在实际工业中,存在许多难以确定其物理模型的非线性系统[1]. 数据建模方法常用于该类系统的建模. 由于环境干扰、采样及测量误差、异常值等因素的影响,数据建模方法面临着巨大挑战. T-S模型因逼近能力较强,被广泛应用于非线性系统的建模[2-7]. 然而大量研究集中在T-S模型的前件参数辨识. K均值聚类将数据聚成K类,并生成K条模糊规则;FCM聚类[8]使用软聚类方式使子模型的融合变得更加光滑;KFCM聚类[9]对FCM进行核扩展,有效解决了线性不可分问题;GKCA聚类方法[10]使用马氏距离对FCM方法进行改进,使得聚类结果呈现椭球状,用以探索数据分布的形状;FCRM聚类[11-14]对FCM进行改进,使得聚类的结果呈现超平面形状,更贴近线性子模型的要求. 应用于T-S模型的后件参数辨识的方法有迭代最小二乘法(RLS[5]),该方法适用于在线学习,而WRLS[12]为RLS的加权方法,一定程度上提高了模型的鲁棒性能. 文献[3]使用卡尔曼滤波进行参数辨识,该方法可以对参数进行在线预测和修正. 但这些方法并未考虑结构风险,模型的复杂度不能得到有效控制,因而泛化性能不强. 同时,这些方法也很少考虑噪声的影响,特别是非高斯噪声与异常值的影响,致使建模的鲁棒性能较差.
针对上述T-S建模方法的不足,构建全新的目标函数,提出考虑结构风险与鲁棒性能的参数辨识方法,并将该建模方法与几种传统建模方法进行比较.
1. 传统T-S模型
T-S模型的模糊推理由R条If-Then模糊规则组成. 模糊规则r定义如下[5]:
其中,Rk为第k条规则,Akj为相对于输入变量xj的模糊子集,
式中:
式中:N为数据点个数,ei为第i个数据的建模误差. 该后件参数辨识方法已有许多成功的应用,但依然存在许多不足:1)由于没有考虑模型的结构风险,模型的泛化性不强;2)在高斯噪声下有较好的辨识效果,但在非高斯噪声或者异常值下辨识效果差,模型鲁棒性差. 因此,为了提高T-S模型的泛化性和鲁棒性,亟需发展新的T-S建模方法.
2. 鲁棒模糊建模方法
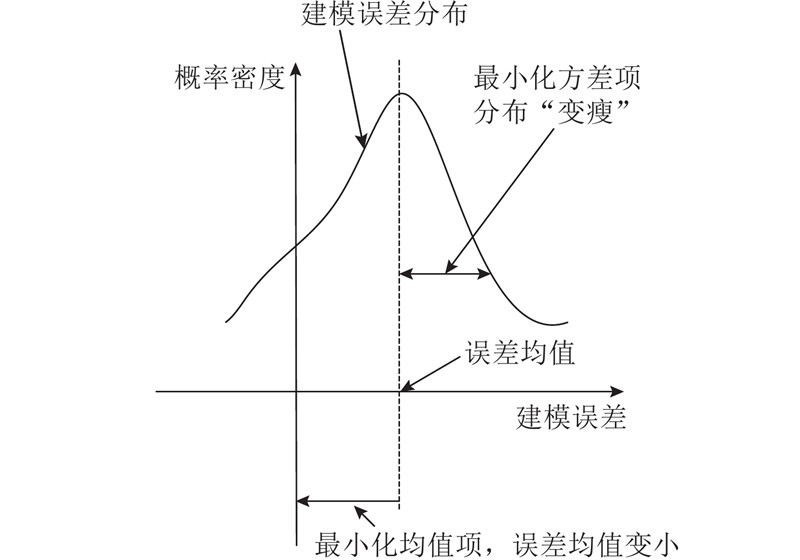
建模误差的均值越小,模型的逼近程度越好,精确性越高. 但仅最小化建模误差的均值,而其方差较大的话,模型受噪声的影响大,鲁棒性不强. 因此,在最小化建模误差均值的同时,应该最小化其方差,从而使模型具有较好的逼近精度和鲁棒性. 为此,构建如图1所示的建模思想,该思想同时最小化建模误差的均值与方差. 由于同时考虑了误差的均值与方差,新的建模方法可以处理非高斯噪声或异常值,优于仅最小化误差平方和的传统建模方法.
图 1
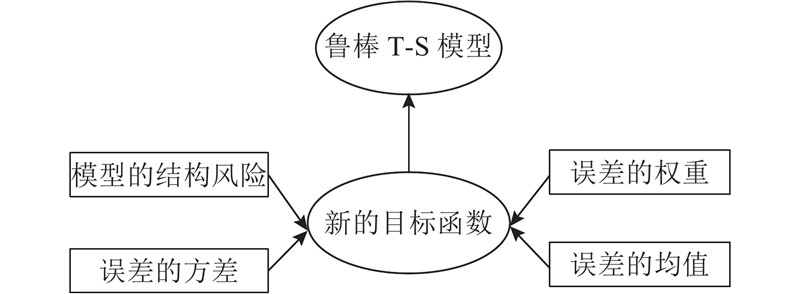
基于上述建模思想,为了提高T-S模型的泛化性和鲁棒性,提出如图2所示的鲁棒模糊建模方法. 该方法通过构建全新的目标函数以获得T-S模型参数
图 2
图 2 鲁棒T-S模糊建模方法目标函数
Fig.2 Objective function of robust T-S fuzzy modeling method
2.1. 新目标函数
构建如下的目标函数:
式中:vk∈(0,1.0],为误差的权重;
该目标函数具有以下特征:
1)第1项
2)第2项
3)第3项
由上述目标函数求解得到的T-S模糊模型具有较好的泛化性、鲁棒性和全局逼近性能,因为该目标函数不仅考虑了模型的结构风险项而且考虑了误差的均值与方差.
2.2. 求解过程
构建拉格朗日函数:
式中:λi为拉格朗日乘子. 优化条件可由下式给出:
由式(11)可得
由式(9)、(12)可得
式中:
由式(7)、(8)、(10)、(13)可建立方程组:
式中:
通过求解式(17)可得
式(18)为最小二乘法问题的通用解形式,当N较大时,可以参考文献[15]进行求解. 由式(7)、(18)得到T-S模型的后件参数为
式中:
式(5)中vi是基于对应样本的误差来求解的,可由式(22)决定[16]:
式中:c1、c2为常系数,通常取值为c1=2.5,c2=3.0;s为统计变量. s的表达式为
式中:IQR为四分位距离,即误差排序序列75%位置的数值与25%位置的数值的差.
权重变量vi是迭代解,可由式(7)~(22)迭代求解. 在实际应用中,迭代1次就足够了[16]. 另外,式(12)的变换形式有
由式(24)可知,当vi=1时,
2.3. 算法总结
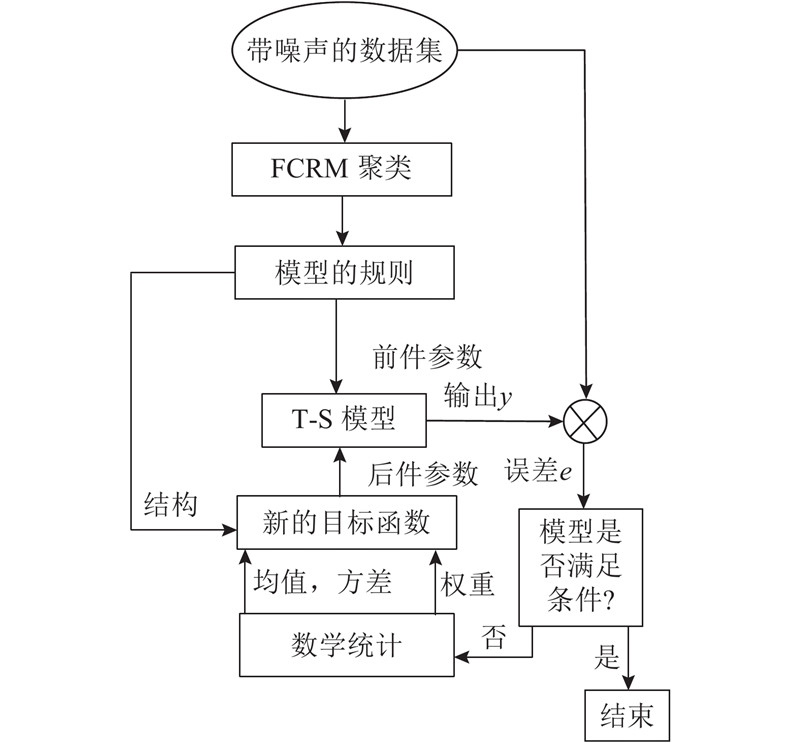
鲁棒T-S模型的建模过程如图3所示,算法流程如下.
图 3
1)收集训练数据
2)求解式(19)、(20),获取后件参数
3)计算误差
3. 算例分析
使用如下均方根误差RMSE和决定系数R-square来评估模型的能力:
式中:T为数据的个数;yk为真实输出;
3.1. 数学算例仿真
产生数据的模型如下:
式中:ym、xm分别为模型的输出和输入;ζ为高斯噪声,
图 4
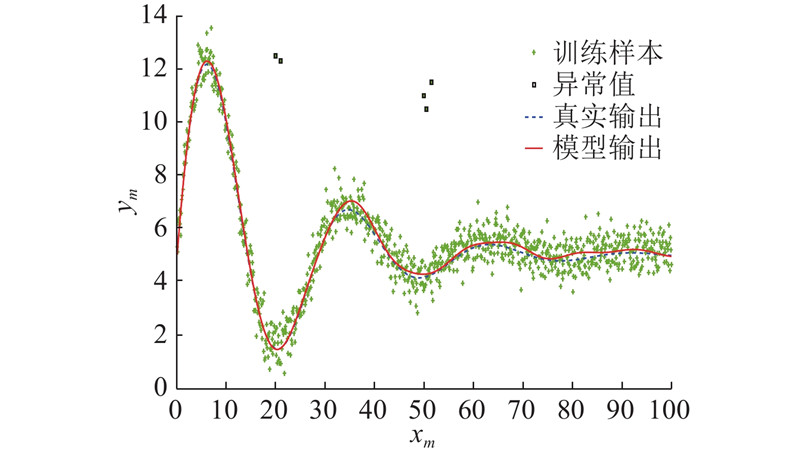
图 4 鲁棒T-S模糊建模方法对含异常值数学算例的建模结果
Fig.4 Modeling result of robust T-S fuzzy modeling method on mathematic case with outliers
表 1 不同建模方法对数学算例拟合结果对比
Tab.1
3.2. 实际液压系统算例
图 5
表 2 液压缸试验台系统参数
Tab.2
| 名称 | 符号 | 数值 | 单位 |
| 运动部件质量 | | 109.5 | kg |
| 柱塞有效面积 | | 0.012 3 | m2 |
| 粘性阻尼系数 | | 2.1×106 | N/(m·s−1) |
| 最大静摩擦力 | | 3.914 9×103 | N |
| 库仑摩擦力 | | 3.473 2×103 | N |
| 临界Stribeck速度 | | 0.001 02 | m/s |
| 粘滞摩擦系数 | | 23 063 | N/(m·s−1) |
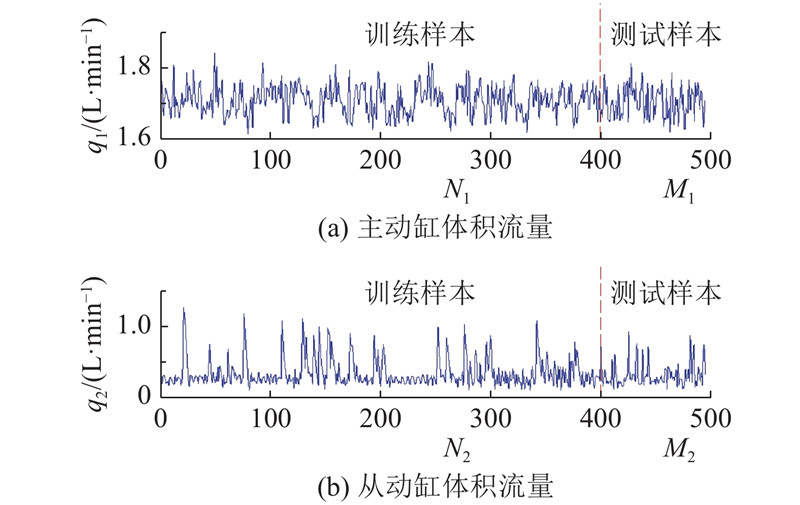
图 6
图 6 液压系统主、从动缸体积流量训练及测试样本
Fig.6 Training and test samples of hydraulic system master and slave cylinder flow
图 7
图 7 鲁棒T-S模糊建模方法对含异常值液压系统的训练结果
Fig.7 Training results of robust T-S fuzzy modeling method for hydraulic system with outliers
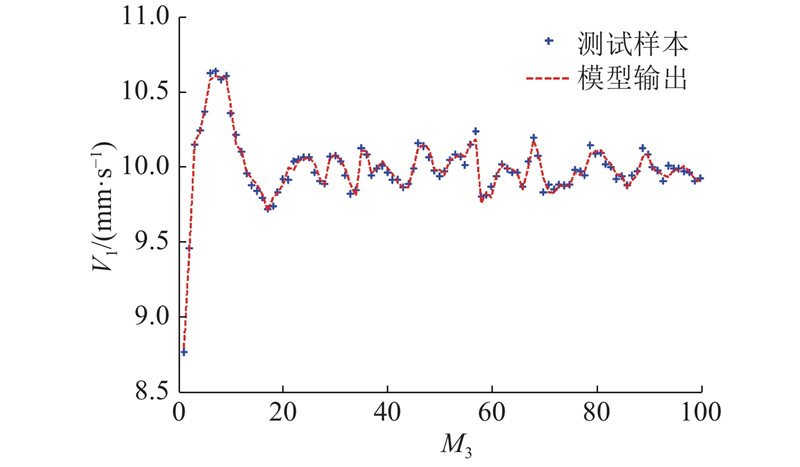
图 8
图 8 鲁棒T-S模糊建模方法对液压系统的测试结果
Fig.8 Test results of robust T-S fuzzy modeling method for hydraulic system
表 3 不同模型对液压系统的训练和测试结果对比
Tab.3
综上,仿真和试验均表明在有噪声的干扰下,提出的方法依然能够获得非线性系统的模型,且建模性能优于传统的建模方法.
4. 结 语
提出基于误差均值与方差最小化的鲁棒T-S模糊建模方法,该方法通过最小化模型的结构风险,提高了模型的泛化性;最小化误差的均值,提高了模型的逼近精度;最小化误差的方差,提高了模型的鲁棒性;数据加权,减少了噪声和异常值对建模的影响. 因此,该方法能有效地获得存在噪声或者异常值的非线性系统的模型. 仿真与试验结果均表明所提出的建模方法能有效获得非线性系统的模型,且优于现有的建模方法. 未来的研究计划可针对实际特定的控制需求,基于提出的鲁棒T-S建模方法,探究非线性系统的控制方法.
参考文献
Two-level modeling based intelligent integration control for time-varying forging processes
[J].
一类非线性系统的扇区模糊建模方法
[J].DOI:10.3969/j.issn.1671-1815.2017.18.013 [本文引用: 1]
Fuzzy modeling approach for a class of sector nonlinear system
[J].DOI:10.3969/j.issn.1671-1815.2017.18.013 [本文引用: 1]
Discrete-time Kalman filter for Takagi-Sugeno fuzzy models
[J].DOI:10.1007/s12530-017-9181-0 [本文引用: 1]
Integrated design and control under uncertainty: a fuzzy modeling approach
[J].
Integrated design of fault-tolerant control for nonlinear systems based on fault estimation and T–S fuzzy modeling
[J].DOI:10.1109/TFUZZ.2016.2598849 [本文引用: 2]
A new TS fuzzy model predictive control for nonlinear processes
[J].DOI:10.1016/j.eswa.2017.06.039
State-space modeling and observer design of Li-Ion batteries using Takagi-Sugeno fuzzy system
[J].DOI:10.1109/TCST.2016.2549270 [本文引用: 1]
Simultaneous structure identification and fuzzy rule generation for Takagi-ugeno models
[J].DOI:10.1109/TSMCB.2008.2006367 [本文引用: 2]
Recursive fuzzy c-means clustering for recursive fuzzy identification of time-varying processes
[J].DOI:10.1016/j.isatra.2011.01.004 [本文引用: 2]
Rule-based modeling: precision and transparency
[J].DOI:10.1109/5326.661100 [本文引用: 2]
T-S fuzzy model identification based on a novel fuzzy c-regression model clustering algorithm
[J].
A novel approach to implement Takagi-Sugeno fuzzy models
[J].DOI:10.1109/TCYB.2017.2701900 [本文引用: 5]
A clustering algorithm based TS fuzzy model for tracking dynamical system data
[J].DOI:10.1016/j.jfranklin.2017.06.014
A novel fuzzy identification method based on ant colony optimization algorithm
[J].DOI:10.1109/ACCESS.2016.2585670 [本文引用: 1]
Weighted least squares support vector machines: robustness and sparse approximation
[J].