三维声学成像作为重要的水下探测技术，在海底地貌测绘、海底施工、水下航行器避障、水下机器人和军事作战等领域的作用日渐凸显，具有广泛的发展前景^[1-3]. 目前，三维成像声纳系统主要安装在船体、潜艇或AUV上. 丹麦Reson公司的SeaBat系列多波束声纳系统^[3]阵元数量少，设备较轻便，但需要对水下场景进行动态扫描，实时性不足，而且图像质量对载体的姿态与运动较敏感，难以进行灵活的水下作业任务. 英国Coda Octopus 公司的Echoscope三维声纳系统^[4]，可进行实时水下三维成像，但其二维平面阵列规模庞大，设备笨重，故在浅港、内河等水域难以通过蛙人或小型潜水器携带设备进行水下作业任务.

为此，一些学者基于稀疏阵列的概念，通过模拟退火算法^[5-6]、遗传算法^[7-8]、压缩感知^[9-10]等算法，对换能器阵列进行稀疏化处理，获得稀疏阵列，减少换能器数量，降低硬件开销. 还有一些学者为了减少平面阵波束形成的计算量，提出chirp zeta transform （CZT）波束形成^[11]、分布式并行子阵波束形成^[12]等算法，相对于传统波束形成，计算量降低了1、2个数量级. 此外，一些学者利用发射线阵和接收线阵组成的十字型阵列代替平面阵列，大大降低阵元数量. Ehrhardt等^[13]进行实际水下对比实验，采集包含十字型阵列在内多种阵列的数据，离线计算出三维图像，结果表明十字型阵列与平面阵列的成像质量相近. 十字型阵列存在扫描水下观测场景所需时间长、实时性不足的问题. 为此，Liu等^[14]提出多频发射（multiple-frequency transmitting，MFT）波束形成算法，降低十字阵列的扫描时间，解决实时性不足的问题；同时，针对接收阵列，利用并行子阵（parallel subarray，PS）波束形成算法，进一步降低计算量. 但在文献[14]中，发射阵列的MFT算法和接收阵列的PS算法都仅仅考虑了理想的远场条件，因此在探测近场目标时，聚焦时延会存在一定偏差，系统性能降低. 此外，PS算法是近似的波束形成算法，对成像质量也会产生一定的影响.

针对上述问题，提出兼顾远场和近场性能的便携式三维声纳系统设计. 系统采用十字型阵列，设备轻便，可胜任水下灵活的作业任务. 针对发射阵列，提出近场条件下优化的MFT算法，将整个水下探测场景根据景深划分为多个聚焦区间，并由菲涅尔近似，为每个聚焦区间配置相应的聚焦参数，保证近场条件下发射聚焦波束的性能. 针对接收阵列，基于修剪快速傅里叶变换（pruned fast Fourier transform，pruned FFT），提出优化的CZT（opitimized CZT，O-CZT）波束形成算法，可实现十字型阵列远场和近场的快速波束形成，同时计算量低于其他波束形成算法.

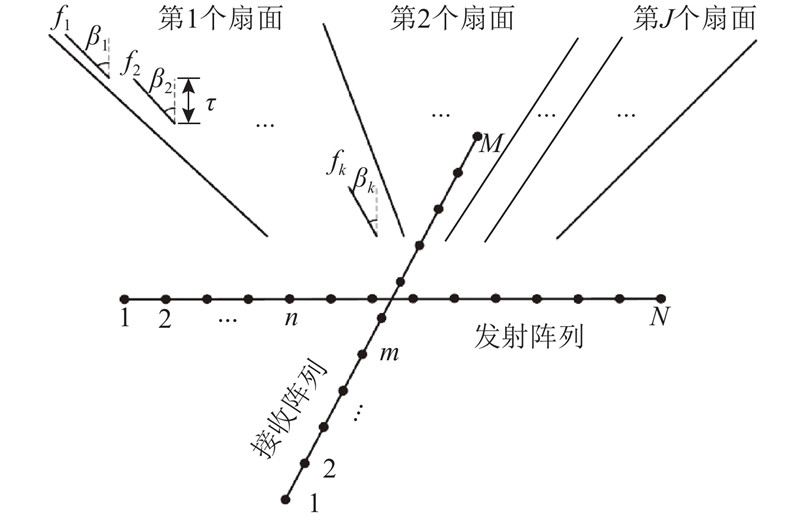
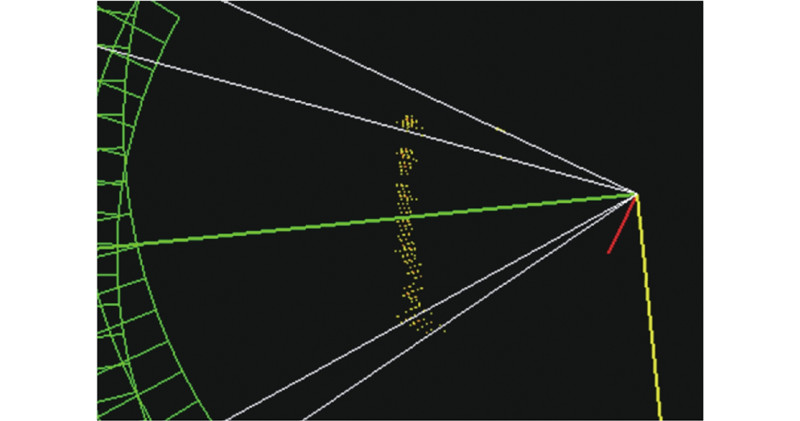
十字型阵列由1条发射阵列和1条接收阵列组成，假设发射阵元数量为N，接收阵元数量为M，阵元间距为d，垂直发射波束方向数为Q，水平接收波束方向数为P. 在远场条件下，MFT算法步骤如下：1）将垂直波束方向分割为J个扇面，在每个扇面内，依次向K个方向（Q=KJ）发射不同频率f_k（k=1，2，···，K）的扇形波束信号，发射脉冲宽度为τ，每个发射频率对应1个垂直波束方向β_k，相邻2个发射频率的频率间隔Δf是固定的；2）等待接收阵列收到回波信号，完成水平方向接收波束形成运算，得到PJ个方向的波束结果；3）对下一个扇面进行相似的操作. 当所有扇面完成上述操作后，可得到整个探测场景内PQ个方向的波束结果. MFT算法的发射过程示意图如图1所示.

发射信号的时域表达式为

(1) $\begin{split} {s_{\rm MFT}} =& {s_n}(t,{f_1},\;{\beta _1}) + {s_n}((t - \tau ),{f_2},\;{\beta _2})+\\ &\cdots + {s_n}((t - (K - 1)\tau ),{f_K},\;{\beta _K}). \end{split}$

式中：

(2) ${s_n}(t,{f_k},{\beta _q}) = \left\{ {\begin{array}{*{20}{l}} {A\sin\; (2{\rm{\text π}}{f_k}(t - {\tau_{{\rm{t}}}^{\rm f}})),}&{0 \leqslant t \leqslant \tau ;}\\ {0,}&{{\text{其他}}{\rm{.}}} \end{array}} \right.$

其中，A为信号幅度；n为发射阵元索引号；β_q为垂直波束方向，q为垂直波束方向的索引号，与扇面号j、频率号k和频率数K的关系为 $q = (j - 1)K + k $； ${\tau_{{\rm{t}}}^{\rm f}}$为发射阵列远场时延参数. ${\tau_{{\rm{t}}}^{\rm f}}$的表达式为

(3) $\tau _{\text{t}}^{\text{f}} = (nd\sin \;{\beta _q})/c.$

式中：c为水中的声速.

MFT波束形成算法通过顺序发射多频信号，有效地将十字型阵列的发射次数从垂直波束方向数Q减小到划分扇面数J，减少了水下场景的扫描时间.

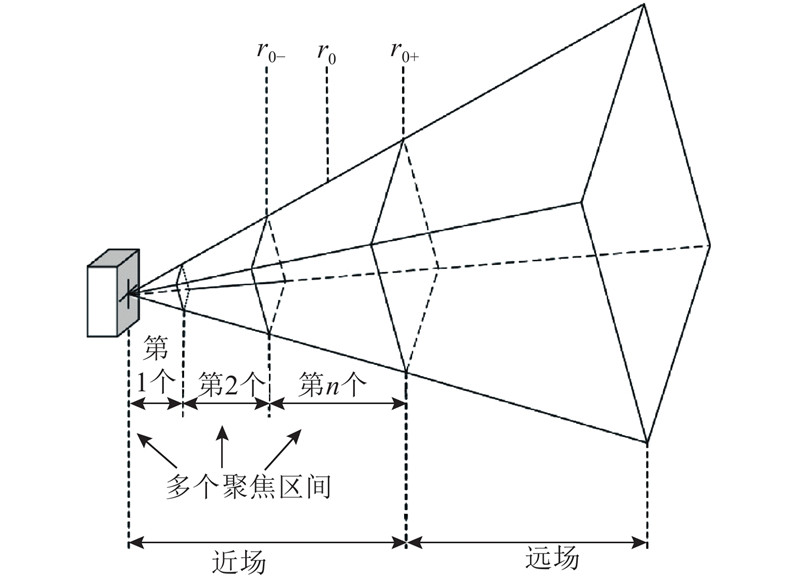
从2个方面对近场条件下MFT算法进行优化：1）根据十字型三维声纳的景深划分聚焦区间；2）由菲涅尔近似，给出MFT算法近场时延参数以及发射阵列的波束图.

动态发射聚焦，即对近场范围内的每个聚焦距离r₀进行1次发射波束形成，这样能获得最佳性能，但所需的发射次数过多会影响成像时间，而且大量的时延参数会增加存储资源的开销. 因此，在实际系统中，为保证系统的实时性以及减少系统的存储空间，可将整个水下观测场景划分为多个聚焦区间，在每个聚焦区间内进行1次发射波束形成，以避免动态发射聚焦带来的成像时间过长和存储空间过大的问题.

系统可以根据景深来划分聚焦区间，一般来说在景深（r₀₋~r₀₊）内，波束图衰减小于3 dB. 多聚焦区间的示意图如图2所示. 景深为聚焦距离r₀、阵列孔径D和发射声波波长λ的函数^[15]，可表示为

(4) ${r_{0 - }} = {r_0} - {r_0}/[{D^2}/(2\lambda {r_0}) + 1],$

(5) ${r_{0 + }} = {r_0} + {r_0}/[{D^2}/(2\lambda {r_0}) - 1].$

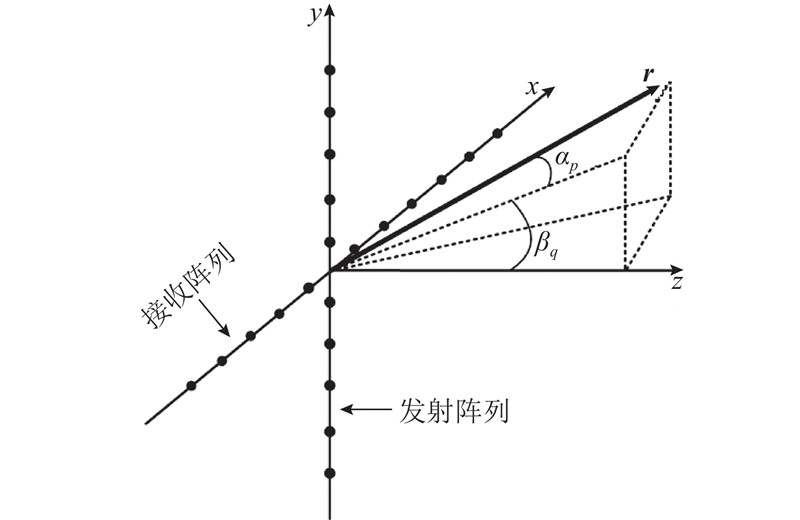
如图3所示，在近场条件下，假设发射波束方向向量为r，接收波束形成方向为α_p（p=1，2，···，P），发射波束形成方向为β_q（q=1，2，···，Q），则发射近场时延参数可表示为

(6) $\tau _{\text{t}}^{\text{n}} = \left[ {{r_0} - ({r_0}^2 + {{\left\| {{u}} \right\|}^2} - 2{r_0}{{r}}{{{u}}^{\text{T}}})} ^{1/2} \right] \Big/c.$

式中：

(7) ${{r}} = {\left[ {\sin \;{\alpha _p},\sin \;{\beta _q},({{\cos }^2}\;{\alpha _p} - {{\sin }^2}\;{\beta _q})}^{1/2} \right]}.$

其中，||·||表示欧式范数；u=（0，y_n，0），为发射阵元的坐标向量.

根据菲涅尔近似^[16]，近场时延参数可以简化为

(8) $\tau _{\text{t}}^{\text{n}} = ({y_n}\sin \;{\beta _q}){/c} - {y_n}^2/(2{r_0}c).$

由式（1）、（2）和（8）可以得到近场条件下发射阵列的波束图为

(9) $\begin{split} &{B_{\rm tr}}(k,\;{\beta _q},\;{r_0}) = \\ &\quad \left| {\sum\limits_{n = 1}^N {{S_n}(k){\rm{\exp }}\;\left[ - {{{\rm{i}}}}2{\rm{\text π}}{f_k}\left(\frac{{{y_n}\sin\; {\beta _q}}}{c} - \frac{{{y_n}^2}}{{2{r_0}c}}\right)\right]} } \right|. \end{split} $

式中：S_n（k）为发射信号s_n（t，f_k，β_q）的DFT运算结果；i为虚数单位；k为DFT的谱线号，对应频率f_k=kf_s/L，其中f_s为接收阵列采样率.

综上所述，近场条件下优化的MFT算法步骤如下：

1）根据景深的定义，由式（4）、（5）划分多个聚焦区间；

2）对第1个聚焦区间，进行多频发射波束形成，采用式（8）给出的菲涅尔近似时延参数，保证近场发射波束性能；

3）接收第1个聚焦区间的回波信号，进行接收波束形成；

4）对其他聚焦区间，重复步骤2）和3）的操作，完成整个探测场景的波束形成.

CZT波束形成是准确且计算量需求小的波束形成算法. Palmese等^[11]通过CZT波束形成算法大幅度降低二维平面阵列三维成像的计算量. 但是目前还没有在远场和近场条件下，对采用MFT算法的十字型阵列CZT波束形成算法的研究. 此外，CZT波束形成算法在计算量方面还有优化的空间.

根据延时-累加波束形成^[1]，时域波束信号可表示为

(10) $b(t,{\alpha _p},{r_0}) = \sum\limits_{m = 0}^{M - 1} {{w_m}} {s_m}(t - \tau _{\rm{r}}^{\rm{n}}).$

式中：s_m（t）为第m个接收阵元的采样信号；w_m为第m个接收阵元的权重，用于抑制旁瓣； $\tau _{\rm{r}}^{\rm{n}} $为接收阵列的近场时延参数. 在近场条件下，即当聚焦距离r₀≤D²/λ时^[15]，采用菲涅尔近似时延参数：

(11) $\tau _{\rm{r}}^{\rm{n}} = ({x_m}\sin \;{\alpha _p}){/c} - {x_m}^2/(2{r_0}c).$

在远场条件下，即当聚焦距离r₀>D²/λ时，二次项（x_m²/2r₀c）可以忽略，则式（11）简化为远场条件下的时延参数.

在数字系统中，通常将时域信号通过离散傅里叶变换（discrete Fourier transform，DFT）转到频域进行计算，式（10）在频域的表达式为

(12) $\begin{split} {B_{{\mathop{\rm re}\nolimits} }}(k,{\alpha _p},{r_0}) =& \left| {\sum\limits_{m = 1}^M {{w_m}{\rm{\exp }}\;\left({{{\rm{i}}}}2{\rm{\text π}}{f_k}\left(\displaystyle\frac{{{x_m}^2}}{{2{r_0}c}}\right)\right){S_m}(k)} }\times \right.\\ &{\kern 1pt} \left. {{\rm{\exp }}\;\left( - {{{\rm{i}}}}2{\rm{\text π}}{f_k}\left(\displaystyle\frac{{{x_m}\sin\; {\alpha _p}}}{c}\right)\right)} \right|. \end{split}$

式中：S_m（k）为时域信号s_m（t）的L点DFT运算结果.

为了利用CZT变换快速计算式（12），可将其变换为

(13) $\begin{split} &{B_{\operatorname{re} }}(k,{\alpha _p},{r_0}) = \\ & \quad\left| {{W^{( - {p^2}/2)}}\sum\limits_{m = 0}^{M - 1} {{v_m}{S_m}(k){H^m}{W^{( - {m^2}/2)}}{W^{{{(p - m)}^2}/2}}} } \right|. \end{split} $

式中：

(14) $H = \exp \;[\left( { - {\rm{i}}2{\text{\text π}}{f_k}d\sin \;{\alpha _i}} \right)/c],$

(15) $W = \exp \;\left( {{\rm{i}}2{{\text π}}{f_k}d\Delta s/c} \right),$

(16) $\Delta s = (\sin \;{\alpha _{\rm{f}}} - \sin \;{\alpha _{\rm{i}}})/(P - 1),$

(17) $\sin {\alpha _p} = \sin {\alpha _{\rm{i}}} + \Delta sp;{\kern 1pt} \;\;p = 0,1,\cdots,P - 1,$

(18) ${v_m} = {w_m}\exp \;\left( {{\rm{i}}2{{\text π}}{f_k}{x_m}^2{/{(2{r_0}c)}}} \right).$

其中，α_i、α_f分别为水平方向初始（第1个）波束方向与终止（最后1个）波束方向.

式（13）可以看作以下2个序列的离散卷积：

(19) ${G_k}(m) = {v_m}{S_m}(k){H^m}{W^{( - {m^2}/2)}},$

(20) ${D_k}(m) = {W^{{m^2}/2}}.$

因此，可利用FFT算法实现两序列快速卷积，从而高效计算水平方向波束形成. 值得说明的是：1）MFT算法中有K个不同的发射频率f_k，因此针对每个阵元采样信号s_m（t），只须计算DFT中的K个结果；2）在远场条件下，二次项（x_m²/2r₀c）近似为零，可以忽略，此时式（13）为O-CZT远场波束形成计算公式；3）根据乘积定理，在远场和近场条件下，十字型阵列整体波束方向图为接收阵列波束方向图与发射阵列波束方向图的乘积，可表示为

(21) $B(k,{\alpha _p},{\beta _q},{r_0}) = {B_{\rm re}}(k,{\alpha _p},{r_0}) \, {B_{\rm tr}}(k,{\beta _q},{r_0}).$

O-CZT波束形成过程如图4所示. 模块1代表O-CZT波束形成输入和输出信号，模块2代表离线计算的参数，模块3代表要在线计算的过程. 其中在线计算过程有以下6个步骤：

1）每个接收阵元的采样信号s_m（t）进行DFT运算，获得K个频率的DFT结果S_m（k）；

2）S_m（k）与参数 ${v_m}{H^m}{W^{( - {m^2}/2)}}$相乘，得到序列G_k（m），其中， ${v_m}{H^m}{W^{( - {m^2}/2)}} $为离线计算并存储在系统中的参数；

3）将序列G_k（m）补零，变为L_a点的序列，进行FFT运算，其中L_a≥M+P−1，同时满足L_a=2^a；

4）将步骤3）中序列G_k（m）FFT的结果与序列D_k（m）FFT的结果对应相乘，其中，序列D_k（m）L_a点FFT是离线计算，并存储在系统中的；

5）将步骤4）中两序列乘积的结果进行L_a点逆快速博里叶变换 (inverse fast Fourier transform, IFFT) 运算，水平方向有P个波束，因此只须保留前P个运算结果；

6）将步骤5）中的IFFT结果与序列 ${{\rm{W}}^{( - {p^2}/2)}}$对应相乘，得到最终的波束结果|B_re|.

在O-CZT波束形成的计算过程中，步骤3）中需要进行L_a点FFT，而输入序列中只有前M个元素（对应接收阵列M个阵元）为非零元素，其余L_a−M个元素为零；同样，在步骤5）L_a点IFFT中，只有前P个结果是需要的，用于计算水平方向P个波束，而不需要计算其余L_a−P个元素. 当只有部分输入元素是非零的或者只有部分输出结果需要计算时，可以通过修剪FFT算法^[17]剪除不必要的计算，提高计算效率，节省计算资源. 根据文献[17]，计算L_a点FFT或IFFT，当只须输出P₂（P₂≥P，且P₂为2的整数幂）个元素时，实数计算量（实数乘法或实数加法）为

(22) ${O_{\rm{pr\_out}}} = 5{L_a}{\log _2}\;{P_2} + {L_a}/4 - 8{P_2} - {{21{L_a}}}/\left({{4{P_2}}}\right).$

同样，修剪FFT算法可用于计算只有M₂（M₂≥M，且M₂为2的整数幂）个元素输入时的L_a点FFT，其实数计算量为

(23) ${O_{\rm{pr\_in}}} = 5{L_a}{\log _2}\;{M_2} + {L_a}/4 - 8{M_2} - {{21{L_a}}}/\left({{4{M_2}}}\right).$

与传统L_a点FFT计算量5L_alog₂ L_a相比，修剪FFT算法的计算量更低，进一步提升了O-CZT波束形成的计算效率.

DM、PS和O-CZT波束形成均属于频域波束形成，因此3种算法第1步均是通过DFT运算将时域信号转为频域信号，每个阵元的时域信号进行L点DFT，抽取1个频率信号所需的实数计算量为

(24) ${O_{{\rm{DFT}}}} = 2L + 2(L - 1) = 4L - 2.$

对于DM波束形成算法，计算1个波束需要M次复数乘法，M−1次复数加法，而每个扇面需要计算PK个波束，故DM算法所需的实数计算量为

(25) $\begin{split} {O_{{\rm{DM}}}} =& ({O_{{\rm{DFT}}}}M + (8M - 2)P)K =\\ &{\kern 1pt} \left[{{({O_{{\rm{DFT}}}}M + (8M - 2)P)Q}}\right]/{J}. \end{split}$

根据文献[14]，进行1个扇面的三维成像时，PS算法的实数计算量为

(26) ${O_{{\rm{PS}}}} = \left[{{({O_{{\rm{DFT}}}}M + (8{M_{\rm F}} - 2){M_{\rm S}}{P_{\rm F}} + 13{M_{\rm S}}P)Q}}\right]/{J}.$

式中：M_F为PS算法中一级子阵的阵元数量，M_S为二级子阵的阵元数量，P_F为一级子阵的波束数.

对于O-CZT波束形成，步骤2）需要M次复数乘法，步骤4）需要L_a次复数乘法，步骤6）需要P次复数乘法，步骤3）、5）采用修剪FFT算法进行优化，计算量如式（22）、（23）所示，故O-CZT波束形成的实数计算量为

(27) $\begin{split} & {O_{{\rm{O{\text{-}} CZT}}}} = \\ &\,\,\,\;\;\left[{{({O_{{\rm{DFT}}}}M \!+\! 6(M \!+\! {L_a} \!\!+\!\! P) \!\!+\!\! {O_{\rm{pr\_in}}} + {O_{\rm{pr\_out}}})Q}}\right]/{J}. \end{split} $

O-CZT波束形成在远场和近场条件下的区别在于对应的参数v_m不同，但由于参数 ${w_m}{H^m}{W^{( - {m^2}/2)}} $是离线计算的，故O-CZT波束形成在远场和近场条件下的在线计算量是相同的.

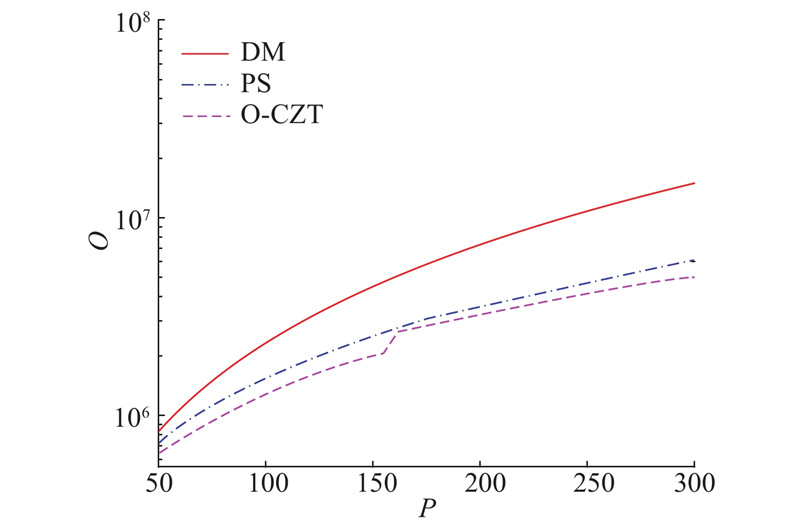
假设M=100，N=100，L=150，J=6，M_F=10，P_F=26，P=Q，3种波束形成算法的实数计算量O随水平波束方向数P的变化趋势如图5所示. 由图可以看出，DM算法的实数计算量最高；PS波束形成算法的计算量居中，O-CZT波束形成算法的计算量最低. L_a≥M+P−1，且L_a为2的整数幂，当50≤P≤157时，149≤M+P−1≤256，此时L_a=256；当157<P≤300时，256<M+P−1<399，此时L_a=512. 故当P从157增大至158时，O-CZT波束形成算法的计算量有阶跃性增长.

当P分别为50、100、150时，DM、PS和O-CZT波束形成算法的计算量如表1所示. 当P=50时，O-CZT算法的计算量比DM算法降低20.5%，比PS算法降低8.3%；当P=150时，O-CZT算法的计算量比DM算法降低57.8%，比PS算法降低24.0%. 可以看出O-CZT波束形成在计算量上的优势.

为验证设计的有效性，在Matlab仿真环境中，对点目标和模拟方框进行成像，并与文献[14]内容进行对比. 仿真环境参数设置为：M=100，N=75，P=100，Q=54，420 kHZ<f_k<580 kHZ，Δf=20 kHz，即K=9，J=6，观测场景角度为100°×50°，采样频率为3 MHz，接收阵元间距d_r=1.5 mm，发射阵元间距d_t=2 mm，DFT点数L=150. 探测距离设为0.5~50.0 m，其中0.5~7.5 m为近场，7.5~50.0 m为远场. 整个场景可划分为5个聚焦区间：0.50~0.65 m、0.65~1.00 m、1.0~2.0 m、2.0~7.5 m、7.5~50.0 m，相应的r₀分别为0.55、0.8、1.4、3.0、25.0 m.

如图6所示为水平方向波束图. 图中，BP为波束图. 假设入射信号的水平角度为0°，当采用O-CZT波束形成，在1.4 m处（完全聚焦），500 kHz信号在水平方向的波束图如图6（a）所示，可以看出，最大旁瓣高度为−13 dB，−3 dB对应的角度分辨率为1.04°；如图6（b）所示为420 kHz信号在水平方向的波束图，可以看出，最大旁瓣高度依然为−13 dB，但由于频率降低，角度分辨率增大至1.24°；如图6（c）所示为2 m处（不完全聚焦，在聚焦区间的边界），500 kHz信号的波束图，可以看出，旁瓣略微升高至−11.7 dB，角度分辨率也增大至1.28°；如图6（d）所示为采用文献[14]的方法，在2 m处，500 kHz信号的波束图，由于该方法没有考虑近场条件，在近场的波束图严重恶化，出现2个主瓣，指向不同的方向，而且旁瓣高度也明显升高至−9.2 dB.

在上述参数配置下，设置3个点目标，其方向（水平，垂直）分别为（30°，8.3°）、（50°，21.3°）、（80°，34.3°），3个点目标分别对应第1扇面的580 kHz信号，第3扇面的500 kHz信号，第5扇面的420 kHz信号. 为观测不同距离的成像效果，进行了3组实验：第1组实验假设目标距离为1.4 m，文献[14]与本研究设计的成像效果分别如图7（a）、7（b）所示；第2组实验假设目标距离为2.0 m，文献[14]与本研究设计的成像效果分别如图7（c）、7（d）所示；第3组实验假设目标距离为10.0 m，文献[14]与本研究设计的成像效果分别如图7（e）、7（f）所示. 目标强度经过归一化处理，图中红色代表目标强度为1，蓝色代表目标强度为0.

文献[14]的发射波束形成与接收波束形成仅考虑了远场条件，因此1.4 m处的点目标成像模糊，指向性差；而随着目标距离变远，在10 m处，点目标成像较为清晰. 而本研究的设计考虑了近场和远场条件，1.4 m处的点目标位于聚焦距离r₀=1.4 m处，点目标成像较清晰，指向性好；2.0 m处的点目标位于聚焦区间1.0~2.0 m的边界，点目标成像稍模糊，但是比文献[14]的成像清晰；10.0 m处的点目标在远场，点目标成像清晰.

为了更直观地进行对比，将目标设置为方框，距阵列中心2.0 m处，文献[14]与本研究设计的成像效果分别如图8（a）、8（b）所示. 通过对比可以发现文献[14]的成像效果较差，方框边缘模糊；而本研究设计的成像效果较好，虽方框位于聚焦区间的边界，但方框边缘依然清晰.

综上所述，相比文献[14]，本研究设计对近场和远场条件下的发射波束形成和接收波束形成进行了优化，因此对近场和远场的目标都能够产生清晰的图像.

设计并实现1台十字型阵列三维声纳原理样机，系统参数与仿真实验的参数一致. 在千岛湖进行水下实验，对2个水下目标进行拍摄. 第1个拍摄目标为1条铁链，如图9所示，铁链长度为2 m，宽度为4 cm，距离样机约为2 m. 如图10所示为拍摄的铁链的三维成像效果，可以看到清晰的链状目标. 第2个拍摄目标为立方体铁框，为增加声波发射面积，缠绕了铁链，如图11所示，铁框的棱长为1 m，每条棱的宽度为10 cm，距离样机约为6 m. 如图12所示为拍摄的立方体铁框的三维成像效果，能够看到清晰的立方体目标. 实际的水下实验表明该小型化三维声纳能够在探测范围内拍摄出清晰的三维图像.

根据仿真实验和实际水下实验，进行如下分析与讨论.

1）为降低扫描时间，采用多频发射波束形成算法，不同发射频率对应不同垂直方向，通过对比图6（a）和6（b），可以发现，频率越低，主瓣宽度越大，对应的角度分辨率增大；420 kHz信号的角度分辨率为1.24°，故在近场完全聚焦的位置以及远场条件下，系统的角度分辨率不大于1.24°.

2）通过对比图6（a）和6（c），可以发现，同1个频率的信号，处于聚焦区间边界2.0 m处的与处于完全聚焦位置1.4 m处的波束图相比，主瓣宽度和旁瓣高度略有增加，因此图7（d）中2.0 m处的点目标成像略大于图7（b）的点目标成像. 由图6（c）与6（d）对比可以看出，在近场条件下，本研究的波束图在主瓣宽度、指向性、旁瓣高度等方面远优于文献[14]方法得出的波束图，图8也进一步证明了本研究方法的优越性.

3）由图7（b）可以看出，在不同垂直方向上，点目标的成像效果略有不同：右上角的点目标为420 kHz信号的成像效果，主瓣较宽，成像点较大；左下角的点目标为580 kHz信号的成像效果，主瓣较窄，点目标较小（指向性好）. 而由图8（b）以及实际的水下实验可以发现，在不同方向上，主瓣宽度的差异并没有对目标整体的成像产生明显的影响，其原因是最小角度分辨率为0.91°（580 kHz信号），最大角度分辨率为1.24°（420 kHz信号），两者差异不大，故对成像影响较小.

4）由图10、12可以看出，该系统可对近场目标实现较为清晰的成像，但由于散点噪声、声波漫反射、声波波长（远低于光的波长）等方面的原因，该系统的成像效果无法与光学图像相比，但其生成的图像可以分辨出目标的轮廓，为水下探测提供了重要的技术手段. 未来将增大该声纳的阵列孔径，提高波束角度分别率，进一步提升水下三维死像质量.

提出兼顾远场和近场性能的便携式三维声纳设计，采用比平面阵轻便的十字型阵列，优化其发射波束形成算法和接收波束形成算法，在远场和近场条件下都能够有效地进行水下成像，同时降低了计算量需求. 实际的水下实验表明，该三维声纳系统能拍摄出清晰的水下三维图像. 未来将增大该声纳的阵列孔径，提高波束角度分辨率，进一步提升水下三维成像质量.