随着城市化进程的加剧，城市土地的不渗透面积激增，改变了城市水文水循环^[1-2]. 城市降雨径流与日俱增，城市排水系统面临着前所未有的挑战. 数值仿真模型有助于实现科学的城市雨水排水管网运行与管理，充分理解模型的特征参数是理解城市水文水资源循环的关键. 模型参数的灵敏度分析是模型构建以及评估的重要环节^[3]. 暴雨径流管理模型（storm water management model，SWMM）是美国国家环保署开发的用于模拟城市暴雨径流以及相关水质演算的雨水管理模型^[4]. SWMM不仅能模拟单一降雨事件，还可以对长期的降雨径流进行动态演算，因此在城市降雨径流模拟中得到了广泛应用^[5-7]. 利用SWMM模拟降雨径流时主要应用到的模块为降雨径流模块以及输送模块，包括水文产汇流计算以及管网流量动态演算，涵盖了SWMM中大部分水文、水力参数，模型校核十分困难. 因此有必要对SWMM进行详细的全局灵敏度分析，筛选出灵敏参数.

参数灵敏度分析的目的是定性或者定量地评价模型输入参数的变化对输出结果的影响，为之后的模型参数校核以及模型优化提供支持^[8]. 已经有许多学者对SWMM进行了参数灵敏度分析，但是大多使用定性方法^[9-15]，计算所得结果只能被用于灵敏参数的筛选和排序，无法对结果作出定量解释；同时缺乏对结果的收敛性分析. Sarrazin等^[16]提出灵敏度分析结果的收敛性是案例独立的，有必要对所得结果进行收敛性分析，确保所选样本数计算得到的最终灵敏度指数是收敛的. 本研究综合考虑SWMM中各类参数的取值情况，在参数取值范围内利用基于方差分解的Sobol方法对研究区内的SWMM模型参数的灵敏度进行定量分析，计算各参数对模型输出结果方差的影响，具体评估各参数的灵敏度，利用重采样技术对结果的收敛性进行简要分析.

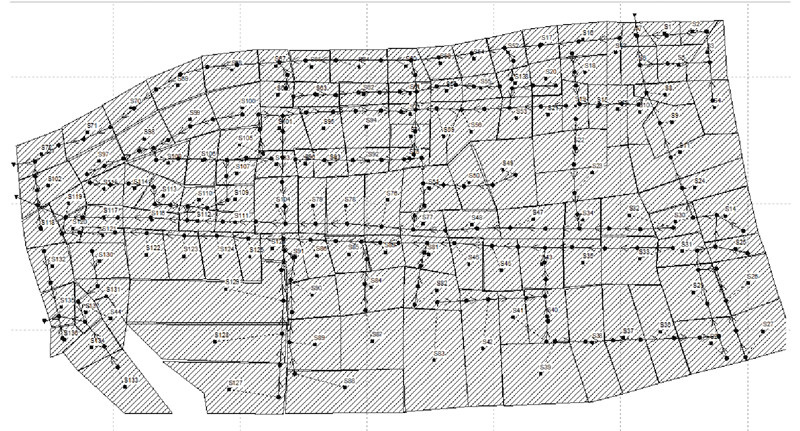
选取我国华东某城市独立的分流制雨水排水管网系统作为研究区域，研究区占地总面积为56.525 hm²，土地利用区域的不透水率约为86%，土地利用情况主要为商住区、住宅区、绿化带、公用街道以及柏油马路等，如表1所示. 表中，I_L为不透水面积百分比估计，A_L为面积，P_L为各类别面积占总研究区面积百分比. 结合区域地形、土地利用类型调查结果和管网GIS数据，将研究区概化为138个汇水单元（主要土地类型为建筑屋顶）、227根管段（主要管材为混凝土）、225个节点和4个排放口，建立研究区的SWMM排水管网模型，如图1所示. 模拟采用的降雨事件为2017年6、7月利用研究区内雨量计监测到的2场次降雨，利用明渠流量计在主要排放口记录体积流量，降雨特征如表2所示.

SWMM的参数可分为测量参数以及待率定参数^[17]. 参照Krebs等^[18]的方法，选取与水文、水力计算模块相关的12类参数进行灵敏度分析. 相关参数取值范围的估计方式主要有3种：GIS数据普查、查阅模型手册、现场调查及文献调研. 基于以上3种方法对参数取值范围进行估算. 实验所用的下渗模型为霍顿模型，将12类参数概化成19个参数，参数具体含义、所属模块及取值范围如表3所示.

在实测参数中，汇水区特征宽度和坡度的测量存在一定难度，因此引入比例因子K_w、K_s. 模型参数的实际输入值等于比例因子乘以测量值：

(1) $ W = {K_{\rm{w}}} \sqrt A. $

式中：W为汇水区的特征宽度，K_w为特征宽度比例因子，A为子汇水区的面积.

汇水区坡度为

(2) $ S = {K_{\rm{s}}}s. $

式中：S为汇水区的实际坡度，K_s为坡度比例因子，s为依据GIS数据分析所得坡度.

与其他蒙特卡洛方法相比，基于方差分解的Sobol方法能够有效求解高度非线性模型中参数间相互作用所产生的灵敏度，计算结果相对稳健可靠，被广泛应用于SWAT、TOPMODEL、WASP等环境领域大型非线性模型中^[19-22]. Sobol方法的主要思想是将函数 $ f(x)$ 分解成 $ {2^p}$ 项递增项之和，通过采样计算参数对模型响应的总方差及各项偏方差，求得各参数的灵敏度. 当输入参数域 $ {I^p}$ 为 $ p$ 维单元体时，将函数 $ f(x)$ 分解为 $ {2^p}$ 个递增项之和^[23]：

(3) $ \begin{split} f(x) = & {f_0} + \sum\limits_{i = 1}^p {{f_i}({x_i})} + \sum\limits_{\mathop {i,j = 1,2, \cdots ,p,}\limits_{i < j} } {{f_{i,j}}({x_i},{x_j})} + \cdots + \\ & {f_{1,2, \cdot \cdot \cdot ,p}}({x_1},{x_2}, \cdots ,{x_p}). \end{split} $

式中： $ {f_0}$ 为常量. 其他项对包含任一变量的积分必定为0，即

(4) $ \int_0^1 {{f_{{i_1},{i_2}, \cdots ,{i_s}}}({x_{{i_1}}},{x_{{i_2}}}, \cdots ,{x_{{i_s}}}){\rm{d}}} {x_{{i_k}}} = 0;\;\;1 \leqslant k \leqslant s\;. $

式（3）中所有项之间都是正交的并且可以表示为函数 $ f(x)$ 的积分：

(5) $ {f_0} = \int_{{I^p}} {f(x){\rm{d}}{{X}}}; \; {{X}} = \{{x_1},{x_2}, \cdots ,{x_p} \} \;, $

(6) $ {f_i}({x_i}) = \int_0^1 \cdots \int_0^1 {f(x)\mathop \prod \limits_{k \ne i} {\rm{d}}{x_k} - {f_0}} \;, $

(7) $ \begin{split} {f_{i,j}}({x_i},{x_j}) = \int_0^1 { \cdots \int_0^1 {f(x)\mathop \prod \limits_{k \ne i,j} {\rm{d}}{x_k} - } } {f_0} - {f_i}({x_i}) - {f_j}({x_j}) . \end{split} $

以此类推，可求得式（3）中其他高阶项. 将式（3）两边平方并且在整个参数域 $ {I^p}$ 内积分，结合式（4），可以得到

(8) $ \begin{split} &\int_{{I^p}} {{{{{\left[ {f(x)} \right]}^2}}}{\rm{d}}{{X}}} - f_0^2 =\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad \\ &\quad \sum\limits_{s = 1}^p {\sum\limits_{{i_1} < {i_2} < \cdots < {i_s}}^p {\int {f_{{i_1},{i_2}, \cdots ,{i_s}}^2{\rm{d}}{x_{{i_1}}}{\rm{d}}{x_{{i_2}}} \cdots {\rm{d}}{x_{{i_s}}}} } } . \end{split} $

函数 $ f(x)$ 的总方差 $ D$ 为

(9) $ D = \int {{{{{\left[ {f(x)} \right]}^2}}}{\rm{d}}{{X}}} - f_0^2. $

偏方差为

(10) $ {D_{{i_1},{i_2}, \cdots ,{i_s}}} = \int {f_{{i_1},{i_2}, \cdots ,{i_s}}^2{\rm{d}}{x_{{i_1}}}{\rm{d}}{x_{{i_2}}} \cdots {\rm{d}}{x_{{i_s}}}}. $

由式（8）可得

(11) $ D = \sum\limits_{s = 1}^p {\sum\limits_{{i_1} < {i_2}< \cdots < {i_s}}^p {{D_{{i_1},{i_2}, \cdots ,{i_s}}}} }. $

全局灵敏度指数为

(12) $ {S_{{i_1},{i_2}, \cdots ,{i_s}}} = {D_{{i_1},{i_2}, \cdots ,{i_s}}}/D;\;1\leqslant {i_1} \leqslant \cdots < {i_s}\leqslant \cdots \leqslant p. $

式中： $ {S_{{i_k}}}$ 为第 $ {i_k}$ 个参数的一阶全局灵敏度指数，用于定量描述参数 $ {x_{{i_k}}}$ 的变化对模型输出结果的影响； $ {S_{{i_k},{i_l}}}$ 为二阶全局灵敏度指数，用于定量描述参数 $ {x_{{i_k}}}$、 $ {x_{{i_l}}}$ 同时变化对模型输出结果的影响；以此类推. 定义总阶全局灵敏度指数 $ S_i^{\text{T}}$为参数各阶灵敏度系数之和，不但反映参数单独变化时所产生的影响，还反映与其他参数交互作用时所产生的影响：

(13) $ S_i^{\text{T}} = 1 - {S_{\sim i}} = 1 - {{{D_{\sim i}}} / D}. $

式中： $ {D_{\sim i}}$ 为除参数 $ {x_i}$ 之外的其他参数共同作用对模型输出结果造成的方差.

在实际过程中，几乎不可能利用解析积分求解SWMM等复杂非线性模型的方差. 本研究利用蒙特卡洛数值积分估计模型输出结果的方差，当模型参数样本数足够大时，计算所得结果逼近解析解. 将SWMM概化为

(14) $ Y = f(X). $

式中： $ X = \{{X_1}, \cdots ,{X_p}\}$ 为 $ p$ 个SWMM参数的集合， $ Y$ 为模型的输出（目标函数值）. 动态演算的SWMM的模型输出不是整个仿真时间序列结果，而是通过目标函数标量化后的值. 选取径流量的均方根误差（root mean square error，RMSE）、峰值流量的绝对百分比误差（absolute percentage error，APE）和峰现时间的绝对误差（absolute error，AE）作为SWMM输出结果的目标函数.

灵敏度计算步骤如下：

1）基于表3通过拉丁超立方采样（Latin hypercube sampling，LHS）在参数分布空间内进行2次互相独立的采样，所得结果分别为样本矩阵 $ {{{M}}_{{1}}}$ 与重采样矩阵 $ {{{M}}_{{2}}}$.

(15) $ \left. \begin{split} &{{{M}}_1} = \left[ {\begin{array}{*{20}{c}} \!\!\! {{X_{11}}}&{{X_{12}}}& \cdots &{{X_{1p}}} \!\!\! \\ \!\!\! {{X_{21}}}&{{X_{22}}}& \cdots &{{X_{2P}}}\\ \vdots &{}\vdots &{} &{} \vdots \!\!\! \\ \!\!\! {{X_{N1}}}&{{X_{N2}}}& \cdots &{{X_{Np}}} \!\!\! \end{array}} \right]\;, \\ & {{{M}}_2} = \left[ {\begin{array}{*{20}{c}} \!\!\! {{{{X}}_{11}^{'}}}&{{{{X}}_{12}^{'}}}& \cdots &{{{{X}}_{1p}^{'}}} \!\!\! \\ \!\!\! {{{{X}}_{21}^{'}}}&{{{{X}}_{22}^{'}}}& \cdots &{{{{X}}_{2p}^{'}}} \!\!\! \\ \vdots &{}\vdots &{} &{} \vdots \\ \!\!\! {{{{X}}_{N1}^{'}}}&{{{{X}}_{N2}^{'}}}& \cdots &{{{{X}}_{Np}^{'}}} \!\!\! \end{array}} \right]. \end{split}\right\} $

式中： $ N$ 为基础样本数，N=5 000； $ p$ 为SWMM参数个数， $ p$=19. 在样本 $ {{{M}}_{{1}}}$、 $ {{{M}}_{{2}}}$ 的基础上，重新采样获得其余19个新的样本矩阵：

(16) $\left. \begin{split} & {{{M}}_{{3_1}}} = \left[ {\begin{array}{*{20}{c}} {{X_{11}}}&{{{{X}}_{12}^{{'}}}}& \cdots &{{{{X}}_{1p}^{{'}}}}\\ {{X_{21}}}&{{{{X}}_{22}^{{'}}}}& \cdots &{{{{X}}_{2p}^{{'}}}}\\ \vdots &{}\vdots &{} &{} \vdots{}\\ {{{X}}_{N1}^{{'}}}&{{{{X}}_{N2}^{{'}}}}& \cdots &{{{{X}}_{Np}^{{'}}}} \end{array}} \right]\;,\; \cdots \;,\\ & {{{M}}_{{3_p}}} = \left[ {\begin{array}{*{20}{c}} {{{{X}}_{11}^{{'}}}}&{{{{X}}_{12}^{{'}}}}& \cdots &{{X_{1p}}}\\ {{{{X}}_{21}^{{'}}}}&{{{{X}}_{22}^{{'}}}}& \cdots &{{X_{2p}}}\\ \vdots &{}\vdots &{} &{} \vdots\\ {{{{X}}_{N1}^{{'}}}}&{{{{X}}_{N2}^{{'}}}}& \cdots &{{X_{Np}}} \end{array}} \right]. \end{split} \right\}$

式中： $ {{{M}}_{{3_1}}}$ 的第1列来自 $ {{{M}}_{\rm{1}}}$ 的第1列， $ {{{M}}_{{3_p}}}$ 的第 $ p$ 列来自 $ {{{M}}_{\rm{1}}}$ 的第 $ p$ 列.

2）将步骤1）中采样得到的包含 $ {{{M}}_{\rm{1}}}$、 $ {{{M}}_{\rm{2}}}$ 在内的21个样本矩阵共计105 000组参数组分别代入1.1节建立的SWMM排水管网模型中进行计算，对所获得的结果进行3类输出变量（径流量、峰值流量、峰现时间）的目标函数值计算.

3）将步骤2）中所得目标函数值代入式（17）～（22）计算SWMM各参数 $ {X_i}$ 对应的灵敏度指数.

(17) $ \begin{split} \mathop D\limits^ \wedge (Y) = & \frac{1}{{2N - 1}}\sum\limits_{r = 1}^N {\Big[ {f^2}({X_{r1}},{X_{r2}}, \cdots ,{X_{rp}}) + } \\ & {f^2}({{X'_{r1}}},{{X'_{r2}}}, \cdots ,{{X'_{rp}}}) \Big] - \mathop {{f_0^2}}\limits^{{ \wedge \,}} , \end{split} $

(18) $ \begin{split} \mathop {{f_0^2}}\limits^{{ \wedge \,}} = \frac{1}{N}\sum\limits_{r = 1}^N {f({X_{r1}},{X_{r2}}, \cdots ,{X_{rp}}) \times } f({{X'_{r1}}},{{X'_{r2}}}, \cdots ,{{X'_{rp}}}), \end{split} $

(19) $ \begin{split} &\mathop {{D_i}}\limits^ \wedge = \frac{1}{{N - 1}}\sum\limits_{r = 1}^N {\Big[ f({X_{r1}},{X_{r2}}, \cdots ,{X_{rp}}) \times } \\ & \;\;\; f({{X'_{r1}}},{{X'_{r2}}}, \cdots ,{{X}}_{{{r}}\left( {{{i - 1}}} \right)}^{{'}},{X_{ri}},{{X}}_{{{r}}\left( {{{i + 1}}} \right)}^{{'}}, \cdots ,{{X'_{rp}}})\Big] - \mathop {{f_0^2}}\limits^{{ \wedge \,}} , \end{split} $

(20) $ \begin{split} &\mathop {{D_{\sim i}}}\limits^ \wedge = \frac{1}{{N - 1}}\sum\limits_{r = 1}^N {\Big[ f({{X'_{r1}}},{{X'_{r2}}}, \cdots ,{{X'_{rp}}}) \times } \\ &\;\;\; f({{X'_{r1}}},{{X'_{r2}}}, \cdots ,{{X}}_{{{r}}\left( {{{i - 1}}} \right)}^{{'}},{X_{ri}}, {{X}}_{{{r}}\left( {{{i + 1}}} \right)}^{{'}},\cdots ,{{X'_{rp}}})\Big] - \mathop {{f_0^2}}\limits^{{ \wedge \,}} , \end{split} $

(21) $ {S_i} = {{{D_i}}}/{{D(Y)}}, $

(22) $ S_i^{\text{T}} = 1 - {{{D_{\sim i}}}}/{{D(Y)}}. $

式中： $ ({X_{r1}},{X_{r2}}, \cdots ,{X_{rp}})$ 来自 $ {{{M}}_{{1}}}$， $({X'_{r1}},{X'_{r2}}, \cdots ,{X'_{rp}})$ 来自 $ {{{M}}_{{2}}}$， $({X'_{r1}},{X'_{r2}},\cdots, {{X}}_{{{r}}\left( {{{i - 1}}} \right)}^{{'}},X_{ri},{{X}}_{{{r}}\left( {{{i + 1}}} \right)}^{{'}},\cdots,{X'_{rp}})$ 来自 $ {{{M}}_{{3_i}}}$， $ \hat \cdots$ 表示估计值，S_i为第i个参数的第一阶全局灵敏度指数.

4）根据 $ {S_i}$ 的大小对SWMM参数进行灵敏度排序，筛选出灵敏参数；对比分析各参数对3类不同输出变量的灵敏度以及在不同雨强下的敏感度. 采用蒙特卡洛数值积分计算敏感度，非灵敏参数第1阶灵敏度稍小于0（而不是等于0），因此以第1阶灵敏度指数为零作为灵敏参数筛选标准^[24-25].

选取径流量、峰值流量以及峰现时间3个对雨水排水系统模拟有重要意义的输出变量，使用Sobol方法计算7月8日场次降雨Rain1下SWMM参数对各输出变量的灵敏度，如表4所示. 可以看出，各参数对不同输出变量的灵敏度存在差异. 径流量计算所得的5个灵敏参数N_i、K_w、K_s、C₁、s_i同时也是另外2类输出变量计算所得的灵敏参数；对于峰值流量及峰现时间，霍顿模型衰减系数被筛选为灵敏参数；对于峰现时间，屋顶不渗透百分比和无洼地蓄水不渗透百分比也是灵敏参数，但是灵敏度相对较小，说明模型对于不同输出变量的关键灵敏参数是一样的，不同输出变量额外筛选出的灵敏参数对模型结果影响较小.

N_i是最灵敏参数，对3类输出变量的第1阶灵敏度指数均大于0.4（总阶灵敏度均大于0.6），远大于排在第2位的K_w，说明模型结果的方差绝大部分是由N_i所造成的，N_i对模型结果影响较大.

混凝土管曼宁糙率系数对于3类输出变量的灵敏度指数差异较大，对于径流量、峰值流量、峰现时间的第1阶灵敏度指数分别为0.011、0.037、0.102（总阶灵敏度指数分别为0.092、0.169、0.233），说明管道曼宁糙率系数的灵敏度指数取决于输出状态变量的类型，对峰现时间最为敏感. 曼宁公式可以合理解释这个结果，糙率越大，管道流速越小，峰值出现时间越长.

不渗透性百分比被识别为非灵敏参数，与前人研究^{[9, 26]}所得出的结论不相符，原因是本研究将城市地表模型概化为6类土地利用类型，将不同土地类型的不渗透率限制在较窄的合理取值范围之内，当不渗透率在此范围内变化时，对模型的最终输出结果影响较小. 这从侧面反映出，当地表土地利用数据精度较高时，所建模型不需要率定不渗透性，可以取经验值. 从GIS相关数据中获取的子汇水区坡度及特征宽度比例因子是排名靠前的灵敏参数，对模型结果影响较大，说明K_s、K_w依旧是待率定参数. 由表4还可以看出，各灵敏参数与其他参数相互作用所造成的结果方差（总阶灵敏度指数与一阶灵敏度指数之差）均约为10%，灵敏参数间的耦合性较强，不宜使用Morris一次一个变量法对参数进行灵敏度分析；被识别为非灵敏参数的总阶灵敏度指数较接近（0.05~0.07），需要计算二阶及三阶灵敏度指数，深入研究非灵敏参数的总阶灵敏度指数是由参数间的相互作用所产生的还是由模型的特征结构所决定的.

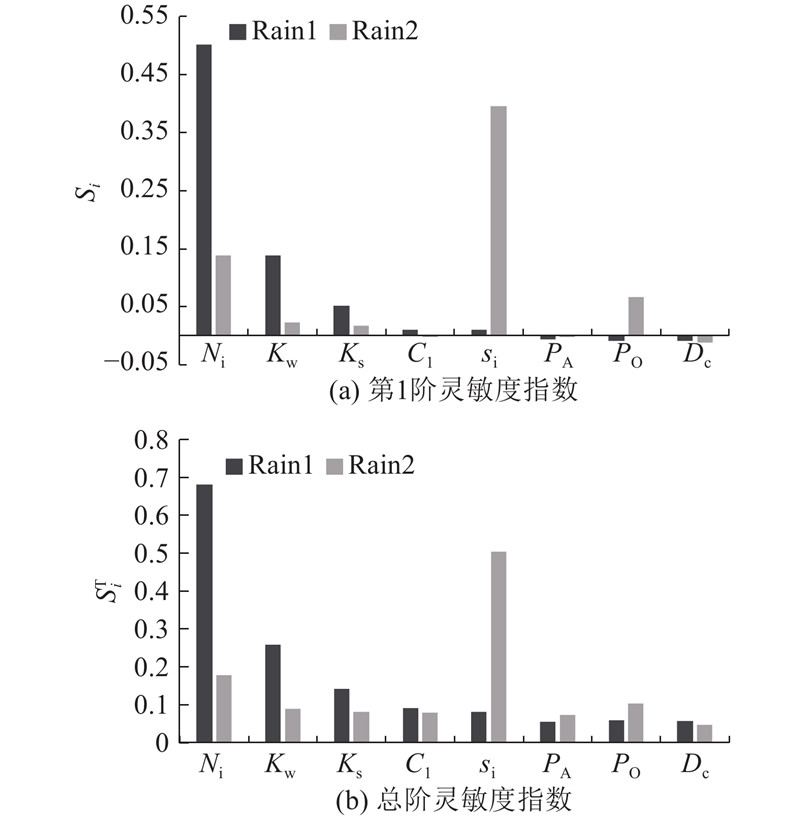
SWMM灵敏度分析的相关研究^{[9, 27]}表明，降雨强度对参数灵敏度有较大影响. 选取6月28日场次降雨Rain2与7月8日场次降雨Rain1作为对比情景，研究雨强对SWMM参数灵敏度的影响. Rain2雨强较小、历时较短，不计算参数对峰值流量以及峰现时间的影响，只比较参数对2场次降雨下径流量计算结果的影响（如表5和图2所示）.

由表4、5可知，在较大的雨强条件下，N_i是最灵敏参数并且对径流量起决定性作用（第1阶灵敏度指数达到0.502），之后依次是K_w、K_s、C₁、s_i，其中s_i第1阶灵敏度指数仅为0.010；在较小的雨强条件下，最灵敏参数是s_i，第1阶灵敏度指数达到0.396，远高于第2位N_i的0.139，同时P_O也被识别为灵敏参数（第1阶灵敏度指数为0.067），位列第3，高于第1阶灵敏度指数分别为0.023、0.017的K_w与K_s，C₁被识别为非灵敏参数. 说明在小雨强的条件下，占地面积约为86%的不渗透地区的洼地储蓄深度使雨量多数存储在不渗透地区，径流量较小甚至不产流；无洼地蓄水不渗透性百分比的改变间接影响了不渗透地区的洼地储蓄总容量，从而影响最终的降雨径流量，因此P_O展现出较高的灵敏度. 降雨的存储过程发生在汇流过程之前，N_i、K_w和K_s等汇流过程参数的灵敏度大大减小，但是仍表现出一定的灵敏性. 在大雨强的条件下，洼地储蓄部分很快被降雨所填满，在取值范围内改变s_i对最终的降雨径流量的影响较小（s_i的第1阶灵敏度值仅为0.010），同理P_O也表现为非灵敏参数.

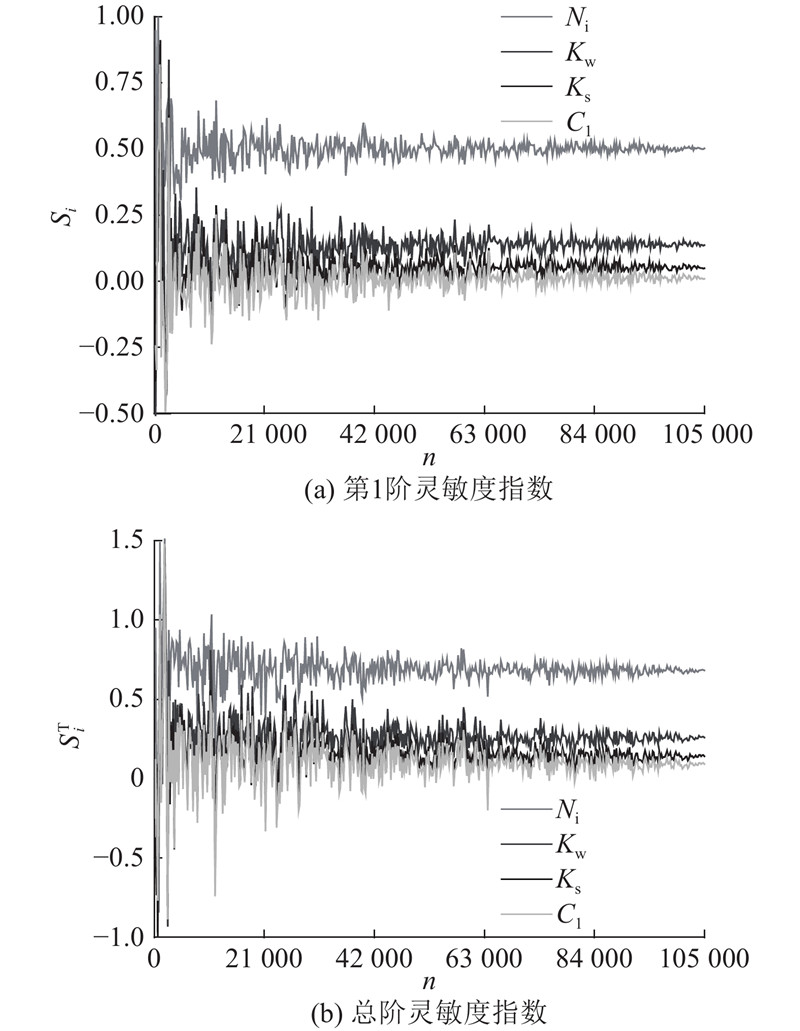
为了分析计算所得灵敏度指数的收敛性，确保所得结果稳健可靠，采用重采样方法在5 000个基础样本中分别抽取10、20、 $ \cdots $、5 000个子样本共500组，计算Rain1的径流量灵敏度指数，对应的SWMM运算次数n分别为210、420、 $ \cdots $、105 000次，主要灵敏参数的收敛情况如图3所示. 由图可以看出，在模型运行63 000次（基础样本数为3 000）之前计算所得的Sobol灵敏度指数上下波动幅度较大，除了最灵敏参数N_i，另外3个灵敏参数的排序不稳定；在模型运行84 000次（基础样本数为4 000）之后，计算所得的Sobol灵敏度指数上下波动幅度减小并最终趋于稳定. 由此可见研究选取基础样本数为5 000时计算所得Sobol灵敏度指数是稳健可靠的.

（1）SWMM中不同输出变量，如径流量、峰值流量和峰现时间的关键灵敏参数大致相同，分别为N_i、K_w、K_s、C₁、s_i. N_i对3类输出变量都是最灵敏参数；C₁对3类输出变量的灵敏度指数差异较大，对峰值流量和峰现时间更为敏感.

（2）在不同雨强下，SWMM中水文水力模块的灵敏参数及相关排序有差异，尤其是与不渗透性洼地储蓄相关的2个参数s_i与P_O差异明显. 在较大雨强下，P_O被识别为非灵敏参数，s_i的灵敏度排序为第5位；在较小雨强下，P_O被识别为灵敏参数，s_i代替N_i成为最灵敏参数.

利用基于方差分解的Sobol方法对SWMM参数全局灵敏度进行定量分析，计算各参数的一阶灵敏度指数与总阶灵敏度指数，结果直观反映出各参数对SWMM计算结果方差的影响，对SWMM校核时的参数选择有参考作用. 受限于SWMM的计算量，没有计算各灵敏参数的二阶灵敏度指数，缺乏对灵敏参数两两间互相作用的定量评价，之后的研究将着力于解决上述问题.