波浪能是海洋能中品位最高、分布最广的能源形式之一[1],作为清洁的可再生能源,对缓解能源危机、减少对传统化石燃料的依赖、改善环境污染等问题具有重要的现实意义. 离岸式振荡水柱(off-shore oscillating water column,off-shore OWC)波能转换装置由于结构简单、易于安装维护、转换效率高等优点而被广泛应用,其基本工作原理是利用海浪上下起伏运动造成气室内外空气压强差,推动气室顶部的空气透平旋转,从而把波浪能转换成机械能.
国内外学者已对OWC波能转换装置进行了不少研究. Evans[2]和Falnes[3]在线性波理论框架下,提出OWC波能转换理论. Evans[4]对早期理论进行改进,将OWC气室内的压强简化为均匀分布的空气压强,并允许气室内水体的自由液面在空间上发生变形,不需要一定保持为完整的平面,得到OWC装置最大和最优效率的解析表达式. Evans等[5]应用特征函数展开法,研究有限水深情况下OWC简化模型的水动力学特性,通过近似表征流体流动在结构大变形处的奇异行为,有效提升数值计算的计算效率和数值精度. 在物理模型试验方面,Ambli等[6]提出多共振振荡水柱装置,利用港口效应聚集波浪能,提高能量转换效率. 梁贤光等[7]研究在不同入射波参数和管口情况下,OWC气室内的水面运动情况. 史宏达等[8-9]对沉箱式防波堤兼作岸式波力发电装置在非规则波下的能量转换效率进行试验研究. 在数值方面,You[10]运用数值手段考察地形对近岸OWC装置工作效率的影响. 史宏达等[11]利用雷诺时均方程和VOF模型,计算波浪的传播和水柱在气室内的振荡情况. 宁德志等[12-13]基于域内源造波技术的时域高阶边界元方法,研究岸式OWC波能转换装置,得到共振频率与前墙吃水深度、墙体厚度及气室宽度之间的关系. Kamath 等[14]依据达西方程,模拟不同输出阻尼系数下的OWC水动力学响应特性. Luo等[15]考虑入射波波高变化对波能捕获效率的影响. Wang等[16]分析波浪的非线性和黏性效应对OWC装置工作效率的影响.
从理论求解和数值模拟2个角度出发,首先基于势流理论,采用匹配特征函数展开法求解微幅波与离岸式振荡水柱波能转换装置相互作用的边界值问题,其次利用商业软件FLUENT建立二维完全非线性波-OWC数值模型,深入研究一系列参数对装置能量转换效率的影响,参数包括OWC装置的吃水深度、气室宽度以及墙体厚度等. 此外,基于经过验证的OWC数值模型,进一步研究入射波波高变化对OWC装置转换效率的影响情况.
1. OWC理论模型的建立
1.1. 控制方程和边界条件
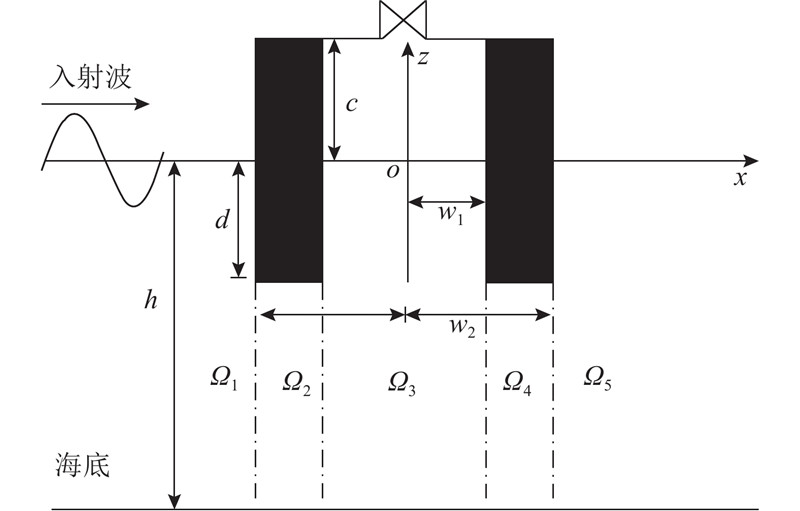
如图1所示,OWC波能转换装置安装于静水深为h的波浪水槽中,气室尺寸为2w1c. 装置吃水深度为d,墙体厚度为w2−w1. 将直角坐标系的原点置于气室内静水面的中点,x轴与静水面重合,z轴垂直向上,波浪沿x轴正向传播. 根据边界条件的差异,将整个流场划分为5个区域(Ω1、Ω2、Ω3、Ω4、Ω5). 记入射波频率为ω,速度势在复数域中可表示为
图 1
图 1 离岸式振荡水柱波能转换装置示意图
Fig.1 Sketch of off-shore oscillating water column wave enery device
相应的自由表面边界条件为
式中:pc为拟封闭气室内的压强,g为重力加速度,ρ为海水密度.
由于结构物处于固定状态,物面及海底边界条件均为
式中:n为物面法线方向,指向流体区域外. 此外,ϕ(x, z)在远场还需满足Sommerfeld辐射边界条件.
1.2. 求解过程
波浪与OWC装置相互作用的过程可分为波浪衍射及辐射问题,即
式中:ϕS为衍射势,在气室内外气压一致时,由波浪与OWC装置前后2个墙体相互作用产生;ϕR为在没有入射波的情况下,气室内压力振荡作用于液面而产生的辐射速度势.
1.2.1. 衍射问题求解
在区域Ω1、Ω3、Ω5中,上部为自由表面边界(在式(2)中令pc=0),下部为不可穿透的海底边界. 因此,可将速度势展开为特征函数基
式中:k为行进波的波数. k、km可分别由以下方程求出:
取k0=−ik,将相应区域的速度势分别展开为
式中:A为入射波振幅,
在区域Ω2、Ω4中,上下为不可穿透的固壁边界,相应的速度势展开为
式中:
对于结构物尖角附近流体运动存在奇异性的问题,采用Deng等[17]的处理方法,在区域间的公共界面上引入正交多项式将速度分布函数近似展开. 速度分布函数表达式为
式中:
式中:Γ为Gamma函数,C为盖根堡多项式.
在获得各区域速度势展开式及公共界面上速度分布函数的基础上,应用区域间的速度连续条件及压力连续条件,构建能求解出所有未知系数的线性方程组.
1.2.2. 辐射问题求解
在辐射问题中,气室内液面上存在气压波动,因此区域Ω3的上边界为非齐次边界条件,即式(2)中
1.2.3. PTO模型
假定气室内空气可压,Sarmento 等[18]提出关联线性能量输出(power take-off, PTO)装置与气室内空气质量变化的方程:
式中:M为空气质量,ρc为空气密度,V为气室体积,V0、
取
式中:
采用Deng等[17]的方式,式(20)可以改写为
式中:
根据Deng等[17]的研究,1个周期内被转换的波浪能为
将其除以入射波的波能流
2. OWC数值模型的建立
2.1. 控制方程
考虑二维不可压缩流体,其流动控制方程包括连续方程和N-S方程:
式中:u、w分别为x轴和z轴2个方向上的速度分量,p为流体压强,ν为流体运动黏滞系数.
采用VOF方法追踪水气交界面的波动,aq为体积分数函数,其定义为单元内第q相流体所占体积与该单元的体积之比. aq=1表示第q相流体占据整个流体单元;aq=0表示在整个流体单元内不含第q相流体. 若aq
式中:q=0为空气相,q=1为水相.
此外,aq还应满足体积分数连续方程:
2.2. 造波及消波方法
借助FLUENT软件的用户自定义函数(user-defined function, UDF),在入射边界给定线性波的速度表达式及相应波面函数生成入射波. 入射波的波浪要素有自由液面高度η,水平方向速度u,垂直方向速度w,可以分别表示为
由于压力出口边界条件不能保证波浪完全透射,为避免出口边界处反射波的形成,在水槽末端设置阻尼消波区,其实现方法是在动量方程中添加1个消波阻尼源项,表达式为
式中:x1为消波区的起点,x2为消波区的终点,β为消波系数,vi为速度分量.
2.3. 边界条件及离散格式
边界条件的设置如下:
1)上边界与右边界设为压力出口边界条件;左边界设为速度入口边界条件;下边界与OWC装置表面设为固壁边界条件.
2)控制方程中的扩散项采用中心差分格式离散,动量方程和压力方程的对流项分别采用二阶迎风格式和Body Force Weighted格式,采用PISO算法求解压力与速度耦合方程.
2.4. 空气透平的处理
OWC气室上方孔口处存在1个线性空气透平,气室内的压强与孔口处的空气流速呈线性关系. 通过引入多孔阶跃层来代替该线性透平,阶跃层满足达西定律:
式中:Δp为气室内外压强差,Δm为阶跃层厚度,μ为空气动力黏滞系数,
式中:ρw为水的密度;ρa为空气密度;M=Lvρa,L为PTO处孔径;pa为大气压强. α可以表示为
式中:b为气室宽度.
此外,理论模型中的χ与C有如下转换关系:
2.5. 波能捕获效率的计算
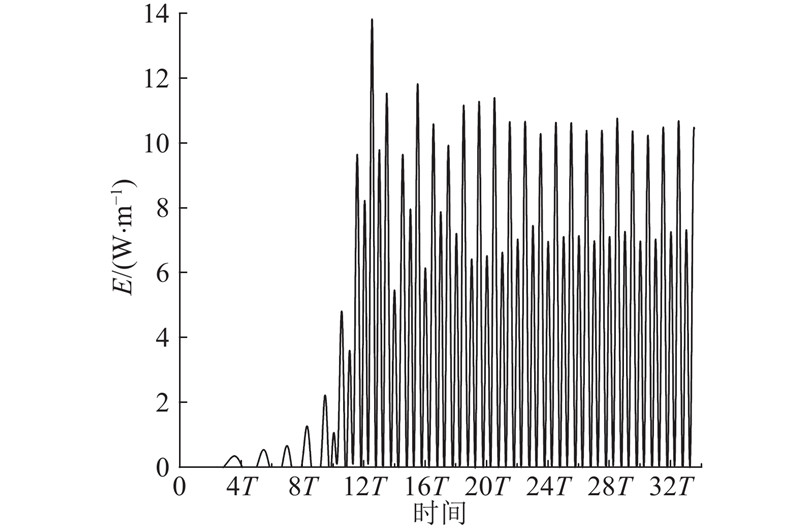
对于入射波波流能的计算,通常采用基于势流理论得到的理论公式(41)进行求解. 考虑到理论解与实际情况存在一定的偏差,为了准确计算OWC装置的波能捕获效率,本研究采用断面积分法,根据式(42)直接计算入射波传播过程中监控断面处的波能通量E,并将监控得到的波能流结果按式(43)取周期平均,记为Pw.
式中:pD为动压压强,p为静压压强,
式中:Pw为监控断面处波能通量的周期平均值,T为周期.
图 2
图 2 单位宽度入射波波能通量的时程曲线
Fig.2 Time history curves of incident wave energy flux per unit width
图 3
式中:Pt为捕获的能量,pc为气室内的压强,vn为孔口处的空气流速. OWC装置的波能捕获效率的表达式为
2.6. OWC数值模型验证
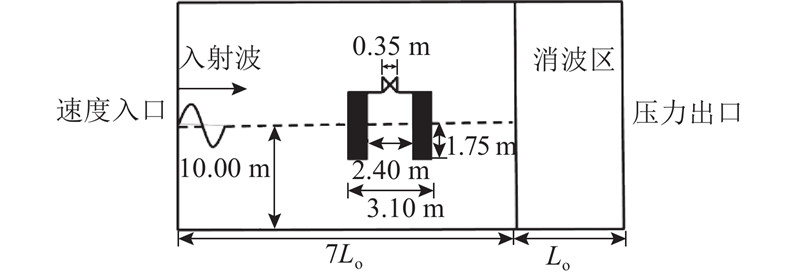
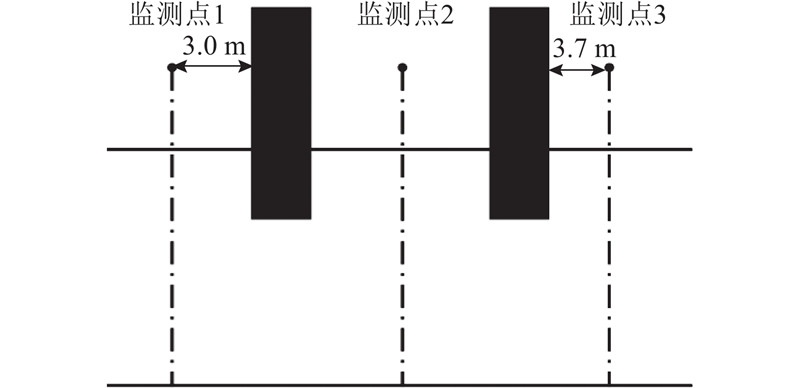
如图4所示,水槽总长为8Lo,水槽末端设置消波区,长度为Lo,OWC气室宽度为2.40 m。气室高度为1.00 m,前后墙吃水深度为1.75 m,墙体厚度为0.35 m,PTO处孔径为0.35 m. 经网格收敛性验证,单位波长内划分80个网格,自由液面处网格加密,单位波高内划分10个网格,时间步长
图 4
图 4 波浪-振荡水柱波能转换装置水槽数值模型示意图
Fig.4 Sketch of numerical tank model for wave-oscillating water column wave enery device
表 1 波能转换效率数值模拟验证中的不同入射波况
Tab.1
| 波况 | λ/m | T/s | 波况 | λ/m | T/s | |
| 1 | 9.8 | 2.51 | 6 | 18.9 | 3.48 | |
| 2 | 11.7 | 2.74 | 7 | 20.0 | 3.59 | |
| 3 | 12.9 | 2.88 | 8 | 21.4 | 3.71 | |
| 4 | 14.0 | 3.00 | 9 | 23.8 | 3.92 | |
| 5 | 16.5 | 3.26 | 10 | 33.7 | 4.76 |
图 5
图 5 振荡水柱波能转换装置气室及附近的水面波动与流场图
Fig.5 Water surface fluctuation and flow field inside and near oscillating water column wave energy device chamber
图 6
图 8
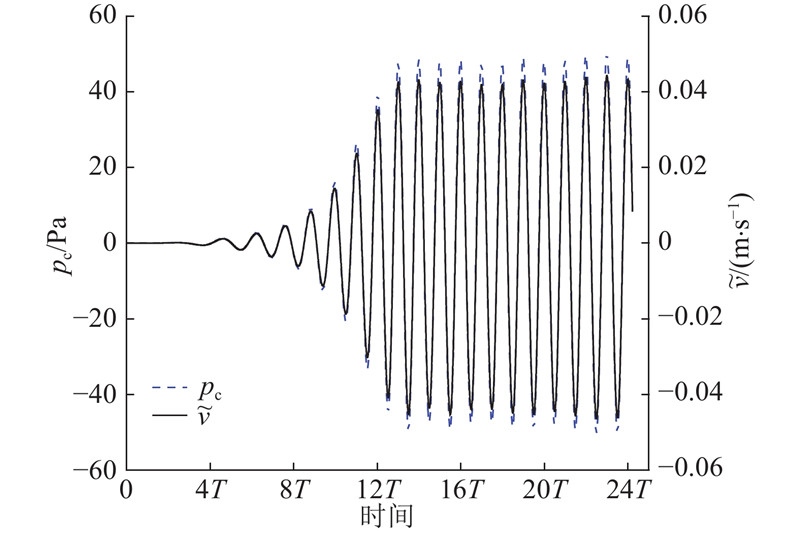
图 8 振荡水柱波能转换装置气室内的压强与PTO出口流速
Fig.8 Static pressure within oscillating water column wave energy device chamber and outlet velocity for PTO
图 7
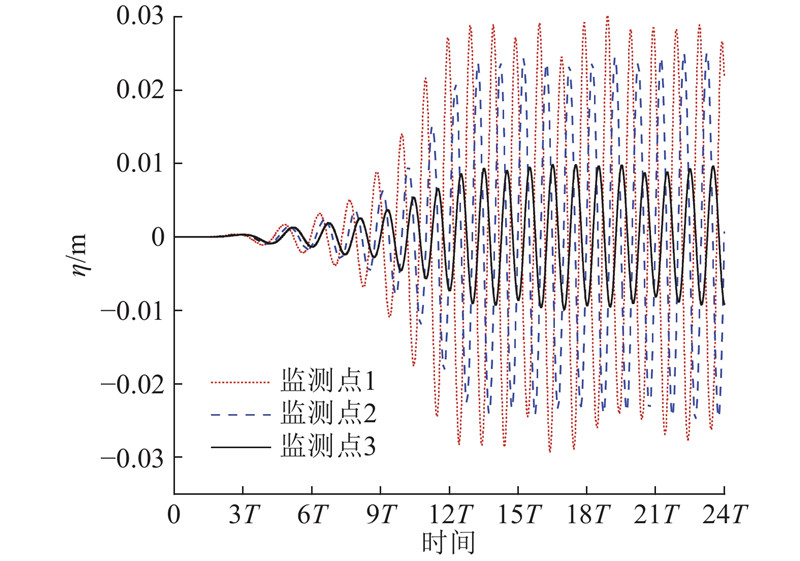
图 7 振荡水柱波能转换装置前、中、后方的波面升沉曲线
Fig.7 Time series of surface elevations before, inside and after oscillating water column wave energy device chamber
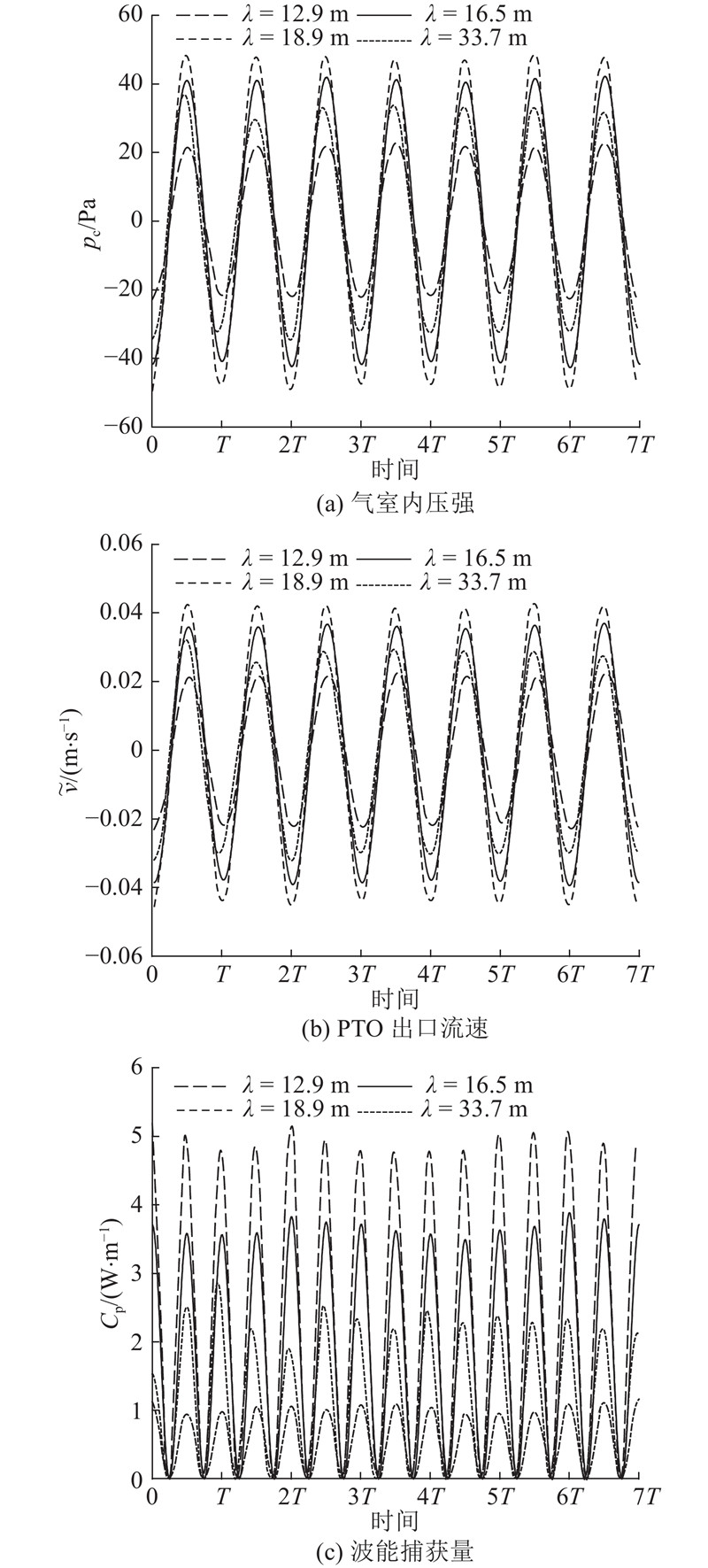
考虑到入射波长对OWC装置波能吸收效率的影响,如图9所示为在波高为0.04 m,波长分别为12.9、16.5、18.9、33.7 m的情况下,OWC气室内压强pc,PTO出口流速
图 9
图 9 振荡水柱波能转换装置气室内压强、PTO出口流速以及波能捕获量的时程曲线
Fig.9 Time history curves of pressure within oscillating water column wave energy device chamber, outlet velocity for PTO and absorbed wave power
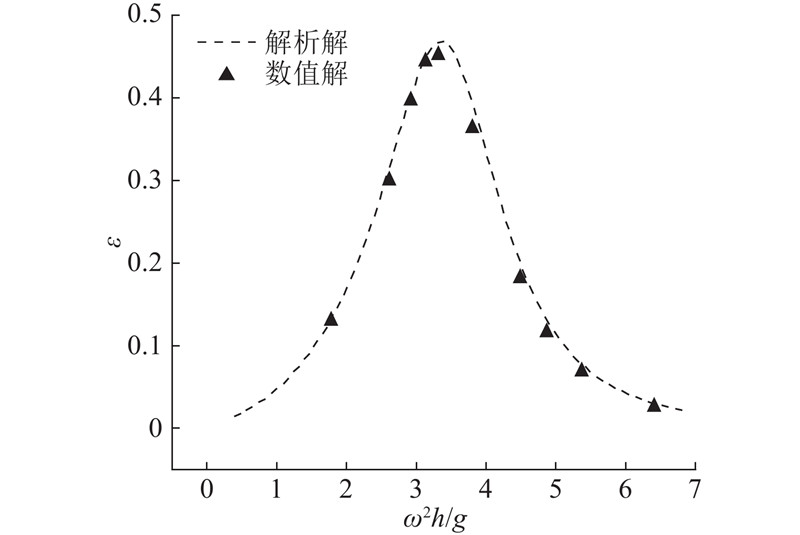
为了验证OWC数值模型的准确性,将10组波况下得到的波能吸收效率与解析解进行对比. 在数值模拟中选取的相对波高较小,因此水体黏性耗散和波浪非线性效应对结果的影响可以忽略不计. 由图10可以看出,在工况6下,当入射波周期为3.48 s时,OWC装置的能量捕获效率ε最高,达到约46%,其波频率接近共振频率,约为1.8 Hz. 当入射波频率远离结构物共振频率时,波能的吸收效率下降. 由图10可以看出,数值结果与解析解吻合良好.
图 10
图 10 不同波浪频率下震荡水柱波能转换装置的能量转换效率
Fig.10 Energy conversion efficiency versus different incident wave frequencies in oscillating water column wave energy device
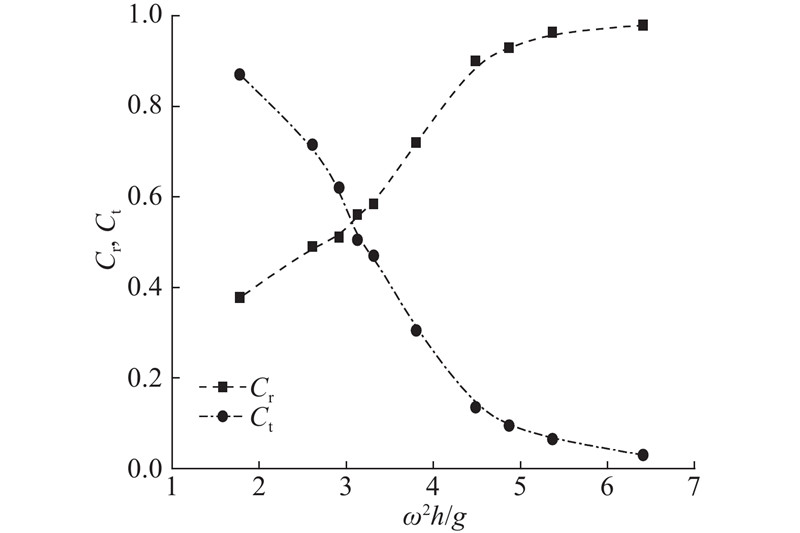
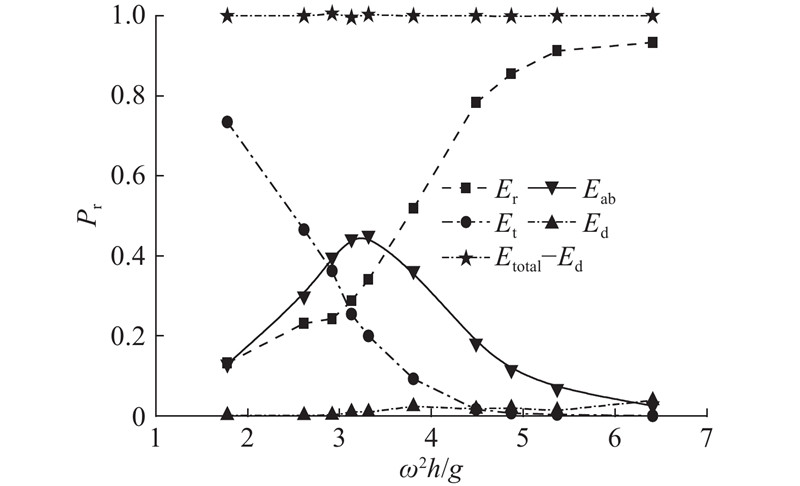
进一步分析能量的守恒情况. 采用Goda两点法分离入射波与反射波波高,如图11所示为不同波浪频率下得到的反射系数Cr和透射系数Ct,采用B样条曲线进行数据拟合. 可以看出,入射波长的增大导致反射系数减小,大部分入射波能透过前墙传入气室,同时透射系数也逐渐增大,更多的波能透射出去. 采用式(41)计算反射波与透射波波能流. 根据能量守恒原理可知,入射波波能流Etotal=反射波波能流Er+透射波波能流Et+OWC装置捕获的能量Eab+能量耗散Ed. 如图12所示为不同波浪频率下各部分能量占入射波波能流的比值Pr,图中的曲线为B样条曲线,其中能量耗散占比较小,这是由于墙体厚度相对于波长较小. 如图5所示也反映出墙体附近没有明显的涡旋存在. 若忽略能量的耗散,各部分能量总和约等于入射波波能流,进一步验证了模型的有效性,所建立的OWC数值模型能够准确模拟波浪与OWC装置的相互作用.
图 11
图 11 不同波浪频率下反射系数和透射系数
Fig.11 Reflection and transmission coefficients versus different incident wave frequencies
图 12
图 12 不同波浪频率下各组成部分的能量占比
Fig.12 Proportion of energy of each component versus different incident wave frequencies
3. 结构尺寸对波能捕获效率的影响
在水深一定的情况下,OWC结构尺寸是影响其工作效率的主要因素,现考虑墙体吃水深度、墙体厚度以及气室宽度对波能转换效率的影响. 计算域水深为10 m,入射波波高为0.04 m.
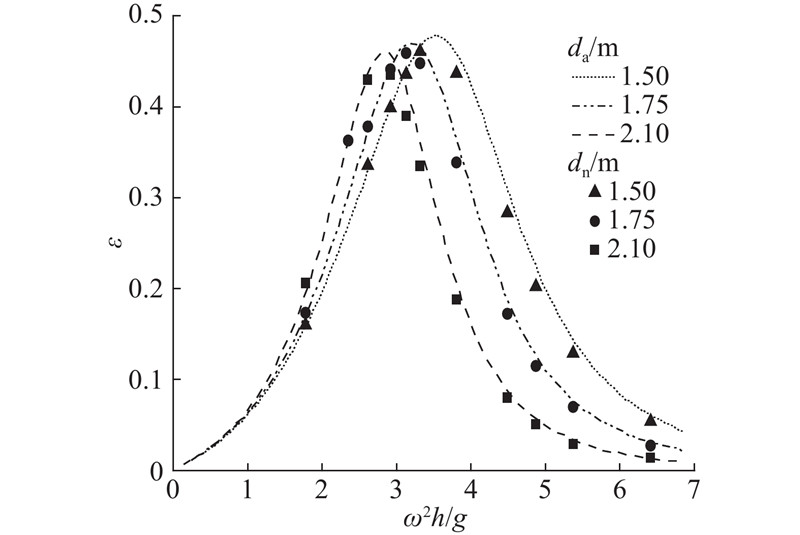
在OWC墙体厚度为0.35 m,气室宽度为2.80 m,装置吃水深度分别为1.50、1.75、2.10 m时,不同频率下OWC装置的能量转换效率如图13所示. 图中,da、dn分别为d的解析解和数值解. 由图可以看出在当前计算范围内,改变吃水深度对低频区的波能转换效率的影响较小,而在高频区,吃水深度的增大导致转换效率明显下降. 这是因为在低频区吃水深度相对波长较小,能量转换效率对吃水深度的变化不敏感,而在高频区吃水深度相对波长较大,能量转换效率对吃水深度的变化较敏感. 同时,可以看出吃水深度的增大,会导致装置高效频率带宽变窄,峰值向低频区移动. 这是由于吃水深度的增加,使得气室内水体质量增大,从而导致OWC的共振频率减小.
图 13
图 13 不同墙体吃水深度下波能转换效率随入射波频率变化
Fig.13 Wave energy conversion efficiency versus different incident wave frequencies for different immersion depths
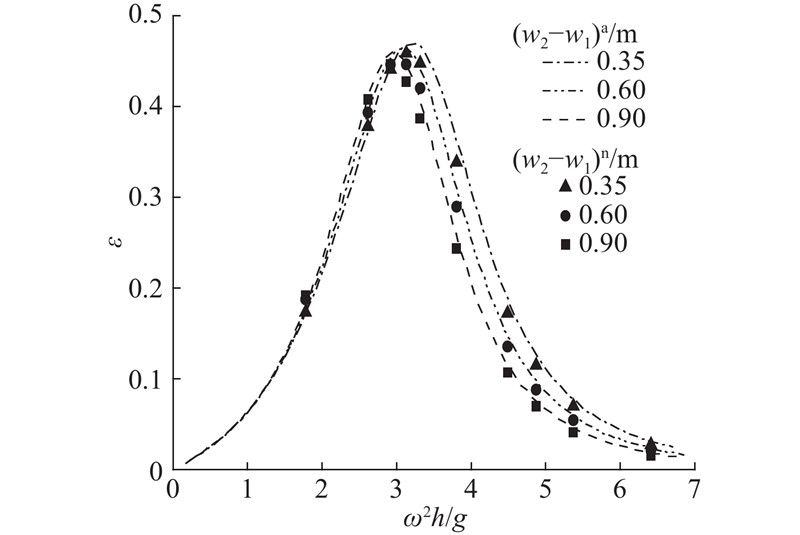
在OWC装置吃水深度为1.75 m,气室宽度为2.80 m,墙体厚度分别为0.35、0.60、0.90 m的情况下,不同频率下OWC装置的能量转换效率如图14所示. 图中,(w2−w1)a、(w2−w1)n分别为w2−w1的解析解和数值解. 可以看出,墙体厚度对低频区波能转换效率的影响较小,在高频区,墙体厚度的增大导致波能转换效率明显下降. 此外,墙体厚度的增大,导致OWC波能转换效率峰值向低频区移动.
图 14
图 14 不同墙体厚度下波能转换效率随入射波频率变化
Fig.14 Wave energy conversion efficiency versus different incident wave frequencies for different thickness of walls
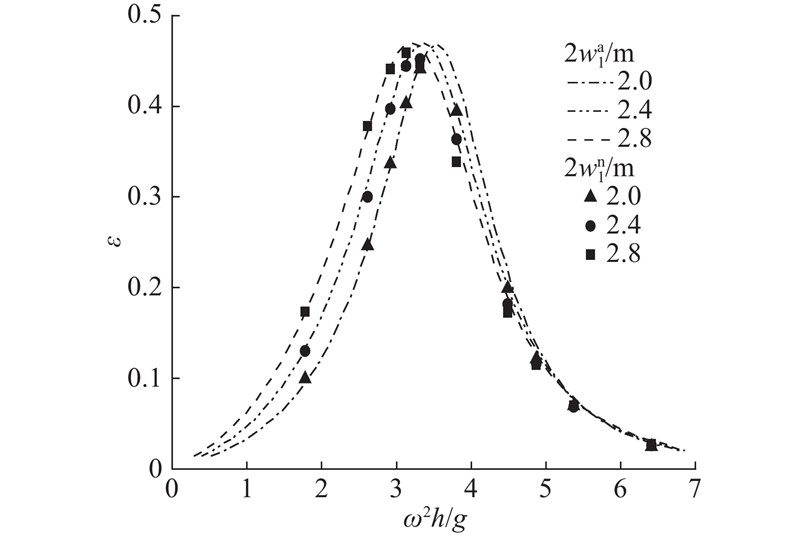
在OWC装置吃水深度为1.75 m,前后墙厚度为0.35 m,气室宽度分别为2.0、2.4、2.8 m时,不同频率下OWC装置的能量转换效率如图15所示. 图中,
图 15
图 15 不同气室宽度下波能转换效率随入射波频率的变化
Fig.15 Wave energy conversion efficiency versus different incident wave frequencies for different chamber widths
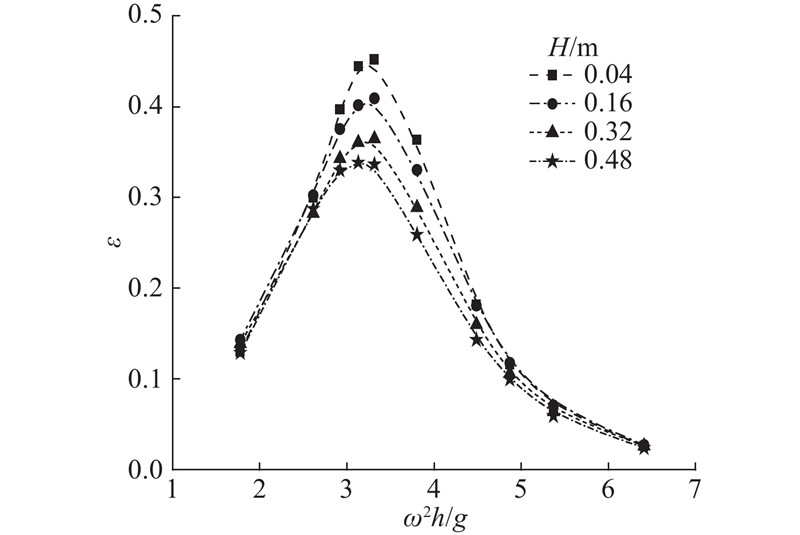
4. 入射波波幅对波能转换效率的影响
图 16
图 16 不同波幅下波能转换效率随入射波频率的变化
Fig.16 Wave energy conversion efficiency versus different incident wave frequencies for different incident wave amplitudes
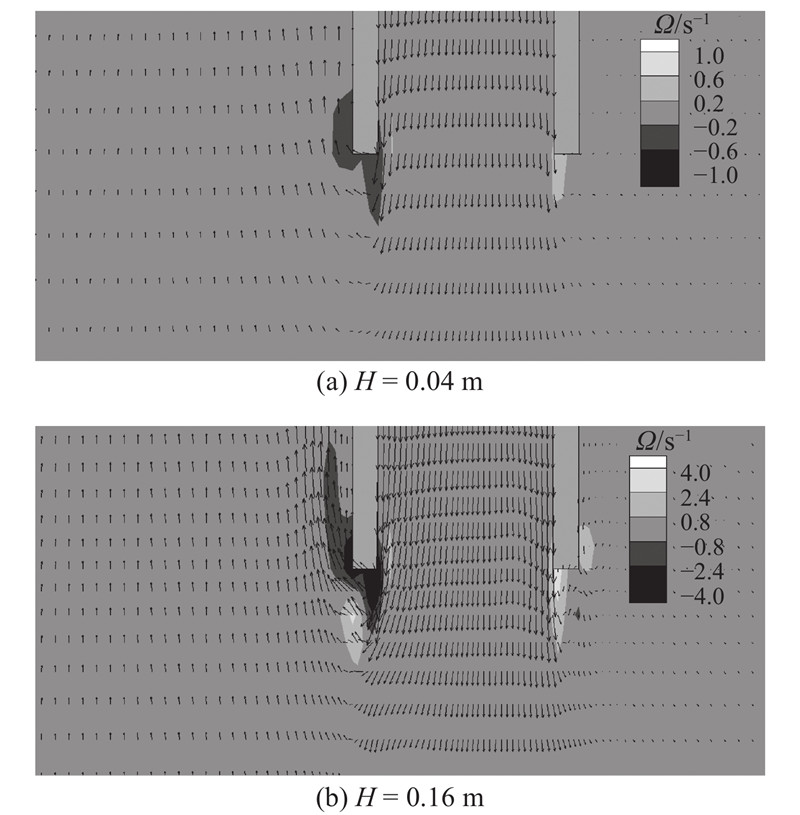
图 17
图 17 不同入射波波幅下振荡水柱波能转换装置底部附近流场、涡量分布
Fig.17 Flow fields and vorticities near bottom of oscillating water column wave energy device for different incident wave amplitudes
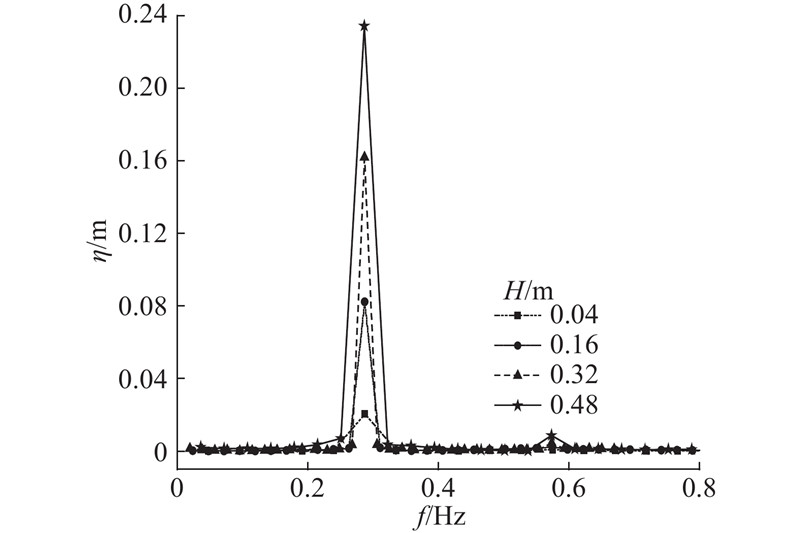
此外,通过FFT变换得到不同波幅下的入射波频谱,如图18所示. 由图可以看出,当H=0.16 m时非线性效应不明显,无高阶波的出现,而当H=0.48 m时非线性效应增强,在频率0.574 Hz附近出现二阶波,即入射波波能从低频波向高频波转移. 由于高频波波能难以传入OWC装置内部,OWC装置波能转换效率下降.
图 18
5. 结 语
从理论和数值上研究OWC装置吃水深度、气室宽度以及墙体厚度对波能转换效率的影响,通过对比发现数值结果与解析解吻合较好. 由结果可知,墙体吃水深度的增加会导致波能转换效率的高效频率带宽变窄,峰值向低频区移动;墙体厚度的增加对低频区波能转换效率的影响较小,但会导致高频区波能转换效率明显下降;气室宽度的增大会导致OWC装置的共振频率向低频区移动,同时在低频区,波能转换效率明显提高,而在高频区略有下降. 此外,波幅的增大带来的黏性及非线性效应会导致OWC装置转换效率下降,在共振频率附近尤为明显. 所建立的OWC数值模型能够准确模拟波与离岸式OWC装置的相互作用,为进一步研究海底地形变化对OWC装置波能转换效率的影响奠定基础.
参考文献
The oscillating water column wave-energy device
[J].DOI:10.1093/imamat/22.4.423 [本文引用: 1]
Radiation impedance matrix and optimum power absorption for interacting oscillators in surface waves
[J].DOI:10.1016/0141-1187(80)90032-2 [本文引用: 1]
Wave-power absorption by systems of oscillating surface pressure distributions
[J].
Hydrodynamic characteristics of an oscillating water column device
[J].DOI:10.1016/0141-1187(95)00008-9 [本文引用: 1]
汕尾100 kW波力电站气室模型性能试验
[J].DOI:10.3969/j.issn.1005-9865.2003.01.020 [本文引用: 1]
Performance experiment of Shanwei 100 kW wave power station’s air-room
[J].DOI:10.3969/j.issn.1005-9865.2003.01.020 [本文引用: 1]
新型沉箱防波堤兼作岸式OWC波能装置的设计及稳定性研究
[J].
Study on new caisson breakwater as OWC
[J].
Hydrodynamic analysis on wave power devices in near-shore zones
[J].
基于VOF模型的OWC气室波浪场数值分析
[J].
Numerical analysis of wave field in OWC chamber using VOF model
[J].
岸式振荡水柱波能转换装置的数值模拟
[J].
Numerical simulation of a land-based oscillating water column wave energy conversion device
[J].
Investigation of hydrodynamic performance of an OWC (oscillating water column) wave energy device using a fully nonlinear HOBEM (higher-order boundary element method)
[J].DOI:10.1016/j.energy.2015.02.012 [本文引用: 1]
Numerical modeling of power take-off damping in an oscillating water column device
[J].DOI:10.1016/j.ijome.2015.01.001 [本文引用: 1]
Nonlinear 2D analysis of the efficiency of fixed oscillating water column wave energy converters
[J].
Nonlinear and viscous effects on the hydrodynamic performance of a fixed OWC wave energy converter
[J].DOI:10.1016/j.coastaleng.2017.10.012 [本文引用: 2]
Wave power extraction by an axisymmetric oscillating-water-column converter supported by a coaxial tube- sector-shaped structure
[J].
Wave generation by an oscillating surface-pressure and its application in wave-energy extraction
[J].DOI:10.1017/S0022112085000234 [本文引用: 2]
Numerical simulation of a heave-only floating OWC (oscillating water column) device
[J].DOI:10.1016/j.energy.2014.08.079 [本文引用: 1]
Numerical energy balance analysis for an onshore oscillating water column-wave energy converter
[J].