桥式起重机在工业生产中主要承担物料吊运、设备安放等重要任务。由于长期承受变幅载荷作用,其桥架结构易出现裂纹萌生与扩展现象,进而导致金属结构疲劳破坏[1 -2 ] 。因此,开展桥式起重机疲劳寿命预测研究,对保障设备稳定运行、降低事故风险具有重要意义。
目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究。陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性。唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估。Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测。
在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测。范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命。戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估。
随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破。雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集。付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测。文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法。Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测。然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间。
为此,本文从物理模型与数据模型相融合的角度,提出一种基于物理信息神经网络(physics-informed neural network, PINN)的桥式起重机疲劳寿命预测方法。首先,采用BiLSTM网络构建数据模型,通过对历史应力时序数据的深度学习,实现对桥式起重机应力状态的高精度预测;其次,基于断裂力学理论,采用时序数据特征提取与载荷等效转换技术,建立描述结构疲劳损伤演化的物理模型;而后,将PINN作为融合框架,将Paris模型的微分方程嵌入网络架构,构建包含数据拟合与物理约束的混合预测模型,实现对桥式起重机疲劳寿命的准确预测;最后,搭建桥式起重机实际运行实验平台,基于长期监测数据对模型预测结果进行有效性验证与精度评估。
1 问题描述及解决方案
与常规设备相比,影响起重机寿命的因素是多元的。在载荷特征方面,常规设备承受的载荷往往是静态载荷或低波动循环载荷,载荷的随机性不强,而起重设备承受的动态载荷的占比较高,载荷的随机性较强,应力幅值的波动较大,导致起重机疲劳寿命预测的偏差较大;在工作环境方面,常规设备的环境条件往往较为良好,起重机则常受到不良环境的影响,如:铸造起重机面临高温环境,港口起重机处于盐雾环境,塔式起重机在建筑工地中面临粉尘、雨水侵蚀,都会加速疲劳损伤;在运行工况方面,常规设备的工况较稳定,可以用相对统一的载荷循环次数建立寿命预测模型,而起重机应用场景的差异较大,无法运用统一的载荷循环次数来建立寿命预测模型。
桥式起重机在长期服役过程中承受着多种多样的随机载荷,导致其桥架结构裂纹萌生处出现疲劳裂纹扩展直至发生疲劳断裂[19 ] ,从而引发重大的安全事故。为了确保桥式起重机在设计预期寿命内安全服役,亟须对其桥架结构关键部位的疲劳寿命进行准确的预测。目前,基于传统力学的疲劳寿命预测方法包括应力寿命法、应变寿命法和断裂力学法等[20 ] 。传统的预测方法存在计算量大、求解过程繁琐等问题。随着计算机运行能力的提升,以机器学习、深度学习为代表的人工智能技术在起重机疲劳寿命预测中得到广泛应用,诸如随机森林模型、神经网络模型等。人工智能技术具备求解计算量大和理论建模难的复杂问题的能力,对起重机疲劳寿命的预测具有较强的能力。
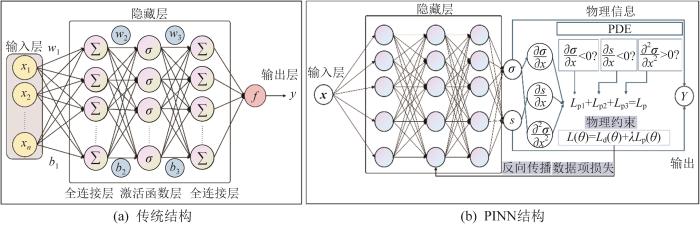
神经网络结构如图1 所示。图1 (a)所示为传统的全连接神经网络结构。由输入层接收多维原始特征数据x 1 x 2 x n w b f y 。该网络纯粹依赖数据驱动学习统计关联性,未融入物理先验信息,因此当面对起重机复杂工况下的强物理约束场景时,易因脱离物理逻辑而出现预测偏差。
图1
图1
神经网络结构
Fig.1
Neural network structure
随着PINN与深度残差神经网络的提出[21 ] ,神经网络在引入物理规律方面有了很大的进展。PINN是一类将物理先验信息嵌入深度学习框架的特殊人工神经网络,其结构如图1 (b)所示。PINN将满足物理方程(如微分方程或其他约束项)的残差项作为损失函数,通过网络计算物理量梯度(如σ/ x、 s/ x 、2 σ/ x 2 等),将物理损失L p L d
为此,本文提出一种数据与力学模型相融合的方法。在断裂力学框架下,将满足Paris模型的微分方程作为物理约束嵌入神经网络结构,赋予模型明确的物理意义。在桥式起重机疲劳寿命预测时,PINN的训练不仅包含测试应力之间的数据项损失,还包括对违反应力与剩余寿命之间物理约束条件的惩罚,最终,将物理损失与数据损失相融合,并作为整个模型的总损失,来预测桥式起重机的疲劳寿命。
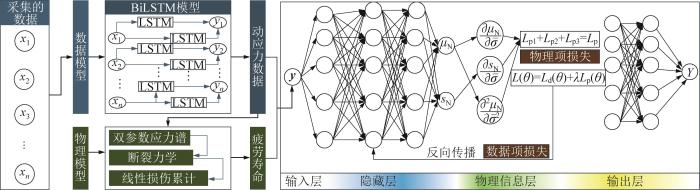
本文所提出的桥式起重机疲劳寿命预测模型的总体框架如图2 所示。其包括5个部分:1)将传感器数据进行特征处理后,作为BiLSTM的输入,得到数据模型下动应力数据预测结果。2)将预测好的动应力数据运用Miner理论与断裂力学方法进行寿命计算,得出疲劳寿命预测结果。3)将BiLSTM预测得到的动应力数据作为PINN的输入,疲劳寿命作为其输出。4)根据断裂力学理论,将疲劳寿命均值和方差的偏导数作为损失函数的物理损失项并加入权重λ
图2
图2
桥式起重机疲劳寿命预测模型总体框架
Fig.2
Overall framework of fatigue life prediction model for bridge crane
2 PINN 模型的构建
2.1 数据模型
由于传感器采集的数据较少,且需要对数据进行清洗,得到的数据不足以满足神经网络训练的需要。在模型训练过程中,需动态地对输入数据进行随机变换,并用生成对抗网络生成与原始数据分布相似的新样本。加入了新样本的模型的精度不高,故需要将数据增强,并利用BiLSTM网络对数据进行训练。其中,LSTM网络是一种常见的循环神经网络模型,用来处理序列数据,具有记忆长短期信息的能力[22 ] 。LSTM网络通过引入门控机制解决梯度消失或梯度爆炸的问题,可有效处理长期依赖和短期记忆的问题。假定桥式起重机相同类型的传感器有n 个,则在某一时刻t ,传感器采集到的数据x t = x 1 , t x 2 , t ⋯ x n , t x t ∈ R n × 1
x = x 1 x 2 ⋯ x t ⋯ x T (1)
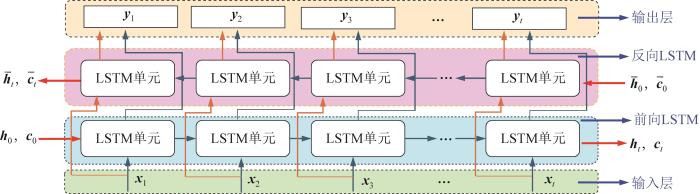
BiLSTM网络结合了2个方向的LSTM层,通过前后向时序数据的输入,更好地找出序列中的潜在联系,弥补了单一LSTM网络仅考虑前向时序数据的不足[23 ] 。BiLSTM网络模型的结构如图3 所示。将传输的时序数据x = [ x 1 x 2 ⋯ x t ] c t -1 ,并由当前时刻的LSTM单元和前一时刻的LSTM单元给出相应的隐藏状态信息 h t -1 ,其输出由最后时刻的输入及前一时刻的隐藏状态决定;反向LSTM层对输入序列的未来数据信息进行学习,输出与前向LSTM层一致;两者输出特征进行堆叠,形成最终的输出y = [ y 1 y 2 ⋯ y t ]
h t = L S T M x t , h t - 1 h t ¯ = L S T M x t , h ¯ t - 1 y t = W 1 h t + W 2 h t ¯ + b t (2)
式中: h t h t ¯ W 1 和 W 2 分别为正向和反向输出的权重参数, b t
图3
图3
BiLSTM 网络模型
Fig.3
BiLSTM network model
2.2 物理模型
以BiLSTM模型获取的动应力时序数据为基础,采用雨流计数法提取双参数应力谱,分别获得应力幅值谱和应力均值谱。通过式(3)将双参数应力谱转换为应力变程序列后,针对变幅应力变程,依据式(4)的转换机制将其等效为等效应力变程。该方法通过时序数据特征提取与载荷等效转换,实现变幅载荷工况下起重机疲劳损伤时应力特征的量化分析。
σ D = 2 σ a + σ m σ - 1 / σ b 1 + σ - 1 / σ b (3)
式中:σ D σ a σ m σ - 1 R =-1时材料的疲劳强度,σ b
σ ¯ = ∑ α i σ D i j j (4)
式中:σ ¯ σ D i α i j
桥式起重机的桥架结构是典型的焊接结构件,其断裂失效机制与结构初始缺陷及裂纹演化过程密切相关。焊接接头因存在不均匀的熔合线组织、残余应力集中区及微观缺陷(如气孔、夹渣),易成为疲劳裂纹萌生的敏感区域。基于断裂力学理论,将裂纹尺寸和扩展速率作为结构损伤评估参数。计算疲劳裂纹扩展寿命时需重点关注裂纹扩展第2阶段(中速率稳定扩展阶段)的动力学特性。在该阶段,裂纹增大速率与应力强度因子幅值呈现显著的对数线性关系,可通过Paris公式定量描述为:
d a d N = C K m (5)
式中:a 为裂纹长度,N 为应力循环次数,K C 和m 均为材料常数。
K = K m a x - K m i n = Y σ ¯ π a (6)
在等幅值的应力作用下,对Paris公式积分,可以得到由初始裂纹尺寸到临界裂纹尺寸的疲劳裂纹扩展寿命。在此基础上,考虑重载程度及工作应力的不确定性,引入应力谱系数和放大系数,可得:
N f = 1 K p f g C Y σ ¯ π m 0.5 m - 1 1 a 0 0.5 m - 1 - 1 a f 0.5 m - 1 (7)
式中:N f 为疲劳裂纹扩展寿命;a 0 为初始裂纹长度;a f 为临界裂纹长度;f g 为放大系数,其取值见GB/T 41510—2022《起重机械安全评估规范 通用要求》[24 ] ;K p 为应力谱系数。
K p = ∑ n i n T σ i σ m a x m y (8)
式中:ni 为与不同的结构应力相对应的应力循环数;nT 为结构的应力循环数,即n T = ∑ n i σ i σ m a x σ i σ m a x σ i m y
2.3 网络模型
网络模型的构建思路是将数据模型与物理模型相融合,并引入PINN中。在小样本数据场景下,将神经网络作为函数逼近器来拟合偏微分方程(partial differential equation, PDE)的解[25 ] ,同时将物理约束条件作为损失函数的一部分。假设函数u = u σ ¯
u + N u , λ = 0 (9)
式中:N u , λ λ u
定义f u σ ¯ u r σ ¯ = f u σ ¯ + N u , λ L 可表示为:
L = L d + L r L d = M - 1 ∑ c = 1 M f u σ ¯ c - u c 2 + L n L r = M - 1 ∑ c = 1 M r σ ¯ c 2 + λ L p θ (10)
式中:σ ¯ c u c L n θ c 为样本点数量,c =1, 2, …, M 。
损失函数作为神经网络参数优化的核心目标,用于度量真实值与预测值之间的差异。其L n
L n = - M - 1 ∑ c = 1 M δ c l o g g f u σ ¯ σ ¯ μ N , s N + 1 - δ c l o g 1 - G f u σ ¯ σ ¯ μ N , s N (11)
式中:g f u · · G f u · · δ c δ c δ c μ N s N
损失函数中的物理驱动部分主要包括2种物理约束项损失,即基于物理方程残差的约束项r · 式(12),后者可表示为式(13)。
r · = f u σ ¯ + N u , λ (12)
L p = m a x 0 , ∂ P p r e ∂ σ ¯ (13)
当∂ P p r e / ∂ σ ¯
μ N ∝ 1 - σ ¯ / M 1 q σ ¯ m 1 - M 2 / σ ¯ p M 1 = 1 - R σ c M 2 = σ t h (14)
式中:σ c σ t h K c K t h p 和q 均为不小于1的校准参数;取m
d μ N d σ ¯ ∝ - q M 1 1 - σ ¯ M 1 q - 1 σ ¯ - m 1 - M 2 σ ¯ - p - m 1 - σ ¯ M 1 q σ ¯ - m - 1 1 - M 2 σ ¯ - p - p 1 - σ ¯ M 1 q σ ¯ - m - 2 1 - M 2 σ ¯ - p - 1 < 0 (15)
d 2 μ N d σ ¯ 2 ∝ - q M 1 - q - 1 M 1 1 - σ ¯ M 1 q - 2 σ ¯ - m 1 - M 2 σ ¯ - P - m 1 - σ ¯ M 1 q - 1 σ ¯ - m - 1 1 - M 2 σ ¯ - p - p M 2 1 - σ ¯ M 1 q - 1 σ ¯ - m - 2 1 - M 2 σ ¯ - p - 1 - m - q M 1 1 - σ ¯ M 1 q - 1 σ - m - 1 1 - M 2 σ ¯ - p - m + 1 1 - σ ¯ M 1 q σ - m - 2 1 - M 2 σ ¯ - p - p M 2 1 - σ ¯ M 1 q σ - m - 3 1 - M 2 σ ¯ - p - 1 - p M 2 - q M 1 1 - σ ¯ M 1 q - 1 σ - m - 2 1 - M 2 σ ¯ - p - 1 - ( m + 2 ) 1 - σ ¯ M 1 q σ - m - 3 1 - M 2 σ ¯ - p - 1 - ( p + 1 ) M 2 1 - σ ¯ M 1 q σ - m - 4 1 - M 2 σ ¯ - p - 2 > 0 (16)
随着应力变程减小,疲劳寿命的方差增大,这表明疲劳寿命具有异方差性。在微小裂纹下,当施加的应力变程较小时,疲劳寿命的大部分时间耗费在小裂纹扩展。在恒定的低应力下,裂纹萌生且受到材料表面局部粗糙度、微观组织不均匀性等因素的影响而增大,结构件的疲劳寿命差异增大,即疲劳寿命的标准差s N d s N / d σ ¯ Δ σ ¯ s N Δ s N 式(17)所示。
d s N d σ ¯ = l i m Δ σ ¯ → 0 Δ s N Δ σ ¯ < 0 (17)
在PINN的物理项损失项L p θ λ
L p θ = λ 1 L p 1 θ + λ 2 L p 2 θ + λ 3 L p 3 θ (18)
对于任意的物理损失项,通过当前样本点的输入是否满足物理约束来判定其是否违反物理规律,可表示为:
L p 1 θ = M - 1 ∑ c = 1 M I d μ N d σ ¯ > 0 · d μ N d σ ¯ 2 L p 2 θ = M - 1 ∑ c = 1 M I d s N d σ ¯ > 0 · d s N d σ ¯ 2 L p 3 θ = M - 1 ∑ c = 1 M I d 2 μ N d σ ¯ 2 < 0 · d 2 μ N d σ ¯ 2 2 (19)
当d μ N / d σ ¯ > 0 I d μ N / d σ ¯ > 0 I d μ N / d σ ¯ < 0 d s N / d σ ¯ > 0 I d s N / d σ ¯ > 0 I d s N / d σ ¯ < 0 d 2 μ N / d σ ¯ 2 < 0 I d 2 μ N / d σ ¯ 2 < 0 I d 2 μ N / d σ ¯ 2 < 0
通过构造复合损失函数的方式将物理约束添加到网络中。在复合损失函数中,数据项损失是强制将实验数据进行拟合得出的误差;物理项损失则将神经网络的输出与物理关系保持一致,并引入惩罚因子λ λ λ
3 实验验证
本文以DQ40 kg-1.8 m-1.3 m小型通用桥式起重机为研究对象。其整机性能参数:工作级别为A5,额定起重质量为25 kg,小车及吊具的质量为18 kg,主梁长度为2 000 mm,最大起升高度为1 000 mm,小车运行速度为0.2~0.25 m/s,大车运行速度为0.15~0.2 m/s,小车轮距为400 mm。起重机运行实验平台如图4 所示,其工作循环过程如图5 所示。
图4
图4
起重机运行实验平台
Fig.4
Crane operation experiment platform
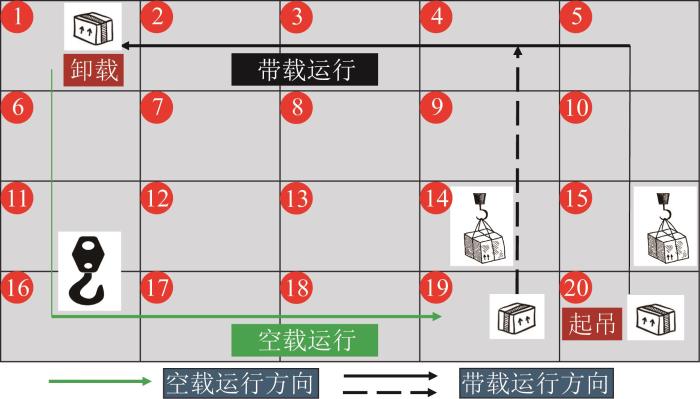
图5
图5
起重机工作循环过程
Fig.5
Working cycle process of crane
起重机工作循环过程为:从区域20开始起吊货物,到达指定的1号区域(卸货区)将货物卸载,并沿空载运行方向空载返回至区域19,第1个工作循环结束;在区域19再次起吊,运行至1号区域将货物卸载,沿空载运行方向空载返回至区域18,第2个工作循环结束;以此类推,起重机分别从区域18、区域17、区域16、区域15、区域14、区域13和区域12起吊货物,并将货物放置在1号区域,卸载后空载运行至相应区域。
3.1 数据预处理
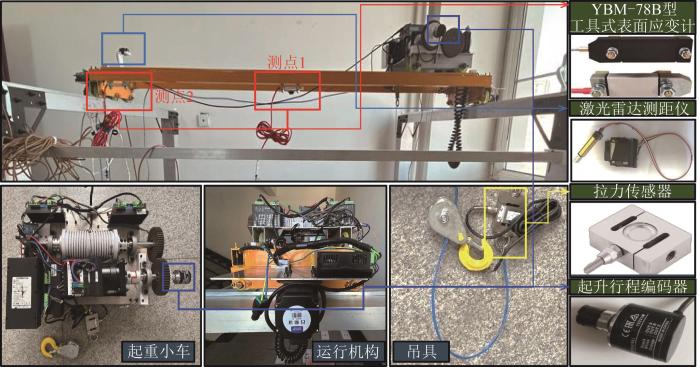
在起重机正常运行状态下采集实验数据。传感器的布置位置如图6 所示。在主梁跨中位置及端部位置安装YBM-78B型工具式表面应变计,用于采集起重机运行过程中桥架结构测点部位的应变;在起重小车的起升机构处安装E6B2-CWZ6C增量式旋转编码器,用于采集货物的起升高度;在大车端梁上安装激光雷达测距仪,用于采集小车位置信息和大车位置信息;在吊具上安装S形拉压力传感器,用于采集起升拉力。除应变的采样频率为100 Hz外,其余参数的采样频率均为10 Hz。各参数的采集范围如表1 所示。
图6
图6
传感器布置位置
Fig.6
Layout positions of sensors
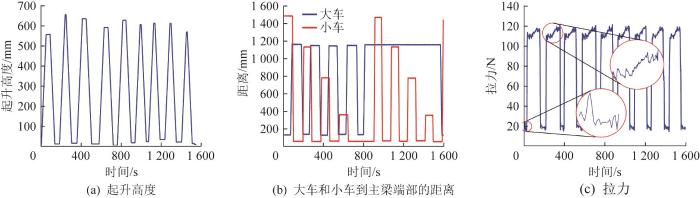
在不同负载下采集各参数。以8.85 kg负载为例,9个工作循环周期内参数采集结果如图7 所示。由图可知:在货物起吊过程中起升高度呈快速上升趋势,起升拉力出现振荡,其归因于起升冲击效应;当货物起吊至指定高度后,大车和小车开始向卸货区移动,此时起升高度不变,拉力随着大小车的移动出现变化,其归因于大小车运行冲击效应;在货物卸载阶段,吊具高度开始下降,拉力随着货物卸载而骤减。整个工作过程呈现周期性变化。
图7
图7
负载为8.85 kg 时参数采集结果
Fig.7
Parameter acquisition results with load of 8.85 kg
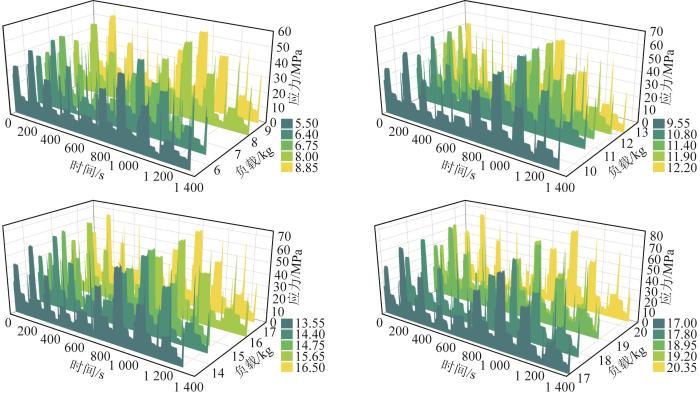
将采集的应变信息通过式(20)转换为应力数据,结果如图8 所示。
σ = E × ε × 10 6 (20)
式中:σ E E = 2.06 × 10 5 ε
图8
图8
原始应力时间历程
Fig.8
Original stress-time history
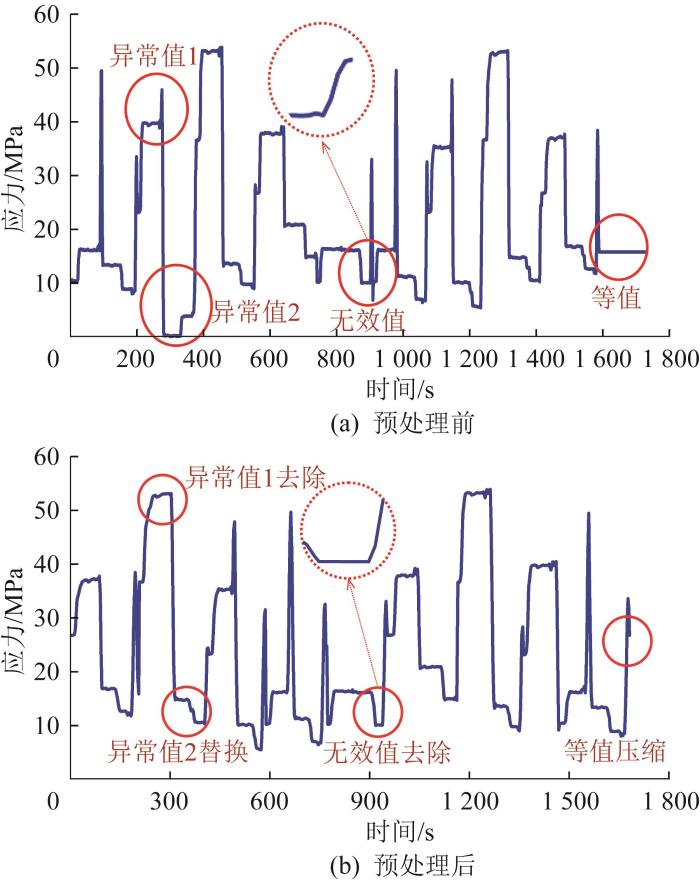
为了便于物理模型的应用,需要对原始应力时序数据进行预处理,包括异常值处理、无效幅值去除和数据压缩等。对于异常值数据,采用异常值去除和异常值替换的方法对错误数据进行修正;对于无效幅值数据,将无效值删除并用前后项数据的均值来代替;对于等值信息,对等值信息进行压缩,具体处理方法可参见文献[26 ]。数据预处理后应力时间历程如图9 所示。负载为8.85 kg时预理前后应力数据的对比如图10 所示。
图9
图9
预处理后应力时间历程
Fig.9
Processed stress-time history
图10
图10
负载为8.85 kg 时预处理前后应力数据对比
Fig.10
Comparison of stress data with load of 8.85 kg before and after preprocessing
对比图8 和图9 可知,对20组不同负载下的应力时序数据进行处理后,数据显著精简。该处理方法在保证训练效率的同时不会对运算精度产生影响,应力数据可直接应用于后续物理模型的构建和网络模型的训练,这为物理模型的双参数应力转换奠定了基础。
3.2 数据模型参数确定
将采集到的各参数时序数据作为模型输入特征,对应参数的应力数据作为目标输出标签,构建用于BiLSTM模型训练的样本数据集。以8∶2的比例将其划分为训练集和测试集,前者用于模型参数的学习与优化,后者用于评估模型在未知数据上的泛化能力。同时,采用归一化方法消除量纲差异,提升训练效率。
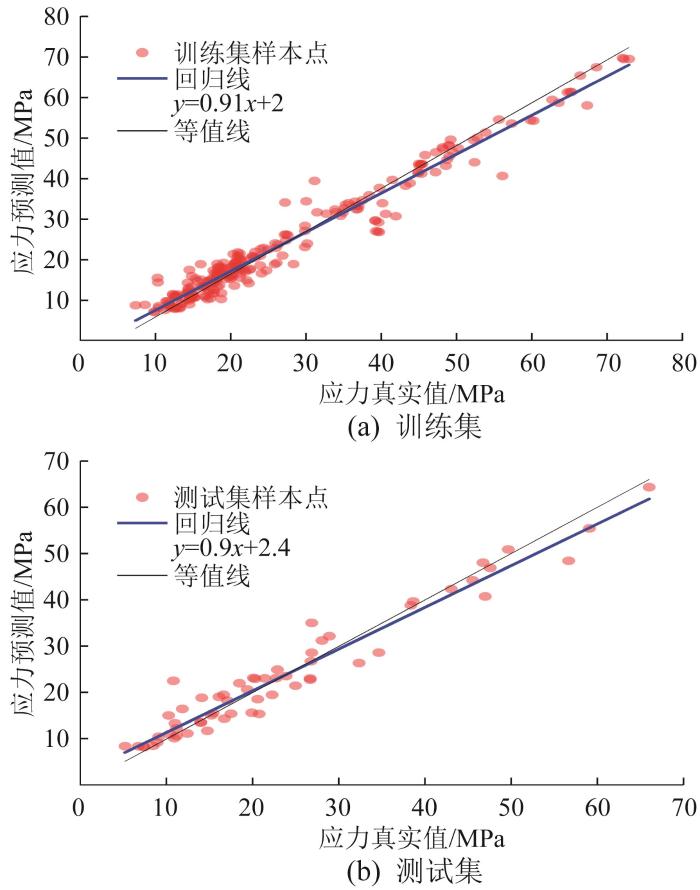
将BiLSTM模型隐藏层的维度设置为64,添加dropout层防止模型过拟合,将丢弃率设置为0.2,添加Relu激活函数层以及全连接层,并将regression层作为输出层;设置模型的训练周期为100轮,每轮迭代次数为203,用Adam梯度下降算法动态调整学习率,初始学习率为0.01,经80轮训练后学习率下降为0.001;每轮训练之后,打乱整个训练集,当达到最大训练轮次后,输出最终的训练结果进行反归一化操作,并将结果与对应的目标值进行比较,结果如图11 (a)所示。在此基础上对测试集进行验证,达到最大轮次后输出结果并进行比较,结果如图11 (b)所示。BiLSTM模型的评价指标(平均绝对误差E MA 、均方根误差E RMS 、拟合优度R 2 )值如表2 所示。
图11
图11
BiLSTM 模型相关测试结果
Fig.11
Test results related to BiLSTM model
由图11 可知,大部分样本点贴近回归线,表明模型对数据具有较强的拟合能力,模型回归线的斜率与等值线接近,截距较小,预测偏差整体可控,且在0~30 MPa低应力区域样本点密集,在高应力区域样本点稀疏,符合实验结果。结合表2 可知,BiLSTM模型在训练集和测试集中的表现高度一致,即E MA 、E RMS 均较接近,预测偏差稳定,模型的泛化能力较好。
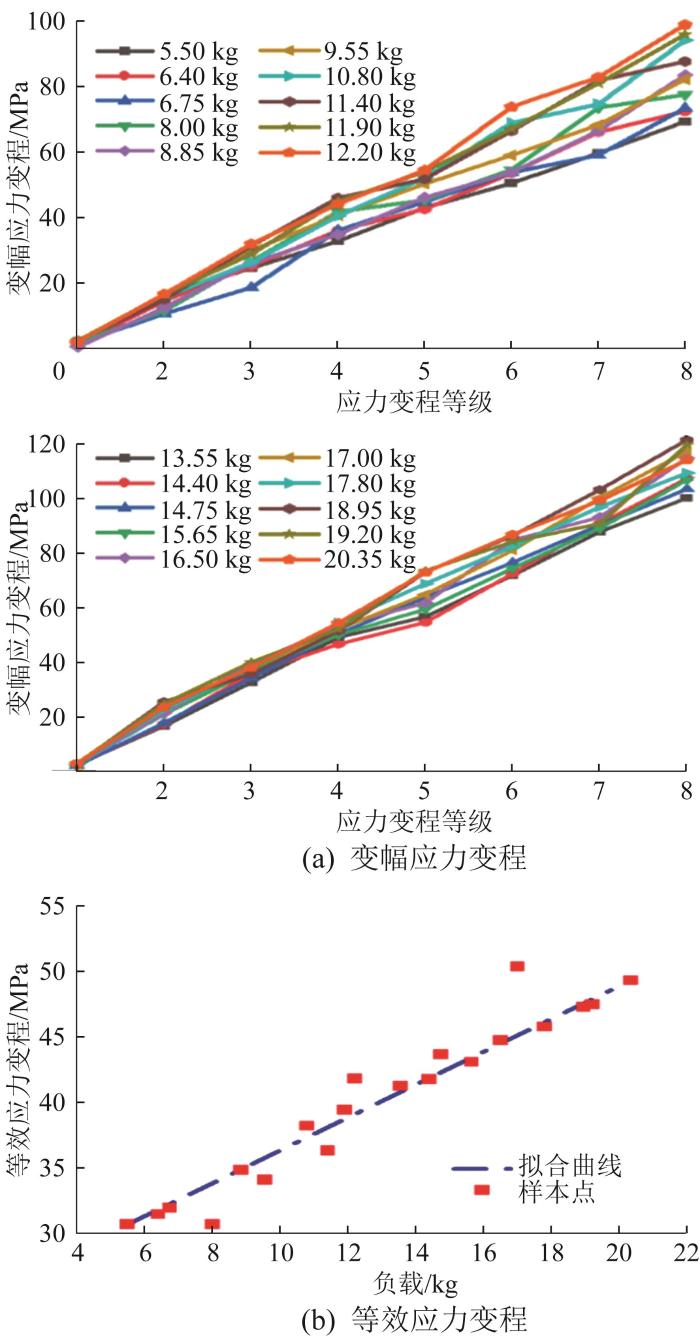
将数据模型中的应力数据带入物理模型,采用雨流计数法提取到双参数应力谱,利用式(3)将不同负载下的双参数应力谱转换成变幅载荷下的应力变程,结果如图12 (a)所示。在此基础上,结合式(4),取材料常数j =2,得出不同负载下的等效应力变程,如图12 (b)所示。
图12
图12
应力变程
Fig.12
Stress range
3.3 网络模型参数配置
将数据模型的动应力数据经对数转换后得到动应力数据的对数值,并带入物理神经网络,作为物理神经网络模型的输入,并将疲劳寿命作为网络模型的输出。
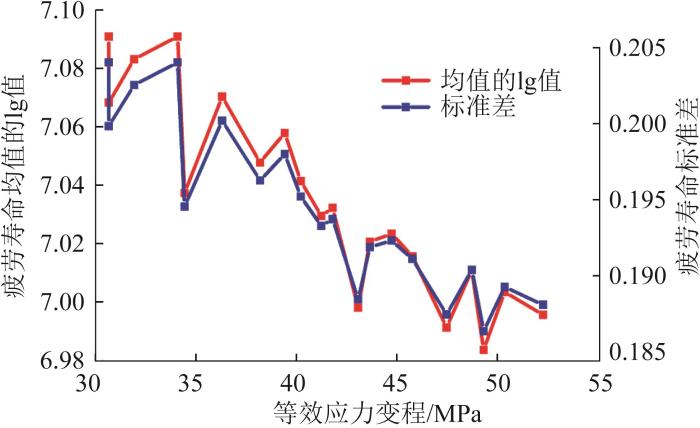
物理神经网络初始参数的设置:训练数量为1 040轮,学习率为1×10-3 ,优化器设置为Adam优化器,输入维度为1,隐藏层神经元个数为128,物理项惩罚因子为2 000,梯度衰减率为0.9。将tanh x 和leaky x 作为物理神经网络的激活函数,第1个激活函数层选用tanh x 函数,第2个激活函数层选用leaky x 函数。在训练过程中,将对数状态下的应力数据转化为dlarray数据格式,带入全连接层,计算相应目标的统计量参数(疲劳寿命均值的lg值、疲劳寿命标准差),结果如图13 所示。
图13
图13
目标统计量参数
Fig.13
Target statistic parameters
由图13 可知,随着等效应力变程的增大,疲劳寿命均值呈现振荡式下降趋势,同时寿命标准差亦呈振荡式递减趋势。标准差的减小直观反映了疲劳寿命数据存在异方差性,意味着在较高应力水平下疲劳寿命数据的离散程度降低。由此,表明所构建的模型描述的疲劳寿命与应力变程的关系符合物理实际,模型具备良好的物理一致性。
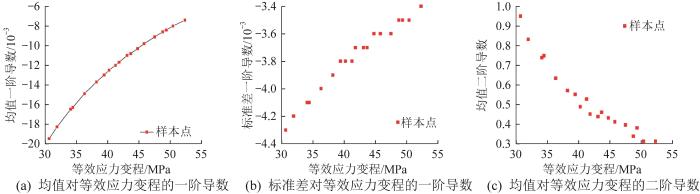
在网络模型的训练过程中,计算疲劳寿命均值对等效应力变程的一阶导数和二阶导数,以及寿命标准差对等效应力变程的一阶导数,结果如图14 所示。
图14
图14
疲劳寿命均值和标准差对等效应力变程的导数
Fig.14
Derivative of mean and standard deviation of fatigue life to equivalent stress range
由图14 (a)和图14 (b)可知:疲劳寿命均值和标准差的一阶导数均为负值,且寿命均值和标准差有单调递减的趋势;随着应力水平的增大,寿命均值和标准差的一阶导数缓慢趋向于0。由图14 (c)可知:寿命均值的二阶导数为正,符合应力—寿命曲线的变化趋势,具备物理一致性。
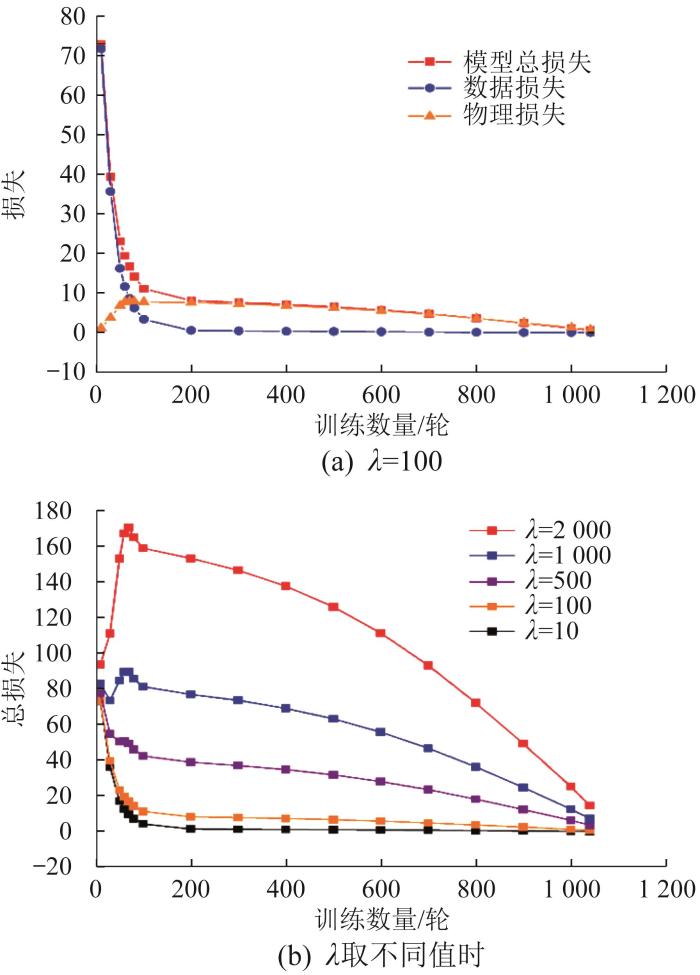
在模型训练过程中,网络模型的数据项损失随着训练的进行而迅速收敛,如图15 (a)所示。模型总损失则因惩罚因子的不同而不同,模型收敛速度存在差异,如图15 (b)所示。
图15
图15
PINN 损失
Fig.15
Loss of PINN
由图15 (a)可知:当模型训练达到100轮时,模型数据项损失已经达到阈值;在训练达到200轮之后,模型整体损失主要为物理信息损失,表明物理信息损失在模型训练后期起到主导作用。由图15 (b)可知:较大的惩罚因子使模型在训练初期能更好地表示模型违反物理定律的程度;过大的惩罚因子会导致预测结果的拟合程度降低,减弱模型的预测性能;较小的惩罚因子在模型训练后期无法修正模型的物理一致性。
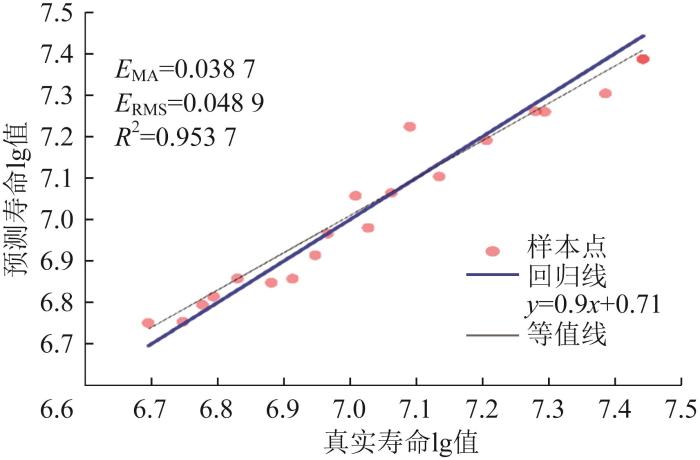
因此,选择λ 图16 所示。
图16
图16
预测寿命与真实寿命的对比
Fig.16
Comparison between predicted life and actual life
由图16 可知,模型的样本点整体在回归线附近,个别点离回归线较远,但对整体拟合精度的影响不大。在模型评价指标中,E MA =0.038 7,E RMS =0.048 9,R 2
3.4 结果分析与讨论
将PINN、卷积神经网络(convolutional neural network, CNN)模型、支持向量回归(support vector regression, SVR)模型、K近邻(K-nearest neighbors, KNN)模型进行比较,来验证本文所提出模型的科学性和适用性。各模型参数设置如下。CNN模型参数:Covn2D池化层的神经元个数为128,Covn2D池化层的神经元个数为64,全连接层的神经元个数为128。SVR模型参数:核函数类型为Gaussian,RBF核参数为0.1,惩罚参数为0.1,其他参数采用默认值。KNN模型参数:K =5,距离度量方式为Euclidean,其他参数采用默认值。各模型预测的疲劳寿命如图17 所示,其评价指标如表3 所示。
图17
图17
各模型预测的疲劳寿命
Fig.17
Fatigue life derived from each model
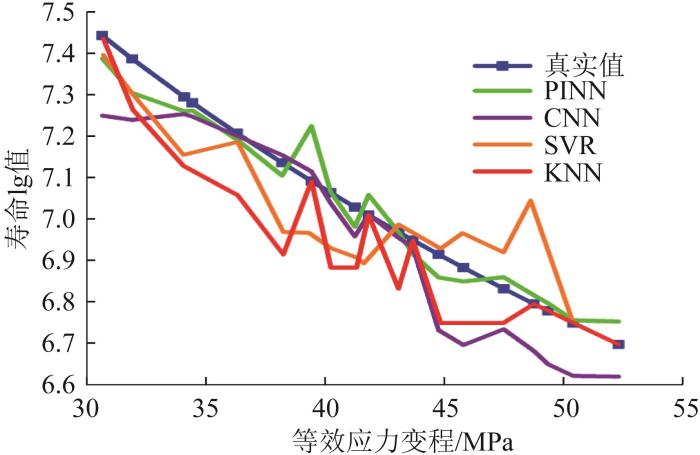
由图17 可知:整体来看,疲劳寿命的预测值随着应力水平的增大而减小,符合物理规律;相比于PINN,在等效应力变程较大时,CNN模型的预测精度较低,而SVR、KNN模型在预测时波动性较大,鲁棒性较低;PINN预测的寿命值在真实值附近变化,精度较高,拟合度较强。由表3 可知,相比于CNN、SVR、KNN,PINN的E MA 分别减少了54.4%、61.3%和43.7%,E RMS 分别减少了55%、65.8%和35.4%,同时R 2
CNN、SVR、KNN模型均为纯数据驱动,依赖数据分布,缺乏针对物理规律的主动约束,因此在多因素耦合的寿命预测中易失效。PINN通过“数据+物理”的双约束,突破了纯数据驱动模型的局限性,在数据稀缺、物理机制明确的场景中表现出独特的优势。
4 结 论
1)本文提出了一种基于PINN的桥式起重机疲劳寿命预测方法。将起重机疲劳寿命机理模型与神经网络融合,实现了对桥式起重机疲劳寿命的精确预测,有效弥补了传统方法对数据依赖性强、物理约束不足的缺陷。通过物理信息与数据的双重驱动,确保了疲劳寿命预测结果的精准度与可靠性,为起重机疲劳寿命预测提供了新的技术路径与研究思路。
2)提出的PINN充分结合了BiLSTM的时序数据分析能力和物理信息的约束,提升了模型预测结果对物理逻辑的可解释性,并增强了模型的泛化能力,使模型预测结果更可靠。
3)以DQ40 kg-1.8 m-1.3 m小型通用桥式起重机为实验对象,采用所提出的疲劳寿命预测方法进行预测实验。根据预测值和真实值,得到E MA =0.038 7,E RMS =0.048 9,R 2
4)当前,PINN的应用在理论研究上发展迅速,但是在实际工程尤其在桥式起重机中的应用仍属起步阶段。并且,起重机的工况复杂性会导致物理方程本身的不确定性,导致物理约束失去意义,模型性能可能会下降。如何高效地将物理模型准确移植到具体场景中,使其适用于实际工况,需今后作进一步的研究。
参考文献
View Option
[1]
高沛 桥式起重机预测性维护系统关键技术研究
[D]. 太原 : 中北大学 , 2023 .
[本文引用: 1]
GAO P Bridge crane predictive maintenance system key technology research
[D]. Taiyuan : North University of China , 2023 .
[本文引用: 1]
[2]
[本文引用: 1]
ZHANG X L CHEN X F LI B et al Review of life prediction for mechanical major equipments
[J]. Journal of Mechanical Engineering , 2011 , 47 (11 ): 100 -116 .
DOI:10.3901/jme.2011.11.100
[本文引用: 1]
[3]
陈琳 , 秦义校 , 高梁 , 等 基于刚柔耦合动力学的铸造起重机结构疲劳寿命研究
[J]. 起重运输机械 , 2025 (5 ): 29 -36 .
[本文引用: 1]
CHEN L QIN Y X GAO L et al Research on fatigue life of casting crane structure based on rigid-flexible coupling dynamics
[J]. Hoisting and Conveying Machinery , 2025 (5 ): 29 -36 .
[本文引用: 1]
[4]
李现春 , 胡晓兵 , 李毅 , 等 基于nCode Design-Life的重型起重设备疲劳寿命预测研究
[J]. 机械 , 2017 , 44 (8 ): 1 -6 .
LI X C HU X B LI Y et al Research on fatigue life prediction of heavy lifting equipment based on nCode Design-Life
[J]. Machinery , 2017 , 44 (8 ): 1 -6 .
[5]
闫梦煜 , 魏国前 , 段若尘 考虑非线性累积损伤的铸造起重机疲劳性能分析
[J]. 机械强度 , 2024 , 46 (4 ): 977 -983 .
[本文引用: 2]
YAN M Y WEI G Q DUAN R C Fatigue performance analysis of casting cranes considering non-linear cumulative damage
[J]. Journal of Mechanical Strength , 2024 , 46 (4 ): 977 -983 .
[本文引用: 2]
[6]
唐涛 , 张飞庆 , 佘玲娟 基于名义应力法的高强钢泵车臂架疲劳寿命研究
[J]. 工程机械 , 2016 , 47 (3 ): 12 -17 , 6 .
[本文引用: 1]
TANG T ZHANG F Q SHE L J A study on fatigue life of high-strength steel pump truck boom frames based on nominal stress process
[J]. Construction Machinery and Equipment , 2016 , 47 (3 ): 12 -17 , 6 .
[本文引用: 1]
[7]
徐格宁 , 张永才 , 张魏唯 铸造起重机金属结构疲劳裂纹扩展分析
[J]. 机械设计与制造 , 2020 (3 ): 13 -17 .
[本文引用: 1]
XU G N ZHANG Y C ZHANG W W Fatigue crack growth analysis of metal structure of casting crane
[J]. Machinery Design & Manufacture , 2020 (3 ): 13 -17 .
[本文引用: 1]
[8]
LEHNER P KREJSA M PAŘENICA P et al Fatigue damage analysis of a riveted steel overhead crane support truss
[J]. International Journal of Fatigue , 2019 : 105190 .
[本文引用: 1]
[9]
G Á , PALMA E DE PAULA R Crane girder fatigue life determination using SN and LEFM methods
[J]. Engineering Failure Analysis , 2017 , 79 : 812 -819 .
[10]
XU B WU Q Stress fatigue crack propagation analysis of crane structure based on acoustic emission
[J]. Engineering Failure Analysis , 2020 , 109 : 104206 .
[本文引用: 1]
[11]
王大荣 , 任京 , 宋奎 , 等 岸桥前主梁安全监测及蠕变长短期记忆神经网络预测
[J]. 湘潭大学学报(自然科学版) , 2025 , 47 (4 ): 44 -52 .
[本文引用: 1]
WANG D R REN J SONG K et al Safety monitoring of front girder of quayside container crane and creep prediction by long short-term memory neural network
[J]. Journal of Xiangtan University (Natural Science Edition) , 2025 , 47 (4 ): 44 -52 .
[本文引用: 1]
[12]
[本文引用: 1]
FAN X N XU G N WANG A H Evaluation method of remaining fatigue life for crane based on the acquisition of the equivalent load spectrum by the artificial neural network
[J]. Journal of Mechanical Engineering , 2011 , 47 (20 ): 69 -74 .
DOI:10.3901/jme.2011.20.069
[本文引用: 1]
[13]
戚其松 , 李成刚 , 董青 , 等 起重机生命周期载荷谱预测及基于疲劳寿命的结构优化设计
[J]. 工程设计学报 , 2023 , 30 (3 ): 380 -389 .
[本文引用: 2]
QI Q S LI C G DONG Q et al Prediction of load spectrum for crane life cycle and structural optimal design based on fatigue life
[J]. Chinese Journal of Engineering Design , 2023 , 30 (3 ): 380 -389 .
[本文引用: 2]
[14]
[本文引用: 1]
LEI Y G JIA F ZHOU X et al A deep learning-based method for machinery health monitoring with big data
[J]. Journal of Mechanical Engineering , 2015 , 51 (21 ): 49 -56 .
DOI:10.3901/jme.2015.21.049
[本文引用: 1]
[15]
刘丽 , 裴行智 , 雷雪梅 基于时间卷积注意力网络的剩余寿命预测方法
[J]. 计算机集成制造系统 , 2022 , 28 (8 ): 2375 -2386 .
[本文引用: 1]
LIU L PEI X Z LEI X M Temporal convolutional attention network for remaining useful life estimation
[J]. Computer Integrated Manufacturing Systems , 2022 , 28 (8 ): 2375 -2386 .
[本文引用: 1]
[16]
付玲 , 佘玲娟 , 颜镀镭 , 等 基于内嵌物理信息与注意力机制Bi LSTM神经网络的臂架系统疲劳损伤预测模型
[J]. 机械工程学报 , 2024 , 60 (13 ): 205 -215 . doi:10.3901/jme.2024.13.205
[本文引用: 1]
FU L SHE L J YAN D L et al Fatigue damage prediction framework of the boom system based on embedded physical information and attention mechanism BiLSTM neural network
[J]. Journal of Mechanical Engineering , 2024 , 60 (13 ): 205 -215 .
DOI:10.3901/jme.2024.13.205
[本文引用: 1]
[17]
文井辉 , 伍荣森 , 李帅永 , 等 基于DRSN和优化BiLSTM的轴承剩余寿命预测方法
[J]. 计算机集成制造系统 , 2024 , 30 (5 ): 1877 -1888 .
[本文引用: 1]
WEN J H WU R S LI S Y et al Bearing residual life prediction method based on DRSN and optimized BiLSTM
[J]. Computer Integrated Manufacturing Systems , 2024 , 30 (5 ): 1877 -1888 .
[本文引用: 1]
[18]
ZHOU T T JIANG S HAN T et al A physically consistent framework for fatigue life prediction using probabilistic physics-informed neural network
[J]. International Journal of Fatigue , 2023 , 166 : 107234 .
[本文引用: 1]
[19]
孙宝晗 , 颜廷俊 基于P-S-N曲线的岸边起重机疲劳寿命预估的研究
[J]. 中国水运 , 2024 (19 ): 134 -136 .
[本文引用: 1]
SUN B H YAN T J Study on fatigue life prediction of quayside crane based on P-S-N curve
[J]. China Water Transport , 2024 (19 ): 134 -136 .
[本文引用: 1]
[20]
张剑 桥架型起重机疲劳寿命预测和结构可靠性分析
[D]. 南京 : 南京航空航天大学 , 2022 .
[本文引用: 1]
ZHANG J Fatigue life prediction and structural reliability analysis of bridge crane
[D]. Nanjing : Nanjing University of Aeronautics and Astronautics , 2022 .
[本文引用: 1]
[21]
张颛利 , 孙兴悦 , 陈旭 基于物理信息神经网络的金属多轴疲劳寿命预测进展
[J]. 机械强度 , 2025 , 47 (2 ): 44 -52 .
[本文引用: 1]
ZHANG Z L SUN X Y CHEN X Development in metal multiaxial fatigue life prediction based on physics-informed neural network
[J]. Journal of Mechanical Strength , 2025 , 47 (2 ): 44 -52 .
[本文引用: 1]
[22]
WEI W CHEN S J CHEN C et al HEN: a novel hybrid explainable neural network based framework for robust network intrusion detection
[J]. Science China Information Sciences , 2024 , 67 (7 ): 170304 .
[本文引用: 1]
[23]
WEN J DENG Y Q PENG W L et al Linguistic steganalysis via fusing multi-granularity attentional text features
[J]. Chinese Journal of Electronics , 2023 , 32 (1 ): 76 -84 .
[本文引用: 2]
[24]
中国机械工业联合会 起重机械安全评估规范 通用要求 : [S]. 北京 : 中国标准出版社 , 2022 .
[本文引用: 1]
China Machinery Industry Federation Safety assessment rules for lifting appliances—General requirements : [S]. Beijing : Standards Press of China , 2022 .
[本文引用: 1]
[25]
LI J H LI B Solving forward and inverse problems of the nonlinear Schrödinger equation with the generalized- symmetric Scarf-II potential via PINN deep learning
[J]. Communications in Theoretical Physics , 2021 , 73 (12 ): 125001 .
[本文引用: 1]
[26]
乌云图 , 李娜 , 蔡晋辉 岸边集装箱桥式起重机疲劳寿命预测
[J]. 中国测试 , 2018 , 44 (4 ): 14 -18 .
[本文引用: 1]
WU Y T LI N CAI J H The fatigue life prediction of quayside container bridge crane
[J]. China Measurement & Test , 2018 , 44 (4 ): 14 -18 .
[本文引用: 1]
桥式起重机预测性维护系统关键技术研究
1
2023
... 桥式起重机在工业生产中主要承担物料吊运、设备安放等重要任务.由于长期承受变幅载荷作用,其桥架结构易出现裂纹萌生与扩展现象,进而导致金属结构疲劳破坏[1 -2 ] .因此,开展桥式起重机疲劳寿命预测研究,对保障设备稳定运行、降低事故风险具有重要意义. ...
桥式起重机预测性维护系统关键技术研究
1
2023
... 桥式起重机在工业生产中主要承担物料吊运、设备安放等重要任务.由于长期承受变幅载荷作用,其桥架结构易出现裂纹萌生与扩展现象,进而导致金属结构疲劳破坏[1 -2 ] .因此,开展桥式起重机疲劳寿命预测研究,对保障设备稳定运行、降低事故风险具有重要意义. ...
机械重大装备寿命预测综述
1
2011
... 桥式起重机在工业生产中主要承担物料吊运、设备安放等重要任务.由于长期承受变幅载荷作用,其桥架结构易出现裂纹萌生与扩展现象,进而导致金属结构疲劳破坏[1 -2 ] .因此,开展桥式起重机疲劳寿命预测研究,对保障设备稳定运行、降低事故风险具有重要意义. ...
机械重大装备寿命预测综述
1
2011
... 桥式起重机在工业生产中主要承担物料吊运、设备安放等重要任务.由于长期承受变幅载荷作用,其桥架结构易出现裂纹萌生与扩展现象,进而导致金属结构疲劳破坏[1 -2 ] .因此,开展桥式起重机疲劳寿命预测研究,对保障设备稳定运行、降低事故风险具有重要意义. ...
基于刚柔耦合动力学的铸造起重机结构疲劳寿命研究
1
2025
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
基于刚柔耦合动力学的铸造起重机结构疲劳寿命研究
1
2025
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
基于nCode Design-Life的重型起重设备疲劳寿命预测研究
0
2017
基于nCode Design-Life的重型起重设备疲劳寿命预测研究
0
2017
考虑非线性累积损伤的铸造起重机疲劳性能分析
2
2024
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
... Acquisition range of each parameter
Table 1 参数 采集范围 参数 采集范围 负载/kg [5 , 23 ] 大车到主梁端部的距离/mm [100, 1 300] 应变/µm [0, 300] 小车到主梁端部的距离/mm [100, 1 500] 起升高度/mm [0, 1 000] 起升拉力(含吊具)/N [13 , 206]
在不同负载下采集各参数.以8.85 kg负载为例,9个工作循环周期内参数采集结果如图7 所示.由图可知:在货物起吊过程中起升高度呈快速上升趋势,起升拉力出现振荡,其归因于起升冲击效应;当货物起吊至指定高度后,大车和小车开始向卸货区移动,此时起升高度不变,拉力随着大小车的移动出现变化,其归因于大小车运行冲击效应;在货物卸载阶段,吊具高度开始下降,拉力随着货物卸载而骤减.整个工作过程呈现周期性变化. ...
考虑非线性累积损伤的铸造起重机疲劳性能分析
2
2024
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
... Acquisition range of each parameter
Table 1 参数 采集范围 参数 采集范围 负载/kg [5 , 23 ] 大车到主梁端部的距离/mm [100, 1 300] 应变/µm [0, 300] 小车到主梁端部的距离/mm [100, 1 500] 起升高度/mm [0, 1 000] 起升拉力(含吊具)/N [13 , 206]
在不同负载下采集各参数.以8.85 kg负载为例,9个工作循环周期内参数采集结果如图7 所示.由图可知:在货物起吊过程中起升高度呈快速上升趋势,起升拉力出现振荡,其归因于起升冲击效应;当货物起吊至指定高度后,大车和小车开始向卸货区移动,此时起升高度不变,拉力随着大小车的移动出现变化,其归因于大小车运行冲击效应;在货物卸载阶段,吊具高度开始下降,拉力随着货物卸载而骤减.整个工作过程呈现周期性变化. ...
基于名义应力法的高强钢泵车臂架疲劳寿命研究
1
2016
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
基于名义应力法的高强钢泵车臂架疲劳寿命研究
1
2016
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
铸造起重机金属结构疲劳裂纹扩展分析
1
2020
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
铸造起重机金属结构疲劳裂纹扩展分析
1
2020
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
Fatigue damage analysis of a riveted steel overhead crane support truss
1
2019
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
Crane girder fatigue life determination using SN and LEFM methods
0
2017
Stress fatigue crack propagation analysis of crane structure based on acoustic emission
1
2020
... 目前,在基于机理模型的起重机疲劳寿命预测方面,不少学者已进行了研究.陈琳等 [3 -5 ] 针对铸造起重机、门式起重机等设备的金属结构疲劳问题,提出了基于刚柔耦合动力学、有限元静力学及实际载荷谱特性的分析方法,研究了起重机结构损伤和疲劳寿命特性.唐涛等[6 -7 ] 获取了材料及焊接接头的应力—寿命曲线,采用名义应力法,开展疲劳裂纹扩展分析,对起重机结构疲劳寿命进行预测,对其剩余寿命进行了评估.Lehner等[8 -10 ] 利用Monte Carlo方法生成时变载荷序列,结合有限元仿真技术,对在役钢结构、铸造机轨道横梁、龙门吊箱型梁等进行了疲劳寿命预测. ...
岸桥前主梁安全监测及蠕变长短期记忆神经网络预测
1
2025
... 在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测.范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命.戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估. ...
岸桥前主梁安全监测及蠕变长短期记忆神经网络预测
1
2025
... 在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测.范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命.戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估. ...
基于人工神经网络获取起重机当量载荷谱的疲劳剩余寿命估算方法
1
2011
... 在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测.范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命.戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估. ...
基于人工神经网络获取起重机当量载荷谱的疲劳剩余寿命估算方法
1
2011
... 在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测.范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命.戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估. ...
起重机生命周期载荷谱预测及基于疲劳寿命的结构优化设计
2
2023
... 在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测.范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命.戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估. ...
... Acquisition range of each parameter
Table 1 参数 采集范围 参数 采集范围 负载/kg [5 , 23 ] 大车到主梁端部的距离/mm [100, 1 300] 应变/µm [0, 300] 小车到主梁端部的距离/mm [100, 1 500] 起升高度/mm [0, 1 000] 起升拉力(含吊具)/N [13 , 206]
在不同负载下采集各参数.以8.85 kg负载为例,9个工作循环周期内参数采集结果如图7 所示.由图可知:在货物起吊过程中起升高度呈快速上升趋势,起升拉力出现振荡,其归因于起升冲击效应;当货物起吊至指定高度后,大车和小车开始向卸货区移动,此时起升高度不变,拉力随着大小车的移动出现变化,其归因于大小车运行冲击效应;在货物卸载阶段,吊具高度开始下降,拉力随着货物卸载而骤减.整个工作过程呈现周期性变化. ...
起重机生命周期载荷谱预测及基于疲劳寿命的结构优化设计
2
2023
... 在基于数据驱动的起重机疲劳寿命预测方法方面,王大荣等[11 ] 基于岸边集装箱桥式起重机关键部位的变形实测数据与有限元仿真数据,结合长短期记忆神经网络,对起重机前主梁的蠕变进行了预测.范小宁等[12 ] 针对起重机使用工况的不确定性和高度随机性,运用人工神经网络技术获取了其疲劳剩余寿命.戚其松等[13 ] 利用神经网络准确预测了起重机服役期间的载荷谱特征,并结合断裂力学理论与结构承载特性分析方法,对起重机关键部位的疲劳寿命进行了评估. ...
... Acquisition range of each parameter
Table 1 参数 采集范围 参数 采集范围 负载/kg [5 , 23 ] 大车到主梁端部的距离/mm [100, 1 300] 应变/µm [0, 300] 小车到主梁端部的距离/mm [100, 1 500] 起升高度/mm [0, 1 000] 起升拉力(含吊具)/N [13 , 206]
在不同负载下采集各参数.以8.85 kg负载为例,9个工作循环周期内参数采集结果如图7 所示.由图可知:在货物起吊过程中起升高度呈快速上升趋势,起升拉力出现振荡,其归因于起升冲击效应;当货物起吊至指定高度后,大车和小车开始向卸货区移动,此时起升高度不变,拉力随着大小车的移动出现变化,其归因于大小车运行冲击效应;在货物卸载阶段,吊具高度开始下降,拉力随着货物卸载而骤减.整个工作过程呈现周期性变化. ...
基于深度学习理论的机械装备大数据健康监测方法
1
2015
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于深度学习理论的机械装备大数据健康监测方法
1
2015
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于时间卷积注意力网络的剩余寿命预测方法
1
2022
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于时间卷积注意力网络的剩余寿命预测方法
1
2022
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于内嵌物理信息与注意力机制Bi LSTM神经网络的臂架系统疲劳损伤预测模型
1
2024
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于内嵌物理信息与注意力机制Bi LSTM神经网络的臂架系统疲劳损伤预测模型
1
2024
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于DRSN和优化BiLSTM的轴承剩余寿命预测方法
1
2024
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于DRSN和优化BiLSTM的轴承剩余寿命预测方法
1
2024
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
A physically consistent framework for fatigue life prediction using probabilistic physics-informed neural network
1
2023
... 随着数据规模和计算机算力的爆炸式增长,以深度学习为代表的机器学习技术在众多工程领域得到应用,物理信息与神经网络的融合研究也实现了重要突破.雷亚国等[14 -15 ] 针对机械大数据的特性,充分发挥深度学习在特征提取中的优势,将时间卷积注意力网络应用在机械设备健康监测领域和C-MAPSS(commercial modular aero-propulsion system simulation,商用模块化航空推进系统仿真)数据集.付玲等[16 ] 提出了一种基于物理信息嵌入与注意力机制的双向长短期记忆(bi-directional long short-term memory, BiLSTM)网络模型,用于臂架系统疲劳损伤预测.文井辉等[17 ] 提出了基于深度残差收缩网络(deep residual shrinkage network, DRSN)和优化BiLSTM的轴承剩余寿命预测方法.Zhou等[18 ] 提出了一种物理一致性疲劳寿命预测框架,基于概率物理信息神经网络并融合疲劳损伤机制,实现了对多种金属材料参数化疲劳寿命分布的预测.然而,在起重机疲劳寿命预测中机理模型与神经网络融合方面,仍存在进一步探索的空间. ...
基于P-S-N曲线的岸边起重机疲劳寿命预估的研究
1
2024
... 桥式起重机在长期服役过程中承受着多种多样的随机载荷,导致其桥架结构裂纹萌生处出现疲劳裂纹扩展直至发生疲劳断裂[19 ] ,从而引发重大的安全事故.为了确保桥式起重机在设计预期寿命内安全服役,亟须对其桥架结构关键部位的疲劳寿命进行准确的预测.目前,基于传统力学的疲劳寿命预测方法包括应力寿命法、应变寿命法和断裂力学法等[20 ] .传统的预测方法存在计算量大、求解过程繁琐等问题.随着计算机运行能力的提升,以机器学习、深度学习为代表的人工智能技术在起重机疲劳寿命预测中得到广泛应用,诸如随机森林模型、神经网络模型等.人工智能技术具备求解计算量大和理论建模难的复杂问题的能力,对起重机疲劳寿命的预测具有较强的能力. ...
基于P-S-N曲线的岸边起重机疲劳寿命预估的研究
1
2024
... 桥式起重机在长期服役过程中承受着多种多样的随机载荷,导致其桥架结构裂纹萌生处出现疲劳裂纹扩展直至发生疲劳断裂[19 ] ,从而引发重大的安全事故.为了确保桥式起重机在设计预期寿命内安全服役,亟须对其桥架结构关键部位的疲劳寿命进行准确的预测.目前,基于传统力学的疲劳寿命预测方法包括应力寿命法、应变寿命法和断裂力学法等[20 ] .传统的预测方法存在计算量大、求解过程繁琐等问题.随着计算机运行能力的提升,以机器学习、深度学习为代表的人工智能技术在起重机疲劳寿命预测中得到广泛应用,诸如随机森林模型、神经网络模型等.人工智能技术具备求解计算量大和理论建模难的复杂问题的能力,对起重机疲劳寿命的预测具有较强的能力. ...
桥架型起重机疲劳寿命预测和结构可靠性分析
1
2022
... 桥式起重机在长期服役过程中承受着多种多样的随机载荷,导致其桥架结构裂纹萌生处出现疲劳裂纹扩展直至发生疲劳断裂[19 ] ,从而引发重大的安全事故.为了确保桥式起重机在设计预期寿命内安全服役,亟须对其桥架结构关键部位的疲劳寿命进行准确的预测.目前,基于传统力学的疲劳寿命预测方法包括应力寿命法、应变寿命法和断裂力学法等[20 ] .传统的预测方法存在计算量大、求解过程繁琐等问题.随着计算机运行能力的提升,以机器学习、深度学习为代表的人工智能技术在起重机疲劳寿命预测中得到广泛应用,诸如随机森林模型、神经网络模型等.人工智能技术具备求解计算量大和理论建模难的复杂问题的能力,对起重机疲劳寿命的预测具有较强的能力. ...
桥架型起重机疲劳寿命预测和结构可靠性分析
1
2022
... 桥式起重机在长期服役过程中承受着多种多样的随机载荷,导致其桥架结构裂纹萌生处出现疲劳裂纹扩展直至发生疲劳断裂[19 ] ,从而引发重大的安全事故.为了确保桥式起重机在设计预期寿命内安全服役,亟须对其桥架结构关键部位的疲劳寿命进行准确的预测.目前,基于传统力学的疲劳寿命预测方法包括应力寿命法、应变寿命法和断裂力学法等[20 ] .传统的预测方法存在计算量大、求解过程繁琐等问题.随着计算机运行能力的提升,以机器学习、深度学习为代表的人工智能技术在起重机疲劳寿命预测中得到广泛应用,诸如随机森林模型、神经网络模型等.人工智能技术具备求解计算量大和理论建模难的复杂问题的能力,对起重机疲劳寿命的预测具有较强的能力. ...
基于物理信息神经网络的金属多轴疲劳寿命预测进展
1
2025
... 随着PINN与深度残差神经网络的提出[21 ] ,神经网络在引入物理规律方面有了很大的进展.PINN是一类将物理先验信息嵌入深度学习框架的特殊人工神经网络,其结构如图1 (b)所示.PINN将满足物理方程(如微分方程或其他约束项)的残差项作为损失函数,通过网络计算物理量梯度(如σ/ x、 s/ x 、2 σ/ x 2 等),将物理损失L p L d
基于物理信息神经网络的金属多轴疲劳寿命预测进展
1
2025
... 随着PINN与深度残差神经网络的提出[21 ] ,神经网络在引入物理规律方面有了很大的进展.PINN是一类将物理先验信息嵌入深度学习框架的特殊人工神经网络,其结构如图1 (b)所示.PINN将满足物理方程(如微分方程或其他约束项)的残差项作为损失函数,通过网络计算物理量梯度(如σ/ x、 s/ x 、2 σ/ x 2 等),将物理损失L p L d
HEN: a novel hybrid explainable neural network based framework for robust network intrusion detection
1
2024
... 由于传感器采集的数据较少,且需要对数据进行清洗,得到的数据不足以满足神经网络训练的需要.在模型训练过程中,需动态地对输入数据进行随机变换,并用生成对抗网络生成与原始数据分布相似的新样本.加入了新样本的模型的精度不高,故需要将数据增强,并利用BiLSTM网络对数据进行训练.其中,LSTM网络是一种常见的循环神经网络模型,用来处理序列数据,具有记忆长短期信息的能力[22 ] .LSTM网络通过引入门控机制解决梯度消失或梯度爆炸的问题,可有效处理长期依赖和短期记忆的问题.假定桥式起重机相同类型的传感器有n 个,则在某一时刻t ,传感器采集到的数据x t = x 1 , t x 2 , t ⋯ x n , t x t ∈ R n × 1
Linguistic steganalysis via fusing multi-granularity attentional text features
2
2023
... BiLSTM网络结合了2个方向的LSTM层,通过前后向时序数据的输入,更好地找出序列中的潜在联系,弥补了单一LSTM网络仅考虑前向时序数据的不足[23 ] .BiLSTM网络模型的结构如图3 所示.将传输的时序数据x = [ x 1 x 2 ⋯ x t ] c t -1 ,并由当前时刻的LSTM单元和前一时刻的LSTM单元给出相应的隐藏状态信息 h t -1 ,其输出由最后时刻的输入及前一时刻的隐藏状态决定;反向LSTM层对输入序列的未来数据信息进行学习,输出与前向LSTM层一致;两者输出特征进行堆叠,形成最终的输出y = [ y 1 y 2 ⋯ y t ] . 可表示为: ...
... Acquisition range of each parameter
Table 1 参数 采集范围 参数 采集范围 负载/kg [5 , 23 ] 大车到主梁端部的距离/mm [100, 1 300] 应变/µm [0, 300] 小车到主梁端部的距离/mm [100, 1 500] 起升高度/mm [0, 1 000] 起升拉力(含吊具)/N [13 , 206]
在不同负载下采集各参数.以8.85 kg负载为例,9个工作循环周期内参数采集结果如图7 所示.由图可知:在货物起吊过程中起升高度呈快速上升趋势,起升拉力出现振荡,其归因于起升冲击效应;当货物起吊至指定高度后,大车和小车开始向卸货区移动,此时起升高度不变,拉力随着大小车的移动出现变化,其归因于大小车运行冲击效应;在货物卸载阶段,吊具高度开始下降,拉力随着货物卸载而骤减.整个工作过程呈现周期性变化. ...
1
2022
... specific-use="noneIndent">式中:N f 为疲劳裂纹扩展寿命;a 0 为初始裂纹长度;a f 为临界裂纹长度;f g 为放大系数,其取值见GB/T 41510—2022《起重机械安全评估规范 通用要求》[24 ] ;K p 为应力谱系数. ...
1
2022
... specific-use="noneIndent">式中:N f 为疲劳裂纹扩展寿命;a 0 为初始裂纹长度;a f 为临界裂纹长度;f g 为放大系数,其取值见GB/T 41510—2022《起重机械安全评估规范 通用要求》[24 ] ;K p 为应力谱系数. ...
Solving forward and inverse problems of the nonlinear Schr?dinger equation with the generalized- symmetric Scarf-II potential via PINN deep learning
1
2021
... 网络模型的构建思路是将数据模型与物理模型相融合,并引入PINN中.在小样本数据场景下,将神经网络作为函数逼近器来拟合偏微分方程(partial differential equation, PDE)的解[25 ] ,同时将物理约束条件作为损失函数的一部分.假设函数u = u σ ¯
岸边集装箱桥式起重机疲劳寿命预测
1
2018
... 为了便于物理模型的应用,需要对原始应力时序数据进行预处理,包括异常值处理、无效幅值去除和数据压缩等.对于异常值数据,采用异常值去除和异常值替换的方法对错误数据进行修正;对于无效幅值数据,将无效值删除并用前后项数据的均值来代替;对于等值信息,对等值信息进行压缩,具体处理方法可参见文献[26 ].数据预处理后应力时间历程如图9 所示.负载为8.85 kg时预理前后应力数据的对比如图10 所示. ...
岸边集装箱桥式起重机疲劳寿命预测
1
2018
... 为了便于物理模型的应用,需要对原始应力时序数据进行预处理,包括异常值处理、无效幅值去除和数据压缩等.对于异常值数据,采用异常值去除和异常值替换的方法对错误数据进行修正;对于无效幅值数据,将无效值删除并用前后项数据的均值来代替;对于等值信息,对等值信息进行压缩,具体处理方法可参见文献[26 ].数据预处理后应力时间历程如图9 所示.负载为8.85 kg时预理前后应力数据的对比如图10 所示. ...