近年来,以磁流变液为介质的磁流变阻尼器受到广泛关注,通过控制输入电流可对其输出阻尼力进行连续调节,有效提高了振动控制性能[4-6]。然而,现有针对磁流变阻尼器的研究大多聚焦于提高输出阻尼力,对刚度特性的主动调控仍缺乏有效手段,导致振动控制系统固有频率的调节范围受限,难以满足宽频域振动抑制需求。Liu等[7]首次提出了双磁流变阻尼器串并联架构,实现了阻尼-刚度双调节,但离散布局导致其整体结构复杂且体积过大。Greiner-Petter等[8]提出了分腔式磁流变半主动机构,基于分腔式液压拓扑实现了刚度-阻尼双参数的三模态切换,但因受限于磁流变阀二元特性引发的阶跃式刚度突变,刚度无法实现连续可调。Sun等[9]通过上下布置2个阻尼缸筒与串联弹簧,实现了刚度与阻尼的调节,但该结构的轴向尺寸过大,导致应用空间有限。Deng等[10]采用内外缸筒并联架构,将双磁流变阻尼器集成于单体装置内,配合串联双刚度弹簧组,构建了军用车辆专用的磁流变座椅悬架,但内外缸筒嵌套结构导致悬架径向尺寸增大,易引发运动干涉问题。基于此,设计一种结构紧凑的变刚度变阻尼磁流变阻尼器十分必要。
为充分提高磁流变阻尼器的性能,许多学者针对磁流变阻尼器的优化设计开展了大量研究[11-13]。Jiang等[14]提出了基于NSGA-Ⅱ(non-dominated sorting genetic algorithm-Ⅱ,非支配排序遗传算法-Ⅱ)的多目标协同优化策略,根据所建立的磁路参数化模型,以最大阻尼力可调范围和最小电磁线圈匝数为目标,通过Pareto前沿解集实现了磁路几何参数与电磁特性的协同优化。仿真和实验结果表明,优化后的磁流变阻尼器性能更优。Wang等[15]针对超精密机床的多源振动,利用磁流变阻尼器设计了减振工作台,并采用改进鹈鹕优化算法(improved pelican optimization algorithm, IPOA)来优化其结构参数,以实现减振能力最大化。结果表明:经IPOA优化后,磁流变阻尼器的最大阻尼力更大且阻尼可控范围更宽,能满足超精密机床振动抑制的要求。Hu等[16]在建立多物理场耦合模型的基础上,结合代理模型和DOE(design of experiment,试验设计)进行多目标优化,有效地提高了磁流变阻尼器的输出阻尼力及其动态可调范围。Liu等[17]采用拟牛顿优化算法对基于B样条曲线的磁流变阻尼器进行了优化,优化后该阻尼器的最大阻尼力及阻尼力动态可调范围均得到了提升。然而,上述优化方法均是将多目标优化转换为单目标优化,无法有效衡量优化目标之间的权重关系,同时在求解3个及以上的优化目标时存在收敛性不足、种群多样性低等问题。
针对传统液压阻尼器的刚度系数和阻尼系数固定以及减振性能不佳等问题,本文设计了一种变刚度变阻尼磁流变阻尼器,其结构简单紧凑,并能连续调节刚度系数与阻尼系数。同时,针对传统优化方法对3个及以上目标的优化效果不佳的问题,提出了一种基于NSGA-III的多目标优化方法。选取刚度可调范围、输出阻尼力及其可调范围作为目标,对变刚度变阻尼磁流变阻尼器进行多目标优化设计,在体积受限情况下进一步提升阻尼器的刚度和阻尼性能。
1 磁流变阻尼器的结构与工作原理
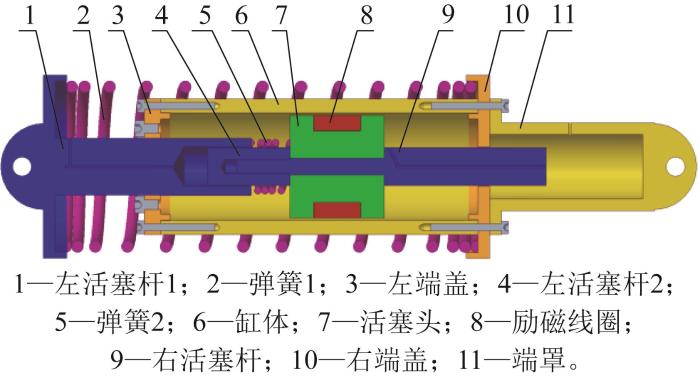
本文所设计的变刚度变阻尼磁流变阻尼器的结构如图1所示,主要由活塞杆、弹簧、端盖、缸体、活塞头、励磁线圈和端罩等组成。阻尼器缸体内充满磁流变液,活塞头上缠绕励磁线圈,活塞头与缸体内表面之间形成阻尼间隙,构成变阻尼装置;阻尼器缸体外侧与弹簧1并联,左活塞杆与活塞头之间由弹簧2串联,构成变刚度装置。
图1
图1
变刚度变阻尼磁流变阻尼器结构示意图
Fig.1
Structure diagram of variable stiffness and variable damping magnetorheological damper
当磁流变阻尼器受到外界振动激励时,活塞杆带动活塞头在缸体内作往复运动,磁流变液在活塞头挤压作用下流过阻尼间隙,励磁线圈通入电流时将产生电磁场并垂直通过阻尼间隙,此时阻尼间隙处磁流变液的屈服应力增大,进而阻碍活塞头运动。通过调节励磁线圈的电流大小,即可实现输出阻尼力的连续可调。将弹簧1与弹簧2的刚度系数设置为不同,且弹簧2能达到的最大弹力大于磁流变液在最大电流下产生的屈服应力;弹簧1跟随活塞杆一起运动,其压缩量和拉伸量与活塞头位移相同。弹簧2位于左活塞杆1与活塞头之间,左活塞杆1与左活塞杆2之间可发生相对滑动,产生的位移差即为弹簧2的拉伸量或压缩量,其大小与输出阻尼力有关。当无电流输入时,磁流变液的屈服应力很小,弹簧2仅需产生微小变形即可克服磁流变液的屈服应力并带动活塞头运动。此时,阻尼器的工作状态可视作仅弹簧1被压缩变形,其刚度即为阻尼器的等效刚度;当输入电流逐渐增大时,磁流变液的屈服应力逐渐增大,弹簧2需要产生更大的变形才能克服该屈服应力并推动活塞头。此时,弹簧2的变形量随输出阻尼力的增大而增大。在该工作模式下,两弹簧均被压缩变形,阻尼器的等效刚度由弹簧1与弹簧2共同提供,且随输入电流的增大而增大,从而实现刚度的连续可调。
综上所述,左活塞杆1在带动活塞头运动时受到弹簧1与弹簧2的阻碍,弹簧2依靠左活塞杆1与左活塞杆2的位移差产生弹力以带动活塞头运动,弹簧2产生的弹力与输出阻尼力有关,输出阻尼力增大,弹簧2为带动活塞头运动而产生的弹力随之增大,则阻尼器的等效刚度增大。通过调节励磁线圈的电流大小来改变输出阻尼力的大小,从而实现阻尼器的变阻尼与变刚度特性。
2 磁流变阻尼器数学模型的建立
2.1 阻尼力数学模型
所设计的变刚度变阻尼磁流变阻尼器的工作模式为剪切阀式,其输出阻尼力Fα 由磁致阻尼力Fτ 与黏滞阻尼力Fη 组成,表达式分别为:
式中:c为修正系数,其取值一般为2~3;l1为活塞头侧翼磁轭长度;τy为磁流变液的剪切屈服应力;Ap为活塞头面积;g为阻尼间隙厚度;D为活塞头直径;v为活塞头速度;η为磁流变液的零场黏度;l为活塞头长度。
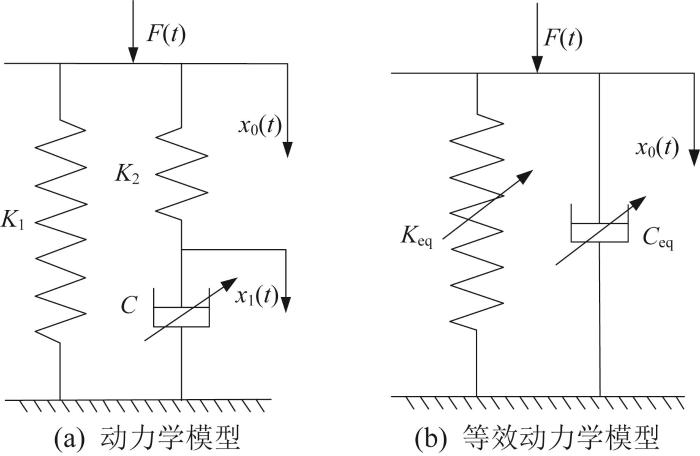
2.2 动力学模型
图2
图2
磁流变阻尼器的动力学模型及其等效模型
Fig.2
Dynamics model and its equivalent model of magnetorheological damper
根据图2(a)所示的动力学模型,可得阻尼器系统的振动微分方程:
设弹簧1处所受的力为F1
单独对F2
式中:s为拉普拉斯变换中的复数变量。
设激励位移x0
联立
根据图2(b)所示的等效动力学模型,该阻尼器的力输出方程可表示为:
结合
3 磁流变阻尼器性能仿真分析
图3
图3
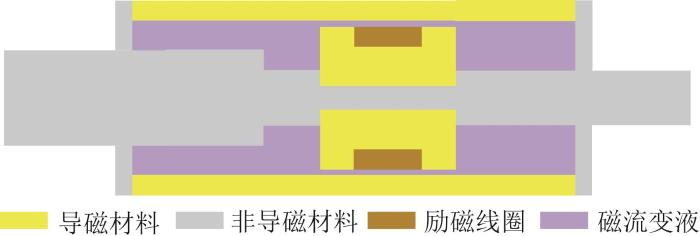
磁流变阻尼器的磁流耦合仿真模型
Fig.3
Magnetic-flux coupling simulation model of magnetorheological damper
3.1 电磁场仿真分析
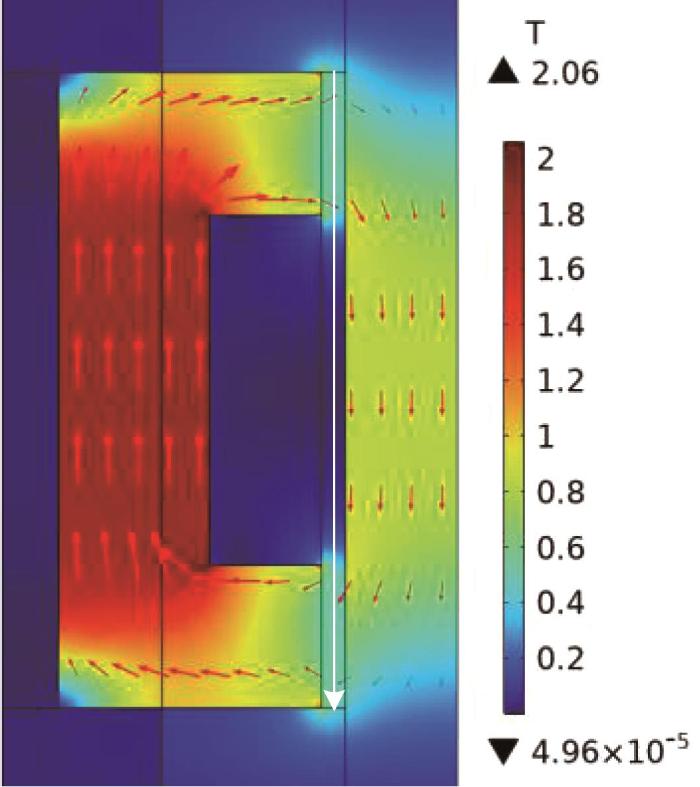
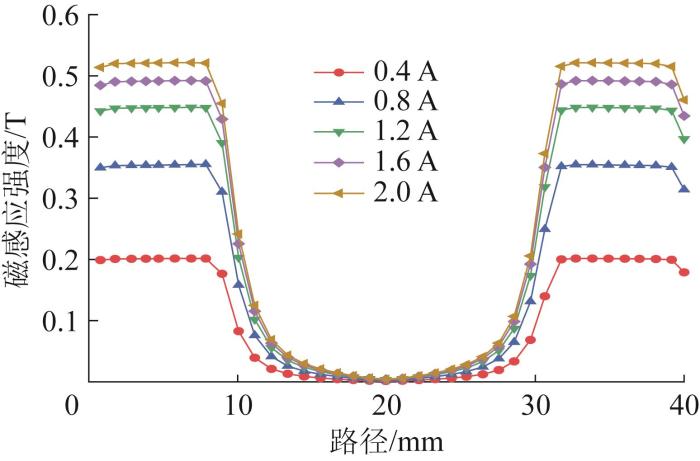
对磁流变阻尼器进行电磁场仿真分析,对励磁线圈施加电流载荷,范围为0.4~2.0 A,步长为0.4 A。当加载电流为2.0 A时,活塞头轴对称截面的磁感应强度分布如图4所示。仿真结果表明,阻尼间隙内的磁感应强度分布较为均匀,仅两端存在轻微漏磁现象。在该磁场回路中,磁感应强度的最大值位于活塞头中部,约为2.06 T。
图4
图4
活塞头轴对称截面的磁感应强度分布
Fig.4
Distribution of magnetic induction intensity in the axisymmetric cross-section of piston head
图5
图5
不同电流下阻尼间隙内磁感应强度的分布曲线
Fig.5
Distribution curves of magnetic induction intensity in the damping gap under different currents
3.2 刚度和阻尼性能仿真分析
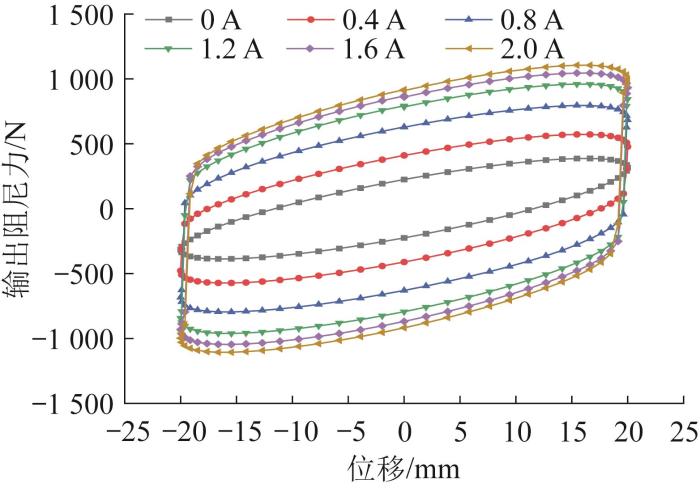
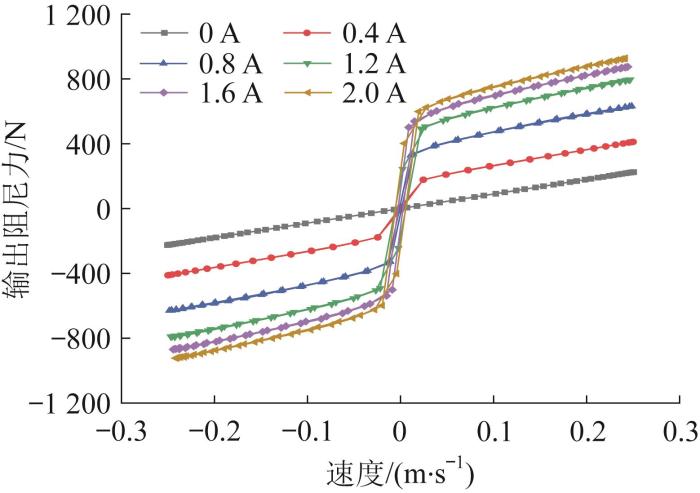
在仿真过程中,采用Bingham-Papanastasiou本构模型来描述磁流变液(非牛顿流体)的流体属性,将流动状态简化为单相层流模型,同时严格限定磁流变液为不可压缩介质,并忽略温度变化的影响。沿轴对称方向对阻尼器左活塞杆1施加振幅x0=20 mm、频率f=2 Hz的正弦激励,并以0.4 A为电流载荷的步长,从0.4 A到2.0 A逐步加载,通过仿真分析不同电流下磁流变阻尼器的输出阻尼力随激励位移、活塞头速度的变化情况。
图6
图6
不同电流下的输出阻尼力—位移曲线
Fig.6
Output damping force-displacement curves under different currents
图7
图7
不同电流下的输出阻尼力—速度曲线
Fig.7
Output damping force-velocity curves under different currents
图8
图8
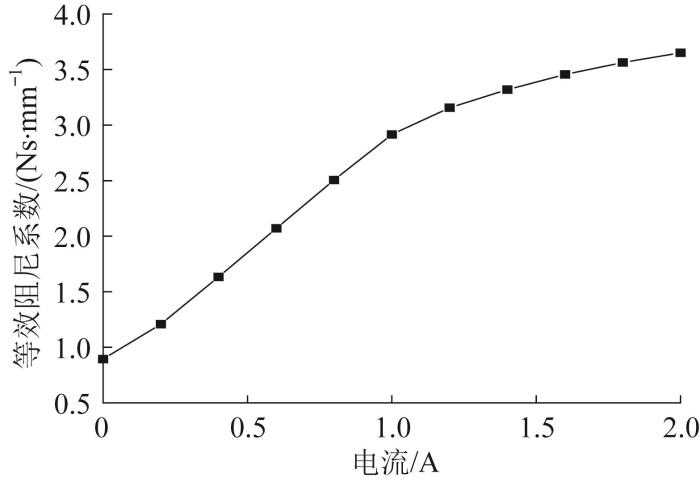
等效阻尼系数随电流的变化曲线
Fig.8
Variation curve of equivalent damping coefficient with current
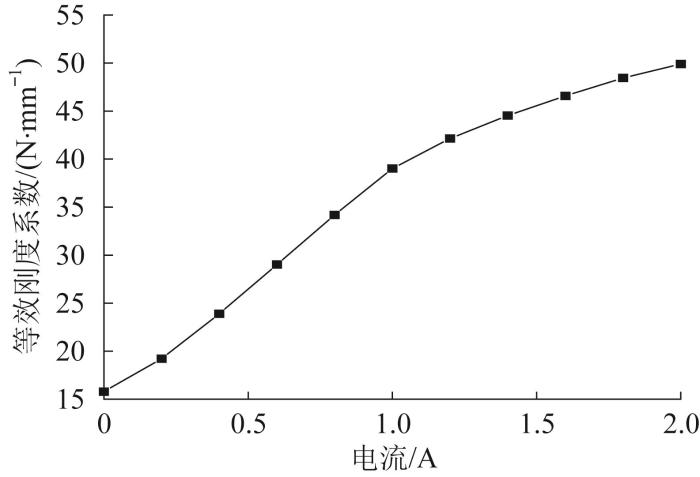
图9
图9
等效刚度系数随电流的变化曲线
Fig.9
Variation curve of equivalent stiffness coefficient with current
4 磁流变阻尼器结构优化设计
4.1 基于NSGA-Ⅲ的优化设计流程
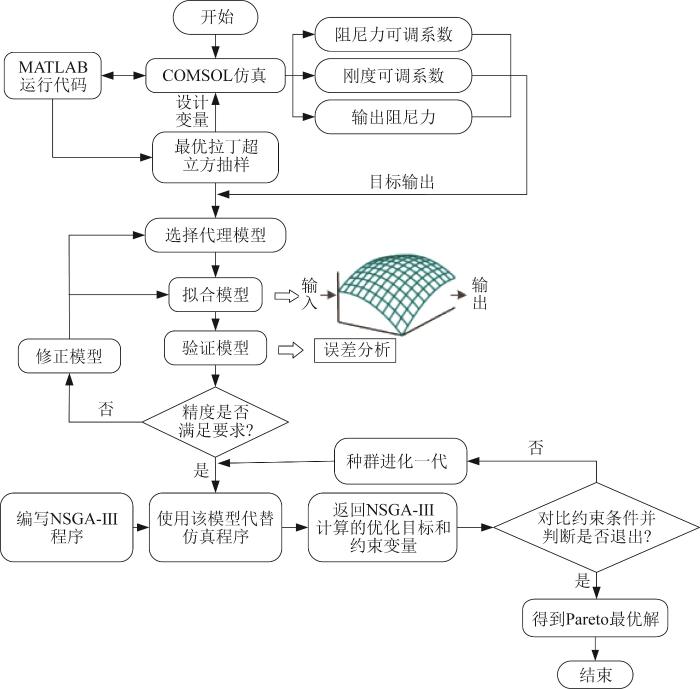
为提升变刚度变阻尼磁流变阻尼器的性能,以拓展其应用领域,需对其关键结构参数进行优化设计。本文采用基于NSGA-Ⅲ的多目标优化算法对所设计的磁流变阻尼器进行结构优化,具体流程如图10所示。首先,基于MATLAB与COMSOL的联合仿真平台,计算不同设计变量下阻尼器的输出阻尼力、阻尼力可调系数及刚度可调系数。然后,采用最优拉丁超立方抽样方法生成设计矩阵,并基于设计矩阵对代理模型进行拟合与构建;同时,对比不同代理模型的拟合效果,最终选出最优代理模型,并使用该模型对阻尼器结构进行优化。最后,利用NAGA-Ⅲ进行多目标优化,得到符合要求的Pareto最优解集。
图10
图10
磁流变阻尼器的多目标优化设计流程
Fig.10
Flow of multi-objective optimization design for magnetorheological damper
4.2 目标函数建立
在有限体积内,合理地设计非导磁材料与导磁材料的位置与尺寸,可提高有效阻尼间隙内的磁感应强度,同时避免导磁材料过早发生磁饱和现象。对于变刚度变阻尼磁流变阻尼器,其主要性能指标有3个,即输出阻尼力、阻尼力可调范围与刚度可调范围。其中,输出阻尼力Fα 可由
刚度可调范围β定义为最大刚度与最小刚度之比,可表示为:
式中:Kmax、Kmin分别为最大刚度和最小刚度。
由
表1 设计变量的取值范围
Table 1
| 设计变量 | 最小值 | 最大值 |
|---|---|---|
| 缸体壁厚dh/mm | 4 | 8 |
| 绕线槽深度d/mm | 4 | 9 |
| 侧翼磁轭长度l1/mm | 8 | 12 |
| 阻尼间隙厚度g/mm | 1 | 2 |
| 弹簧1刚度系数K1/(N·mm-1) | 10 | 20 |
| 弹簧2刚度系数K2/(N·mm-1) | 100 | 200 |
4.3 多目标优化流程
考虑到输出阻尼力、阻尼力可调范围和刚度可调范围这3个指标之间存在一定的矛盾关系,需要同时进行优化,这就构成了一个典型的多目标优化问题。在处理此类多目标优化问题时,关键在于如何平衡不同目标,以达成整体最优的效果。
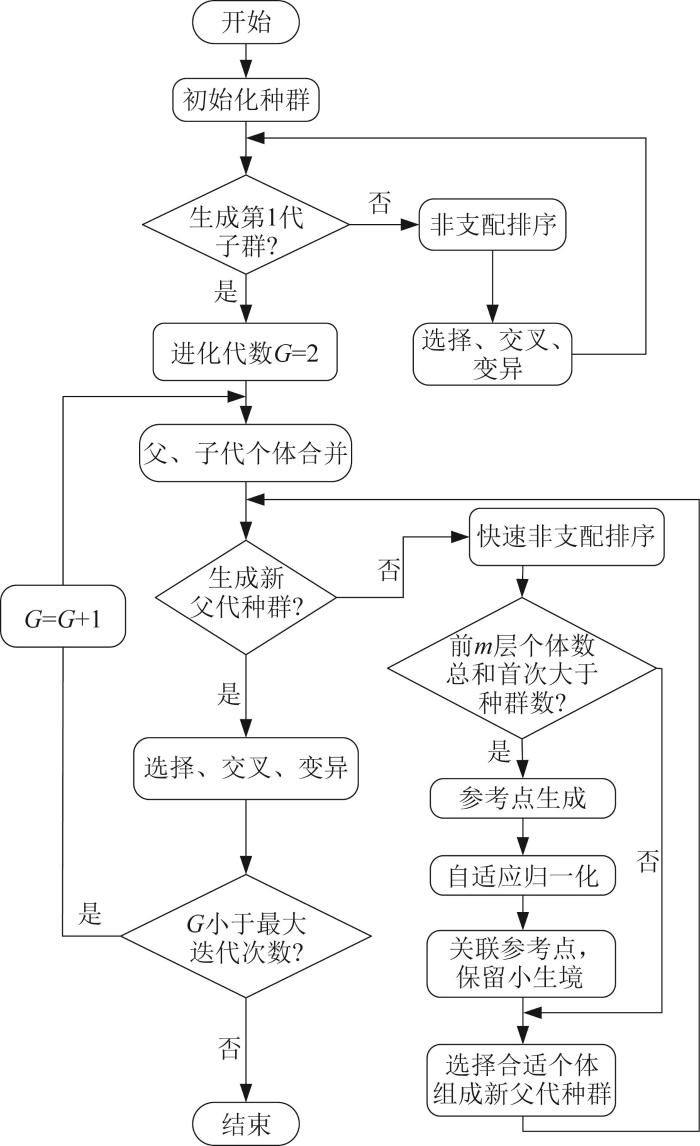
NSGA-III在多目标优化问题的求解中展现出良好性能。图11所示为NSGA-III的基本寻优流程,其核心思想是借助参考点引导的选择机制和环境选择策略来挑选下一代种群,以此来解决多目标优化问题[19-20]。其中:参考点引导的选择机制能够根据预设的参考方向,将个体分配到不同的参考点区域,优先保留与参考点匹配度高的个体,从而兼顾不同的优化目标。在优化过程中,随着搜索代数的增加,种群的多样性可能会逐渐降低,NSGA-III可通过环境选择策略来维持种群的多样性和均匀分布。此外,环境选择策略还能保持个体之间的适当距离,防止种群过度聚集在局部区域,陷入局部最优。这些机制相互配合,有助于在保证最优解多样性的同时提高计算效率,最终获得一个满足多约束条件的优质解集合。
图11
4.4 代理模型构建
一般而言,DOE抽取的样本数量越多,基于这些样本数据构建的代理模型越能精准地逼近有限元仿真结果[23]。然而,随着抽样次数的增加,代理模型精度的提升程度将逐渐减弱。因此,本文采用最优拉丁超立方抽样方法,以确保代理模型的精度与抽样效率。
鉴于不同代理模型各具特点,本文选择响应面模型(一阶和二阶)、卷积神经网络模型、径向基神经网络模型和PSO-BP(particle swarm optimization- back propagation,粒子群优化-反向传播)神经网络模型这4种模型中拟合效果最好的模型作为后续优化使用的代理模型。以100次抽样产生的设计矩阵作为原始数据,分别利用不同代理模型对磁流变阻尼器的3个性能指标进行拟合,得到各代理模型的拟合指标,如表2所示。其中:拟合指标包括均方根误差(root mean square error, RMSE)和决定系数R2。
表2 各代理模型的拟合指标
Table 2
| 代理模型 | RMSE | R2 | ||||
|---|---|---|---|---|---|---|
| α | β | Fα/N | α | β | Fα | |
| 一阶响应面模型 | 0.41 | 0.37 | 199.3 | 0.81 | 0.80 | 0.89 |
| 二阶响应面模型 | 0.12 | 0.17 | 49.4 | 0.96 | 0.91 | 0.98 |
| 卷积神经网络模型 | 0.17 | 0.30 | 132.6 | 0.96 | 0.83 | 0.97 |
| 径向基神经网络模型 | 0.15 | 0.28 | 62.1 | 0.97 | 0.84 | 0.98 |
| PSO-BP神经网络模型 | 0.08 | 0.15 | 51.7 | 0.99 | 0.96 | 0.99 |
对比表2中各代理模型的RMSE与R2可发现,除了二阶响应面模型拟合的输出阻尼力Fα 的RMSE外,PSO-BP神经网络模型的RMSE最小且R2最接近1。基于此,最终选择PSO-BP神经网络模型作为后续优化求解的代理模型。
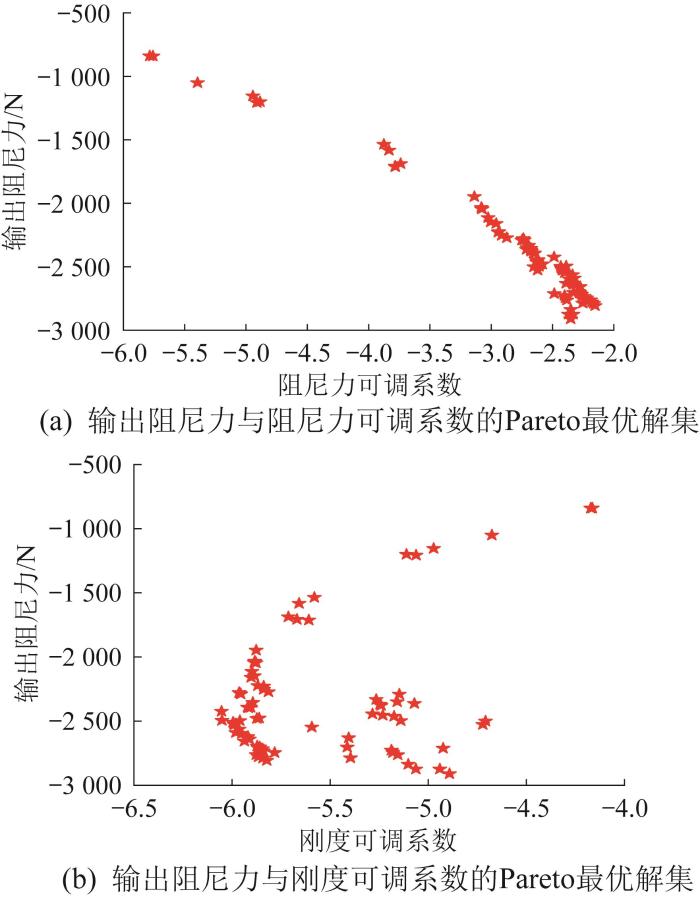
NSGA-Ⅲ的参数设置如下:初始种群大小为80,最大迭代次数为100,交叉比例为0.8,变异概率为0.5。经过迭代运算,得到了磁流变阻尼器性能指标的Pareto最优解集,如图12所示。其中:图12(a)为输出阻尼力与阻尼力可调系数的解集,图12(b)为输出阻尼力与刚度可调系数的解集。由图12(a)可知,输出阻尼力与阻尼力可调系数成反比。由图12(b)可知,输出阻尼力与刚度可调系数呈非线性关系,当输出阻尼力小于2 000 N时,输出阻尼力与刚度可调系数大致成正比;但当输出阻尼力大于2 000 N时,输出阻尼力与刚度可调系数的关系不明显。分析原因在于:等效刚度已达到取值范围内的最大值,输出阻尼力的增大对刚度可调系数的影响很小。
图12
图12
磁流变阻尼器性能指标的Pareto最优解集
Fig.12
Pareto optimal solution set for performance indicators of magnetorheological damper
4.5 优化前后阻尼器的性能对比
优化前后磁流变阻尼器的关键参数如表3所示。
表3 磁流变阻尼器关键参数的优化结果
Table 3
| 参数 | 优化前 | 优化后 |
|---|---|---|
| 缸体壁厚dh/mm | 7.0 | 4.1 |
| 绕线槽深度d/mm | 7.0 | 6.7 |
| 侧翼磁轭长度l1/mm | 9.0 | 8.8 |
| 阻尼间隙厚度g/mm | 1.5 | 1.7 |
| 弹簧1刚度系数K1/(N·mm-1) | 15 | 10 |
| 弹簧2刚度系数K2/(N·mm-1) | 150 | 130 |
图13
图13
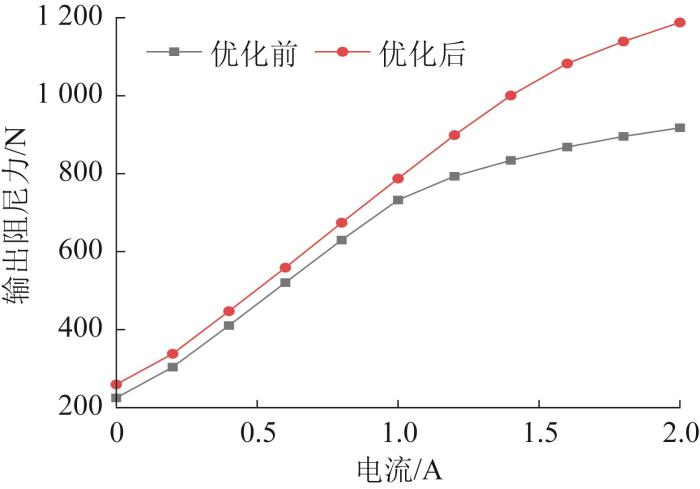
优化前后输出阻尼力随电流的变化曲线
Fig.13
Variation curves of output damping force with current before and after optimization
图14
图14
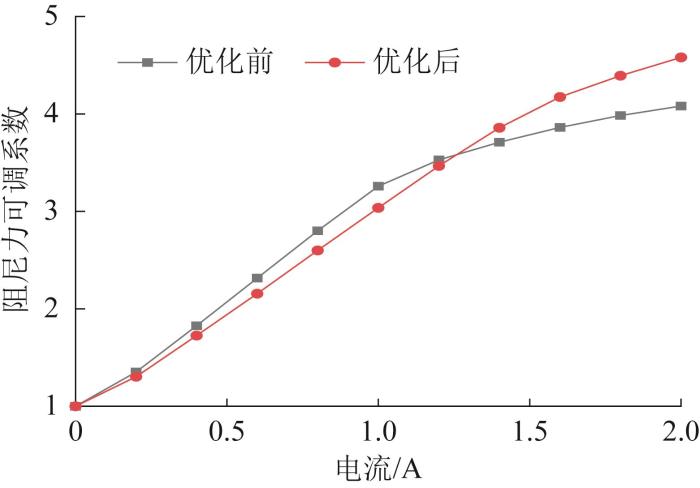
优化前后阻尼力可调系数随电流的变化曲线
Fig.14
Variation curves of adjustable damping force coefficient with current before and after optimization
图15
图15
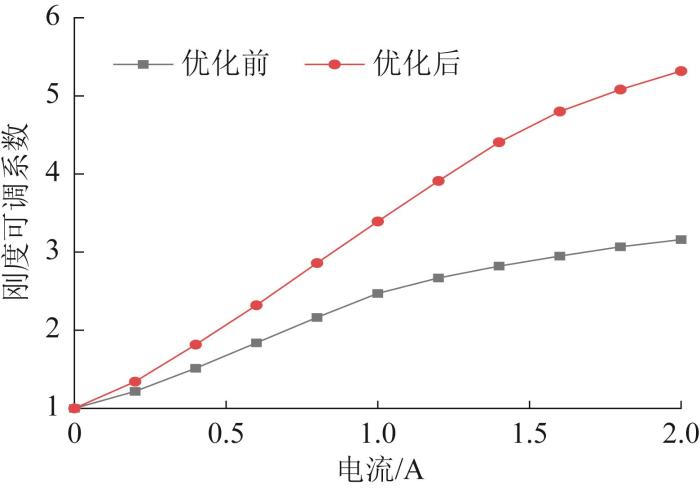
优化前后刚度可调系数随电流的变化曲线
Fig.15
Variation curves of adjustable stiffness coefficient with current before and after optimization
5 结 论
1)设计了一种变刚度变阻尼磁流变阻尼器,将2个刚度系数不同的弹簧分别与磁流变阻尼器串、并联,进而通过调节励磁线圈的电流来实现刚度系数和阻尼系数的连续可调。同时,建立了磁流变阻尼器的阻尼力数学模型和动力学模型,并通过仿真分析验证了其结构设计的合理性。
2)基于NSGA-Ⅲ对变刚度变阻尼磁流变阻尼器进行了优化设计。通过对比优化前后磁流变阻尼器的主要性能指标可知,当加载电流为2.0 A时,优化后的输出阻尼力可达1 188.2 N,相比优化前提高了29.5%;阻尼力可调系数由4.1提高到4.6,刚度可调系数由3.2提高到5.3,相比优化前分别提高了12.2%和65.6%。结果表明,优化后的变刚度变阻尼磁流变阻尼器的刚度和阻尼性能均明显提升,这可为车辆悬架或建筑隔振系统中磁流变阻尼器的设计与优化提供参考。

本文链接:https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.119
参考文献
旋转式摩擦阻尼器滞回性能及其在多阶段抗震中的应用
[J].
Hysteretic performance of the rotational friction damper and its application in multi-stage seismic design
[J].
工程车辆座椅悬架多维振动控制研究
[J].
Multi-dimensional vibration control of engineering vehicle seat suspension
[J].
动力装备和建筑楼盖的动力吸振研究
[J].
Research on dynamic vibration absorption for power equipment and building floor
[J].
A review of magnetorheological fluid damper technology and its applications
[J].
全通道内置阀式磁流变阻尼器的设计及性能分析
[J].
Design and performance analysis of full fluid channel magnetorheological damper with built-in valve
[J].
利用负刚度磁流变阻尼器的单层球面网壳三维隔震研究
[J].
Three-dimensional seismic isolation of single-layer spherical lattice shells using magnetorheological negative stiffness dampers
[J].
Semi-active vibration isolation system with variable stiffness and damping control
[J].
A semi-active magnetorheological fluid mechanism with variable stiffness and damping
[J].
A new generation of magnetorheological vehicle suspension system with tunable stiffness and damping characteristics
[J].
Design and verification of a seat suspension with variable stiffness and damping
[J].
Development of low-cost optimal magneto-rheological damper for automotive application
[J].
振动能量采集型磁流变阻尼器优化设计及性能分析
[J].
Optimal design and performance analysis of vibration energy harvesting type magnetorheological dampers
[J].
Design and geometric parameter optimization of hybrid magnetorheological fluid damper
[J].
Multi-objective optimization design for a magnetorheological damper
[J].
A smart structural optimization method of magnetorheological damper for ultra-precision machine tool
[J].
Optimal design and performance analysis of magnetorheological damper based on multiphysics coupling model
[J].
Design and optimization of a magnetorheological damper based on B-spline curves
[J].
具有内外线圈结构的磁流变阀压降性能分析
[J].
Analysis of pressure drop performance of magnetorheological valve with inner and outer excitation coils
[J].
改进NSGA-Ⅲ的高维多目标柔性作业车间低碳调度方法研究
[J].
Research on low-carbon scheduling method for high-dimensional multi-objective flexible job shop improved by NSGA-Ⅲ
[J].
Mooring optimization for net-cage group system based on NSGA-III multi-objective genetic algorithm
[J].
基于代理模型的风机主轴疲劳优化
[J].
Fatigue optimization of fan main shaft based on the surrogate model
[J].
风电齿轮箱迷宫密封泄漏量分析及结构优化设计
[J].
Leakage analysis and structural optimization design of labyrinth seal in wind power gearbox
[J].