折纸结构起源于民间的手工折纸艺术，指由轻薄材料沿折痕折展而成的复杂三维结构^[1]。折纸结构具备轻量化、大变形、可重构和易制备等特点^[2-3]，目前已被广泛应用于多个工程领域，如卫星上的太阳能帆^[4]、应变传感器^[5]、微型机器人^[6]和折纸机械臂^[7]等。此外，部分折纸结构还具有负泊松比、多稳态和准零刚度等力学特性^[8]，其在机械超材料研究领域备受关注^[9]。

折纸结构的多稳态特性是指其在折展过程中存在多个力学平衡位置。这种特性使得折纸结构具有快速变形、可储能和负刚度等优势^[10-12]。近年来，针对折纸结构的多稳态特性分析、动静力学模型构建以及基于多稳态折纸结构的高性能软体机器人设计的研究日益增多^[13-14]。目前，分析折纸结构双稳态特性的方法一般为：先建立势能模型，再分析不同几何结构参数对力—位移本构关系的影响^[15]。Silverberg等^[16]对方形扭转折纸结构的力学特性进行了研究，并分析了折痕刚度、折面刚度及折痕夹角对其双稳态特性的影响。邱海等^[17]从SMO（stacked Miura origami，堆叠型三浦折纸）结构的弹性势能出发，建立了SMO串联结构的静力学模型，并研究了双胞SMO串联结构由双稳态特性引发的非线性动力学行为。Wang等^[18]研究了不同形状及折痕等效刚度对非刚性折纸结构双稳态特性的影响，并基于Hessian矩阵提出了一种判断折纸结构是否具有多稳态特性的方法。然而，部分折纸结构的稳态特性受折痕长度、折痕夹角的影响很小，且部分应用场景下折纸结构的整体尺寸受到一定限制。针对这一问题，Faber等^[19]受昆虫可折叠翅膀的启发，采用低弹性模量材料制作单顶点四折痕折纸结构的折痕。相较于传统折纸结构中折痕仅起等效卷簧的作用，基于该方法制作的折痕在折展过程中可实现拉伸变形，丰富了折纸结构的运动形式。Flores等^[20]将Waterbomb折纸结构的折痕由直线替换为圆弧，并分析了圆弧曲率对该折纸结构稳态特性的影响。

现有研究虽在一定程度上实现了在较少调节折纸结构尺寸参数的同时获得更好的稳态特性，但解决方法往往依赖硅胶等低弹性模量材料^[21]，而对普通薄片材料依靠尺寸无关参数调节稳态特性的方法缺乏深入研究。研究表明，折纸结构的稳态特性主要受初始折展角度的影响，且对于普通薄片材料而言，初始折展角度源自折展过程中折痕处产生的弹塑性变形，这种弹塑性变形主要受折纸结构制成时的折痕角度、预折叠角度等尺寸无关参数的影响。

基于此，本文以三浦折纸结构为研究对象，分析尺寸无关参数对其稳态特性的影响。首先，对三浦折纸结构的构型与势能模型进行介绍，并分析比较折痕长度、相邻折痕夹角和初始折展角度等参数对势能模型影响的显著性。然后，分析并比较三浦折纸结构初始折展角度的影响因素，并对改变初始折展角度后的力学特性进行实验分析。最后，基于三浦折纸结构设计水上折纸机器人，并通过实验分析尺寸无关参数对机器人游动速度的影响。

三浦折纸结构由4个折面及4条公共折痕组成。现有关于三浦折纸结构的研究大多集中在多层结构堆叠下的负泊松比行为分析和双胞堆叠下的双稳态特性分析等方面，缺乏对单胞三浦折纸结构双稳态特性的研究。

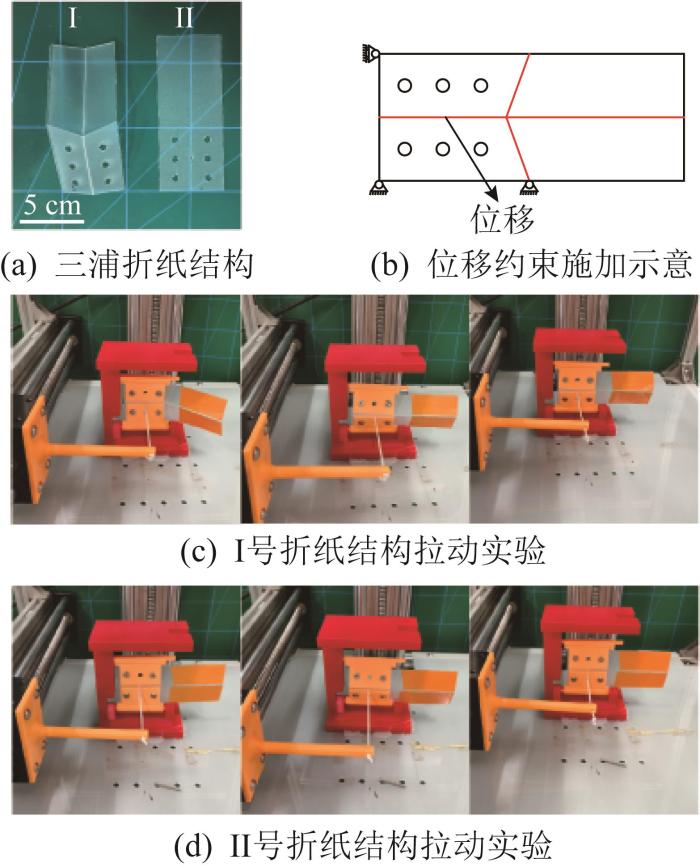
图1(a)展示了2个几何尺寸相同的三浦折纸结构（I和Ⅱ），其制作材料均为0.4 mm厚的PP（polypropylene，聚丙烯）薄板，折痕由激光切割机使用6.7%的能量在预定位置进行激光切割制成。两者的主要区别为：I号折纸结构经预折叠后在残余应力的作用下发生变形，其初始折展角度发生变化；Ⅱ号折纸结构未经过预折叠处理。在开展拉动实验时，为增强视觉效果，在折纸结构上粘贴橙色胶带。利用夹具对2个折纸结构分别施加图1(b)所示的位移约束。结果发现，在位移约束所导致的变形不超过折痕弹性极限的情况下，卸载后Ⅰ号折纸结构出现第二稳态，如图1(c)所示；而Ⅱ号折纸结构在卸载后恢复至初始状态，不具备双稳态特性，如图1(d)所示。由此可知，单胞三浦折纸结构在特定条件下存在双稳态特性，且这种特性不仅与其尺寸参数相关，还与其初始折展角度有关。下文将针对各参数对单胞三浦折纸结构稳态特性的影响展开分析。

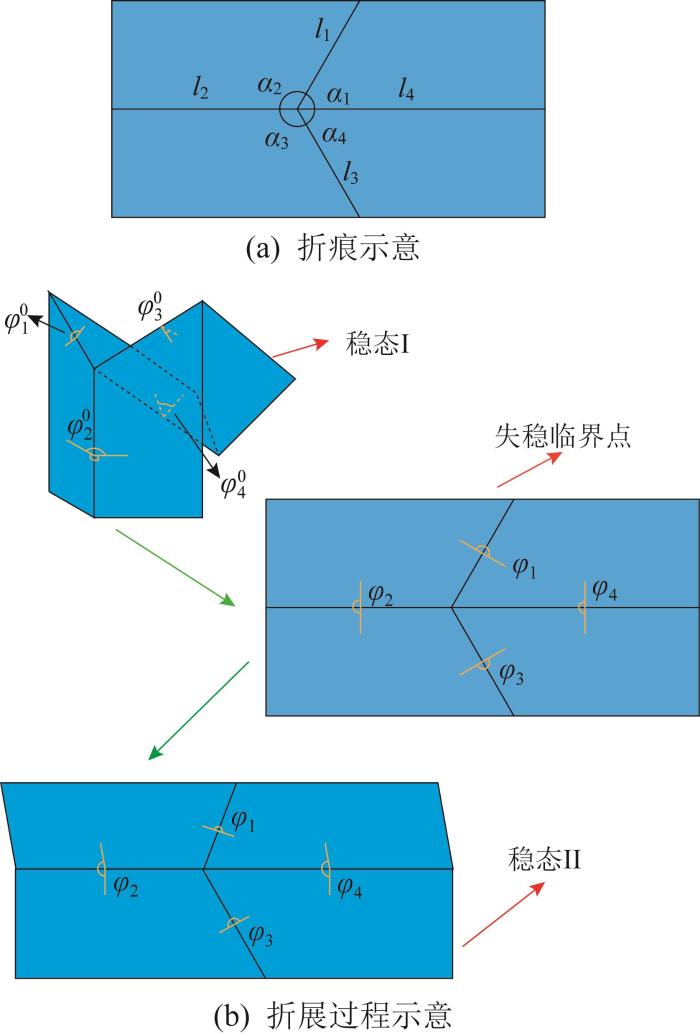
三浦折纸结构的尺寸参数包括折痕长度li和相邻折痕夹角αi(i=1, 2, …, 4)，如图2(a)所示。这些基本尺寸参数满足以下关系：

如图2(b)所示，三浦折纸结构的折展过程为：先由稳态Ⅰ展开至失稳临界点（即完全展平状态），再由失稳临界点折展至稳态Ⅱ。通过各相邻折面之间的二面角φi来描述三浦折纸结构的折展过程，定义稳态Ⅰ下的二面角为初始折展角度φi0。

通过研究发现，三浦折纸结构的失稳临界点总处于完全展平状态，且由2个稳态折展至失稳临界点的过程并不完全相同，本文将其分为2段来讨论。当三浦折纸结构处于失稳临界点时，φ2=π，故以φ2作为自变量，以φ2=π作为分段讨论的分界点。则可得，当φ2<π时，各二面角φi与相邻折痕夹角αi之间满足如下关系^[22]：

其中：

联立式(1)与式(2)，变换可得：

其中：

当φ2>π时，各二面角φi之间满足如下关系：

折纸结构的不同稳态对应其势能曲线上的各个局部极小值点。因此，在讨论折纸结构的多稳态特性时，应先分析其应变能。三浦折纸结构属于典型的刚性折纸结构，其折面变形量相较于折痕变形量可忽略不计。基于此，三浦折纸结构在折展过程中所储存的势能可等效为折痕储存的势能。假设ki表示第i条折痕的等效弹性系数，则三浦折纸结构的弹性势能E可表示为：

由式(5)可知，三浦折纸结构的弹性势能E与折痕等效弹性系数ki、二面角φi和初始折展角度φi0相关。根据材料力学的相关知识，ki与折痕长度、折痕厚度的三次方成正比，与折痕宽度成反比。由于本文研究的三浦折纸结构的折痕加工方法为使用激光切割机对预定折痕处进行切割，折痕宽度与折痕厚度均在0.1 mm以下，可调整范围很小，且因受加工条件限制，在实验分析时难以通过精准改变这2个参数来验证其对弹性势能的影响，因此在后续分析中将其设为定值。

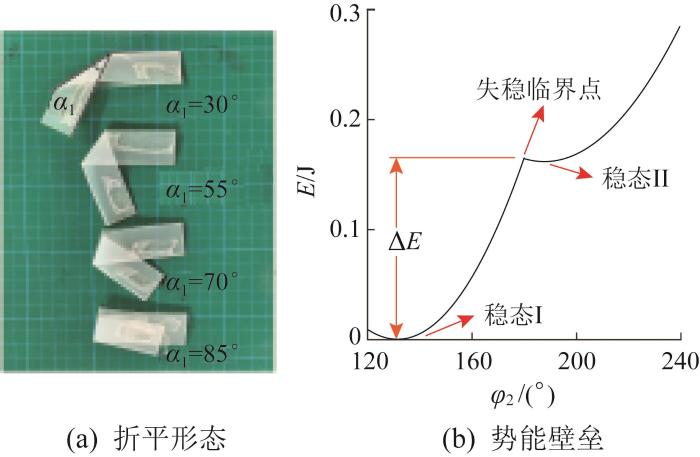
对于折痕长度li而言，由式(1)可知，独立参数包括l1、l2、l4三项，l3可由l1确定。在实际应用中，固定三浦折纸结构的夹具的尺寸通常与l1、l2相关，故通常不通过改变l1、l2来调整折纸结构的稳态特性。此外，为防止结构设计过于臃肿，三浦折纸结构各折痕长度间的关系一般为：l1最小，l2次之，l4最大。在设计时，取l1=25 mm，l2=50 mm，l4=70~130 mm。对于相邻折痕夹角αi与初始折展角度φi0，由式(2)和式(3)可知，两者中均只有1个独立参数。如图3(a)所示，相邻折痕夹角α1不同的三浦折纸结构在折展过程中的形态有较大差异，因此在实验设计时α1的限定范围取55°~85°。结合式(2)可知，φi0的可选范围为0°~180°，在实验设计时取60°~180°。选择l₄、α1、φ20作为三浦折纸结构弹性势能的影响因子。使用Minitab软件，根据田口实验设计法，选择L₉(3³)正交表来分析各因子对三浦折纸结构弹性势能影响的显著性，具体因素水平如表1所示。

通常情况下，双稳态结构的势能壁垒越高，表示超过失稳临界点后所释放的能量越多，即具有越大的失稳输出力，实际应用价值越高。考虑到三浦折纸结构的失稳临界点与稳态Ⅰ间的势能壁垒远大于失稳临界点与稳态Ⅱ间的势能壁垒，以失稳临界点与稳态Ⅰ间的势能壁垒ΔE作为响应值，如图3(b)所示。假设单位长度（1 mm）折痕的等效弹性系数为1×10^-4 N/(°)，通过MATLAB软件计算得到对应的势能壁垒，具体实验方案及对应结果如表2所示。

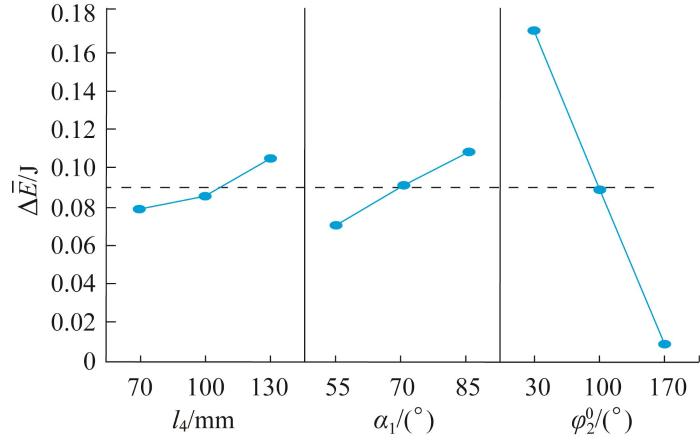
使用Minitab软件对表2中的数据进行处理，得到三浦折纸结构势能壁垒ΔE均值的响应结果，如表3所示。由势能壁垒极差以及排秩结果可以看出，初始折展角度对三浦折纸结构势能壁垒的影响远大于其余2项尺寸参数。由此说明，在不调整尺寸参数的情况下，三浦折纸结构能够通过改变初始折展角度来实现稳态特性的调整。

根据上述结果，绘制三浦折纸结构势能壁垒均值ΔE¯的主效应图，如图4所示。由图4可知，初始折展角度越小，三浦折纸结构的势能壁垒越大。

折纸结构的折痕通常由激光切割薄片材料或由硅胶凝固制成。对于由硅胶等材料制成的折纸结构，其初始折展角度取决于模具形状，能精确地制得预设的初始折展角度。但由于硅胶材料存在刚度较低、质量较大等问题，在很多应用场景下折纸结构的材料通常选用PP或PVC（polyvinyl chloride，聚氯乙烯）薄板。对于由此类材料制成的折纸结构，其初始折展角度取决于折展过程中的弹塑性变形。

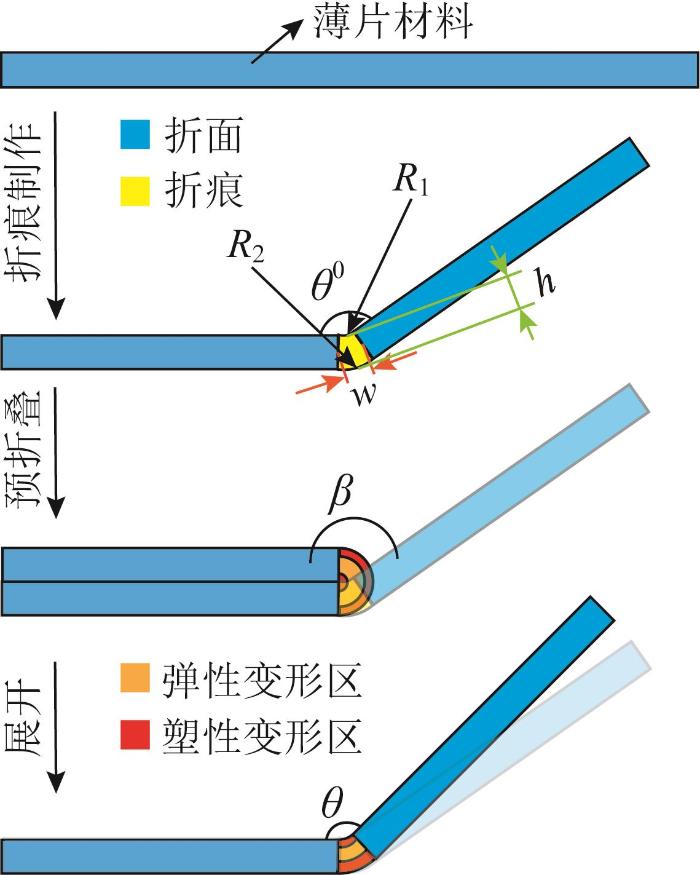
如图5所示，定义单折痕折纸结构的折痕初始制成角度为θ⁰。当将折纸结构沿折痕进行预折叠后，若预折叠角度β超过折痕弹性变形极限，则折痕处发生塑性变形，当该结构自然展开时，由于存在残余应力，其折叠角只能恢复至变形后的角度θ，此角度即为单折痕折纸结构的初始折展角度φ⁰。

由弹塑性力学知识可知，当单折痕折纸结构预折叠后，在残余应力的影响下，其初始折展角度φ⁰与折痕弹性模量E_c、折痕厚度h、折痕制成角度θ⁰、预折叠角度β和折痕宽度w等相关。对于多折痕折纸结构，其初始折展角度φi0还需要考虑各相邻折面二面角间的相互影响。多折痕折纸结构由预折叠状态展开时可视为线弹性卸载，卸载后折叠角θ_i 与预折叠角度β_i 满足以下关系：

根据式(3)，三浦折纸结构的初始折展角度φi0与相邻折痕夹角αi有关，而折痕的等效弹性系数ki与折痕长度、折痕厚度的三次方成正比。由此可知，三浦折纸结构的初始折展角度φi0除了受折痕制成角度、预折叠角度等尺寸无关参数的影响外，还受折痕长度、相邻折痕夹角等尺寸参数的影响。

采用田口实验设计法分析折痕长度、相邻折痕夹角和折痕制成角度对三浦折纸结构初始折展角度的影响。对于折痕弹性模量E_c而言，由于改变材料后难以保证折痕厚度与折痕宽度等参数完全一致，因此在实验中折纸结构的材料均选用PP薄板。对于折痕厚度h和折痕宽度w，因受实验条件限制，无法直接分析这2个参数对初始折展角度的影响，故在实验时通过在相同厚度（0.4 mm）的PP薄板上切割折痕，以保证初始折展角度不受这2个参数的影响。由于调整折痕长度l1、l2与相邻折痕夹角α_i 等参数会对三浦折纸结构的尺寸与折展形态造成一定影响，因此仅选择l4作为影响因子，其取值范围为70~130 mm；l1、l2分别设为26.6 mm和50 mm，α1设为70°。对于预折叠角度β（各折痕的预折叠角度相等，即β_i =β），0.4 mm厚的PP薄板在切割出折痕后沿折痕弯折90°~100°为其弹性变形极限，结合最大预折叠角度通常为180°，在实验时取β=120°~180°。对于折痕制成角度θ0（各折痕的初始制成角度相等，即θ_i⁰=θ⁰），其理论取值范围为0°~180°，本文取30°~170°，实验中折痕制成角度的调整步骤（见图6）如下：1）利用激光切割折痕；2）使用封口夹对折痕局部加热至150 ℃左右；3）将折痕加热软化后的折纸结构放置在可旋转至任意角度的模具上；4）待折痕冷却后，可得到任意折痕制成角度的折纸结构。综上，三浦折纸结构初始折展角度各影响因素的具体水平值如表4所示。

为方便测量，以稳态Ⅰ下三浦折纸结构的折痕2与折痕4的夹角γ0来评估初始折展角度的大小，如图7所示。γ0满足：

由式(7)可知，γ0与各初始折展角度均呈正相关，即γ0越小，各初始折展角度越小。使用Minitab软件选择L₉(3³)正交表，设计相应的田口实验，如表5所示。

使用Minitab软件对表5中的实验数据进行处理，得到初始折展角度均值（γ₀均值）响应结果，如表6所示。由极差与排秩结果可以看出，折痕制成角度θ⁰对γ0均值的影响最大，即折痕制成角度对初始折展角度的影响最为显著。

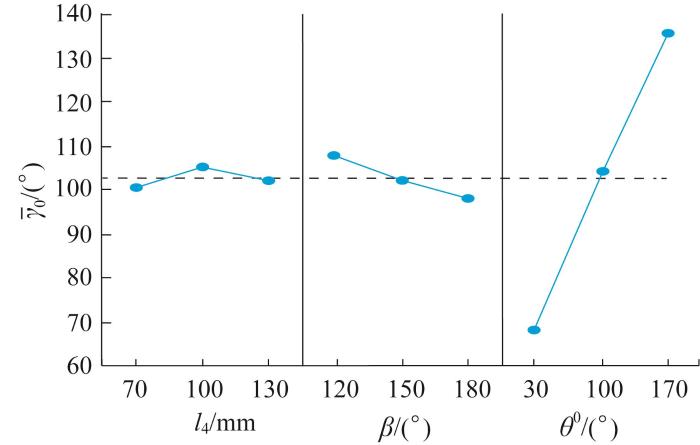
根据上述结果，绘制三浦折纸结构初始折展角度均值γ¯0的主效应图，如图8所示。从图8中可以看出，三浦折纸结构的初始折展角度与折痕制成角度呈正相关，与预折叠角度呈负相关。调整三浦折纸结构初始折展角度的最佳策略为：在预折叠角度最大的情况下，尽可能减小折痕制成角度。

为验证初始折展角度对三浦折纸结构稳态特性的影响最大，设计了如下实验：将三浦折纸结构放置在夹具中，夹具限制折纸结构沿x轴方向的位移，允许折纸结构沿z轴与y轴方向移动，如图9(a)所示。其中：Ⅰ、Ⅱ号实验装置分别用于测量折纸结构由稳态Ⅰ与稳态Ⅱ折展至失稳临界点过程中的力—位移关系。将测力计固定在滑动导轨上，利用步进电机控制器对导轨施加每次上升或下降0.5 mm的脉冲信号，并利用测力计读取对应的支承力F数值。

在折展过程中，三浦折纸结构可视为单自由度结构，折展至φ2时的等效力矩M可由弹性势能E对φ2求导获得。则由稳态Ⅱ至失稳临界点过程中的等效力矩M为：

稳态Ⅰ至失稳临界点过程中的等效力矩M为：

其中：

通过受力分析，可得支承力F与等效力矩M的关系：

三浦折纸结构在z轴方向上相较于初始位置的位移D为：

联立式(10)和式(11)，可得支承力F与位移D间的关系式：

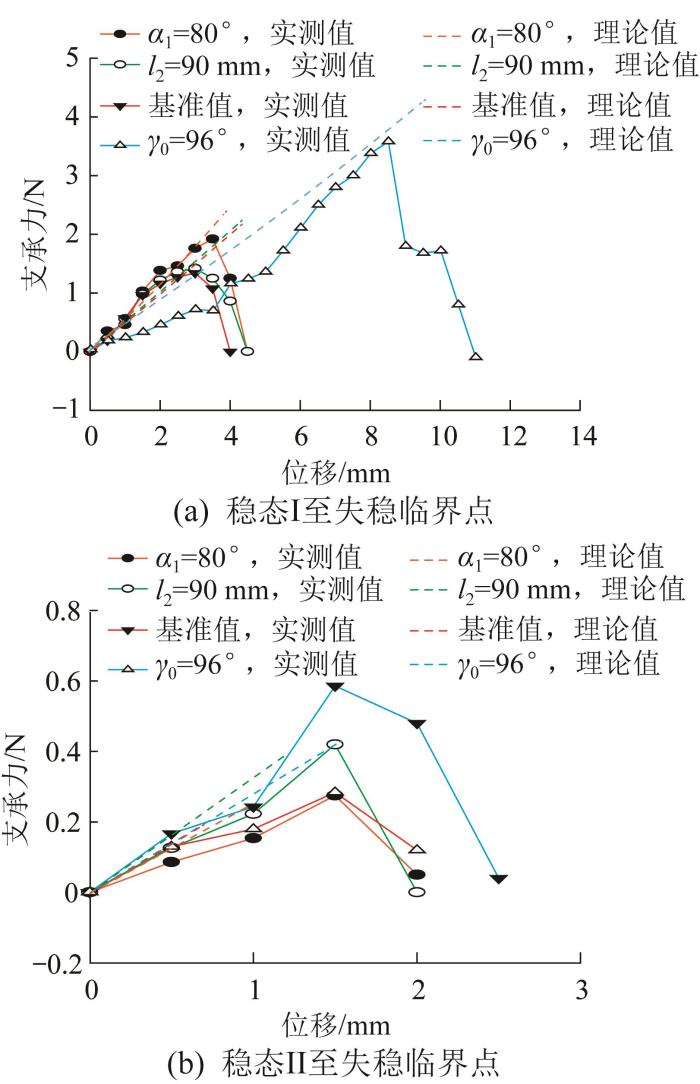
在本文实验中，设定三浦折纸结构各参数的基准值如下：l1=l3=26.6 mm、l2=50 mm、l4=70 mm、γ0=128°、α1=70°。通过更改α₁、l₂和γ₀的值来验证支承力理论模型的正确性，分别取α₁=80°、l₂=90 mm、γ₀=96°三种情况（其余参数均与基准值相同）。不同情况下三浦折纸结构由稳态Ⅰ折展至失稳临界点与由稳态Ⅱ折展至失稳临界点过程中的力—位移曲线分别如图10(a)与图10(b)所示。从图10中可以看出，力—位移曲线的理论结果与实测结果之间存在一定误差；但从整体趋势上来看，理论结果与实测结果均表明，初始折展角度对支承力和失稳行程的影响最为显著，而折痕长度与相邻折痕夹角等尺寸参数的影响很小。

三浦折纸结构力—位移曲线的理论结果与实测结果的误差主要集中在以下两方面：1）稳态Ⅰ与稳态Ⅱ到失稳临界点的实测位移比理论位移高1~2 mm，这可能是因为在求理论位移时将折面设为了刚性，忽略了折面的变形，而实验中折面存在一定幅度的变形以及夹具与折纸结构为过盈配合；2）实测支承力与理论支承力存在一定误差，且γ₀=96°时稳态Ⅰ至失稳临界点过程中的实测支承力明显小于理论支承力，这可能是因为夹具存在一定摩擦与自重，以及理论模型作了一定简化。

为分析三浦折纸结构失稳时间随初始折展角度的变化规律，设计了以下实验，实验装置采用图9(b)中的Ⅱ号装置。具体实验方案如下：先将三浦折纸结构由稳态Ⅱ折展至失稳临界点，随后录制其由失稳临界点折展至稳态Ⅰ的过程，并使用MATLAB软件按30帧/s的速率将视频差分为图像，以此记录三浦折纸结构失稳所需的时间。实验用三浦折纸结构的其余参数不变，均与2.2节中的基准值一致，仅初始折展角度变化（分别取γ₀=87°、114°、128°）。

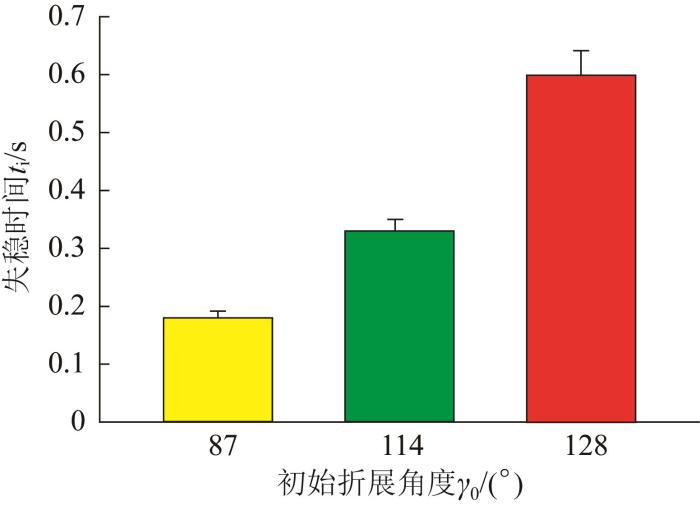
不同初始折展角度γ₀下三浦折纸结构的失稳时间t_i如图11所示。由图11可知，随着初始折展角度的减小，三浦折纸结构的失稳时间逐渐缩短。结果表明，初始折展角度越小，三浦折纸结构的失稳速度越快。

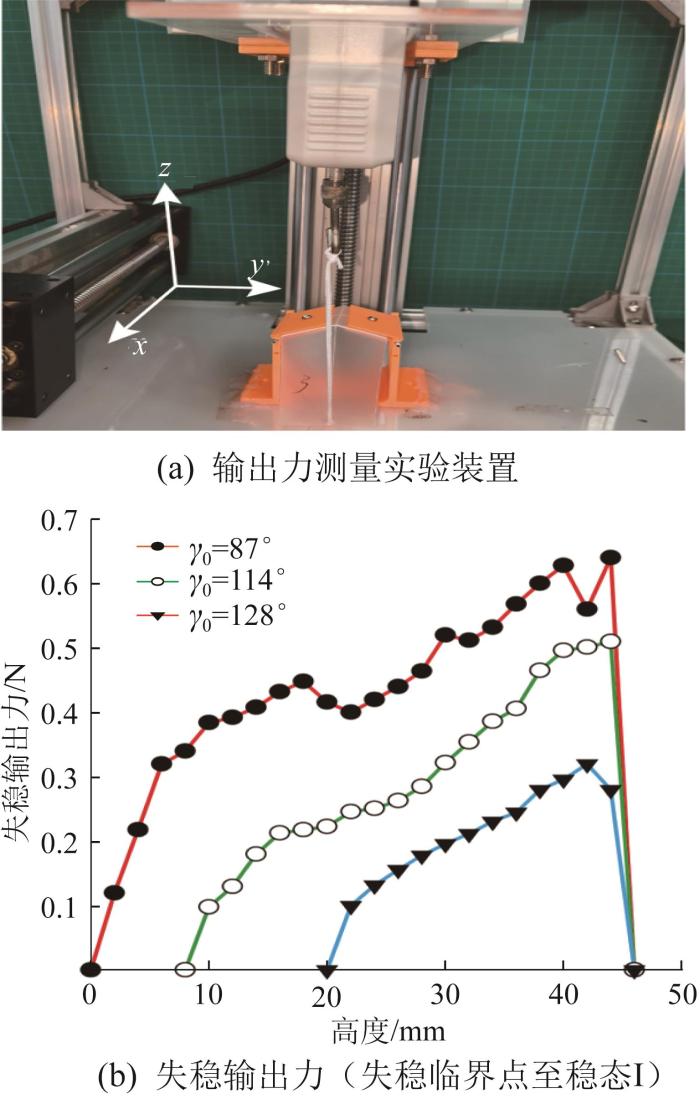
为分析三浦折纸结构失稳时折痕4（长度为l₄）末端输出力随初始折展角度的变化规律，设计了以下实验，实验装置整体采用图9(b)中的Ⅱ号装置，区别在于：尼龙绳与折纸结构的连接点由折痕2的中点改为折痕4的末端点，测力计由固定改为可沿x轴方向水平移动，如图12(a)所示。实验方案如下：利用丝杆带动折纸结构末端向上移动，每次向上移动的距离为2 mm，同时通过导轨带动测力计移动，以使尼龙绳始终保持竖直状态，同步读取测力计数值。实验用三浦折纸结构的其余参数不变，均与2.2节中的基准值一致，仅初始折展角度变化（分别取γ₀=87°、114°、128°）。不同初始折展角度下测得的失稳输出力如图12(b)所示。由图可知，随着初始折展角度的减小，在相同行程下三浦折纸结构失稳时沿竖直方向提供的输出力增大。

为展示通过调整尺寸无关参数来调节三浦折纸结构稳态特性的可行性，设计了一种基于三浦折纸结构的水上折纸机器人，其运动机理受海龟与青蛙的游动方式启发。如图13(a)和图13(b)所示，海龟与青蛙游动时脚掌先快速向后拍动以增大自身向前滑动的距离，滑动结束后缓慢将脚掌移回原处以减小回退距离。机器人通过三浦折纸结构的双稳态特性来实现这一运动机理：首先，通过驱动装置使折纸结构由稳态Ⅰ折展至失稳临界点；随后，折纸结构释放储存在势能壁垒中的能量，使得机器人向前游动；当游动停止后，由驱动装置将折纸结构折展回稳态Ⅰ，由于存在势能壁垒，使得该过程的速度降低，减小了机器人的回退距离，如图13(c)所示。

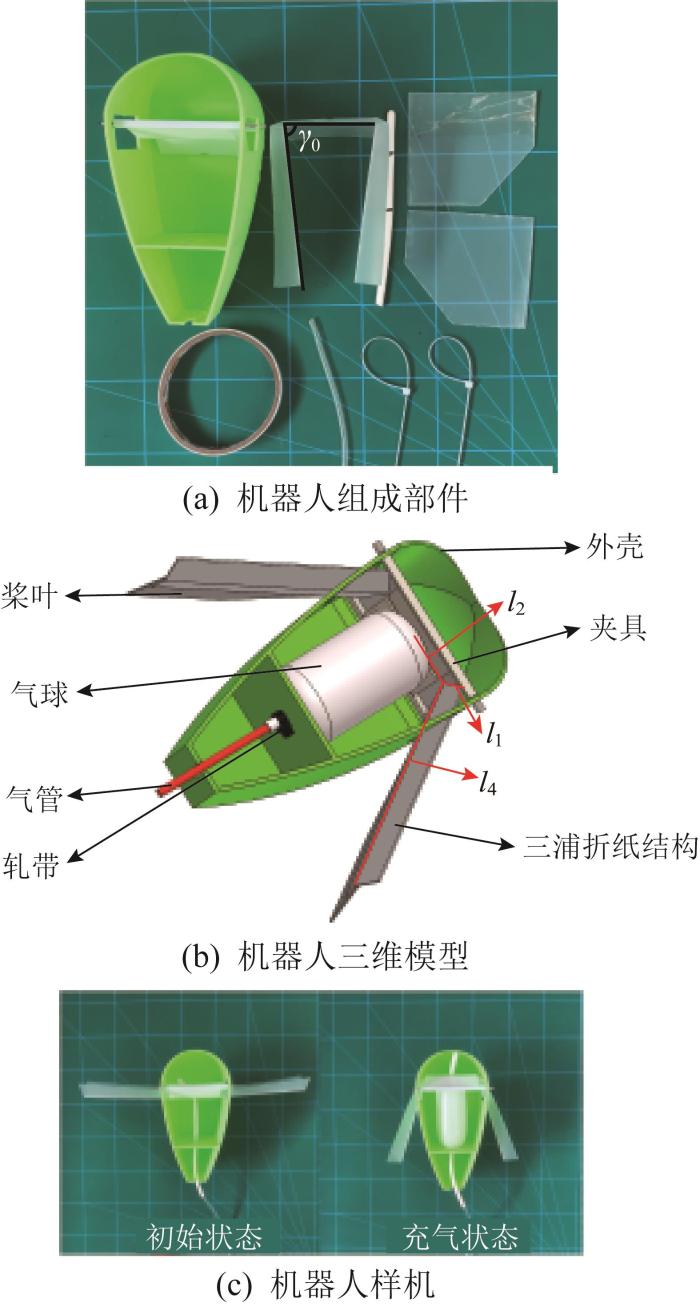
水上折纸机器人的组成部件如图14(a)所示，主要由外壳、夹具、三浦折纸结构、桨叶、气球和气管组成，其三维模型如图14(b)所示。其中，机器人驱动装置由气球与气管构成，通过气球充放气带动三浦折纸结构与桨叶运动。机器人样机的初始状态与充气状态如图14(c)所示。

由水上折纸机器人的运动机理可知，其游动速度受势能壁垒的影响，且势能壁垒越大，游动速度越快。机器人外壳尺寸由夹具尺寸决定，而夹具尺寸由三浦折纸结构尺寸参数决定。在狭小环境下，通过调整尺寸参数来调节机器人游动速度缺乏适用性，而采用调整折痕制成角度与预折叠角度等尺寸无关参数的方法适用性更广。

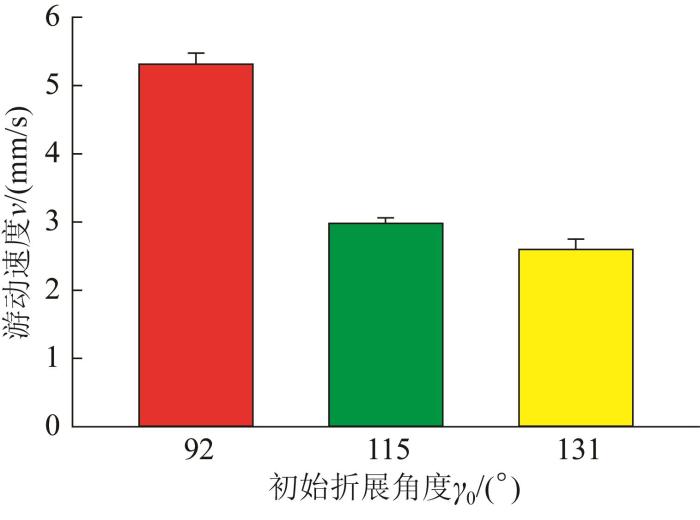
机器人样机中的三浦折纸结构由2个相同的单胞三浦折纸结构并联组成，如图15所示。每个三浦折纸结构的具体尺寸如下：l1=l3=26.6 mm、l2= 30 mm、l4=70 mm、α1=70°。在折痕制成角度与预折叠角度均为180°的情况下折展后γ₀=131°，通过调整折痕制成角度可将γ₀减小至92°左右。初始折展角度调整前后机器人的游动过程如图16所示，机器人游动速度v与初始折展角度γ₀的关系如图17所示。从图17中可以看出，在不改变机器人样机尺寸的条件下，通过调整初始折展角度可使机器人的游动速度提升70%。由此可知，通过调整三浦折纸结构尺寸无关参数来调节其稳态特性具有一定的实际应用价值。

本文依托单胞三浦折纸结构的双稳态特性，分析了不同参数对三浦折纸结构稳态特性及其初始折展角度的影响，得到了以下结论。

1）初始折展角度对三浦折纸结构势能壁垒的影响最为显著，且两者呈负相关。

2）折痕制成角度对三浦折纸结构初始折展角度的影响最为显著，且两者呈正相关。

3）通过相关实验分析了调整初始折展角度对三浦折纸结构失稳时间、失稳输出力等稳态特性的影响。在不改变机器人样机尺寸的情况下，通过调整三浦折纸结构的初始折展角度，使得机器人的游动速度提升了70%，验证了本文研究的实用价值。

本文所提出的通过调整尺寸无关参数来调节稳态特性的方法拓展了三浦折纸结构双稳态特性分析的路径，同时对后续三浦折纸结构双稳态特性的研究与应用有一定参考价值。