基于NSGA-Ⅱ和TOPSIS法的横波可控震源振动器平板疲劳寿命优化

doi:10.3785/j.issn.1006-754X.2025.04.141

基于NSGA-Ⅱ和TOPSIS法的横波可控震源振动器平板疲劳寿命优化

陈振^,¹^,², 冉庆杰^,^,¹, 英晓洋¹, 陈能鹏¹, 魏超成¹, 王乔木¹

1.西南石油大学机电工程学院，四川成都 610500

2.页岩气评价与开采四川省重点实验室，四川成都 610500

Fatigue life optimization of sheer wave vibroseis vibrator baseplate based on NSGA-Ⅱ and TOPSIS method

CHEN Zhen^,¹^,², RAN Qingjie^,^,¹, YING Xiaoyang¹, CHEN Nengpeng¹, WEI Chaocheng¹, WANG Qiaomu¹

1.School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China

2.Sichuan Key Laboratory of Shale Gas Evaluation and Exploitation, Chengdu 610500, China

通讯作者: 冉庆杰（2000—），男，硕士生，从事可靠性分析、疲劳寿命预测研究，E-mail: 1638785198@qq.com，https://orcid.org/0009-0001-5918-3740

收稿日期: 2024-05-20 修回日期: 2024-07-12

基金资助:

页岩气评价与开采四川省重点实验室资助项目. YSK2022013
四川省科技厅自然科学基金面上项目. 2024NSFSC0094

First author contact: CHEN Z, RAN Q J, YING X Y, et al. Fatigue life optimization of sheer wave vibroseis vibrator baseplate based on NSGA-Ⅱ and TOPSIS method[J]. Chinese Journal of Engineering Design, 2025, 32(2): 272-280.

Received: 2024-05-20 Revised: 2024-07-12

作者简介 About authors

陈　振（1985—），男，副教授，硕士生导师，博士，从事油气装备疲劳行为、可靠性设计和安全评价及理论等研究，E-mail:117976897@qq.com , E-mail：117976897@qq.com

摘要

横波可控震源振动器平板作为页岩气勘探中的关键部件，其疲劳寿命直接影响可控震源的使用寿命和勘探精度。然而，传统的振动器平板疲劳寿命优化方法未考虑平板与平板齿间焊接残余应力的影响，导致平板结构在抗疲劳优化设计方面效果不佳。为此，使用局部灵敏度法对平板疲劳寿命进行敏感性分析，确定了焊接残余应力为影响疲劳寿命的关键因素。随后，建立了平板的各向最大焊接残余应力与焊接速度和焊接层间温度之间的数学模型，并以各向最大焊接残余应力为约束，以疲劳寿命为优化目标，建立相应的优化模型。最后，利用NSGA-Ⅱ（non-dominated sorting genetic algorithm-Ⅱ，非支配排序遗传算法-Ⅱ）获取Pareto解集，并结合熵权法和TOPSIS（technique for order preference by similarity to ideal solution，逼近理想解排序）法确定最佳优化方案：焊接速度为10.23 mm/s，焊接层间温度为105 ℃。结果表明，优化后平板的疲劳寿命为10.23年，相比优化前提高了17.72%。研究结果可为横波可控震源振动器平板的疲劳寿命优化提供科学有效的理论方法和工程指导。

关键词： 横波可控震源 ; 振动器平板 ; 疲劳寿命 ; 焊接残余应力 ; NSGA-Ⅱ ; TOPSIS法

Abstract

The sheer wave vibroseis vibrator baseplate is a key component in shale gas exploration, and its fatigue life directly affects the service life of vibroseis and the exploration accuracy. However, traditional optimization methods for vibrator baseplate fatigue life ignore the welding residual stress between the baseplate and the baseplate teeth, resulting in poor performance in anti-fatigue optimization design for the baseplate structure. Therefore, the local sensitivity method was used to conduct a sensitivity analysis for the fatigue life of the baseplate, and the welding residual stress was determined as the key factor affecting the fatigue life. Subsequently, mathematical models between the maximum welding residual stresses in all directions of the baseplate and the welding speed and interlayer temperature were established. Meanwhile, with the maximum welding residual stresses in all directions as the constraints and the fatigue life as the optimization target, the corresponding optimization model was constructed. Finally, the NSGA-Ⅱ (non-dominated sorting genetic algorithm-Ⅱ) was used to obtain the Pareto solution set, and the best optimization scheme was determined by combining the entropy weight method and the TOPSIS (technique for order preference by similarity to ideal solution): the welding speed was 10.23 mm/s and the welding interlayer temperature was 105 ℃. The results showed that the fatigue life of the optimized baseplate was 10.23 years, which was 17.72% higher than that before optimization. The research results can provide scientific and effective theoretical methods and engineering guidance for the fatigue life optimization of the sheer wave vibroseis vibrator baseplate.

Keywords： sheer wave vibroseis ; vibrator baseplate ; fatigue life ; welding residual stress ; NSGA-Ⅱ ; TOPSIS method

PDF (3735KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈振, 冉庆杰, 英晓洋, 陈能鹏, 魏超成, 王乔木. 基于NSGA-Ⅱ和TOPSIS法的横波可控震源振动器平板疲劳寿命优化[J]. 工程设计学报, 2025, 32(2): 272-280 doi:10.3785/j.issn.1006-754X.2025.04.141

CHEN Zhen, RAN Qingjie, YING Xiaoyang, CHEN Nengpeng, WEI Chaocheng, WANG Qiaomu. Fatigue life optimization of sheer wave vibroseis vibrator baseplate based on NSGA-Ⅱ and TOPSIS method[J]. Chinese Journal of Engineering Design, 2025, 32(2): 272-280 doi:10.3785/j.issn.1006-754X.2025.04.141

对于页岩气勘探开发，横波可控震源具有抗干扰能力强且不受土壤中水饱和度影响的优势。横波可控震源激发的地震波通过地下岩石介质传播，勘探精度较高。振动器平板是横波可控震源与大地耦合的关键部件，其疲劳寿命直接影响可控震源的使用寿命和勘探精度^[1]。因此，对振动器平板的疲劳寿命进行优化成为提高横波可控震源使用寿命和勘探精度的关键环节。近年来，众多学者通过引入多目标优化算法来实现装备或零部件的疲劳寿命优化，但忽略了焊接残余应力与工作载荷应力的耦合作用，导致疲劳寿命的预测精度低及优化效果不佳^[2-3]。为此，本文拟在考虑焊接残余应力的基础上对振动器平板开展疲劳寿命优化，即通过构建疲劳寿命与焊接工艺参数的映射模型，实现基于焊接工艺参数优选的疲劳寿命优化。

近年来，随着焊接结构在工程装备中的广泛应用，其疲劳寿命优化逐渐成为研究热点。早在1871年，Wohler首次提出了S—N曲线和疲劳极限的概念，明确了应力是疲劳破坏的决定性因素，为金属材料的疲劳损伤评估奠定了理论基础^[4]。1945年，Miner^[5]提出了线性疲劳累积损伤理论并推导了相应的计算公式。丁彦闯等^[6]提出了基于累积损伤约束的焊接接头抗疲劳优化设计方法，通过采用虚拟疲劳试验与Kriging近似模型相结合的优化策略，实现了某焊接接头在疲劳可靠性约束下的轻量化设计。张红卫等^[7]采用有限元分析法建立了考虑焊接残余应力的桥壳疲劳寿命预测模型，明确了在疲劳寿命预测中考虑焊接残余应力的必要性。针对焊接结构的疲劳寿命优化，许多学者采用结构优化的方式来实现。丁勇等^[8]评估了模数式桥梁伸缩缝的疲劳寿命，并提出了4种结构优化方法，实现了伸缩缝结构强度和疲劳寿命的提升。周杰等^[9]利用虚拟样机仿真技术建立了车辆行走系统模型与路面不平度模型，并结合疲劳寿命预测方法实现了传动轴结构的优化设计。许期英等^[10]对汽车横向稳定杆进行了疲劳寿命优化设计，解决了横向稳定杆断裂失效的问题。Lukić等^[11]基于一阶可靠度分析法对焊接接头的疲劳可靠性进行了优化。王剑等^[12]基于结构应力法对焊接结构的疲劳寿命进行了灵敏度分析，并建立了结构应力、疲劳寿命对设计参数的灵敏度方程。Rizzo等^[13]结合断裂力学和可靠性理论，通过灵敏度分析识别了船舶焊接接头疲劳裂纹扩展的影响因素，并对其进行了优化设计。叶红玲等^[14]建立了以质量最小为目标的连续体结构疲劳寿命拓扑优化模型，并对优化模型进行了求解。宋烨空等^[15]利用响应面法建立了以最小疲劳寿命、最大等效应力为目标函数的关节轴承静态疲劳特性优化模型，并利用NSGA-Ⅱ（non-dominated sorting genetic algorithm-Ⅱ，非支配排序遗传算法-Ⅱ）进行了求解，有效地提高了该轴承的最小疲劳寿命。

综上，许多学者通过建立优化目标与设计参数间的近似模型来寻求焊接结构疲劳寿命的最优解。然而，近似模型对实际优化问题的拟合精度存在不确定性，导致所得解集分布不均，这不利于筛选符合工程实际的疲劳寿命优化方案。基于此，本文结合NSGA-Ⅱ^[15-16]和TOPSIS（technique for order preference by similarity to ideal solution，逼近理想解排序）法对横波可控震源振动器平板的疲劳寿命进行优化。首先，结合应力耦合准则与修正的S—N曲线，对影响平板疲劳寿命的关键因素进行局部灵敏度分析；然后，以焊接工艺参数（焊接速度、焊接层间温度）为设计变量、各向最大焊接残余应力为约束条件，建立平板疲劳寿命优化模型；最后，利用NSGA-Ⅱ求解Pareto解集，并结合熵权法和TOPSIS法确定可提升平板疲劳寿命的最佳焊接工艺参数。

1 耦合焊接残余应力的振动器平板疲劳寿命灵敏度分析

横波可控震源作为先进的勘探装备，能够产生频率和振幅均可精确调控的连续横波信号，且具有高效能、操作安全及成本效益显著的特点，其在油气勘探、地质结构研究等领域得到了广泛应用。横波可控震源的结构如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 横波可控震源结构

Fig.1 Structure of shear wave vibroseis

振动器平板作为耦合横波可控震源与大地的关键部件，承受震源车身重力与振动器交变激振力的共同作用，且其与平板齿的焊接部位又受到焊接残余应力的影响，在长期交变循环载荷作用下易发生疲劳破坏，影响使用寿命。因此，需对耦合焊接残余应力的振动器平板疲劳寿命进行优化。

1.1　疲劳分析方法

S—N曲线表征材料或结构疲劳寿命与应力水平之间的关系，其准确性将直接影响结构疲劳寿命的预测精度和优化效果。对于横波可控震源振动器平板，全尺寸平板的S—N曲线难以直接获取，需对其母材的S—N曲线进行修正。参考文献[17]，得到修正后的平板S—N曲线，可表示为：

l g N = 23.593 3 - m l g S - m l g 2.40

(1)

式中：N为循环次数；m为平板的材料常数，结合文献[18-19]可得 $m = 7.314 4$ ；S为最大应力，本文取等效焊接残余应力与工作载荷应力的耦合应力。

耦合应力S的计算式如下：

S = σ^{0} + σ^{f}

(2)

式中：σ⁰为平板与平板齿焊缝处的等效焊接残余应力，由等效应变公式计算得到，其值取决于焊接速度与焊接层间温度；σ^f为平板的工作载荷应力。

在运用修正S—N曲线进行疲劳寿命预测时，最大应力水平是由最大耦合应力经Goodman公式修正后得到的，修正后可表示为：

S = \frac{600 (σ_{m a x}^{0} - σ_{m i n}^{0})}{1 200 - σ_{m a x}^{0} - σ_{m i n}^{0} - 2 σ^{f}}

(3)

其中：

\{\begin{array}{l} σ_{m a x}^{0} = σ^{0} + σ_{m a x}^{f} \\ σ_{m i n}^{0} = - σ^{0} + σ_{m i n}^{f} \end{array}

式中： $σ_{m i n}^{0}$ 、 $σ_{m a x}^{0}$ 为等效焊接残余应力的最小、最大值， $σ_{m i n}^{f}$ 、 $σ_{m a x}^{f}$ 为工作载荷应力的最小、最大值。

联立式(1)至式(3)，可得循环次数N与等效焊接残余应力和工作载荷应力的关系，具体如下：

\begin{array}{l} N = 10 e x p \{\overset{}{\underset{}{\overset{}{23.593 3 - m l g 2.40 -}}} \\ m l g [\frac{600 (2 σ^{0} + σ_{m a x}^{f} - σ_{m i n}^{f})}{1 200 - 2 σ^{f} - σ_{m a x}^{f} - σ_{m i n}^{f}}]\} \end{array}

(4)

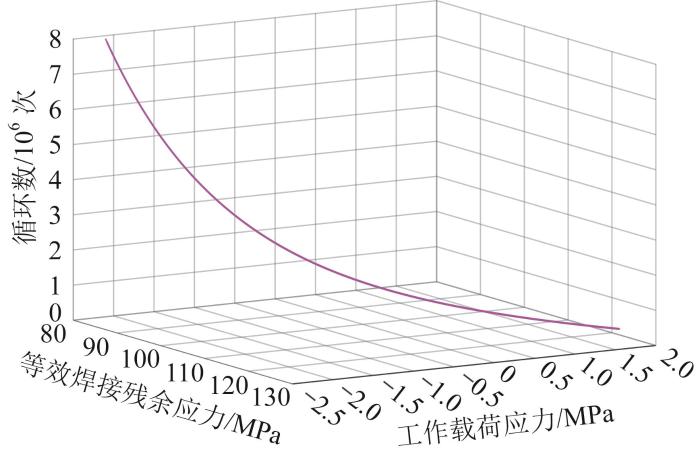
结合振动器平板的材料参数和焊接工艺参数，利用式(4)绘制其疲劳寿命曲线，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 振动器平板疲劳寿命曲线

Fig.2 Fatigue life curve of vibrator baseplate

1.2　基于修正 S — N 曲线的局部灵敏度分析

在对振动器平板疲劳寿命进行优化前，需对其影响因素进行量化评价。为此，基于上文建立的循环次数与等效焊接残余应力和工作载荷应力的关系式，对振动器平板疲劳寿命的影响因素进行局部灵敏度分析^[20]。通过求导分别计算得到循环次数相对于等效焊接残余应力和工作载荷应力的一阶灵敏度方程，具体推导如下：

\frac{d N}{d σ^{0}} = l n 10 \cdot 10 e x p \{23.593 3 - m l g 2.40 - m l g [\frac{600 (2 σ^{0} + σ_{m a x}^{f} - σ_{m i n}^{f})}{1 200 - 2 σ^{f} - σ_{m a x}^{f} - σ_{m i n}^{f}}]\} (\frac{- 2 m l g e}{2 σ^{0} + σ_{m a x}^{f} - σ_{m i n}^{f}})

(5)

\frac{d N}{d σ^{f}} = l n 10 \cdot 10 e x p \{23.593 3 - m l g 2.40 - m l g [\frac{600 (2 σ^{0} + σ_{m a x}^{f} - σ_{m i n}^{f})}{1 200 - 2 σ^{f} - σ_{m a x}^{f} - σ_{m i n}^{f}}]\} (\frac{- 2 m l g e}{1 200 - 2 σ^{f} - σ_{m a x}^{f} - σ_{m i n}^{f}})

(6)

由上述灵敏度公式可知，循环次数与等效焊接残余应力呈负相关，即若要使循环次数最大，则需将等效焊接残余应力降至最低。

基于式(5)和式(6)，定义振动器平板疲劳寿命影响因素的灵敏度比值β：

β = \frac{d N / d σ^{0}}{d N / d σ^{f}} = \frac{1 200 - 2 σ^{f} - σ_{m a x}^{f} - σ_{m i n}^{f}}{2 σ^{0} + σ_{m a x}^{f} - σ_{m i n}^{f}}

(7)

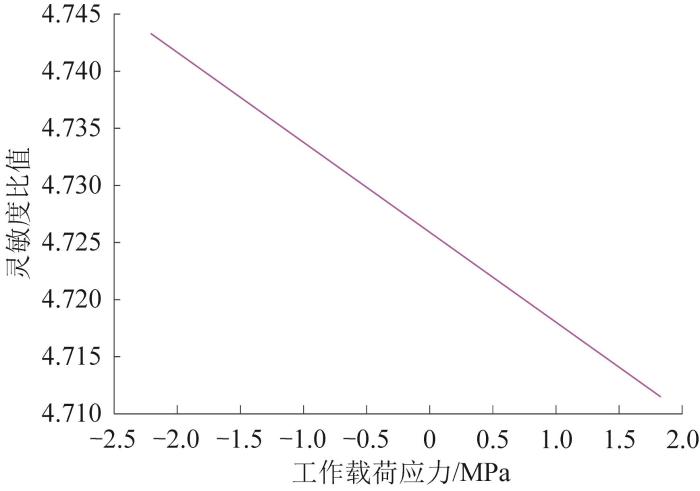
基于文献[17]中获得的振动器平板焊缝处的等效焊接残余应力，利用式(7)绘制不同工作载荷应力下平板疲劳寿命影响因素的灵敏度比值曲线，如图3所示。由图3可知，在一定的工作载荷应力范围内，随着工作载荷应力的增大，灵敏度比值 $β > > 1$ ，说明等效焊接残余应力对平板焊缝处疲劳寿命的影响远大于工作载荷应力，其为影响疲劳寿命的主导因素。因此，可通过优化焊接残余应力来提高平板的疲劳寿命。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 振动器平板疲劳寿命影响因素的灵敏度比值曲线

Fig.3 Sensitivity ratio curve of factors influencing on fatigue life of vibrator baseplate

2 振动器平板疲劳寿命优化模型的构建与求解

2.1　焊接残余应力的变化规律分析

为了实现通过优选焊接工艺参数来优化焊接残余应力，利用焊接有限元软件SYSWELD对不同焊接工艺参数组合下振动器平板焊缝处焊接残余应力的变化规律进行数值模拟（平板焊接模型参见文献[17]）。其中，焊接速度、焊接层间温度的取值如表1所示。

表1 焊接速度与焊接层间温度的取值

Table 1 Values of welding speed and welding interlayer temperature

设计变量	取值
焊接速度/(mm/s)	6、8、10、12
焊接层间温度/℃	100、150、200、250

新窗口打开| 下载CSV

通过数值模拟分析得到不同焊接速度、焊接层间温度下振动器平板焊缝处沿X、Y、Z向的最大焊接残余应力，如表2所示。

表2 不同焊接工艺参数下振动器平板的各向最大焊接残余应力

Table 2 Maximum welding residual stresses in all directions of vibrator baseplate under different welding process parameters

焊接速度/(mm/s)	焊接层间温度/℃	最大焊接残余应力/MPa
焊接速度/(mm/s)	焊接层间温度/℃	X向	Y向	Z向
6	100	490.75	185.90	110.83
	150	490.67	168.63	102.93
	200	489.55	153.98	93.24
	250	488.44	150.05	90.42
8	100	470.42	186.93	135.47
	150	498.04	165.73	112.91
	200	496.80	153.67	100.52
	250	523.02	169.67	118.79
10	100	460.20	114.02	108.28
	150	499.89	110.48	81.70
	200	493.83	131.13	98.51
	250	501.36	170.83	115.58
12	100	501.91	128.10	100.62
	150	529.27	135.32	94.56
	200	514.95	141.41	108.94
	250	511.10	136.43	125.22

新窗口打开| 下载CSV

根据表2数据，利用二元回归法拟合得到振动器平板焊缝处各向最大焊接残余应力与焊接速度和焊接层间温度间的数学模型，具体表达式如下：

\{\begin{array}{l} \begin{array}{l} σ_{x, m a x} = 163.3 + 100.5 v + 1.112 T + 0.819 5 v T - 20.66 v^{2} - 0.025 74 T^{2} - 0.033 59 v^{2} T - \\ 0.000 606 6 v T^{2} + 1.025 v^{3} + 5.629 \times 10^{- 5} T^{3} \end{array} \\ \begin{array}{l} σ_{y, m a x} = - 2 983 + 1 122 v + 8.778 T - 2.46 v T - 122.7 v^{2} + 0.015 09 T^{2} + 0.147 3 v^{2} T - 0.008 534 v T^{2} + \\ 0.001 477 v^{2} T^{2} + 4.211 v^{3} - 7.323 \times 10^{- 5} v^{3} T^{2} \end{array} \\ σ_{z, m a x} = - 426.1 + 236.5 v - 1.31 T - 0.103 8 v T - 26.22 v^{2} + 0.004 056 T^{2} + 0.009 288 v^{2} T - 5.664 \times 10^{- 7} v T^{2} + 0.895 4 v^{3} \end{array}

(8)

式中：σ_x_,_max、σ_y_,_max、σ_z_,_max分别为X、Y、Z向最大焊接残余应力，v为焊接速度，T为焊接层间温度。

上述振动器平板焊缝处X、Y、Z向最大焊接残余应力拟合模型的相关系数分别为0.953 9、0.996 4、0.928 3，说明拟合模型的精度较高。

为了验证式(8)所示拟合模型的准确性，取焊接速度为8 mm/s，焊接层间温度为120、180、220 ℃，通过数值模拟分析得到振动器平板焊缝处各向最大焊接残余应力，并将焊接工艺参数代入式(8)计算对应的应力值，将两者进行对比并计算相对误差，结果如表3所示。

表3 振动器平板各向最大焊接残余应力的仿真值与计算值对比（ v=8 mm/s）

Table 3 Comparison of simulation values and calculation values of maximum welding residual stresses in all directions of vibrator baseplate (v=8 mm/s)

焊接层间温度/℃	X向最大焊接残余应力			Y向最大焊接残余应力			Z向最大焊接残余应力
焊接层间温度/℃	仿真值/MPa	计算值/MPa	相对误差/%	仿真值/MPa	计算值/MPa	相对误差/%	仿真值/MPa	计算值/MPa	相对误差/%
120	501.78	488.78	-2.59	177.53	174.22	-1.86	114.02	118.50	3.93
180	507.39	500.22	-1.41	161.40	155.07	-3.92	94.39	97.94	3.76
220	508.07	502.56	-1.08	154.70	157.71	1.95	99.00	100.27	1.28

新窗口打开| 下载CSV

由表3可知，各向最大焊接残余应力计算值与仿真值的相对误差不超过4%，且变化趋势高度吻合，说明所构建的拟合模型可准确反映振动器平板焊缝处各向最大焊接残余应力的变化趋势。

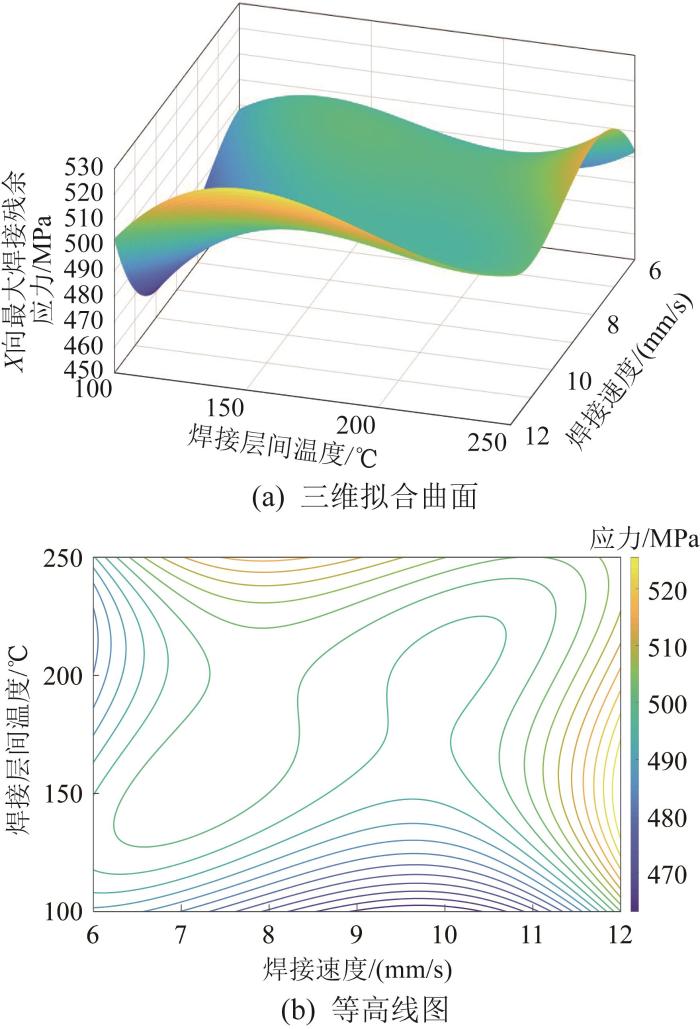
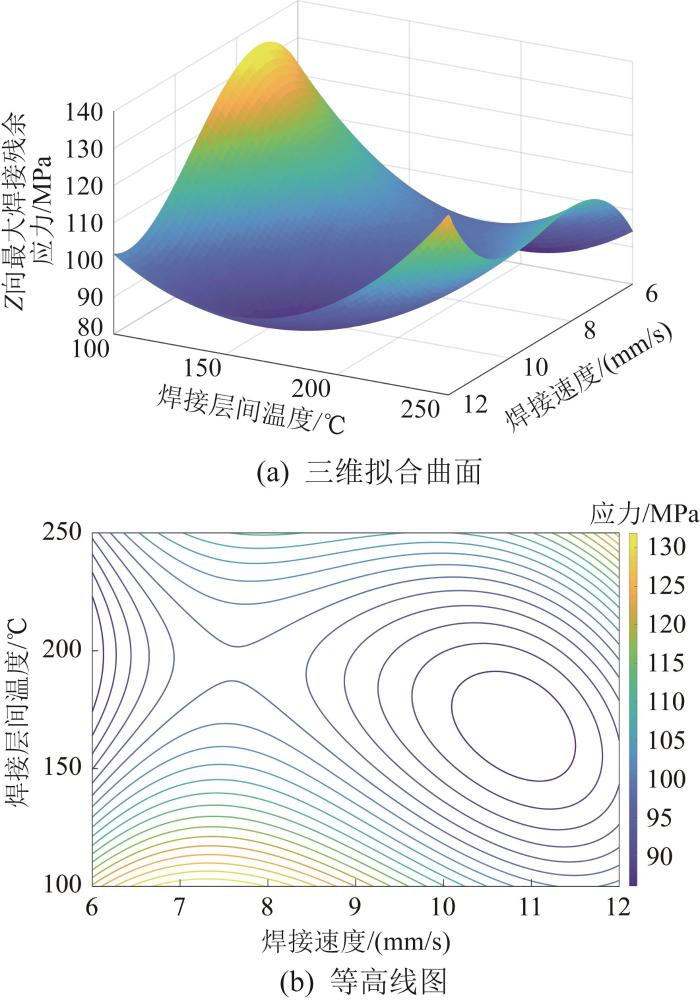
根据式(8)中的X向最大焊接残余应力数学关系式，结合表2中焊接速度与焊接层间温度的多种组合方案，利用MATLAB软件绘制振动器平板焊缝处X向最大焊接残余应力的三维拟合曲面与对应的等高线图，以观察其变化规律，结果如图4所示。其中：图4(a)所示为三维拟合曲面，直观展示了焊接速度与焊接层间温度对X向最大焊接残余应力的影响规律；图4(b)所示为对应等高线图，便于识别最优焊接工艺参数区间。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 振动器平板 X 向最大焊接残余应力的变化规律

Fig.4 Variation law of maximum welding residual stress in X direction of vibrator baseplate

由图4可知：当焊接速度为9~11 mm/s、焊接层间温度为100~150 ℃时，等高线密集，X向最大焊接残余应力的变化梯度较大，说明此参数区间内焊接速度和焊接层间温度的影响较大；当焊接速度为10 mm/s、焊接层间温度为100 ℃时，X向最大焊接残余应力较小；而当焊接速度为8 mm/s、焊接层间温度为250 ℃以及焊接速度为12 mm/s、焊接层间温度为150 ℃时，X向最大焊接残余应力较大。

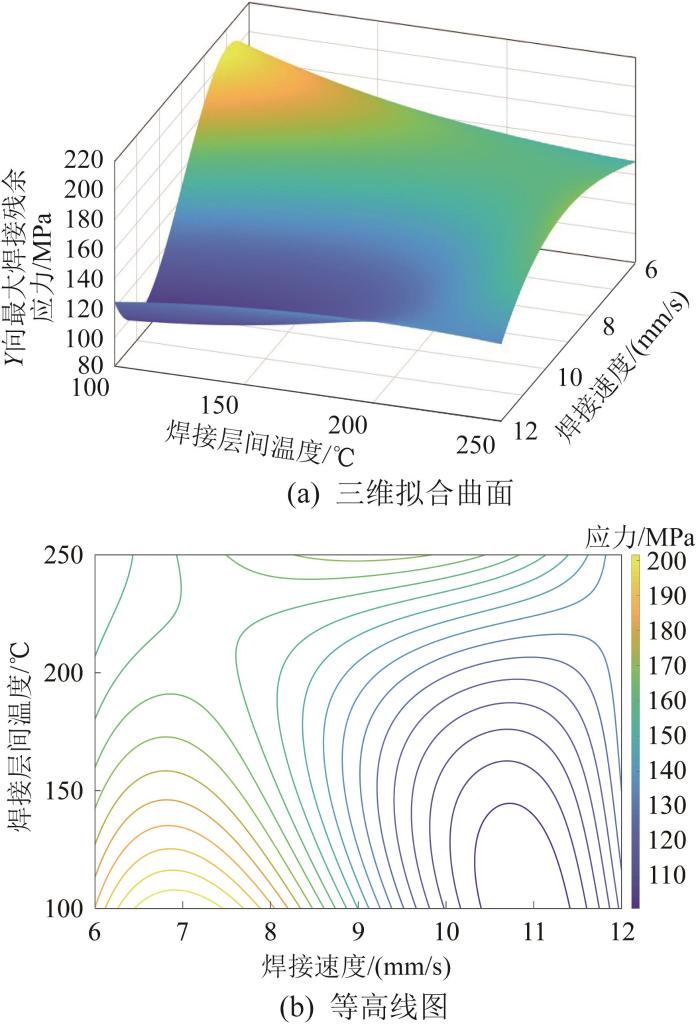
同理，绘制振动器平板焊缝处Y向最大焊接残余应力随焊接工艺参数变化的三维拟合曲面及对应的等高线图，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 振动器平板 Y 向最大焊接残余应力的变化规律

Fig.5 Variation law of maximum welding residual stress in Y direction of vibrator baseplate

由图5可知，当焊接速度为10~12 mm/s、焊接层间温度为100~150 ℃时，Y向最大焊接残余应力较小且变化平缓，说明该参数区间内焊接速度和焊接层间温度的影响较小；当焊接速度为6~8 mm/s、焊接层间温度为100~150 ℃时，Y向最大焊接残余应力较大且变化梯度较大，即焊接工艺参数的影响较大。

随后，绘制振动器平板焊缝处Z向最大焊接残余应力随焊接工艺参数变化的三维拟合曲面及对应的等高线图，如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 振动器平板 Z 向最大焊接残余应力的变化规律

Fig.6 Variation law of maximum welding residual stress in Z direction of vibrator baseplate

由图6可知，当焊接速度为10~12 mm/s、焊接层间温度为100~200 ℃时，Z向最大焊接残余应力变化平缓，说明该参数区间内焊接速度和焊接层间温度的影响较小；当焊接速度为6~9 mm/s、焊接层间温度为100~150 ℃时，Z向最大焊接残余应力较大且变化梯度较大，即焊接工艺参数的影响较大。

综上，出现焊接残余应力极小值时对应的焊接工艺参数区间如下：焊接速度为10~12 mm/s、焊接层间温度为100~150 ℃。

2.2　优化模型的建立与求解

基于运用二元回归法确定的振动器平板焊缝处各向最大焊接残余应力与焊接工艺参数之间的数学模型，建立以疲劳寿命最大（即X、Y、Z向焊接残余应力最小）为优化目标、各向最大焊接残余应力为约束的多目标优化模型，具体如下：

\{\begin{array}{l} f i n d σ_{x}, σ_{y}, σ_{z} \\ m a k e L_{F} \to m a x \\ s . t . σ_{x, m a x}, σ_{y, m a x}, σ_{z, m a x} \\ v \in [10, 12] m m / s \\ T \in [100, 150] ℃ \end{array}

(9)

式中： $σ_{x} 、 σ_{y} 、 σ_{z}$ 分别为X、Y、Z向焊接残余应力；L_F为疲劳寿命，计算方法参见文献[17]。

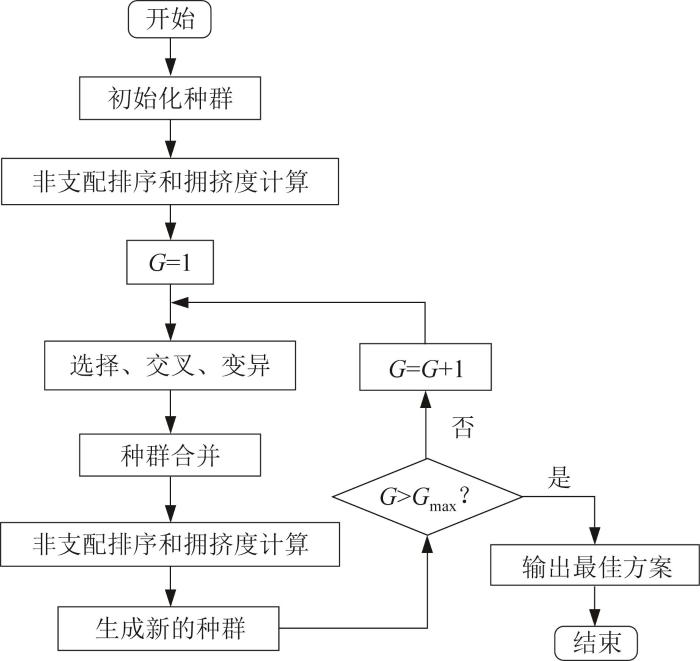
鉴于NSGA-Ⅱ可保证非劣最优解的均匀分布，且其在多目标优化求解中具有计算迭代次数少、收敛快的优势，本文运用NSGA-Ⅱ来求解上述优化模型的Pareto解集。NSGA-Ⅱ的求解流程如图7所示。本文中NSGA-Ⅱ的参数设置如表4所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 NSGA-Ⅱ的求解流程

Fig.7 Solution process of NSGA-Ⅱ

表4 NSGA-Ⅱ的参数设置

Table 4 Parameter setting for NSGA-Ⅱ

参数	数值	参数	数值
交叉概率	0.9	变异概率	0.1
交叉分布指数	20	变异分布指数	20
种群数量/个	400	迭代数/次	200

新窗口打开| 下载CSV

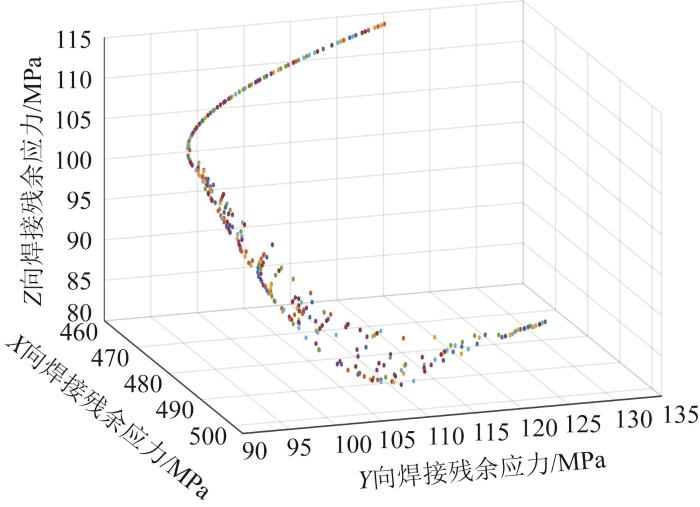
利用MATLAB软件编程求解得到振动器平板焊接残余应力的Pareto解集，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 基于NSGA-Ⅱ的振动器平板焊接残余应力的Pareto解集

Fig.8 Pareto solution set of welding residual stress of vibrator baseplate based on NSGA-Ⅱ

图8展示了利用NSGA-II求解得到的焊接残余应力Pareto解集的分布特征，基于该Pareto解集对振动器平板的疲劳寿命进行优化，以确定多目标优化模型在不同权重下的最优解。

3 基于熵权法和TOPSIS法的振动器平板疲劳寿命优化

3.1　焊接工艺参数对焊接残余应力的影响权重分析

由于本文的3个优化目标涉及贡献度的差异，需对3个优化目标进行评估，得到其影响权重比。以3个优化目标为评估指标，基于Pareto最优解集及综合权重，采用熵权法和TOPSIS法^[21]对图8所示的Patero解集进行评估并排序。

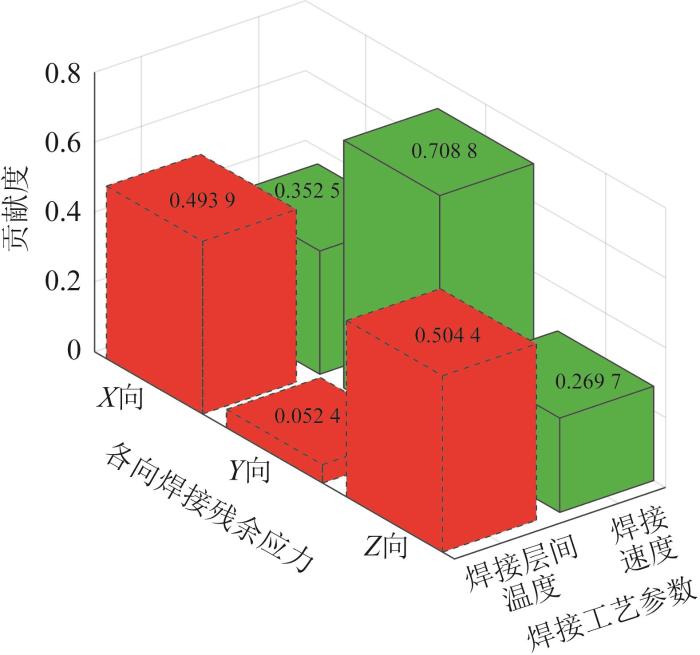
基于上文建立的振动器平板焊缝处各向最大焊接残余应力与焊接工艺参数的拟合关系式，通过灵敏度分析得到焊接速度与焊接层间温度对X、Y、Z向焊接残余应力这3个性能指标的贡献度，如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 焊接工艺参数对各向焊接残余应力的贡献度

Fig.9 Contribution degree of welding process parameters to welding residual stresses in all directions

3.2　基于熵权法和TOPSIS法的疲劳寿命优化

采用熵权法和TOPSIS法对焊接工艺参数的影响程度进行全面评估。首先，构建基于TOPSIS法的决策矩阵 X ：

X = [\begin{matrix} x_{11} x_{12} \dots x_{1 n} \\ x_{21} x_{22} \dots x_{2 n} \\ ⋮ ⋮ ⋮ \\ x_{m 1} x_{m 2} \dots x_{m n} \end{matrix}]

(10)

式中： $x_{i j}$ 为第j个焊接工艺参数对第i个性能指标的贡献度， $i = 1, 2, \dots, m$ ， $j = 1, 2, \dots, n$ ；m为性能指标数量，n为焊接工艺参数数量。

利用式(11)对决策矩阵中各元素进行正则化处理，得到处理后的决策矩阵 r。

r_{i j} = \frac{x_{i j}}{\sqrt[]{\sum_{i = 1}^{m} x_{i j}^{2}}}

(11)

利用式(12)计算正则化处理后决策矩阵 r 中各元素的特征比重p_ij，得到特征比重矩阵 p。

p_{i j} = \frac{r_{i j}}{\sum_{i = 1}^{m} r_{i j}}

(12)

结合式(13)计算第i个性能指标的熵值e_i，由此得到对应的熵值矩阵 e。

e_{i} = \frac{1}{l n n} \sum_{j = 1}^{n} p_{i j} l n p_{i j}

(13)

利用熵权法，即式(14)计算得到第i个性能指标的权重系数ω_i，由此得到对应的权重矩阵 ω。

ω_{i} = \frac{1 - e_{i}}{\sum_{i = 1}^{m} (1 - e_{i})}

(14)

将权重矩阵 ω 与决策矩阵 r 相乘，计算得到加权决策矩阵 V ：

V = [\begin{matrix} v_{11} v_{12} \dots v_{1 n} \\ v_{21} v_{22} \dots v_{2 n} \\ ⋮ ⋮ ⋮ \\ v_{m 1} v_{m 2} \dots v_{m n} \end{matrix}]

(15)

式中： $v_{i j}$ 为第j个焊接工艺参数对第i个性能指标影响的加权综合评价值。

在TOPSIS法中，正理想解 V⁺ 和负理想解 V^- 的定义如下：

\{\begin{array}{l} V^{+} = [m a x v_{i 1} m a x v_{i 2} \dots m a x v_{i n}] \\ V^{-} = [m i n v_{i 1} m i n v_{i 2} \dots m i n v_{i n}] \end{array}

(16)

各性能指标对应的正、负理想解之间的距离采用欧式距离公式进行计算，表达式为：

\{\begin{array}{l} d_{i}^{+} = \sqrt[]{\sum_{j = 1}^{n} {({V_{j}}^{+} - ν_{i j})}^{2}} \\ d_{i}^{-} = \sqrt[]{\sum_{j = 1}^{n} {({V_{j}}^{-} - ν_{i j})}^{2}} \end{array}

(17)

则各性能指标与对应正理想解的贴近度η_j 的计算式为：

η_{j} = \frac{d_{j}^{-}}{d_{j}^{+} + d_{j}^{-}}

(18)

由式(18)可知，贴近度越大，说明在该焊接工艺参数下性能指标越接近正理想解，即综合性能越优。因此，本文将贴近度定义为评价各焊接工艺参数对各向焊接残余应力的综合贡献度。

根据图9所示的各焊接工艺参数对各向焊接残余应力的贡献度以及上述理论计算公式，首先采用熵权法计算各焊接工艺参数对各向焊接残余应力的影响权重，如表5所示。

表5 焊接工艺参数对各向焊接残余应力的影响权重

Table 5 Influence weight of welding process parameters on welding residual stresses in all directions

性能指标	焊接速度	焊接层间温度
X向焊接残余应力	0.113 0	0.158 2
Y向焊接残余应力	0.198 5	0.014 7
Z向焊接残余应力	0.084 2	0.157 5

新窗口打开| 下载CSV

随后，采用TOPSIS法求解各向焊接残余应力与正、负理想解的贴近度并进行排序，结果如表6所示。

表6 各向焊接残余应力与正、负理想解的贴近度及其排序

Table 6 Closeness degree and sequence of welding residual stresses in all directions to their positive and negative ideal solutions

性能指标	$d_{j}^{+}$	$d_{j}^{-}$	η_j	排序结果
X向焊接残余应力	0.085 5	0.146 4	0.631 2	1
Y向焊接残余应力	0.143 5	0.114 3	0.443 3	3
Z向焊接残余应力	0.114 3	0.142 8	0.555 5	2

新窗口打开| 下载CSV

基于利用NSGA-II求得的Pareto解集，结合上述优化决策评判体系选取最佳优化方案：X、Y、Z向焊接残余应力分别为460.02、114.40、111.65 MPa。该方案对应的焊接速度为10.23 mm/s，焊接层间温度为105 ℃。

根据所确定的优化方案，通过应力耦合原则，结合Miner准则和修正的S—N曲线进行疲劳寿命计算，确定优化后振动器平板的疲劳寿命为10.23年，与文献[17]中仅耦合焊接残余应力后所预测的疲劳寿命8.69年相比提高了17.72%。

4 结论

本文针对横波可控震源振动器平板在考虑焊接残余应力耦合作用时的疲劳寿命进行优化，创新地以焊接工艺参数为设计变量、各向最大焊接残余应力为约束条件，建立了平板疲劳寿命优化模型，并运用NSGA-Ⅱ和TOPSIS法确定了最优方案。

1）基于运用二元回归法拟合得到的振动器平板各向最大焊接残余应力与焊接工艺参数之间的数学模型，建立了振动器平板疲劳寿命的多目标优化模型。随后，运用NSGA-Ⅱ求得焊接残余应力的Pareto解集，再通过熵权法和TOPSIS法确定了各焊接工艺参数对各向焊接残余应力的影响权重以及各向焊接残余应力与正、负理想解的贴近度。综合Pareto解集、影响权重和贴近度，确定最优焊接方案为：焊接速度为10.23 mm/s，焊接层间温度为105 ℃。此时，各向焊接残余应力分别为460.02、114.40、111.65 MPa。

2）根据最佳优化方案，计算振动器平板疲劳寿命，与优化前疲劳寿命相比提高了17.72%。由此说明，本文建立的振动器平板疲劳寿命多目标优化模型具有可行性，为基于焊接工艺参数优选的平板疲劳寿命优化提供了新思路。

3）本文的优化方法以NSGA-Ⅱ求得的Pareto解集为基础，采用熵权法和TOPSIS法进行最优方案的筛选。相比于传统的优化方法，本文优化方法在相同的迭代次数和优化难度下可得到更加准确的优化结果，且优化效率更高。同时，该优化方法对约束条件具有较强适应性，即使增加约束条件数量，其求解难度和计算成本也不会显著增加，并维持较高的迭代效率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陈振

可控震源振动器平板疲劳寿命和疲劳可靠性分析研究

［D］. 成都：西南石油大学， 2016. doi：10.1111/ffe.12467