本文链接:
近年来,国内外学者针对可变构型仿生移动机器人开展了广泛研究[11-13]。Zhang等[14]提出了一种由3段履带式移动机构串联铰接而成的蛇形机器人,其能够被动适应崎岖地形。Nodehi等[15]提出了一种基于绳驱的单履带式蛇形机器人,其可通过弯曲身体实现灵活转向。为了进一步提高机器人的运动灵活性,Fukuoka等[16]提出了一种能够灵活穿越狭窄空间的五段轮式蛇形机器人。Wang等[17]设计了一种基于主动关节的六段蠕虫型机器人,其可通过调节各关节的振幅来实现整体不同幅度的摆动。Bi等[18]提出了一种基于模块化弹性关节的仿蠕虫机器人,并通过优化伸缩关节的步态使机器人能够快速穿过狭窄缝隙。然而,受限于身体节段的数量和离散的运动方式,大多数蛇形与仿蠕虫机器人的变形灵活性仍有待提高,制约了其在曲折狭窄空间中平顺通过的能力。
为此,本文提出了一款仿变形虫可重构履带机器人。首先,通过模拟变形虫胞质颗粒的刚柔转换特性,融合俯仰关节与偏航关节,设计了一种基于闩锁结构的可锁定履带模块。机器人通过逐个调整前端履带模块的偏航关节角并锁定,同时依次解锁后端履带模块,以实现在前进过程中连续改变自身几何形态。然后,基于相邻履带模块之间的位置关系获取机器人的形态矩阵,并通过对关节角序列的迭代分析建立机器人的运动学模型。最后,通过开展仿真和样机测试实验来验证机器人的运动性能。
1 机器人结构设计与工作原理介绍
1.1 仿变形虫设计理念
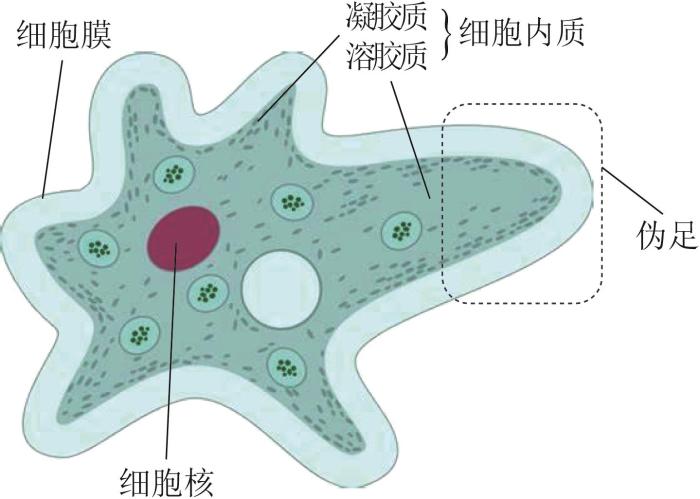
变形虫是一种微小的单细胞生物,其利用胞质颗粒的重组,可实现灵活变形。胞质颗粒存在凝胶和溶胶两种模态,且模态之间能相互转换。变形虫的外部支撑层由许多刚性的凝胶质颗粒构成,而内部身体则由大量液态的溶胶质颗粒组成,其结构组成如图1所示。区别于大多数爬行生物躯干蠕动或足式摆动的运动方式,变形虫通过伪足生长的方式来实现延伸运动,表现出极强的变形能力。具体为:内部的溶胶质颗粒不断向外流动并转换为凝胶质,实现尖端外翻并生成伪足,以向前延长身体;同时,后端的凝胶质颗粒转换为溶胶质并向内流动,实现身体后部的收缩;当完成收缩运动后,外侧的溶胶质颗粒重新转换为凝胶质,以使身体形态保持稳定。基于大量胞质颗粒的位置重组和模态转换,变形虫可随时重构自身形态,实现沿任意方向的运动与灵活变形,这为可重构机器人的设计提供了一种新的灵感。
图1
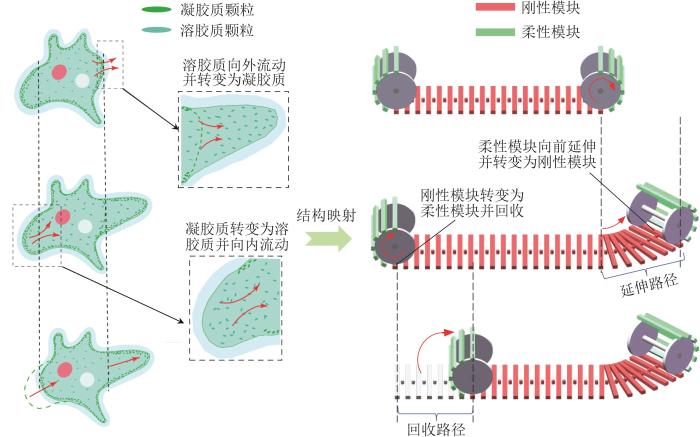
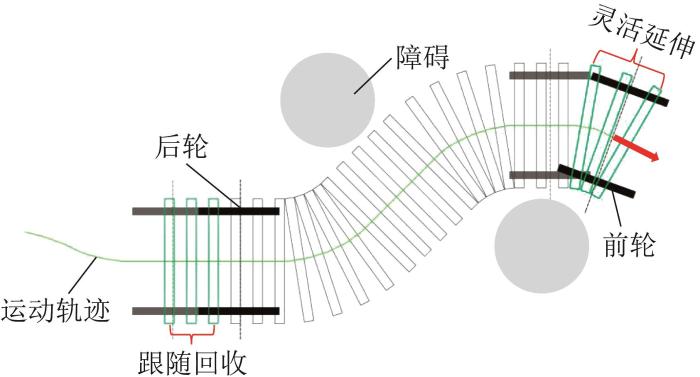
受变形虫灵活变形运动的启发,模仿其胞质颗粒重组机制,提出了一种基于可锁定机构的仿变形虫可重构履带机器人,设计理念如图2所示。该机器人的外部结构由闭环履带链组成,其中:顶部履带模块间为柔性自由连接,底部相邻履带模块间的连接状态可在刚性与柔性之间相互切换。通过前轮带动前端顶部柔性履带链节滚动到底部并转换为刚性状态,同时后端底部履带链节转换为柔性状态并由后轮回收到顶部,由此机器人完成一次变形前进运动。重复上述变形运动过程,机器人可沿底部履带构建的刚性支撑路径实现连续变形的前进运动。此外,履带链节之间在偏航方向上具有多种稳定的连接角度。通过依次选取不同的连接角度,机器人可实现灵活连续的平面变形运动。这种极度灵活的变形机制可使机器人躲避复杂地形中的障碍,极大地扩展了移动机器人的作业地形与应用场景。
图2
图2
仿变形虫可重构履带机器人的设计理念
Fig.2
Design concept of amoeba-like reconfigurable tracked robot
1.2 机器人结构设计
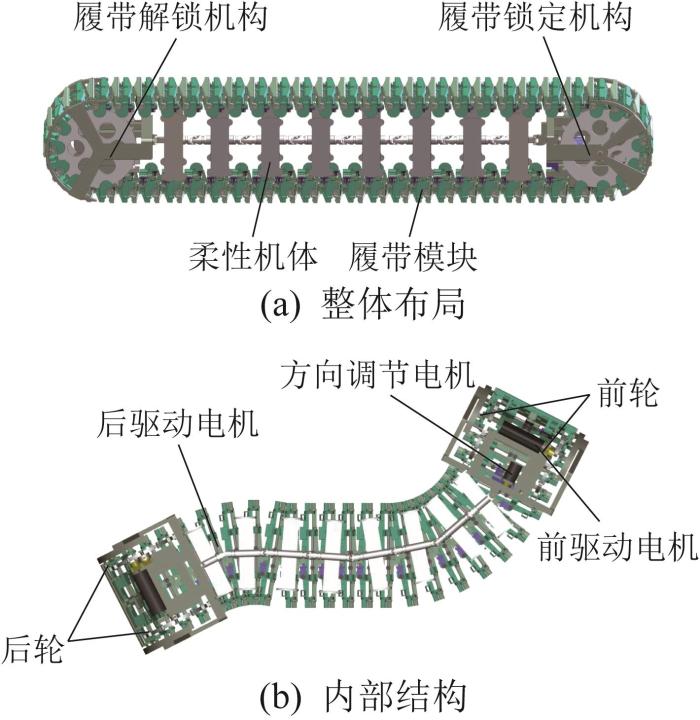
面向狭窄障碍空间的高通过性需求,区别于传统履带机器人的双链差速转向方式,仿变形虫可重构履带机器人采用可横向弯曲的单履带链驱动,在有效缩短宽度的同时可实现灵活蜿蜒运动。该机器人的运动仅由3个电机驱动,机体头部和尾部分别布置1个驱动电机以提供牵引力,前进方向由安装在机体头部的方向调节电机控制。机器人整体结构主要由模块化可锁定履带、履带锁定机构、履带解锁机构和柔性机体组成,如图3所示。履带链节之间的关节经特殊设计,包含俯仰关节和偏航关节。其中:偏航关节可被锁定,以使履带链节保持为刚性构型。在机器人前进过程中,头部的履带锁定机构依次调整前部自由履带链节间偏航关节的摆动角并逐个锁定,则可将底部履带构建为刚性的支撑路径,以决定前进方向。同时,尾部的履带解锁机构主动跟随并重置关节的自由度,以向头部提供新的自由履带。组合不同的关节锁定角,即可生成特定形状的刚性路径。不断地锁定与解锁可使机器人在前进过程中重构自身形态,实现灵活的变形运动以适应复杂环境。
图3
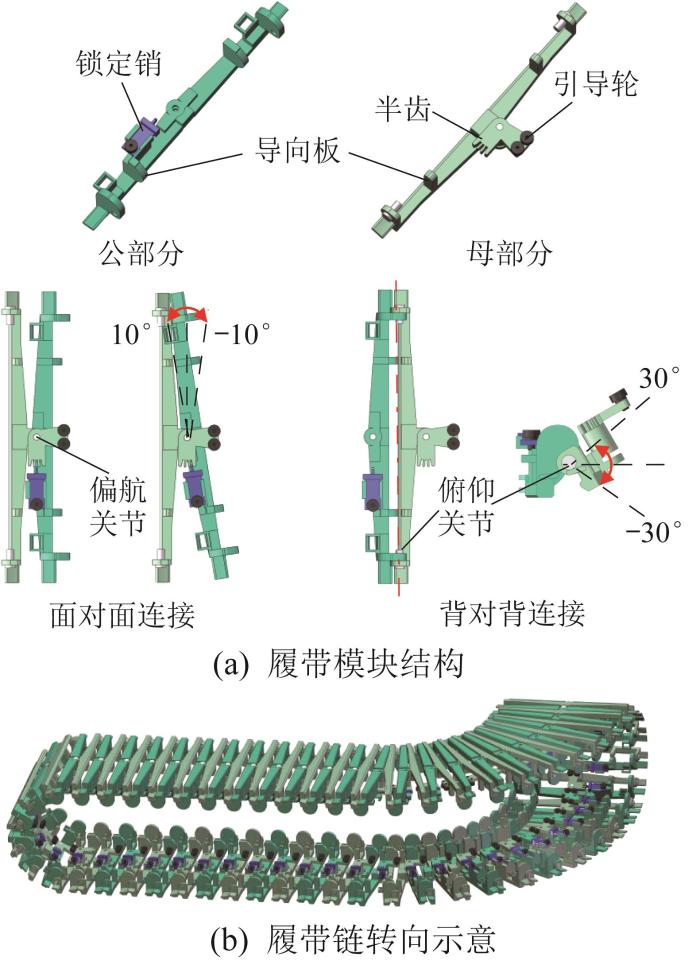
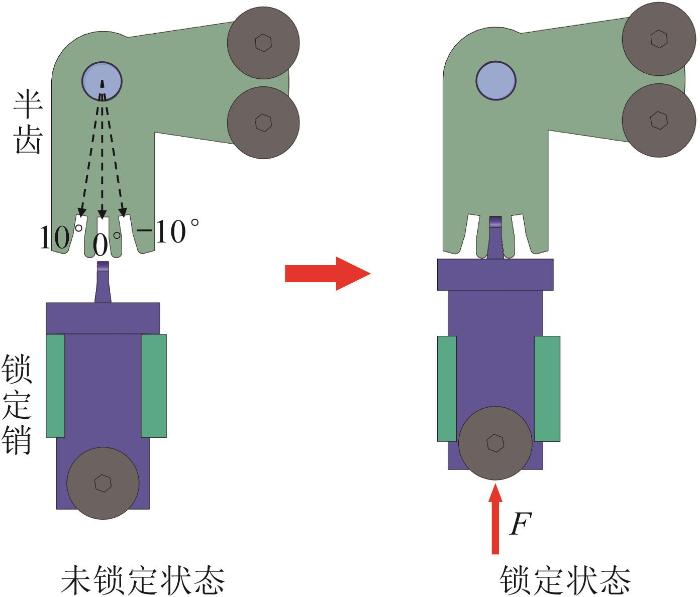
1)模块化可锁定履带设计。
图4
图4
模块化可锁定履带的结构与转向示意图
Fig.4
Structure and steering diagram of modular lockable track
图5
2)履带锁定机构设计。
履带锁定机构位于机器人头部,可为机器人提供牵引力,并调整履带关节的锁定角。履带锁定机构主要包括驱动电机、前轮、方向调节电机、导向滑块、锁定楔形块、导向轮和前导轨,如图6所示。该机构能够调节履带偏航关节的摆动角并锁定,从而将底部履带构建为刚性的支撑路径,以引导机器人前进。
图6
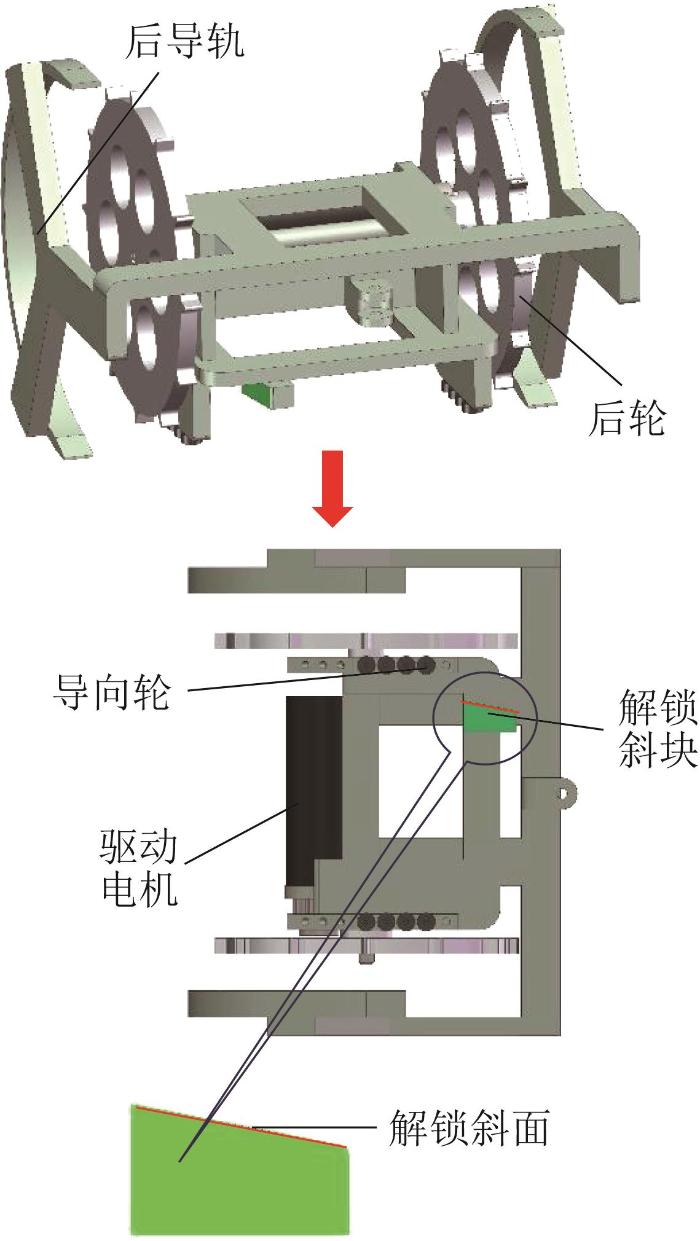
3)履带解锁机构设计。
履带解锁机构位于机器人尾部,主要包括后轮、驱动电机、解锁斜块、导向轮和后导轨,如图7所示。该机构能被动解锁履带的偏航自由度,并引导履带与后轮平顺啮合,以持续提供新的自由履带。在后轮的驱动下,解锁斜面可推动锁定销回到初始位置,使得锁定销与半齿分离,从而使偏航关节解锁为自由状态。
图7
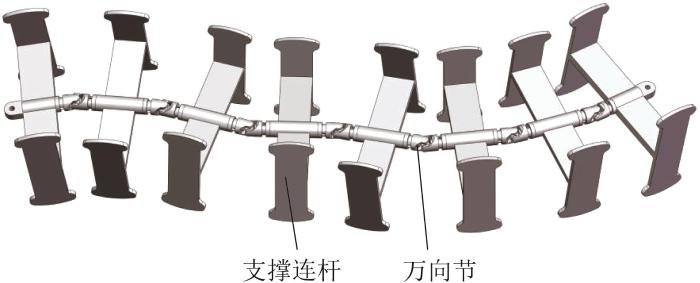
4)柔性机体设计。
柔性机体由万向节铰接的多个支撑连杆串联组成,其可自由摆动的柔性构型能够被动适应刚性履带的多样化变形,如图8所示。无论是在平地行驶还是在被动适应崎岖地形时,柔性机体均能支撑顶部松散的履带,以避免其与底部履带发生干涉,从而保障机器人平顺运行。
图8
1.3 机器人形态重构原理
所设计的机器人采用可三维弯曲的单履带链环作为行走机构,由独立的前轮和后轮共同驱动前进。基于履带的可锁定设计,机器人前进时通过头部依次调整并锁定履带模块的偏航关节角,以将底部履带构建为刚性的支撑路径,从而决定前进方向;尾部在跟随的同时解锁各个关节,以回收该路径,从而使机器人实现连续滚动。通过依次选取不同的关节锁定角,可生成特定形状的路径。此外,由于内部机体完全柔性,机器人可在前进过程中被动适应所生成路径的形状,从而实现重构变形。
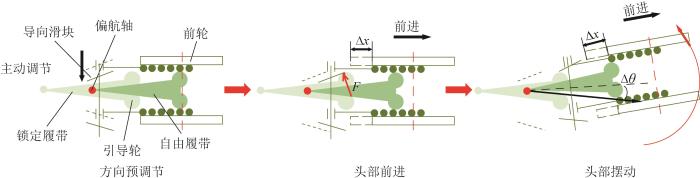
当机器人转向时,偏航关节的角度调整过程包括方向预调整、头部前进和头部摆动三步,如图9所示。其中:方向预调整为方向调节电机推动导向滑块向左或向右移动,以便后续导向滑块的斜面引导前侧自由履带摆动。当机器人头部前进后,导向滑块斜面将与后侧锁定履带的引导轮接触。随着头部继续前进,导向滑块斜面与引导轮之间的接触力使头部发生摆动,并带动自由履带沿偏航关节旋转。
图9
当偏航关节摆动至最大角度后,机器人头部继续前进,即可实现偏航关节的自动锁定。具体来说,在前轮的牵引下,机器人头部下侧的锁定楔形块通过其斜面的导向作用将锁定销推入半齿,以限制两侧履带链节的相对摆动,从而实现偏航关节的锁定。
偏航关节的锁定角包括以下3种:10°,0°,-10°(左转为正,右转为负),如图10所示,其锁定过程如下:
图10
1)0°锁定。首先,导向滑块固定在初始中间位置,机器人头部保持直线前进;然后,在前轮的驱动下,解锁斜块引导锁定销移动,使其轻松滑入半齿的0°凹口以完成锁定。
2)10°锁定。首先,方向调节电机带动导向滑块左移到特定位置,使其斜面1接触引导轮;然后,在前轮的驱动与斜面1的导向作用下,机器人头部向左摆动10°;最后,解锁斜块引导锁定销移动,使其轻松滑入半齿的10°凹口以完成锁定。
3)-10°锁定。首先,方向调节电机带动导向滑块右移到特定位置,使其斜面2接触引导轮;然后,在前轮的驱动与斜面2的导向作用下,机器人头部向右摆动10°;最后,解锁斜块引导锁定销移动,使其轻松滑入半齿的-10°凹口以完成锁定。
在机器人头部锁定机构对履带关节角进行调整与锁定的同时,尾部解锁机构对关节进行解锁,以保证机器人连续运行。由于底部的履带始终为刚性状态,可作为支撑路径引导机器人前进,因此头部向前不断放置新的履带链节,即可实现路径延伸,而尾部可同步回收底部履带以实现路径裁剪。基于头部锁定与尾部解锁的配合,机器人可沿履带所构建的路径不断前进。通过组合不同数量的偏航关节(偏转10°或-10°),机器人能够在前进过程中随时调整头部的延伸方向,生成多样化的曲线路径,且任意部位严格跟随,整体运动轨迹呈高度一致性,适用于蜿蜒曲折的狭窄空间。机器人的重构运动原理如图11所示。
图11
2 机器人运动学建模与形态分析
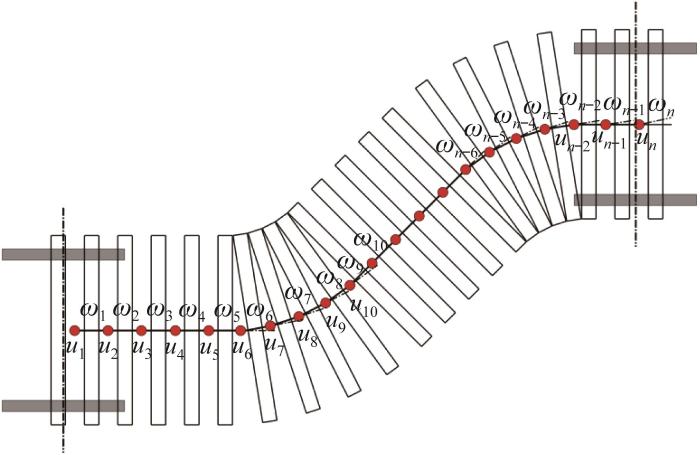
基于上述重构运动原理,机器人可沿由底部锁定履带构建的路径前进,故底部履带的位置与关节角直接决定了机器人的位置状态。在平面运动中,底部履带可视为由关节连接的多连杆串联系统,如图12所示。
图12
基于右手定则,依次建立机器人底部履带各偏航关节的坐标系。通过逐个创建相邻关节的齐次坐标变换矩阵,来准确描述各偏航关节间的位置关系。在任一时刻下的路径中,定义底部履带最后端的偏航关节为起始点,将变换矩阵逐个相乘以确定路径中各偏航关节的位置坐标。随着履带的延伸与回收,计算并更新底部履带各偏航关节的位置坐标,如此循环迭代可实现机器人的运动学建模。通过仅含关节角序列和固有履带模块参数的运动学模型,即可精确描述机器人的位置和形态。
2.1 基于偏航关节的坐标变换
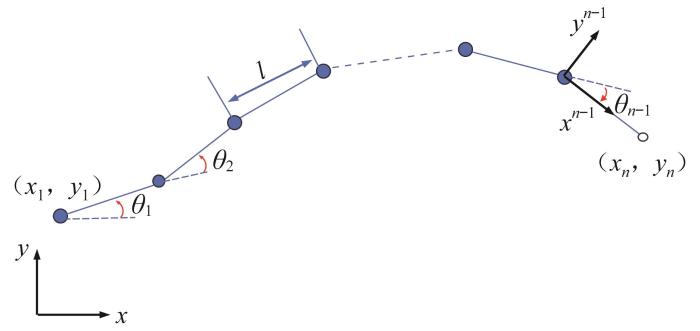
在机器人的运动过程中,其底部履带可等效为多连杆串联机构,机构简图如图13所示。
图13
在分析关节坐标系的相对位置关系时,往往同时存在平行移动和绕轴转动。因此,在描述局部坐标系在世界坐标系中的位姿时,须同时考虑平移变换和旋转变换。为便于分析,将坐标系的变换过程分解为坐标系原点之间的平移变换和坐标系之间的欧拉角旋转变换。
为计算坐标系之间的变换矩阵,需要先基于右手定则分别确立相邻关节坐标系的轴向方向,然后通过平移、旋转得到其映射变换关系。如图14所示,前一个关节的坐标系O-XbYbZb变换为下一个关节的坐标系O″-Xb″Yb″Zb″的过程分为以下2步:1)坐标系O-XbYbZb沿Yb轴方向平移e,使坐标系原点与下一个关节的坐标系原点O″重合,得到坐标系O′-Xb′Yb′Zb′;2)坐标系O′-Xb′Yb′Zb′通过欧拉角旋转变换
图14
根据图14,得到坐标系O-XbYbZb与O′-Xb′Yb′Zb′之间的平移矩阵 D
同理,得到坐标系O′-Xb′Yb′Zb′与O″-Xb″Yb″Zb″之间的旋转矩阵 R
将平移矩阵与旋转矩阵组合,得到相邻关节之间的齐次坐标变换矩阵 T,可表示为:
基于上述齐次坐标变换矩阵,底部履带中各偏航关节坐标系之间的位置关系可描述为:
式中:
2.2 机器人运动学模型
在平面运动过程中,初始状态下底部履带各偏航关节的摆动角用矩阵序列可描述为:
式中:ωi 为偏航关节的摆动角,可取10°,0°,-10°。
基于齐次坐标变换矩阵的迭代分析,可得机器人的初始位置状态
式中: si 为偏航关节i的位置向量;l为履带链节固有长度,本文取l=3 cm;x1、y1为起始偏航关节的位置坐标。
基于初始位置状态
机器人尾部前进的X、Y向位移Xt、Yt分别为:
综上可知,当前进k个履带链节长度后,机器人的位置状态更新为 S(k):
通常情况下,狭窄障碍空间下机器人的通过性受到转弯半径的制约。基于上述分析,履带偏航关节连续弯曲时,机器人能够以最小曲率半径实现转向,则其最小转弯半径R可表示为:
鉴于偏航关节的摆动角最大可取10°以及履带链节固有长度l=3 cm,可得机器人的最小转弯半径R=17.1 cm。
2.3 机器人形态分析
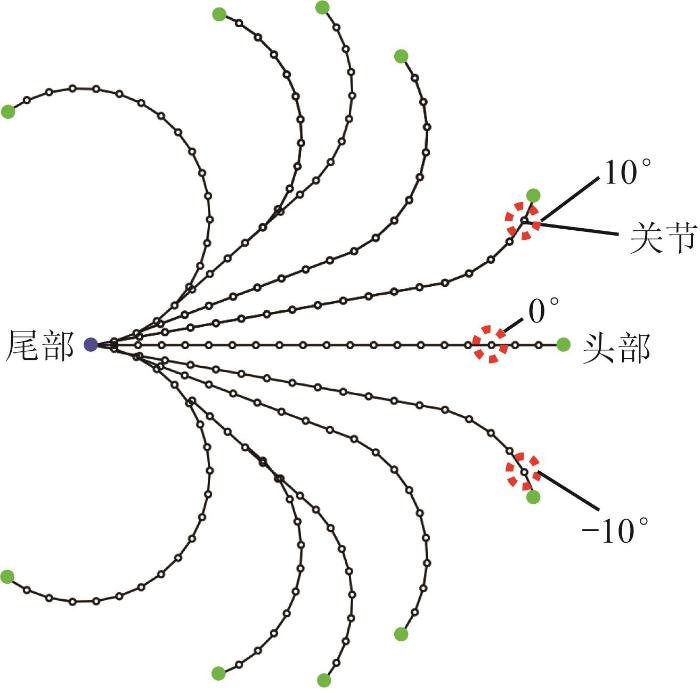
仿变形虫机器人可生成多样化的形态,以实现在狭小环境下的灵活避障。为评估本文所设计的机器人的避障能力,对其整体的形态变化范围进行分析,以描述其运动灵活性。由上文分析可知,底部履带的关节角序列决定了机器人的整体形态,基于偏航关节的3种锁定角,以尾部为起始点,通过遍历底部履带偏航关节角的各种组合,获取机器人的所有形态,如图15所示。
图15
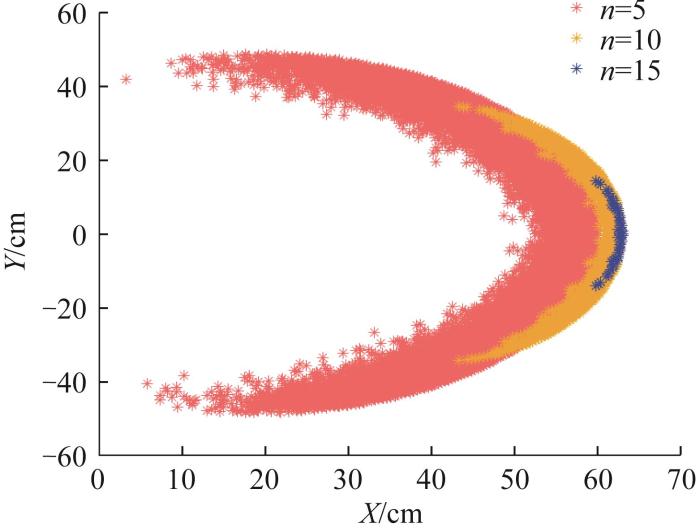
为方便表示,隐藏机体位置,仅用头部可达空间表示机器人的形态变化范围,并将其作为灵活性指标。因受限于固定的关节锁定角,履带模块的数量直接影响机器人的灵活性。基于此,利用MATLAB软件开展仿真模拟,分析底部履带模块数量与头部可达空间之间的关系。在机器人总长度(60 cm)的约束条件下,考虑设计尺寸的限制,底部履带模块数量最多取20个,本文分别选取5,10,20个履带模块并计算任意形态下的头部位置,从而得到头部可达空间,结果如图16所示。
图16
分析图16可知,当机器人长度一定时,底部履带模块的数量越多,其头部可达空间的面积越大,即机器人的运动灵活性越强。在机器人长度为60 cm的条件下,底部履带模块的数量可取20个,远超同尺寸下蛇形机器人躯干的关节数量,说明具备更强的灵活性。
3 机器人运动性能测试实验
为测试仿变形虫可重构履带机器人的运动性能,制作机器人样机并搭建相应的实验平台。机器人样机尺寸(长
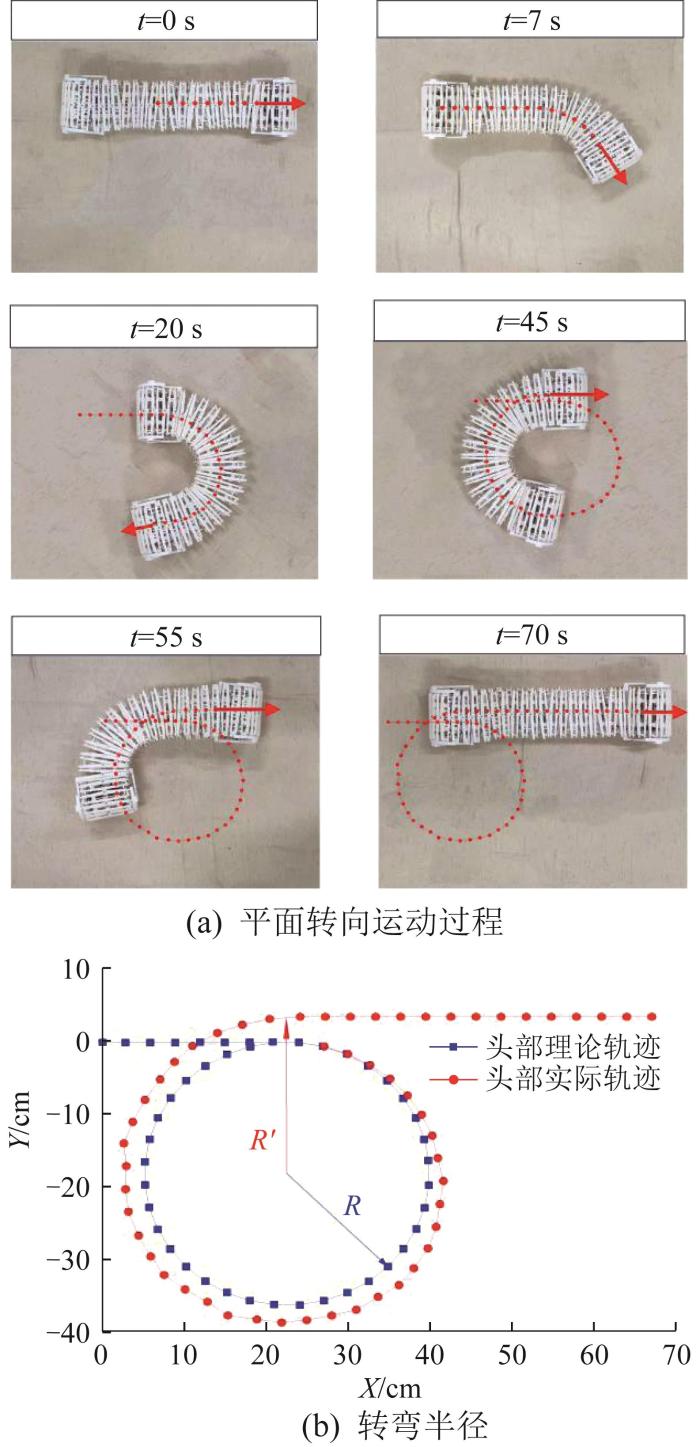
3.1 平面转向实验
图17
3.2 避障实验
履带的偏航关节具有3种锁定角,通过机器人头部依次选取不同的锁定角并将偏航关节锁定,则底部履带可构建出一条蜿蜒的路径,以引导机器人实现避障运动。为了测试机器人在狭窄环境下的避障性能,在地面上布置3个相距20 cm的障碍,开展机器人避障实验,如图18所示。结果表明,机器人可沿底部履带构建的路径前进以实现灵活避障,验证了机器人在狭窄空间中的通过能力。
图18
3.3 地形自适应实验
履带的俯仰关节可自由摆动,能够根据地形被动调整其俯仰角,从而使机器人具备一定的地形自适应能力。为验证机器人的自适应性能,在室外砖地、野外草地、障碍地形、斜坡地形下分别开展通过性测试实验,如图19所示。实验结果表明,配合俯仰关节的被动适应,该机器人具备良好的自适应能力,可穿越各类崎岖地形。
图19
4 结 论
面向复杂狭窄环境下的巡检作业需求,本文设计了一款仿变形虫可重构履带机器人,并制作了机器人样机和开展了验证实验。所得结论如下:
1)受变形虫的重组变形机制启发,设计了模块化可重构履带机器人。通过模拟变形虫胞质颗粒的刚柔转换特性,融合俯仰关节与偏航关节,设计了基于闩锁结构的可锁定履带模块。配合头部的履带锁定机构与尾部的履带解锁机构,机器人可在前进过程中连续改变自身形态,实现灵活的蜿蜒运动。
2)基于关节角描述的相邻履带模块间的位置关系,计算了机器人的形态矩阵。同时,通过对关节角序列的迭代分析,建立了机器人的运动学模型,并通过仿真分析了机器人的形态变化范围,验证了其运动灵活性。
3)通过开展平面转向实验,得到机器人的实际最小转弯半径为17.7 cm。在多障碍组成的狭小环境下开展了避障实验,验证了机器人的灵活避障性能。在砖地、草地、障碍地形、斜坡地形下分别开展通过性测试实验,验证了机器人的复杂地形自适应性能。
综上,本文提出的仿变形虫可重构履带机器人具备丰富的形态,且能够严格跟随底部履带构建的曲线路径前进,整个身体的运动轨迹一致且无多余摆动。该机器人在障碍密布或蜿蜒曲折的狭小空间中具备优异的通过性,适用于地震废墟、工厂车间、管道、洞穴等复杂场景下的巡检作业任务。研究结果为移动机器人的仿生结构设计提供了一种新思路。未来,将开展机器人结构优化及柔顺控制方法研究,以进一步提高机器人的运动性能与可靠性。
参考文献
A hybrid obstacle-avoidance method of spatial hyper-redundant manipulators for servicing in confined space
[J].
Modeling and control of hybrid 3-D gaits of snake-like robots
[J].
轻型蛇形机器人系统设计及分段运动规划策略研究
[D].
Lightweight snake robot system design and segmented motion planning strategy research
[D].
多关节蛇形机器人的结构设计和运动实现
[J].
Structure design and motion realization of multi-joint snakelike robot
[J].
水下蛇形机器人关节旋转机构建模与运动分析
[J].
Modeling and kinematic analysis of joint rotating mechanism for underwater snake-like robots
[J].
基于3-RSR并联机构的蛇形机器人本体构型设计与运动性能研究
[J].
Body configuration design and kinematic performance research of snake-like robot based on 3-RSR parallel mechanism
[J].
基于仿生水母的水下机器人结构设计与试验研究
[J].
Structural design and experimental study of underwater robots based on biomimetic jellyfish
[J].DOI:10.3969/j.issn.1001-4551.2024.04.020 [本文引用: 1]
爬壁机器人悬摆式磁吸附机构的设计与优化
[J].
Design and optimization of pendulous magnetic adsorption mechanism for wall-climbing robots
[J].
关节电机驱动六足机器人仿生结构设计与柔顺运动控制
[J].
Biomimetic structure design and compliant motion control for hexapod robot driven by joint motors
[J].
蛇形机器人: 仿生机理、结构驱动和建模控制
[J].
Snake robotics: bionic mechanism, structure, actuation, modeling and control
[J].DOI:10.3901/jme.2022.07.075 [本文引用: 1]
微型仿尺蠖软体机器人的设计与实验
[J].
Design and experiment of miniature inchworm-like soft robot
[J].
基于连续体模型的蛇形机器人质心速度跟踪控制方法
[J].
Tracking control method of the centre-of-mass velocity for a snake-like robot based on the continuum model
[J].DOI:10.13973/j.cnki.robot.2017.0829
蛇形机器人步态产生及步态分析
[J].
Gait generation and analysis for snake-like robots
[J].DOI:10.3724/sp.j.1218.2011.00371 [本文引用: 1]
A novel reconfigurable robot for urban search and rescue
[J].
Porcospino, spined single-track mobile robot for inspection of narrow spaces
[J].
Mechanical designs for field undulatory locomotion by a wheeled snake-like robot with decoupled neural oscillators
[J].
Tracking displacement of a worm-like robot with multiple sensor configurations
[J].
A worm-snake-inspired metameric robot for multi-modal locomotion: Design, modeling, and unified gait control
[J].