本文链接:
磁流变阻尼器作为磁流变假肢的主要作动部件,其性能的优劣在很大程度上决定着假肢的性能[5-7]。Saini等[8]设计了一种具有旁通阀结构的旋转式磁流变阻尼器,降低了磁流变假肢的制造复杂度,但增大了其外形体积。强彦等[9]设计了一种用于磁流变假肢的孔隙结合式磁流变阻尼器,减小了阻尼器的结构尺寸。Yang等[10]为了得到更大的阻尼力,设计了三线圈磁流变阻尼器,提高了其阻尼性能,但由于体积过大,无法在磁流变假肢中运用。易锋等[11]设计了单轴式磁流变假肢膝关节,同时将计算力矩(computing torque,CT)控制与比例微分(proportional derivative,PD)控制相结合,实现了对磁流变假肢的有效控制;该磁流变阻尼器体积较小,但是在人站立期间无法提供较大的阻尼力。
为了使磁流变阻尼器更好地运用在假肢中,国内外学者对磁流变阻尼器进行了优化[12-14],提升了其性能,使磁流变假肢更加便捷实用。Fu等[15]分析了磁流变阻尼器的迟滞效应对小腿摆动角度的影响,并提出了滑模控制法来加以消除。Liu等[16]基于B样条曲线对假肢中磁流变阻尼器的结构尺寸进行优化,最大限度地增大了磁流变阻尼器的可控输出阻尼力。Seid等[17]针对磁流变假肢质量大的问题,通过响应面法实现了其轻量化,使阻尼器质量减小了71%。Gao等[18]针对磁流变假肢的能耗及质量问题,采用粒子群算法进行了其结构优化,减小了阻尼器的消耗功率及质量。Kumar等[19-20]利用多目标遗传算法和神经网络,使假肢中的磁流变阻尼器在满足阻尼力需求的同时,实现了体积的最小化。Saini等[21]提出了一种融合等效磁法和有限元静磁法的优化方法,采用该方法可以缩短优化时间,更容易设计出具有较优结构的磁流变假肢。
根据上述研究可知,磁流变假肢中的磁流变阻尼器存在体积过大、输出阻尼力较小、液流通道利用率较低等问题,阻碍其在磁流变假肢中的应用。因此,应最大限度地提高液流通道的空间利用率,使磁流变阻尼器在有限体积内输出较大的阻尼力。
作者设计了一种全通道内置阀式磁流变阻尼器。基于阀式工作模式,通过布置导磁楔形环和隔磁环引导磁力线穿过全部液流通道,并采用多目标遗传优化算法对磁流变阻尼器的结构参数进行优化,使磁流变阻尼器体积小,输出阻尼力大,能满足磁流变假肢的使用要求。
1 磁流变阻尼器的结构及工作原理
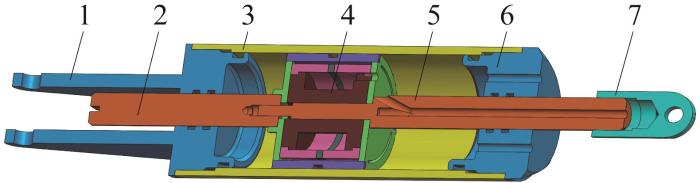
图1
图1
全通道内置阀式磁流变阻尼器结构
1—左端盖;2—左活塞杆;3—缸体;4—活塞头;5—右活塞杆;6—右端盖;7—右吊耳。
Fig.1
Structure of full fluid channel MRD with bulit-in valve
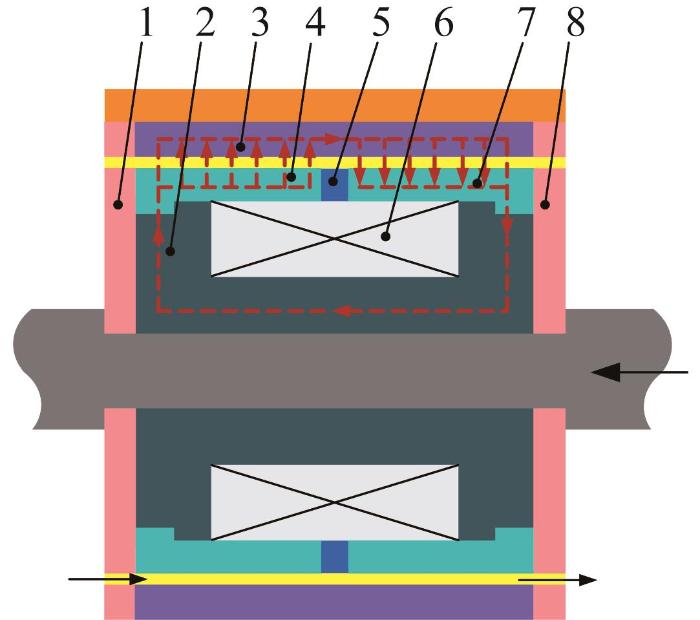
磁流变阻尼器活塞头的结构如图2所示。其中:左楔形环与右楔形环之间设有隔磁环,左、右楔形环与线圈绕线架通过绕线架上的阶梯式轴肩间隙配合;内置导磁缸体通过左、右压板间隙配合确定轴向定位,径向定位则通过左、右压板圆周上设置的小凹槽与其两端面设置的小凸台间隙配合确定。通过有序布置不导磁压板、导磁楔形环及隔磁环,引导磁路先沿着左楔形环穿过磁流变液和内置导磁缸体,后回穿磁流变液和右楔形环,最后到达绕线架,使得有效阻尼通道几乎为全通道,从而提高磁场利用率,在体积有限的情况下增大阻尼器的输出阻尼力。
图2
图2
磁流变阻尼器活塞头结构
1—左压板;2—线圈绕线架;3—内置导磁缸体;4—左楔形环;5—隔磁环;6—励磁线圈;7—右楔形环;8—右压板。
Fig.2
Structure of piston head of MRD
由图2可知,左、右楔形环与内置导磁缸体之间存在间隙,设计间隙厚度为1 mm。当活塞杆在外加激励下带动活塞头向左运动时,左腔内的磁流变液通过该间隙向右腔流动;当活塞杆在外加激励下带动活塞头向右运动时,磁流变液的流向随之相反。当励磁线圈通入电流时,由电磁感应产生的磁力线穿过间隙的磁流变液,磁流变液产生磁流变效应,随之产生屈服应力,阻碍活塞头的往复运动,从而达到阻尼效果。通过调节电流的大小,就能控制磁流变阻尼器的输出阻尼力。
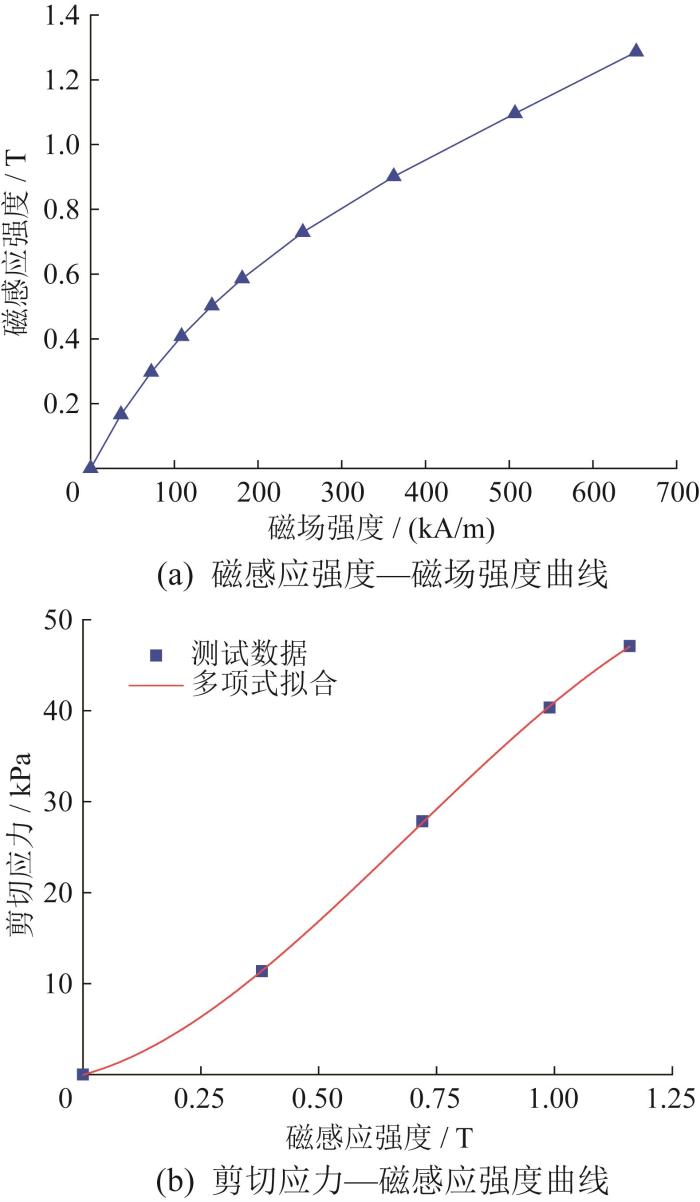
图3
通过多项式拟合,剪切应力τ与磁感应强度B的关系可表示为:
式中:a1=-305.9 kPa/T5,a2=728.3 kPa/T4,a3=-637.6 kPa/T3,a4=272.9 kPa/T2,a5=-9.117 kPa/T,a6=0.141 3 kPa。
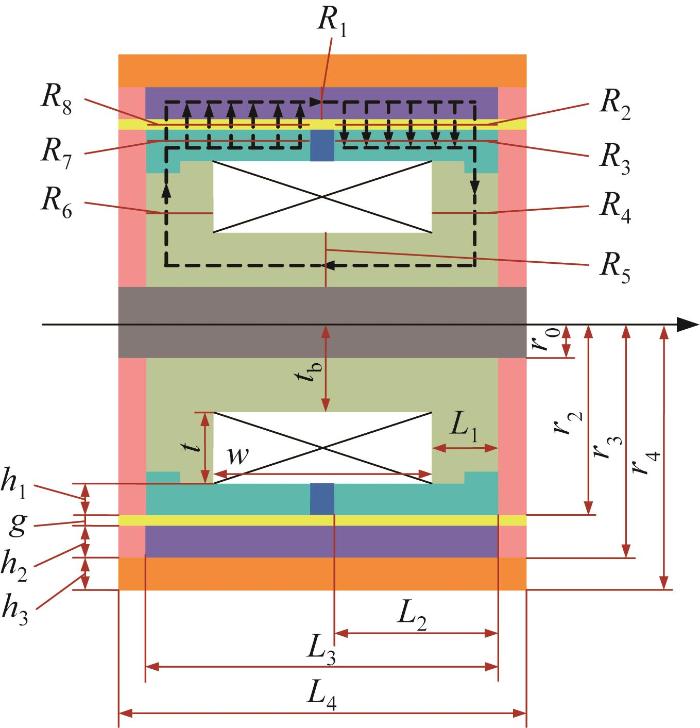
2 磁流变阻尼器磁路分析
图4
图4
全通道内置阀式磁流变阻尼器磁路示意图
Fig.4
Schematic diagram of magnetic circuit of full fluid channel MRD with bulit-in valve
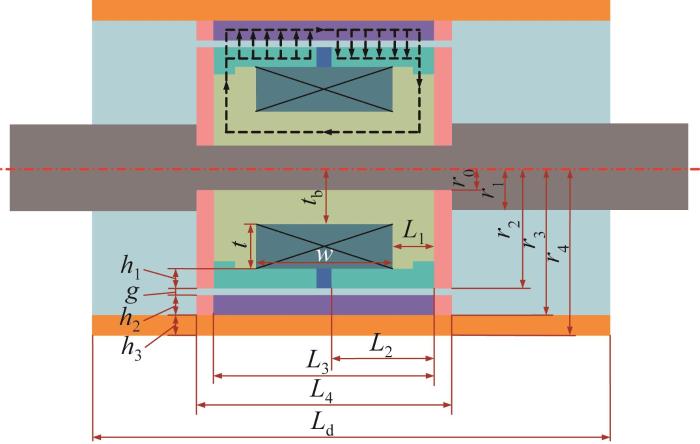
表1 磁流变阻尼器尺寸参数 (mm)
Table1
| 尺寸参数 | 数值 |
|---|---|
| 绕线槽深度t | 6.5 |
| 绕线槽小径tb | 8.0 |
| 绕线槽轴向长度w | 16.0 |
| 楔形环厚度h1 | 3.0 |
| 内置导磁缸体厚度h2 | 3.0 |
| 缸体厚度h3 | 3.0 |
| 阻尼间隙g | 1.0 |
| 活塞杆小半径r0 | 3.0 |
| 活塞杆大半径r1 | 6.0 |
| 液流通道处小半径r2 | 17.5 |
| 活塞头半径r3 | 21.5 |
| 缸体外径r4 | 24.5 |
| 活塞头侧翼磁轭轴向长度L1 | 5.0 |
| 楔形环轴向长度L2 | 12.0 |
| 内置导磁缸体轴向长度L3 | 26.0 |
| 活塞头长度L4 | 30.0 |
| 缸体长度Ld | 108.0 |
闭合磁路第i部分的磁阻Ri 表示为:
式中:li 为第i部分的有效长度,μi 为第i部分的相对磁导率,μ0为真空磁导率,Si 为第i部分的界面面积。
内置导磁缸体处的磁阻R1为:
式中:μ1为导磁材料的相对磁导率,取μ1=1 000。
阻尼通道处的磁阻R2和R8为:
式中:μ2为磁流变液的相对磁导率,取μ2=2.5。
楔形环处的磁阻R3和R7为:
活塞头侧翼的磁阻R4和R6为:
活塞头中部的磁阻R5为:
整个磁路的总磁阻Rm为:
各部分的磁通量Φi 表示为:
则:
式中:N为励磁线圈匝数,I为外加电流。
3 磁流变阻尼器输出阻尼力数学模型的建立
磁流变阻尼器活塞头的液流通道分布如图5所示。活塞头左、右楔形环外表面与内置导磁缸体内表面之间形成的液流通道为轴向圆环阻尼间隙,为了便于计算,轴向圆环流道可以近似视作平板间隙模式。磁流变阻尼器工作时的总压降包括两部分,即在轴向圆环间隙中产生的黏滞压降Δpη 和磁滞压降Δpτ。
图5
图5
磁流变阻尼器活塞头液流通道分布示意图
Fig.5
Schematic diagram of fluid channel distribution of piston head of MRD
黏滞压降Δpη 计算如下:
式中:η为零场黏度;v为活塞头往复运动速度;Sd为活塞头与磁流变液的有效接触面积。
磁滞压降Δpτ 计算如下:
式中:c为修正系数,取c=2~3;τy为阻尼间隙处磁流变液的屈服应力。
液流通道内总压降Δp=Δpη +Δpτ。
因此全通道内置阀式阻尼器的输出阻尼力F表示为:
4 磁流变阻尼器电磁场仿真分析
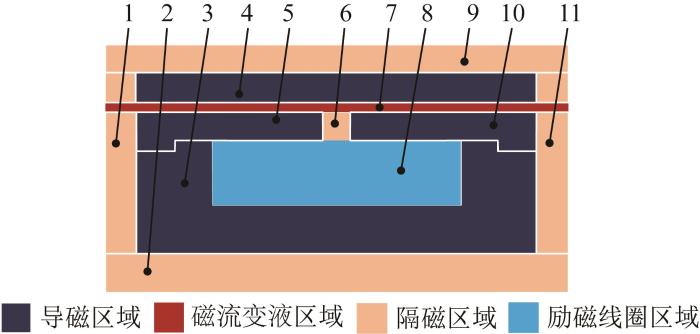
利用ANSYS软件对全通道内置阀式磁流变阻尼器进行仿真。由于磁流变阻尼器为对称结构,建立其1/2实体的有限元模型,如图6所示。针对各零部件材料导磁特性的差异,将磁流变阻尼器的仿真模型划分为导磁区域、磁流变液区域、隔磁区域和励磁线圈区域。
图6
图6
磁流变阻尼器有限元模型
1—左压板;2—活塞杆;3—线圈绕线架;4—内置导磁缸体;5—左楔形环;6—隔磁环;7—磁流变液;8—励磁线圈;9—缸体;10—右楔形环;11—右压板。
Fig.6
Finite element model of MRD
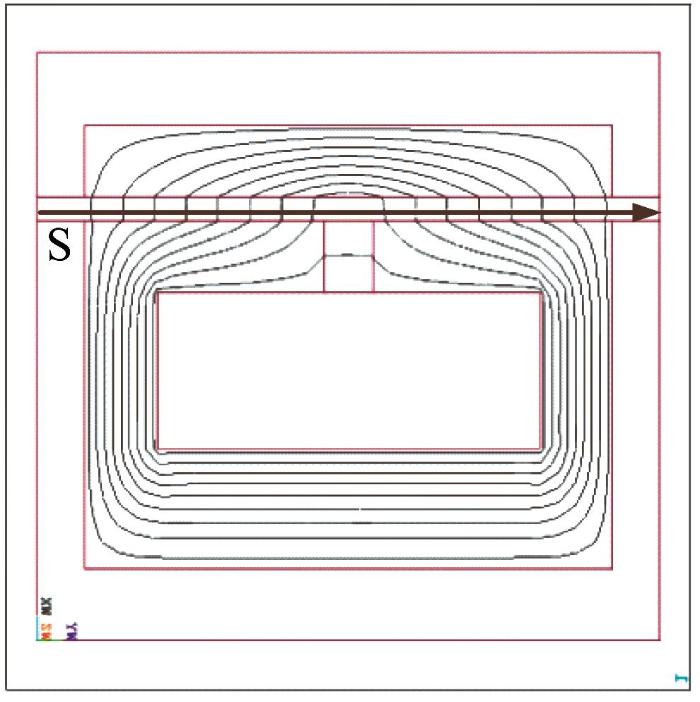
在设置加载激励和模型的边界约束条件之后,对阻尼器有限元模型进行仿真求解,得到的磁力线分布如图7所示。由图可知,隔磁环两侧的磁力线均穿过磁流变液,形成有效的液流通道。另外,有少部分磁力线直接穿过隔磁环,这是由隔磁环厚度较小造成的。磁力线以隔磁环为中心左右对称分布,并且左、右楔形环与内置导磁缸体之间形成的有效液流通道处的磁力线分布和变化基本相同,故下文选择路径S进行磁流变阻尼器仿真分析,为后续计算剪切应力和输出阻尼力提供相关的数据。
图7
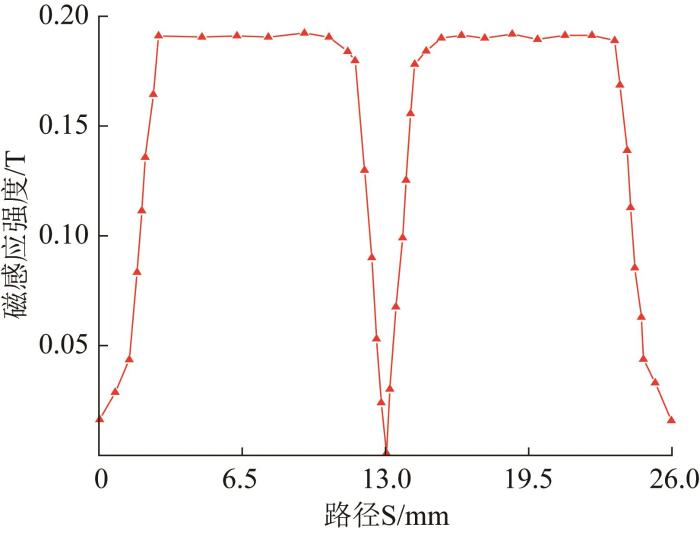
当电流为2 A时,路径S上磁感应强度的分布如图8所示。由图可知:磁感应强度从下方楔形环入口端开始不断增大至最大值,越接近励磁线圈的中心区域,磁感应强度越大,磁力线在隔磁环处开始转向,从最大值逐渐减小:隔磁环左右两侧的磁感应强度是对称的。
图8
图8
电路为2 A时路径S上磁感应强度分布
Fig.8
Magnetic induction flux distribution on path S with current of 2 A
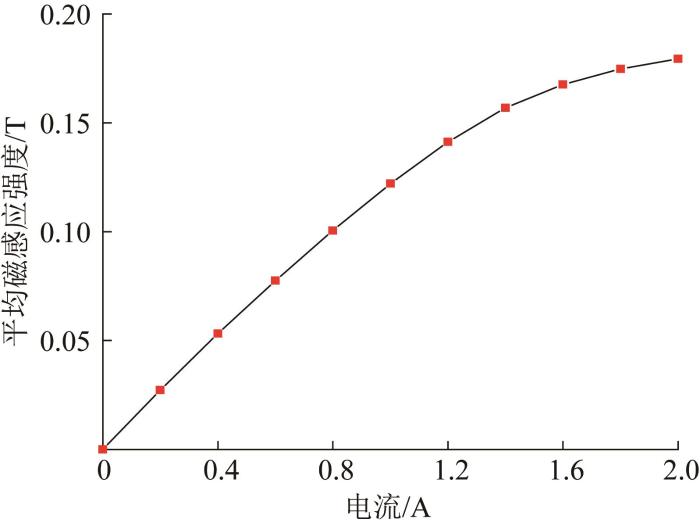
平均磁感应强度随电流的变化曲线如图9所示。由图可知:平均磁感应强度随着电流的增大而逐渐增大;当电流为0~1.4 A时,平均磁感应强度与电流呈线性关系,此后平均磁感应强度的变化逐渐趋于平缓。
图9
图9
平均磁感应强度随电流的变化曲线
Fig.9
Change curve of average magnetic flux density with current
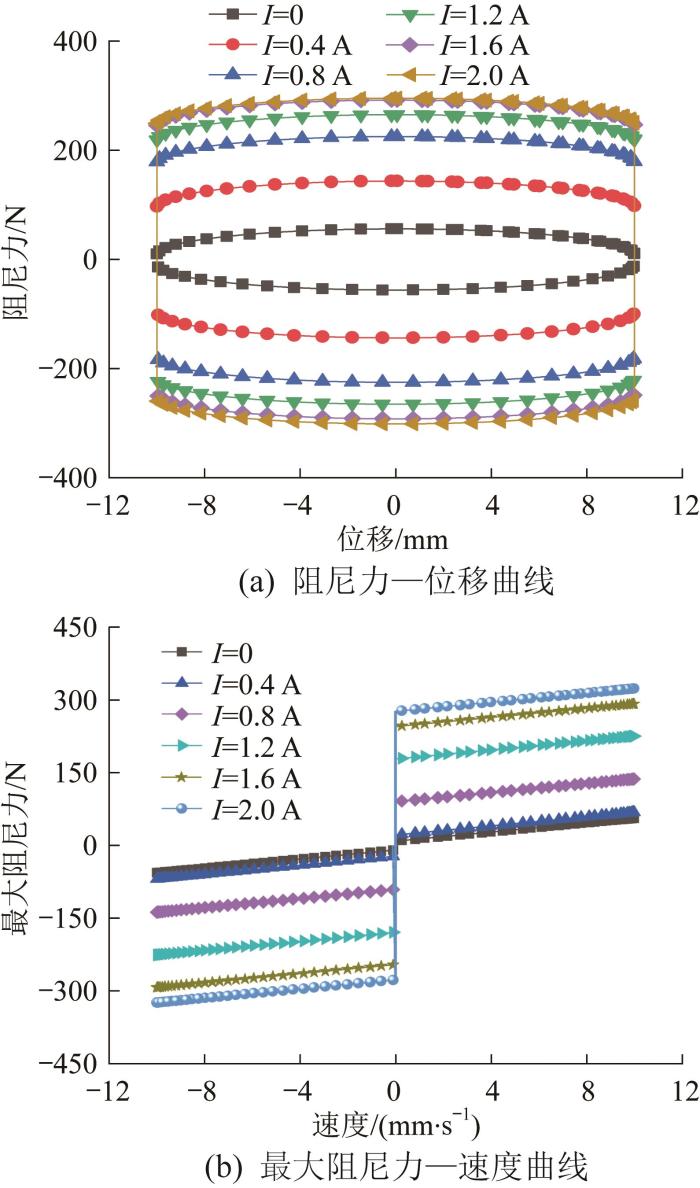
仿真中设置振幅z=10 mm、频率f=1 Hz的正弦激励,则不同电流下磁流变阻尼器的阻尼特性曲线如图10所示。由图(a)可知:阻尼力—位移曲线呈平滑的“回”字形;线圈未通入电流时,阻尼力接近76.63 N,此时阻尼力为黏滞阻尼力,不受人工控制,而由阻尼器的结构尺寸确定。由图(b)可知:在阻尼器压缩和拉伸运动过程中,最大阻尼力—速度曲线呈镜像的“Z”字形;在电流一定的情况下,阻尼力随着活塞头往复运动速度的提高而增大,但变化不显著,这是由于在通入电流的情况下,黏滞压降对总压降的影响不大;当外加电流为2 A时,最大阻尼力可达到330 N,能够满足磁流变假肢的阻尼力需求。
图10
图10
不同电流下磁流变阻尼器阻尼特性曲线
Fig.10
Damping characteristc curves of MRD under different currents
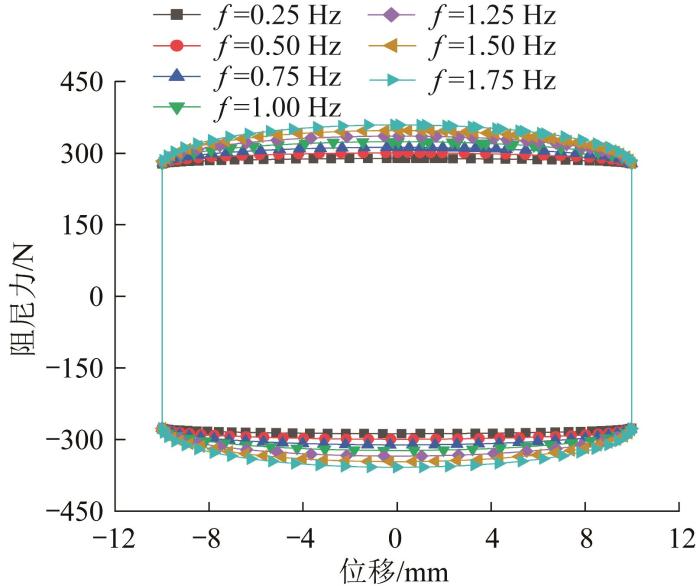
图11
图11
不同频率下阻尼力—位移曲线
Fig.11
Damping force-displacement curves under different frequencies under different frequencies
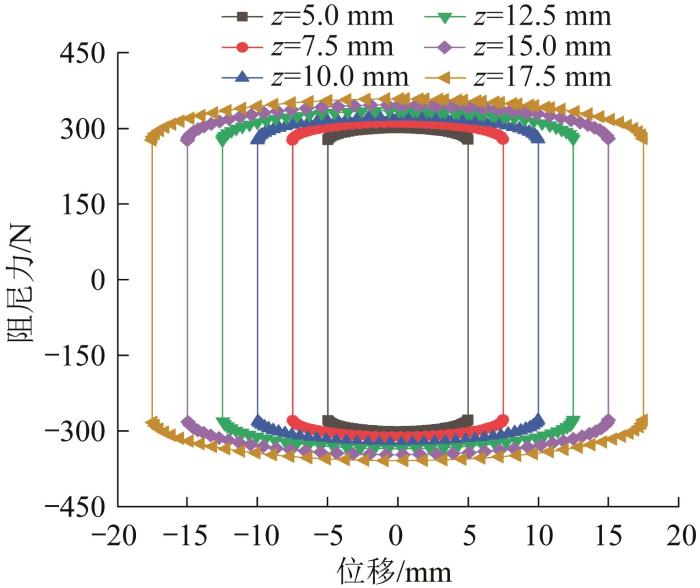
图12
图12
不同振幅下阻尼力—位移曲线
Fig.12
Damping force-displacement curves under different amplitudes
5 磁流变阻尼器结构参数优化
为了兼顾磁流变阻尼器的输出阻尼力和体积,采用NSGA-Ⅱ多目标遗传算法优化阻尼器参数,使阻尼器在具有较小体积的同时具备较大的输出阻尼力。
输出阻尼力F应尽可能大和阻尼器体积V尽可能小,故目标函数设置为:
优化参数设置为:活塞头侧翼磁轭轴向长度L1、绕线槽深度t、绕线槽小径tb、绕线槽轴向长度w、楔形环厚度h1和内置导磁缸体厚度h2。各变量的取值范围如表2所示。
表2 磁流变阻尼器优化参数取值范围 (mm)
Table 2
| 优化参数 | 取值范围 |
|---|---|
| 活塞头侧翼磁轭轴向长度L1 | 3~7 |
| 绕线槽深度t | 5~8 |
| 绕线槽小径tb | 6~10 |
| 绕线槽轴向长度w | 8~24 |
| 楔形环厚度h1 | 2~4 |
| 内置导磁缸体厚度h2 | 2~4 |
参数优化的约束条件为:
式中:M为自然数。
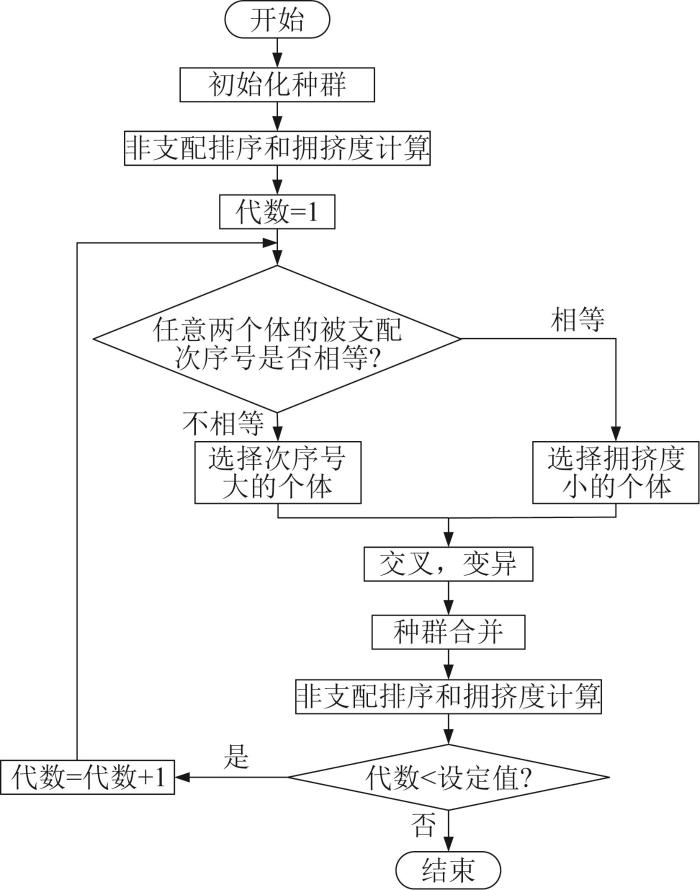
NSGA-Ⅱ多目标遗传算法的流程如图13所示。优化中,设置初始种群规模为50,最大迭代次数为200,交叉概率为0.8,变异概率为0.05。根据
图13
优化前后磁流变阻尼器结构参数值如表3所示。优化后阻尼器活塞头的体积为20 190 mm3,减小了24.4%。
表3 优化前后磁流变阻尼器结构参数值
Table 3
| 优化参数 | 优化前 | 优化后 |
|---|---|---|
| V/mm3 | 26 717 | 20 190 |
| L1/mm | 5 | 3 |
| t/mm | 6.5 | 8 |
| tb/mm | 8 | 8 |
| w/mm | 16 | 20 |
| h1/mm | 3 | 2 |
| h2/mm | 3 | 2 |
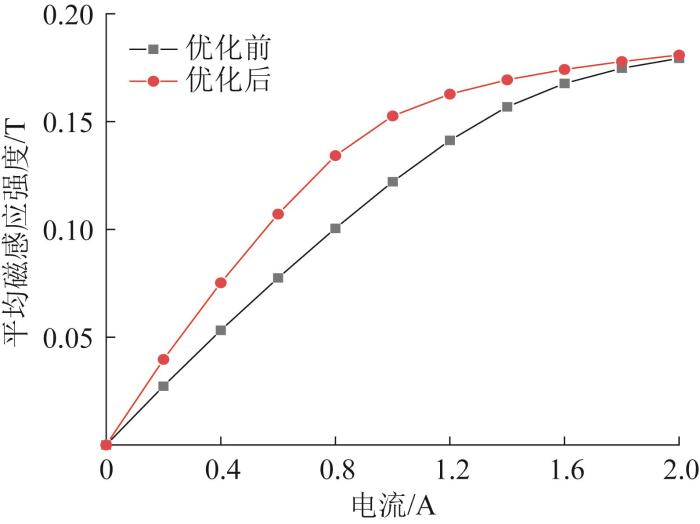
优化前后平均磁感应强度随电流的变化曲线如图14所示。由图可知:当电流为0~2.0 A时,优化后平均磁感应强度相比于优化前有所增大;当电流为1.0 A时,优化后平均磁感感应强度从0.122 T提高到0.153 T,提升幅度最大,为25.4%;当电流增大到1.4 A后,平均磁感应强度增速变缓且趋于平稳。
图14
图14
优化前后平均磁感应强度随电流的变化曲线
Fig.14
Change curves of average magnetic flux density with current before and after optimization
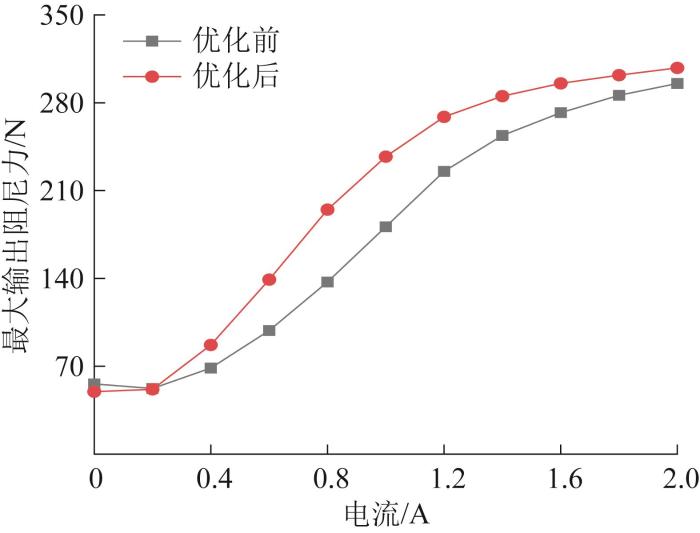
优化前后最大输出阻尼力随电流的变化曲线如图15所示。由图可知:当电流为0 时,优化前的零场阻尼力略大于优化后,这是由于优化后活塞头直径小于优化前,有效面积Sd减小所致;当电流为2.0 A时,最大输出阻尼力由优化前的295.38 N增大到优化后的307.77 N,增加了4.1%,同时阻尼器活塞头的体积减小了24.4%。
图15
图15
优化前后最大输出阻尼力随电流的变化曲线
Fig.15
Change curves of maximum output damping force with current before and after optimization
6 磁流变阻尼器性能测试与分析
全通道内置阀式磁流变阻尼器的样机如图16所示。优化前、后励磁线圈的匝数分别为170和260。
图16
为了分析阻尼器的动力学性能,建立了阻尼器力学性能测试系统,如图17所示。该系统由激振台、磁流变阻尼器、直流电源、电液加载控制器及计算机等组成。待测的阻尼器一端与上方横梁相连,另一端与下方动力杆相连;直流电源为阻尼器提供励磁电流;电液加载控制器与激振台相连,用于驱动液压系统中的伺服阀,并起到数据转换和传输的功能,最终可基于激振台提供不同的振动激励,驱动阻尼器作相应的拉伸;计算机与电液加载控制器相连,用于控制程序运行和采集反馈的输出信号。
图17
6.1 阻尼器动力学性能测试
设置激振台作振幅为10 mm、振动频率为1 Hz的正弦运动,调整直流电源,对磁流变阻尼器输入不同的电流,得到优化前后不同电流下阻尼力—位移曲线,如图18所示。由图可知:当电流为0~2.0 A时,优化前后阻尼力均随着电流的增大而增大,优化前最大阻尼力从76.6 N增大到307.80 N,优化后最大阻尼力从72.21 N增大到333.75 N。
图18
图18
优化前后不同电流下阻尼力—位移曲线
Fig.18
Damping force-displacement curves under different currents before and after optimization
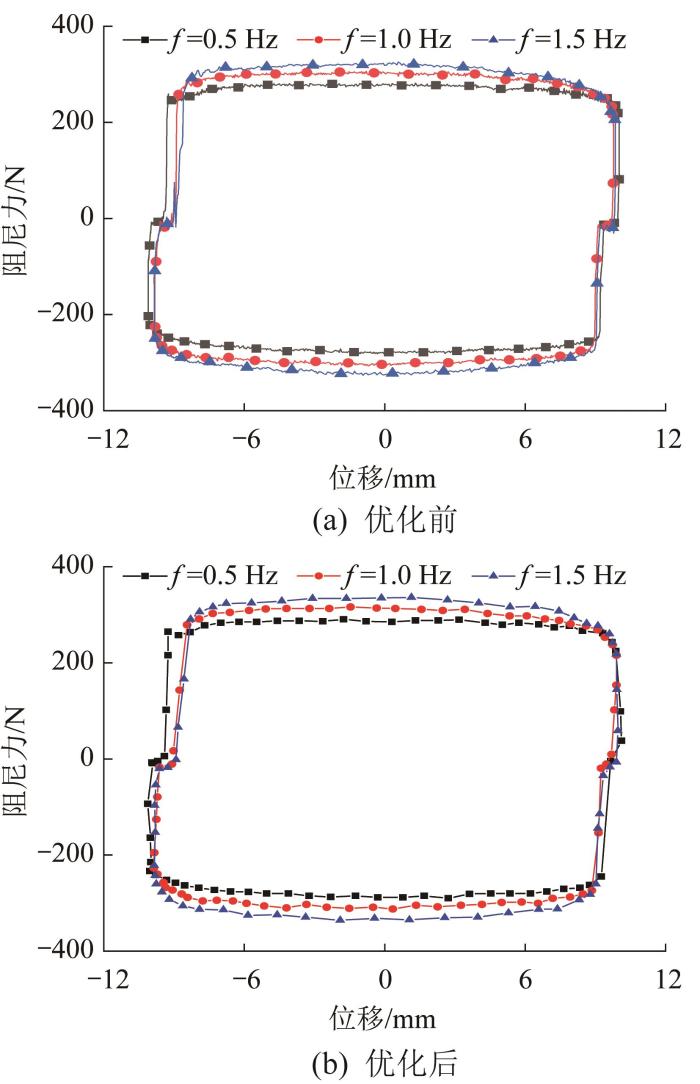
当正弦激励幅值为10 mm、电流为2.0 A时,优化前后不同频率下阻尼力—位移曲线如图19所示。由图可知:在不同频率下阻尼器具有相同的运动规律,阻尼力随着频率的增大而略微增大。原因是频率增大可使活塞头的运动速度提高,从而使阻尼力增大。
图19
图19
优化前后不同频率下阻尼力—位移曲线
Fig.19
Damping force-displacement curves under different frequencies before and after optimization
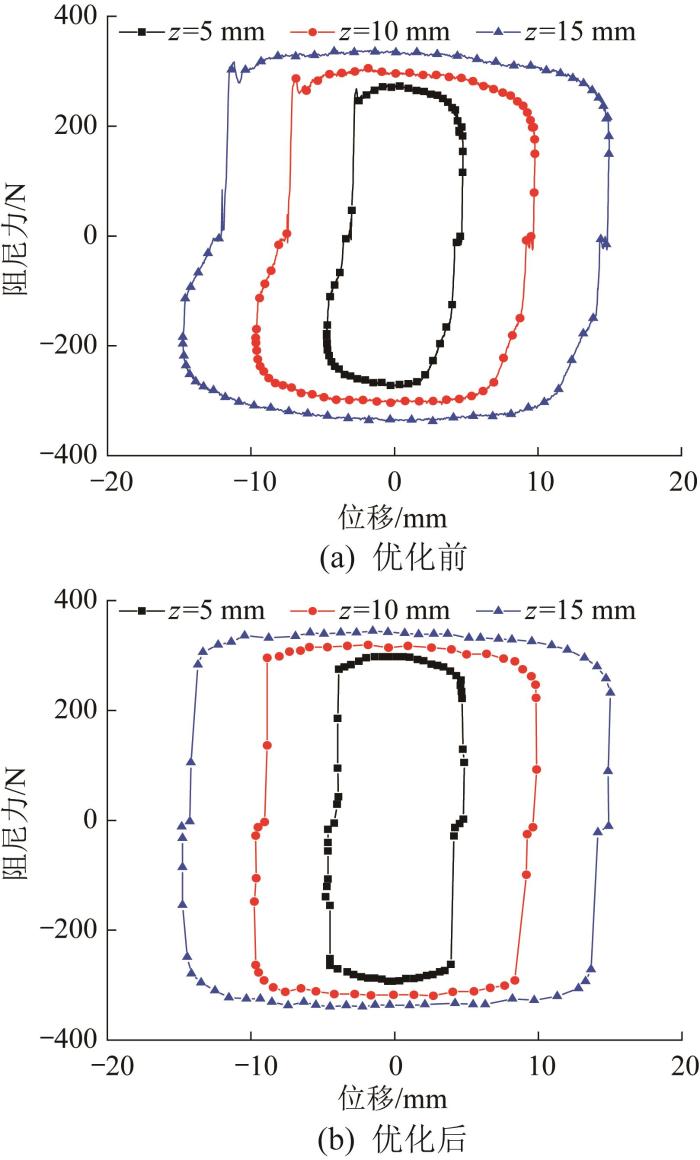
当正弦激励频率为1 Hz、电流为2.0 A时,优化前后不同振幅下阻尼力—位移曲线如图20所示。由图可知:阻尼力随着振幅的增大而略微增大。这是因为增大幅值也会使活塞头的运动速度提高,导致黏滞阻尼力增大,而黏滞阻尼力占总阻尼力的比重较小,因此阻尼力随振幅的变化并不明显。
图20
图20
优化前后不同振幅下阻尼力—位移曲线
Fig.20
Damping force-displacement curves under different amplitudes before and after optimization
6.2 优化前后阻尼器动力学性能对比分析
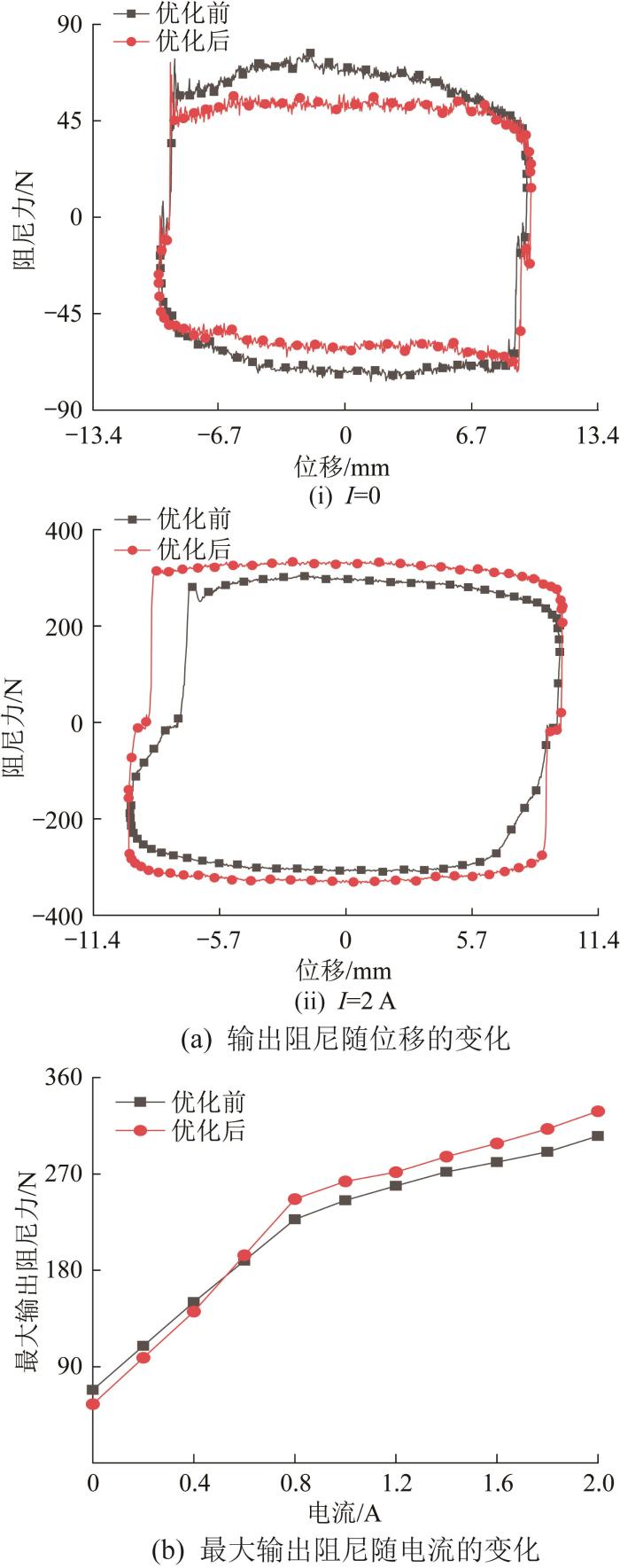
当激振台的振幅10 mm、频率为1 Hz时,优化前后输出阻尼力的对比如图21所示。
图21
图21
优化前后阻尼器输出阻尼力对比
Fig.21
Comparison of maximum output damping force before and after optimization
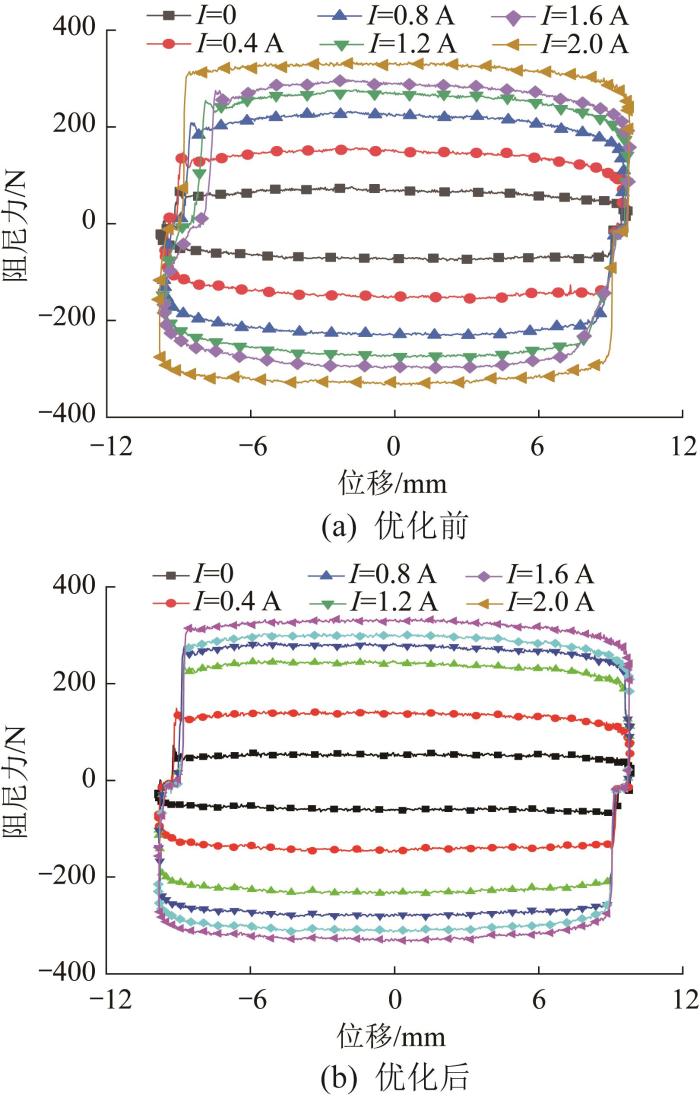
由图21(a)可知:输出阻尼力随位移变化的趋势一致。表明采用所设计的优化方法可以在确保阻尼器具有较大输出阻尼力的同时减小活塞头尺寸。
由图21(b)可知:当电流较小时,优化后最大输出阻尼力略小于优化前;当电流较大时,优化后最大输出阻尼力略大于优化前;当电流为0.6 A时,优化前、后的最大输出阻尼力基本相等。这是由于当电流较小时,输出阻尼力主要为黏滞阻尼力,而当电流较大时,输出阻尼力主要为磁滞阻尼力。当电流为1.0 A时,优化后的最大阻尼力为263.11 N,比优化前的245.22 N增大了17.89 N;当电流为2.0 A时,优化后的最大阻尼力为333.76 N,比优化前的309.76增大了24 N。
7 结 论
1)针对假肢膝关节中的磁流变阻尼器受到空间尺寸限制而无法输出大阻尼力的问题,设计了一种全通道内置阀式磁流变阻尼器。通过设置导磁楔形环和隔磁环,引导磁力线穿过全部液流通道,使阻尼器的有效液流通道几乎为全部流道;采用多目标遗传算法对所设计的阻尼器的结构参数进行优化,同时进行了阻尼器性能仿真和测试。优化后阻尼器活塞头体积减小了24.4%,最大阻尼力提高了24 N。
2)当工作电流为2 A时,优化前磁流变阻尼器最大输出阻尼力的仿真值为295.38 N,测试值为309.76 N,误差为4.6%;优化后最大输出阻尼力的仿真值为307.77 N,测试值为333.76 N,误差为7.6%。研究结果表明,在不减小输出阻尼力的基础上,可减小活塞头体积,有效解决了磁流变假肢中磁流变阻尼器在有限空间内无法输出较大阻尼力的问题。
参考文献
国务院新闻办发表《平等、参与、共享: 新中国残疾人权益保障70年》白皮书
[J].
The state council information office of the People’s Republic of China issued white paper: Equality, participation and sharing: 70 years of protecting the rights and interests of persons with disabilities in the PRC
[J].
Design and control of a prosthetic leg for above-knee amputees operated in semi-active and active modes
[J].
智能假肢膝关节的优化设计及运动学分析
[J].
Optimum design and dynamics analysis of intelligent prosthetic knee joint
[J].
A novel four-bar linkage prosthetic knee based on magnetorheological effect: Principle, structure, simulation and control
[J].
Design, analysis and optimization of a hybrid fluid flow magnetorheological damper based on multiphysics coupling model
[J].
A review of advances in magnetorheological dampers: Their design optimization and applications
[J].
Dynamic performance of a novel integral magnetorheological damper-rotor system
[J].
Design of bypass rotary vane magnetorheological damper for prosthetic knee application
[J].
用于四连杆下假肢的孔隙结合式磁流变液阻尼器设计
[J].
Design of pore combined magnetorheological fluid damper for four link lower prosthesis
[J].
Dynamic modeling of large-scale magnetorheological damper systems for civil engineering applications
[J].
单轴式磁流变假肢膝关节设计及CT+PD轨迹跟踪控制
[J].
Designing uniaxial magnetorheological damper-based prosthetic knee and CT+PD trajectory tracking control
[J].
Multi-objective optimization design for a magnetorheological damper
[J].
Development of low-cost optimal magneto-rheological damper for automotive application
[J].
Design and geometric parameter optimization of hybrid magnetorheological fluid damper
[J].
A magnetorheological damper-based prosthetic knee (MRPK) and sliding mode tracking control method for an MRPK-based lower limb prosthesis
[J].
Design and optimization of a magnetorheological damper based on B-spline curves
[J].
Design and evaluation of a magnetorheological damper based prosthetic knee
[J].
Optimal design of a magnetorheological damper used in smart prosthetic knees
[J].
Optimal design of magnetorheological valve using the coupling of FE magnetic analysis and MOGA optimization for prosthetic ankle
[J].
Geometric optimization of magnetorheological damper for prosthetic ankles using artificial neural networks
[J].
Design, fabrication and characterization of an optimal magnetorheological (MR) damper for prosthetic knee application
[D].
Prototype of robotic ankle-foot prosthesis with active damping using magnetorheological fluids
[J].