基于螺旋接触线的五轴侧铣刀具定位方法

doi:10.3785/j.issn.1006-754X.2024.03.183

基于螺旋接触线的五轴侧铣刀具定位方法

李忠朋^,^,¹, 张立强^,^,¹, 刘钢¹^,²^,³

1.上海工程技术大学机械与汽车工程学院，上海 201620

2.机械工业航空大型复杂薄壁构件智能制造技术重点实验室，上海 201620

3.成都智远先进制造技术研究院，四川成都 610511

Five-axis flank milling tool positioning method based on spiral contact line

LI Zhongpeng^,^,¹, ZHANG Liqiang^,^,¹, LIU Gang¹^,²^,³

1.School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

2.Key Laboratory of Machinery Industry for Intelligent Manufacturing of Large Complex Thin-Walled Parts, Shanghai 201620, China

3.Institute of Chengdu Zhiyuan Advanced Manufacturing Technology, Chengdu 610511, China

通讯作者: 张立强（1979—），男，教授，硕士生导师，博士，从事复杂曲面数控加工研究，E-mail: zhanglq@sues.edu.cn，https://orcid.org/0000-0002-6415-8689

收稿日期: 2023-06-30 修回日期: 2023-09-04

基金资助:

国家自然科学基金资助项目. 51775328

Received: 2023-06-30 Revised: 2023-09-04

作者简介 About authors

李忠朋（1999—），男，硕士生，从事五轴侧铣加工路径规划研究，E-mail:M310121104@sues.edu.cn，https://orcid.org/0009-0000-9991-6630 , E-mail：M310121104@sues.edu.cn

摘要

针对五轴侧铣加工非可展直纹面时刀具与设计曲面相互干涉的问题，提出了一种基于螺旋接触线的刀具定位方法。首先，基于Z-buffer法建立单个刀位下的误差解析模型，以评估刀具定位方法的优劣。其次，根据非可展直纹面的扭转特性，构造刀轴矢量的数学模型，同时分析刀具-工件接触线的性质及参数表达式。再次，考虑实际加工中的非线性加工误差，通过运动学变换对全局刀位进行路径插补优化。最后，基于改进两点偏置法、最小二乘法及所提出的方法进行仿真分析并对比3种方法所产生的误差，同时基于后2种方法进行实验验证。仿真和实验结果表明，所提出的方法能够有效减小侧铣加工中的原理误差，可为非可展直纹面的五轴侧铣加工提供一定的参考依据。

关键词： 五轴侧铣 ; 非可展直纹面 ; 螺旋接触线 ; 路径优化 ; 原理误差

Abstract

A tool positioning method based on spiral contact line is proposed to address the problem of mutual interference between tool and design surface during five-axis flank milling of undevelopable ruled surfaces. Firstly, an analytical error model under a single tool position was established based on the Z-buffer method to evaluate the advantages and disadvantages of the tool positioning method. Secondly, a mathematical model of the tool axis vector was constructed based on the torsional characteristics of the undevelopable ruled surfaces, and the properties and parametric expressions of the tool-workpiece contact line were analyzed. Thirdly, considering the non-linear machining errors in actual machining, the path interpolation optimization for the global tool position was carried out by kinematics transformation. Finally, the simulation analysis was conducted based on the improved two-point offset method, the least square method and the proposed method, and the errors generated by the three methods were compared, with the latter two methods being used for experimental verification. The simulation and experimental results show that the proposed method can effectively reduce the principle error in flank milling, which can provide a certain reference for five-axis flank milling of undevelopable ruled surfaces.

Keywords： five-axis flank milling ; undevelopable ruled surface ; spiral contact line ; path optimization ; principle error

PDF (3565KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李忠朋, 张立强, 刘钢. 基于螺旋接触线的五轴侧铣刀具定位方法[J]. 工程设计学报, 2024, 31(5): 575-584 doi:10.3785/j.issn.1006-754X.2024.03.183

LI Zhongpeng, ZHANG Liqiang, LIU Gang. Five-axis flank milling tool positioning method based on spiral contact line[J]. Chinese Journal of Engineering Design, 2024, 31(5): 575-584 doi:10.3785/j.issn.1006-754X.2024.03.183

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.03.183

在航空航天、汽车及造船等行业中，具有直纹面^[1]尤其是非可展直纹面^[2]的零件十分常见，如凸轮、叶轮和涡轮叶片等^[3]。五轴侧铣技术^[4]通过线接触的方式去除工件表面的材料，具有较高的材料去除率和加工效率，且所加工的工件表面的质量往往比点铣高。然而，较大的刀具-工件接触面积给精确生成刀位和刀具路径带来了巨大的挑战。例如：在使用圆柱形刀具侧铣加工具有扭转特性的非可展直纹面时，不合理的刀位规划会引起过切误差或欠切误差。从本质上看，这些几何误差为不可避免的原理误差^[5]，只要使用合理的刀位优化方法，即可将误差控制在给定的公差范围内。

近年来，众多的国内外学者针对非可展直纹面侧铣加工中的刀具路径规划问题展开了广泛研究。根据优化原理和优化效果，五轴侧铣加工刀具路径优化方法可分为2类：局部优化法和整体优化法。局部优化法是通过调整单个刀位来实现刀具旋转表面与工件表面的最佳匹配。Liu^[6]提出了单点偏置法和两点偏置法，这2种方法虽简单且易实现，但其产生的误差（尤其是过切误差）过大。Redonnet等^[7]提出了三点规划法，三点中的两点是直纹面2条边界准线上的点，剩余一点是直纹面直母线上的点。Bedi等^[8]令刀具沿直纹面的边界准线滑动，并限制刀尖点运动方向与直纹面准线相切，由此得到一系列离散刀位。Menzel等^[9]在文献[8]方法的基础上限制直纹面母线与刀具曲面相切，提出了改进的刀具定位三步法。Gong等^[10]提出了用于刀位规划的三点偏置法，即先将直纹面向刀具方向偏置与圆柱形刀具半径相等的距离，再在偏置面上选取3条不同的曲线，并令刀轴沿其中2条曲线滑移，直到剩余一条曲线距离刀轴线最近，从而确定最优刀位。Yan等^[11]基于免疫粒子群算法计算得到使误差取得最小值时的刀位，在一定程度上减小了侧铣加工误差。Sun等^[12-13]提出了一种旋转式三点偏置法，其与三点偏置法的不同之处在于：该方法通过旋转的方式得到刀位。整体优化法通过控制刀具面族包络向设计表面整体逼近，以实现刀具路径优化。Pechard等^[14]首次从减小整体误差入手，提出了一种刀具路径全局规划方法，即通过调整刀轴轨迹面来使刀具包络面最小二乘逼近非可展直纹面，但由于是将刀轴上的点沿直纹面法向投影来度量刀具路径的几何偏差，使得计算结果存在一定的误差，故该方法有一定的局限性。Gong等^[15]利用等距包容原理将圆柱形刀具侧铣加工中的路径规划问题转换为刀轴轨迹面向直纹面等距面的最小二乘逼近问题，然后根据包络曲面的建模，提出了针对任意回转刀具路径规划的最小二乘优化方法。何改云等^[16]基于序列二次规划算法提出了一种使加工包络面与设计表面相互匹配的方法，实现了刀具加工轨迹的优化并取得了良好的加工效果。陈力智等^[17]利用奇异值分解算法求解基于三点偏置刀位偏差补偿的轴迹面拟合模型，得到了圆锥刀具的最优侧铣加工路径。Chu等^[18]基于同步扰动随机逼近算法和类电磁机制算法，通过最小化误差确定了描述刀具位姿的3条参数曲线。

上述刀具路径的整体优化法虽可有效提高设计表面的整体加工精度，但该类方法及相关技术在实际工程中很少使用。在五轴侧铣加工刀具路径优化中，关键要点在于优化方法的精度、稳健性、效率和简便性。在现有的刀具定位方法中，离散刀位确定方法具有良好的鲁棒性和简便性，但该方法的准确性与所建立的优化模型紧密相关。基于此，本文根据非可展直纹面的扭转特性确定刀位，提出了一种基于螺旋接触线的刀具定位方法。同时，通过仿真分析与实验对所提出的方法与改进两点偏置法和最小二乘法进行比较，旨在为非可展直纹面的五轴侧铣加工提供参考。

1 五轴侧铣加工误差建模

在对设计表面进行数控加工的过程中，常采用圆柱形刀具来对非可展直纹面进行五轴侧铣加工。被加工表面的加工误差通常与机床、夹具和刀具的加工精度、理论误差以及由力或热引起的变形等有关。为了将由理论误差或原理误差所引起的误差占比降至最低，学者们对不同刀具路径规划方法的加工误差模型进行了深入研究。刀具路径规划方法的优劣会直接影响设计表面的加工精度，由此产生的误差为几何误差^[19]。若刀具过度浸入设计表面，则几何误差属于过切误差；相反，则属于欠切误差。考虑到几何误差本质上为设计表面与刀具包络面之间的偏差，而在获得所有的刀位前无法确定刀具包络面的整体形状，因此很难单独定位刀具并同时考虑实际加工误差。

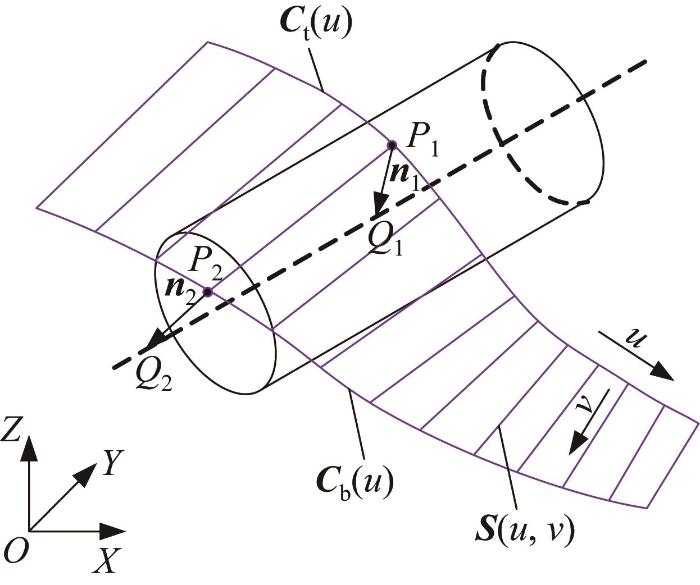
为此，本文基于Z-buffer法^[20]提出了一种误差解析模型，可简便、快捷地求解得到在不考虑其他误差源情况下被加工表面的几何误差。该方法的求解过程类似于“割草”过程，如图1所示。首先，将设计表面离散成适量的点云数据；然后，在每个样本点处沿曲面法向的正反向分别延长R（R为刀具半径），则以样本点为中点的向量即为“草”。当刀具沿特定的轨迹扫掠过这些“草”之后，它们的长度被不同程度地削减，削减后“草”的剩余长度即为加工误差。若刀具与“草”相交于设计表面正向，则产生欠切误差；反之，则产生过切误差。为了计算“草”的剩余长度，则须求解某一刀位处刀具表面与“草”的交点。由此可知，误差建模的关键在于线面的布尔求交。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于Z-buffer法的误差模型

Fig.1 Error model based on Z-buffer method

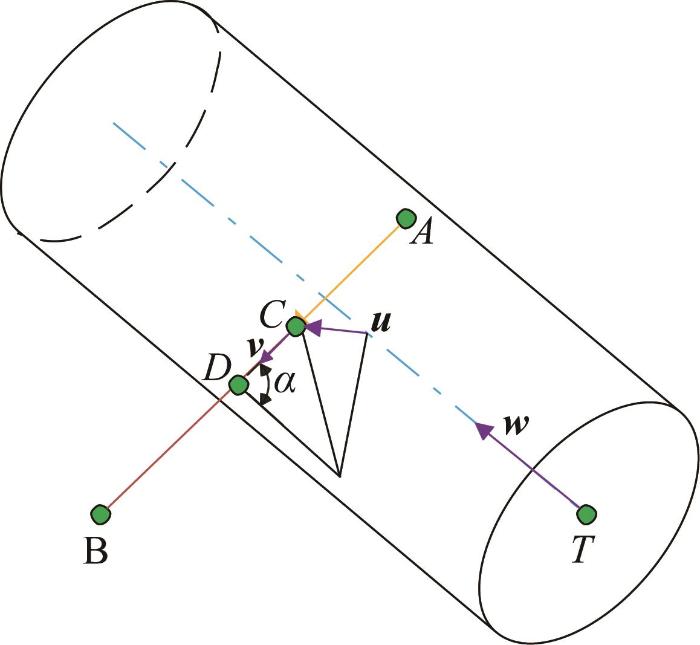
如图2所示，假设此时刀具的中心点为T，“草”的2个端点分别为A和B，将线段AB与圆柱形刀具表面的交点记为D。为了求解得到交点D的坐标，须先找到线段AB上距离刀轴最近的点C。根据图2所示的几何关系，可得：

T + x w + y u + z v = B

其中：

u = v \times w

v = \frac{\vec{A B}}{‖\vec{A B}‖}

式中： T 、 B 分别为点T和点B的位置矢量， v 、 w 分别为单位刀轴矢量和“草”的单位矢量。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 线面布尔求交示意

Fig.2 Schematic of Boolean quadrature for line and surface

求解上述以x、y、z为未知变量的线性方程组，即可求得点C和点D的位置矢量 C 、 D，分别表示为：

C = T + x w + y u

D = C + (\sqrt[]{R^{2} - y^{2}} / s i n α) v

其中：

α = a r c c o s (v \cdot w)

式中： $α$ 为单位刀轴矢量 w 与线段AB的夹角。

在得到交点D的坐标之后，即可求得设计表面某一点处的几何误差e，由e的正负可判断误差的性质：当e为正值时，为欠切误差；当e为负值时，为过切误差。

e = R - ‖\vec{A D}‖

2 基于螺旋接触线的刀具定位方法

在实际对设计表面进行五轴侧铣加工刀具路径规划的过程中，一般先进行局部优化，即先对单个刀位进行优化，随后采用最小二乘法等方法进行整体优化。本文所提出的基于螺旋接触线的刀具定位方法则是先对离散的刀位进行规划，然后对求得的所有离散刀位中的相邻刀位进行补偿计算，从而得到最终的整体刀具路径轨迹。

2.1　离散刀位的确定

在五轴侧铣加工过程中，直纹面是常见的设计表面之一。直纹面是由母线沿2条边界准线扫掠而形成的，其参数表达式为：

S (u, v) = (1 - v) C_{b} (u) + v C_{t} (u), 0 \leq u \leq 1, 0 \leq v \leq 1

(5)

式中：u、v为曲面参数， $C_{t} (u)$ 、 $C_{b} (u)$ 分别为上下准线的参数表达式。

通常情况下，直纹面的上下准线为B样条曲线^[21]，则式(5)可改写为：

\begin{array}{l} S (u, v) = (1 - v) \sum_{i = 0}^{m} N_{i, k} (u) d_{b} + v \sum_{i = 0}^{m} N_{i, k} (u) d_{t}, \\ 0 \leq u \leq 1, 0 \leq v \leq 1 \end{array}

(6)

式中： $N_{i, k} (u)$ 为B样条曲线的基函数， $d_{t}$ 、 $d_{b}$ 分别为上下准线控制顶点的位置矢量，i为控制顶点的序号，k为B样条曲线的次数。

当上下准线在同一u处的法矢（或切矢）不共线时，则直纹面为非可展直纹面，即满足以下条件：

{\overset{•}{C}}_{t} (u) \times {\overset{•}{C}}_{b} (u) \cdot ({\overset{•}{C}}_{t} (u) - {\overset{•}{C}}_{b} (u)) \neq 0

(7)

式中： ${\overset{•}{C}}_{t} (u)$ 、 ${\overset{•}{C}}_{b} (u)$ 分别为上下准线在u处的切矢。

由于非可展直纹面具有扭转特性和不可展性，母线外法向距离为刀具半径的点不可能同时位于圆柱形刀具的刀轴上。因此，在五轴侧铣加工非可展直纹面时，会不可避免地产生原理误差^[2]。为此，提出了一种类似于两点偏置法的刀具定位方法。如图3所示，P₁和P₂为非可展直纹面 $S (u, v)$ 上同一直母线的2个端点，其分别位于上下准线上，Q₁和Q₂分别为P₁和P₂沿直纹面法向偏置相同距离后所得到的点。本文刀具定位方法的限定条件为：使母线两端点的几何误差为0，即以Q₁与Q₂的连线方向作为刀轴矢量的方向。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 刀具定位示意

Fig.3 Schematic of tool positioning

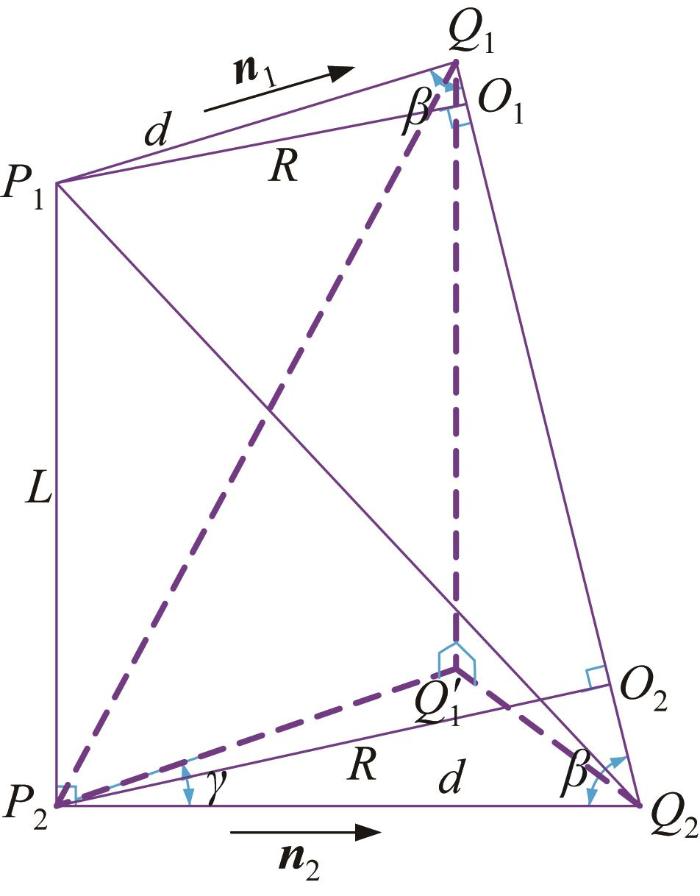
刀具定位的关键在于偏置距离的确定，将偏置距离记为d。为方便求解，将偏置距离求解转换为刀轴位置求解，如图4所示。假设直母线P₁P₂的长度为L，P₁O₁和P₂O₂均垂直于Q₁Q₂，P₁Q₁与Q₁Q₂之间的夹角为 $β$ ，由几何关系可知，P₂Q₂与Q₁Q₂之间的夹角也为 $β$ ；直母线P₁P₂处的扭转角为 $γ$ ，即P₁处直纹面的法向量 n₁与P₂处直纹面的法向量 n₂在以直母线为法向量的平面内的投影矢量之间的夹角，可表示为：

γ = a r c c o s \frac{n_{1 p} \cdot n_{2 p}}{‖n_{1 p} \cdot n_{2 p}‖}

(8)

其中：

\{\begin{matrix} n_{1 p} = n_{1} + P_{12} (n_{1} \cdot P_{12} - 1) \\ n_{2 p} = n_{2} + P_{12} (n_{2} \cdot P_{12} - 1) \end{matrix}

P_{12} = \frac{\vec{P_{1} P_{2}}}{‖\vec{P_{1} P_{2}}‖}

式中： n_1p、 n_2p分别为法向量 n₁、 n₂的投影矢量。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 刀轴位置确定示意

Fig.4 Schematic of tool axis position determination

根据图4所示的几何关系，可得：

\{\begin{array}{l} c o s β \sqrt[]{4 d^{2} s i n^{2} (γ / 2) + L^{2}} = 2 d s i n^{2} (γ / 2) \\ d s i n β = R \end{array}

(9)

由式(9)可求得关于 $β$ 的方程：

a c o s^{4} β + b c o s^{2} β + c = 0

(10)

其中：

\{\begin{array}{l} a = L^{2} \\ b = - [L^{2} + 4 R^{2} s i n^{2} (γ / 2)] \\ c = 4 R^{2} s i n^{4} (γ / 2) \end{array}

联立式(9)和式(10)，可求得偏置距离d：

d = R / s i n [a r c c o s (\frac{- b + \sqrt[]{b^{2} - 4 a c}}{2 a})]

(11)

在已知夹角 $β$ 和偏置距离d后，可根据几何关系求解点O₁和点O₂的坐标。此时以点O₂作为刀具底面的中心，以直线O₁O₂所在的单位矢量作为单位刀轴矢量，从而可确定刀具刀尖点的位置和姿态。

2.2　刀具-工件接触线分析

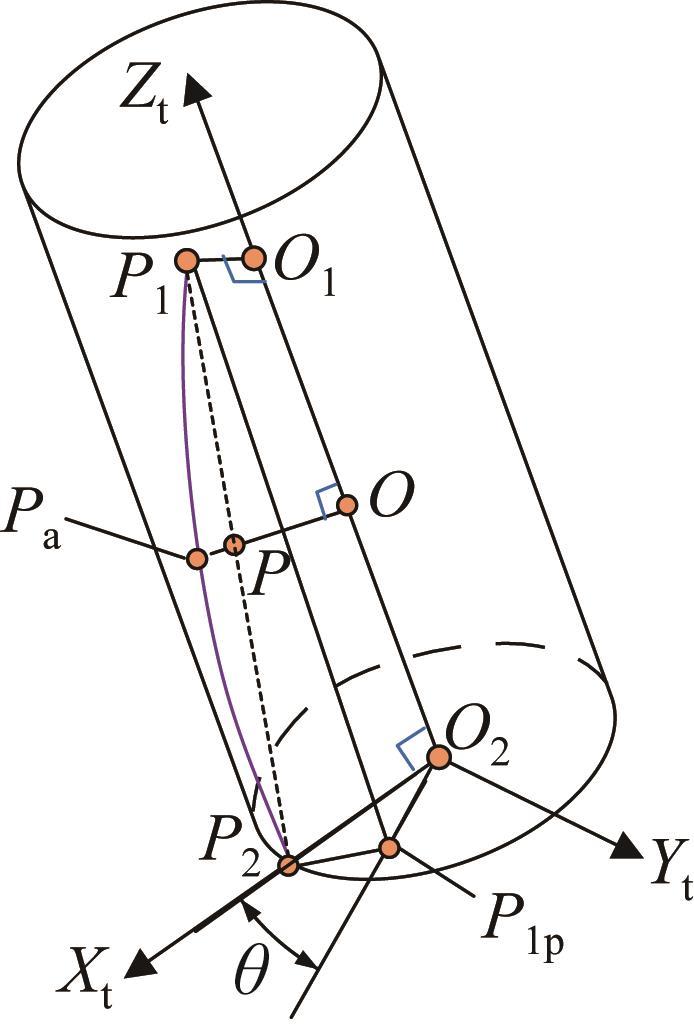
由直纹面的加工目的可知，加工时圆柱形刀具与工件的最佳接触线为直纹面的直母线P₁P₂。但由于非可展直纹面具有扭转特性，使得加工过程中实际的接触线并不能与直母线重合。如图5所示，点O为刀轴O₁O₂上一离散采样点，点P为直母线P₁P₂上一点，且OP垂直于刀轴矢量。延长OP交曲线 $\overset{̑}{P_{1} P_{2}}$ 于点P_a，OP_a的长度等于刀具半径。将点P_a称为对应于采样点O的特征点，所有的特征点组成特征线。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 刀具-工件实际接触线示意

Fig.5 Schematic of actual tool-workpiece contact line

根据以上描述，特征点为刀具回转曲面浸入工件表面最深的点，这意味着特征点位于刀具包络面上。由此可知，特征点为侧铣加工刀具-工件接触线上的一个接触点，则特征线即为刀具-工件接触线。鉴于OP_a垂直于刀轴O₁O₂，而接触点P_a又位于刀具的回转曲面上，则 $\vec{O P_{a}}$ 实际上为刀具回转曲面在接触点处的主法向量，故曲线 $\overset{̑}{P_{1} P_{2}}$ 为刀具表面的测地线^[22]。因刀具外表面为圆柱面，由测地线的几何特性可知，刀具与工件的接触线 $\overset{̑}{P_{1} P_{2}}$ 为螺旋线^[23]。

如图5所示，以O₂为原点建立刀具坐标系O₂-X_tY_tZ_t：以点O₂与点P₂的连线作为X_t轴，以刀轴O₁O₂作为Z_t轴，最后根据右手定则确定Y_t轴。图5中，点P_1p为点P₁在X_tO₂Y_t平面上的投影点， $θ$ 为X_t轴与O₂P_1p之间的夹角。在刀具坐标系O₂-X_tY_tZ_t中，刀具-工件接触线的参数表达式如下：

\{\begin{matrix} x_{p} = R c o s φ \\ y_{p} = R s i n φ \\ z_{p} = l φ \end{matrix}

(12)

其中：

l = \frac{O_{1} O_{2}}{θ}

式中： $φ$ 为螺旋角， $φ \in [0, θ]$ 。

2.3　整体刀具路径规划

在五轴侧铣加工过程中，2个相邻刀位之间的刀位通常以直线插补的方式计算得到。然而，直线插补是对后处理之后的刀具中心点和旋转轴的旋转角度进行线性插值，这会对在后处理之前所规划的刀具路径产生影响，从而产生非线性误差^[24]。另外，为了能使用本文所构建的误差模型来计算刀具沿规划路径加工工件表面时所产生的几何误差，有必要对2个相邻刀位之间的刀具运动进行研究。

采用［ T, w ］来表示五轴侧铣加工中的刀位，则相邻2个刀位分别为 $C_{n} = [T_{n}, w_{n}]$ 和 $C_{n + 1} = [T_{n + 1}, w_{n + 1}]$ 。按照传统的刀位插补算法，相邻2个刀位之间的刀位如下：

\begin{array}{l} C (t) = [(1 - t) T_{n} + t T_{n + 1}, (1 - t) w_{n} + t w_{n + 1}], \\ 0 \leq t \leq 1 \end{array}

(13)

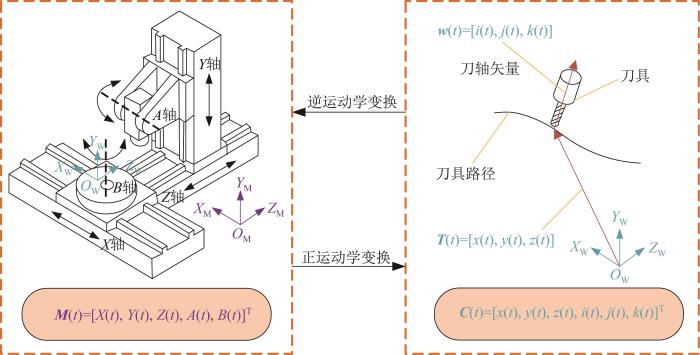
然而，使用传统的刀位插补算法易产生偏差。这是因为插补运算是由数字控制器在机床坐标系中完成的，而从工件坐标系到机床坐标系的逆运动学变换是非线性的。为了不失一般性，以A-B型（A表示摆头，B表示转台）五轴机床（见图6）为例进行说明，运动学变换可利用D-H法^[25]进行建模。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 五轴侧铣加工的运动学变换

Fig.6 Kinematics transformation for five-axis flank milling

如图6所示，正运动学变换的本质是将刀位从机床坐标系O_M-X_MY_MZ_M转换到工件坐标系O_W-X_WY_WZ_W中。令 $M (t) = {[X (t), Y (t), Z (t), A (t), B (t)]}^{T}$ 表示刀位文件经后处理之后得到的刀位， $C (t) = {[x (t), y (t), z (t), i (t), j (t), k (t)]}^{T}$ 表示刀位文件中的刀位。对于A-B型五轴机床而言， $C (t)$ 与 $M (t)$ 的转换关系如下：

\begin{array}{l} {[X (t), Y (t), Z (t)]}^{T} = R_{B} (t) \cdot R_{A} (t) \cdot \\ {[x (t), y (t), z (t)]}^{T} \end{array}

(14)

[\begin{matrix} i (t) \\ j (t) \\ k (t) \end{matrix}] = [\begin{matrix} - c o s A (t) s i n B (t) \\ - s i n A (t) \\ c o s A (t) c o s B (t) \end{matrix}]

(15)

其中：

R_{A} (t) = [\begin{matrix} 1 & 0 & 0 \\ 0 & c o s A (t) & - s i n A (t) \\ 0 & s i n A (t) & c o s A (t) \end{matrix}]

R_{B} (t) = [\begin{matrix} c o s B (t) & 0 & - s i n B (t) \\ 0 & 1 & 0 \\ s i n B (t) & 0 & c o s B (t) \end{matrix}]

式中： $R_{A} (t)$ 、 $R_{B} (t)$ 分别为绕A轴和B轴旋转的旋转矩阵。

在机床坐标系中，对相邻2个刀位 $M_{n}$ 和 $M_{n + 1}$ 进行线性插补运算：

M (t) = (1 - t) M_{n} + t M_{n + 1}, 0 \leq t \leq 1

(16)

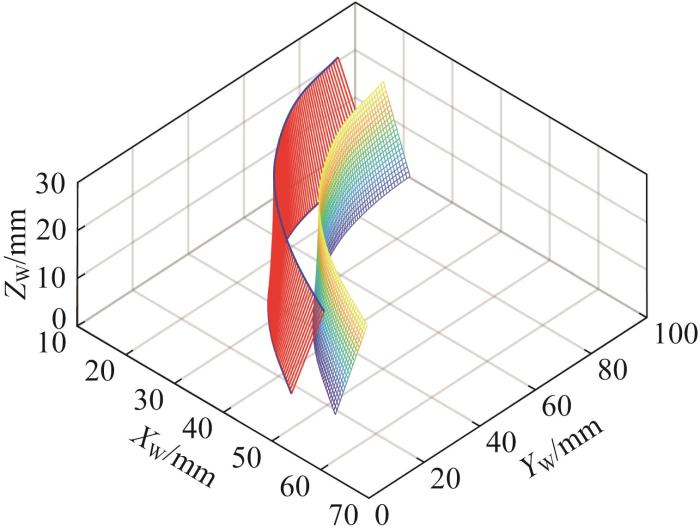
随后，利用式(17)将插补得到的刀位转换到工件坐标系中。遍历所有离散刀位，即可得到考虑非线性插补误差的刀位。利用MATLAB-R2021b软件绘制全局刀位的分布情况，如图7所示。

C (t) = F K T (M (t)), 0 \leq t \leq 1

(17)

式中：FKT $()$ 为正运动学变换函数。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于螺旋接触线的全局刀位分布图

Fig.7 Global tool position diagram based on spiral contact line

3 仿真分析与实验验证

3.1　仿真算例

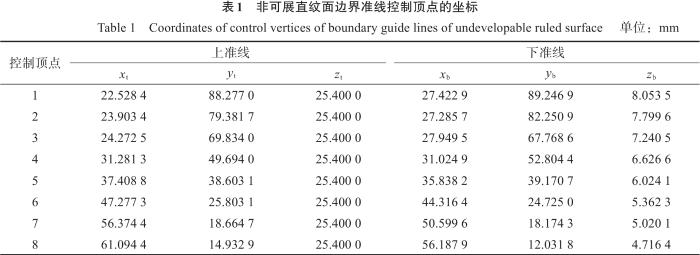
为了验证本文所提出的基于螺旋接触线的刀具定位方法的有效性，选取一个典型的非可展直纹面^[26]并利用MATLAB-R2021b软件进行仿真分析。目标非可展直纹面边界准线控制顶点的坐标如表1所示。分别使用改进的两点偏置法（两点是指同一直母线上1/4处和3/4处的两点）、最小二乘法^[19]以及本文方法对目标非可展直纹面的五轴侧铣加工刀具路径进行规划，并对其加工误差的分布情况和最大加工误差进行比较。在对加工误差进行仿真计算时，非可展直纹面u向和v向的网格划分精度为100×21。

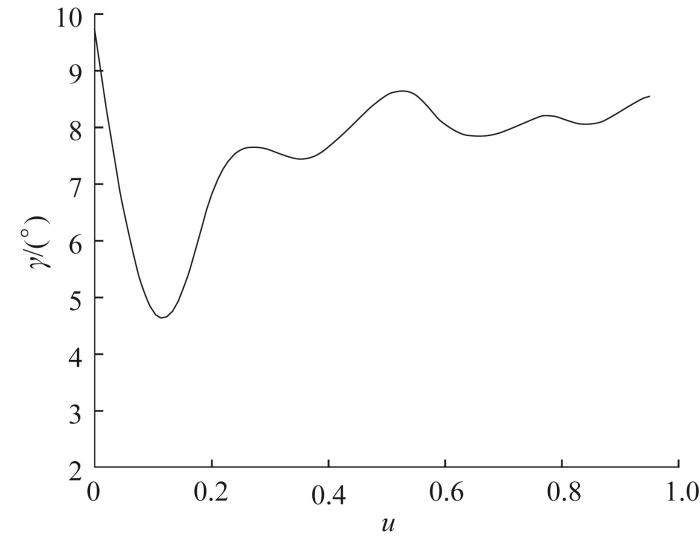
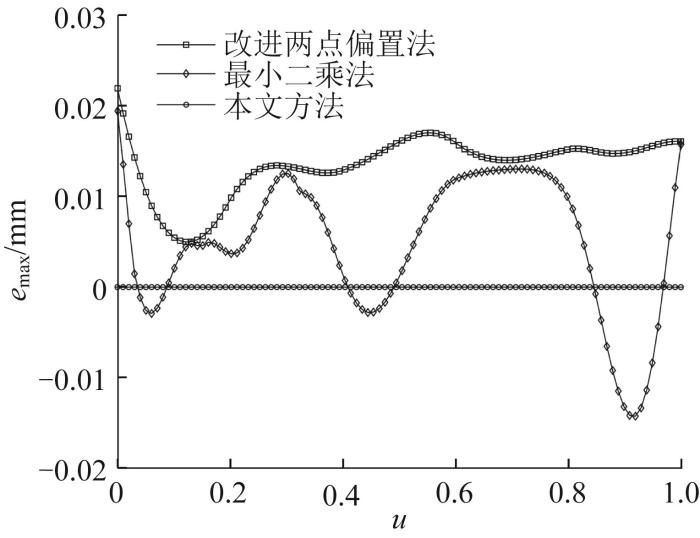
目标非可展直纹面的扭转角γ的变化曲线如图8所示。基于上述3种刀具路径规划方法对目标曲面侧铣加工刀具路径上的每一个刀位进行仿真计算。为了验证本文方法的优越性，对基于1节中侧铣加工误差模型计算得到的各刀具路径规划方法的原理误差进行对比，并对比刀具路径中每一个刀位处的最大加工误差e_max，其中沿刀具轨迹方向（u向）的最大加工误差分布规律如图9所示，最大过切误差e_o,_max、最大欠切误差e_u,_max及对应极差如表2所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 非可展直纹面的扭转角变化曲线

Fig.8 Torsion angle variation curve of undevelopable ruled surface

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同刀位下最大加工误差的分布规律

Fig.9 Distribution law of maximum machining error under different tool positions

表2 不同方法下最大加工误差的对比 (mm)

Table 2 Comparison of maximum machining error under different methods

误差	改进两点偏置法	最小二乘法	本文方法
极差	0.102 7	0.078 2	0.028 9
e_{o, max}	-0.080 8	-0.058 8	-0.028 9
e_{u, max}	0.021 9	0.019 4	0

新窗口打开| 下载CSV

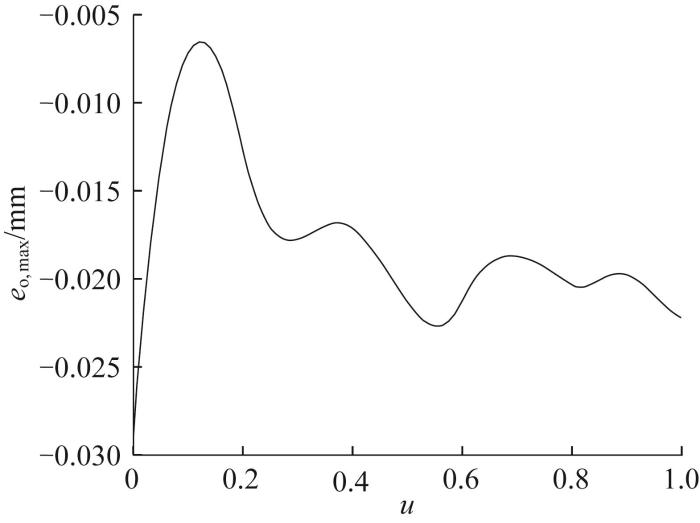
根据图9和表2，本文方法所产生的最大过切误差和最大欠切误差均小于其他2种方法。值得注意的是，本文方法产生的最大欠切误差为0，即该方法只会产生过切误差。对本文方法所产生的过切误差的分布规律进行分析，如图10所示。对比图8和图10可看出，本文方法所产生的最大过切误差的变化规律与非可展直纹面扭转角的变化规律基本一致，即扭转角越大，对应的过切误差越大，这也印证了引起原理误差的本质原因。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 本文方法下最大过切误差的分布规律

Fig.10 Distribution law of maximum overcut error under the method in this paper

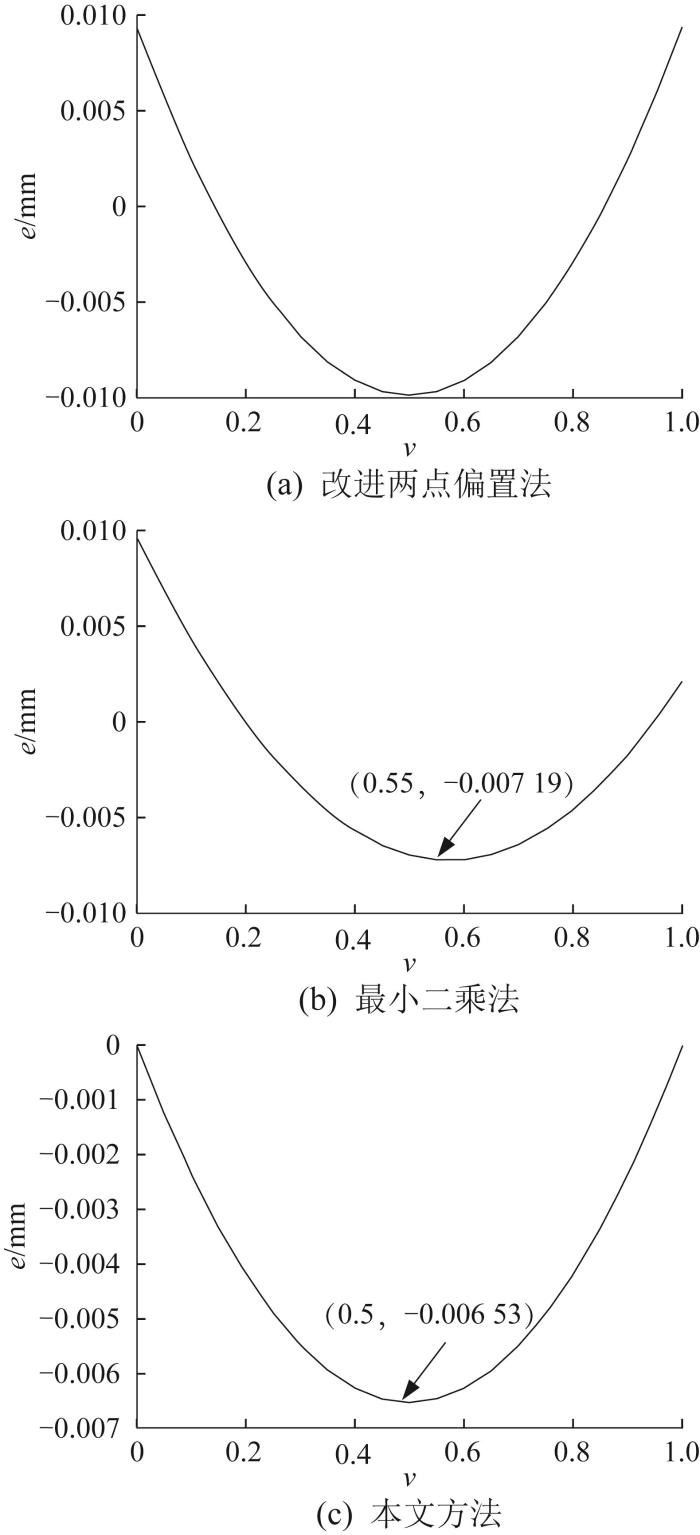
为了进一步对比3种刀具路径规划方法的差异性，对非可展直纹面同一母线处的加工误差分布规律进行分析，结果如图11所示。因本文方法的刀具定位原理与两点偏置法相似，由图11可以看到，本文方法下加工误差的分布规律与改进两点偏置法下的相似，加工误差分布大致呈关于 $v = 0.5$ 对称。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 单个刀位下的加工误差分布规律

Fig.11 Distribution law of machining error under a single tool position

3.2　实验验证

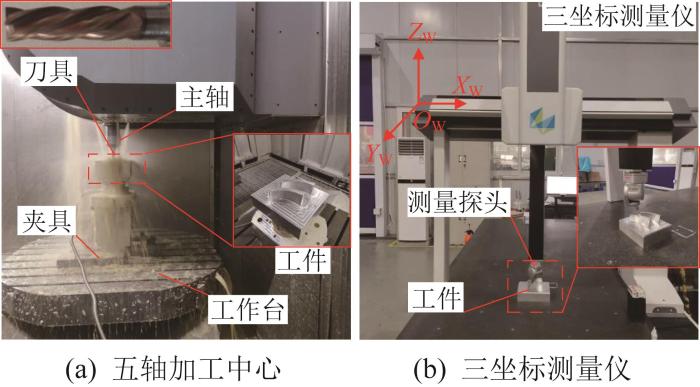
为了进一步验证本文方法的有效性，在图12(a)所示的A-B型HMC-C100P立卧转换式五轴加工中心开展加工实验。所需加工的工件表面为非可展直纹面（相关参数与3.1节同），工件材料为7050-T7451铝合金。根据3.1节，已知最小二乘法优于改进两点偏置法，故不再使用基于改进两点偏置法得到的刀位开展加工实验。在五轴侧铣加工中，选用直径为16 mm的平底圆柱形铣刀，刀具材料为硬质合金。设精加工阶段的径向切深为1 mm，轴向切深为30 mm；加工中心主轴转速为2 000 r/min，每齿进给量为0.02 mm。在完成加工实验后，使用图12(b)所示的Hexagon三坐标测量仪分别对基于2种方式加工的工件表面上的采样点进行坐标测量。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 五轴加工中心与三坐标测量仪

Fig.12 Five-axis machining center and three-coordinate measuring instrument

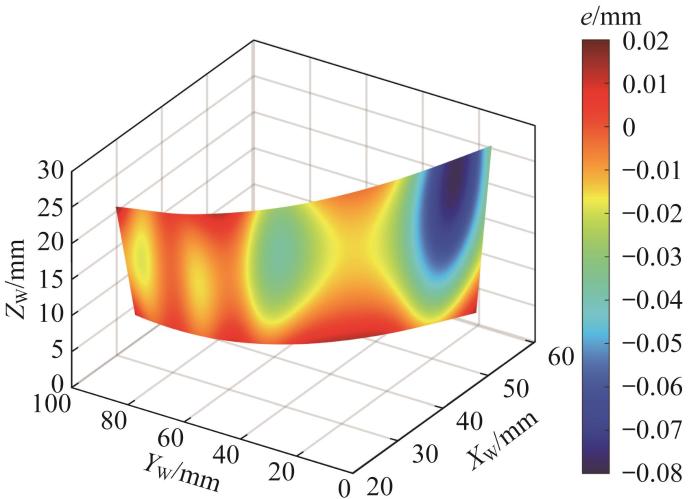
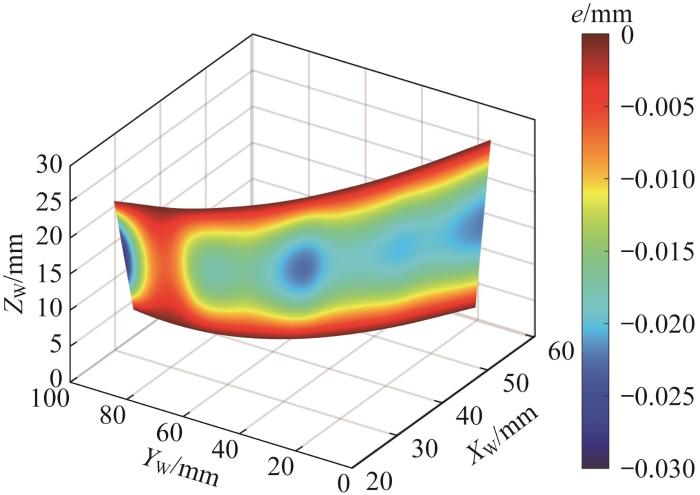
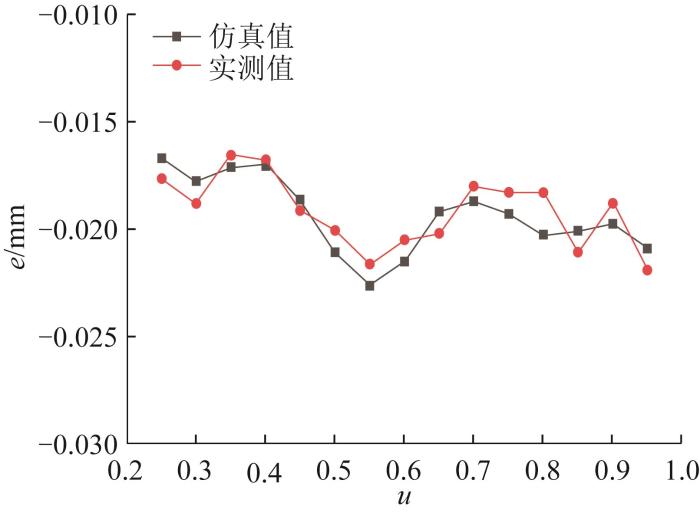
根据三坐标测量结果，对最小二乘法和本文方法下的加工误差进行分析，结果分别如图13和图14所示。通过对比可以发现，最小二乘法所产生的加工误差总体上比本文方法所产生的大，尤其是局部过切误差要大很多。此外，本文方法所产生的加工误差分布大致呈关于 $v = 0.5$ 对称，这是由本文方法的刀具定位原理所导致的。基于本文方法加工得到非可展直纹面后，均匀地在 $v = 0.45$ 上取15个采样点，这些采样点对应的 $u \in [0.25, 0.95]$ 。对这些采样点处的加工误差仿真值与实测值进行对比，结果如图15所示。由图15可以看出，仿真结果与实测结果之间相差无几，两者的最大相对误差为9.84%，验证了基于螺旋接触线的刀具定位方法是有效的。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 最小二乘法下加工误差的分布云图

Fig.13 Machining error distribution nephogram under least square method

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 本文方法下加工误差的分布云图

Fig.14 Machining error distribution nephogram under the method in this paper

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 本文方法下加工误差的仿真值与实测值对比（ v=0.45）

Fig.15 Comparison between simulated and measured machining error values under the method in this paper （v=0.45）

4 结论

本文针对五轴侧铣加工非可展直纹面时产生的原理误差问题，提出了一种基于螺旋接触线的刀具定位方法。通过基于Z-buffer法的误差解析模型来评估单个刀位下的加工误差；在考虑实际加工中非线性误差的情况下，通过仿真以及侧铣切削加工实验证明了本文所提出方法的有效性。仿真和实验结果表明，相比于改进的两点偏置法和最小二乘法，本文方法可有效减小侧铣加工中的原理误差，尤其是欠切误差，这在非可展直纹面的五轴侧铣加工中有一定的工程应用价值。但是，本文所提出的基于螺旋接触线的刀具定位方法仅适用于圆柱形刀具，未来可针对锥形刀具开展相关研究。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

YAO

C L

， HE

G Y

， SANG

Y C

， et al.

Tool path regeneration in five-axis flank milling for ruled surface based on error distribution

［J］. Proceedings of the Institution of Mechanical Engineers， Part B： Journal of Engineering Manufacture， 2022， 236（13）： 1751-1759.