工程设计学报

工程设计学报, 2024, 31(3): 348-356 doi: 10.3785/j.issn.1006-754X.2024.03.170

可靠性与保质设计

基于振动响应分析的海底管道悬空内检测研究

马文滨,,1,2, 段志文1,2,3, 李想1,2, 张行,1,2

1.中国石油大学（北京） 机械与储运工程学院，北京 102249

2.中国石油大学（北京） 高端油气装备智能设计与制造研究中心，北京 102249

3.国家管网集团北方管道有限责任公司 秦皇岛输油气分公司，河北 秦皇岛 066001

Study on submarine pipeline suspension internal detection based on vibration response analysis

MA Wenbin,,1,2, DUAN Zhiwen1,2,3, LI Xiang1,2, ZHANG Hang,1,2

1.College of Mechanical and Transportation Engineering, China University of Petroleum (Beijing), Beijing 102249, China

2.Center of Advanced Oil and Gas Equipment, China University of Petroleum (Beijing), Beijing 102249, China

3.Qinhuangdao Oil and Gas Transportation Branch, National Pipe Network Group North Pipeline Co. , Ltd. , Qinhuangdao 066001, China

通讯作者: 张　行（1988—），男，湖北黄冈人，副教授，博士，从事油气智能装备设计理论与服役可靠性研究，E-mail: zhanghang@cup.edu.cn

收稿日期: 2023-05-23   修回日期: 2023-08-21  

基金资助: 国家自然科学基金青年基金资助项目.  51805542
国家自然科学基金面上项目.  52275141
中国石油大学（北京）科研基金资助项目.  2462023QNXZ012

Received: 2023-05-23   Revised: 2023-08-21  

作者简介 About authors

马文滨（2001—），男，重庆人，硕士生，从事悬空检测技术与装备研究，E-mail:18883487151@163.com，https://orcid.org/0009-0007-0627-7456 , E-mail：18883487151@163.com

摘要

铺设于海床中的海底管道常因洋流冲刷、船舶锚拽等自然或人为因素而处于悬空状态，易造成管道变形、腐蚀、损伤和开裂泄漏等问题，严重影响管线安全。针对DN200海底管道的悬空内检测，设计了一种内检测机器人并对其进行了动力学分析。同时，联合ANSYS与ADAMS软件建立了柔性管道-土耦合模型，开展了悬空管道内检测仿真分析。采用快速傅里叶变换和短时傅里叶变换方法对内检测机器人在复杂激励耦合条件下的振动响应信号进行处理，通过分析机器人的振动加速度实现了对悬空管段的有效识别。研究结果为油气管道悬空内检测提供了新思路。

关键词： 海底管道 ; 悬空 ; 内检测机器人 ; 动力学分析 ; 振动响应

Abstract

Submarine pipelines laid in the seabed are often suspended due to natural or man-made factors such as ocean current erosion and ship anchoring, which can easily cause pipeline deformation, corrosion, damage, cracking and leakage, seriously affecting the safety of pipelines. Aiming at the suspension internal detection for DN200 submarine pipelines, an internal detection robot was designed, and its dynamics analysis was conducted. Meanwhile, a flexible pipeline-soil coupling model was established by combining ANSYS and ADAMS software, and the internal detection simulation analysis for suspended pipelines was carried out. The fast Fourier transform and the short-time Fourier transform were used to process the vibration response signal of the internal detection robot under complex excitation coupling conditions, and the effective identification of the suspended pipeline section was realized by analyzing the vibration acceleration of the robot. The research results provide a new idea for the internal detection of oil and gas pipelines in suspension.

Keywords： submarine pipeline ; suspension ; internal detection robot ; dynamics analysis ; vibration response

PDF (4384KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

马文滨, 段志文, 李想, 张行. 基于振动响应分析的海底管道悬空内检测研究[J]. 工程设计学报, 2024, 31(3): 348-356 doi:10.3785/j.issn.1006-754X.2024.03.170

MA Wenbin, DUAN Zhiwen, LI Xiang, ZHANG Hang. Study on submarine pipeline suspension internal detection based on vibration response analysis[J]. Chinese Journal of Engineering Design, 2024, 31(3): 348-356 doi:10.3785/j.issn.1006-754X.2024.03.170

随着海洋油气事业的发展，从海上油气平台到陆地的石油与天然气运输管道的里程逐渐增大。海底油气管道通常铺设于海床中，是运输海洋石油和天然气最经济安全的方式之一[1]。但随着海底管道网络的快速扩张和其他海上活动的日益频繁，由轮船锚链拉拽造成的海底管道变形问题越来越多[2]。同时，受洋流冲击、海啸、海底地震等自然活动的影响，海底管道易裸露于海床之上，导致海底管道腐蚀、损伤甚至开裂泄漏[3]。目前，海底管道悬空问题已成为海洋油气资源开发面临的主要风险和危害之一，严重威胁了管线安全。若不及时处理这一问题，则可能会造成重大的海洋污染事故和巨大的经济损失。近年来，国内外学者针对海底管道悬空内检测技术开展了大量研究。1993年，英国剑桥大学的Köpke与Hunt博士[4-5]首次提出了基于振动理论的管道悬空内检测方法，即先采用清管器搭载激振装置的方式来激励管道，再通过采集、分析管道的振动响应信号来评估管道的悬空状态。该方法首次采用频率响应函数对管道的悬空状态进行评价。西南石油大学的潘峰等人[6]、中国石油大学的Liao等人[7-10]开展了海底管道悬空内检测的数值模拟与室内实验研究，通过扫频激振方式对被检管道施加激励，利用安装在管道外部的加速度传感器来采集管道的振动响应信号，并采用频率响应函数、傅里叶变换等多种方法，结合共振频率变化指标对被检管道的悬空状态进行了分析与评价，精确地识别出了悬空管段的位置及长度。中国石油大学的张行等人[11-12]为突破扫频激振所需辅助设备多、成本高的限制，开展了基于力锤激励的海底管道悬空内检测机器人的研究，并成功研制了一种适用于外径为508 mm的海底管道的内检测机器人，该机器人采用间歇激励管道、间歇采集管道振动响应的检测方案；完成管道振动响应信号的采集后，他们采用短时傅里叶变换、改进希尔伯特-黄变换等方法对管道的安全性进行了分析与评价。

综上所述，目前海底管道悬空内检测主要是通过直接采集、分析管道振动响应信号来实现的。但是，在实际应用中，很难实现海底管道振动响应信号的直接采集。为解决这一问题，笔者设计了一种新型的海底管道悬空内检测机器人，该机器人能够直接通过其本体的振动响应信号来间接分析和识别悬空管道，旨在为油气管道悬空内检测研究提供新思路。

1 海底管道悬空内检测机器人的结构及工作原理

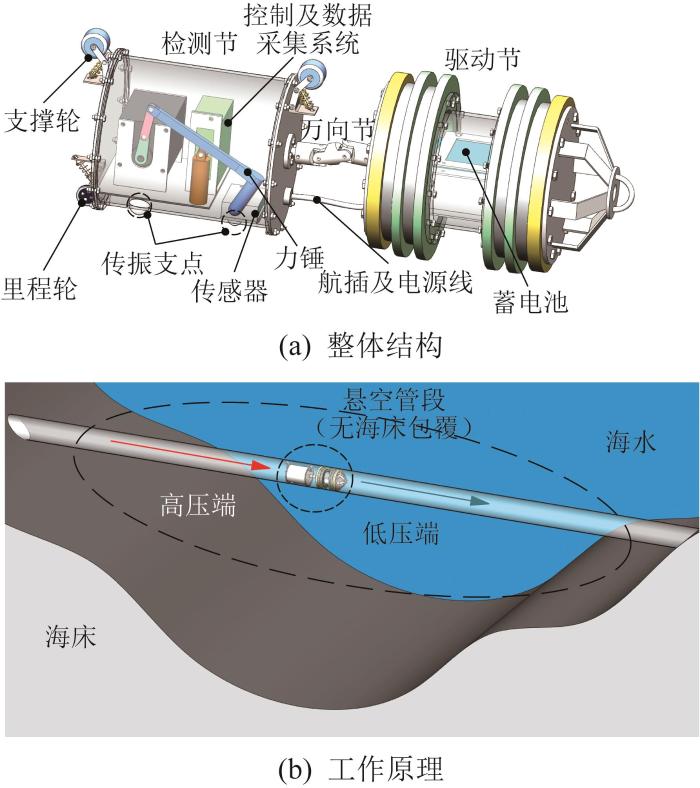
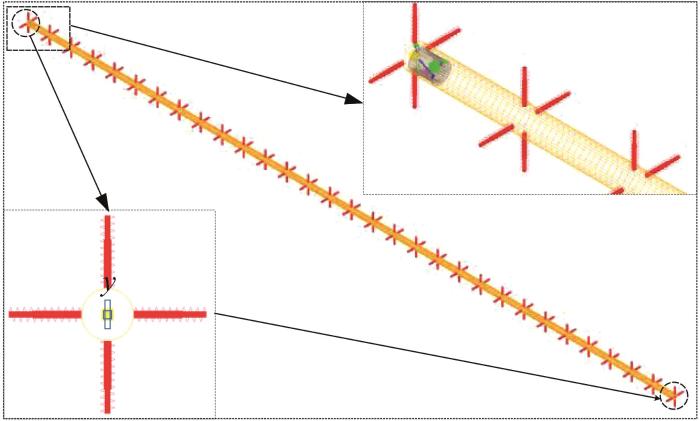
本文针对DN200海底管道的悬空内检测问题，设计了一种新型的海底管道悬空内检测机器人，其整体结构和工作原理如图1所示。该机器人主要由驱动节与检测节组成，两者通过万向节连接。其中，驱动节为清管器，其外部装有密封盘，密封盘与海底管道内壁呈面-面接触，以保证驱动节的密封性能；驱动节内部装有蓄电池，可为检测节的各执行元件提供电源。检测节外部装有支撑轮、里程轮与传振支点，内部装有激振系统、电机控制系统、里程数据采集系统与振动响应信号采集系统。检测节外部的2组支撑轮组件采用滑块配合弹簧缓冲的结构，能够将检测节传振支点紧压在海底管道内壁，以形成点-面接触。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   海底管道悬空内检测机器人的整体结构和工作原理

Fig.1   Overall structure and working principle of submarine pipeline suspension internal detection robot


如图1(b)所示，海底管道悬空内检测机器人的驱动方式为：驱动节一侧为高压端，另一侧为低压端，两侧形成的压差为驱动节提供动力，驱动节牵引检测节于管内行进。在行进过程中，检测节内的力锤敲击检测节本体，检测节本体通过与管道紧密接触的传振支点将力锤的激振力传递至管道，以实现对管道的间接激励；管道受激后产生的振动通过检测节上的传振支点有效地传递回检测节内部。与此同时，位于检测节内部的三轴加速度传感器精准地采集检测节本体的振动响应信号。对所采集的机器人检测节本体的振动响应—时间数据进行短时傅里叶变换处理，通过分析处理后的振动响应数据以及里程轮所采集的里程数据来快速确定悬空管段的位置。

2 机器人动力学分析及柔性管道-土耦合仿真模型建立

2.1　机器人动力学分析

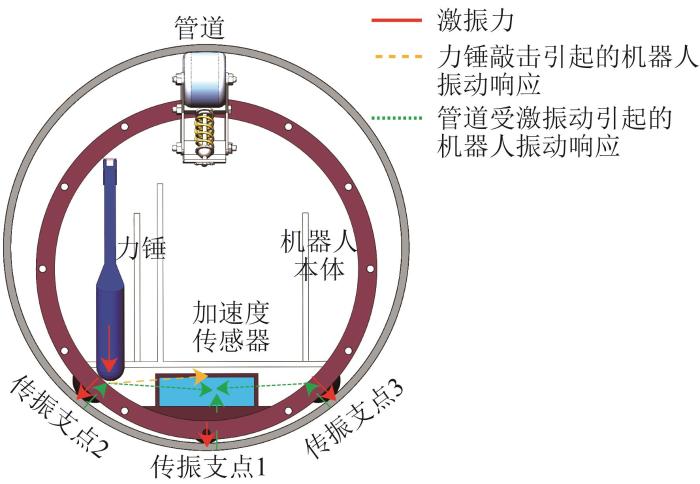
对本文所设计的海底管道悬空内检测机器人受激后的状态进行了动力学分析，如图2所示。该机器人在管道内作业时的振动响应较为复杂。在管道内部，机器人受到双向激励：一方面来自力锤敲击，另一方面来自管道的受激振动。力锤先对机器人本体施加激振力，引起其自身产生振动响应；随后，机器人自身的振动响应通过检测节外壁的传振支点1，2，3对管道进行激励，管道受激后产生的振动响应通过传振支点1，2，3反向传递至机器人本体。因此，加速度传感器采集到的振动加速度信号是由力锤敲击引起的机器人振动加速度与管道振动引起的机器人振动加速度叠加耦合而成的。本文通过分析机器人的耦合振动响应来间接评价管道的振动响应。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   海底管道悬空内检测机器人受激后的动力学分析示意

Fig.2   Schematic of dynamics analysis of submarine pipeline suspension internal detection robot under excitation


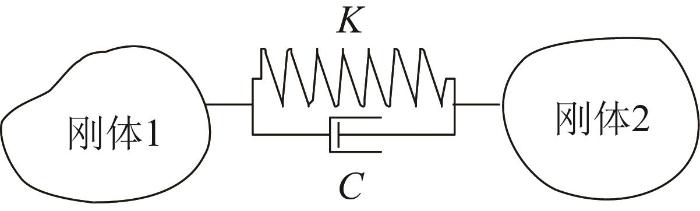
海底管道悬空内检测模型较为复杂，涉及的接触力与弹簧力众多。合理计算并设置力锤与机器人检测节内壁之间的接触力是构建其碰撞模型的关键。力锤与机器人检测节内壁的碰撞模型本质上是一种刚体碰撞模型[13-14]。简化的刚体碰撞模型如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   刚体碰撞模型

Fig.3   Rigid body collision model


根据图3，当力锤与机器人检测节内壁发生碰撞时，两者之间的接触力与弹性力和阻尼力有关，其表达式为：

Fn=Kδne+Cvn

式中：Fn为法向接触力，N；K为接触刚度系数，N/m；δn为接触点处的法向穿透深度，m；e为力指数；C为阻尼系数，N·s/m；vn为接触点处的法向相对速度，m/s。

接触刚度系数K的大小与相互接触的两物体的材料及结构类型有关，其计算式如下[15]：

K=43R12E

其中：

1R=1R1+1R21E=1-μ12E1+1-μ22E2

式中：R为综合曲率半径，m；E为综合弹性模量，N/m2；R1为力锤接触点的当量半径，m；R2为检测节内壁接触点的当量半径，m；E1为力锤材料的弹性模量，N/m2；E2为检测节内壁材料的弹性模量，N/m2；μ1为力锤材料的泊松比；μ2为检测节内壁材料的泊松比。

根据力锤与机器人检测节内壁的接触点的当量半径（R1=7.5×10-3 m，R2=8.2×10-2 m），以及对应材料的弹性模量（E1=E2=2.07×1011 N/m2）和泊松比（μ1=μ2=0.29），利用式(2)和式(3)计算得到综合曲率半径R、综合弹性模量E和接触刚度系数K。综上，力锤与机器人检测节内壁的碰撞仿真模型的参数设置如表1所示。

表1   碰撞仿真模型参数设置

Table 1  Parameter setting for collision simulation model

参数数值
综合曲率半径/m6.872×10-3
综合弹性模量/(N/m2）1.139×1011
接触刚度系数/(N/m)398.2
阻尼系数/(N·s/m)0.4
力指数1.5
法向穿透深度/m1×10-4
静摩擦系数0.3
动摩擦系数0.1
静平移速度/(m/s)1×10-4
摩擦平移速度/(m/s)1×10-3

新窗口打开| 下载CSV


2.2　柔性管道-土耦合仿真模型建立

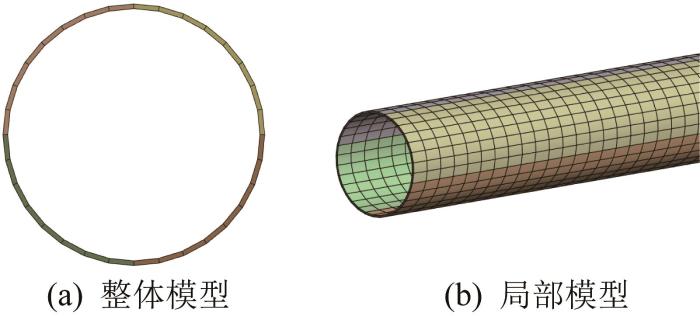
海洋油气管道的铺设方式与陆上管道相似，即：先在海床上挖沟，再将油气管道铺设于沟中并进行掩埋。因此，所检测的海底管道处于管-土耦合状态。在耦合状态下，被检管道受激后产生的振动响应在管道不同位置处并不相同，且管道整体的振动响应会受到管道各位置之间相互作用的影响。因此，不能将管道视作刚体进行研究，而是应当基于有限元思想，将管道视作由大量微元组成的柔性体[16-20]。本文采用ANSYS与ADAMS软件联合仿真的方式，对所设计的机器人在检测海底管道悬空状态时的耦合振动响应进行研究。

利用ANSYS软件构建海底管道的有限元模型，如图4所示。其中，管道的长度为30 m，外径为219 mm，内径为211 mm，厚度为4 mm；单个管道片单元的径向厚度为4 mm，轴向长度为50 mm。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   海底管道有限元模型

Fig.4   Finite element model of submarine pipeline


将海底管道有限元模型导入ADAMS软件，并在柔性管道外部与ADAMS软件中的参考地面（ground）之间设置具有一定刚度和阻尼的管-土弹簧来模拟管道与海床土壤之间的相互作用。基于ADAMS软件构建的柔性管道-土耦合仿真模型如图5所示。本文于柔性管道外侧的垂向、水平方向加设管-土弹簧；在管道两端设置固定块，并在固定块上加设垂向平移副，以限制管道两端因受力而发生扭转。通过对相应柔性管道外部的管-土弹簧设置刚度和阻尼来模拟铺设状态正常的管道，刚度系数设为400 000 N/m，阻尼系数设为100 N·s/m；通过卸载相应柔性管道外部的管-土弹簧的刚度与阻尼来模拟悬空管道[21]。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   柔性管道-土耦合仿真模型

Fig.5   Flexible pipeline-soil coupling simulation model


3 基于机器人振动响应信号的海底管道悬空内检测

海底管道悬空内检测机器人以0.5 m/s的速度在管道内匀速行进，力锤每秒对机器人检测节内壁激振1次；仿真时间为60 s，步长为0.001 s。

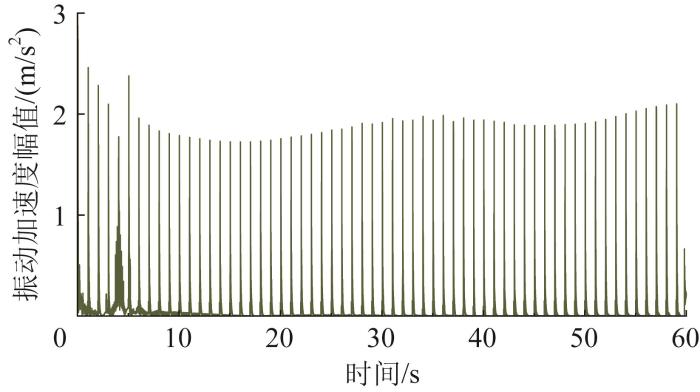
3.1　正常管道内检测

在柔性管道-土耦合仿真模型中，将30 m长的管道设置为铺设状态正常的管段，以开展正常管道内检测仿真分析。机器人在正常管段内连续进行检测作业时的振动加速度幅值的变化情况如图6所示。由图6可知，在正常管道内，机器人在不同管道位置处的振动加速度幅值不同，但基本维持在2 m/s2左右。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   正常管段内机器人的振动加速度幅值

Fig.6   Vibration acceleration amplitude of robot in normal pipeline section


3.2　悬空管道内检测

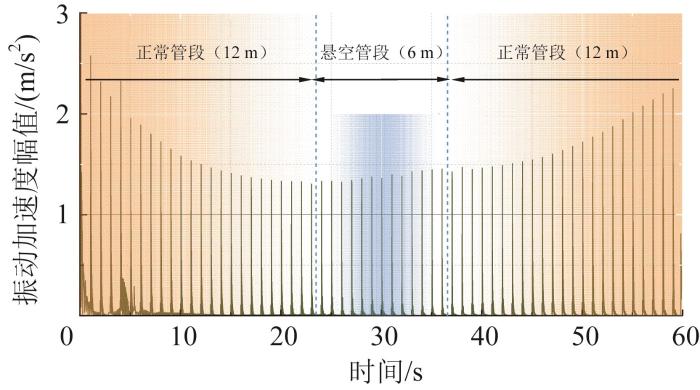
在柔性管道-土耦合仿真模型中，将中间部分6 m长的管道设为悬空管段，其余部分均为铺设状态正常的管道，同样开展管道内检测仿真分析。机器人在正常管段和悬空管段内连续进行检测作业时的振动加速度幅值的变化情况如图7所示。由图7可知，在由正常管段至悬空管段的检测过程中，机器人的振动加速度幅值由2.6 m/s2逐渐减小至1.3 m/s2；在由悬空管段至正常管段的检测过程中，机器人的振动加速度幅值由1.3 m/s2逐渐增大至2.3 m/s2。通过对比图6和图7发现，机器人在经过悬空管段时，其振动加速度会有一定幅度的下降，则可以通过观察机器人振动加速度的变化情况来判断管道的悬空位置，初步证明了通过分析机器人的振动响应来间接分析管道的悬空状态是有效、可行的。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   正常管段和悬空管段内机器人的振动加速度幅值

Fig.7   Vibration acceleration amplitude of robot in normal pipeline section and suspended pipeline section


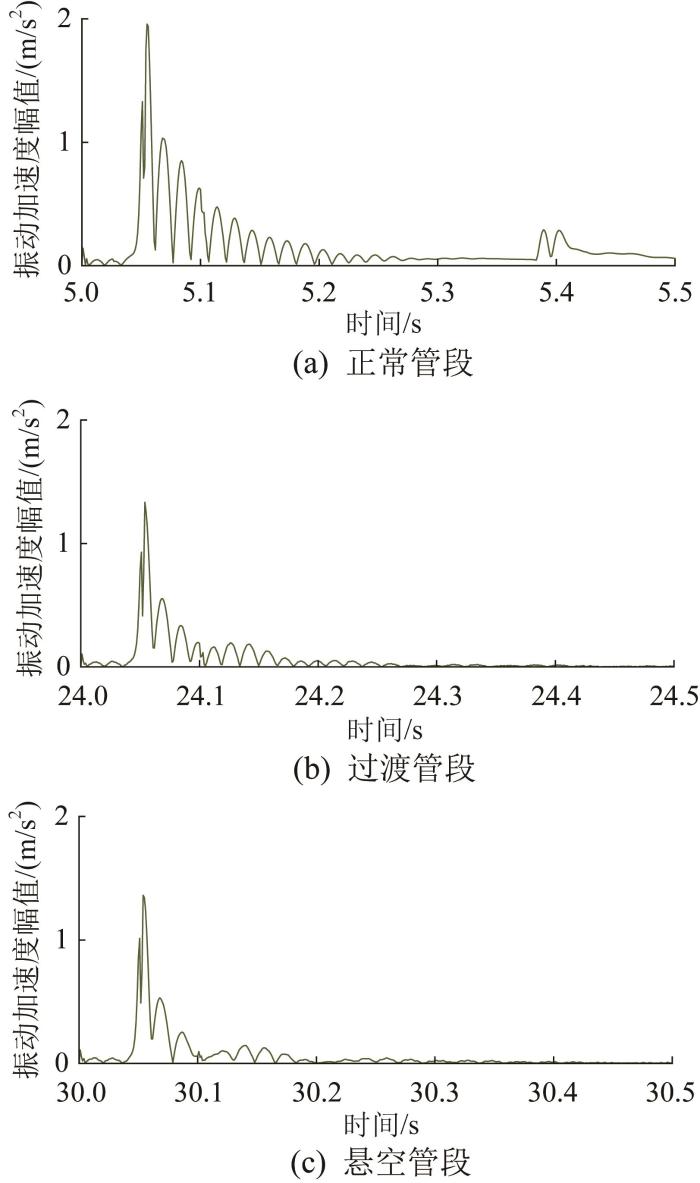
为进一步探究机器人在由正常管段向悬空管段行进检测时的振动响应，将正常管段与悬空管段之间的一段管道设为过渡管段（长0.25 m），并对不同管段内机器人的振动加速度信号进行时域分析、基于快速傅里叶变换的频域分析以及基于短时傅里叶变换的频域分析。

1）时域分析。

基于图7，分别提取机器人行经正常管段、过渡管段、悬空管段时的振动加速度幅值的变化情况（均取0.5 s），结果如图8所示。通过对比发现：在正常管段检测时，机器人的振动加速度幅值普遍大于行经过渡管段及悬空管段时的振动加速度幅值，且在正常管段检测时，机器人振动加速度的振荡更为剧烈；在悬空管段检测时，机器人的振动加速度幅值明显减小，振动加速度振荡也变缓。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   机器人在不同管段内的振动加速度时域特性

Fig.8   Time-domain characteristics of vibration acceleration of robot in different pipeline sections


出现上述结果的原因主要是正常管段、过渡管段、悬空管段周围的土壤覆盖程度不同。正常管段完全被周围土壤覆盖，周围土壤对管道周向施加的压力限制了管道受激后的振动响应，因此正常管段受激后的振动能量无法有效耗散，从而导致部分振动能量反向传递至机器人，造成机器人在正常管段检测时的振动加速度幅值较大且振荡剧烈。悬空管段周围无土壤覆盖，管道周向无压力限制，管道作自由振动，使得大部分振动能量自行耗散，则反向传递至机器人的振动能量减少，故机器人检测时的振动加速度幅值减小且振荡变缓。对于过渡管段，由于土壤对管道的覆盖不完全，机器人检测时的振动加速度幅值介于上述2种情况之间。

2）基于快速傅里叶变换的频域分析。

对机器人在正常管段、过渡管段、悬空管段开展检测作业时的振动加速度进行快速傅里叶变换，得到相应的幅频特性曲线，如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   机器人在不同管段内的振动加速度幅频特性

Fig.9   Amplitude-frequency characteristics of vibration acceleration of robot in different pipeline sections


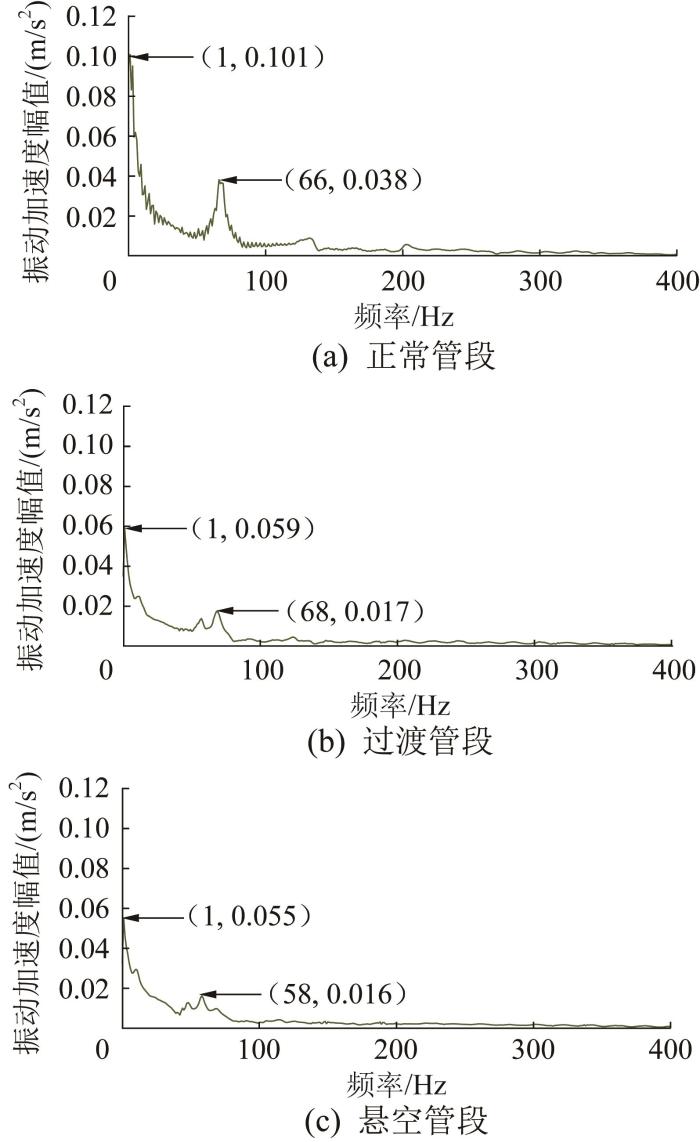
观察图9可知：机器人在正常管段、过渡管段、悬空管段检测时，其振动加速度的频率为0~100 Hz，第1个振动加速度峰值均出现在1 Hz处，第2个振动加速度峰值分别出现在66，68，58 Hz处。机器人在正常管段检测时的振动加速度峰值分别为0.101，0.038 m/s2，分别大于在过渡管段的0.059，0.017 m/s2以及在悬空管段的0.055，0.016 m/s2。综上，当机器人由正常管段向悬空管段行进检测时，其振动加速度峰值呈下降趋势。

3）基于短时傅里叶变换的频域分析。

快速傅里叶变换只能反映信号的频域特性，而无法对信号的时域特性进行分析。为了更直观地观察信号在时域与频域中的特性，Gabor于1946年提出了短时傅里叶变换[22-24]。对图7所示的机器人振动加速度信号进行短时傅里叶变换，得到对应的时频功率幅值谱，如图10所示。从图10中可以观察出，机器人在正常管段与悬空管段的振动加速度功率幅值差异明显，尤其是0~30 Hz与50~80 Hz频段；越接近悬空管段中心，机器人振动加速度的功率幅值越小。

图10

新窗口打开| 下载原图ZIP| 生成PPT

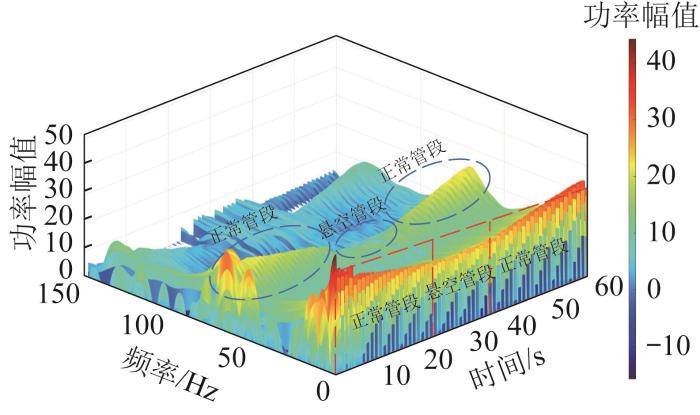
图10   机器人振动加速度的时频功率幅值谱

Fig.10   Time-frequency power amplitude spectrum of robot vibration acceleration


3.3　不同长度的悬空管道内检测

1）时域分析。

为研究悬空管段长度不同时机器人振动响应的变化规律，在上述6 m悬空管段内检测仿真的基础上，开展8 m悬空管段和4 m悬空管段的内检测仿真。当机器人行进至8，6，4 m悬空管段中心位置处开展检测作业后（取0.5 s），采集机器人的振动加速度信号，结果如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   机器人在不同长度悬空管段内的振动加速度幅值

Fig.11   Vibration acceleration amplitude of robot in suspended pipeline sections with different lengths


通过对比图11能够发现：

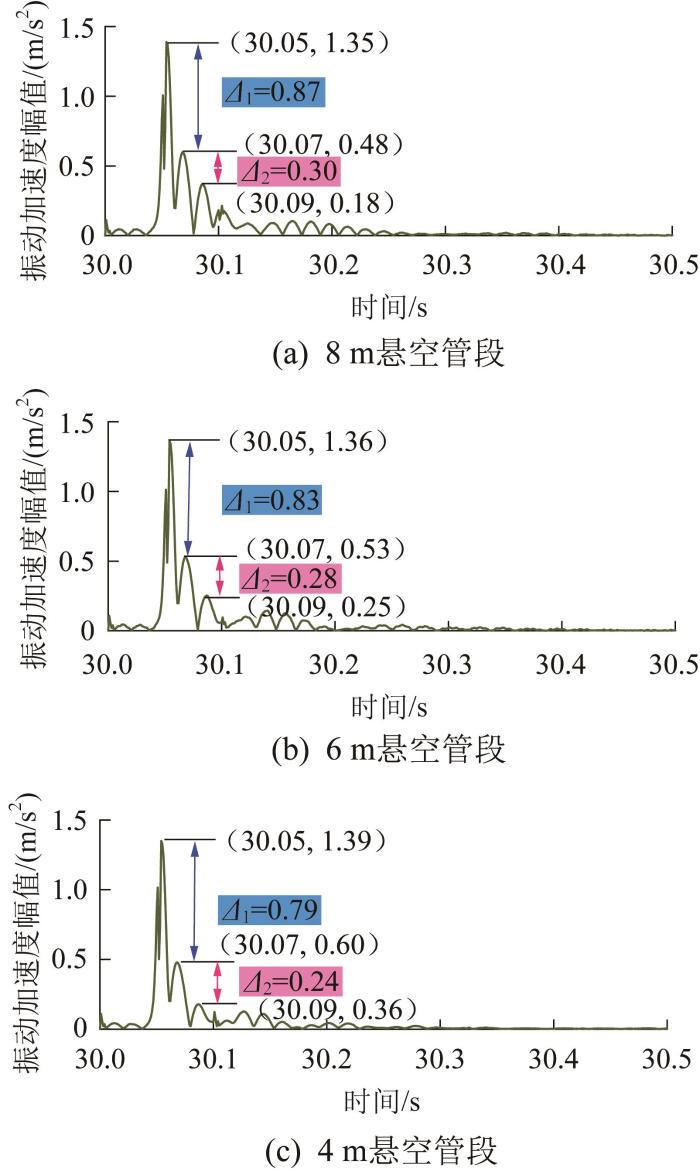
随着悬空管段的缩短，机器人在悬空管段中心位置作业后的振动加速度幅值变大。当悬空管段为8，6，4 m时，机器人的第1个振动加速度峰值分别为1.35，1.36，1.39 m/s2；第2个振动加速度峰值分别为0.48，0.53，0.60 m/s2；第3个振动加速度峰值分别为0.18，0.25，0.36 m/s2。

另外，随着悬空管段的缩短，机器人振动加速度的衰减幅度变小。当悬空管段为8 m时，第1个振动加速度峰值至第2个振动加速度峰值衰减了0.87 m/s2；当悬空管段为6 m时，第1个振动加速度峰值至第2个振动加速度峰值衰减了0.83 m/s2；当悬空管段为4 m时，第1个振动加速度峰值至第2个振动加速度峰值衰减了0.79 m/s2。同样的，当悬空管段为8，6，4 m时，机器人第2个振动加速度峰值至第3个振动加速度峰值的衰减规律与第1个振动加速度峰值至第2个振动加速度峰值的衰减规律相同，分别衰减了0.30，0.28，0.24 m/s2。

2）基于短时傅里叶变换的频域分析。

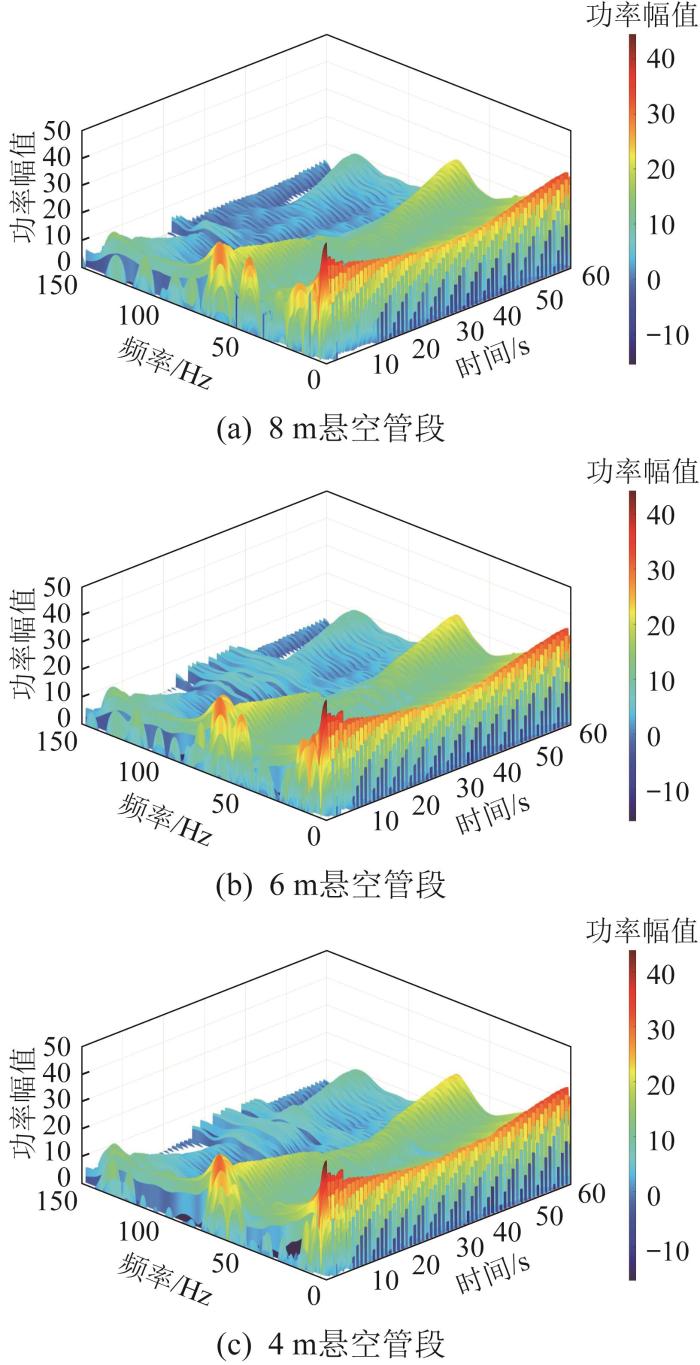
对机器人在含8，6，4 m悬空管段的管道内行进检测时的振动加速度信号进行短时傅里叶变换，得到的时频功率幅值谱如图12所示。通过对比发现，当悬空管段分别为8，6，4 m时，机器人振动加速度的功率幅值均呈现在正常管段高、在悬空管段低的趋势，对应的频段为0~30 Hz与50~80 Hz。为进一步探究这2个频段内机器人振动加速度功率幅值的变化情况，提取0~30 Hz与50~80 Hz频段内的振动加速度功率幅值时域图进行分析。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   悬空管段长度不同时机器人振动加速度的时频功率幅值谱

Fig.12   Time-frequency power amplitude spectrum of robot vibration acceleration with different lengths of suspended pipeline sections


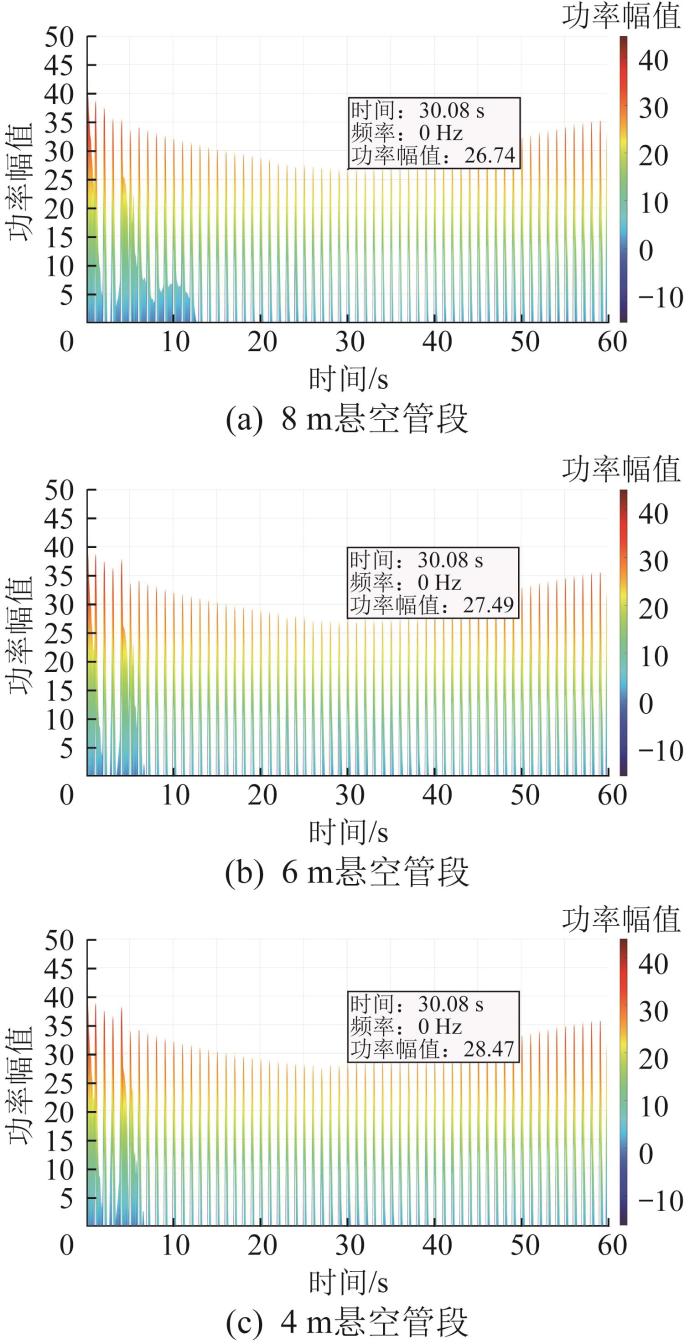
在0~30 Hz频段内，悬空管段长度不同时机器人的振动加速度功率幅值在时域上的变化情况如图13所示。通过对比发现，机器人在8，6，4 m悬空管段中心位置处的振动加速度功率幅值分别为26.74，27.49，28.47。随着悬空管段的缩短，机器人在悬空管段中心位置处的振动加速度功率幅值逐渐升高。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   悬空管段长度不同时机器人振动加速度的功率幅值时域图（0~ 30 Hz频段）

Fig.13   Time-domain diagram of power amplitude of robot vibration acceleration with different lengths of suspended pipeline sections (frequency range of 0~30 Hz)


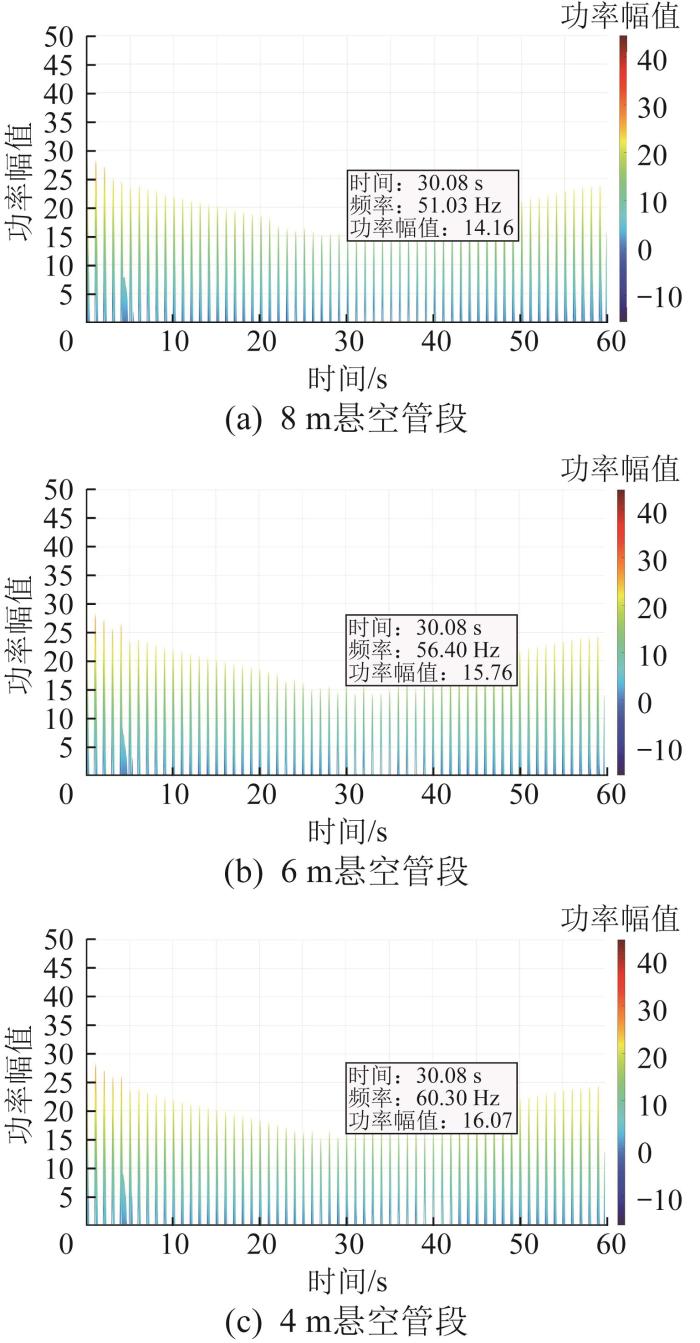
在50~80 Hz频段内，悬空管段长度不同时机器人的振动加速度功率幅值在时域上的变化情况如图14所示。通过对比发现，机器人在8，6，4 m悬空管段中心位置处的振动加速度功率幅值分别为14.16，15.76，16.07，对应的频率分别为51.03，56.40，60.30 Hz。由此可知，在50~80 Hz频段内，随着悬空管段的缩短，机器人在悬空管段中心位置处的振动加速度功率幅值逐渐增大，对应的频率也逐渐增大。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   悬空管段长度不同时机器人振动加速度的功率幅值时域图（50~80 Hz频段）

Fig.14   Time-domain diagram of power amplitude of robot vibration acceleration with different lengths of suspended pipeline sections (frequency range of 50~80 Hz)


4 结 论

通过对海底管道悬空内检测机器人结构进行创新设计以及开展海底管道悬空内检测仿真分析，验证了基于机器人本体振动响应信号的海底管道悬空内检测方法的可行性。通过对机器人在正常管段、过渡管段、悬空管段内开展检测作业时的振动加速度信号进行时域、频域处理与分析，得出如下结论。

1）当机器人由正常管段向悬空管段行进检测时，机器人振动加速度的振荡程度变缓，振动加速度峰值呈下降趋势；越接近悬空管段，机器人的振动加速度功率幅值越小。

2）机器人在悬空管段内开展检测作业时，其振动能量主要来自0~30 Hz、50~80 Hz频段。通过观察这2个频段内机器人振动加速度的时频功率幅值谱，即能够清晰地识别出悬空管段。

3）随着悬空管段的缩短，机器人在悬空管段中心位置处的振动加速度逐渐增大，但振动加速度由一个峰值衰减至下一峰值的幅度逐渐变小；随着悬空管段的缩短，机器人在悬空管段中心位置处的振动加速度的功率幅值及对应的频率均呈增大趋势。

参考文献

高鹏.

2021年中国油气管道建设新进展

［J］.国际石油经济，2022，30（3）：12-19. doi：10.3969/j.issn.1004-7298.2022.03.002

DOI:10.3969/j.issn.1004-7298.2022.03.002      [本文引用: 1]

GAO P.

New progress in China's oil and gas pipeline construction in 2021

［J］. International Petroleum Economics， 2022， 30（3）： 12-19.

DOI:10.3969/j.issn.1004-7298.2022.03.002      [本文引用: 1]

LIU Y， HU H， ZHANG D.

Probability analysis of damage to offshore pipeline by ship factors

［J］. Transportation Research Record， 2013， 2326（1）： 24-31.

[本文引用: 1]

徐兴雨，齐静静，陈凯，等.

埕岛油田海底管道悬空特征及其影响因素

［J］.海洋地质前沿，2023，39（1）：77-84.

[本文引用: 1]

XU X Y， QI J J， CHEN K， et al.

Suspension characteristics and influencing factors of submarine pipelines in the Chengdao Oilfield

［J］. Marine Geology Frontiers， 2023， 39（1）： 77-84.

[本文引用: 1]

KÖPKE U G， HUNT H E M.

Identification of support conditions of buried pipes using a vibrating pig

［J］. Proceedings of the Institution of Mechanical Engineers， Part E： Journal of Process Mechanical Engineering， 1993， 207（1）： 29-40.

[本文引用: 1]

KÖPKE U G.

Transverse vibration of buried pipelines due to internal excitation at a point

［J］. Proceedings of the Institution of Mechanical Engineers， Part E： Journal of Process Mechanical Engineering， 1993， 207（1）： 41-59.

[本文引用: 1]

潘峰，唐东林，陈印，等.

管道腐蚀缺陷超声信号的PSO-SVM模式识别研究

［J］.机械科学与技术，2020，39（5）：751-757.

[本文引用: 1]

PAN F， TANG D L， CHEN Y， et al.

Ultrasonic signal pattern recognition of pipeline corrosion defects with PSO-SVM

［J］. Mechanical Science and Technology for Aerospace Engineering， 2020， 39（5）： 751-757.

[本文引用: 1]

LIAO N S， ZHANG H， ZHANG S M， et al.

A method for identifying support conditions of buried subsea gas pipelines based on forced vibration signal analysis

［J］. Proceedings of the Institution of Mechanical Engineers， Part M： Journal of Engineering for the Maritime Environment， 2019， 233（1）： 218-228.

[本文引用: 1]

LIAO N S， ZHANG H， ZHANG S M.

Experiment for identifying free span of buried gas pipeline under internal excitation load

［J］. International Journal of Pressure Vessels and Piping， 2019， 169： 215-222.

廖宁生，张行，张仕民，等.

移动振动激励下的管道悬空内检测试验研究

［J］.石油矿场机械，2018，47（5）：60-64. doi：10.3969/j.issn.1001-3482.2018.05.013

DOI:10.3969/j.issn.1001-3482.2018.05.013     

LIAO N S， ZHANG H， ZHANG S M， et al.

Experimental research of pipeline free span detection under moving vibration excitation

［J］. Oil Field Equipment， 2018， 47（5）： 60-64.

DOI:10.3969/j.issn.1001-3482.2018.05.013     

张行，杜书强，张仕民，等.

基于管内主动激励的管道悬空检测模拟分析

［J］.石油机械，2017，45（8）：105-110.

[本文引用: 1]

ZHANG H， DU S Q， ZHANG S M， et al.

Simulation analysis of pipeline free span detection based on inner pipe active excitation

［J］. China Petroleum Machinery， 2017， 45（8）： 105-110.

[本文引用: 1]

张行，李振林， 啜广山，等.

海底管道悬空锤击内检测方法及振动信号分析

［J］.石油机械，2023，51（3）：68-75.

[本文引用: 1]

ZHANG H， LI Z L， CHUO G S， et al.

Internal detection method and vibration signal analysis of suspended hammering of submarine pipelines

［J］. China Petroleum Machinery， 2023， 51（3）： 68-75.

[本文引用: 1]

贾邦龙，帅健，张银辉.

海底管道悬空段状态检测及安全性评价

［J］.油气储运，2021，40（6）：658-663. doi：10.6047/j.issn.1000-8241.2021.06.008

DOI:10.6047/j.issn.1000-8241.2021.06.008      [本文引用: 1]

JIA B L， SHUAI J， ZHANG Y H.

State detection and safety evaluation of submarine suspended pipeline

［J］. Oil & Gas Storage and Transportation， 2021， 40（6）： 658-663.

DOI:10.6047/j.issn.1000-8241.2021.06.008      [本文引用: 1]

黄维璇，李四平.

刚体碰撞问题的Hamilton原理及其应用

［J］.中国科学：物理学 力学 天文学，2023，53（5）：77-88. doi：10.1360/sspma-2022-0351

DOI:10.1360/sspma-2022-0351      [本文引用: 1]

HUANG W X， LI S P.

Hamilton's principle for rigid body collision problems and its applications

［J］. Scientia Sinica Physica， Mechanica & Astronomica， 2023， 53（5）： 77-88.

DOI:10.1360/sspma-2022-0351      [本文引用: 1]

黄杰，陈浩，刘国军，等.

埋地铁磁管道环焊缝非开挖定位技术研究

［J］.机械科学与技术，2020，39（7）：1048-1052.

[本文引用: 1]

HUANG J， CHEN H， LIU G J， et al.

Research of non-excavation positioning technology of girth weld in underground ferromagnetic pipeline

［J］. Mechanical Science and Technology for Aerospace Engineering， 2020， 39（7）： 1048-1052.

[本文引用: 1]

胡玉飞，张建超，陈湛，等.

内部激励下高速动车齿轮箱振动响应评估

［J］.北京交通大学学报，2022，46（4）：148-156. doi：10.11860/j.issn.1673-0291.20210173

DOI:10.11860/j.issn.1673-0291.20210173      [本文引用: 1]

HU Y F， ZHANG J C， CHEN Z， et al.

Evaluation of gearbox vibration response in high-speed train under internal excitation

［J］. Journal of Beijing Jiaotong University， 2022， 46（4）： 148-156.

DOI:10.11860/j.issn.1673-0291.20210173      [本文引用: 1]

赵密，杜修力.

时间卷积的局部高阶弹簧-阻尼-质量模型

［J］.工程力学，2009，26（5）：8-18.

[本文引用: 1]

ZHAO M， DU X L.

High-order model of spring-dashpot-mass model for localizing time convolution

［J］. Engineering Mechanics， 2009， 26（5）： 8-18.

[本文引用: 1]

刘兴华.

洪水冲刷作用下悬空管道力学响应特性研究

［J］.油气田地面工程，2022，41（2）：11-16，21. doi：10.3969/j.issn.1006-6896.2022.02.003

DOI:10.3969/j.issn.1006-6896.2022.02.003     

LIU X H.

Study on mechanical response characteristics of suspended pipelines under flood scouring

［J］. Oil-Gas Field Surface Engineering， 2022， 41（2）： 11-16， 21.

DOI:10.3969/j.issn.1006-6896.2022.02.003     

许利惟，刘旭，陈福全.

塌陷作用下埋地悬空管道的力学响应分析

［J］.工程力学，2018，35（12）：212-219，228.

XU L W， LIU X， CHEN F Q.

Mechanical analysis of buried suspended pipeline under the action of collapse

［J］. Engineering Mechanics， 2018， 35（12）： 212-219， 228.

KANTARDGI I G， GOGIN A G.

Submarine pipeline stability under stream and waves action

［J］. Power Technology and Engineering， 2021， 55： 367-372.

XIE Y， MA X F， NING H F.

Formation and failure mechanism of submarine suspension pipeline

［J］. Oil & Gas Storage and Transportation， 2017， 36： 1436-1442.

[本文引用: 1]

PENG X L， HAO H， LI Z X.

Application of wavelet packet transform in subsea pipeline bedding condition assessment

［J］. Engineering Structures， 2012， 39： 50-65.

[本文引用: 1]

LEE J Y.

Variable short-time Fourier transform for vibration signals with transients

［J］. Journal of Vibration and Control， 2015， 21（7）： 1383-1397.

[本文引用: 1]

SAFIZADEH M S， LAKIS A A， THOMAS M.

Using short-time Fourier transform in machinery diagnosis

［C］//Proceedings of the 4th WSEAS International Conference on Electronic， Signal Processing and Control. Wisconsin， Apr. 25-27， 2005.

张泽宇，惠记庄，石泽.

小波包最优基分解树的降噪滤波方法研究

［J］.机械科学与技术，2020，39（1）：28-34.

[本文引用: 1]

ZHANG Z Y， HUI J Z， SHI Z.

Research on denoising and filtering method based on wavelet packet optimal base decomposition tree

［J］. Mechanical Science and Technology for Aerospace Engineering， 2020， 39（1）： 28-34.

[本文引用: 1]

/

〈 〉