<img src="https://www.zjujournals.com/gcsjxb/images/1006-754X/images/logo.png" class="img-responsive">

图1 混凝土3D打印流程

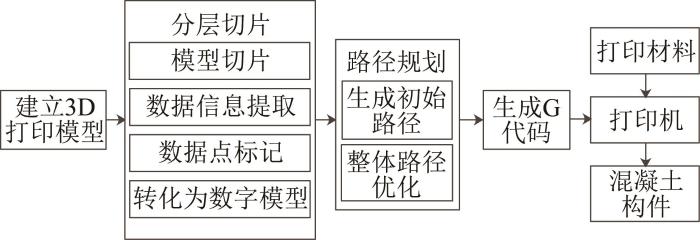
Fig.1 Concrete 3D printing flow

2 混凝土3D打印路径规划算法

2.1　算法流程

如图2所示，基于连续顶点分区的混凝土3D打印路径规划流程主要包括以下4个步骤^[14]：1）根据需求，建立待打印混凝土构件的3D打印模型；2）对混凝土构件的3D打印模型进行分层切片处理并提取各切片模型的特征，尤其是顶点以及顶点之间相连接的边，以形成计算机可识别的数字模型；3）基于哈密顿回路算法将数字模型划分为几个连续的分区；4）使用遗传算法寻找所形成分区之间的最短路径。

图2

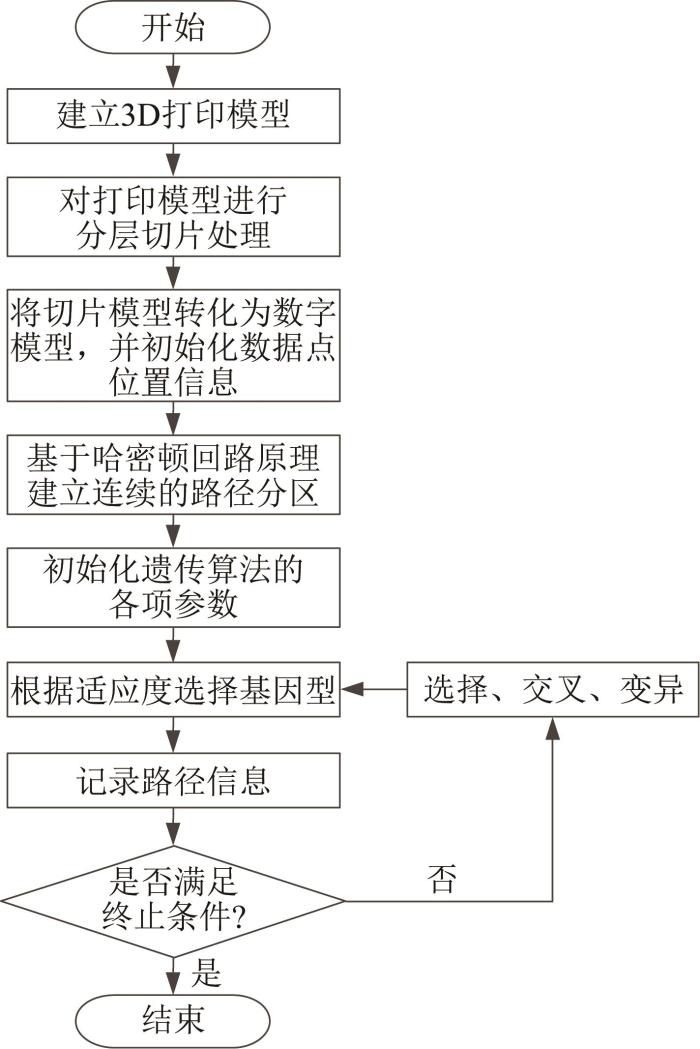
图2 基于连续顶点分区的混凝土3D打印路径规划流程

Fig.2 Concrete 3D printing path planning process based on continuous vertex partitioning

2.2　连续顶点分区方法

哈密顿回路是指在一个无向图中，经过图中所有顶点且每个顶点恰好经过一次的一条回路^[15]。本文基于哈密顿回路的原理来寻找混凝土构件切片模型中多个连续性较强的路径分区。

在将混凝土构件3D打印模型切片转化为数字模型后，提取模型中的各个几何顶点并按顺序将其编号为 $V_{1}$ ， $V_{2}$ ，…， $V_{n}$ ，将对应顶点坐标分别记为 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ ，…， $(x_{n}, y_{n})$ 。通过构建邻接矩阵 T 来描述各个顶点之间的连接状况，即根据各顶点的坐标，利用式(1)计算各顶点之间的欧氏距离d_ij 并存入邻接矩阵 T。邻接矩阵 T 中各元素记为权重，权重为0表示顶点不相连。邻接矩阵 T 的表达式如式(2)所示。

d_{i j} = \sqrt[]{{(x_{j} - x_{i})}^{2} + {(y_{j} - y_{i})}^{2}}

(1)

T = [\begin{matrix} 0 & 1 & 1 & \dots & 0 \\ 1 & 0 & 2 & \dots & 0 \\ 1 & 2 & 0 & \dots & 3 \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 3 & \dots & 0 \end{matrix}]

(2)

对邻接矩阵 T 进行循环遍历，以判断是否存在哈密顿回路^[10]。设初始搜索深度d=0，随机选择顶点 $V_{i}$ 作为起点并将其加入当前分区，枚举与 $V_{i}$ 相邻的且未被访问过的顶点 $V_{1}$ ， $V_{2}$ ， $\dots$ ， $V_{j}$ ，比较邻接矩阵 T 中 $T_{1 i}$ ， $T_{2 i}$ ， $\dots$ ， $T_{j i}$ 的值，将权重最大的顶点 $V_{j}$ 加入当前分区，并将邻接矩阵 T 中的T_ji 和T_ij 置为0；随后，令d=d+1，以顶点 $V_{j}$ 为起点继续递归搜索。若枚举所有相邻的且未被访问过的顶点失败，则回溯到上一顶点，继续寻找其他路径。若当前的搜索深度 $d$ = $n - 1$ ，且当前顶点与起点相邻，则找到一条哈密顿回路，即形成了一个分区，将当前分区放入二维数组 $A_{1}$ 。重复上述过程，直到完成所有哈密顿回路的搜索。在完成哈密顿回路的搜索后，对切片模型中未处理的边（即邻接矩阵中行和列不为0所对应的边）继续进行分区处理。随机选择一个还有边连接的顶点V_r 作为起点并将其加入当前分区，根据上述规则枚举和增加顶点，直到当前顶点没有相邻顶点，即形成一个分区并将其放入二维数组 $A_{1}$ 中。重复上述过程，直到邻接矩阵 T 中各元素的值全部为0。随机生成的二维数组 $A_{1}$ 可表示为：

A_{1} = \{\begin{matrix} V_{1} & V_{5} & \dots & V_{2} \\ V_{3} & V_{2} & \dots & V_{7} \\ ⋮ & ⋮ & ⋮ \\ V_{n - 1} & V_{n} & \dots & V_{n - 3} \end{matrix}\}

(3)

定义二维数组 $A$ ，将 $A_{1}$ 中各分区的起点、终点的坐标放入二维数组 $A$ 中。随机生成的二维数组 $A$ 可表示为：

A = \{\begin{matrix} x_{1} & y_{1} & x_{2} & y_{2} \\ x_{3} & y_{3} & x_{4} & y_{4} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ x_{n - 1} & y_{n - 1} & x_{n} & y_{n} \end{matrix}\}

(4)

2.3　基于遗传算法的整体路径优化

遗传算法是一种模拟自然选择和遗传机制的优化算法，属于演化计算技术^[16]。鉴于遗传算法在解决优化问题中的高效性，本文选择遗传算法来寻找连接各路径分区的最短路径^[17]，以实现整体路径的优化。基于遗传算法的混凝土3D打印路径的优化步骤如下。

步骤1　确定初始化参数。

在遗传算法中，初始化参数的选择对算法性能和优化结果至关重要。在本文中，设染色体长度与二维数组 $A$ 中的分区数量保持一致；种群大小、交叉概率和变异概率均根据分区数量进行调整；终止条件设置为最大迭代次数为 $m$ 。

步骤2　计算适应度。

在遗传算法中，采用适应度函数来量化评估种群中每个个体对于解决特定问题或达成特定目标的适宜程度^[18]，以确定可在进化过程中生存下来的个体。在本文中，首先，从二维数组A中读取所有分区对应的起点和终点的坐标；然后，运用式(1)计算得到各个分区起点、终点与其他分区起点、终点之间的相对距离，并生成随机路径，路径按照随机排序的顺序遍历所有分区。最后，按照顺序将路径中各相邻分区相邻顶点之间的相对距离相加，得到所在路径的距离之和，记为 $d_{k}$ 。定义适应度函数 $F (s) = 1 / d_{k}$ ，适应度值越大，表示路径质量越好。

步骤3　遗传操作。

1）选择。选择操作是指选择适应度值较大的个体作为下一代进化的父代。本文采用轮盘赌选择的方法，选择较短的路径作为父代。利用式(5)计算每条路径的累积概率 $P (s_{a})$ 。质量更好的路径，有更大的概率被选中。

P (s_{a}) = \frac{F (s_{a})}{\sum_{b = 1}^{N} F (s_{b})}

(5)

2）交叉。交叉操作是模拟基因的重组过程。本文通过将2个父代个体对应的路径分区及该分区内2个端点的排列顺序进行交叉，以生成新的路径。

3）变异。变异操作是模拟基因的突变过程。在本文中，交叉操作是随机选择路径，将路径分区或该分区内2个端点的顺序进行随机交换，以产生新的路径。

步骤4　终止判断。

若达到最大迭代次数 $m$ ，则终止计算并输出最优路径，包括分区顺序以及各分区起点和终点的坐标；否则重复执行选择、交叉和变异等操作，直到达到最大迭代次数。

3 混凝土3D打印仿真与实验分析

3.1　3D打印路径的评价指标

在混凝土3D打印领域，打印路径的质量直接影响最终混凝土构件的成形质量和性能。一条高质量的打印路径应具备高连续性和平滑的特点。常用的打印路径评价指标包括打印喷头覆盖总长度、打印喷头空行程、打印喷头启停次数以及总打印时间等。通过优化上述评价指标，能够显著提升混凝土3D打印的效率和可靠性，进而有效提升打印质量^[19]。

1）打印喷头覆盖总长度。打印喷头覆盖总长度是指打印喷头在移动过程中经过的距离总和。在同一打印模型中，打印喷头覆盖总长度越短，说明所采用的路径规划算法的效果越优。

2）打印喷头空行程。空行程是指打印过程中打印喷头移动但不下料的距离。在同一打印模型中，较小的空行程意味着打印路径更短、打印喷头移动更少以及打印过程更高效。

3）打印喷头的启停次数。在混凝土3D打印中，打印喷头的启动、暂停可能会造成混凝土物料堆积，如图3所示。启停次数过多会影响混凝土构件的成形质量。合理规划打印路径可以减少打印喷头的启停次数，从而提高打印效率和打印质量。

图3

图3 打印喷头启停造成的混凝土物料堆积

Fig.3 Concrete material accumulation caused by start and stop of print nozzle

4）打印时间。在混凝土3D打印中，打印时间是指混凝土构件成形所需的时间，表征打印效率和路径规划算法性能^[20]。打印时间越短表示打印效率越高，即路径规划算法越优异。

3.2　混凝土3D打印仿真

利用CIMCO Edit8软件开展混凝土3D打印仿真分析，以验证本文基于连续顶点分区的路径规划算法（下文简称本文算法）的可行性，并与已有的采用欧拉回路的混凝土3D打印路径规划算法（下文简称欧拉回路算法）、Cura软件算法以及Dijkstra算法进行对比。

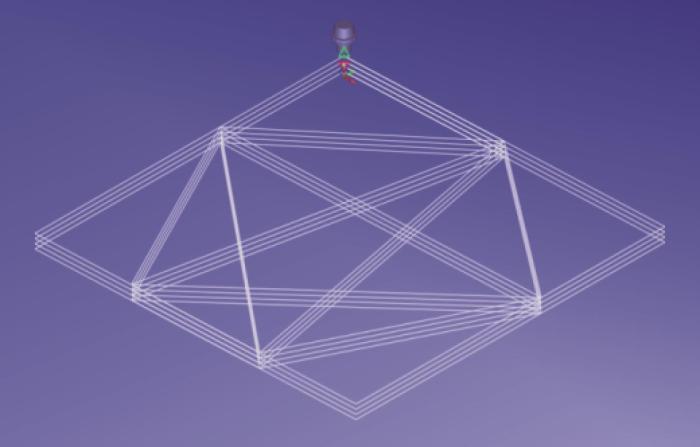
混凝土构件1：长、宽、高分别为1 000 mm、1 000 mm、48 mm，共4层。混凝土构件1的仿真成形结果如图4所示。将欧拉回路算法中的蚁群数量设为50，本文算法中的遗传迭代次数设为30。基于欧拉回路算法和本文算法的混凝土构件1的打印路径分区效果如图5所示。基于不同算法的混凝土构件1的打印路径规划仿真结果如表1所示。

图4

图4 混凝土构件1的仿真成形结果

Fig.4 Simulation forming result of concrete component 1

图5

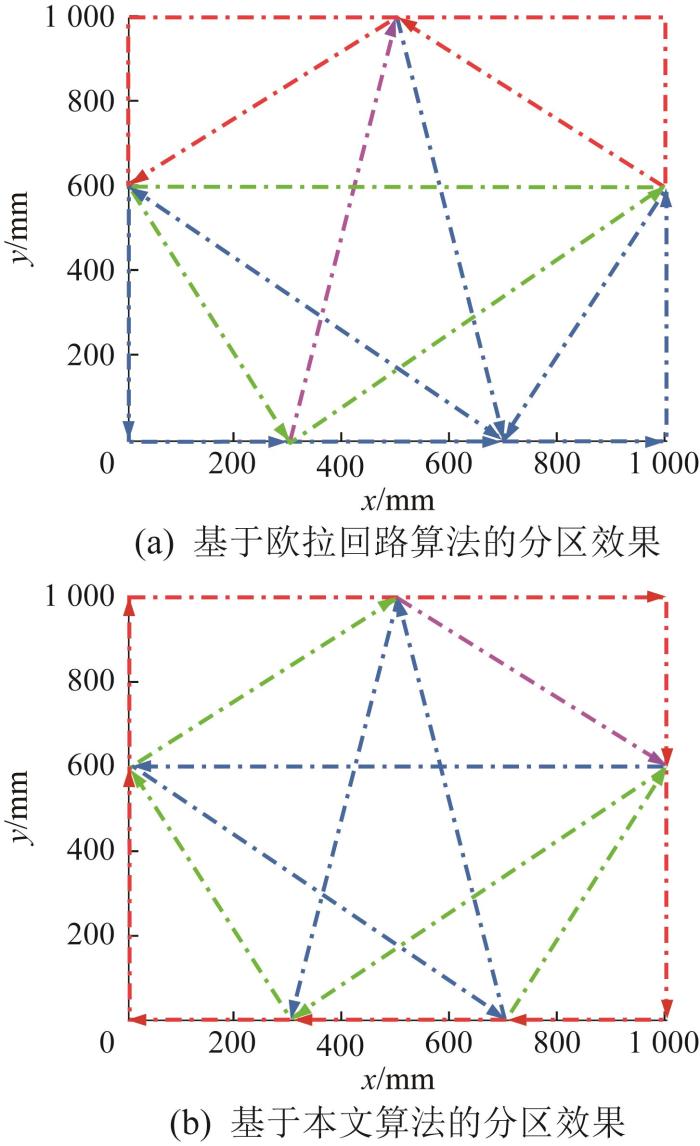
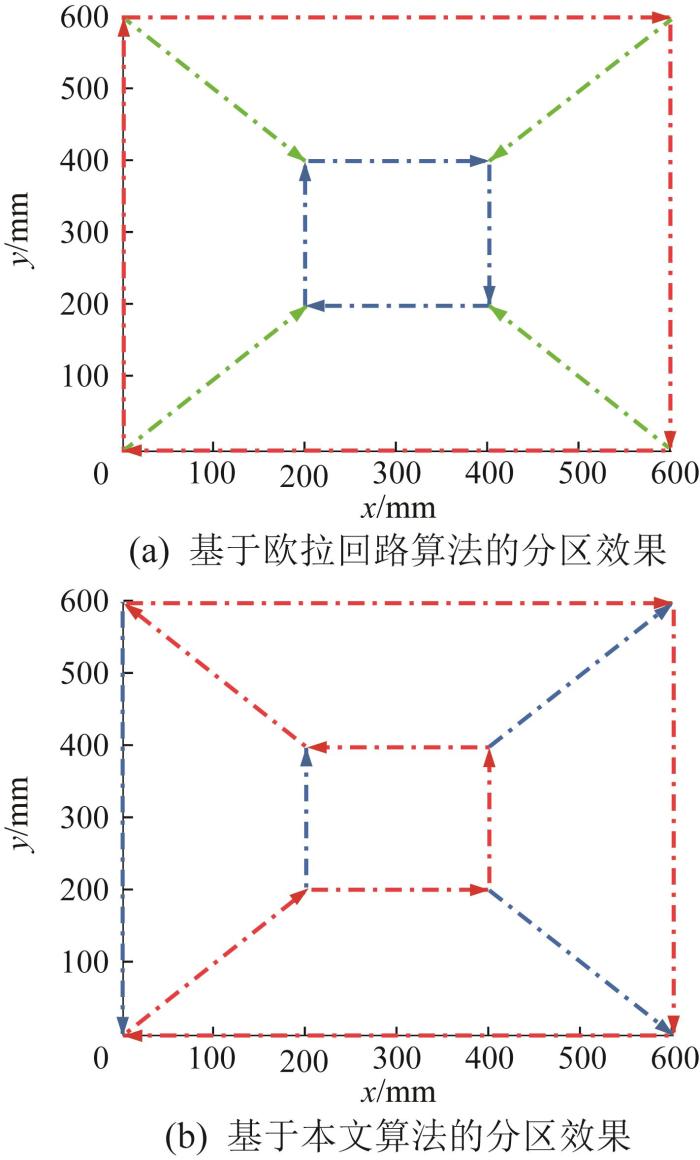
图5 混凝土构件1的打印路径分区效果对比

Fig.5 Comparison of printing path partition effect of concrete component 1

表1 基于不同算法的混凝土构件1的打印路径规划仿真结果

Table 1 Simulation results of printing path planning for concrete component 1 based on different algorithms

算法	打印喷头覆盖总长度/mm	打印喷头空行程/mm	打印喷头启停数/次	打印时间/s
本文算法	51 659	3 580	8	183
欧拉回路算法	53 820	5 740	16	212
Cura软件算法	61 250	13 171	27	278
Dijkstra算法	58 340	10 260	23	245

由表1结果可知，相较于欧拉回路算法，采用本文算法的打印路径规划方案能够减小37.6%的空行程、减少50.0%的启停次数以及缩短13.7%的打印时间；相较于Cura软件算法，采用本文算法的打印路径规划方案能够减小72.8%的空行程、减少70.4%的启停次数以及缩短34.2%的打印时间；相较于Dijkstra算法，采用本文算法的打印路径规划方案能够减小65.1%的空行程、减少65.2%的启停次数以及缩短25.3%的打印时间。

混凝土构件2：长、宽、高分别为600 mm、600 mm、48 mm，共4层。混凝土构件2的仿真成形结果如图6所示。同样地，将欧拉回路算法中的蚁群数量设为50，本文算法中的遗传迭代次数设为30。基于欧拉回路算法和本文算法的混凝土构件2的打印路径分区效果如图7所示。基于不同算法的混凝土构件2的打印路径规划仿真结果如表2所示。

图6

图6 混凝土构件2的仿真成形结果

Fig.6 Simulation forming result of concrete component 2

图7

图7 混凝土构件2的打印路径分区效果对比

Fig.7 Comparison of printing path partition effect of concrete component 2

表2 基于不同算法的混凝土构件2的打印路径规划仿真结果

Table 2 Simulation results of printing path planning for concrete component 2 based on different algorithms

算法	打印喷头覆盖总长度/mm	打印喷头空行程/mm	打印喷头启停数/次	打印时间/s
本文算法	23 389	3 760	11	132
欧拉回路算法	26 024	5 100	15	149
Cura软件算法	30 182	10 553	22	181
Dijkstra算法	29 332	9 703	18	163

由表2结果可知，相较于欧拉回路算法，采用本文算法的打印路径规划方案能够减小26.3%的空行程、减少26.7%的启停次数以及缩短11.4%的打印时间；相较于Cura软件算法，采用本文算法的打印路径规划方案能够减小64.4%的空行程、减少50.0%的启停次数以及缩短27.1%的打印时间；相较于Dijkstra算法，采用本文算法的打印路径规划方案能够减小61.2%的空行程、减少38.9%的启停次数以及缩短19.0%的打印时间。

综上，相较于其他的路径规划算法，采用本文算法进行路径规划能够显著地减小打印喷头的空行程、减少打印喷头的启停次数以及缩短打印时间。由此可得，在混凝土的3D打印中，使用本文算法进行打印路径规划可有效提高打印效率和节约成本。

3.3　混凝土3D打印实验

为了进一步验证本文算法在实际混凝土3D打印中的可靠性和实用性，基于本文算法、欧拉回路算法、Cura软件算法和Dijkstra算法开展混凝土3D打印实验并对比成形构件的外观和质量。每种路径规划算法下均打印3个混凝土构件。其中：构件1的长、宽、高分别为600 mm、600 mm、48 mm，共4层；构件2的长、宽、高分别为1 038 mm、1 000 mm、24 mm，共2层；构件3的长、宽、高分别为600 mm、520 mm、48 mm，共4层。本文所使用的混凝土3D打印机的控制器为DDCS V3.1，其打印喷头的直径为30 mm，最大移动速度为100 mm/s；混凝土构件的每一层高度均为12 mm。图8所示为基于不同算法的混凝土构件的打印成形效果。

图8

图8 基于不同算法的混凝土构件打印成形效果对比

Fig.8 Comparison of print forming effect of concrete components based on different algorithms

由图8结果可知，采用欧拉回路算法、Cura软件算法和Dijkstra算法规划的打印路径存在连续性较差和打印喷头启停次数过多的问题，导致局部混凝土物料堆积和混凝土构件成形质量较差。相比之下，基于本文算法规划的打印路径连续性较高且相对平滑，实现了混凝土构件成形质量的有效提升。

基于不同算法的混凝土构件打印路径规划实验结果如表3所示。表3结果显示，在相同的打印喷头移动速度下，基于本文算法的打印路径规划方案至少减小了35.9%的打印喷头空行程、减少了27.8%的打印喷头启停次数以及缩短了14.9%的打印时间。因此，在混凝土3D打印中，应用本文算法可有效地提高混凝土构件的成形质量和降低生产成本，这意味着本文算法具有广阔的应用前景。

表3 基于不同算法的混凝土构件打印路径规划实验结果

Table 3 Experimental results of printing path planning for concrete components based on different algorithms

构件	算法	打印喷头覆盖总长度/mm	打印喷头空行程/mm	打印喷头启停数/次	打印时间/s
构件1	本文算法	21 101	4 264	11	195
	欧拉回路算法	23 490	6 653	17	224
	Cura软件算法	34 502	17 665	24	253
	Dijkstra算法	36 972	20 135	22	258
构件2	本文算法	16 304	3 384	13	150
	欧拉回路算法	19 601	6 681	18	179
	Cura软件算法	23 381	10 461	23	202
	Dijkstra算法	21 987	9 067	21	232
构件3	本文算法	16 201	900	4	131
	欧拉回路算法	18 301	3 100	9	163
	Cura软件算法	28 572	13 271	13	194
	Dijkstra算法	30 008	14 707	10	212

3.4　结果分析

综合上述混凝土3D打印路径规划的仿真结果与实验结果可知，与其他的路径规划算法相比，基于连续顶点分区的路径规划算法有效提升了混凝土3D打印路径的质量，主要体现在以下方面。

1）所采用的哈密顿回路算法是一种顶点遍历算法，能够确保打印喷头在打印过程中不会重复经过同一个顶点，减少了打印喷头的启停次数，从而缩短了打印时间、降低了打印过程的不稳定性和减少了成形构件的缺陷。

2）采用遗传算法来获得各路径分区之间的最短连接路径，尽可能地减小了打印喷头在打印过程中的空行程，以确保连续打印路径的最大化，有效地提高了打印效率和打印质量。

仿真和实验结果证明了本文算法的可行性和实用性，其在混凝土3D打印领域的应用前景非常广阔。

3.5　本文算法的迭代次数讨论

对于本文算法，遗传算法中的迭代次数m对算法的运行效率以及打印喷头空行程有重要影响。从理论上看，随着迭代次数m的增加，遗传算法搜索解空间的机会增加，即更有可能趋近全局最优解^[21]。但是，过多的迭代次数不仅会增加计算成本和算法执行时间，还可能会使算法陷入局部最优解，从而无法获得最优的打印路径。因此，针对实际应用中的混凝土3D打印路径规划问题，须综合考虑路径规划的复杂性、解空间的大小，以合理设定遗传算法中的迭代次数m。

对于常见的混凝土构件，本文算法通常会将其打印路径划分为2~6个分区。通过打印实验系统地分析不同迭代次数m下本文算法的运行时间以及打印喷头空行程的变化情况，结果如表4所示。

表4 不同迭代次数下本文算法的运行时间以及打印喷头的空行程

Table 4 Running time of algorithm in this paper and empty travel of print nozzle under different iterations

分区数量/ 个	迭代数/次	算法运行时间/s	打印喷头空行程/mm
2	20	0.34	243
	40	0.78	243
	60	1.42	243
3	40	1.12	337
	60	2.18	325
	80	3.67	325
4	60	3.55	458
	80	3.98	419
	100	5.03	382
5	80	4.93	687
	100	5.86	612
	120	7.34	612
6	100	7.42	945
	120	9.09	863
	140	10.93	825

由表4结果可知，在分区数量较少的情况下，迭代次数对路径规划速度和打印喷头空行程的影响不太明显。然而，当分区数量增加时，在相同的分区条件下，迭代次数的增加会使路径规划速度变慢，但会减小打印喷头的空行程。但当迭代次数达到一定数量时，可能会导致路径规划时间增加，从而导致优化效果变差。因此，在混凝土3D打印路径的规划过程中，应根据具体情况选择合适的迭代次数，以提高路径规划的效率。

4 结论

目前，混凝土3D打印技术的发展突飞猛进，但是关于混凝土3D打印路径规划算法的研究仍较少。本文提出了一种基于连续顶点分区的混凝土3D打印路径规划算法，该算法结合哈密顿回路算法和遗传算法对打印路径进行规划和优化，可为混凝土3D打印技术提供新思路，有望推动混凝土3D打印技术在建筑施工领域的广泛应用。但是，本文算法也存在很多不足，如待打印的混凝土构件不连续时，基于本文算法的打印效率较低，这是未来需要进一步研究的问题。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

盛蕾，武雷.

3D打印混凝土技术研究综述

［J］.混凝土与水泥制品，2021（10）：7-11.

SHENG

， WU

Summary of 3D printed concrete technology research

［J］. China Concrete and Cement Products， 2021（10）： 7-11.

DOI:10.3969/j.issn.1672-6413.2018.06.012 [本文引用: 1]

[2]

王猛

增材制造直接分层和路径规划技术研究

［J］.机械工程与自动化，2018（6）：34-35，38. doi：10.3969/j.issn.1672-6413.2018.06.012

WANG

Research on direct slicing and path planning technology of additive manufacturing

［J］. Mechanical Engineering & Automation， 2018（6）： 34-35， 38.

DOI:10.3969/j.issn.1672-6413.2018.06.012 [本文引用: 1]

[3]

汤寄予，席义斌，高丹盈，等.

3D打印混凝土的可打印性研究综述

［J］.混凝土与水泥制品，2022（12）：18-23.

TANG

J Y

， XI

Y B

， GAO

D Y

， et al.

Review on printability of 3D printed concrete

［J］. China Concrete and Cement Products， 2022（12）： 18-23.

[4]

崔凤英，李晓微.

3D打印路径规划研究

［J］.青岛科技大学学报（自然科学版），2020，41（2）：101-105.

CUI

F Y

， LI

X W

Research on 3D printing path planning

［J］. Journal of Qingdao University of Science and Technology （Natural Science Edition）， 2020， 41（2）： 101-105.

[5]

马宗方，万伟鹏，宋琳，等.

采用欧拉回路的混凝土3D打印路径优化算法

［J］.机械科学与技术： 1-7（2023-02-21）［2023-07-15］..

URL [本文引用: 1]

Z F

， WAN

W P

， SONG

， et al.

Path optimization algorithm for concrete 3D printing using the Euler circuit

［J］. Mechanical Science and Technology for Aerospace Engineering： 1-7 （2023-02-21）［2023-07-15］. .

URL [本文引用: 1]

[6]

WAN

， WANG

， MA

G W

Continuous and adaptable printing path based on transfinite mapping for 3D concrete printing

［J］. Automation in Construction， 2022， 142： 104471.

[7]

FOK

K Y

， GANGANATH

， CHENG

C T

， et al.

A 3D printing path optimizer based on christofides algorithm

［C］//2016 IEEE International Conference on Consumer Electronics. Nantou， Taiwan， China， May 27-29， 2016.

DOI:10.3778/j.issn.1002-8331.2012-0438 [本文引用: 1]

[8]

王祎，葛静怡，薛昕惟，等.

改进Q学习的薄壁结构3D打印路径规划

［J］.计算机工程与应用，2022，58（12）：299-303. doi：10.3778/j.issn.1002-8331.2012-0438

WANG

， GE

J Y

， XUE

X W

， et al.

Path planning for complex thin-walled structures in 3D printing： improved Q-learning method

［J］. Computer Engineering and Applications， 2022， 58（12）： 299-303.

DOI:10.3778/j.issn.1002-8331.2012-0438 [本文引用: 1]

[9]

曹俊峰

面向3D混凝土打印的双螺旋路径规划算法研究与施工作业系统搭建

［D］.武汉：华中科技大学，2021.

CAO

J F

Research on 3D concrete printing-oriented double helix path planning algorithm and construction operation system construction

［D］. Wuhan： Huazhong University of Science and Technology， 2021.

DOI:10.3969/j.issn.1674-4993.2022.03.031 [本文引用: 1]

[10]

高遵海，陈倬.

图的路径运算矩阵与哈密顿回路等路径问题

［J］.华中科技大学学报（自然科学版），2021，49（2）：32-36. doi：10.13245/j.hust.210204

DOI:10.13245/j.hust.210204 [本文引用: 2]

GAO

Z H

， CHEN

Path-operation matrices of graph for solving Hamilton cycles and other path problems

［J］. Journal of Huazhong University of Science and Technology （Natural Science Edition）， 2021， 49（2）： 32-36.

DOI:10.13245/j.hust.210204 [本文引用: 2]

[11]

王港华

基于遗传算法的小规模TSP问题研究分析

［J］. 物流工程与管理，2022，44（3）：111-114. doi：10.3969/j.issn.1674-4993.2022.03.031

WANG

G H

Research analysis of small-scale TSP problem based on genetic algorithm

［J］. Logistics Engineering and Management， 2022， 44（3）： 111-114.

DOI:10.3969/j.issn.1674-4993.2022.03.031 [本文引用: 1]

[12]

胡作玄，王献芬.

两个古老的回路问题

［J］.科学世界，2007（5）：82-89.

Z X

， WANG

X F

Two ancient circuit problems

［J］. Science World， 2007（5）： 82-89.

[13]

张大旺，王栋民.

3D打印混凝土材料及混凝土建筑技术进展

［J］.硅酸盐通报，2015，34（6）：1583-1588.

ZHANG

D W

， WANG

D M

Progress of 3D print of concrete materials and concrete construction technology

［J］. Bulletin of the Chinese Ceramic Society， 2015， 34（6）： 1583-1588.

DOI:10.3969/j.issn.1674-6635.2022.07.010 [本文引用: 1]

[14]

黄舒弈，张宇，徐卫国.

机器人3D打印建筑的打印路径规划方法探索

［J］.建筑技艺，2022，28（7）：79-81. doi：10.3969/j.issn.1674-6635.2022.07.010

HUANG

S Y

， ZHANG

， XU

W G

Exploring tool path planning methods of the robotic 3DP construction

［J］. Architecture Technique， 2022， 28（7）： 79-81.

DOI:10.3969/j.issn.1674-6635.2022.07.010 [本文引用: 1]

[15]

叶志琳

基于邻接矩阵和递归算法的哈密顿回路研究

［J］.佳木斯大学学报（自然科学版），2022，40（4）：164-167.

Z L

Research on Hamiltonian loop based on adjacency matrix and recursive algorithm

［J］. Journal of Jiamusi University （Natural Science Edition）， 2022， 40（4）： 164-167.

DOI:10.3969/j.issn.1671-1807.2023.08.042 [本文引用: 1]

[16]

陈旭

基于遗传算法的移动机器人路径规划研究综述

［J］.科技和产业，2023，23（8）：274-278. doi：10.3969/j.issn.1671-1807.2023.08.042

CHEN

Summary of research on path planning of mobile robot based on genetic algorithms

［J］. Science Technology and Industry， 2023， 23（8）： 274-278.

DOI:10.3969/j.issn.1671-1807.2023.08.042 [本文引用: 1]

[17]

尹雅楠

基于改进遗传算法的无人机航迹规划与任务分配方法研究

［D］.石家庄：河北科技大学，2023.

YIN

Y N

Research on UAV path planning and task allocation method based on improved genetic algorithm

［D］. Shijiazhuang： Hebei University of Science and Technology， 2023.

[18]

刘树赵，邹德旋，罗鸿赟，等.

改进遗传算法求解旅行商问题

［J］.计算机时代，2023（5）：66-71.

LIU

S Z

， ZOU

D X

， LUO

H Y

， et al.

Improved genetic algorithm to solve traveling salesman problem

［J］. Computer Era， 2023（5）： 66-71.