双异步电机驱动双质体振动系统同步滑模控制

doi:10.3785/j.issn.1006-754X.2023.00.067

双异步电机驱动双质体振动系统同步滑模控制

余乐^,^,¹^,², 侯勇俊², 赵永强¹, 汪玉琪¹

1.陕西理工大学工程训练中心，陕西汉中 723001

2.西南石油大学机电工程学院，四川成都 610500

Synchronous sliding mode control of double-mass vibration system driven by two asynchronous motors

YU Le^,^,¹^,², HOU Yongjun², ZHAO Yongqiang¹, WANG Yuqi¹

1.Engineering Training Center, Shaanxi University of Technology, Hanzhong 723001, China

2.School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China

收稿日期: 2023-03-31 修回日期: 2023-05-18

基金资助:

国家自然科学基金资助项目. 51074132
陕西省教育厅专项科研计划项目. 21JK0557

Received: 2023-03-31 Revised: 2023-05-18

作者简介 About authors

余乐（1989—），男，陕西汉中人，工程师，博士生，从事机械系统动力学、振动利用与控制工程等研究，E-mail:len1166@126.com，https://orcid.org/0000-0001-5176-4105 , E-mail：len1166@126.com

摘要

针对2个异步电机安装在2个不同质体上的振动系统在部分参数条件下不能同步运转或同步相位差不满足设计要求的问题，提出采用主从控制结构和滑模控制算法对异步电机进行矢量控制，以使振动系统实现0或π相位差的同步运转。首先，基于拉格朗日方程建立了振动系统的运动微分方程，并推导了其固有频率的表达式。然后，设计了振动系统异步电机的控制器，并分别证明了其稳定性。最后，在MATLAB/Simulink环境中建立了振动系统的机电-控制仿真模型，开展了自同步和控制同步仿真并进行了对比。结果表明：所设计的控制器可使振动系统实现0或π相位差的同步运转。研究结果可为双异步电机驱动双质体振动系统的研制提供参考。

关键词： 异步电机 ; 双质体振动系统 ; 同步运转 ; 滑模控制

Abstract

Aiming at the problem that the vibration system with two asynchronous motors installed on two different mass bodies cannot run synchronously or the synchronous phase difference does not meet the design requirements under the condition of some parameters, the vector control for asynchronous motors is proposed by using master-slave control structure and sliding mode control algorithm, so that the vibration system can implement 0 or π phase difference synchronous operation. Firstly, the motion differential equations of the vibration system were established according to the Lagrange equation, and the natural frequency expressions were derived. Then, the controllers for asynchronous motors in the vibration system were designed and their stability was proved respectively. Finally, the electromechanical-control simulation model of the vibration system was established in MATLAB/Simulink environment, and the self-synchronization and control synchronization simulation were carried out and compared. The results showed that the designed controllers could make the vibration system implement 0 or π phase difference synchronous operation. The research results can provide reference for the development of double-mass vibration system driven by two asynchronous motors.

Keywords： asynchronous motor ; double-mass vibration system ; synchronous operation ; sliding mode control

PDF (2855KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

余乐, 侯勇俊, 赵永强, 汪玉琪. 双异步电机驱动双质体振动系统同步滑模控制. 工程设计学报[J], 2023, 30(5): 608-616 doi:10.3785/j.issn.1006-754X.2023.00.067

YU Le, HOU Yongjun, ZHAO Yongqiang, WANG Yuqi. Synchronous sliding mode control of double-mass vibration system driven by two asynchronous motors. Chinese Journal of Engineering Design[J], 2023, 30(5): 608-616 doi:10.3785/j.issn.1006-754X.2023.00.067

在煤炭、化工、建筑和粮食等领域，振动机械常被用于输送、筛分、干燥物料^[1]。其中，自同步振动筛因结构简单、维护方便而被广泛应用^[2-3]。自同步是指2个或多个偏心转子无需刚性连接即可实现同转速运转，即转子间的相位差保持恒定。因此，在利用同步现象之前必须解决2个问题：一个是振动系统能否实现同步运动，另一个是在同步运动过程中的相位差是否满足要求。这2个问题将直接影响振动系统的响应。

自同步现象最早由Huygens于1665年发现^[4]，他观察到2个悬挂在薄板上的钟摆在摇动一段时间后可以同步摆动。进入20世纪后，Blekhman等^[5-6]对2个偏心转子的同步运动进行了研究，并提出了自同步理论；闻邦椿等^[2-3]分析了振动机械的自同步特性，并将相关理论应用到工程实践中。近年来，Zhang等^[7-9]采用改进的小参数方法分别对由2个和多个激振电机驱动的振动系统进行了理论和实验研究；Djanan等^[10-11]研究了一种激振电机在平板上运动的振动系统的同步运动；贺斌等^[12-13]对一种2个激振电机安装在同一个质体上的双质体振动系统进行了研究。与此同时，学者们纷纷开展了多电机驱动振动系统的控制同步研究。Kong等^[14-15]研究了由多个激振电机驱动的振动系统的控制同步运动及其索末菲（Sommerfeld）效应。Fang等^[16-18]提出了转子耦合摆振动系统，并对其自同步运动和控制同步运动进行了深入的研究。黄志龙等^[19-20]在考虑物料影响的情况下，采用相邻交叉耦合控制策略对多种多电机驱动的振动系统进行了控制同步研究。张康等^[21-22]采用不同的滑模控制策略对多个直线电机进行了同步控制并开展了实验研究。

然而，上述文献的研究对象主要是激振电机安装在同一质体上的振动系统，而较少涉及激振电机安装在不同质体上的振动系统。为了减小地基载荷、占地面积以及实现对物料的多级筛分，侯勇俊等^[23]提出了一种激振电机（异步电机）安装在不同质体上的双质体振动系统，并对其同步性展开了研究。结果表明：一些结构参数对振动系统的同步相位差有显著影响，在部分参数条件下振动系统甚至不能实现自同步运转，这均会影响振动系统的稳态响应和工作效率。

通常当同步相位差为0或π时，双质体振动系统的激振力可以最大程度地叠加或者抵消，故0或π相位同步通常为工程应用所需的工作状态。为了进一步提升振动系统的工作性能，笔者拟采用主从控制结构和滑模控制算法对异步电机进行矢量控制，以实现0或π相位同步。当振动系统的固有频率与激振频率相近时，其振幅会快速变化。利用这一特性，在工程应用中只需更换不同刚度的弹簧而不改变其他条件即可改变质体的振幅。因此，本文主要讨论弹簧刚度对振动系统同步运动的影响以及所设计控制器对弹簧刚度不同的振动系统的同步控制效果。

1 双质体振动系统的动力学模型

双质体振动系统主要由上质体、下质体、激振电机（异步电机）、弹簧和底座等组成，其动力学模型如图1所示。其中：弹簧是对称放置的；2个异步电机上所带的偏心块用2个偏心转子表示。当振动系统工作时，2个安装在不同质体上的异步电机产生的激振力通过中间弹簧相互传递。这样既可以减小每个质体的载荷，又能使2个质体以不同的轨迹运动。在动力学建模时，先推导振动系统的动能、势能和能量耗散函数，再代入拉格朗日方程以推导振动系统的运动微分方程。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双质体振动系统的动力学模型

Fig.1 Dynamics model of double-mass vibration system

图1中：o₁-X₁Y₁和o₂-X₂Y₂分别为上振动体（上质体和异步电机1的装配体）和下振动体（下质体和异步电机2的装配体）的绝对坐标系； $o_{1}^{'} - X_{1}^{'} Y_{1}^{'}$ 和 $o_{2}^{'} - X_{2}^{'} Y_{2}^{'}$ 分别为平行于o₁-X₁Y₁和o₂-X₂Y₂的相对坐标系； $o_{1}^{'} - X_{1}^{″} Y_{1}^{″}$ 和 $o_{2}^{'} - X_{2}^{″} Y_{2}^{″}$ 分别为相对于 $o_{1}^{'} - X_{1}^{'} Y_{1}^{'}$ 和 $o_{2}^{'} - X_{2}^{'} Y_{2}^{'}$ 的旋转坐标系； $o_{1}^{'}$ 和 $o_{2}^{'}$ 分别为上、下振动体的质心，静止时 $o_{i}^{'}$ 与 $o_{i}$ ( $i = 1, 2$ )重合； $o_{i}^{″}$ (i=1, 2)为偏心转子i的旋转中心；l_i 为原点 $o_{i}$ 与 $o_{i}^{″}$ 之间的距离；φ_i 为偏心转子i的角位移；β_i 为连线 $o_{i} o_{i}^{″}$ 与X_i 轴之间的夹角；r_i 为偏心转子i的等效半径。令 $Φ_{1}^{″}$ 、 $Φ_{2}^{″}$ 分别表示偏心转子1，2的质心在坐标系 $o_{1}^{'} - X_{1}^{″} Y_{1}^{″}$ 和 $o_{2}^{'} - X_{2}^{″} Y_{2}^{″}$ 中的坐标， $Φ_{1}$ 、 $Φ_{2}$ 分别表示偏心转子1，2的质心在坐标系o₁-X₁Y₁和o₂-X₂Y₂中的坐标，则根据图1，可得：

\{\begin{array}{l} Φ_{1}^{″} = [\begin{array}{l} l_{1} c o s β_{1} + r_{1} c o s φ_{1} \\ l_{1} s i n β_{1} + r_{1} s i n φ_{1} \end{array}] \\ Φ_{2}^{″} = [\begin{array}{l} l_{2} c o s β_{2} + r_{2} c o s φ_{2} \\ l_{2} s i n β_{2} + r_{2} s i n φ_{2} \end{array}] \end{array}

Φ_{1} = Φ_{1}^{'} + Γ_{1} Φ_{1}^{″}, Φ_{2} = Φ_{2}^{'} + Γ_{2} Φ_{2}^{″} \begin{matrix}  \end{matrix}

其中：

Φ_{1}^{'} = [\begin{array}{l} x_{1} \\ y_{1} \end{array}]

Φ_{2}^{'} = [\begin{array}{l} x_{2} \\ y_{2} \end{array}]

Γ_{i} = [\begin{matrix} c o s ψ_{i} & - s i n ψ_{i} \\ s i n ψ_{i} & c o s ψ_{i} \end{matrix}]

式中： $Φ_{1}^{'}$ 、 $Φ_{2}^{'}$ 分别为上、下振动体质心的位移向量；x_i 、y_i 分别为振动体质心沿X_i 、Y_i 方向的位移；ψ_i 为振动体质心旋转的角位移。

由此可得，振动系统的动能T为：

\begin{array}{l} T = \frac{1}{2} \sum_{i = 1}^{2} M_{i} ({\dot{x}}_{i}^{2} + {\dot{y}}_{i}^{2}) + \frac{1}{2} \sum_{i = 1}^{2} J_{z i} {\dot{ψ}}_{i}^{2} + \\ \frac{1}{2} \sum_{i = 1}^{2} (J_{o i} + m_{o i} r_{i}^{2}) {\dot{φ}}_{i}^{2} + \frac{1}{2} \sum_{i = 1}^{2} m_{o i} {\dot{Φ}}_{i}^{T} {\dot{Φ}}_{i} \end{array}

式中：M₁、M₂分别为上、下振动体的质量；m_o_i 为偏心转子i的质量；J_z1、J_z2分别为上、下振动体的转动惯量；J_o_i 为异步电机i的转轴的转动惯量。

振动系统的势能E为：

\begin{array}{l} E = \frac{1}{2} k_{x 2} x_{2}^{2} + \frac{1}{2} k_{y 2} y_{2}^{2} + \frac{1}{2} k_{ψ 2} ψ_{2}^{2} + \\ \frac{1}{2} k_{x 1} {(x_{2} - x_{1})}^{2} + \frac{1}{2} k_{y 1} {(y_{2} - y_{1})}^{2} + \\ \frac{1}{2} k_{ψ 1} {(ψ_{2} - ψ_{1})}^{2} \end{array}

式中：k_xi 、k_yi 、k_ψi 分别为沿X_i 、Y_i 和质心旋转方向的弹簧刚度，其中 $k_{x i} = k_{y i} / 3$ 。

振动系统的能量耗散函数D为：

\begin{array}{l} D = \frac{1}{2} f_{x 2} {\dot{x}}_{2}^{2} + \frac{1}{2} f_{y 2} {\dot{y}}_{2}^{2} + \frac{1}{2} f_{ψ 2} {\dot{ψ}}_{2}^{2} + \\ \frac{1}{2} f_{1} {\dot{φ}}_{1}^{2} + \frac{1}{2} f_{2} {\dot{φ}}_{2}^{2} + \frac{1}{2} f_{x 1} {({\dot{x}}_{2} - {\dot{x}}_{1})}^{2} + \\ \frac{1}{2} f_{y 1} {({\dot{y}}_{2} - {\dot{y}}_{1})}^{2} + \frac{1}{2} f_{ψ 1} {({\dot{ψ}}_{2} - {\dot{ψ}}_{1})}^{2} \end{array}

式中：f_xi 、f_yi 、f_ψi 分别为沿X_i 、Y_i 和质心旋转方向的弹簧阻尼，其中 $f_{x i} = 0.001 k_{x i}$ ， $f_{y i} = 0.001 k_{y i}$ ；f_i 为异步电机i的转轴的阻尼。

则振动系统的广义力 Q 可表示为：

Q = {[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & T_{e 1} & T_{e 2} \end{matrix}]}^{T}

式中：T_e1、T_e2分别为异步电机1，2的电磁转矩。

拉格朗日方程可表示为：

\frac{d}{d t} (\frac{\partial T}{\partial \dot{q}}) - \frac{\partial T}{\partial q} + \frac{\partial E}{\partial q} + \frac{\partial D}{\partial \dot{q}} = Q

其中：

q = {[\begin{matrix} x_{1} & x_{2} & y_{1} & y_{2} & ψ_{1} & ψ_{2} & φ_{1} & φ_{2} \end{matrix}]}^{T}

式中： q 为振动系统的广义坐标。

将式(3)至式(6)代入式(7)，即可得振动系统的运动微分方程：

\{\begin{array}{l} M_{1} {\ddot{x}}_{1} - f_{x 1} ({\dot{x}}_{2} - {\dot{x}}_{1}) - k_{x 1} (x_{2} - x_{1}) = m_{o 1} r_{1} ({\ddot{φ}}_{1} s i n φ_{1} + {\dot{φ}}_{1}^{2} c o s φ_{1}) \\ M_{2} {\ddot{x}}_{2} + f_{x 2} {\dot{x}}_{2} + f_{x 1} ({\dot{x}}_{2} - {\dot{x}}_{1}) + k_{x 2} x_{2} + k_{x 1} (x_{2} - x_{1}) = \\ m_{o 2} r_{2} ({\ddot{φ}}_{2} s i n φ_{2} + {\dot{φ}}_{2}^{2} c o s φ_{2}) \\ M_{1} {\ddot{y}}_{1} - f_{y 1} ({\dot{y}}_{2} - {\dot{y}}_{1}) - k_{y 1} (y_{2} - y_{1}) = m_{o 1} r_{1} (- {\ddot{φ}}_{1} c o s φ_{1} + {\dot{φ}}_{1}^{2} s i n φ_{1}) \\ M_{2} {\ddot{y}}_{2} + f_{y 2} {\dot{y}}_{2} + f_{y 1} ({\dot{y}}_{2} - {\dot{y}}_{1}) + k_{y 2} y_{2} + k_{y 1} (y_{2} - y_{1}) = \\ m_{o 2} r_{2} (- {\ddot{φ}}_{2} c o s φ_{2} + {\dot{φ}}_{2}^{2} s i n φ_{2}) \\ J_{z 1} {\ddot{ψ}}_{1} - f_{ψ 1} ({\dot{ψ}}_{2} - {\dot{ψ}}_{1}) - k_{ψ 1} (ψ_{2} - ψ_{1}) = \\ m_{o 1} r_{1} l_{1} [- {\ddot{φ}}_{1} c o s (φ_{1} - β_{1}) + {\dot{φ}}_{1}^{2} s i n (φ_{1} - β_{1})] \\ J_{z 2} {\ddot{ψ}}_{2} + f_{ψ 2} {\dot{ψ}}_{2} + f_{ψ 1} ({\dot{ψ}}_{2} - {\dot{ψ}}_{1}) + k_{ψ 2} ψ_{2} + k_{ψ 1} (ψ_{2} - ψ_{1}) = \\ m_{o 2} r_{2} l_{2} [- {\ddot{φ}}_{2} c o s (φ_{2} - β_{2}) + {\dot{φ}}_{2}^{2} s i n (φ_{2} - β_{2})] \\ (J_{o 1} + m_{o 1} r_{1}^{2}) {\ddot{φ}}_{1} + f_{1} {\dot{φ}}_{1} = T_{e 1} + T_{L 1} \\ (J_{o 2} + m_{o 2} r_{2}^{2}) {\ddot{φ}}_{2} + f_{2} {\dot{φ}}_{2} = T_{e 2} + T_{L 2} \end{array}

其中：

\begin{array}{l} T_{L 1} = m_{o 1} r_{1} ({\ddot{x}}_{1} s i n φ_{1} - {\ddot{y}}_{1} c o s φ_{1}) - m_{o 1} l_{1} r_{1} [{\ddot{ψ}}_{1} c o s (φ_{1} - β_{1}) + {\dot{ψ}}_{1}^{2} s i n (φ_{1} - β_{1})] \\ T_{L 2} = m_{o 2} r_{2} ({\ddot{x}}_{2} s i n φ_{2} - {\ddot{y}}_{2} c o s φ_{2}) - m_{o 2} l_{2} r_{2} [{\ddot{ψ}}_{2} c o s (φ_{2} - β_{2}) + {\dot{ψ}}_{2}^{2} s i n (φ_{2} - β_{2})] \end{array}

式中： $T_{L 1}$ 、 $T_{L 2}$ 分别为异步电机1，2的负载转矩。

2 双质体振动系统的固有频率

对式(8)的前2个方程进行Laplace变换，可得：

\{\begin{array}{l} M_{1} S^{2} {\bar{x}}_{1} (S) - f_{x 1} S {\bar{x}}_{2} (S) + f_{x 1} S {\bar{x}}_{1} (S) - k_{x 1} {\bar{x}}_{2} (S) + \\ k_{x 1} {\bar{x}}_{1} (S) = {\bar{f}}_{1} (S) \\ M_{2} S^{2} {\bar{x}}_{2} (S) + f_{x 2} S {\bar{x}}_{2} (S) + f_{x 1} S {\bar{x}}_{2} (S) - f_{x 1} S {\bar{x}}_{1} (S) + \\ k_{x 2} {\bar{x}}_{2} (S) + k_{x 1} {\bar{x}}_{2} (S) - k_{x 1} {\bar{x}}_{1} (S) = {\bar{f}}_{2} (S) \end{array}

式中：S为Laplace算子； ${\bar{x}}_{i} (S)$ 为 $x_{i}$ 的Laplace变换； ${\bar{f}}_{i} (S)$ 为 $m_{o i} r_{i} ({\ddot{φ}}_{i} s i n φ_{i} + {\dot{φ}}_{i}^{2} c o s φ_{i})$ 的Laplace变换。

将式(9)整理成矩阵形式：

X (S) [\begin{matrix} {\bar{x}}_{1} (S) \\ {\bar{x}}_{2} (S) \end{matrix}] = [\begin{matrix} {\bar{f}}_{1} (S) \\ {\bar{f}}_{2} (S) \end{matrix}]

特征方程 $X (S)$ 的行列式可以表示成如下形式：

\begin{array}{l} |X (S)| = |\begin{matrix} M_{1} S^{2} + f_{x 1} S + k_{x 1} & - f_{x 1} S - k_{x 1} \\ - f_{x 1} S - k_{x 1} & M_{2} S^{2} + f_{x 2} S + f_{x 1} S + k_{x 2} + k_{x 1} \end{matrix}| = \\ M_{1} M_{2} S^{4} + [M_{2} f_{x 1} + M_{1} (f_{x 1} + f_{x 2})] S^{3} + \\ [M_{2} k_{x 1} + M_{1} (k_{x 1} + k_{x 2}) + f_{x 1} f_{x 2}] S^{2} + \\ (f_{x 1} k_{x 2} + f_{x 2} k_{x 1}) S + k_{x 1} k_{x 2} \end{array}

令 $|X (S)| = 0$ 以求解S，其解可表示为：

\{\begin{array}{l} S_{11} = - a_{1} + j ω_{x r 1}, S_{12} = - a_{1} - j ω_{x r 1} \\ S_{21} = - a_{2} + j ω_{x r 2}, S_{22} = - a_{2} - j ω_{x r 2} \end{array}

式中：a₁、a₂为衰减系数；ω_x_r1、ω_xr2为振动系统X方向的固有频率。

同理，可得振动系统Y方向的固有频率ω_y_r1和ω_y_r2。由于在实际工程应用中通常要求振动体上每个点的轨迹相同，因此异步电机的旋转中心与振动体的质心重合（即 $l_{1} = l_{2} = 0^{} m$ ），不考虑质心旋转方向的振动。

本文双质体振动系统选用2个相同的异步电机，振动系统和异步电机的参数分别如表1和表2所示。根据表2中异步电机的参数，可得其角频率（即激振频率）为157 rad/s。将表1中振动系统的参数代入式(12)，可计算得到当k_y₁=1 062 kN/m时，振动系统X方向的固有频率与激振频率相同；当k_y₁=443 kN/m时，振动系统Y方向的固有频率与激振频率相同。

表1 双质体振动系统的参数

Table 1 Parameters of double-mass vibration system

参数	量值
振动体质量M₁、M₂	48.45 kg
振动体转动惯量J_z1、J_z2	5 kg·m²
中间弹簧Y向刚度k_y₁	10~2 000 kN/m
下质体弹簧Y向刚度k_y₂	500 kN/m
中间弹簧Y向阻尼f_y₁	10~2 000 N·s/m
下质体弹簧Y向阻尼f_y₂	500 N·s/m
偏心转子质量m_o1、m_o2	3 kg
偏心转子等效半径r₁、r₂	0.02 m
异步电机转轴的转动惯量J_o1、J_o2	0.01 kg·m²

新窗口打开| 下载CSV

表2 异步电机的参数

Table 2 Parameters of asynchronous motor

参数	量值
电压	220 V
频率	50 Hz
极对数	2
转子的电阻	0.54 $Ω$
定-转子互感	0.13 H
定子电感	0.20 H
转子电感	0.20 H

新窗口打开| 下载CSV

3 双质体振动系统的控制器设计

交流异步电机的数学模型为非线性高阶系统，其在d-q坐标系下的电压、磁链方程^[24]如下：

[\begin{array}{l} U_{s d} \\ U_{s q} \\ U_{r d} \\ U_{r q} \end{array}] = [\begin{matrix} R_{s} + p L_{s} & - ω_{T} L_{s} & p L_{m} & - ω_{T} L_{m} \\ ω_{T} L_{s} & R_{s} + p L_{s} & ω_{T} L_{m} & p L_{m} \\ p L_{m} & - ω_{s} L_{m} & R_{r} + p L_{r} & - ω_{s} L_{r} \\ ω_{s} L_{m} & p L_{m} & ω_{s} L_{r} & R_{r} + p L_{r} \end{matrix}] [\begin{array}{l} I_{s d} \\ I_{s q} \\ I_{r d} \\ I_{r q} \end{array}]

[\begin{matrix} ϕ_{s d} \\ ϕ_{s q} \\ ϕ_{r d} \\ ϕ_{r q} \end{matrix}] = [\begin{matrix} L_{s} & 0 & L_{m} & 0 \\ 0 & L_{s} & 0 & L_{m} \\ L_{m} & 0 & L_{r} & 0 \\ 0 & L_{m} & 0 & L_{r} \end{matrix}] [\begin{matrix} I_{s d} \\ I_{s q} \\ I_{r d} \\ I_{r q} \end{matrix}]

式中： $R_{s}$ 、 $R_{r}$ 分别为定子、转子的电阻； $L_{m}$ 、 $L_{s}$ 、 $L_{r}$ 分别为定-转子互感、定子电感和转子电感； $ω_{T}$ 、 $ω_{s}$ 分别为定子的同步转速和转差转速；U、I、 $ϕ$ 分别为电压、电流、磁链；p为微分算子，p=d/dt。

在同步旋转M-T坐标系中，有：

T_{e} = \frac{3}{2} n_{p} L_{m} I_{s q} ϕ_{r} / L_{r}

式中： $n_{p}$ 为极对数； $ϕ_{r}$ 为转子总磁链。

根据式(15)，将式(8)的后2个公式改写成如下形式：

\{\begin{array}{l} (J_{o 1} + m_{o 1} r_{1}^{2}) {\ddot{φ}}_{1} + f_{1} {\dot{φ}}_{1} = K_{T 1} u_{1} + T_{L 1} \\ (J_{o 2} + m_{o 2} r_{2}^{2}) {\ddot{φ}}_{2} + f_{2} {\dot{φ}}_{2} = K_{T 2} u_{2} + T_{L 2} \end{array}

其中：

K_{T 1} = K_{T 2} = \frac{3}{2} n_{p} L_{m} ϕ_{r} / L_{r}

式中：u_i (i=1, 2)为所设计的控制器。

本文通过对2个异步电机进行矢量控制来实现其同步运转。异步电机的矢量控制原理如图2所示。参照文献[16-18]，采用主从控制结构和滑模控制算法分别设计2个异步电机的控制器：对于电机1，只控制其转速；对于电机2，只控制其与电机1之间的相位差。由此可实现2个异步电机的0或π相位差同步运转。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 异步电机的矢量控制原理

Fig.2 Vector control principle for asynchronous motor

3.1　主电机转速控制

设异步电机1（主电机）的目标转速为 $ω_{d}$ ，实际转速为 $ω_{1}$ ；异步电机2（从电机）的实际转速为 $ω_{2}$ ，则转速跟踪误差e₁为：

e_{1} = ω_{1} - ω_{d}

(17)

对式(17)求导，并将式(16)中的第1个方程代入，则可得：

{\dot{e}}_{1} = \frac{1}{(J_{o 1} + m_{o 1} r_{1}^{2})} (K_{T 1} u_{1} - f_{1} ω_{1} + T_{L 1}) - {\dot{ω}}_{d}

(18)

设计滑模函数 $s_{1}$ ：

s_{1} = e_{1} + c_{1} \int_{0}^{t} e_{1} (τ) d τ

(19)

式中： $c_{1}$ 为正实数。

对 $s_{1}$ 求关于时间的导数，并结合式(18)可得^[16-18]：

{\dot{s}}_{1} = \frac{1}{(J_{o 1} + m_{o 1} r_{1}^{2})} (K_{T 1} u_{1} - f_{1} ω_{1} + T_{L 1}) - {\dot{ω}}_{d} + c_{1} e_{1}

(20)

假设 ${\dot{s}}_{1} = 0$ 并忽略扰动 $T_{L 1}$ ，则异步电机1的等效控制器u_e1可表示为：

u_{e 1} = \frac{1}{K_{T 1}} (J_{o 1} + m_{o 1} r_{1}^{2}) ({\dot{ω}}_{d} - c_{1} e_{1}) + \frac{1}{K_{T 1}} f_{1} ω_{1}

(21)

为了增强振动系统的稳定性，设计鲁棒控制器u_h1：

u_{h 1} = - \frac{1}{K_{T 1}} (J_{o 1} + m_{o 1} r_{1}^{2}) ε_{1} s g n (s_{1})

(22)

其中：

s g n (s_{1}) = \{\begin{matrix} 1, & s_{1} > 0 \\ 0, & s_{1} = 0 \\ - 1, & s_{1} < 0 \end{matrix}

式中： $ε_{1}$ 为大于零的常数。

根据式(21)和式(22)，异步电机1的转速滑模控制器u₁为：

\begin{array}{l} u_{1} = \frac{1}{K_{T 1}} (J_{o 1} + m_{o 1} r_{1}^{2}) ({\dot{ω}}_{d} - c_{1} e_{1}) + \frac{1}{K_{T 1}} f_{1} ω_{1} - \\ \frac{1}{K_{T 1}} (J_{o 1} + m_{o 1} r_{1}^{2}) ε_{1} s g n (s_{1}) \end{array}

(23)

将式(23)代入式(20)，整理可得：

{\dot{s}}_{1} = - ε_{1} s g n (s_{1}) + \frac{T_{L 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})}

(24)

定义Lyapunov函数V₁为：

V_{1} = \frac{s_{1}^{2}}{2}

(25)

由式(25)可知，当 $V_{1} = 0$ 时， $s_{1} = 0$ ；当 $V_{1} > 0$ 时， $s_{1} \neq 0$ 。对式(25)求导，可得：

\begin{array}{l} {\dot{V}}_{1} = s_{1} {\dot{s}}_{1} = s_{1} [- ε_{1} s g n (s_{1}) + \frac{T_{L 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})}] = \\ - ε_{1} |s_{1}| + \frac{s_{1} T_{L 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} \leq - [ε_{1} - \frac{|T_{L 1}|}{(J_{o 1} + m_{o 1} r_{1}^{2})}] |s_{1}| \end{array}

(26)

由式(26)可知，当 $ε_{1} > |T_{L 1}| / (J_{o 1} + m_{o 1} r_{1}^{2})$ 时， ${\dot{V}}_{1} \leq 0$ ，则有 $\underset{t \to \infty}{l i m} s_{1} (t) = 0$ 。

根据式(19)，可得：

{\dot{e}}_{1} + c_{1} e_{1} = 0

(27)

由式(27)可知，固有 $\underset{t \to \infty}{l i m} e_{1} (t) = 0$ 。

3.2　从电机相位控制

异步电机1和异步电机2之间相位差的追踪误差e₂可表示为：

e_{2} = Δ φ - Δ φ_{d}

(28)

式中： $Δ φ$ 为2个异步电机的相位差， $Δ φ = φ_{1} - φ_{2}$ ； $Δ φ_{d}$ 为目标相位差。

结合式(16)和追踪误差e₂的二阶导数，可得：

\begin{array}{l} {\ddot{e}}_{2} + \frac{f_{1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} {\dot{φ}}_{1} - \frac{f_{2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} {\dot{φ}}_{2} = \\ \frac{K_{T 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} u_{1} + \frac{T_{L 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} - \\ \frac{K_{T 2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} u_{2} - \frac{T_{L 2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} \end{array}

(29)

设计滑模函数 $s_{2}$ ^[16-18]：

s_{2} = c_{2} e_{2} + {\dot{e}}_{2}

(30)

式中： $c_{2}$ 为正实数。

令 ${\dot{s}}_{2} = 0$ ，并结合式(28)和式(29)，则异步电机2的等效控制器u_e2可表示为：

\begin{array}{l} u_{e 2} = [\frac{K_{T 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} u_{1} + \frac{T_{L 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} - \\ \frac{T_{L 2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} - \frac{f_{1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} {\dot{φ}}_{1} + \\ \frac{f_{2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} {\dot{φ}}_{2} + c_{2} ({\dot{φ}}_{1} - {\dot{φ}}_{2})] \frac{(J_{o 2} + m_{o 2} r_{2}^{2})}{K_{T 2}} \end{array}

(31)

同理，为了增强振动系统的稳定性，设计鲁棒控制器u_h2^[25]：

u_{h 2} = \frac{1}{K_{T 2}} (J_{o 2} + m_{o 2} r_{2}^{2}) f (e_{2}) s g n (s_{2})

(32)

其中：

f (e_{2}) = \{\begin{array}{l} \frac{λ}{ε_{2}}, \\ \frac{λ |e_{2}|}{|e_{2}| + 1}, \end{array} \begin{matrix} \begin{array}{l} |e_{2}| > δ \\ |e_{2}| \leq δ \end{array} \end{matrix}

0 < ε_{2} < 1

，

δ > 0

，

λ > 0

根据式(31)和式(32)，异步电机2的相位差滑模控制器u₂为：

\begin{array}{l} u_{2} = [\frac{K_{T 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} u_{1} + \frac{T_{L 1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} - \\ \frac{T_{L 2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} - \frac{f_{1}}{(J_{o 1} + m_{o 1} r_{1}^{2})} {\dot{φ}}_{1} + \\ \frac{f_{2}}{(J_{o 2} + m_{o 2} r_{2}^{2})} {\dot{φ}}_{2} + c_{2} ({\dot{φ}}_{1} - {\dot{φ}}_{2})] \frac{(J_{o 2} + m_{o 2} r_{2}^{2})}{K_{T 2}} + \\ \frac{1}{K_{T 2}} (J_{o 2} + m_{o 2} r_{2}^{2}) f (e_{2}) s g n (s_{2}) \end{array}

(33)

将式(33)代入式(30)，整理可得：

{\dot{s}}_{2} = - f (e_{2}) s g n (s_{2})

(34)

定义Lyapunov函数V₂为：

V_{2} = \frac{s_{2}^{2}}{2}

(35)

由式(35)可知，当 $V_{2} = 0$ 时， $s_{2} = 0$ ；当 $V_{2} > 0$ 时， $s_{2} \neq 0$ 。对式(35)求导，可得：

{\dot{V}}_{2} = s_{2} {\dot{s}}_{2} = - s_{2} f (e_{2}) s g n (s_{2}) = - f (e_{2}) |s_{2}|

(36)

显然，可得 ${\dot{V}}_{2} \leq 0$ ，故有 $\underset{t \to \infty}{l i m} s_{2} (t) = 0$ 。结合式(30)可得：

c_{2} e_{2} + {\dot{e}}_{2} = 0

(37)

由式(37)可知， $\underset{t \to \infty}{l i m} e_{2} (t) = 0$ 。

4 双质体振动系统同步仿真分析

根据双质体振动系统的运动微分方程、所设计的控制器以及电源-电机模块，在MATLAB/Simulink环境中建立振动系统的机电-控制仿真模型。为了检验所设计控制器的可行性和鲁棒性，首先，讨论在自同步状态（即控制器不介入）下弹簧刚度对振动系统同步特性的影响；然后，对自同步状态下不能同步以及同步相位差不能实现0或π的工况进行控制同步仿真；最后，对比自同步仿真与控制同步仿真的结果。双质体振动系统和异步电机的参数设置参见表1和表2。

4.1　自同步仿真分析

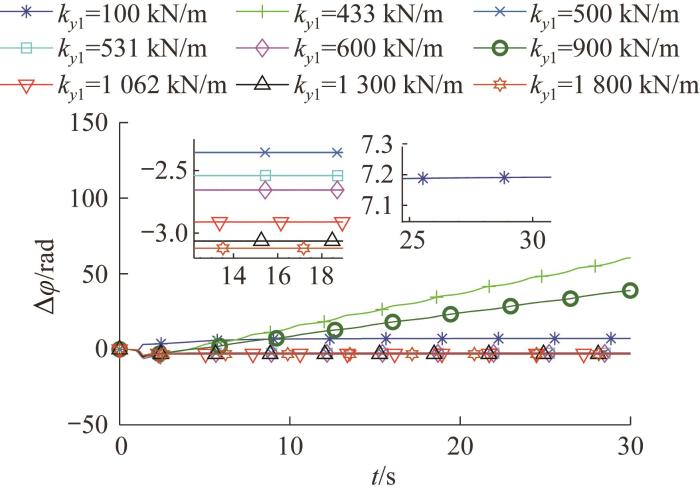
图3所示为自同步状态下弹簧刚度不同时双质体振动系统的相位差随时间的变化曲线，图中曲线最终收敛说明振动系统实现了自同步运动。从图3中可以看出，该振动系统的运动呈现3种状态：1）相位差 $Δ φ = 0 . 91_{} r a d$ 时的同向同步运动状态；2）相位差为 $- 3.12 \leq Δ φ \leq - 2 . 35_{} r a d$ 时的反向同步运动状态；3）相位差发散时的不同步运动状态。随着弹簧刚度 $k_{y 1}$ 的增大，相位差曲线经历了收敛—发散—收敛—发散—收敛的过程。当k_y₁=443 kN/m时，相位差曲线发散，根据式(12)，此时Y方向的固有频率与激振频率相同，均为157 rad/s；当k_y₁=900 kN/m时，相位差曲线也发散，此时X方向的固有频率为146.3 rad/s，略小于激振频率157 rad/s；当k_y₁=1 062 kN/m，相位差曲线收敛，此时X方向的固有频率与激振频率相同。结果表明，当X方向共振时，双质体振动系统可以实现同步运动，此时其相位差 $Δ φ = - 2 . 90_{} r a d$ 。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同弹簧刚度下双质体振动系统的相位差仿真结果

Fig.3 Phase difference simulation results of double-mass vibration system under different spring stiffness

通过仿真得到k_y₁=443 kN/m和k_y₁=1 062 kN/m时双质体振动系统的响应和异步电机的转速，结果分别如图4和图5所示。由图可知，当k_y₁=443 kN/m时，异步电机不能以恒定的转速运转，其转速在 $149.4 ~ 158 . 1_{} r a d / s$ 内波动；振动系统各个方向的振幅均不恒定，即无恒定的运动轨迹。当k_y₁=1 062 kN/m时，异步电机的转速在 $151.4 ~ 152 . 4_{} r a d / s$ 内波动，可以看作以恒定的转速运转；振动系统各个方向的振幅恒定，即运动轨迹恒定。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 k_y₁=443 kN/m时双质体振动系统的自同步仿真结果

Fig.4 Self-synchronization simulation results of double-mass vibration system with k_y₁=443 kN/m

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 k_y₁=1 062 kN/m时双质体振动系统的自同步仿真结果

Fig.5 Self-synchronization simulation results of double-mass vibration system with k_y₁=1 062 kN/m

4.2　控制同步仿真

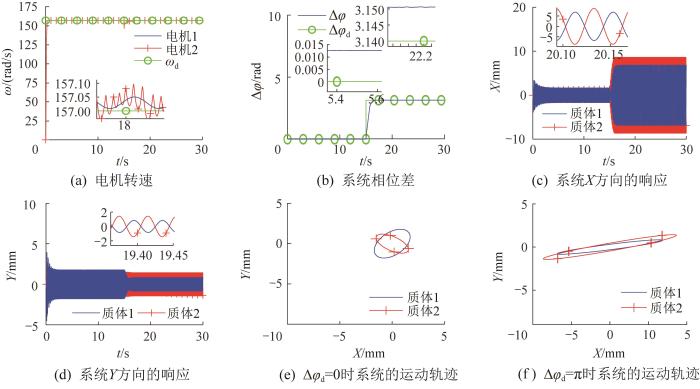
分别采用图4和图5对应的参数对双质体振动系统的异步电机进行滑模矢量控制，得到k_y₁=443 kN/m和k_y₁=1 062 kN/m时振动系统的控制同步仿真结果，分别如图6和图7所示。其中：主电机的目标转速 $ω_{d} = 157_{} r a d / s$ ；主从电机间的初始目标相位差 $Δ φ_{d} = 0$ ，t=15 s时目标相位差 $Δ φ_{d} = π$ 。由图6和图7可知，相位差曲线最终趋于收敛，双质体振动系统各个方向的振幅恒定，说明其处于稳定的同步运转状态。根据图6(a)、(b)和图7(a)、(b)，可知所设计的控制器的跟踪效果良好。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 k_y₁=443 kN/m时双质体振动系统的控制同步仿真结果

Fig.6 Control synchronization simulation results of double-mass vibration system with k_y₁=443 kN/m

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 k_y₁=1 062 kN/m时双质体振动系统的控制同步仿真结果

Fig.7 Control synchronization simulation results of double-mass vibration system with k_y₁=1 062 kN/m

对比图4和图6可知，通过对异步电机进行滑模矢量控制可使原本不能同步运转的双质体振动系统同步运转且可以调节相位差。对比图6(e)和图6(f)所示的振动系统的稳定运动轨迹可知，当目标相位差为π时振动系统的Y方向响应显著增大，上、下质体的运动轨迹均为与水平方向夹角大约为60°的椭圆轨迹。

对比图5和图7可知，通过对异步电机进行滑模矢量控制可以改变双质体振动系统的相位差。在自同步运转时，振动系统的相位差为-2.90 rad；在控制同步运转时，振动系统的相位差可以为0或π。对比7(e)和图7(f)可知，当目标相位差为π时，振动系统的X方向响应显著增大，上、下质体的运动轨迹均为与水平方向夹角大约为10°的椭圆轨迹。

5 结论

1）本文采用主从控制结构和滑模控制算法分别设计了双质体振动系统的2个异步电机的控制器。同时，在MATLAB/Simulink环境中建立了振动系统的机电-控制仿真模型，并进行了自同步和控制同步仿真。通过对比自同步和控制同步的仿真结果，验证了所设计控制器的可行性和鲁棒性。

2）当Y方向共振时，双质体振动系统不能实现自同步运动；当X方向共振时，该振动系统可以实现相位差为 $- 2 . 90_{} r a d$ 的自同步运动；但当X方向的固有频率略小于激振频率（即 $k_{y 1} = 900_{} k N / m$ ）时，振动系统不能实现自同步运动。

3）所设计的控制器可以使双质体振动系统实现0或π相位差的同步运转。当X方向和Y方向共振（即 $k_{y 1} = 443_{} k N / m$ 和 $k_{y 1} = 1 062_{} k N / m$ ）时，相位差为 $π$ 的同步运动有利于振动系统共振规律的利用。利用此规律，在不改变异步电机激振频率的情况下，仅采用质径积较小的异步电机即可实现所需的振幅，有利于节约能源。

4）X方向共振的双质体振动系统可用于设计振动运输设备；Y方向共振的系统可用于设计振动筛分设备。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[2]

闻邦椿，刘树英，何勍.振动机械的理论与动态设计方法［M］.北京：机械工业出版社，2001：307-312.

[本文引用: 2]

WEN

B C

， LIU

S Y

， HE

. Theory and dynamic design method of vibration machinery［M］. Beijing： China Machine Press， 2001： 307-312.

[本文引用: 2]

[3]

闻邦椿，刘树英，陈照波，等.机械振动理论及应用［M］.北京：高等教育出版社，2009：64-84.

[本文引用: 2]

WEN

B C

， LIU

S Y

， CHEN

Z B

， et al. Theory of mechanical vibration and its applications［M］. Beijing： Higher Education Press， 2009： 64-84.

[本文引用: 2]

[4]

阿尔卡季·皮科瓦夫斯基，迈克尔·罗森布拉姆，于尔根·库尔特斯.同步——非线性科学中的通用概念［M］. 高宏，胡琦琳，张朋波，等，译.北京：科学出版社，2018：1-20.