大转动惯量缠绕机加减速曲线优化设计

doi:10.3785/j.issn.1006-754X.2023.00.052

大转动惯量缠绕机加减速曲线优化设计

窦方健^,^,¹, 邱清盈^,^,¹, 管成¹, 邵锦杰¹, 吴海峰²

1.浙江大学机械工程学院，浙江杭州 310027

2.中国核工业集团有限公司第八研究所，上海 201800

Optimization design of acceleration and deceleration curve of winding machine with large moment of inertia

DOU Fangjian^,^,¹, QIU Qingying^,^,¹, GUAN Cheng¹, SHAO Jinjie¹, WU Haifeng²

1.School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China

2.The Eighth Research Institute, China National Nuclear Corporation, Shanghai 201800, China

通讯作者: 邱清盈（1970—），男，浙江杭州人，副教授，博士，从事机械优化设计和创新设计方法研究，E-mail: medesign@zju.edu.cn，https://orcid.org/0000-0001-6884-3125

收稿日期: 2022-12-29 修回日期: 2023-04-06

基金资助:

浙江省重点科技计划项目. 2019C01053
2018智能制造新模式应用项目. 110201D01801

Received: 2022-12-29 Revised: 2023-04-06

作者简介 About authors

窦方健（1997—），男，江苏常熟人，硕士生，从事电机加减速曲线优化研究，E-mail:2397351750@qq.com,https://orcid.org/0000-0002-9108-9244 , E-mail：2397351750@qq.com

摘要

针对大转动惯量碳纤维缠绕机的加速和减速阶段运行不平稳、传动件易失效破坏等问题，提出了一种基于改进型Sigmoid加减速曲线的主轴运行曲线优化方案。首先，利用五次多项式对传统Sigmoid加减速曲线的跃变处进行补偿，以约束曲线起始点、衔接点、终止点的速度、加速度和急动度（加加速度）。然后，基于改进曲线的速度与加速度函数建立缠绕机的负载扭矩、电机输出功率、主轴强度与刚度以及缠绕圈数的数学模型，并以各阶段运行时长为设计变量、以电机最大输出功率最小和总运行时长最短为优化目标对曲线进行多目标优化，根据缠绕圈数、传动件强度与刚度等的约束条件，利用多目标遗传算法NSGA-Ⅱ（non-dominated sorting genetic algorithm-Ⅱ，非支配排序遗传算法-Ⅱ）求解模型的非支配解集，并利用比重选取函数选择最优解。最后，通过AMESim-ADAMS联合仿真对比加减速曲线优化前后缠绕机的运行效果。结果表明：优化后缠绕机的总运行时长、最大加速度、最大负载扭矩和最大输出功率分别降低了41.7%，75.8%，75.5%和72.8%，且主轴的运行曲线更加平滑，验证了优化方案的可行性。研究结果为大转动惯量旋转设备的运行不平稳或传动件失效问题提供了一种新的解决思路。

关键词： 大转动惯量 ; 缠绕机 ; 加减速曲线 ; 多目标优化 ; 遗传算法

Abstract

Aiming at the problems of unstable operation and easy failure of transmission parts during acceleration and deceleration of carbon fiber winding machine with large moment of inertia, an optimization scheme of spindle operation curve based on improved Sigmoid acceleration and deceleration curve was proposed. Firstly, the quintic polynomial was used to compensate the mutation of the traditional Sigmoid acceleration and deceleration curve by constraining the velocity, acceleration and jerk of the starting point, connecting point and ending point of the curve. Then, the mathematical models of load torque, motor output power, strength and stiffness of spindle and number of winding coils were established based on the velocity and acceleration functions of the improved curve. The multi-objective optimization for the curve was carried out with the operating time of each stage as the design variables and the maximum motor output power and total operating time as the optimization objectives. Under the constraints of the number of winding coils, strength and stiffness of transmission parts and so on, the non-dominated solution set was solved by the multi-objective genetic algorithm NSGA-Ⅱ(non-dominated sorting genetic algorithm-Ⅱ), and the optimal solution was selected by the proportion selection function. Finally, through AMESim-ADAMS co-simulation, the operation effects of winding machine before and after acceleration and deceleration curve optimization were compared. The results showed that the total operating time, maximum acceleration, maximum load torque and maximum output power of the optimized winding machine were reduced by 41.7%, 75.8%, 75.5% and 72.8%, and the spindle operation curve was smoother, which verified the feasibility of the optimization scheme. The research results provide a new solution for the problem of unstable operation or transmission parts failure of rotating equipment with large moment of inertia.

Keywords： large moment of inertia ; winding machine ; acceleration and deceleration curve ; multi-objective optimization ; genetic algorithm

PDF (2619KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

窦方健, 邱清盈, 管成, 邵锦杰, 吴海峰. 大转动惯量缠绕机加减速曲线优化设计. 工程设计学报[J], 2023, 30(4): 503-511 doi:10.3785/j.issn.1006-754X.2023.00.052

DOU Fangjian, QIU Qingying, GUAN Cheng, SHAO Jinjie, WU Haifeng. Optimization design of acceleration and deceleration curve of winding machine with large moment of inertia. Chinese Journal of Engineering Design[J], 2023, 30(4): 503-511 doi:10.3785/j.issn.1006-754X.2023.00.052

近年来，碳纤维材料在工业生产中被广泛应用，碳纤维制备专用设备的需求量随之增大^[1-2]。在碳纤维材料的制备过程中，须将丝状材料缠绕成形，因此要设计相应的缠绕机和缠绕方法。

目前，已有不少学者对碳纤维制备用缠绕机及缠绕方法展开了研究。例如：王征等人^[3]针对碳纤维增强碳/碳坩埚预制体缠绕效率低的问题，设计了一种柔性缠绕成形系统，实现了自动缠绕。Dackweiler等人^[4]针对T形管道接口处碳纤维缠绕问题，推导了缠绕路径模型，并结合微分几何方法计算了测地线和非测地线的曲线。Li等人^[5]针对碳纤维生产过程中断丝的在线检测和跟踪问题，提出了一种基于卷积神经网络的机器视觉方法，用于跟踪碳纤维缠绕丝，进而准确地定位断丝处。杨海^[6]针对缠丝机械臂运行轨迹的平滑性，设计了一种以缠绕时间、耗能、轨迹平滑性为目标函数的执行器末端轨迹多目标优化模型，消除了缠绕张力的波动。李浩等人^[7]针对碳纤维立体织机引纬机构的剑杆运行波动大的问题，采用2个异相位小模数齿轮同时啮合1根齿条的方法提高了其传动平稳性。张鹏等人^[8]考虑碳纤维缠绕机主轴径向跳动和结构尺寸的约束，设计了以主轴质量最小为目标的主轴结构优化模型。

然而，针对大转动惯量缠绕机运行曲线优化的研究鲜有报道。在实际应用中，现有碳纤维缠绕机由于自身转动惯量较大，运行时负载扭矩较大，易造成传动件失效破坏；此外，主轴转动时的加速度波动也会影响缠绕机运行的平稳性。因此，在缠绕机结构确定的情况下，如何设计其运行曲线并按需求优化以实现稳定运行成为研究重点。

考虑到缠绕机运行平稳问题，首先针对传统Sigmoid加减速曲线^[9]的速度跃变缺陷，采用五次多项式进行分段匹配补偿，设计了一种改进型Sigmoid加减速曲线作为主轴的运行曲线，以使主轴转动的速度与加速度曲线连续平滑且无突变。然后在改进曲线的基础上，考虑传动件的强度与刚度、缠绕圈数和加减速阶段运行时长的约束条件，以各阶段运行时长为设计变量、以电机最大输出功率最小和总运行时长最短为优化目标，建立加减速曲线的多目标优化模型，并利用多目标遗传算法NSGA-Ⅱ（non-dominated sorting genetic algorithm-Ⅱ，非支配排序遗传算法-Ⅱ）求解Pareto前沿^[10-11]，并通过定义比重选取函数，根据用户需求选取最优解，从而得到主轴的优化运行曲线。

1 碳纤维缠绕机介绍

中国核工业集团有限公司设计的碳纤维缠绕机的结构如图1所示。其中：芯模的材料为45号碳钢，形状呈直径较大的圆筒状，中间含有4块加强板；芯模外层缠绕碳纤维。由于芯模和碳纤维层的总转动惯量较大，缠绕机在加减速过程中的负载扭矩较大，负载扭矩所产生的扭转切应力直接影响主轴的强度与刚度以及联轴器的强度。此外，缠绕机以瞬间驱动电机的方式运行会造成联轴器的柱销剪断或主轴变形失效，严重时甚至造成主轴扭断；且长时间的启停冲击与运行振动也会导致传动件的寿命缩短。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 碳纤维缠绕机结构示意

Fig.1 Structure diagram of carbon fiber winding machine

在碳纤维缠绕机整体结构确定的情况下，更换强度更高的传动件须改变对应配合零件或固定支架的结构尺寸，大大增加了时间和经济成本。因此，在不更换传动件和紧固件的情况下，如何设计与优化缠绕机主轴的运行曲线以解决上述问题是本文研究的关键所在。

2 缠绕机加减速曲线设计

传统的Sigmoid速度曲线是Sigmoid函数的一种变形式^[9]。与三次多项式曲线比较，Sigmoid函数在(-∞, +∞)内高阶可导，当实际环境中存在外界扰动时，Sigmoid加减速曲线的跟踪效果更佳，加速度振荡更少，从而使系统运行更平稳。因此，本文采用Sigmoid加减速曲线对碳纤维缠绕机主轴的运行曲线进行设计与优化。

以加速阶段为例，设加速时长为T₁，总运行时长为T_z，匀速速度为v_m，则传统的Sigmoid加速曲线 $g (t)$ 可表示为：

g (t) = \frac{v_{m}}{1 + e^{- \frac{12}{T_{1}} (t - \frac{T_{1}}{2})}}

式中：t为时间。

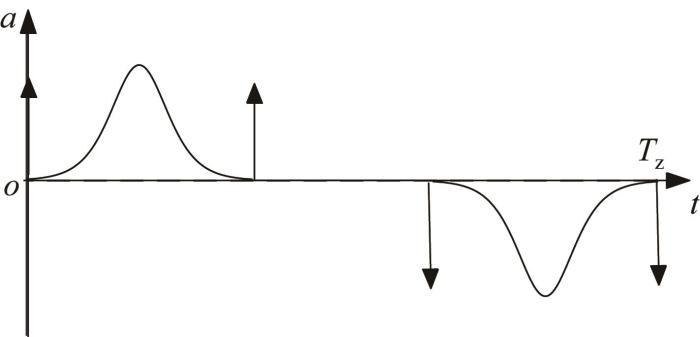
由于式(1)中存在指数函数，加速阶段的初始时刻与末端时刻的理论计算速度分别为 $g (0) = v_{m} / (1 + e^{6})$ 和 $g (T_{1}) = v_{m} / (1 + e^{- 6})$ 。在无补偿情况下，该加速曲线无法完全达到初始速度0和目标速度v_m，出现了速度跃变的现象（见图2），即速度曲线不连续，导致该跃变时刻的加速度在理论上趋近无穷大，存在突变（见图3）。这样容易引起扭矩突增，使得缠绕机在该时刻附近运行不平稳并产生振动，有损传动件与电机的寿命。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 传统Sigmoid速度曲线

Fig.2 Traditional Sigmoid velocity curve

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 传统Sigmoid加速度曲线

Fig.3 Traditional Sigmoid acceleration curve

2.1　加速阶段的分段匹配

设定加速阶段初始段补偿曲线的时间区间为 $[0, τ_{1})$ ，Sigmoid加速曲线的时间区间为 $[τ_{1}, T_{1} - τ_{1})$ ，末尾段补偿曲线的时间区间为 $[T_{1} - τ_{1}, T_{1}]$ ，对 $g (t)$ 进行区间变换，变换后的 $g (t)$ 可表示为：

g (t) = \frac{v_{m}}{1 + e^{- \frac{12}{T_{1} - 2 τ_{1}} (t - \frac{T_{1}}{2})}}

(2)

分别求解 $g (t)$ 的一阶、二阶导数，可得：

\{\begin{array}{l} \dot{g} (t) = \frac{12 v_{m}}{T_{1} - 2 τ_{1}} \cdot \frac{Q}{{(1 + Q)}^{2}} \\ \ddot{g} (t) = \frac{12^{2} v_{m}}{(T_{1} - 2 τ_{1})^{2}} \cdot \frac{Q (Q - 1)}{{(1 + Q)}^{3}} \end{array}

(3)

其中：

Q = e^{- \frac{12}{T_{1} - 2 τ_{1}} (t - \frac{T_{1}}{2})}

式中：Q为中间变量。

设初始段的多项式速度曲线 $V (t)$ 为：

V (t) = a_{5} t^{5} + a_{4} t^{4} + a_{3} t^{3} + a_{2} t^{2} + a_{1} t + a_{0}

(4)

式中：a_i 为多项式的系数。

则初始段的加速度曲线 $A (t)$ 和急动度（加加速度）曲线 $J (t)$ 可表示为：

\{\begin{array}{l} A (t) = 5 a_{5} t^{4} + 4 a_{4} t^{3} + 3 a_{3} t^{2} + 2 a_{2} t + a_{1} \\ J (t) = 20 a_{5} t^{3} + 12 a_{4} t^{2} + 6 a_{3} t + 2 a_{2} \end{array}

(5)

为使加速阶段的速度和加速度曲线连续平滑且无突变，多项式系数的求解约束包括：1）起始点或末端点的速度、加速度和急动度均为0；2）曲线衔接点处速度、加速度、急动度的连续性要求。综上，求解约束可表示为：

\{\begin{array}{l} V (0) = 0 \\ A (0) = 0 \\ J (0) = 0 \\ V (τ_{1}) = g (τ_{1}) = \frac{v_{m}}{1 + e^{6}} \\ A (τ_{1}) = \dot{g} (τ_{1}) = \frac{12 e^{6} v_{m}}{(T_{1} - 2 τ_{1}) (1 + e^{6})^{2}} \\ J (τ_{1}) = \ddot{g} (τ_{1}) = \frac{12^{2} e^{6} (e^{6} - 1) v_{m}}{(T_{1} - 2 τ_{1})^{2} (1 + e^{6})^{3}} \end{array}

(6)

根据式(6)，计算得到各个多项式系数a_i 的值：

\{\begin{array}{l} a_{0} = 0 \\ a_{1} = 0 \\ a_{2} = 0 \\ a_{3} = \frac{τ_{1}^{2} \ddot{g} (τ_{1}) - 8 τ_{1} \dot{g} (τ_{1}) + 20 g (τ_{1})}{2 τ_{1}^{3}} \\ a_{4} = \frac{- τ_{1}^{2} \ddot{g} (τ_{1}) + 7 τ_{1} \dot{g} (τ_{1}) - 15 g (τ_{1})}{τ_{1}^{4}} \\ a_{5} = \frac{τ_{1}^{2} \ddot{g} (τ_{1}) - 6 τ_{1} \dot{g} (τ_{1}) + 12 g (τ_{1})}{2 τ_{1}^{5}} \end{array}

(7)

为方便计算，设末尾段的多项式速度曲线 $V (t)$ 为：

V (t) = \sum_{i = 0}^{5} b_{i} (t - T_{1} + τ_{1})^{i}

(8)

式中：b_i 为多项式的系数。

则末尾段的加速度曲线 $A (t)$ 和急动度曲线 $J (t)$ 可表示为：

\{\begin{array}{l} A (t) = \sum_{i = 1}^{5} i b_{i} (t - T_{1} + τ_{1})^{i - 1} \\ J (t) = \sum_{i = 2}^{5} i (i - 1) b_{i} (t - T_{1} + τ_{1})^{i - 2} \end{array}

(9)

末尾段的约束条件同上，表示为：

\{\begin{array}{l} V (T_{1} - τ_{1}) = g (T_{1} - τ_{1}) = \frac{v_{m}}{1 + e^{- 6}} \\ A (T_{1} - τ_{1}) = \dot{g} (T_{1} - τ_{1}) = \frac{12 e^{- 6} v_{m}}{(T_{1} - 2 τ_{1}) (1 + e^{- 6})^{2}} \\ J (T_{1} - τ_{1}) = \ddot{g} (T_{1} - τ_{1}) = \frac{12^{2} e^{- 6} (e^{- 6} - 1) v_{m}}{(T_{1} - 2 τ_{1})^{2} (1 + e^{- 6})^{3}} \\ V (T_{1}) = v_{m} \\ A (T_{1}) = 0 \\ J (T_{1}) = 0 \end{array}

(10)

由此计算得到多项式系数b_i 的值：

\{\begin{array}{l} b_{0} = g (T_{1} - τ_{1}) \\ b_{1} = \dot{g} (T_{1} - τ_{1}) \\ b_{2} = \frac{\ddot{g} (T_{1} - τ_{1})}{2} \\ b_{3} = \frac{- 3 τ_{1}^{2} \ddot{g} (T_{1} - τ_{1}) - 12 τ_{1} \dot{g} (T_{1} - τ_{1}) - 20 g (T_{1} - τ_{1}) + 20 v_{m}}{2 τ_{1}^{3}} \\ b_{4} = \frac{3 τ_{1}^{2} \ddot{g} (T_{1} - τ_{1}) + 16 τ_{1} \dot{g} (T_{1} - τ_{1}) + 30 g (T_{1} - τ_{1}) - 30 v_{m}}{2 τ_{1}^{4}} \\ b_{5} = \frac{- τ_{1}^{2} \ddot{g} (T_{1} - τ_{1}) - 6 τ_{1} \dot{g} (T_{1} - τ_{1}) - 12 g (T_{1} - τ_{1}) + 12 v_{m}}{2 τ_{1}^{5}} \end{array}

(11)

综上，改进型Sigmoid加速曲线 $g_{1} (t)$ 可表示为：

g_{1} (t) = \{\begin{array}{l} a_{5} t^{5} + a_{4} t^{4} + a_{3} t^{3}, 0 \leq t < τ_{1} \\ \frac{v_{m}}{1 + e^{- \frac{12}{T_{1} - 2 τ_{1}} (t - \frac{T_{1}}{2})}}, τ_{1} \leq t < T_{1} - τ_{1} \\ \sum_{i = 0}^{5} b_{i} (t - T_{1} + τ_{1})^{i}, T_{1} - τ_{1} \leq t \leq T_{1} \end{array}

(12)

2.2　减速阶段的分段匹配

设匀速阶段的运行时长为T₂，减速阶段的运行时长为T₃，则总运行时长T_z=T₁+T₂+T₃。为了方便减速曲线公式的推导与计算，以横坐标轴为时间轴，以纵坐标轴为速度轴，将减速阶段的速度曲线看作运行时长为T₃、多项式补偿部分时长为 $τ_{2}$ 的Sigmoid加速曲线先以纵坐标轴为基准进行镜像，再沿横坐标轴右侧平移T_z所得到的运行曲线。

未镜像前的Sigmoid减速曲线 $h (t)$ 及其各阶导数可表示为：

\{\begin{array}{l} h (t) = \frac{v_{m}}{1 + e^{- \frac{12}{T_{3} - 2 τ_{2}} (t - \frac{T_{3}}{2})}} \\ \dot{h} (t) = \frac{12 v_{m}}{T_{3} - 2 τ_{2}} \cdot \frac{U}{{(1 + U)}^{2}} \\ \ddot{h} (t) = \frac{12^{2} v_{m}}{(T_{3} - 2 τ_{2})^{2}} \cdot \frac{U (U - 1)}{{(1 + U)}^{3}} \end{array}

(13)

其中：

U = e^{- \frac{12}{T_{3} - 2 τ_{2}} (t - \frac{T_{3}}{2})}

式中：U为中间变量。

设未镜像前减速阶段初始段和末尾段的多项式速度曲线分别如式(14)和式(15)：

V (t) = c_{5} t^{5} + c_{4} t^{4} + c_{3} t^{3} + c_{2} t^{2} + c_{1} t + c_{0}

(14)

V (t) = \sum_{i = 0}^{5} k_{i} (t - T_{3} + τ_{2})^{i}

(15)

式中：c_i 、k_i 为多项式的系数。

为了使减速阶段的速度和加速度曲线连续平滑且无突变，多项式系数的求解约束同2.1节所述，由此可计算得到多项式系数c_i 、k_i 的值：

\{\begin{array}{l} c_{0} = 0 \\ c_{1} = 0 \\ c_{2} = 0 \\ c_{3} = \frac{τ_{2}^{2} \ddot{h} (τ_{2}) - 8 τ_{2} \dot{h} (τ_{2}) + 20 h (τ_{2})}{2 τ_{2}^{3}} \\ c_{4} = \frac{- τ_{2}^{2} \ddot{h} (τ_{2}) + 7 τ_{2} \dot{h} (τ_{2}) - 15 h (τ_{2})}{τ_{2}^{4}} \\ c_{5} = \frac{τ_{2}^{2} \ddot{h} (τ_{2}) - 6 τ_{2} \dot{h} (τ_{2}) + 12 h (τ_{2})}{2 τ_{2}^{5}} \end{array}

(16)

\{\begin{array}{l} k_{0} = h (T_{3} - τ_{2}) \\ k_{1} = \dot{h} (T_{3} - τ_{2}) \\ k_{2} = \frac{\ddot{h} (T_{3} - τ_{2})}{2} \\ k_{3} = \frac{- 3 τ_{2}^{2} \ddot{h} (T_{3} - τ_{2}) - 12 τ_{2} \dot{h} (T_{3} - τ_{2}) - 20 h (T_{3} - τ_{2}) + 20 v_{m}}{2 τ_{2}^{3}} \\ k_{4} = \frac{3 τ_{2}^{2} \ddot{h} (T_{3} - τ_{2}) + 16 τ_{2} \dot{h} (T_{3} - τ_{2}) + 30 h (T_{3} - τ_{2}) - 30 v_{m}}{2 τ_{2}^{4}} \\ k_{5} = \frac{- τ_{2}^{2} \ddot{h} (T_{3} - τ_{2}) - 6 τ_{2} \dot{h} (T_{3} - τ_{2}) - 12 h (T_{3} - τ_{2}) + 12 v_{m}}{2 τ_{2}^{5}} \end{array}

(17)

通过镜像和平移后的改进型Sigmoid减速曲线 $h_{1} (t)$ 可表示为：

h_{1} (t) = \{\begin{array}{l} \sum_{i = 0}^{5} k_{i} (T_{z} - t - T_{3} + τ_{2})^{i}, T_{1} + T_{2} \leq t < T_{1} + T_{2} + τ_{2} \\ \frac{v_{m}}{1 + e^{- \frac{12}{T_{3} - 2 τ_{2}} (T_{z} - t - \frac{T_{3}}{2})}}, T_{1} + T_{2} + τ_{2} \leq t < T_{z} - τ_{2} \\ \sum_{i = 3}^{5} c_{i} (T_{z} {- t)}^{i}, T_{z} - τ_{2} \leq t \leq T_{z} \end{array}

(18)

2.3　改进型Sigmoid加减速曲线

综上，改进型Sigmoid加减速曲线 $v (t)$ 及其对应的加速度曲线 $a (t)$ 分别表示为：

v (t) = \{\begin{array}{l} g_{1} (t), 0 \leq t < T_{1} \\ v_{m}, T_{1} \leq t < T_{1} + T_{2} \\ h_{1} (t), T_{1} + T_{2} \leq t \leq T_{z} \end{array}

(19)

a (t) = \dot{v} (t)

(20)

改进型Sigmoid速度和加速度曲线分别如图4和图5所示。由图可知，改进后的速度曲线及加速度曲线连续平滑且无突变，有效解决了速度跃变和加速度突变的问题，可使缠绕机运行更平稳。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 改进型Sigmoid速度曲线

Fig.4 Improved Sigmoid velocity curve

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 改进型Sigmoid加速度曲线

Fig.5 Improved Sigmoid acceleration curve

3 缠绕机加减速曲线优化

考虑在设备设计中采用低功率电机可大大降低电机的采购成本，故本文将缠绕机的电机最大输出功率最小作为其中一个优化目标，以便设计时选择更廉价的低功率电机。同时，考虑用户对经济效益的要求，须控制运行时长，故本文将总运行时长最短作为另一个优化目标。综上，如何选取加减速曲线各阶段的运行时长，以使电机最大输出功率和总运行时长均达到理想解并满足传动件的强度与刚度以及缠绕圈数的要求，是本文的研究重点。

3.1　加减速曲线优化相关的数学模型

3.1.1　负载扭矩模型

在芯模产生的负载扭矩较大的情况下，主轴轴承的摩擦力矩和纤维的缠绕力矩相对很小，在分析传动件的强度时可忽略，故缠绕机的负载扭矩 $M_{T} (t)$ 为：

M_{T} (t) = J_{m} a (t)

(21)

式中：J_m为芯模、碳纤维层和卡盘的总转动惯量。

3.1.2　电机输出功率模型

设减速器的传动效率为η₁，联轴器的传动效率为η₂，则电机的输出功率 $P (t)$ 可表示为：

P (t) = \frac{|J_{m} a (t) \cdot v (t)|}{η_{1} η_{2}}

(22)

3.1.3　主轴的强度与刚度模型

主轴受到芯模等零件重力所引起的弯矩与负载扭矩的作用，因此按照弯扭合成强度进行校核与计算。零件重力所引起的弯矩不随角速度或角加速度的变化而变化，而负载扭矩随角加速度的变化而变化。参考文献[12-13]，可推导得到主轴强度校核中的计算应力σ_ca、疲劳校核中的计算安全系数S_ca、静强度校核中的计算安全系数S_sca以及刚度校核中的单位长度扭转角 $φ$ ，分别为：

σ_{c a} = \frac{\sqrt[]{M^{2} + 0 . 6^{2} m a x \{M_{T}^{2} (t)\}}}{W}

(23)

S_{c a} = \frac{S_{σ}}{\sqrt[]{1 + \frac{S_{σ}^{2} (K_{τ} + ϕ_{τ})^{2} m a x \{M_{T}^{2} (t)\}}{4 τ_{- 1}^{2} W_{T}^{2}}}}

(24)

S_{s c a} = \frac{S_{s σ}}{\sqrt[]{1 + S_{s σ}^{2} \frac{m a x \{M_{T}^{2} (t)\}}{τ_{s} W_{τ}^{2}}}}

(25)

φ = \frac{180 °}{π} \cdot \frac{m a x \{|M_{T} (t)|\}}{G I_{P}}

(26)

式中：M为强度校核中危险截面的弯矩；W为危险截面的抗弯截面系数；S_σ 为考虑法向应力的计算安全系数；K_τ 为考虑扭转切应力时的综合影响系数； $ϕ_{τ}$ 为碳钢系数；τ_-1为材料的剪切疲劳极限；W_T为疲劳校核中危险截面的抗扭截面系数；S_s_σ 为考虑法向应力的安全系数；τ_s为材料的抗扭屈服极限；W_τ 为静强度校核中危险截面的抗扭截面系数；G为剪切弹性模量；I_P为轴截面极惯性矩。

3.1.4　缠绕圈数模型

缠绕机运行时须控制缠绕丝线的总圈数。通过主轴运行曲线的速度公式对时间积分，可得到缠绕圈数的数学模型：

n = \frac{\int_{0}^{T_{1}} g_{1} (t) d t + v_{m} T_{2} + \int_{T_{1} + T_{2}}^{T_{z}} h_{1} (t) d t}{2 π}

(27)

3.2　加减速曲线的多目标优化模型

缠绕机加减速曲线的多目标优化模型关系如图6所示。基于含设计变量T₁、T₂、T₃的速度曲线 $v (t)$ 和加速度曲线 $a (t)$ 得到缠绕机的负载扭矩、电机输出功率、主轴的强度与刚度和缠绕圈数的数学模型，进而得到目标函数，并根据运行要求确定约束条件。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 缠绕机加减速曲线的多目标优化模型关系

Fig.6 Multi-objective optimization model relationships for acceleration and deceleration curve of winding machine

根据图6，可知：

1）设计变量。

X = [T_{1} T_{2} T_{3}]^{T}

(28)

2）优化目标。

m i n F (X) = m i n {[T_{z} m a x \{P (t)\}]}^{T}

(29)

3）约束要求。

主轴的强度与刚度约束包括以下方面：强度约束、疲劳强度约束、静强度约束以及刚度约束。联轴器的强度约束即作用扭矩不超过许用扭矩。此外，根据用户需求设定加速和减速阶段时间约束范围为0~6 s，缠绕丝线总圈数为n_z。

故约束条件可表示为：

\{\begin{array}{l} n - n_{z} = 0 \\ \begin{matrix} T_{1} \in (0, 6] s \\ T_{2} \in (0, 6] s \end{matrix} \\ \begin{array}{l} σ_{c a} \leq [σ_{- 1}] \\ \begin{array}{l} S - S_{c a} \leq 0 \\ S_{s} - S_{s c a} \leq 0 \\ φ \leq [φ] \end{array} \end{array} \\ m a x \{|M_{T} (t)|\} \leq M_{L} \end{array}

(30)

式中：[σ_-1]为材料许用弯曲应力；S为疲劳安全系数；S_s为按屈服强度计算的设计安全系数； $[φ]$ 为单位长度允许的扭转角；M_L为联轴器的许用扭矩。

3.3　优化算法与选取策略

本文采用多目标遗传算法NSGA-II^[14-18]求解多目标的Pareto前沿，具体算法流程参见文献[14]，本文不再赘述。设种群数目为200，迭代次数为300，交叉率为0.8，变异率为0.2。同时，定义权重选取函数 $E (\cdot)$ ，可根据需求在Pareto前沿上选择E值最小的一组解作为最终解。

E (F_{1}, F_{2}) = β \frac{F_{1} - F_{1 m i n}}{F_{1 m a x} - F_{1 m i n}} + (1 - β) \frac{F_{2} - F_{2 m i n}}{F_{2 m a x} - F_{2 m i n}}

(31)

式中：F₁、F₂为解得的Pareto前沿中一对非支配解，即2个目标函数的值；F_{1 min}、F_{1 max}分别为第1个目标函数在Pareto前沿中的最小值、最大值；F_{2 min}、F_{2 max}分别为第2个目标函数在Pareto前沿中的最小值、最大值；β为用户设定的权重系数，根据用户需求调整选取函数 $E (\cdot)$ 对于不同目标的侧重程度。

3.4　多目标优化结果

缠绕机的主要参数如表1所示。本文设补偿段运行时长 $τ_{1}$ 为加速阶段运行时长T₁的1/10、 $τ_{2}$ 为减速阶段运行时长T₃的1/10。

表1 缠绕机主要参数

Table 1 Main parameters of winding machine

参数	量值	参数	量值
J_m	1 129.14 kg·m²	S_s_σ	18.415
η₁	0.94	τ_s	313.2 MPa
η₂	0.99	W_τ	8.284×10^-5 m³
v_m	2.094 4 rad/s	G	8.1×10⁴ MPa
T₂	3 s	I_P	1.868×10^-6 m³
M	1 214.56 N·m	n_z	2.3圈
W	4.142×10^-5m³	[σ_-1]	70 MPa
S_σ	3.780 5	S	1.5
K_τ	3.028 7	S_s	1.6
$ϕ_{τ}$	0.05	$[φ]$	1.5°
τ_-1	200 MPa	M_L	6 300 N·m
W_T	8.284×10^-5 m³

新窗口打开| 下载CSV

通过多目标优化后得到Pareto前沿，用户设定选取函数的权重系数β=0.5，选取Pareto前沿中E_min对应的点，如图7所示，得到各设计变量的最优解和目标函数值，结果如下：

\{\begin{array}{l} T_{1} = 3.572 s \\ T_{2} = 3.332 s \\ T_{3} = 3.564 s \end{array}

(32)

\{\begin{array}{l} T_{z} = 10.468 s \\ m a x \{P (t)\} = 3.318 k W \end{array}

(33)

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 缠绕机加减速曲线多目标优化模型的Pareto前沿

Fig.7 Pareto frontier of multi-objective optimization model for acceleration and deceleration curve of winding machine

4 仿真验证

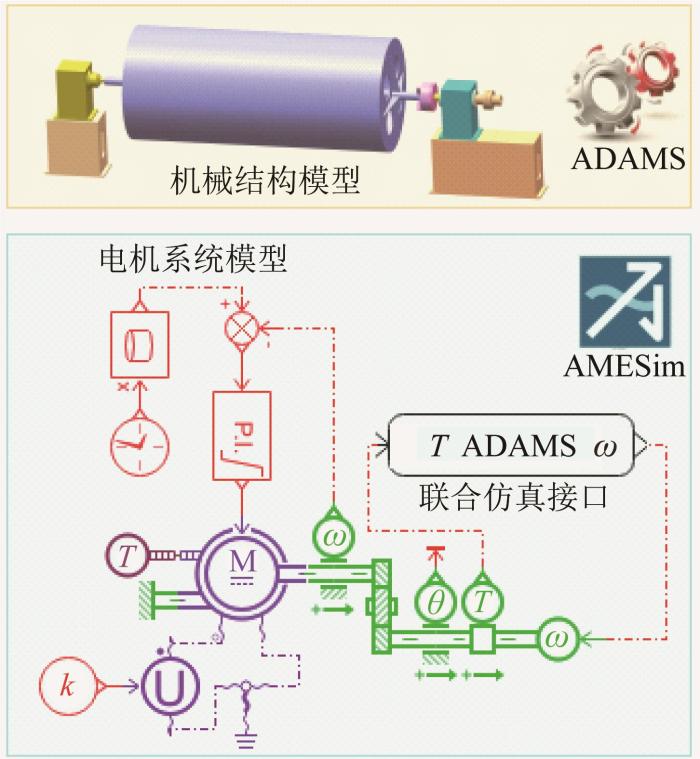
采用ADAMS软件建立缠绕机的机械结构模型，同时利用AMESim软件中的电机库与机械库建立缠绕机的电机系统模型，通过联合仿真接口交互信息并进行仿真，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 缠绕机的AMESim-ADAMS联合仿真模型

Fig.8 AMESim-ADAMS co-simulation of winding machine

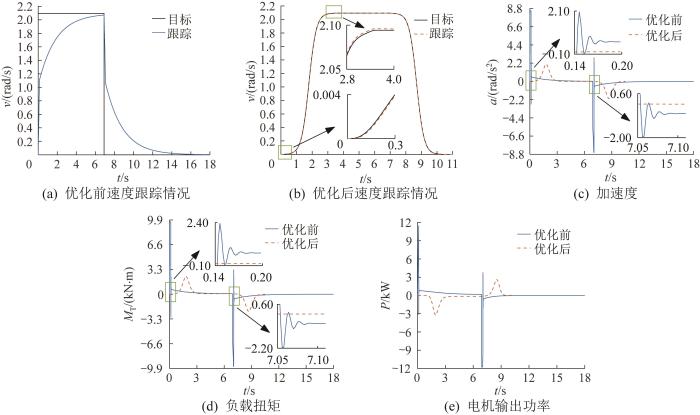
将式(32)的最终解代入式(19)，可得主轴的改进速度曲线 $v (t)$ ，并通过 $v (t)$ 与减速比i_T相乘得到优化后电机的速度曲线 $v_{d} (t)$ ，作为PI（proportional-integral，比例-积分）控制器的输入信号；而瞬时驱动即输入信号为v_m与减速比i_T相乘的阶跃信号。基于缠绕圈数约束进行理论计算，可得阶跃信号的时长为6.9 s。以0.002 s的采样时间对电机的速度曲线进行插值离散化，将离散化数据作为PI控制器的跟踪目标进行仿真分析，并与优化前进行对比。通过仿真可得，优化前后缠绕机的运行效果如图9所示，优化效果如表2所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 优化前后缠绕机运行效果对比

Fig.9 Comparison of operation effect of winding machine before and after optimization

表2 优化前后缠绕机运行性能对比

Table 2 Comparison of operation performance of winding machine before and after optimization

优化前后	总运行时长T_z/s	最大加速度a_max/(rad/s²)	最大负载扭矩M_{T max}/(N·m)	最大输出功率P_max/kW
改进率/%	41.7	75.8	75.5	72.8
优化前	17.98	8.552	9 650.01	11.810
优化后	10.48	2.067	2 366.78	3.211

新窗口打开| 下载CSV

由图9和表2可知：在优化前的瞬时驱动方式下，缠绕机主轴的启动与制动阶段耗时较长，总运行时长达到17.98 s，而优化后运行时长仅为10.48 s，缩短了41.7%，提高了生产效率；优化前主轴在加速和减速阶段起始时刻的加速度发生突变，冲击较大，引起局部振动，有损传动件寿命，而优化后主轴的加速度曲线连续平滑且无突变，减小了启停时的振动，其最大加速度较优化前降低了75.8%，冲击减小，使得缠绕机运行更平稳；优化前缠绕机运行中负载扭矩最大值达到9 650.01 N·m，不满足联轴器许用扭矩和主轴强度与刚度的要求，易发生传动件失效破坏，而优化后的负载扭矩最大值为2 366.78 N·m，相比优化前减小了75.5%，保证了传动件对强度与刚度的要求，且无扭矩突增现象；优化后电机系统的最大输出功率远小于瞬时驱动的情况，输出功率最大值减小了72.8%，选用价格更低的低功率电机即可满足运行需求。

5 结论

本文设计的改进型Sigmoid加减速曲线，能够消除缠绕机主轴运行曲线的加速度突变；通过对主轴运行曲线进行多目标优化，使总运行时长、最大加速度、最大负载扭矩和最大输出功率相较于优化前分别减小了41.7%，75.8%，75.5%和72.8%。结果表明，优化设计后的运行曲线可以极大地减小大转动惯量缠绕机转动过程中的负载扭矩、启停冲击和振动，使得缠绕机运行更加平稳，从而大大减小了传动件因负载扭矩过大或运行不平稳而失效的风险。

不过，在实际的控制中，加速度轨迹会受轨迹插补时间的影响，并不完全等同于速度曲线的一阶导数，后续可进一步研究实际运行中离散轨迹曲线的优化与控制。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LIU

， XU

G W

， JIANG

X M

Discrete global sliding mode control for time-delay carbon fiber multilayer diagonal loom

［J］. IEEE Access， 2017， 5： 15326-15331.