精密机床直线进给系统误差均化机理研究

doi:10.3785/j.issn.1006-754X.2023.00.023

精密机床直线进给系统误差均化机理研究

孙光明^,^,¹^,², 张大卫¹, 孙铭泽³, 徐鹏飞¹, 陈发泽¹, 李志军⁴

1.天津大学机构理论与装备设计教育部重点实验室，天津 300072

2.天津城建大学控制与机械工程学院，天津 300384

3.天津理工大学机械工程学院，天津 300082

4.天津大学内燃机燃烧学国家重点实验室，天津 300072

Research on error averaging mechanism of linear feed system for precision machine tools

SUN Guangming^,^,¹^,², ZHANG Dawei¹, SUN Mingze³, XU Pengfei¹, CHEN Faze¹, LI Zhijun⁴

1.Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education, Tianjin University, Tianjin 300072, China

2.School of Control and Mechanical Engineering, Tianjin Chengjian University, Tianjin 300384, China

3.School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300082, China

4.State Key Laboratory of Engines, Tianjin University, Tianjin 300072, China

收稿日期: 2022-07-18 修回日期: 2022-09-19

基金资助:

国家重点研发计划项目.  2018YFB1701201
天津市自然科学基金青年项目.  22JCQNJC01000
天津市企业特派员项目.  22YDTPJC00260

Received: 2022-07-18 Revised: 2022-09-19

作者简介 About authors

孙光明（1987—），男，河南驻马店人，讲师，博士，从事精密机床误差测量、分析与补偿技术研究，E-mail:gmsun@tju.edu.cn，https://orcid.org/0000-0002-0961-9964 , E-mail：gmsun@tju.edu.cn

摘要

精密机床直线进给系统的误差均化现象是机床精度设计中的重点关注问题。以精密卧式加工中心中典型的双导轨四滑块直线进给系统为研究对象，重点研究滚动导轨副几何误差与工作台运动误差之间的均化机理。首先，利用基于传递函数的等效刚度法，建立了导轨几何误差与工作台运动误差之间的映射关系，并以法向直线度误差为例揭示了误差均化机理。然后，建立了双导轨四滑块直线进给系统有限元模型，分析了导轨几何误差与工作台运动误差的均化系数。最后，开展了误差均化机理分析实验，通过测量导轨几何误差和工作台运动误差并计算误差均化系数，验证了理论分析与仿真分析的正确性。研究结果为机床的精度设计提供了理论依据。

关键词： 精密机床 ; 直线进给系统 ; 误差均化 ; 均化系数

Abstract

The phenomenon of error averaging in the linear feed system of precision machine tools is a key concern in machine tool accuracy design. Taking a typical linear feed system with double guide rails and four sliders in precision horizontal machining center as the research object, the averaging mechanism between the geometric error of rolling guide rail pair and the motion error of workbench was emphatically studied. Firstly, the equivalent stiffness method based on transfer function was used to establish the mapping relationship between the geometric error of guide rail and the motion error of workbench, and the error averaging mechanism was revealed by taking the normal straightness error as an example. Then, the finite element model of the linear feed system with double guide rails and four sliders was established, and the averaging coefficients of the geometric error of guide rail and the motion error of workbench were analyzed. Finally, an error averaging mechanism analysis experiment was conducted to verify the correctness of the theoretical analysis and simulation analysis by measuring the geometric error of guide rail and the motion error of workbench and calculating the error averaging coefficient. The research results provide a theoretical basis for the accuracy design of machine tools.

Keywords： precision machine tool ; linear feed system ; error averaging ; averaging coefficient

PDF (5153KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙光明, 张大卫, 孙铭泽, 徐鹏飞, 陈发泽, 李志军. 精密机床直线进给系统误差均化机理研究. 工程设计学报[J], 2023, 30(2): 200-211 doi:10.3785/j.issn.1006-754X.2023.00.023

SUN Guangming, ZHANG Dawei, SUN Mingze, XU Pengfei, CHEN Faze, LI Zhijun. Research on error averaging mechanism of linear feed system for precision machine tools. Chinese Journal of Engineering Design[J], 2023, 30(2): 200-211 doi:10.3785/j.issn.1006-754X.2023.00.023

直线进给系统是精密机床的重要部件之一，其运动精度直接影响整机精度^[1-3]。直线进给系统由床身、直线滚动导轨副和工作台按特定顺序装配而成^[4-5]。在装配过程中，制造误差逐渐累积和传递，但导轨安装基面—导轨—工作台的误差传递并非严格按照1∶1的比例，而是存在一个小于1的均化系数，这种现象称为误差均化作用。误差均化的机理及影响因素不明确一直是制约机床精度设计的瓶颈问题。

针对机床直线进给系统的误差均化问题，国内外学者开展了许多研究。Park等^[6-7]最早利用有限元仿真法来研究静压导轨几何误差与工作台运动误差之间的关系。Shamoto等^[8]采用半解析方法分析了由静压导轨支撑的进给系统的位姿误差与导轨直线度误差之间的关系。Park等^[9]利用基于传递函数的等效刚度法，结合静力学模型建立了静压导轨几何误差与工作台运动误差之间的数学模型，通过分析发现油膜作用力的幅值随着轮廓误差波长的增大而增大。Ekinci等^[10-11]以气浮导轨为研究对象，利用静力平衡法研究了其几何误差与工作台运动误差之间的关系。Khim等^[12]利用基于传递函数的等效刚度法，研究了由滚动导轨副支撑的进给系统的运动误差与导轨几何误差之间的关系，并提出了提高各部件运动精度的方法。薛飞等^[13-14]以静压导轨为研究对象，运用油膜厚度均化分析方法计算了不同轮廓误差分量对应的运动误差和静态均化系数，结果表明：轮廓误差分量的波长、油垫长度及运动直线度评定长度对导轨静态均化效应具有显著影响。随后，他们又计算了不同直线度误差分量对应的运动误差和静态均化系数，深入研究了导轨的几何误差形态和主要设计参数对误差均化作用的影响。Qi等^[15]提出了一种考虑三维轮廓误差的静压导轨误差均化效应分析方法，并建立了单垫和双垫静压导轨的误差均化模型，深入地分析了导轨宽度和长度方向上的轮廓误差对误差均化效应的影响。Zha等^[16]提出了一种基于误差均化效应的静压导轨运动精度公差设计方法，该方法考虑了导轨的波长、振幅和相位参数，先基于平均油膜厚度建立了导轨的运动精度分析模型，再根据导轨几何误差与工作台运动误差之间的关系，计算得到导轨的直线度误差，实现了导轨的公差设计。刘锡尧等^[17]采用有限差分法推导了气浮导轨在各个平衡位置处的力学参数，并利用最小包容法求解其运行直线度，进而建立了平面气浮导轨的物理模型。Zhao等^[18]建立了气体静压轴承的动平衡方程，并推导了其气体润滑控制方程，进而获得了该轴承在气体润滑和直接接触时的误差均化效应，结果表明：轮廓误差的波长是主要影响因素，波长越小，误差均化效果越好。He等^[19]提出了分层误差建模方法，将直线进给系统的误差分为基面层、导轨层、滑块层和工作台层等4个层面，深入研究了各层误差之间的传递机理，但未涉及误差均化的研究。Ni等^[20]以由滚动导轨副支撑的进给系统为研究对象，基于静力平衡法和传递函数法，验证了误差均化现象的存在，并阐述了误差均化产生的原因，但未对误差均化系数进行定量化研究。综上所述，目前关于机床误差均化机理的研究主要集中在静压导轨的误差均化机理上，而对滚动导轨误差均化机理的研究较少且缺乏定量分析，暂未明确误差均化系数。此外，还缺乏对误差均化作用传递规律的研究。

基于此，笔者以精密卧式加工中心中典型的双导轨四滑块直线进给系统为研究对象，从理论上建立滚动导轨几何误差与工作台运动误差之间的映射模型，以分析误差均化的机理。在此基础上，建立直线进给系统有限元模型，对误差均化机理进行仿真分析。最后，通过实验来验证理论分析和仿真分析的正确性，旨在为滚动导轨副到导轨安装基面的公差分配提供指导。

1 误差均化机理理论分析

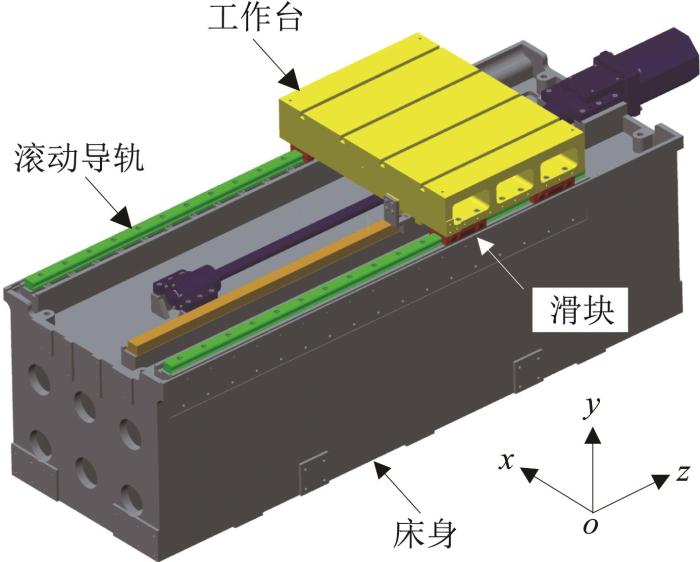
以典型的双导轨四滑块直线进给系统为研究对象，如图1所示，每条滚动导轨通过2个滑块与工作台连接，工作台在滚动导轨副的支撑下作往复直线运动。图中：x方向为工作台水平面内运动方向的垂直方向，y方向为工作台的垂直方向，z方向为工作台的运动方向。在对该直线进给系统进行理论建模时，分为单滑块误差传递建模和滚动导轨副误差均化建模两方面。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双导轨四滑块直线进给系统

Fig.1 Linear feed system with double guide rails and four sliders

1.1　导轨几何误差作用下滑块的受力分析

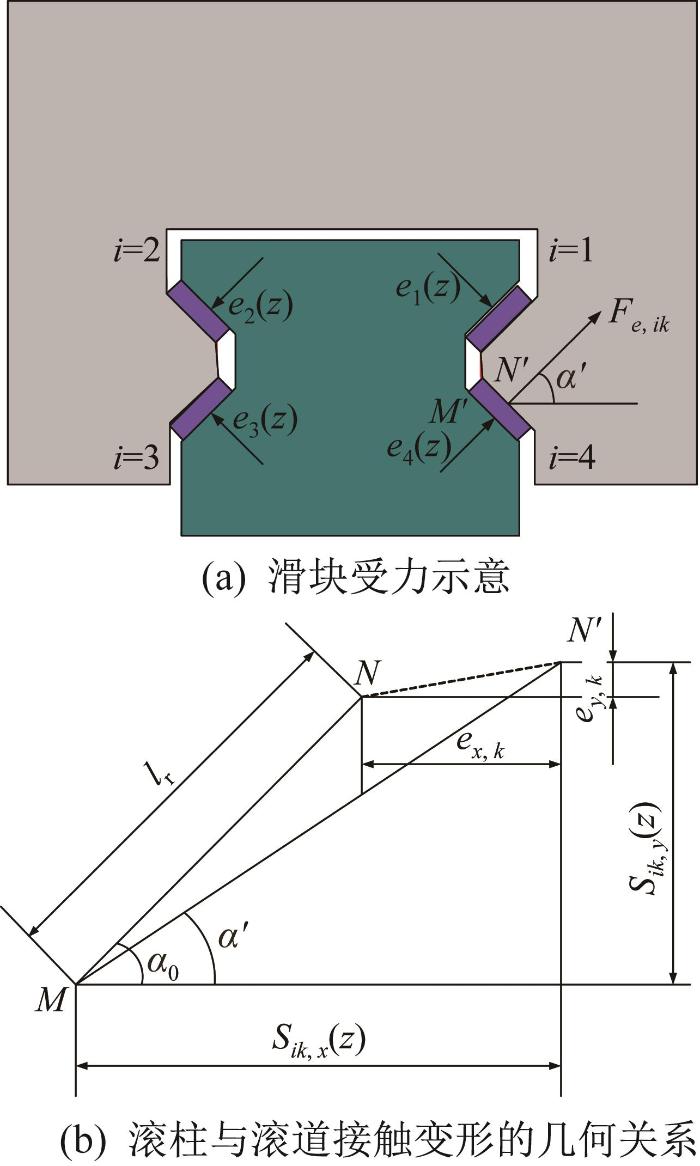
在直线进给系统运行过程中，导轨的几何误差（即直线度误差）引起滑块的受力发生变化，进而影响工作台的运动误差。在分析滑块受力时，假设导轨与滑块之间的滚柱为弹性体，其他部件为刚体。单滑块的力学模型如图2所示。图中：M和M ′分别为滚柱与导轨滚道的理想和实际接触点，在理想状态下，即各零部件无几何误差的状态下M与M ′重合；N和N ′分别为滚柱与滑块滚道的理想和实际接触点；α₀和α ′分别为理想和实际接触角；e_i $(z)$ 为导轨位置z处第i（i=1, 2, …, 4）个导轨滚道面的几何误差；e_x_,_k 、e_y_,_k 分别为第k个滚柱所在位置处的导轨几何误差在x、y方向上的分量；l_r为滚柱与导轨滚道和滑块滚道接触点的初始距离；F_e_,_ik 为第i列的第k个滚柱所受的赫兹接触力，其计算式如下^[12]：

F_{e, i k} = C {ξ_{e, i k}}^{\frac{10}{9}}

(1)

其中：

C = 3 . 81^{- \frac{10}{9}} l^{\frac{8}{9}} [\frac{E}{2 (1 - ν^{2})}]

式中： $ξ_{e, i k}$ 为第i列的第k个滚柱的弹性变形量；C为简化系数；l为滚柱的接触长度；E为弹性模量；ν为泊松比。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 单滑块力学模型

Fig.2 Single slider mechanical model

在导轨几何误差的作用下，假设弹性变形只发生在滚柱上，则可得：

e_{x} (z) = e_{i, x} (z)

(2)

e_{y} (z) = e_{i, y} (z)

(3)

\begin{array}{l} ξ_{e, i k} (z) = \sqrt[]{S_{i k, x}^{2} (z) + S_{i k, y}^{2} (z)} |c o s (α_{0} - α')| - \\ |D - p_{r}| \end{array}

(4)

其中：

S_{i k, x} (z) = l_{r} c o s α_{0} + |e_{x, k} (z)|

S_{i k, y} (z) = l_{r} s i n α_{0} + |e_{y, k} (z)|

α^{'} = a r c t a n (\frac{S_{i k, y} (z)}{S_{i k, x} (z)})

式中： $S_{i k, x} (z)$ 、 $S_{i k, y} (z)$ 为导轨几何误差作用下导轨滚道面与滑块滚道面的曲率中心在x、y方向上的相对距离；p_r为滚柱的预紧量；D为滚柱直径。

根据图2(a)，4条滚道中的滚柱均受到赫兹接触力，且上面2列（i=1, 2）滚柱的受力方向朝下，下面2列（i=3, 4）滚柱的受力方向朝上。以向上为正方向，则滑块所受的合力f_e $(z)$ 为：

f_{e} (z) = (\sum_{i = 3}^{4} \sum_{k = 1}^{n} F_{e, i k} (z) - \sum_{i = 1}^{2} \sum_{k = 1}^{n} F_{e, i k} (z)) s i n α^{'}

(5)

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 导轨几何误差作用下滑块的受力分析

Fig.3 Force analysis of slider under the action of geometric error of guide rail

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 双导轨四滑块直线进给系统静力平衡模型

Fig.4 Static balance model of linear feed system with double guide rails and four sliders

根据传递函数理论，将滑块所受的力与导轨几何误差幅值之比定义为等效刚度 $K (ω)$ ：

K (ω) = \frac{f_{e} (ω)}{e (ω)}

(6)

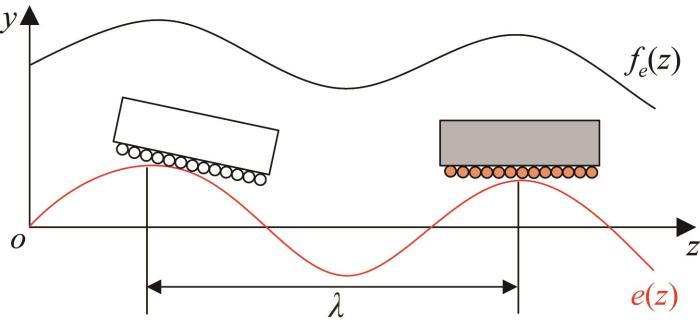
式中：ω为导轨几何误差的频率，ω=2π/λ，其中λ为导轨几何误差的波长，如图3所示。

1.2　直线进给系统误差均化建模

双导轨四滑块直线进给系统的受力状态如图4所示。

将导轨几何误差 $e (z)$ 展开为空间周期为导轨长度L的傅里叶级数：

e (z) = \sum_{t = 1}^{\infty} (a_{t} c o s \frac{2 π t}{L} z + b_{t} s i n \frac{2 π t}{L} z)

(7)

式中：a_t 、b_t 为傅里叶级数的系数。

将基于滑块中心处导轨几何误差计算得到的接触力等效为滑块的整体受力，即：

\begin{array}{l} f_{e, j} (z) = f_{e} (z + Z_{j}) = \\ \sum_{t = 1}^{\infty} K (\frac{2 π t}{L}) [a_{t} c o s \frac{2 π t}{L} (z + Z_{j}) + \\ b_{t} s i n \frac{2 π t}{L} (z + Z_{j})] \end{array}

(8)

式中: Z_j 为第j个滑块的中心到工作台中心的z向距离；f_e_,_j $(z)$ 为第j个滑块在导轨的几何误差作用下所受的力。

因此，滚动导轨副在空间中的受力平衡方程如下：

\{\begin{array}{l} \sum_{j = 1}^{4} f_{x, j} (z) = 0 \\ f_{x, j} (z) = f_{e x, j} (z) - K_{x} (0) x_{j} (z) \\ \sum_{j = 1}^{4} f_{y, j} (z) = 0 \\ f_{y, j} (z) = f_{e y, j} (z) - K_{y} (0) y_{j} (z) \\ \sum_{j = 1}^{4} (f_{x, j} (z) Y_{j} + f_{y, j} (z) X_{j}) = 0 \\ \sum_{j = 1}^{4} f_{y, j} (z) Z_{j} = 0 \\ \sum_{j = 1}^{4} f_{x, j} (z) Z_{j} = 0 \end{array}

(9)

式中：f_x_,_j $(z)$ 、f_y_,_j $(z)$ 分别为第j个滑块在x、y方向上所受的合力；f_ex_,_j $(z)$ 、f_ey_,_j $(z)$ 分别为在导轨几何误差作用下滑块在x、y方向上所受的力；K_x $(0)$ 、K_y $(0)$ 分别为滑块在x、y方向上的静刚度；x_j $(z)$ 、y_j $(z)$ 分别为导轨几何误差引起的第j个滑块在x、y方向上的位移；X_j 、Y_j 分别为第j个滑块的中心到工作台中心的x、y向距离。在已知的双导轨四滑块直线进给系统中，X_j 、Y_j 、Z_j 为常数，且因4个滑块在同一个平面上，则Y₁=Y₂=Y₃=Y₄，下文计算时统一用Y_c表示。

假设ε_x $(z)$ 、ε_y $(z)$ 和ε_z $(z)$ 分别为工作台的俯仰误差、偏摆误差和滚转误差，δ_x $(z)$ 、δ_y $(z)$ 为工作台的x、y向直线度误差，则滑块位移与工作台运动误差的关系为：

x_{j} (z) = δ_{x} (z) + Z_{j} ε_{y} (z) + Y_{c} ε_{z} (z)

(10)

y_{j} (z) = δ_{y} (z) - Z_{j} ε_{x} (z) + X_{j} ε_{z} (z)

(11)

联立式(6)至式(11)，可得工作台运动误差与导轨几何误差的关系：

ε_{x} (z) = \frac{K_{y} (ω) (- e_{y, 12} (z) + e_{y, 11} (z) + e_{y, 21} (z) - e_{y, 22} (z))}{4 |Z_{1}| K_{y} (0)}

(12)

ε_{y} (z) = \frac{K_{x} (ω) (e_{x, 12} (z) + e_{x, 11} (z) - e_{x, 21} (z) - e_{x, 22} (z))}{4 K_{x} (0) |Z_{1}|}

(13)

ε_{z} (z) = \frac{K_{y} (ω) (- e_{y, 12} (z) - e_{y, 11} (z) + e_{y, 21} (z) + e_{y, 22} (z)) |Z_{1}|}{4 K_{y} (0) X_{1}^{2}}

(14)

\begin{array}{l} δ_{x} (z) = \frac{K_{x} (ω) (e_{x, 12} (z) + e_{x, 11} (z) + e_{x, 21} (z) + e_{x, 22} (z))}{8 K_{x} (0)} + \\ \frac{K_{y} (ω) (- e_{y, 12} (z) - e_{y, 11} (z) + e_{y, 21} (z) + e_{y, 22} (z)) |Z_{1}| Y_{c}}{4 K_{y} (0) X_{1}^{2}} \end{array}

(15)

δ_{y} (z) = \frac{K_{y} (ω) (e_{y, 12} (z) + e_{y, 11} (z) + e_{y, 21} (z) + e_{y, 22} (z))}{8 K_{y} (0)}

(16)

式中：K_x $(ω)$ 、K_y $(ω)$ 为在导轨几何误差作用下导轨滑块副的x、y向等效刚度；e_x_{, 11}、e_y_{, 11}为第1条导轨上第1个滑块处的x、y向几何误差，e_x_{, 12}、e_y_{, 12}、e_x_{, 21}、e_y_{, 21}、e_x_{, 22}、e_y_{, 22}以此类推。

1.3　误差均化理论分析结果

将工作台的运动误差与导轨几何误差的比值定义为均化系数。以y向（法向）直线度误差的均化系数n_e 为例进行分析，其计算式为：

n_{e} = \frac{δ_{y} (ω)}{e_{y} (ω)}

(17)

式中： $δ_{y} (ω)$ 为工作台y向直线度误差的幅值； $e_{y} (ω)$ 为导轨y向几何误差的幅值。

1）导轨几何误差波长的影响。

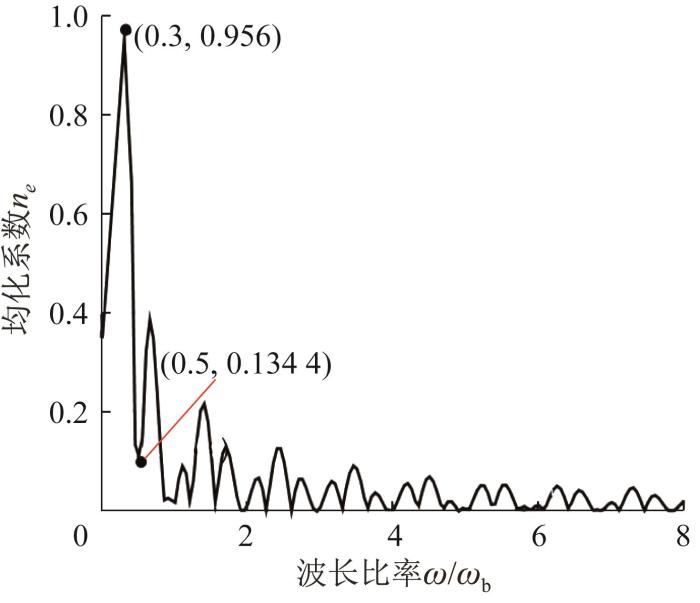
令ω_b表示波长为滑块长度l_b时所对应的频率，并将ω_b视为基准频率。利用MATLAB软件进行计算分析，得到工作台y向直线度误差的均化系数随导轨y几何误差波长比率ω/ω_b的变化规律，结果如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 导轨几何误差波长对工作台直线度误差均化系数的影响

Fig.5 Effect of wavelength of guide rail geometric error on error averaging coefficient of workbench straightness error

从图5中可以看出，当导轨y向几何误差的波长比率ω/ω_b>0.5，即λ<0.5l_b时，工作台y向直线度误差均化系数随波长比率的增大呈波动性减小；当波长比率ω/ω_b<0.5，即λ>2l_b时，y向直线度误差均化系数随波长比率的减小而增大。这是因为随着波长比率的增大，在滑块长度范围内，导轨几何误差的频率增大，且其波峰和波谷出现的次数增加，滚柱之间的受力差异减小，从而降低了滑块受力的波动性，使得工作台的直线度误差也相应减小，故均化效果变好。反之，随着波长比率的减小，滚柱之间的受力差异变大，使得工作台的直线度误差波动增大，均化效果变差。

2）导轨几何误差幅值的影响。

为研究导轨y向几何误差幅值对工作台y向直线度误差均化系数的影响，分别计算导轨y向几何误差幅值为2，5，10 μm时的均化系数，结果如图6所示。由图可知，随着导轨y向几何误差幅值的变化，工作台y向直线度误差均化系数基本没有变化，这说明导轨几何误差幅值对均化作用的影响较小。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 导轨几何误差幅值对工作台直线度误差均化系数的影响

Fig.6 Effect of amplitude of guide rail geometric error on error averaging coefficient of workbench straightness error

2 误差均化机理仿真分析

在理论建模时，假设导轨与滑块之间的滚柱为弹性体，其他部件为刚体，且弹性变形只发生在滚柱上，但这与实际状态不完全符合。因此，本节利用有限元法来分析导轨几何误差对直线进给系统误差均化作用的影响规律。

2.1　有限元建模

2.1.1　单滑块有限元建模

以THK SRG R45导轨副为分析对象，采用弹簧单元法建立单滑块有限元模型，其材料属性设置如表1所示。

表1 单滑块有限元模型材料属性设置

Table 1 Material attribute setting for single slider finite element model

参数	导轨和滑块	工作台
材料	马氏体不锈钢	QT500
密度/(g/cm³)	7.75	7.0
弹性模量/GPa	206	162
泊松比	0.3	0.293

新窗口打开| 下载CSV

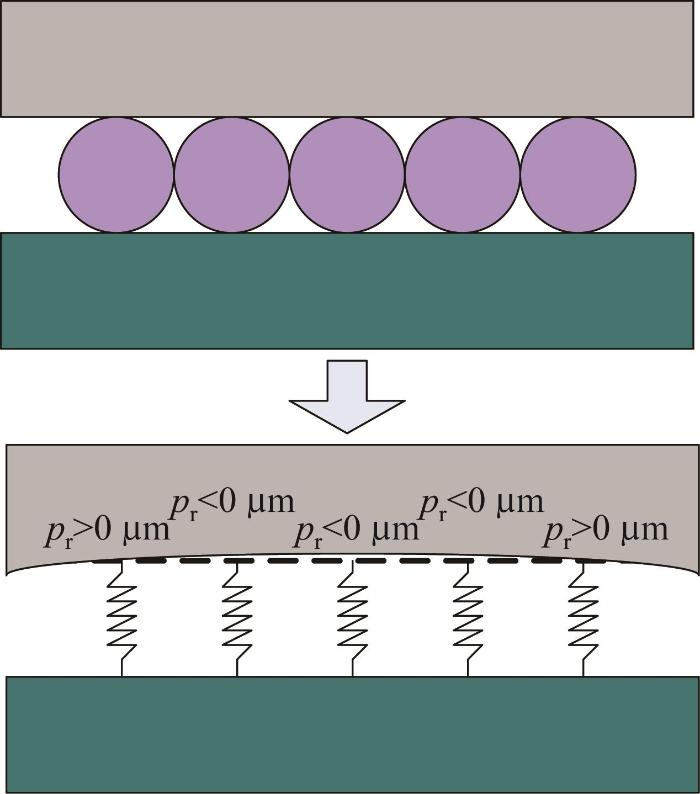
在进行单滑块有限元建模时，将滚柱等效为弹簧，通过改变弹簧的长度（即预紧量）来模拟导轨的几何误差^[21]，如图7所示。滚柱与滚道面接触的几何关系如图8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 滚柱预紧量与导轨几何误差的映射关系

Fig.7 Mapping relationship between roller pre-tightening and geometric error of guide rail

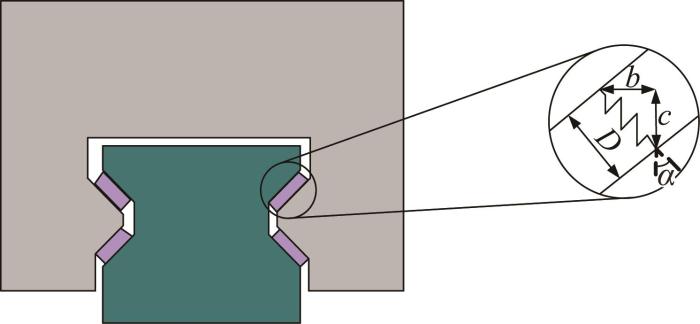
图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 滚柱与滚道面接触的几何关系

Fig.8 Geometric relationship of contact between roller and raceway surface

当预紧量p_r>0 μm时，弹簧压缩，滚柱与滚道面之间产生的预紧量为：

p_{r} = \sqrt[]{{(b + e_{x})}^{2} + {(c + e_{y})}^{2}} - D

(18)

式中：c、b分别为滚柱直径D在x、y方向上的分量。

当预紧量p_r<0 μm时，弹簧拉伸，滚柱与滚道面之间产生的预紧量为：

p_{r} = \sqrt[]{{(b - e_{x})}^{2} + {(c - e_{y})}^{2}} - D

(19)

基于弹簧单元法建立的单滑块有限元模型如图9所示。为验证所构建模型的正确性，对其进行刚度校核，并与制造商提供的刚度参数进行对比。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 基于弹簧单元法的单滑块有限元模型

Fig.9 Single slider finite element model based on spring element method

在进行滚动导轨副等效建模时，按照式(1)中导轨副受力与变形量的关系对滚柱刚度进行非线性拟合，并与制造商提供的刚度进行对比，结果如图10所示。根据拟合曲线的曲率，可得单个滚柱的接触刚度K_N=2.77×10⁵ N/mm。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 单个滚柱的接触刚度曲线对比

Fig.10 Comparison of contact stiffness curves of single roller

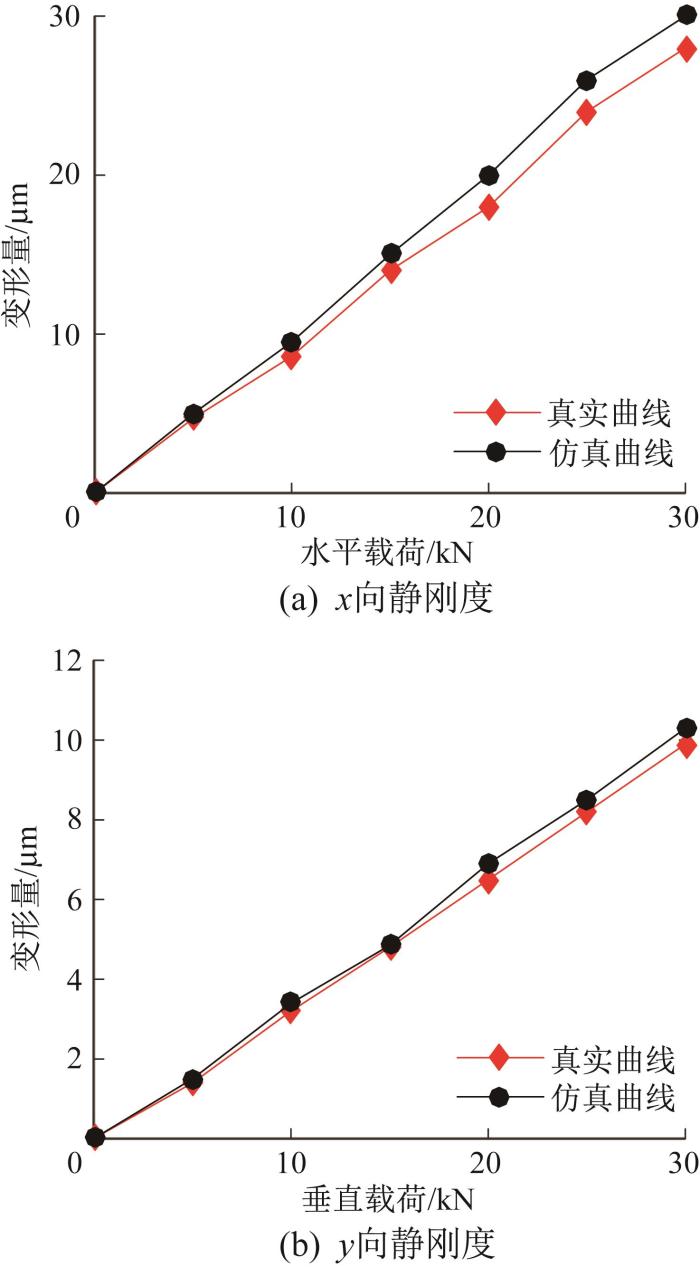
通过有限元仿真分析得到滑块的静刚度曲线，并与制造商提供的静刚度曲线进行对比，结果如图11所示。由图11可以看出，基于有限元模型计算得到的滑块静刚度与真实静刚度高度接近：在水平载荷作用下，两者的最大相对误差为11.1%；在垂直载荷作用下，两者的最大相对误差为7.1%。上述结果验证了有限元模型的正确性。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 滑块的静刚度曲线对比

Fig.11 Comparison of static stiffness curves of slider

2.1.2　直线进给系统有限元建模

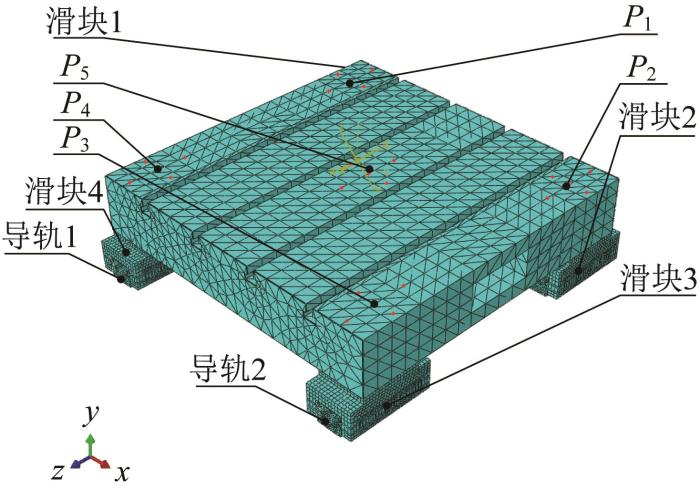
在对直线进给系统进行有限元建模时，对其关键零部件进行简化，原则是保证简化前后工作台的刚度、质量一致。所构建的双导轨四滑块直线进给系统有限元模型如图12所示，其中导轨只保留了与滑块连接的部分，在仿真分析时，以静仿动。假设工作台沿z轴正方向运动，取工作台的4个角P₁、P₂、P₃、P₄和中心P₅处的25个点，用于计算工作台的运动误差；将导轨分为8段，每隔150 mm取1个数据，每次分析共取9个数据。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 双导轨四滑块直线进给系统有限元模型

Fig.12 Finite element model of linear feed system with double guide rails and four sliders

2.2　仿真分析结果

导轨几何误差形态一般有拱形误差、单调误差和波形误差三种，如图13所示。其中：拱形误差呈抛物线分布，误差函数为g_e=± $p {(z - q)}^{2}$ +τ，分为正拱形和倒拱形两种；单调误差可看作半个拱形误差；波形误差可等效为多个拱形误差。本文以正拱形误差为例，通过改变误差函数中的参数来改变误差形态，进而分析导轨的不同几何误差形态对直线进给系统误差均化作用（以直线度误差为例）的影响。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 导轨几何误差形态示意

Fig.13 Schematic diagram of geometric error form of guide rail

1）调整系数p。

当正拱形误差函数g_e= $- p {(z - q)}^{2}$ +τ中的系数p发生变化时，拱形误差幅值会发生变化。调整系数p（令p=-1.372 6 $\times$ 10^-8，-1.143 9 $\times$ 10^-8，-9.151 0 $\times$ 10^-9），并保持q=0，τ=0.010不变，通过有限元仿真得到对应的导轨几何误差形态，结果如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同系数p对应的导轨几何误差形态

Fig.14 Geometric error forms of guide rail corresponding to different coefficients p

通过有限元仿真分析可得，3种不同系数p对应的导轨几何误差形态下工作台的直线度误差如图15所示。由图15(a)可知，3种误差形态下工作台x向直线度误差的均化系数分别为0.256 6，0.256 4，0.258 2；由图15(b)可知，3种误差形态下工作台y向直线度误差的均化系数分别为0.439 1，0.427 3，0.471 1。综上可知，改变导轨几何误差的幅值，工作台x向直线度误差的均化系数保持在0.25左右，y向直线度误差的均化系数保持在0.45左右，均化系数基本没有变化，与理论分析结果一致。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 系数p对工作台直线度误差的影响

Fig.15 Influence of coefficient p on straightness error of workbench

2）调整系数q。

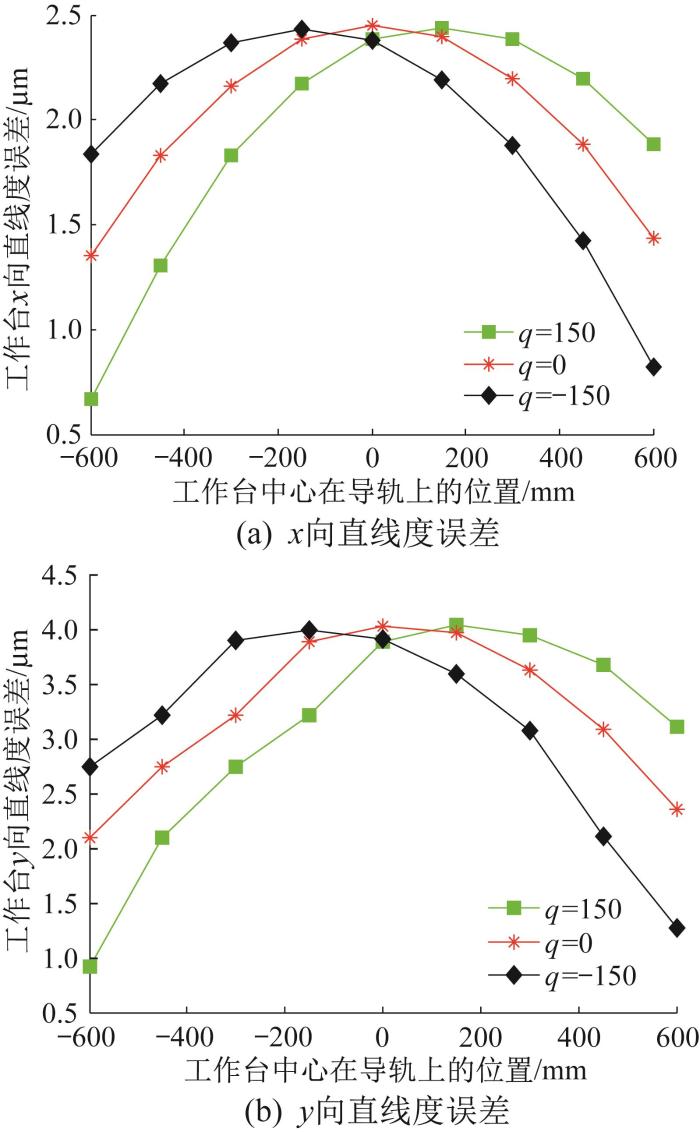
调节正拱形误差函数g_e=± $p {(z - q)}^{2}$ +τ中的系数q时，拱形误差会产生左右偏置，其幅值会发生变化。调整系数q（令q=150，0，-150），并保持p=-1.143 9 $\times$ 10^-8，τ=0.010不变，通过有限元仿真分析得到对应的导轨几何误差形态，结果如图16所示。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 不同系数q对应的导轨几何误差形态

Fig.16 Geometric error forms of guide rail corresponding to different coefficients q

通过有限元仿真分析可得，3种不同系数q对应的导轨几何误差形态下工作台的直线度误差如图17所示。由图17(a)可知，3种误差形态下工作台x向直线度误差的均化系数分别为0.270 1，0.256 4，0.254 3；由图17(b)可知，3种误差形态下工作台y向直线度误差的均化系数分别为0.456 8，0.438 7，0.463 0。综上可知，通过改变系数q来调整导轨几何误差幅值时，工作台直线度误差均化系数的仿真结果基本保持不变，与理论分析结果一致。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 系数q对工作台直线度误差的影响

Fig.17 Influence of coefficient q on straightness error of workbench

3) 调整系数τ。

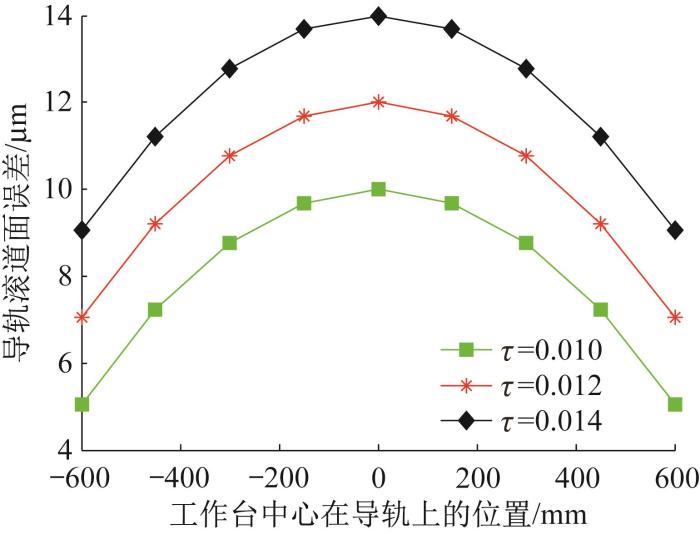
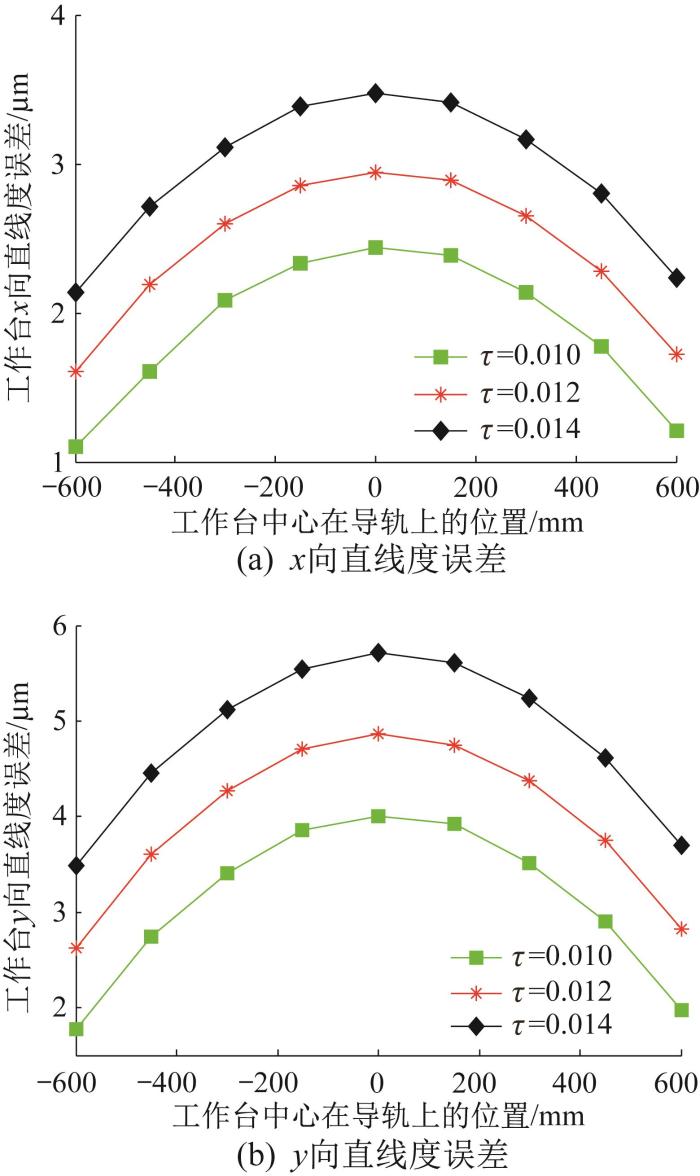
当正拱形误差函数g_e=± $p {(z - q)}^{2}$ +τ中的系数τ发生变化时，拱形误差的幅值不变。调整系数τ（令τ=0.010，0.012，0.014），并保持p=-1.143 9 $\times$ 10^-8，q=0不变，通过有限元仿真分析得到对应的导轨几何误差形态，结果如图18所示。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 不同系数 τ 对应的导轨几何误差形态

Fig.18 Geometric error forms of guide rail corresponding to different coefficients τ

通过有限元仿真分析可得，3种不同系数τ对应的导轨几何误差形态下工作台的直线度误差如图19所示。由图19(a)可知，3种误差形态下工作台x向直线度误差的均化系数分别为0.260 4，0.257 9，0.259 9；由图19(b)可知，3种误差形态下工作台y向直线度误差的均化系数分别为0.430 7，0.432 1，0.429 1。综上可知，当改变系数τ时，工作台x、y向直线度误差均化系数的仿真结果均变化不大，与理论分析结果一致。

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 系数 τ 对工作台直线度误差的影响

Fig.19 Influence of coefficient τ on straightness error of workbench

3 实验验证

3.1　实验装置

在自行设计的直线进给系统误差均化机理分析实验台上开展实验。实验台的具体参数如表2所示，其中导轨型号为SRG45R2QZZZCO+1650LSR-Ⅱ。实验中所采用的仪器和工具如表3所示。实验共开展2次，以验证导轨几何误差幅值对直线进给系统误差均化作用的影响规律。在实验过程中，通过刮研导轨基面来改变导轨的几何误差幅值。

表2 误差均化机理分析实验台参数 (mm)

Table 2 Parameters of experimental platform for error averaging mechanism analysis

参数	数值
床身	1 800×600×485
工作台	570×550×102
导轨跨距	474
滑块间距	443

新窗口打开| 下载CSV

表3 误差均化机理分析实验所用仪器及工具

Table 3 Instruments and tools used in error averaging mechanism analysis experiment

仪器及工具	用途	备注
光电准直仪	用于测量导轨安装基面、滑块面和工作台的直线度误差	AIM系列，分辨率为0.01 $''$ ，精度为0.1 $''$
扭矩扳手	对导轨的固定螺栓施加规定的拧紧力矩	力矩为5~60 Nm
水平仪	平行度测量和角度调整	0.02 mm/m

新窗口打开| 下载CSV

3.2　实验结果

在不同的实验条件下，采用光电准直仪对左导轨、右导轨和工作台的直线度误差分别进行测量，测量现场如图20所示。

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 导轨和工作台的直线度误差测量现场

Fig.20 Measurement site of straightness error of guide rail and workbench

1）第1次实验结果。

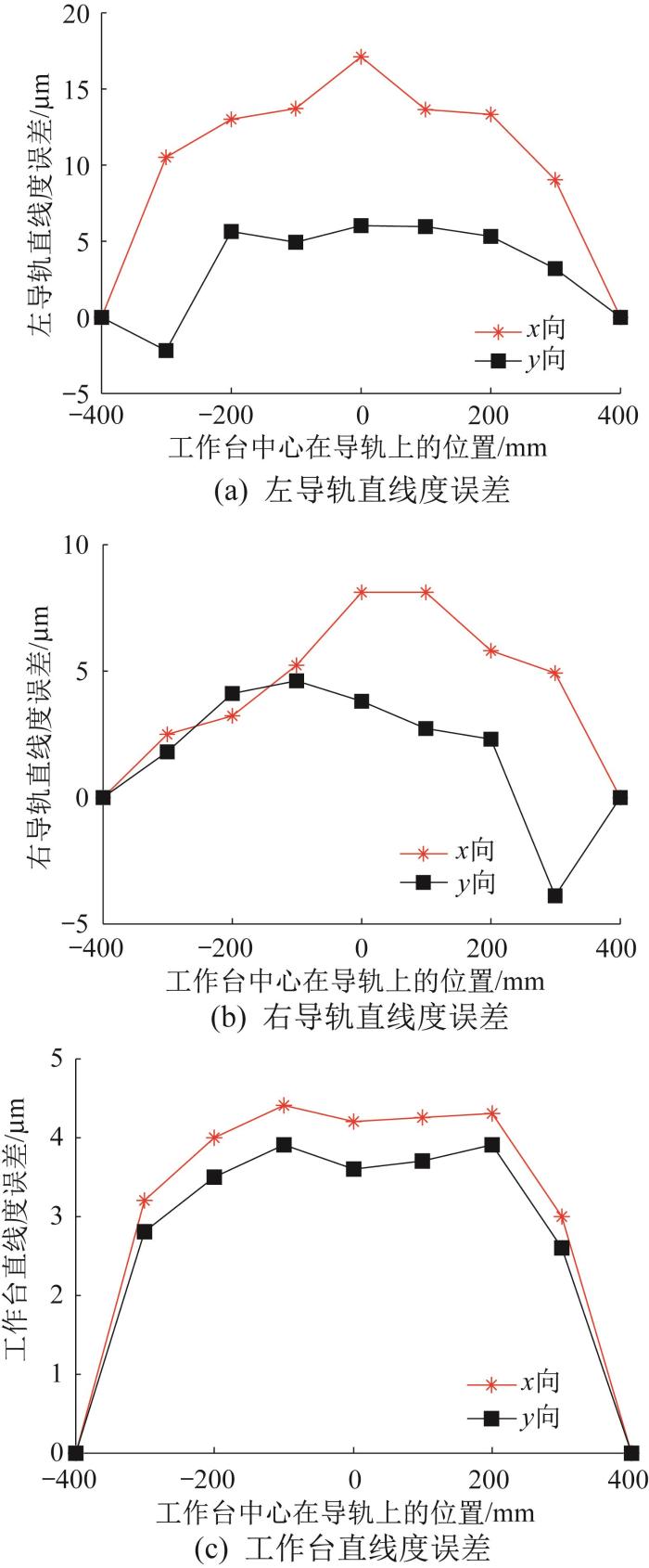
在气温为18.82 ℃，气压为100.801 kPa，相对湿度为46.74 %，材料温度为19.12 ℃的条件下开展第1次测量实验，得到的左导轨、右导轨和工作台的直线度误差如图21所示。根据测量数据，得到直线进给系统的误差传递关系，如表4所示。

图21

新窗口打开| 下载原图ZIP| 生成PPT

图21 导轨和工作台的直线度误差测量结果（第1次实验）

Fig.21 Measurement results of straightness error of guide rail and workbench (1st experiment)

表4 第1次实验中直线进给系统的误差传递情况 (μm)

Table 4 Error transmission of linear feed system in the first experiment

部件	直线度误差
部件	x向	y向
左导轨	6.600	6.100
右导轨	13.700	8.100
导轨副	10.150	7.100
工作台	2.820	3.070

新窗口打开| 下载CSV

利用上述实验数据计算得到x、y向直线度误差的均化系数，并对比实验结果与仿真结果，如表5所示。由表5可以看出，x、y向直线度误差的均化系数分别为0.278和0.432，第1次实验的结果与仿真结果高度接近，验证了仿真分析的正确性。

表5 直线度误差均化系数的实验与仿真结果比较（第1次实验）

Table 5 Comparison of experimental and simulation results of straightness error averaging coefficient (1st experiment)

比较项	直线度误差均化系数
比较项	x向	y向
相对误差/%	6.9	5.4
仿真值	0.260	0.410
实验值	0.278	0.432

新窗口打开| 下载CSV

2）第2次实验。

在气温为18.09 ℃，气压为100.791 kPa，相对湿度为39.71 %，材料温度为18.34 ℃的条件下，对左导轨、右导轨以及工作台的直线度误差分别进行测量，测量结果如图22所示。根据测量数据，得到直线进给系统的误差传递情况，如表6所示。

图22

新窗口打开| 下载原图ZIP| 生成PPT

图22 导轨和工作台的直线度误差测量结果（第2次实验）

Fig.22 Measurement results of straightness error of guide rail and workbench (2nd experiment)

表6 第2次实验中直线进给系统的误差传递情况 (μm)

Table 6 Error transmission of linear feed system in the second experiment

部件	直线度误差
部件	x向	y向
左导轨	19.470	8.050
右导轨	9.530	8.220
导轨副	14.500	8.135
工作台	4.830	4.160

新窗口打开| 下载CSV

利用上述实验数据计算得到x、y向直线度误差的均化系数，并对比实验结果与仿真结果，如表7所示。由表7可以看出，x、y向直线度误差的均化系数分别为0.333和0.511，第2次实验的结果与仿真结果有一定的误差，但在数值上仍高度接近，同样验证了仿真分析的正确性。

表7 直线度误差均化系数的实验与仿真结果比较（第2次实验）

Table 7 Comparison of experimental and simulation results of straightness error averaging coefficient (2nd experiment)

比较项	直线度误差均化系数
比较项	x向	y向
相对误差/%	28.1	24.6
仿真值	0.260	0.410
实验值	0.333	0.511

新窗口打开| 下载CSV

通过2次实验分析可知：x向直线度误差的均化系数为0.278~0.333；y向直线度误差的均化系数为0.432~0.511，且随着导轨直线度误差幅值的变化，均化系数的变化不大，这与仿真结果基本一致，验证了理论分析和仿真分析的正确性。

4 结论

误差均化是在机床精度设计过程中必须关注的重要问题。本文以典型的双导轨四滑块直线进给系统为研究对象，从理论建模、仿真分析和实验验证等方面深入研究了误差均化机理及其影响因素，得到以下结论。

1）直线进给系统误差均化的内在机理为：在导轨几何误差作用下，系统中各零部件产生的弹性变形抵消了一部分导轨几何误差，致使滑块与工作台所承受的作用力减小，从而使得工作台的运动误差幅值小于导轨的几何误差幅值。

2）随着导轨几何误差幅值的增大，工作台的运动误差增大，但误差均化系数基本没有变化。

3）在相同导轨几何误差的作用下，工作台x向运动误差的均化系数小于y向。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LIU

， CHEN

M S

， SUN

Y W

Global toolpath modulation-based contour error pre-compensation for multi-axis CNC machining

［J］. The International Journal of Advanced Manufacturing Technology， 2023， 125（7/8）： 3171-3189.