随着集成电路工艺特征尺寸的缩小和芯片中器件面积的减小,电路布线所占面积增大.多值逻辑电路因携带的信息密度较高,可减少电路连线,节省芯片面积.因此,研究多值逻辑电路与系统设计具有重要意义.文献[1]基于多值代数提出了用于多值数字电路设计的CMOS门通用集,并应用于四路选择器和四值触发器的设计与实现.文献[2]利用多值逻辑(四值逻辑)模代数运算,提出模4中的算术运算及其CMOS电路实现. CMOS动态三值逻辑电路[3]、纳米场效应管三值逻辑门和算术运算电路[4]、纳米场效应管三值全加器电路[5]、单电子晶体管(single electron transistor,SET)和MOSFET组合构成的多值逻辑电路和存储电路[6],受到了较多关注.目前,多值逻辑CMOS集成电路由二值CMOS集成电路实现.文献[7]提出了一种新的CMOS传输管逻辑电路和互补CMOS逻辑电路混合型的高速CMOS二值全加器电路.三值T门是一种通用逻辑模块(器件),利用三值T门模块可实现任意三值逻辑函数.根据多值逻辑电路设计原理[8],将三值T门电路分为阈门逻辑电路和三值逻辑信号传输电路两部分.用CMOS传输门可构成三值T门的信号传输电路部分.阈门逻辑电路可将三值逻辑信号转换为二值逻辑信号,并作为CMOS传输门的栅极信号.基于上述原理,本文提出了三值T门模块电路的设计,该模块是用二值CMOS管设计的,其三值信号传输部分由CMOS传输门实现,阈值逻辑信号产生部分由互补CMOS电路实现,即采用混合型逻辑电路构建.不同于文献[8]提出的三值T门电路,本文提出的三值T门电路未用变阈值MOS管.
三值T门逻辑网络的化简(最小化)及其计算机算法,是三值逻辑电路与系统领域一个重要的研究课题.文献[9]提出了基于多值T门组合电路模块分解方法的多值T门电路化简方法.文献[10]研究了三值逻辑函数简化的不相交积之和(reduced disjoint sum-of-products,RDSOP)形式的代数理论,提出采用混合控制变量排序的三值T门组合网络的化简和设计的一种代数方法.但在该文给出的算法的第2步,求取待实现函数在其变量集上合适的划分,缺少相关定理和选取依据.本文基于三值逻辑函数RDSOP形式的代数理论,讨论求取待实现函数在其变量集上选取合适划分的相关定理及其选取依据,提出三值T门组合网络设计(化简)的一种混合控制变量排序算法,该算法可使待设计的三值T门网络最小化,易实现三值T门组合网络的自动综合.将该三值T门模块用于三值T门网络的仿真实验,结果表明,该三值T门网络的逻辑功能正确,算法有效.
1 三值格代数系统和三值T代数系统的基本运算和定理设逻辑值集合为L={0,1,2},全序关系为2 > 1 > 0.对于变量x, y∈L及常量j∈L,引进具有补运算的三值格代数系统,“或”(取大)、“与”(取小)、“阈”(文字)3种基本运算和补运算[8],分别为
| $ \left\{ \begin{array}{l} x + y \buildrel \Delta \over = \max \left( x,y \right),x\cdot y\triangleq \min \left( x,y \right),\\ {}^j{x^j} \buildrel \Delta \over = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 2,\\ 0, \end{array}&\begin{array}{l} 当\;x = j,\\ 当\;x \ne j, \end{array} \end{array}} \right. \end{array} \right. $ | (1) |
| $ \bar x \buildrel \Delta \over = 2 - x,x \in L, $ | (2) |
式中,符号“-”为算术减法运算,符号“·”可以省略.式(1)的3种基本运算已构成代数完备系统,即三值格代数系统.由式(1)和式(2)组成含有冗余运算的三值格代数系统.在该代数系统中,0与2互补,1自补.为了简化符号,常将jxj简记为xj.由式(1)和式(2),易证得下述性质:
| $ {x^i} \cdot {x^j} = 0,i \ne j;i,j \in L, $ |
| $ {x^0} + {x^1} + {x^2} = 2, $ |
| $ x = 0 \cdot {x^0} + 1 \cdot {x^1} + 2 \cdot {x^2} = 1 \cdot {x^1} + {x^2}, $ |
| $ \overline {{x^0}} = {x^1} + {x^2},\overline {{x^1}} = {x^0} + {x^2},\overline {{x^1}} = {x^0} + {x^1}, $ |
注意到,在该代数系统中,一元运算x, x0, x1, x2已不是相互独立的运算.x,x0,
三值T门实现的T运算(T算子)定义为[9]
| $ T\left( {{f_0},{f_1},{f_2};x} \right) = {f_i},x = i, $ | (3) |
式中x, fi∈{0, 1, 2},其中x为T门的控制(地址)变量,fi, 0≤i≤2为T门的数据输入.式(3)所示的T运算构成一个代数完备系统,即三值T代数系统.在三值格代数系统中,式(3)可表示为
| $ T\left( {{f_0},{f_1},{f_2};x} \right) = {f_0} \cdot {x^0} + {f_1} \cdot {x^1} + {f_2} \cdot {x^2}. $ | (4) |
在三值格代数系统中,设有一个定义在变量集X={x1, x2, …, xn}上的n变量三值函数f(X)∈{0, 1, 2},其中xi∈{0, 1, 2},1≤i≤n.变量集X上各变量重新排序后取划分为
| $ \prod\limits_{{i_2} \cdots {i_n}} { = \left\{ {{x_{{i_1}}};{x_{{i_2}}}, \cdots ,{x_{{i_n}}}} \right\}} = \left\{ {{B_1};{B_2}} \right\}, $ | (5) |
式中,is∈{1, 2, …, n}, 1≤s≤n, X的子集B1和B2称为划分块,满足B1∩B2=
| $ f = {f_{x_{{i_1}}^0}} \cdot x_{{i_1}}^0 + {f_{x_{{i_1}}^1}} \cdot x_{{i_1}}^1 + {f_{x_{{i_1}}^2}} \cdot x_{{i_1}}^2, $ | (6) |
式(6)为推广的展开定理,其中fxi10, fxi11, fxi12分别为函数f关于xi10, xi11, xi12的函数限制[11](又称为剩余子函数),xi1称为限制变量.fxi10, fxi11, fxi12分别为变量xi1被赋值0,1,2时所得的f值,即
| $ {f_{x_{{i_1}}^0}} = f\left| {_{{x_{{i_1}}} = 0}} \right.,{f_{x_{{i_1}}^1}} = f\left| {_{{x_{{i_1}}} = 1}} \right.,{f_{x_{{i_1}}^2}} = f\left| {_{{x_{{i_1}}} = 2}} \right.. $ | (7) |
定义1 对于三值格代数系统,一个定义在变量集X={x1, x2, …, xn}上的n变量三值函数f及定义在X的子集{xi1, xi2, …, xil}上的积项p=xi1ji1 xi2ji2…xiljil,其中jis∈{0, 1, 2}, i1≤is≤il, 求函数f关于积项p的函数限制的运算,称为限制运算,定义为
| $ {f_p} = {f_{x_{{i_1}}^{{j_{{i_1}}}}x_{{i_2}}^{{j_{{i_2}}}} \cdots x_{{i_l}}^{{j_{{i_l}}}}}} = f\left| {_{{x_{{i_1}}}{x_{{i_2}}} \cdots {x_{{i_l}}} = {j_{{i_1}}}{j_{{i_2}}} \cdots {j_{{i_l}}}}} \right.. $ | (8) |
定义2 变量集X={x1, x2, …, xn}上某个变量xi(i∈{1, 2, …, n})的文字xij(j∈L, 当j=0, 1, 2时分别为xi0, xi1, xi2)之剩余文字xij′定义为xij′∈{xij′|j′∈L, j′≠j},即
| $ x_i^{0'} \in \left\{ {x_i^1,x_i^2} \right\},x_i^{1'} \in \left\{ {x_i^0,x_i^2} \right\},x_i^{2'} \in \left\{ {x_i^0,x_i^1} \right\}. $ | (9) |
三值函数中所含变量的个数n定义为该函数的Ln空间(超立方体)的维数,称为该函数的维数,并称该函数为n维函数.一个n维函数在空间Ln上共有3n个点.每个点的变量取值,对应于相应文字组成的最小项.函数值为0的点(0值点)对应的最小项(0值最小值)在该函数表达式中可以不列出.1值点和2值点分别对应于该函数所含的1值最小项和2值最小项.用该函数中全部最小项表示的式子称为该函数的最小项表达式,其中,0值最小值可忽略不计.最小项表达式也称最小项展开式,可通过对该函数的每个变量依次利用推广的展开定理即式(6)展开得到.例如,一个二变量三值函数的最小项表达式为
| $ \begin{array}{l} f\left( {{x_1},{x_2}} \right) = {a_0} \cdot {m_0} + {a_1} \cdot {m_1} + \cdots + {a_8} \cdot {m_8} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;f\left( {0,0} \right) \cdot {x_1}^0{x_2}^0 + f\left( {0,1} \right) \cdot {x_1}^0{x_2}^1 + \cdots + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;f\left( {2,2} \right) \cdot {x_1}^2{x_2}^2, \end{array} $ |
式中,x1, x2, f(x1, x2)∈L={0, 1, 2},该函数可用二维平面中的点表示,如图 1所示,其中0值最小值可省略.

|
图 1 二变量函数的平面图形表示 Fig. 1 The plane graphic representation of the two variable functions |
对于定义在变量集X={x1, x2, …, xn}上的n变量三值函数f,将X中的变量排序后划分为
| $ \prod\limits_{{i_{t + 1}} \cdots {i_n}} { = \left\{ {{x_{{i_1}}},{x_{{i_2}}}, \cdots ,{x_{{i_l}}};{x_{{i_{l + 1}}}}, \cdots ,{x_{{i_n}}}} \right\}} = \left\{ {{B_1};{B_2}} \right\}, $ | (10) |
对子集B1中的每个变量,依次利用推广的展开定理即式(6),可导出该函数按照划分式(10)的展开式为
| $ f = \sum\limits_{r = 0}^{{3^l} - 1} {{f_{{p_r}}} \cdot {p_r}} , $ | (11) |
式中,积项pr=xi1ji1 xi2ji2…xiljil,fpr为函数f关于积项pr的函数限制,r为l重组(ji1, ji2, …, jil)的取值组成的三进制数的十进制数表示.在式(11)中,由于各积项pr,0≤r≤3l-1,是互不相交的;由式(8)可得,相应的各函数限制fpr(0≤r≤3l-1)是互不相交的.因此,各积项fpr·pr的最小项集合是互不相交的.将具备条件:fpr∈{0, 1, 2, xg},xg∈B2的函数限制称为平凡子函数(trivial sub-function,TS).此时, 式(11)中相应的积项d·pr称为d值积项,d∈{0, 1, 2, xg}.
在一个n变量三值函数的RDSOP形式[10]中,一个积项p所含该函数的最小项数目称为该函数的尺度(大小),用符号“‖p‖”表示.例如,一个文字xij,j∈{0, 1, 2},i∈{1, 2, …, n},所含该函数的最小项数目为‖xij‖=3n-1.
定理1[10] 一个定义在变量集X={x1, x2, …, xn}上的三值函数f及X上的一个划分式(10),在函数f的一个RDSOP形式[10]中,若有一个d值积项d·pk,其中d∈{1, 2},pk∈pr,pr=(xi1ji1, xi2ji2, …, xiljil),jis∈{0, 1, 2},i1≤is≤il,0≤r≤3l-1, 则函数f关于pk的函数限制fpk=d的充分必要条件为
| $ \left\| {\left( {d \cdot {p_k}} \right)} \right\| = {3^{n - l}}. $ |
证明 充分性.当d∈{1, 2}时,积项d·pk所表示的函数f的最小项集合有3n-l个最小项,即‖(d·pk)‖=3n-l.由该RDSOP形式中每个积项的最小项集合互不相交,可知该RDSOP形式中除d·pk外,其余每个积项中都至少有一个文字出现在剩余文字集合{xi1j′i1, xi2j′i2, …, xilj′il}中.由式(8)可求得,当xi1 xi2…xil=ji1ji2…jil时,该RDSOP形式中有一积项pk=2,其余积项均为0,故得fpk=d.
必要性.若fpk=d∈{1, 2},由式(8)可知,fpk中只含除pk中l个不同变量外的其余变量,共(n-l)个变量,组成3n-l个子最小项,且这些子最小项之和为2.而将积项fpk·pk展开成f的最小项之和为fpk·pk=d·2·pk,将该式右边的逻辑值2以上述3n-l个子最小项之和代入后,可得该积项d·pk含有函数f的3n-l个d值最小项,即‖(d·pk)‖=3n-l.证毕.
定理2[10] 一个定义在变量集X={x1, x2, …, xn}上的三值函数f及X上的一个划分式(10),在函数f的RDSOP形式[10]中,若有一个积项d·pk=xg· pk,其中pk∈pr,pr=(xi1ji1, xi2ji2, …, xiljil),jis∈{0, 1, 2},i1≤is≤il,0≤r≤3l-1,xg为函数f中除pk中各不同文字外的一个变量.则函数f关于pk的函数限制fpk=xg的充分必要条件为
| $ \left\| {\left( {{x_g} \cdot {p_k}} \right)} \right\| = {3^{n - l}}. $ |
证明 充分性.当d=xg时,xg·pk=0·pkxg0+1·pkxg1+2·pkxg2,而积项0·pkxg0, 1·pkxg1和2·pkxg2均含有该函数f的3n-l-1个最小项,故得‖(xg·pk)‖=3n-l,其中0·pkxg0表示f的3n-l-1个0值最小项不在此RDSOP形式中.同样, 利用RDSOP形式中各积项的不相交性,由式(8)可求得
| $ {f_{{p_k}}} = 0 \cdot x_g^0 + 1 \cdot x_g^1 + 2 \cdot x_g^2 = {x_g}. $ |
必要性.若fpk=d=xg,则得积项xg·pk=0·pkxg0+1·pkxg1+2·pkxg2,同理可知,积项0·pkxg0, 1·pkxg1和2·pkxg2分别含有函数f的0值,1值和2值最小项的个数均为3n-l-1.故得
| $ \begin{array}{l} \left\| {\left( {{x_g} \cdot {p_k}} \right)} \right\| = \left\| {\left( {0 \cdot {p_k}x_g^0} \right)} \right\| + \left\| {\left( {1 \cdot {p_k}x_g^1} \right)} \right\| + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {\left( {2 \cdot {p_k}x_g^2} \right)} \right\| = {3^{n - l}}, \end{array} $ |
其中0·pkxg0表示函数f的3n-l-1个0值最小项不在此RDSOP形式中.证毕.
推论1 一个定义在变量集X={x1, x2, …, xn}上的三值函数f及X上的划分式(10),在函数f的RDSOP形式中,若有da值积项pa,da·pa=da· (xi1ji1, xi2ji2, …, xiljil),其中,jis∈{0, 1, 2},i1≤is≤il,da∈{1, 2, xga}, xga∈B2,且满足‖(da·pa)‖≥‖(dq·pq)‖, 1≤q≤m,其中m为该RDSOP形式中除积项da·pa外其余dq值积项的数目,dq∈{1, 2, xgq}, xgq为集合X除pq中所含文字外的一个变量.则按照划分式(10),将该函数f按式(11)展开(分解)所得到的各函数限制中,有平凡子函数fpa=da.
证明 由式(11)、定理1和定理2,可推得该推论成立.
需注意,对某个(或某些)pq,若有‖(da·pa)‖= ‖(dq·pq)‖,可推得fpq=dq为平凡子函数,此时,pq中变量集X含有不同文字的数目也为l个.
推论2 一个定义在变量集X={x1, x2, …, xn}上的三值函数f及X上的一个划分式(10),在函数f的RDSOP形式中,若有积项pb=(xi1ji1, xi2ji2, …, xiljil),其中jis∈{0, 1, 2},i1≤is≤il,该积项不含在该RDSOP形式中,或‖(0·pb)‖=3n-l,并且在该RDSOP形式中,其余每个关于该划分式(10)的积项都至少含有一个文字属于剩余文字集合{xi1j′i1, xi2j′i2, …, xilj′il},则得fpb=0.
证明 由式(11)和定理1,可推得该推论成立.
由推论1和推论2,求得平凡子函数的维数为(n-l),称之为(n-l)维平凡子函数.可以看出,平凡子函数的维数越高,对T门网络化简越有利.对于混合控制变量排序算法,T门网络化简(最小化)目标是在待实现函数的每级网络中,使待实现函数按照扩展的展开定理即式(6)展开后得到的非平凡子函数类型(nontrivial sub-function patterns,NTSP)的数目最小,此时得到的T门网络称为最小化T门网络.
2 三值T门组合网络设计实例 2.1 三值T门组合网络设计步骤Step 1 将待实现的函数化为RDSOP形式.并对所用T门数目的变量num赋初值num:=1.
Step 2 由推论1和推论2,求取该函数变量集X上(或求取该函数每个不能用单个T门实现的非平凡子函数关于X的子集上)合适的划分,使函数(或相关子函数)按照扩展的展开定理即式(6)展开后得到的非平凡子函数类型数目最小(min).
Step 3 利用限制运算,按照所选划分,求出各函数限制.检验各函数限制是否能用单个T门实现:“N”(非平凡子函数类型的序数)表示不能用单个T门实现,“S”(非平凡子函数类型的序数)表示能用单个T门实现.将表示所用T门数目的变量num之值修改为num:=num+(min).
Step 4 在求出的函数限制中,判断是否有不能用单个T门实现的非平凡子函数,若有,则重复step2~step3.否则,输出设计结果.该算法的程序流程图如图 2所示.

|
图 2 算法流程图 Fig. 2 Flow-process diagram of algorithm |
例 用三值T门通用逻辑模块实现4变量函数f的最小化T门网络:
| $ \begin{array}{l} f = 1 \cdot \sum {\left( {1,12,13,14,15,16,17,25,28,30,36,} \right.} \\ \;\;\;\;\;\;39,42,43,44,45,46,48,50,52,55,69,70,71,\\ \;\;\;\;\;\;\left. {72,77,79} \right) + 2 \cdot \sum {\left( {6,7,8,21,22,23,26,32,} \right.} \\ \;\;\;\;\;\;33,34,35,53,54,60,61,62,66,67,68,73,\\ \;\;\;\;\;\;\left. {75,80} \right). \end{array} $ |
解 算法的执行过程如下:
Step 1 利用代数化简法[10],将待实现的函数f转化为RDSOP形式:
| $ \begin{array}{l} f = 1 \cdot x_2^1x_3^2 + 2 \cdot x_2^0x_3^2 + {x_2} \cdot x_1^0x_3^1 + 1 \cdot x_2^0x_3^0x_4^1 + \\ \;\;\;\;\;\;1 \cdot x_2^2x_3^2x_4^1 + 1 \cdot x_1^1x_3^1x_4^0 + 2 \cdot x_1^2x_2^1x_3^1 + \\ \;\;\;\;\;\;2 \cdot x_2^2x_3^2x_4^2 + {x_1} \cdot x_2^2x_3^0x_4^1 + 1 \cdot x_1^1x_2^1x_3^0x_4^0 + \\ \;\;\;\;\;\;1 \cdot x_1^1x_2^2x_3^0x_4^0 + 1 \cdot x_1^1x_2^2x_3^1x_4^2 + 1 \cdot x_1^2x_2^2x_3^0x_4^0 + \\ \;\;\;\;\;\;1 \cdot x_1^2x_2^2x_3^1x_4^2 + 2 \cdot x_1^1x_2^0x_3^1x_4^2 + 2 \cdot x_1^2x_2^0x_3^0x_4^0 + \\ \;\;\;\;\;\;2 \cdot x_1^2x_2^2x_3^1x_4^0,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{num}}: = 1. \end{array} $ | (12) |
Step 2 由最小化目标,求函数f变量集上的划分.由式(12)知,若选取划分{x2, x3; x1, x4}, 可得fx21x32=1, fx20x32=2;若选取划分{x1, x3; x2, x4},可得fx10x31=x2;若选取划分{x3, x4; x1, x2},可得fx30x42=0.可见应选择的划分为{x3; x1, x2, x4}.这样可使下一级网络中各T门数据输入连接的非平凡子函数类型数目最小,有利于T门网络最小化.
Step 3 利用限制运算求函数限制fx30,fx31和fx32.由式(12)得
| $ \begin{array}{l} {f_{x_3^0}} = 1 \cdot x_2^0x_4^1 + {x_1} \cdot x_2^2x_4^1 + 1 \cdot x_1^1x_2^1x_4^0 + \\ \;\;\;\;\;\;\;\;1 \cdot x_1^1x_2^2x_4^0 + 1 \cdot x_1^2x_2^2x_4^0 + 2 \cdot x_1^2x_2^0x_4^0,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\rm{N}},1} \right) \end{array} $ |
| $ \begin{array}{l} {f_{x_3^1}} = {x_2} \cdot x_1^0 + 1 \cdot x_1^1x_4^0 + 2 \cdot x_1^2x_2^1 + 1 \cdot x_1^1x_2^2x_4^2 + \\ \;\;\;\;\;\;\;1 \cdot x_1^2x_2^2x_4^2 + 2 \cdot x_1^1x_2^0x_4^2 + 2 \cdot x_1^2x_2^2x_4^0,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\rm{N}},2} \right) \end{array} $ |
| $ \begin{array}{l} {f_{x_3^2}} = 1 \cdot x_2^1 + 2 \cdot x_2^0 + 1 \cdot x_2^2x_4^1 + 2x_2^2x_4^2,\;\;\;\;\;\left( {{\rm{N}},3} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{num}}: = {\rm{num}} + 3. \end{array} $ |
Step 4 fx30,fx31和fx32均为不能用单个T门实现的非平凡子函数,重复step2~step3, 求得:
| $ {f_{x_3^0x_4^0}} = 1 \cdot x_1^1x_2^1 + 1 \cdot x_1^1x_2^2 + 1 \cdot x_1^2x_2^2 + 2 \cdot x_1^2x_2^0\left( {{\rm{N}},1} \right), $ |
| $ {f_{x_3^0x_4^1}} = 1 \cdot x_2^0 + {x_1} \cdot x_2^2\left( {{\rm{S}},2} \right),\;\;\;\;\;\;{f_{x_3^0x_4^2}} = 0; $ |
| $ {f_{x_3^1x_1^0}} = {x_2},\;\;\;{f_{x_3^1x_1^1}} = 1 \cdot x_4^0 + 1 \cdot x_2^2x_4^2 + 2 \cdot x_2^0x_4^2\left( {{\rm{N}},3} \right), $ |
| $ {f_{x_3^1x_1^2}} = 2 \cdot x_2^1 + 1 \cdot x_2^2x_4^2 + 2 \cdot x_2^2x_4^0\left( {{\rm{N}},4} \right); $ |
| $ \begin{array}{l} {f_{x_3^2x_2^0}} = 2,{f_{x_3^2x_2^1}} = 1,{f_{x_3^2x_2^2}} = 1 \cdot x_4^1 + 2 \cdot x_4^2 = {x_4}.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{num}}: = {\rm{num}} + 4. \end{array} $ |
Step 5 fx30x40, fx31x11, fx31x12均为不能用单个T门实现的非平凡子函数,重复step2~step3, 求得:
| $ {f_{x_3^0x_4^0x_1^0}} = 0,{f_{x_3^0x_4^0x_1^1}} = 1 \cdot x_2^1 + 1 \cdot x_2^2\left( {{\rm{S}},1} \right), $ |
| $ {f_{x_3^0x_4^0x_1^2}} = 1 \cdot x_2^2 + 2 \cdot x_2^0\left( {{\rm{S}},2} \right), $ |
| $ {f_{x_3^1x_1^1x_4^0}} = 1,{f_{x_3^1x_1^1x_4^1}} = 0,{f_{x_3^1x_1^1x_4^2}} = 1 \cdot x_2^2 + 2 \cdot x_2^0\left( {{\rm{S}},2} \right), $ |
| $ \begin{array}{l} {f_{x_3^1x_1^2x_2^0}} = 0,{f_{x_3^1x_1^2x_2^1}} = 2,{f_{x_3^1x_1^2x_2^2}} = 1 \cdot x_4^2 + 2 \cdot x_4^0\left( {{\rm{S}},3} \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{num}}: = {\rm{num}} + 3. \end{array} $ |
Step 6 在求得的函数限制中,若全为能用单个T门实现的非平凡子函数,则输出设计结果.
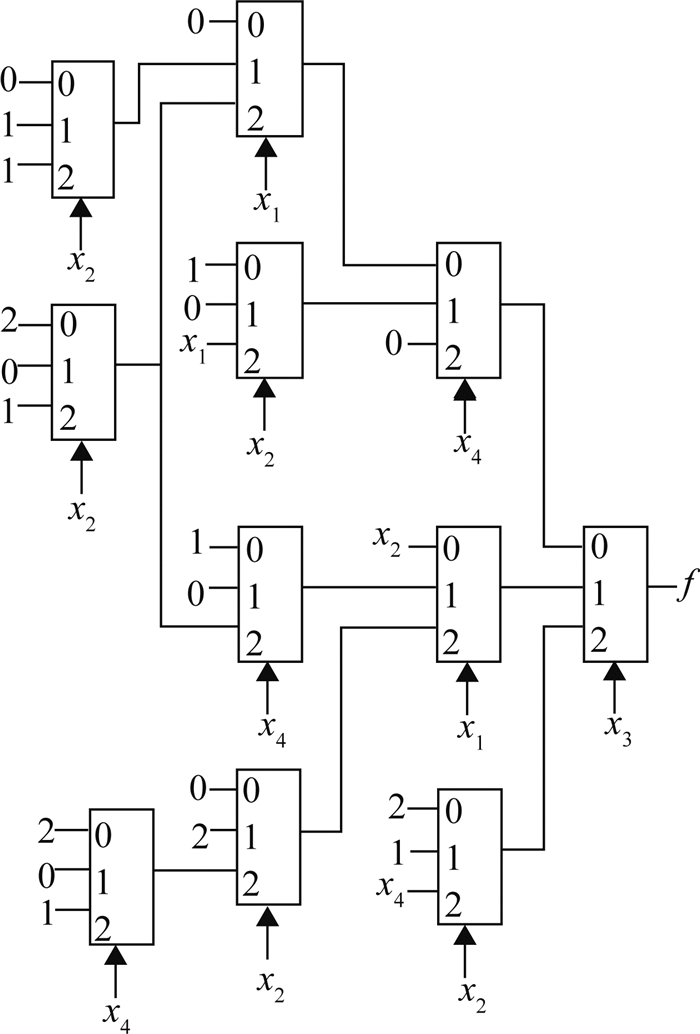
所设计的T门组合网络每级(从输出级计算)所需的T门数目分别为1,3,4,3,共需11个T门.由求得的各个函数限制作待设计的T门逻辑网络图如图 3所示.
|
图 3 实例函数的最小化T门网络实现 Fig. 3 The minimization T gate network of the implementation instance function |
利用三值格代数的基本性质和式(4),由T门逻辑模块表示的T运算(T算子)为
| $ \begin{array}{l} t = T\left( {{f_0},{f_1},{f_2};x} \right) = \\ \;\;\;\;\;\;\;{f_0} \cdot {x^0} + {f_1} \cdot \overline {{x^0}} \overline {{x^2}} + {f_2} \cdot {x^2}. \end{array} $ | (13) |
实验中的T门模块电路用CMOS管实现, 式(13)表示T门模块的逻辑表达式适合用NMOS管实现.利用PMOS管和NMOS管的互补性,可得用CMOS传输门实现T门模块的表达式:
| $ \begin{array}{l} t = T\left( {{f_0},{f_1},{f_2};x} \right) = {f_0} \cdot \left( {{x^0} + \overline {{x_{\rm{p}}}^0} } \right) + \\ \;\;\;\;\;{f_1} \cdot \left( {\overline {{x^0}} + {x_{\rm{p}}}^0} \right) \cdot \left( {\overline {{x^2}} + {x_{\rm{p}}}^2} \right) + {f_2} \cdot \left( {{x^2} + \overline {{x_{\rm{p}}}^2} } \right), \end{array} $ | (14) |
其中,下标“p”表示PMOS管.例如,x0和
|
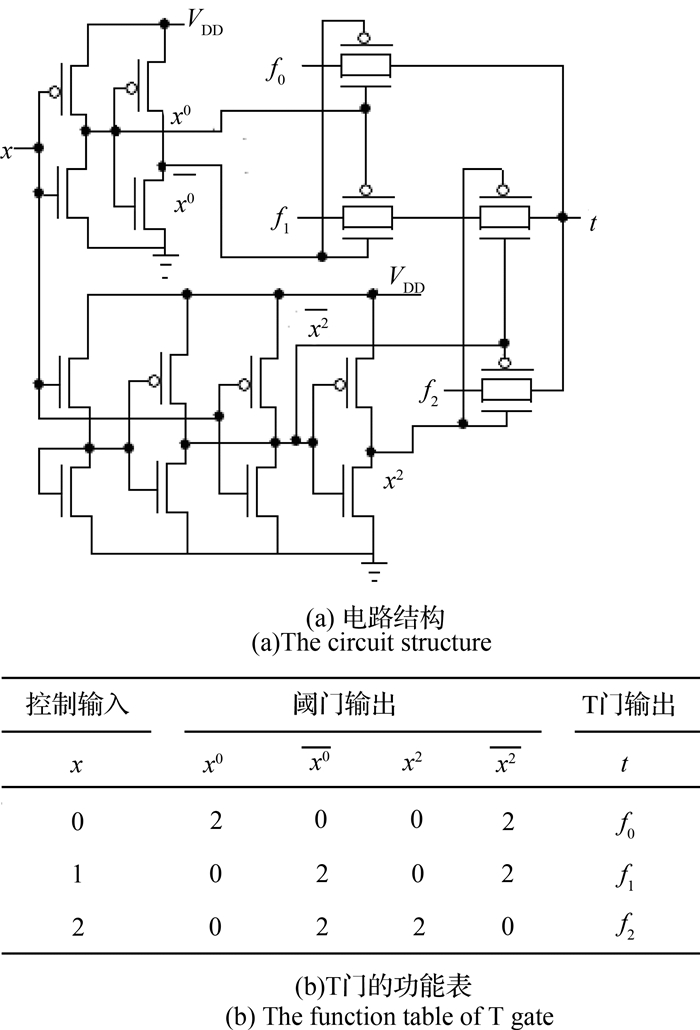
图 4 T门逻辑模块的CMOS管电路实现 Fig. 4 The CMOS transistor circuit implementation of T gate logic module |
应该指出,在图 4(a)所示的T门逻辑模块电路中,阈值逻辑部分采用传统互补CMOS电路实现,共用12个MOS管.该电路中MOS管的扇出系数较大,输出的各阈值逻辑信号可为控制变量相同的T门模块电路中CMOS传输门MOS管的栅极信号公用.
采用HSPICE软件和TSMC 0.18 μm CMOS工艺模型,利用本文提出的T门模块组成对如图 3所示的实例函数的最小化T门网络进行仿真实验.在仿真实验中,共用124个MOS管,其中,NMOS管65个、PMOS管59个.若采用文献[8]提出的变阈值设计的T门模块电路来实现本文的T门网络,则需132个MOS管,其中,NMOS管和PMOS管各66个. NMOS管和PMOS管的宽长比(W/L)分别为(0.36 μm /0.18 μm)和(0.72 μm /0.18 μm).电源VDD=1.8 V,逻辑值0, 1, 2,分别为0, 0.9, 1.8 V.输出端上的负载电容为25 fF.仿真实验的输入和输出波形如图 5所示.由图 5可知,利用本文方法设计的最小化T门网络可以完成正确的逻辑功能.

|
图 5 实例函数的最小化T门网络的仿真实验波形 Fig. 5 Simulation experimental waveform of the minimization T gate network of the implementation instance function |
利用三值格代数和三值T代数的基本运算和性质,讨论了求取待实现函数在其变量集上选取合适划分的定理及其选取判据.基于此,提出了三值T门组合网络设计(化简)的一种混合控制变量排序算法,并给出了应用实例.本文算法可使待实现的三值T门网络化简到最小, 并减少了搜索次数.采用HSPICE软件和TSMC 0.18 μm CMOS工艺模型,利用本文设计的T门模块电路,验证了采用该算法设计的最小化T门组合网络的逻辑功能是正确且有效的.
| [1] | ROMERO M E, MARTINS E M, SANTOS R R D, et al. Universal set of CMOS gates for the synthesis of multiple valued logic digital circuits[J]. IEEE Transactions on Circuits and Systems-1:Regular Papers, 2014, 61(3): 736–749. DOI:10.1109/TCSI.2013.2284187 |
| [2] | PAREL V, GURUMURTHY K S. Arithmetic operations in multi-valued logic[J]. International Journal of VLSI design & Communication Systems, 2010, 1(1): 21–32. |
| [3] | TOTO F, SALETTI R. CMOS dynamic ternary circuit with full logic swing and zero-static power consumption[J]. Electronic Letters, 1998, 34(11): 1083–1084. DOI:10.1049/el:19980754 |
| [4] | LIN S, KIM Y B, LOMBARDI F. CNTFET-based design of ternary logic gates and arithmetic circuits[J]. IEEE Transactions on Nanotechnology, 2011, 10(2): 217–225. DOI:10.1109/TNANO.2009.2036845 |
| [5] | KESHAVARZIAN P, SARIKHANI R. A novel CNTFET-based ternary fall adder[J]. Circuits Syst Signal Processing, 2014, 33(3): 665–679. DOI:10.1007/s00034-013-9672-6 |
| [6] | INOKAWA H, FUJIWARA A, TAKAHASHI Y. A multiple-valued logic and memory with combined single-electron and metal-oxide-semiconductor transistors[J]. IEEE Transactions on Electron Devices, 2003, 50(2): 462–470. DOI:10.1109/TED.2002.808421 |
| [7] | WAIRYA S, NAGARIA R K, TIWARI S. New design methodologies for high-speed mixed-mode CMOS full adder circuits[J]. International Journal of VLSI design & Communication Systems, 2011, 2(2): 78–98. |
| [8] |
吴训威.
多值逻辑电路设计原理[M]. 杭州: 杭州大学出版社, 1994.
WU X W. Design Principles of Multi-Valued Logic Circuits[M]. Hangzhou: Hangzhou University Press, 1994. |
| [9] | FANG K Y, WOJCIK A S. Modular decomposition of combinational multiple-valued circuits[J]. IEEE Transactions on Computers, 1988, 37(10): 1293–1301. DOI:10.1109/12.5993 |
| [10] |
姜恩华, 姜文彬. 三值逻辑函数RDSOP形式的代数理论和T门实现[J].
计算机学报, 2007, 30(7): 1132–1137.
JIANG E H, JIANG W B. Algebra theory of RDSOP forms of ternary logic functions and its implementation with T-gates[J]. Chinese Journal of Computers, 2007, 30(7): 1132–1137. DOI:10.3321/j.issn:0254-4164.2007.07.010 |
| [11] | WANG Y, MCCROSKY C. Solving Boolean equations using ROSOP forms[J]. IEEE Transactions on Computers, 1998, 47(2): 171–177. DOI:10.1109/12.663763 |


