0 引言

自1965年ZEDEH教授首次提出模糊集概念以来, 模糊系统理论在许多研究领域得到了广泛应用, 尤其是常见的Mamdani模糊系统和T-S模糊系统得到了长足的发展和重点关注.1985年, 日本学者TAKAGI与SUGENO (T-S)^[1]基于输入输出数据对率先建立了T-S模糊系统模型, 并将其应用于非线性系统的控制中; 1992年, WANG等^[2]采用正则最小二乘法和模糊基函数研究了Mamdani模糊系统及其特性, 并借助Stone-Weierstrass定理证明了该系统对连续函数具有逼近性, 但对可积函数类的逼近性涉及很少.2000年, 刘普寅等^[3]首次提出分片线性函数概念, 并以此为桥梁研究了广义模糊系统对Lebesgue可积函数的泛逼近性问题.2006年, 刘福才等^[4]也以非线性函数为输出后件, 构造了一类T-S型模糊系统, 并讨论了该系统的逼近性能.2012年, 王贵君等^[5]将Mamdani模糊系统和T-S模糊系统进行合并，建立了混合模糊系统, 并证明该混合系统不仅保持了逼近性能, 而且可通过对输入变量分层来减少模糊规则数.2015年, 张国英等^[6]基于分片线性函数研究了一类非线性T-S型模糊系统对p-可积函数的逼近性；相关研究还可参阅文献[7-8].以上工作为进一步探究模糊系统的逼近性奠定了理论基础.

Bernstein多项式是基于某个给定函数而形成的一个特定型多元多项式, 其在研究高维空间函数逼近或插值问题中发挥了重要作用^[9].2001年, 张恩勤等^[10]以一元多项式为规则后件，研究了一类模糊系统的插值特性, 并借助插值法讨论了该系统的逼近精度问题.但该结果仅限于单输入单输出的一维模糊系统.本文以多元Bernstein多项式为规则后件，构造一类多输入单输出模糊系统, 并利用随机剖分数所确定的Bernstein多项式给出该模糊系统的输出算法.

1 模糊系统的构造

通常, 模糊规则后件对模糊系统的输出值影响较大, 依据不同规则后件建立的模糊系统显然不同.实际上, Mamdani模糊系统的规则后件是一个模糊集, 而T-S模糊系统的规则后件是关于输入变量的多元线性函数, 且Mamdani模糊系统可视为T-S模糊系统的特例.本节将采用多元Bernstein多项式取代规则后件建立异于Mamdani和T-S的一种模糊系统.为此, 首先对前件模糊集族实施一定限制，给出构造模糊系统的几个相关概念.

定义1  设{A₁, A₂, …, A_N}为论域U⊂R上一个模糊集族, 分别给出以下概念:

(1) 若每个模糊集A_i的核满足Ker A_i≠∅, i=1, 2, …, N, 则称{A₁, A₂, …, A_N}在U上是标准的.

(2) 若∀x∈U, ∃i₀∈{1, 2, …, N}，使得A_i0(x)>0, 则称{A₁, A₂, …, A_N}在U上是完备的.完备性强调论域U被所给集族的支撑集完全覆盖, 且不能有空隙.

(3) 若∀x∈Ker (A_j), j=1, 2, …, N, 满足A_i(x)=0(i≠j), 则称{A₁, A₂, …, A_N}在U上是一致的.一致性强调{A₁, A₂, …, A_N}相邻模糊集的隶属函数之间必须相交, 但不能过界.

下面, 再来熟悉有关多元Bernstein多项式的一些概念.因通过线性变换可将一般闭区间[a, b]变换为[0, 1], 故可设[a_i, b_i]=[0, 1], i=1, 2, …, n, 且只要在[0, 1]ⁿ=[0, 1]×[0, 1]×…×[0, 1]上讨论Bernstein多项式的结构问题即可.

设f(x)是[0, 1]ⁿ上的连续函数, m₁, m₂, …, m_n分别为[0, 1]ⁿ空间每个坐标轴上[0, 1]闭区间的等距剖分数.特别地, 当n=1时, [0, 1]上一元Bernstein多项式B_m(f; x)可表示为

$ {B_m}\left( {f;x} \right) = \sum\limits_{k = 0}^m {f\left( {\frac{k}{m}} \right)C_m^k{x^k}{{\left( {1 - x} \right)}^{m - k}}} . $

当n=2时, [0, 1]×[0, 1]上的二元Bernstein多项式B_{m1, m2}(f; (x₁, x₂))可表示为

$ \begin{array}{*{20}{c}} {{B_{{m_1},{m_2}}}\left( {f;\left( {{x_1},{x_2}} \right)} \right) = \sum\limits_{{k_1} = 0}^{{m_1}} {\sum\limits_{{k_2} = 0}^{{m_2}} {f\left( {\frac{{{k_1}}}{{{m_1}}},\frac{{{k_2}}}{{{m_2}}}} \right)C_{{m_1}}^{{k_1}}C_{{m_2}}^{{k_2}}} } \times }\\ {{x_1}^{{k_1}}{x_2}^{{k_2}}{{\left( {1 - {x_1}} \right)}^{{m_1} - {k_1}}}{{\left( {1 - {x_2}} \right)}^{{m_2} - {k_2}}}.} \end{array} $

(1)

一般地, n元Bernstein多项式可表示为

$ \begin{array}{l} {B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)} \right) = \\ \;\;\;\;\;\;\sum\limits_{{k_1} = 0}^{{m_1}} {\sum\limits_{{k_2} = 0}^{{m_2}} { \cdots \sum\limits_{{k_n} = 0}^{{m_n}} {f\left( {\frac{{{k_1}}}{{{m_1}}},\frac{{{k_2}}}{{{m_2}}}, \cdots ,\frac{{{k_n}}}{{{m_n}}}} \right)C_{{m_1}}^{{k_1}}C_{{m_2}}^{{k_2}} \cdots C_{{m_n}}^{{k_n}}} } } \times \\ \;\;\;\;\;\;{x_1}^{{k_1}}{x_2}^{{k_2}} \cdots {x_n}^{{k_n}}{\left( {1 - {x_1}} \right)^{{m_1} - {k_1}}}{\left( {1 - {x_2}} \right)^{{m_2} - {k_2}}} \cdots \times \\ \;\;\;\;\;\;{\left( {1 - {x_n}} \right)^{{m_n} - {k_n}}}. \end{array} $

若记

$ \begin{array}{l} Q_{{m_1},{m_2}, \cdots ,{m_n}}^{{k_1},{k_2}, \cdots ,{k_n}}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right) = C_{{m_1}}^{{k_1}}C_{{m_2}}^{{k_2}} \cdots C_{{m_n}}^{{k_n}}{x_1}^{{k_1}}{x_2}^{{k_2}} \cdots \times \\ \;\;\;\;\;\;\;\;\;\;{x_n}^{{k_n}}{\left( {1 - {x_1}} \right)^{{m_1} - {k_1}}}{\left( {1 - {x_2}} \right)^{{m_2} - {k_2}}} \cdots {\left( {1 - {x_2}} \right)^{{m_2} - {k_2}}}, \end{array} $

则有

$ \begin{array}{l} \sum\limits_{{k_1} = 0}^{{m_1}} {\sum\limits_{{k_2} = 0}^{{m_2}} { \cdots \sum\limits_{{k_n} = 0}^{{m_n}} {Q_{{m_1},{m_2}, \cdots ,{m_n}}^{{k_1},{k_2}, \cdots ,{k_n}}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)} } } = \\ \;\;\;\;\;\;\;\left( {\sum\limits_{{k_1} = 0}^{{m_1}} {C_{{m_1}}^{{k_1}}x_1^{{k_1}}{{\left( {1 - {x_1}} \right)}^{{m_1} - {k_1}}}} } \right) \times \\ \;\;\;\;\;\;\;\left( {\sum\limits_{{k_2} = 0}^{{m_2}} {C_{{m_2}}^{{k_2}}x_2^{{k_2}}{{\left( {1 - {x_2}} \right)}^{{m_2} - {k_2}}}} } \right) \cdots \times \\ \;\;\;\;\;\;\;\left( {\sum\limits_{{k_n} = 0}^{{m_n}} {C_{{m_n}}^{{k_n}}x_n^{{k_n}}{{\left( {1 - {x_n}} \right)}^{{m_n} - {k_n}}}} } \right) = \\ \;\;\;\;\;\;\;{\left( {{x_1} + 1 - {x_1}} \right)^{{m_1}}}{\left( {{x_2} + 1 - {x_2}} \right)^{{m_2}}} \cdots \times \\ \;\;\;\;\;\;\;{\left( {{x_n} + 1 - {x_n}} \right)^{{m_n}}} = 1. \end{array} $

故n元Bernstein多项式可简化为

$ \begin{array}{l} {B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)} \right) = \\ \;\;\;\;\;\;\sum\limits_{{k_1} = 0}^{{m_1}} {\sum\limits_{{k_2} = 0}^{{m_2}} { \cdots \sum\limits_{{k_n} = 0}^{{m_n}} {f\left( {\frac{{{k_1}}}{{{m_1}}},\frac{{{k_2}}}{{{m_2}}}, \cdots ,\frac{{{k_n}}}{{{m_n}}}} \right)} } } \times \\ \;\;\;\;\;\;Q_{{m_1},{m_2}, \cdots ,{m_n}}^{{k_1},{k_2}, \cdots ,{k_n}}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right). \end{array} $

若∀x=(x₁, x₂, …, x_n)∈[0, 1]ⁿ, 则n元Bernstein多项式还可简化为

$ \begin{array}{l} {B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;x} \right) = \\ \sum\limits_{{k_1} = 0}^{{m_1}} {\sum\limits_{{k_2} = 0}^{{m_2}} { \cdots \sum\limits_{{k_n} = 0}^{{m_n}} {f\left( {\frac{{{k_1}}}{{{m_1}}},\frac{{{k_2}}}{{{m_2}}}, \cdots ,\frac{{{k_n}}}{{{m_n}}}} \right)Q_{{m_1},{m_2}, \cdots ,{m_n}}^{{k_1},{k_2}, \cdots ,{k_n}}\left( x \right)} } } . \end{array} $

(2)

现以二元Bernstein多项式为规则后件构造模糊系统, 设二维IF-THEN模糊规则形如：

$ \begin{array}{*{20}{c}} {R:{\rm{IF}}\;{x_1}\;{\rm{is}}\;A_{{m_1}}^1\;{\rm{and}}\;{x_2}\;{\rm{is}}\;A_{{m_2}}^2,}\\ {{\rm{THEN}}\;y\;{\rm{is}}\;{B_{{m_1},{m_2}}}\left( {f;\left( {{x_1},{x_2}} \right)} \right),} \end{array} $

其中，指标变量m₁=1, 2, …, N₁; m₂=1, 2, …, N₂, 而Aⁱ_mi分别是论域U_i⊂R上前件模糊集, i=1, 2, B_{m1, m2}(f; (x₁, x₂))是输出论域V⊂R上的规则后件, 所有可能的模糊规则总数为N₁N₂.

基于上述二维IF-THEN模糊规则、乘积推理机、单点模糊化和中心平均解模糊化, 不难获得新模糊系统的解析表达式：

$ \begin{array}{l} F\left( {{x_1},{x_2}} \right) = \\ \frac{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right){B_{{m_1},{m_2}}}\left( {f;\left( {{x_1},{x_2}} \right)} \right)} } }}{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right)} } }}, \end{array} $

(3)

其中，B_{m1, m2}(f; (x₁, x₂))的下标m₁, m₂分别为x₁和x₂坐标轴上闭区间[0, 1]的剖分数; A¹_m1和A²_m2分别为x₁和x₂轴上一致标准完备的前件模糊集.

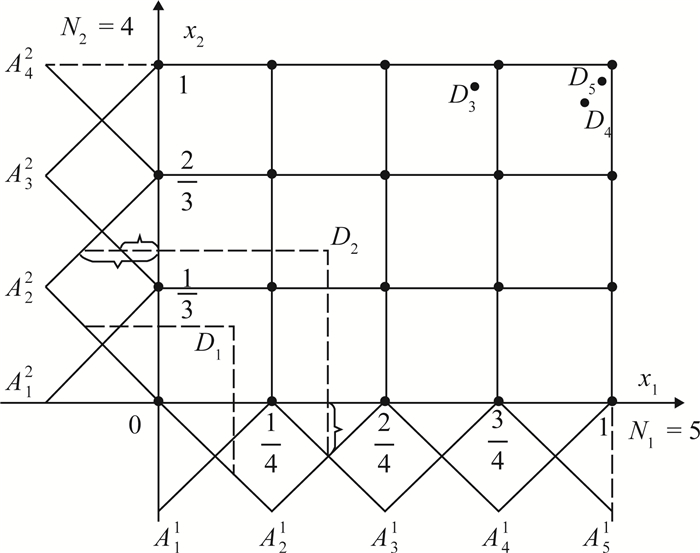
注1  因模糊系统(3)随输入变量(x₁, x₂)随机变化，其所属剖分区域也随之改变, 故称Bernstein多项式B_{m1, m2}(f; (x₁, x₂))的指标变量m₁, m₂为随机剖分数.实际上, 随机剖分数m₁和m₂与论域[0, 1]×[0, 1]上的剖分数N₁和N₂有本质区别, m₁由输入点(x₁, x₂)第1个分量对应x₁轴上的非零前件模糊集随机确定, m₂由第2个分量对应x₂轴上非零前件模糊集随机确定, 参见图 1.

下面, 按图 1所示选取样本点${D_2} = \left( {\frac{3}{8}, \frac{4}{9}} \right)$来说明随机剖分数m₁和m₂是如何随机生成的.例如, 输入点D₂第1分量$\frac{3}{8}$在x₁轴上对应非零模糊集为A₂¹和A₃¹; 第2分量$\frac{4}{9}$在x₂轴上对应非零模糊集为A₂²和A₃².此时共有4条模糊规则, 且随机剖分数m₁, m₂的取值有以下4种情形:

$ \left\{ \begin{array}{l} {m_1} = 2,\;\;\;{m_2} = 2,\\ {m_1} = 2,\;\;\;{m_2} = 3,\\ {m_1} = 3,\;\;\;{m_2} = 2,\\ {m_1} = 3,\;\;\;{m_2} = 3. \end{array} \right. $

同理, 若输入样本点${D_1} = \left( {\frac{3}{{16}}, \frac{2}{9}} \right)$, 则随机剖分数m₁, m₂也有4种取值:

$ \left\{ \begin{array}{l} {m_1} = 1,\;\;\;{m_2} = 1,\\ {m_1} = 1,\;\;\;{m_2} = 2,\\ {m_1} = 2,\;\;\;{m_2} = 1,\\ {m_1} = 2,\;\;\;{m_2} = 2. \end{array} \right. $

特别地，当输入点取图 1中的格点时, 仅对应1条模糊规则, 且该模糊系统的输出计算更简单.例如, 若输入点为$\left( {\frac{3}{4}, \frac{1}{3}} \right)$, 则随机剖分数m₁, m₂仅有1组取值: m₁=4, m₂=2.据此不难计算以二元Bernstein多项式B_{m1, m2}(f; (x₁, x₂))为规则后件的模糊系统的输出值.

类似地, 设n-维模糊规则为:

$ \begin{array}{l} R:{\rm{IF}}\;{x_1}\;{\rm{is}}\;A_{{m_1}}^1\;{\rm{and}}\;{x_2}\;{\rm{is}}\;A_{{m_2}}^2, \cdots ,{x_n}\;{\rm{is}}\;A_{{m_n}}^n,\\ {\rm{THEN}}\;y\;{\rm{is}}\;{B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)} \right). \end{array} $

依乘积推理机、单值模糊化和中心平均解模糊化，可得n维模糊系统的输出为

$ \begin{array}{l} F\left( x \right) = \frac{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } }}{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } }} \times \\ \;\;\;\;\;\;\;\;\;\;\;{B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;x} \right), \end{array} $

(4)

其中，输入变量x=(x₁, x₂, …, x_n)∈[0, 1]ⁿ, 而Aⁱ_mi(i=1, 2, …, n)分别为x_i轴上一致标准完备的前件模糊集, N_i为x_i轴[0, 1]上的剖分数, m_i为x_i轴的随机剖分数, B_{m1, m2}, …, m_n(f; x)按式(3)计算.

特别地, 若取前件模糊集为三角形隶属函数, 则有

$ \begin{array}{l} \sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } = \\ \;\;\;\;\;\sum\limits_{{m_1} = 1}^{{N_1}} {A_{{m_1}}^1\left( {{x_1}} \right)\sum\limits_{{m_2} = 1}^{{N_2}} {A_{{m_2}}^2\left( {{x_2}} \right) \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_n}}^n\left( {{x_n}} \right)} } } = 1. \end{array} $

此时, ∀x=(x₁, x₂, …x_n)∈[0, 1]ⁿ, 模糊系统(4)可进一步简化为

$ \begin{array}{l} F\left( x \right) = \sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } \times \\ \;\;\;\;\;\;\;\;\;\;\;{B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;x} \right). \end{array} $

(5)

至此, 以多元Bernstein多项式为规则后件构造了多输入单输出模糊系统(4)的输出表达式, 并通过选取输入样本点和图 1分析了随机剖分数的生成过程.

2 模糊系统逼近及算法

模糊系统可近似表示某些信息不完整的未知函数, 通常只得知所给函数f在某论域内所有点或局部点的取值(数据对), 并不知该函数的解析表达式.否则, 若f的解析式已知, 再去构造烦琐的模糊系统将毫无意义.因此, 具有逼近性能的模糊系统才更有理论价值.

下面给出可由Bernstein多项式逼近连续函数的一个引理, 进而给出该模糊系统的逼近性证明和输出算法.

引理1^[9]  设f是[0, 1]ⁿ上多元连续函数, 则∀ε>0和x=(x₁, x₂, …, x_n)∈[0, 1]ⁿ, ∃m₁, m₂, …, m_n∈N, 使得|B_{m1, m2, …, mn}(f; x)-f(x)|＜ε.

定理1  设f是[0, 1]ⁿ上一个连续函数, 则对∀ε>0, 存在形如式(4)的基于Bernstein多项式的模糊系统F, 使得∀x=(x₁, x₂, …, x_n)∈[0, 1]ⁿ, 有

$ \left| {F\left( x \right) - f\left( x \right)} \right| < \varepsilon . $

证明  设基于连续函数f(x)的n元Bernstein多项式B_{m1, m2, …, mn}(f; x)如式(2)所示.此外, 给定[0, 1]ⁿ空间一个等距剖分, 且第x_i轴[0, 1]上的剖分数为N_i, i=1, 2, …, n, 其中Aⁱ_mi为对应x_i轴上的前件模糊集, 而m₁, m₂, …, m_n为由输入变量生成的随机剖分数.

此时, 对∀ε>0和x=(x₁, x₂, …, x_n)∈[0, 1]ⁿ, 由式(4)和引理1可得

$ \begin{array}{l} \left| {F\left( x \right) - f\left( x \right)} \right| = \\ \left| {\frac{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } }}{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } }} \times } \right.\\ \left. {\left( {{B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;x} \right) - f\left( x \right)} \right)} \right| \le \\ \frac{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } }}{{\sum\limits_{{m_1} = 1}^{{N_1}} {\sum\limits_{{m_2} = 1}^{{N_2}} { \cdots \sum\limits_{{m_n} = 1}^{{N_n}} {A_{{m_1}}^1\left( {{x_1}} \right)A_{{m_2}}^2\left( {{x_2}} \right) \cdots A_{{m_n}}^n\left( {{x_n}} \right)} } } }} \times \\ \left| {{B_{{m_1},{m_2}, \cdots ,{m_n}}}\left( {f;x} \right) - f\left( x \right)} \right| < \varepsilon . \end{array} $

因此, 以多元Bernstein多项式为规则后件的模糊系统在[0, 1]ⁿ上对连续函数具有逼近性.此结论对进一步研究模糊系统具有重要意义.

注2  通过线性变换可将一般闭区间[a, b]变换为[0, 1], 故此定理可推广至Rⁿ空间中的任意n-维长方体, 即以Bernstein多项式为规则后件的模糊系统可在n-维长方体上逼近连续函数.此外, 直观上看，虽然模糊系统式(4)相对简单, 但要具体计算该系统的输出值却较为复杂.究其原因主要是多元Bernstein多项式的每个分量都有自身的随机剖分数, 从而导致计算步骤烦琐.为此, 接下来将给出该模糊系统的输出算法, 并假设f是[0, 1]ⁿ上的连续函数.

输出算法

第1步  剖分论域.在每个坐标轴x_i(i=1, 2, …, n)所属区间[0, 1]上进行N_i-1等距分割, 分割点为j/N_i, j=0, 1, 2, …, N_i, 相应剖分数为N₁, N₂, …, N_n, 分割后每个轴上小区间长度均为1/(N_i-1).再过每个分点作垂线, 即可获得论域空间[0, 1]ⁿ上的一个剖分.

第2步 定义前件模糊集.在每个坐标轴[0, 1]上以每个分点为峰值点定义一致标准完备的前件模糊集族, 通常取这些模糊集为三角形或梯形隶属函数, 且每个轴上可定义N_i个模糊集, i=1, 2, …, n, 其中两端模糊集的隶属函数图像为半三角形或半梯形, 参见图 1.

第3步  确定随机剖分数.根据所输入样本点x=(x₁, x₂, …, x_n)确定每个分量在所属小区间起作用的非零前件模糊集, 从而获得Bernstein多项式B_{m1, m2, …, mn}(f; x)所有可能的随机剖分数m₁, m₂, …, m_n的若干组合.

第4步  计算B_{m1, m2, …, mn}(f; x).依据所得随机剖分数m₁, m₂, …, m_n的所有可能组合，计算Bernstein多项式B_{m1, m2, …, mn}(f; x)在所给样本点x=(x₁, x₂, …, x_n)处的值.

第5步  计算隶属度值.根据输入样本点x=(x₁, x₂, …, x_n)计算每个坐标轴上对应非零前件模糊集的隶属度值Aⁱ_mj(x_i), i=1, 2, …, n.

第6步  计算系统输出值.将第4和第5步所得值代入式(4), 得模糊系统的最终输出值.

注3  实际中, 通过给定逼近精度ε适当选取第1步所涉及的剖分数N_i, 简单起见，也可选取N₁=N₂=…=N_n.此外, 为计算方便，第2步要求前件模糊集一致标准完备.例如, 取三角形二相波隶属函数, 则每个输入样本点对应的随机剖分数m_i(i=1, 2, …, n)仅有2种取值, 此时模糊系统共有2ⁿ条规则.特别当输入样本点为格点(顶点)时, 所有随机剖分数m_i只有1种取值, 此时, 该系统仅有1条模糊规则.

3 实例分析

上节给出了以Bernstein多项式为规则后件的模糊系统的输出算法.该算法的关键是计算Bernstein多项式在样本点的输出值.下面, 仅以样本点D₂为例给出$F\left( {\frac{3}{8}, \frac{4}{9}} \right)$的详细计算过程.

例1  设二元连续函数f(x₁, x₂)=x₁²+x₂², (x₁, x₂)∈[0, 1]×[0, 1], 前件模糊集的隶属函数选取三角形二相波, 试按式(5)计算二元模糊系统在样本点D₂处的输出值$F\left( {\frac{3}{8}, \frac{4}{9}} \right)$.

解  在不考虑逼近精度的情况下, 先设N₁=5, N₂=4(参见图 1), 2个坐标轴上前件模糊集的隶属函数可通过适当左右平移其中某一个得到.由式(5)有

$ \begin{array}{l} F\left( {\frac{3}{8},\frac{4}{9}} \right) = \\ \sum\limits_{{m_1} = 1}^5 {\sum\limits_{{m_2} = 1}^4 {A_{{m_1}}^1\left( {\frac{3}{8}} \right)A_{{m_2}}^2\left( {\frac{4}{9}} \right){B_{{m_1},{m_2}}}\left( {f;\left( {\frac{3}{8},\frac{4}{9}} \right)} \right)} } . \end{array} $

按照输出算法, 样本点D₂在x₁轴上对应的非零模糊集为A₂¹和A₃¹, 在x₂轴上对应的非零模糊集为A₂²和A₃², 由图 1易得其隶属函数.此时, 共有4条模糊规则, 故随机剖分数也有4组取值, 即

$ \left( {{m_1},{m_2}} \right) = \left( {2,2} \right);\left( {2,3} \right);\left( {3,2} \right);\left( {3,3} \right). $

因此, 模糊系统输出的$F\left( {\frac{3}{8}, \frac{4}{9}} \right)$可进一步表示为

$ \begin{array}{l} F\left( {\frac{3}{8},\frac{4}{9}} \right) = A_2^1\left( {\frac{3}{8}} \right)\left( {A_2^2\left( {\frac{4}{9}} \right){B_{2,2}}\left( {f;\left( {\frac{3}{8},\frac{4}{9}} \right)} \right) + } \right.\\ \;\;\;\;\;\;\left. {A_3^2\left( {\frac{4}{9}} \right){B_{2,3}}\left( {f;\left( {\frac{3}{8},\frac{4}{9}} \right)} \right)} \right) + \\ \;\;\;\;\;\;A_3^1\left( {\frac{3}{8}} \right)\left( {A_2^2\left( {\frac{4}{9}} \right){B_{3,2}}\left( {f;\left( {\frac{3}{8},\frac{4}{9}} \right)} \right)} \right) + \\ \;\;\;\;\;\;A_3^2\left( {\frac{4}{9}} \right){B_{3,3}}\left( {f;\left( {\frac{3}{8},\frac{4}{9}} \right)} \right), \end{array} $

(6)

其中，前件模糊集A₂¹, A₃¹, A₂²和A₃²的隶属函数由图 1很容易确定.例如, A₃¹和A₂²的隶属函数分别为

$ A_3^1\left( {{x_1}} \right) = \left\{ \begin{array}{l} 4{x_1} - 1,\;\;\;\;\;\;\;\;\frac{1}{4} \le {x_1} < \frac{1}{2},\\ 3 - 4{x_1},\;\;\;\;\;\frac{1}{2} \le {x_1} \le \frac{3}{4},\\ 0,\;\;\;\;\;其他; \end{array} \right. $

$ A_2^2\left( {{x_2}} \right) = \left\{ \begin{array}{l} 3{x_2},\;\;\;\;\;\;\;\;0 \le {x_2} < \frac{1}{3},\\ 2 - 3{x_2},\;\;\;\;\;\frac{1}{3} \le {x_2} \le \frac{2}{3},\\ 0,\;\;\;\;\;其他. \end{array} \right. $

不难计算$A_2^1\left( {\frac{3}{8}} \right) = A_3^1\left( {\frac{3}{8}} \right) = \frac{1}{2}$; $A_2^2\left( {\frac{4}{9}} \right) = \frac{2}{3}, A_3^2\left( {\frac{4}{9}} \right) = \frac{1}{3}$.接下来以${B_{2, 2}}\left( {f;\left( {\frac{3}{8}, \frac{4}{9}} \right)} \right)$为例，计算每个Bernstein多项式在样本点D₂处的取值.

由式(1)和f(x₁, x₂)=x₁²+x₂²可得

$ \begin{array}{l} {B_{2,2}}\left( {f;\left( {\frac{3}{8},\frac{4}{9}} \right)} \right) = \\ \sum\limits_{{k_1} = 0}^2 {\sum\limits_{{k_2} = 0}^2 {C_2^{{k_1}}C_2^{{k_2}}f\left( {\frac{{{k_1}}}{2},\frac{{{k_2}}}{2}} \right){{\left( {\frac{3}{8}} \right)}^{{k_1}}}{{\left( {\frac{4}{9}} \right)}^{{k_2}}}{{\left( {\frac{5}{8}} \right)}^{2 - {k_1}}}{{\left( {\frac{5}{9}} \right)}^{2 - {k_2}}}} } = \\ \sum\limits_{{k_2} = 0}^2 {C_2^{{k_2}}f\left( {0,\frac{{{k_2}}}{2}} \right){{\left( {\frac{4}{9}} \right)}^{{k_2}}}{{\left( {\frac{5}{8}} \right)}^2}{{\left( {\frac{5}{9}} \right)}^{2 - {k_2}}}} + \\ \sum\limits_{{k_2} = 0}^2 {2C_2^{{k_2}}f\left( {\frac{1}{2},\frac{{{k_2}}}{2}} \right)\frac{3}{8}{{\left( {\frac{4}{9}} \right)}^{{k_2}}}\frac{5}{8}{{\left( {\frac{5}{9}} \right)}^{2 - {k_2}}}} + \\ \sum\limits_{{k_2} = 0}^2 {C_2^{{k_2}}f\left( {1,\frac{{{k_2}}}{2}} \right){{\left( {\frac{3}{8}} \right)}^2}{{\left( {\frac{4}{9}} \right)}^{{k_2}}}{{\left( {\frac{5}{9}} \right)}^{2 - {k_2}}}} \approx 0.578\;8. \end{array} $

同理, 可算得${B_{2, 3}}\left( {f;\left( {\frac{3}{8}, \frac{4}{9}} \right)} \right) \approx 0.537\;6$, ${B_{3, 2}}\left( {f;\left( {\frac{3}{8}, \frac{4}{9}} \right)} \right) \approx 0.539\;7$, ${B_{3, 3}}\left( {f;\left( {\frac{3}{8}, \frac{4}{9}} \right)} \right) \approx 0.498\;6$.并将其代入式(6)，可立得最终输出值$F\left( {\frac{3}{8}, \frac{4}{9}} \right) \approx 0.545\;5$.

实际上, 所给函数f在样本点$\left( {\frac{3}{8}, \frac{4}{9}} \right)$的实际取值为$f\left( {\frac{3}{8}, \frac{4}{9}} \right) = {\left( {\frac{3}{8}} \right)^2} + {\left( {\frac{4}{9}} \right)^2} \approx 0.338\;2.$.直观来看, 随机选取剖分数N₁=5, N₂=4进行计算, 该系统的输出值与函数在样本点的实际取值接近, 这主要由基于Bernstein多项式的模糊系统具有逼近性所决定.

为更好地研究本文设计系统逼近性的精度及特点，再选取几个样本点计算系统的输出, 并将其输出与函数值及Mamdani模糊系统的输出进行对比.

样本点为${D_1} = \left( {\frac{3}{{16}}, \frac{2}{9}} \right)$, ${D_3} = \left( {\frac{{11}}{{16}}, \frac{{17}}{{18}}} \right)$, ${D_4} = \left( {\frac{{15}}{{16}}, \frac{8}{9}} \right)$和${D_5} = \left( {\frac{{31}}{{32}}, \frac{{17}}{{18}}} \right)$, 如图 1所示, 分别计算以Bernstein多项式为规则后件的模糊系统的输出F(D_i)(i=1, 3, 4, 5)，并分别比较该模糊系统和以往Mamdani模糊系统在样本点的取值.方便起见, 记Mamdani模糊系统在各样本点的输出为M(D_i)(i=1, 2, …, 5).具体计算过程参见例1, 结果见表 1.

从表 1的结果中不难发现, Mamdani模糊系统的输出值误差较为稳定, 这是由于Mamdani模糊系统后件输出只与样本点所在剖分区域的4个顶点有关.而以Bernstein多项式为规则后件的模糊系统的输出受样本点所在区域影响较大, 且样本点离原点越远误差越小，这主要由Bernstein多项式的自身特性所决定.事实上, 以Bernstein多项式为模糊系统的规则后件正是本文的创新点.虽然某些点的输出，本文系统不及Mamdani模糊系统理想, 但当样本点接近(1, 1)点时, 以Bernstein多项式为规则后件的模糊系统的实际输出优于Mamdani模糊系统.例如, 在样本点D₄和D₅处，以Bernstein多项式为规则后件的模糊系统的输出误差明显较Mamdani模糊系统小.

4 结论

构造了依据Bernstein多项式的多元模糊系统, 特别是在前件模糊集选取三角形二相波时获得了更为简化的模糊系统.证明了该模糊系统具有逼近性, 还给出了该系统的输出算法.当然, 计算由随机剖分数确定的Bernstein多项式在样本点的取值尤为重要.事实上, 本文只是在随机给定剖分数基础上设计了输出算法, 实际问题中剖分数是依据逼近精度适当选取的.目前该系统的逼近精度并不十分理想, 有待继续探讨.