2. 台州学院 数学与信息工程学院, 浙江 台州 317000
2. School of Mathematics & Information Engineering, Taizhou University, Taizhou 317000, Zhejiang Province, China
最近,BRAUN等[1]提出了如下带时间约束(time restrictions)的单机排序问题:设有n个工件需在单台机上加工,工件i的加工时间为pi≥0,其中加工时间为0的工件称为零工件.工件i可以在任意长度为pi的时间区间[α, α+pi)内加工并完成,其中α≥0为其开工时刻.除零工件外,同一时刻至多允许1个工件在机器上加工.同时,机器在加工过程中还需满足时间B-约束,即在任意单位时间区间[x, x+1)内至多允许加工B个工件,其中B为给定正整数.该问题可看作一类带资源约束的排序新模型[2],如机动车自动导引、医院手术排程等[3-4]. BRAUN等[1]以极小化工件最大完工时间为目标函数,证明了当B为输入值时问题是NP-难的;当B为常数时,对求解问题的LS算法进行了渐近最坏情况分析,特别是当B=2时证明了LS算法的渐近紧界为4/3. BRAUN等[5]分析得到LPT算法的渐近最坏情况界为2-2/B. ZHANG等[4]改进了上述结果,给出了B=2时的渐近最优算法以及B≥5时的渐近紧界为5/4的改进算法.
BRAUN等[1]将B为常数情形的计算复杂性作为公开问题,ZHANG等[4]猜测B=2的情形属于P问题(多项式时间可解问题).本文分析B=2时最优排序的结构与最优解的性质,并在此基础上设计了一个时间复杂度为O(n log n)的启发式算法;当工件数较少(≤6)时,证明了该算法的最优性.
1 最优排序的结构与性质假设工件的加工时间满足p1≥p2≥…≥pn.为方便叙述,下文仅用加工时间表示对应工件.由文献[1, 4]的结论,不妨假设p1≤1.根据文献[1],一个可行排序可以用工件或其加工时间的排列π来表示,如π=(p[1], p[2], …, p[n]).具体地,首先从0时刻开始加工工件p[1],在加工第i个工件p[i]时,为满足时间B-约束,其开工时间既不能早于p[i-2]的完工时间后一个单位时间,也不能早于p[i-1]的完工时间,每个工件都尽可能早开工,称上述由排列产生可行排序的规则为LR规则.类似地,可以从排列中最后一个工件自右向左产生可行排序,称为RL规则.从排列中任意一个工件向左右两边产生可行排序的规则,称为M规则.根据时间约束的定义及上述规则,显然有以下性质:
性质1 对于给定排列,任意规则产生的可行排序的目标值都相等.
此外,由交换原理和排列两端的对称性,又能得到
性质2 存在最优排列,使得加工时间最小的工件pn,pn-1位于两端.
证明 由排列两端的对称性,仅需证明最小工件pn在最优排列的前端,即第1个位置.设有最优排列
π*=(p[1], p[2], …, p[k-1], pn, p[k+1], …, p[n]),
其中pn位于第k(>1)个位置.交换pn与p[1]的位置(如图 1所示),由于pn < p[1],因此p[2], …, p[k-1]的完工时间均可提前p[1]-pn,从而第k个位置的工件p[1]也可以提前p[1]-pn开工.又因p[1]的加工时间恰好比pn大p[1]-pn,因此交换后p[1]的完工时间与交换前pn的完工时间相同,故其后的工件p[k+1], …, p[n]的开工时间可以保持不变,即交换后的排列对应的目标值与最优排列π*的目标值一致.综上,交换pn到排列前端不改变排列的最优性,命题得证.

|
图 1 性质2证明中交换前后的排序 Fig. 1 Alternative schedules in the proof of property 2 |
性质3 存在最优排列,使得第2位置工件的加工时间不短于第3和第4位置工件的加工时间.
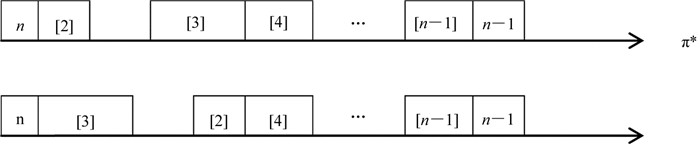
证明 设有最优排列π*=(pn, p[2], p[3], p[4], …, pn-1),其中p[2] < p[3].记π*中p[2]与p[3]之间的空闲时间为Δ,则有p[2]+Δ=1,于是p[3]+Δ≥1,根据时间约束,工件p[4]恰在p[3]完工时刻开工.交换p[2]与p[3]位置后,仍保持其间的空闲时间为Δ(如图 2所示).
|
图 2 性质3证明中交换第2, 3位置工件前后的排序 Fig. 2 Schedules by swapping job 2 and 3 in the proof of property 3 |
由于p[3]+Δ≥1,p[2]+Δ=1, 因此排序仍可行,且工件p[4]可在p[2]完工时刻开工,即排列在交换前后第3,4位置工件的完工时间不变,因此此后的工件完工时间也不变,即交换后的排列仍是最优排列.
由以上证明,设有最优排列π*=(pn, p[2], p[3], p[4], …, pn-1),且p[3]≤p[2] < p[4],则交换p[2]与p[4](见图 3),同理可以证明交换后的排列最优.

|
图 3 性质3证明中交换第2,4位置工件前后的排序 Fig. 3 Schedules by swapping job 2 and 4 in the proof of property 3 |
由性质3及排列两端的对称性,易得
性质4 存在最优排列,使得第n-1位置工件的加工时间不短于第n-2和n-3位置工件的加工时间.
2 基于最优结构的启发式算法根据第1节对最优排序结构的讨论,设计如下启发式算法:
算法W (1)将工件按加工时间从大到小排序,即p1≥p2≥…≥pn;(2)生成排列π=(pn, p1, p3, …, p4, p2, pn-1),并按照M规则产生可行排序.
由于算法的第1步需要对n个工件进行排序,所以其时间复杂性是O(n log n).
定理1 当工件数n≤6时,算法W给出的是最优排序.
证明 当n≤4时,由性质2及排列的两端对称性,算法W给出的排列显然最优.
当n=5时,由性质2至性质4,加工时间最少的工件p5, p4在最优排列的两端,而排在第2位置的工件加工时长长于第3,4位置的工件,排在倒数第2即第4位置的工件加工时长长于第3位置的工件,由此可知,算法W所给的排列(p5, p1, p3, p2, p4)满足上述特征,因此是最优的.
当n=6时,由性质2至性质4及上述类似分析,最优排序必为(p6, p1, p3, p4, p2, p5)和(p6, p1, p4, p3, p2, p5)之一.前者为算法W给出的排列,记为πW,后者记为π,按照M规则产生对应的排序如图 4所示.

|
图 4 由M规则产生的πW与π对应排序 Fig. 4 Schedules of πW and π generated by the M rule |
在πW与π中,显然第2,3位置工件之间的空闲时长相等,第4,5位置工件之间的空闲时长也相等,且满足Δ1+p1=1,Δ2+p2=1.令πW与π中第3,4位置工件之间的空闲时长分别为ΔW和Δ,则根据M规则有:
| $ {{\Delta }^{1}}+{{p}_{3}}+{{\Delta }^{\rm{W}}}\ge 1, {{\Delta }^{2}}+{{p}_{4}}+{{\Delta }^{\rm{W}}}\ge 1, {{\Delta }^{\rm{W}}}\ge 0. $ | (1) |
| $ {{\Delta }^{1}}+{{p}_{4}}+\Delta \ge 1, {{\Delta }^{2}}+{{p}_{3}}+\Delta \ge 1, {{\Delta }^{\rm{W}}}\ge 0. $ | (2) |
由于按照M规则,空闲时间只能由满足时间约束产生,结合式(1),(2),就有
| $ \begin{align} &{{\Delta }^{\rm{W}}}=\max \{1-{{\Delta }^{1}}-{{p}_{3}}, 1-{{\Delta }^{2}}-{{p}_{4}}, 0\}= \\ &\ \ \ \ \ \ \ \ \max \{{{p}_{1}}-{{p}_{3}}, {{p}_{2}}-{{p}_{4}}, 0\}, \\ &\Delta =\max \{1-{{\Delta }^{1}}-{{p}_{4}}, 1-{{\Delta }^{2}}-{{p}_{3}}, 0\}= \\ &\ \ \ \ \ \ \ \max \{{{p}_{1}}-{{p}_{4}}, {{p}_{2}}-{{p}_{3}}, 0\}. \\ \end{align} $ |
注意到p1-p3≤p1-p4,p2-p4≤p1-p4, 所以ΔW≤Δ.从而πW产生的总空闲时长不超过π产生的总空闲时长,故πW是最优的.
文献[4]已证明排列(pn, p1, p2, p3, …, pn-1)是渐近最优的,对比该排列与算法W所给出的排列,并经过类似分析不难得到以下结论:
定理2 当工件数n≥7时,算法W目标值CW与最优值C*必满足
所以当n≥7时,算法W是渐近最优的.然而即使当n=7时,算法W也不是最优的.
实例说明见表 1.
| 表 1 n=7的实例 Table 1 Instance with n=7 |
研究了单机带时间B-约束的排序问题,分析了B=2时最优排序的性质并设计了启发式算法W,证明算法在工件数n≤6时是最优的.当n≥7时,算法W是渐近最优的,但当n=7时,算法也非绝对最优,因此猜想B=2时带时间约束的单机排序可能是NP-难的,未来研究方向是设法给出该问题的计算复杂性证明.
| [1] | BRAUN O, CHUNG F, GRAHAM R. Single-processor scheduling with time restrictions[J]. Journal of Scheduling, 2014, 17: 399–403. DOI:10.1007/s10951-013-0342-0 |
| [2] | LEUNG J. Handbook of Scheduling[M]. Boca Raton: Chapman and Hall, 2004. |
| [3] | EDIS P, OGUZ C, OZKARAHAN I. Parallel machine scheduling with additional resources:Notation, classification, models and solution methods[J]. European Journal of Operational Research, 2013, 230: 449–463. DOI:10.1016/j.ejor.2013.02.042 |
| [4] | ZHANG A, YE F, CHEN Y, et al. Better permutations for the single-processor scheduling with time restrictions[J]. Optimization Letters, 2017, 11: 715–724. DOI:10.1007/s11590-016-1038-0 |
| [5] | BRAUN O, CHUNG F, GRAHAM R. Worst-case analysis of the LPT algorithm for single processor scheduling with time restrictions[J]. OR Spectrum, 2016, 38: 531–540. DOI:10.1007/s00291-016-0431-5 |



