近年来随着数据分析和计算机技术的飞速发展,高维美式期权的定价方法取得了实质性的突破[1-8],但随着美式期权维数的增加, 存在所谓的“维数灾难”问题.为了克服这一难题, 研究者将Monte Carlo模拟美式期权定价作为重要的研究主题[9-10].
假设d维无红利标的资产x=(x1, x2,…,xd)满足几何布朗运动
| $ \frac{{d{x^k}}}{{{x^k}}} = rdt + \sum\limits_{l = i}^d {{\nu _{kl}}d{W_l}} ,i \le k \le d, $ |
其中, r为无风险利率,dWi为标准维纳过程,波动率矩阵V=[νij]由协方差矩阵C=VVT决定,C=[cij]是d×d的协方差矩阵,且cij=ρijσiσj,σk为资产k的波动率,ρij为dWi和dWj的相关系数.假设初始时刻为0,到期时刻为T,把期权有效期划分为c个小时间段,每个时间段长度为
| $ \begin{array}{*{20}{c}} {S_j^i\left( k \right) = S_{j - 1}^i\left( k \right)\exp \left( {\left( {r - \frac{1}{2}\sigma _k^2} \right)\Delta t + } \right.}\\ {\sqrt {\Delta t} \sum\limits_{l = 1}^d {V\left( {k,l} \right)z_j^i\left( l \right)} ,} \end{array} $ | (1) |
其中Sji(k)为资产k在时刻j上第i条路径的模拟价格, k=1,2,…,d,j=1,2,…,N,i=1,2,…,M,zji为d个独立同分布的标准正态变量所组成的向量.
本文研究的美式看跌期权的收益均由标的资产价格的最大值决定,即期权收益为
| $ \max \left\{ {E - \mathop {\max }\limits_{1 \le k \le d} S_j^i\left( k \right),0} \right\}, $ | (2) |
BOYLE等[11]对美式期权的Monte Carlo模拟方法做了详细介绍和综述,其中提到:每生成一列Sti(i= 0,1,…,N)的路径后,一个明显的估计量为
| $ \hat P = \mathop {\max }\limits_{i = 0,1, \cdots ,d} {{\rm{e}}^{ - r{t_i}}}h\left( {{S_{{t_i}}}} \right). $ |
但此估计量是偏高的,即
LONGSTAFF等[14]利用最小二乘法确定了一个“期望函数”,并以期望函数的值作为期权继续持有的价值,与立刻执行的价值进行比较,决定是否提前执行.LSM方法的具体过程为:首先对每条模拟路径,求出tN时刻的期权收益,作为相应路径在tN时刻的期权收益贴现到tN-1时刻的现金流Y关于tN-1时刻d个标的资产的价格向量X的线性回归,用最小二乘法求出回归系数,称所得的函数为条件期望函数.对期权收益为正的路径,将tN-1时刻的X值代入线性回归函数,求得相应的条件期望函数值.然后比较此值与在tN-1时刻执行的收益大小,以确定期权在该路径上是否提前执行,进而计算tN-1时刻期权的价格.最后重复上述过程,依次计算前面各时刻美式期权的价格,直到t1时刻,计算所有路径期权价格的平均值,取该平均值与0时刻期权价值中较大者作为期权价格的最终估计值.需要强调的是,在作线性回归时,LSM方法仅对处于在值状态(期权收益为正)的路径进行回归,其余路径仅作为贴现,从而减少了计算时间,大大提高了算法的效率.
美式期权的后向性质决定了定价时需要把所有模拟路径存储下来,这对计算机存储量的要求很高.CHAN等[15]提出了一种不用存储所有模拟路径的简化算法.该方法主要基于模型中的2个重要性质:计算机生成的随机数具有伪随机性,即随机数可由“种子”确定和几何布朗运动的特点.一方面从式(1) 可以得到所有路径SNi的表达式:
| $ \begin{array}{l} \mathit{\boldsymbol{S}}_N^i = {\mathit{\boldsymbol{S}}_0}\exp \left( {N\left( {r - \frac{{\mathit{\boldsymbol{\sigma }} \cdot \mathit{\boldsymbol{\sigma }}}}{2}} \right)\Delta t + } \right.\\ \left. {\sqrt {\Delta t} V\left( {{\bf{z}}_1^i + {\bf{z}}_2^i + \cdots + {\bf{z}}_N^i} \right)} \right),\\ 1 \le i \le M, \end{array} $ | (3) |
其中S0为初始资产价格向量,σ·σ=(σ12, σ22,…,σd2)T,Sji和zji均为d维向量.可见要计算最终股价模拟值SNi,无须把所有随机数都记录下来,只要求
| $ \begin{array}{l} \mathit{\boldsymbol{S}}_{j - 1}^i\left( k \right) = \mathit{\boldsymbol{S}}_j^i\left( k \right) \times \\ \;\;\;\;\;\;\;\;\exp \left( { - \left( {r - \frac{1}{2}\sigma _k^2} \right)\sqrt {\Delta t} \sum\limits_{l - 1}^d {V\left( {k,l} \right)\mathit{\boldsymbol{z}}_j^i\left( l \right)} } \right), \end{array} $ | (4) |
其中, k=1,2,…,d,j=1,2,…,N,i=1,2,…,M.式(4) 表明,在给定{Sji}i=1M的条件下,要计算{Sj-1i}i=1M,只需要计算随机数向量{zji}i=1M即可,而相应的随机数可由存储的相应种子确定.该方法大大降低了计算机存储量,提高了计算效率,可用于计算多标的资产及路径依赖型的美式期权定价.
1 基于方差缩减的LSM算法 1.1 方差缩减优化方法文献[10-11]详细介绍了各种方差缩减技术的理论依据,并用数值例子进行了比较和分析.本文选用了其中2种方法:对偶变量法和控制变量法.用数值例子比较这2种方法在处理实际问题时的效果.
1.1.1 对偶变量法对偶变量法利用变量之间的负相关性减小方差.就美式期权定价问题而言,需要利用服从标准正态分布的随机数计算期权价格.注意到若i服从标准正态分布,则Sji也如此.具体来说,每次模拟,首先生成随机数序列,并计算期权价格,设算得的期权价格估计为Y1.然后,把每个随机数用其相反数代替,其余方法完全相同,可得到一个期权价格估计,记为Y2.用2个估计的平均值估计期权价格,即
下面讨论对偶变量法的方差缩减效果和运算效率.从理论上说,因为估计量Y1和Y2的方差相同,所以
| $ {\rm{Var}}\left( {\frac{{{Y_1} + {Y_2}}}{2}} \right) = \frac{1}{2}\left( {{\rm{Var}}\left( {{Y_1}} \right) + {\rm{Cov}}\left[ {{Y_1},{Y_2}} \right]} \right). $ | (5) |
如果Cov[Y1, Y2]≤Var(Y1),那么就有Var(YAV)≤Var(Y1).但是YAV的计算量是Y1的2倍,在考虑效率问题时,必须将所需计算量也考虑在内.因此,想要提高计算效率,需满足
| $ 2{\rm{Var}}\left( {{Y_{{\rm{AV}}}}} \right) \le {\rm{Var}}\left( {{Y_{\rm{1}}}} \right), $ | (6) |
此条件等价于Cov[Y1, Y2]≤0.事实上,Y1和Y2都是模拟所生成的随机数的函数,BROADIE等[13]指出,只要Y1关于随机数的函数(记为φ)是单调的,对偶变量法总能起到减小方差的效果.方差缩减比率为
| $ \begin{array}{l} VRE{R_{{\rm{AV}}}} = \frac{{{\rm{Var}}\left( {{Y_{\rm{1}}}} \right)}}{{{\rm{Var}}\left( {{Y_{{\rm{AV}}}}} \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\rm{Var}}\left( {{Y_{\rm{1}}}} \right)}}{{2{\rm{Var}}\left( {\left( {{Y_1} + {Y_2}} \right)/2} \right)}} = \frac{1}{{1 + \rho }}, \end{array} $ | (7) |
其中ρ=Cov[Y1, Y2].ρ越小,方差缩减效果越好.对美式期权来说,φ十分复杂,想要计算Y1和Y2的相关系数也很困难,方差缩减效果只能通过模拟来估计.
1.1.2 控制变量法控制变量法是通过一个与期权价格相关性较大的控制变量来减小方差的.本文利用单一控制变量技术的推广——复合控制变量进行计算.选取基础资产价格向量作为控制变量,每次模拟时,记资产价格向量为Xi=(Xi(1), Xi(2),…,Xi(d)),期权价格的原始估计为Yi,i=1,2,…,M.此时,E(X)是已知的,随机变量X和Y的随机模拟样本(Xi, Yi)是独立同分布的,且其协方差矩阵为
| $ \Sigma = \left[ {\begin{array}{*{20}{c}} {{\Sigma _\mathit{\boldsymbol{X}}}}&{{\Sigma _{\mathit{\boldsymbol{XY}}}}}\\ {\Sigma _{\mathit{\boldsymbol{X}}Y}^T}&{\mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2} \end{array}} \right], $ | (8) |
其中,∑X为d×d矩阵,∑XY为d×1矩阵,标量σY2为Y的方差.最终的估计量定义为
| $ {\mathit{\boldsymbol{Y}}_{{\rm{CV}}}} = \mathit{\boldsymbol{\bar Y}} - {\mathit{\boldsymbol{b}}^T}\left( {\mathit{\boldsymbol{\bar X}} - E\left( \mathit{\boldsymbol{X}} \right)} \right), $ |
其中Y为随机变量Y的粗糙估计量,X为随机向量X的粗糙估计量,b为系数向量.控制变量YCV的方差
| $ \begin{array}{*{20}{c}} {{\rm{Var}}\left( {{\mathit{\boldsymbol{Y}}_{{\rm{CV}}}}} \right) = {\rm{Var}}\left( {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{b}}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}} - E\left[ \mathit{\boldsymbol{X}} \right]} \right)} \right) = }\\ {\mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2 - 2{\mathit{\boldsymbol{b}}^T}{\Sigma _{\mathit{\boldsymbol{XY}}}} + {\mathit{\boldsymbol{b}}^T}{\Sigma _\mathit{\boldsymbol{X}}}\mathit{\boldsymbol{b}},} \end{array} $ | (9) |
其中当系数向量b取最优系数向量
| $ {\mathit{\boldsymbol{b}}^ * } = \Sigma _\mathit{\boldsymbol{X}}^{ - 1}{\Sigma _{\mathit{\boldsymbol{XY}}}} $ |
时,控制变量YCV的方差取最小值:
| $ {\rm{Var}}\left( {{\mathit{\boldsymbol{Y}}_{{\rm{CV}}}}} \right) = \mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2 - \Sigma _{\mathit{\boldsymbol{X}}Y}^T\Sigma _\mathit{\boldsymbol{X}}^{ - 1}{\Sigma _{\mathit{\boldsymbol{XY}}}} = \mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2\left( {1 - {\mathit{\boldsymbol{R}}^2}} \right). $ | (10) |
其中R2= ∑XYT ∑X-1 ∑XY/σY2.此时方差缩减效率为
| $ VRE{R_{{\rm{CV}}}} = \frac{{{\rm{Var}}\left( \mathit{\boldsymbol{Y}} \right)}}{{{\rm{Var}}\left( {{\mathit{\boldsymbol{Y}}_{{\rm{CV}}}}} \right)}} = \frac{{\mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2}}{{\mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{Y}}^2\left( {1 - {\mathit{\boldsymbol{R}}^2}} \right)}} = \frac{1}{{1 - {\mathit{\boldsymbol{R}}^2}}}, $ | (11) |
R2越大,方差缩减效果越好.在实际计算中,最优系数向量的确定步骤为:先用小样本估计样本方差SX与样本协方差SXY,分别代替∑X和∑XY并代入式(10), 计算最优系数向量.要求小样本数目远小于期权定价的模拟数目.
具体来说,首先在模拟M条路径之前,先以完全相同的方法生成m条路径,得到资产价格模拟向量Xi=(Xi(1), Xi(2),…,Xi(d))和期权价格模拟值Yi,i=1,2,…,m.在此基础上,计算随机模拟样本(Xi, Yi)的样本方差SX与样本协方差SXY ,其中SX为d×d矩阵,其第jk个元素为
| $ \frac{1}{{m - 1}}\left( {\sum\limits_{i = 1}^m {X_i^{\left( j \right)}X_i^{\left( k \right)}} - n{{\bar X}^{\left( j \right)}}{{\bar X}^{\left( k \right)}}} \right), $ | (12) |
SXY为d×1矩阵,其第j个元素为
| $ \frac{1}{{m - 1}}\left( {\sum\limits_{i = 1}^m {X_i^{\left( j \right)}{\mathit{\boldsymbol{Y}}_i}} - n{{\bar X}^{\left( j \right)}}\mathit{\boldsymbol{\bar Y}}} \right). $ | (13) |
此时选取的最优系数向量的估计为
首先,按如下顺序生成随机数序列.设N维向量s用于储存随机数种子.先任意给出一个种子s(1),以它开始随机数发生,从t1时刻开始,在每条路径i上,生成一个d维随机数向量,然后生成后面时刻所需的随机数.在每生成M个随机向量后,得到并储存当前种子s(j).重要的是不需要储存任何生成的随机数zji(k),只需求和式
然后,根据式(4) 求得SNi,且只需{zNi}i=1M就可以进一步求出SN-1i.此时,结合LSM方法,决定是否在该时刻执行期权.若结果为即刻执行,则将期权价值向量p中相应路径的数值更新为即刻执行的价值.若结果为继续持有,则不改变向量p中相应路径的数值.按照上述方法,依次向前计算,直到t1时刻.
最后,分别结合对偶变量法和控制变量法对求得的估计值做进一步修正,得到最终估计值,并运用批处理方法计算估计量的方差,因为此两方法都破坏了样本间的独立性.
2 数值例子考虑3个无红利标的资产的美式看跌期权(d=3),期权价值由式(2) 决定,敲定价格为E.3种资产的初始价格S0为(40, 40, 40)T,无风险利率r为0.05,资产的波动率分别为0.2, 0.3和0.5,到期时间为T,假设标的资产之间的相关系数均为ρ,选取M=1 000, N=10,采用Matlab计算,并用文献[11]中的例子进行检验.
表 1分别给出了基本Monte Carlo方法、对偶变量法和控制变量法的计算结果.其中,mean列和std列分别代表重复10次运算的均值和样本标准差,CI(confidence interval)列为由10次运算结果得到的置信度为95%的置信区间,PDE列是用经典积分方法算得的结果;T的单位为月,资产价格的单位为美元.
| 表 1 原始方法、对偶变量法和控制变量法的计算结果 Table 1 Computing results on original、antithetic variates and control variates methods |
为了更明显地比较缩减效果,表 2列出了这2种方法的方差缩减比.其中
| 表 2 对偶变量法和控制变量法的标准差缩减效率 Table 2 Standard deviation reduction efficiency on AV and CV methods |
为了分析计算结果的稳定性,下面对3种方法的均值和标准差做进一步比较.选定T=7, E=40,选取ρ=0,1,对前文所述的方法分别重复50次,作散点图,得到图 1和图 2,图中每个点都代表 10次模拟得到的均值和标准差.
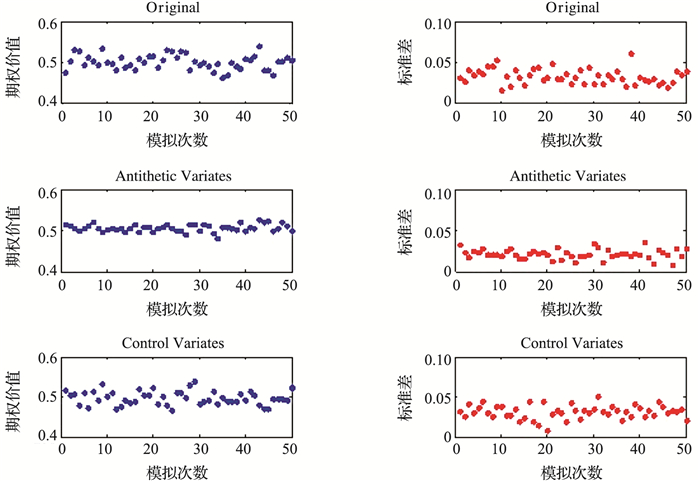
|
图 1 ρ=0, T=7, E=40情形下3种方法的比较 Fig. 1 Comparison of three methods in the case of ρ=0, T=7, E=40 |

|
图 2 ρ=1, T=7, E=40情形下3种方法的比较 Fig. 2 Comparison of three methods in the case of ρ=1, T=7, E=40 |
根据散点图进行横向比较可得,在3种参数选择下,对偶变量法和控制变量法都能起到减小方差的作用,对偶变量法缩减效果十分明显,而控制变量法相对不明显.纵向比较可得,控制变量法在ρ=1时的方差缩减效果比ρ=0时要高,而对偶变量法则表现得比较平均.其原因为控制变量法的缩减效率取决于控制变量与期权价格的相关程度,相关程度越高,效果越好.在本文中,控制变量为模拟股价,期权收益由股价的最大值决定,故两者间的相关系数取决于标的资产间的相关系数.当ρ=0时,标的资产间的相关性低,控制变量的缩减效果并不明显,甚至有几次模拟的标准差比未使用控制变量的标准差最大值还大.当ρ=1时,标的资产间的相关性高,控制变量和期权收益的相关性也高,控制变量的缩减效果较之前有明显提高.而对偶变量法的缩减效率由对偶变量产生的估计量的相关系数决定,与到期时间、资产间相关系数等参数无直接关系,所以对偶变量法在不同参数下表现较为平均.
3 总结充分利用Monte Carlo方法的特点和优势,讨论了一个多目标资产的美式期权定价问题,运用线性回归思想以及几何布朗运动和伪随机数的性质,在LSM方法的基础上,结合存储量减小方法和方差缩减技术,对不同参数下美式期权定价进行了比较和分析.采用对偶变量法和控制变量法缩减基本方差,讨论了决定其方差缩减效果的因素和参数估计的方法.从计算结果看,对偶变量法较控制变量法标准差缩减效果更明显,且对偶变量法在不同参数下的表现比较平均,而控制变量法的效果取决于标的资产间的相关系数,这是由所选取的控制变量所决定的.
然而,需要指出的是,本文的计算结果还不够稳定、收敛性不够高,这也是Monte Carlo方法的缺点之一.若采用拟蒙特卡洛方法(quasi-Monte Carlo),用确定性的低偏差序列(low discrepancy sequences)代替随机点列,可改进Monte Carlo方法的收敛性.如何利用拟蒙特卡洛方法提高算法的收敛性是未来研究的一个重要方向.
| [1] | JIN X, YANG C Y. Efficient estimation of lower and upper bounds for pricing higher-dimensional American arithmetic average options by approximating their payoff functions[J]. International Review of Financial Analysis, 2016, 44: 65–77. DOI:10.1016/j.irfa.2016.01.009 |
| [2] | BALAJEWICZ M, TOIVANEN J. Reduced order models for pricing American options under stochastic volatility and jump-diffusion models[J]. Procedia Computer Science, 2016, 80: 734–743. DOI:10.1016/j.procs.2016.05.360 |
| [3] | CHEN W T, XU X, ZHU S P. A predictor-corrector approach for pricing American options under the finite moment log-stable model[J]. Applied Numerical Mathematics, 2015, 97: 15–29. DOI:10.1016/j.apnum.2015.06.004 |
| [4] | JIN X, LI X, HWEE H T, et al. A computationally efficient state-space partitioning approach to pricing high-dimensional American options via dimension reduction[J]. European Journal of Operational Research, 2013, 231(2): 362–370. DOI:10.1016/j.ejor.2013.05.035 |
| [5] | HU W B, LI S H. The forward-path method for pricing multi-asset American-style options under general diffusion processes[J]. Journal of Computational and Applied Mathematics, 2014, 263: 25–31. DOI:10.1016/j.cam.2013.11.026 |
| [6] | HU Y H, LI Q, CAO Z Y, et al. Parallel simulation of high-dimensional American option pricing based on CPU versus MIC[J]. Concurrency and Computation-practice & Experience, 2015, 27(5): 1110–1121. |
| [7] | BASTANI A F, ZAHMADI Z, DAMIRCHELI D. A radial basis collocation method for pricing American options under regime-switching jump-diffusion models[J]. Applied Numerical Mathematics, 2013, 65: 79–90. DOI:10.1016/j.apnum.2012.10.005 |
| [8] | LABUSCHAGNE C C A, BOETTICHER S T V. Dupire's formulas in the Piterbarg option pricing model[J]. The North American Journal of Economics and Finance, 2016, 38: 148–162. DOI:10.1016/j.najef.2016.09.002 |
| [9] | YU X S, LIU Q. Canonical least-squares Monte Carlo valuation of American options:Convergence and empirical pricing analysis[J]. Mathematical Problems in Engineering, 2014(1): 1–13. |
| [10] |
陈辉. 期权定价的蒙特卡罗模拟方差缩减技术研究[J].
统计与信息论坛, 2008, 23(7): 86–96.
CHEN H. Variance reduction techniques of Monte Carlo simulation methods in options pricing[J]. Statistics & Information Tribune, 2008, 23(7): 86–96. |
| [11] | BOYLE P, BROADIE M, GLASSERMAN P. Monte Carlo methods for security pricing[J]. Journal of Economic Dynamics and Control, 1997, 21: 1267–1321. DOI:10.1016/S0165-1889(97)00028-6 |
| [12] | BARRAQUAND J, MARTINEAU D. Numerical valuation of high dimensional multivariate American securities[J]. Journal of Financial and Quantitative Analysis, 1995, 30: 383–405. DOI:10.2307/2331347 |
| [13] | BROADIE M, GLASSERMAN P. Pricing American-style securities using simulation[J]. Journal of Economic Dynamics and Control, 1997, 21: 1323–1352. DOI:10.1016/S0165-1889(97)00029-8 |
| [14] | LONGSTAFF F A, SCHWARTZ E S. Valuing American options by simulation:A simple least-squares approach[J]. Review of Financial Studies, 2001, 14(1): 113–147. DOI:10.1093/rfs/14.1.113 |
| [15] | CHAN R H, WONG C, YEUNG K. Pricing multi-asset American-style options by memory reduction Monte Carlo methods[J]. Applied Mathematics and Computation, 2006, 179: 535–544. DOI:10.1016/j.amc.2005.11.108 |



