2. 华东师范大学 数学系, 上海 200062
2. Department of Mathematics, East China Normal University, Shanghai 200062, China
图的完美匹配计数已经被证实是NP-难问题, 因此要得到一般图的完美匹配数目是非常困难的.该问题在蛋白质结构预测、量子化学、晶体物理学和计算机科学等领域都有重要应用, 对此问题的研究具有非常重要的理论价值和现实意义[1-9].本文用划分、求和、再递推的方法分别给出了4-1-nC10和2-nT2图的完美匹配数目的计算公式.该方法能够计算许多类图的所有完美匹配的数目.
定义1 若G图的2个完美匹配M1和M2中有一条边不同, 则称M1和M2是G的2个不同的完美匹配.
定义2 设2条长为n的路:P1=u1u2…un+1, P2=v1v2…vn+1, 分别连接路P1与P2的顶点ui与vi(i=1, 2, …, n+1) 得到的图, 称长为n的梯子, 记为Tn.
n个长为10的圈记为
| $ {C^i} = {u_{i1}}{u_{i2}}{u_{i3}}{v_{i2}}{w_{i3}}{w_{i2}}{w_{i1}}{w_{i4}}{v_{i1}}{u_{i4}}\left( {i = 1, 2, ..., n} \right). $ |
连接圈Ci上顶点vi1与vi2, 连接圈Ci与Ci+1的顶点ui2与ui+1, 1, ui3与ui+1, 4, wi3与wi+1, 4, wi2与wi+1, 1(i=1, 2, …, n-1), 再分别连接圈C1与Cn的顶点u14与w14, u11与w11, un3与wn3, un2与wn2, 得到的图记为4-1-nC10, 如图 1所示.
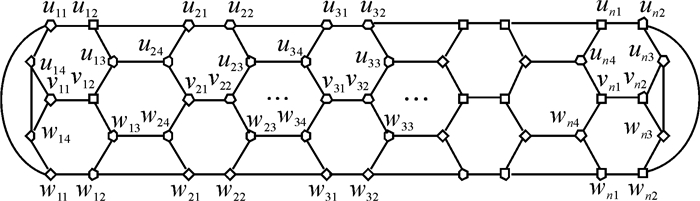
|
图 1 4-1-nC10图 Fig. 1 Graph of 4-1-nC10 |
设n个长为2的梯子T2i, 其顶点集为V(T2i)=ui1, ui2, ui3, vi1, vi2, vi3(i=1, 2, …, n).连接梯子T2i和T2i+1的顶点vi1与ui+1, 1、vi3与ui+1, 3(i=1, 2, …, n-1),再连接梯子T21的顶点u11与u13、T2n的顶点vn1与vn3,得到的图记为2-nT2, 如图 2所示.
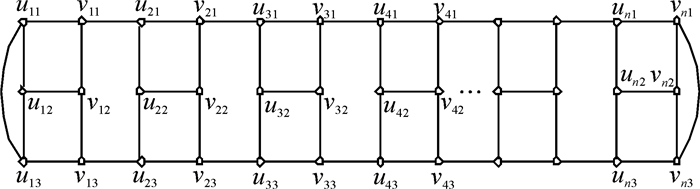
|
图 2 2-nT2图 Fig. 2 Graph of 2-nT2 |
定理1 f(n)表示4-1-nC10图完美匹配的数目, 则
| $ f\left( n \right) = {2^{n-2}} \cdot {\left( {2 + \sqrt 2 } \right)^{n + 1}} + {2^{n-2}} \cdot {\left( {2-\sqrt 2 } \right)^{n + 1}} + 1. $ |
证明 4-1-nC10图是3正则3边连通图, 显然存在完美匹配.欲求f(n), 需定义G1, G2, G3图, 并分别求出其完美匹配的数目.4-1-nC10图删除边u11w11, u14w14后得到的图记为G; 将路u1u2vw的顶点u1, u2, w分别与G图的顶点u11, u14, w14连接,得到的图记为G1; 将路uvw1w2的顶点u, w1, w2分别与G图的顶点u14, w14, w11连接,得到的图记为G2; 将路u1u2的顶点u1, u2分别与G图的顶点u11, u14连接, 再将路w1w2的顶点w1, w2分别与G图的顶点w14, w11连接,得到的图记为G3; G1, G2, G3图分别如图 3~5所示.显然G1, G2, G3图都存在完美匹配, 且
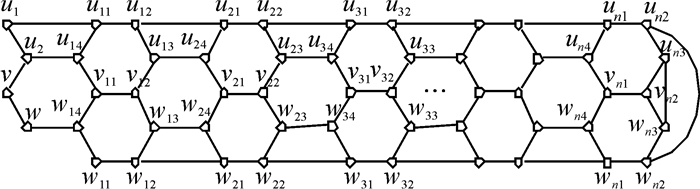
|
图 3 G1图 Fig. 3 Graph of G1 |

|
图 4 G2图 Fig. 4 Graph of G2 |
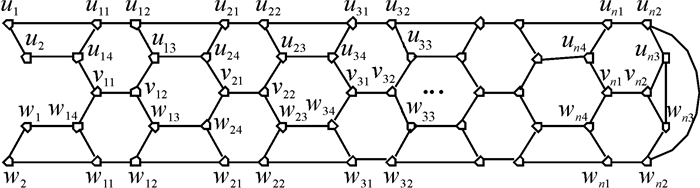
|
图 5 G3图 Fig. 5 Graph of G3 |
设G1, G2, G3图的完美匹配数分别为a(n), b(n), c(n), 则a(n)=b(n).
G1图的完美匹配按饱和顶点u1可划分为以下6种情形:
情形1 由c(n)的定义, G1图包含边u1u11, u2u14, vw, v11v12, w14w11的完美匹配数为c(n-1).
情形2 由a(n)的定义, G1图包含边u1u11, u2u14, vw, v11w14, w11w12的完美匹配数为a(n-1).
情形3 由a(n)的定义, G1图包含边u1u11, u2v, ww14, v11w14, w11w12的完美匹配数为a(n-1).
情形4 由b(n)的定义, G1图包含边u1u11, u2u14, vw, v11w14, w11w12的完美匹配数为b(n-1), 又a(n)=b(n), 所以b(n-1)=a(n-1).
情形5 由c(n)的定义, G1图包含边u1u2, u11u14, vw, v11v12, w14w11的完美匹配数为c(n-1).
情形6 由a(n)的定义, G1图包含边u1u2, u11u13, vw, v11w14, w11w12的完美匹配数为a(n-1).
综上所述,
| $ a\left( n \right) = 4a\left( {n-1} \right) + 2c\left( {n-1} \right). $ | (1) |
G3图的完美匹配按饱和顶点u1可分以下8种情形求得:
情形1 由c(n)的定义, G3图包含边u1u11, u2u14, v11v12, w1w14, w2w11的完美匹配数为c(n-1).
情形2 由a(n)的定义, G3图包含边u1u11, u2u14, w1w2, v11w14, w11w12的完美匹配数为a(n-1).
情形3 由c(n)的定义, G3图包含边u1u11, u2u14, v11v12, w1w2, w14w11的完美匹配数为c(n-1).
情形4 由c(n)的定义, G3图包含边u1u2, u11u14, v11v12, w1w2, w14w11的完美匹配数为c(n-1).
情形5 由c(n)的定义, G3图包含边u1u2, u11u14, v11v12, w1w14, w2w11的完美匹配数为c(n-1).
情形6 由a(n)的定义, G3图包含边u1u2, u11u14, v11w14, w1w2, w11w12的完美匹配数为a(n-1).
情形7 由b(n)的定义, G3图包含边u1u2, u11u12, u14v11, w1w14, w2w11的完美匹配数为b(n-1), 又a(n)=b(n), 所以b(n-1)=a(n-1).
情形8 由b(n)的定义, G3图包含边u1u2, u11u12, u14v11, w1w2, w14w11的完美匹配数为b(n-1), 又a(n)=b(n), 所以b(n-1)=a(n-1).
综上所述,
| $ c\left( n \right) = 4a\left( {n-1} \right) + 4c\left( {n-1} \right). $ | (2) |
4-1-nC10图的完美匹配按饱和顶点u11可分以下5种情形求得:
情形1 由c(n)的定义, 4-1-nC10图包含边u11w11, u14w14, v11v12的完美匹配数为c(n-1).
情形2 由a(n)的定义, 4-1-nC10图包含边u11u14, v11w14, w11w12的完美匹配数为a(n-1).
情形3 由c(n)的定义, 4-1-nC10图包含边u11u14, w11v12, w14w11的完美匹配数为c(n-1).
情形4 由b(n)的定义, 4-1-nC10图包含边u11u12, u14v11, w14w11的完美匹配数为b(n-1), 又a(n)=b(n), 所以b(n-1)=a(n-1).
情形5 4-1-nC10图的完美匹配包含边u11u12, u14w14, v11v12, w11w12, 则该完美匹配一定包含边ui3ui+1, 4, wi3wi+1, 4, ui+1, 1ui+1, 2, vi+1, 1vi+1, 2, wi+1, 1wi+1, 2, i=1, 2, …, n-1.所以4-1-nC10图包含边u11u12, u14w14, v11v12, w11w12的完美匹配恰有1个.
综上所述,
| $ f\left( n \right) = 2a\left( {n-1} \right) + 2c\left( {n-1} \right) + 1. $ | (3) |
将式(1) 和(2) 代入式(3), 得
| $ f\left( n \right) = 16a\left( {n-2} \right) + 12c\left( {n-2} \right) + 1, $ | (4) |
由式(3) 得
| $ f\left( {n-1} \right) = 2a\left( {n-2} \right) + 2c\left( {n-2} \right) + 1, $ | (5) |
式(4)-式(5)×8得
| $ f\left( n \right) = 8f\left( {n-1} \right)-4c\left( {n-2} \right) - 7. $ | (6) |
由式(2) 和(3) 得
| $ c\left( n \right) = 2f\left( n \right)-2, $ | (7) |
由式(6) 和(7) 得
| $ f\left( n \right) = 8f\left( {n-1} \right)-8f\left( {n-2} \right) + 1. $ | (8) |
易知非齐次线性递推式(8) 的特解为1.
齐次线性递推式f(n)=8f(n-1)-8f(n-2) 的通解为
| $ f\left( n \right) = {c_1}{\left( {4 + 2\sqrt 2 } \right)^n} + {c_2}{\left( {4-2\sqrt 2 } \right)^n}. $ | (9) |
由图 6知f(1)=7.由式(3) 知,
f(2)=2a(1)+2c(1)+1.

|
图 6 图 4-1-1×C10的所有完美对集 Fig. 6 All perfect matchings of 4-1-1×C10 graph |
由图 7知a(1)=8.
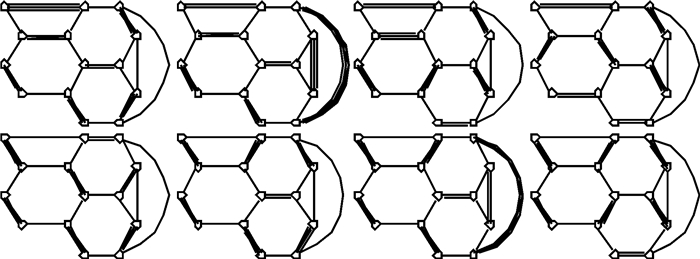
|
图 7 G4图 Fig. 7 Graph of G4 |
由图 8知c(1)=12.所以,

|
图 8 G5图 Fig. 8 Graph of G5 |
f(2)=2×8+2×12+1=41.
因此, 线性递推式(8) 满足f(1)=7, f(2)=41的解为
| $ f\left( n \right) = {2^{n-2}} \cdot {\left( {2 + \sqrt 2 } \right)^{n + 1}} + {2^{n-2}} \cdot {\left( {2-\sqrt 2 } \right)^{n + 1}} + 1. $ |
定理2 g(n)表示2-nT2图的完美匹配数目, 则g(n)=3n+1.
证明 2-nT2图是2边连通3正则图, 显然存在完美匹配.为求g(n), 先定义G6图.删除2-nT2图的边u11u13得到的图记为G6, 如图 9所示.
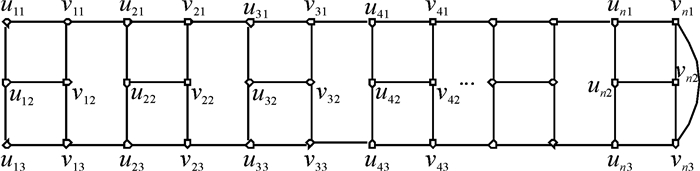
|
图 9 G6图 Fig. 9 Graph of G6 |
显然,G6图存在完美匹配,其完美匹配数记为d(n).G6图的完美匹配按饱和顶点u11的情况可分以下3种情形求得:
情形1 由d(n)的定义, G6图包含边u11v11, u12v12, u13v13的完美匹配数为d(n-1).
情形2 由d(n)的定义, G6图包含边u11v11, u12u13, v12v13的完美匹配数为d(n-1).
情形3 由d(n)的定义, G6图包含边u11u12, v11v12, u13v13的完美匹配数为d(n-1).
综上所述, d(n)=3d(n-1)=3n-1·d(1),易知
| $ d\left( 1 \right) = 3, 所以d\left( n \right) = {3^n}. $ | (10) |
2-nT2图的完美匹配按饱和顶点u11可分以下4种情形求得:
情形1 2-nT2图的完美匹配包含边u11u13, 则其必包含边ui2vi2(i=1, 2, …, n), vi1ui+11, vi3ui+13(i=1, 2, …, n-1), vn1vn3.所以2-nT2图包含边u11u13的完美匹配恰有一个.
情形2 由d(n)的定义, 2-nT2图包含边u11u12, v11v12, u13v13的完美匹配数为d(n-1).
情形3 由d(n)的定义, 2-nT2图包含边u11v11, u12v12, u13v13的完美匹配数为d(n-1).
情形4 由d(n)的定义, 2-nT2图包含边u11v11, u12u13, v12v13的完美匹配数为d(n-1).
综上所述,
| $ g\left( n \right) = 3d\left( {n-1} \right) + 1. $ | (11) |
由式(10) 和(11), 得g(n)=3n+1.
| [1] | LOVÁSZ L, PLUMMER M. Matching Theory[M]. New York: North-Holland Press, 1986. |
| [2] | KRÁL D, SERENI J S, STIEBITZ M. A new lower bound on the number of perfect matchings in cubic graphs[J]. Discrete Math, 2009, 23: 1465–1483. |
| [3] | KARDOS F, KRÁL D, MISKUF J, et al. Fullerene graphs have exponentially many perfect matchings[J]. Journal of Mathematical Chemistry, 2009, 46: 443–447. DOI:10.1007/s10910-008-9471-7 |
| [4] |
唐保祥, 任韩. 几类图完美匹配的数目[J].
南京师大学报:自然科学版, 2010, 33(3): 1–6.
TANG B X, REN H. The number of perfect matching for three specific types of graphs[J]. Journal of Nanjing Normal University: Natural Science Edition, 2010, 33(3): 1–6. |
| [5] |
唐保祥, 李刚, 任韩. 3类图完美匹配的数目[J].
浙江大学学报:理学版, 2011, 38(4): 387–390.
TANG B X, LI G, REN H. The number of perfect matching for three specific types of graphs[J]. Journal of Zhejiang University: Science Edition, 2011, 38(4): 387–390. |
| [6] |
唐保祥, 任韩. 3类特殊图完美对集数的计算[J].
南开大学学报:自然科学版, 2014, 47(5): 11–16.
TANG B X, REN H. The enumeration of perfect matchings in three types of special graphs[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2014, 47(5): 11–16. |
| [7] |
唐保祥, 任韩. 4类图完美匹配数目的递推求法[J].
数学杂志, 2015, 353(2): 626–634.
TANG B X, REN H. Recursive method for finding the number of perfect matchings of the four types of graphs[J]. Journal of Mathematics, 2015, 353(2): 626–634. |
| [8] |
唐保祥, 任韩. 4类图完美匹配的计数[J].
武汉大学学报:理学版, 2011, 58(5): 441–446.
TANG B X, REN H. The number of perfect matchings in four types of graphs[J]. Journal of Wuhan University: Natural Science Edition, 2011, 58(5): 441–446. |
| [9] |
唐保祥, 任韩. 5类图完美匹配的计数[J].
中山大学学报:自然科学版, 2012, 51(4): 31–37.
TANG B X, REN H. The number of perfect matchings in five types of graphs[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(4): 31–37. |


