面向多尺度拓扑优化的渐进均匀化GPU并行算法研究

doi:10.3785/j.issn.1008-9497.2023.06.007

面向多尺度拓扑优化的渐进均匀化GPU并行算法研究

夏兆辉^,¹, 刘健力¹, 高百川¹, 聂涛¹, 余琛^,^,², 陈龙³, 余金桂⁴

1.华中科技大学机械科学与工程学院/智能制造装备与技术全国重点实验室，湖北武汉 430074

2.武汉轻工大学数学与计算机学院，湖北武汉 430023

3.上海理工大学机械工程学院，上海 200093

4.武汉理工大学机电工程学院，湖北武汉 430070

Efficient GPU parallel strategy for multi-scale topology optimization via asymptotic homogenization

XIA Zhaohui^,¹, LIU Jianli¹, GAO Baichuan¹, NIE Tao¹, YU Chen^,^,², CHEN Long³, YU Jingui⁴

1.School of Mechanical Science and Engineering/National Key Laboratory of Advanced Manufacturing Technology，Huazhong University of Science and Technology，Wuhan 430074，China

2.School of Mathematics and Computer Science，Wuhan Polytechnic University，Wuhan 430023，China

3.School of Mechanical Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China

4.School of Mechanical and Electrical Engineering，Wuhan University of Technology，Wuhan 430070，China

通讯作者: ORCID：https：//orcid.org/0000-0002-6814-0638，E-mail：mc_yuchen@whpu.edu.cn.

收稿日期: 2023-07-12 修回日期: 2023-07-20 接受日期: 2023-07-28

基金资助:

国家自然科学基金青年项目. 52005192
国家重点研发计划青年科学家项目. 2022YFB3302900

Received: 2023-07-12 Revised: 2023-07-20 Accepted: 2023-07-28

作者简介 About authors

夏兆辉（1986—），ORCID：https：//orcid.org/0000-0002-0299-6871，男，博士，主要从事CAD/CAE设计分析优化一体化方法与工业软件技术研究. 。

摘要

针对多尺度结构拓扑设计计算效率低等问题，提出了一种基于水平集渐进均匀化的多尺度拓扑优化并行算法。基于通用图形处理器（graphics processing unit，GPU），通过水平集初始化、大型稀疏刚度矩阵方程求解以及本构矩阵并行计算，可大幅提升渐进均匀化算法的效率。实验结果表明，当三维晶胞单元网格细化至分辨率为10万时，多尺度结构拓扑优化GPU并行算法较CPU串行算法快数十倍。

关键词： 多尺度拓扑优化 ; 渐进均匀化 ; 统一计算设备架构（CUDA） ; GPU并行计算

Abstract

In response to the low computational efficiency in the context of multi-scale structural topology design, an efficient asymptotic homogenization GPU parallel strategy is presented. The strategy leverages the graphics processing unit (GPU) and investigates parallel strategies for level set initialization, large sparse stiffness matrix equations solving and constitutive properties computing. Experimental results demonstrate that the computing efficiency of the asymptotic homogenization can be greatly improved by adopting the parallel strategies, in particular, when refining a three-dimensional unit cell grid to a resolution of 100 000, the GPU parallel strategy achieves a speedup of two orders of magnitude compared to the CPU serial.

Keywords： multi-scale topology optimization ; asymptotic homogenization ; compute unified device architecture (CUDA) ; GPU parallel computing

PDF (4553KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

夏兆辉, 刘健力, 高百川, 聂涛, 余琛, 陈龙, 余金桂. 面向多尺度拓扑优化的渐进均匀化GPU并行算法研究. 浙江大学学报(理学版)[J], 2023, 50(6): 722-735 doi:10.3785/j.issn.1008-9497.2023.06.007

XIA Zhaohui, LIU Jianli, GAO Baichuan, NIE Tao, YU Chen, CHEN Long, YU Jingui. Efficient GPU parallel strategy for multi-scale topology optimization via asymptotic homogenization. Journal of Zhejiang University(Science Edition)[J], 2023, 50(6): 722-735 doi:10.3785/j.issn.1008-9497.2023.06.007

0　引言

自然界中的多孔材料如蛛丝、蜂巢、蚁穴等能以低密度实现高刚度和高强度^［1-3］，其高性能结构为科学家和工程师提供了众多设计灵感^［4-6］。近年来，增材制造技术的快速发展进一步推动了先进结构材料的设计^［7-8］，通过将拓扑优化方法和均匀化方法相结合，发展了多尺度拓扑优化方法。假设周期性多孔微结构单元均匀镶嵌在设计域中，当微结构单元的尺寸远小于宏观物体特征尺寸时，其多孔结构特性可通过均匀化方法表现为均质材料特征。进而利用拓扑优化方法对设计域每个微结构单元的几何结构进行优化，在满足约束的前提下使宏观物体性能达到最优。

多孔材料内部周期性结构特征复杂，为降低直接使用有限元分析模拟多孔材料的复杂度，研究了渐进均匀化方法^［9-10］。GUEDES等^［11］的工作表明，渐进均匀化方法是确定微观复合材料整体性能响应的有效工具，将非均质连续体替换为等效均匀化模型，得到基于单元的均匀化材料特性，并指定用具有该均匀化特性的固体材料替代周期性结构。近年来，均匀化方法已被广泛应用于研究复杂周期性材料的整体性能问题^［12-14］，文献［15］将均匀化方法用于多尺度并行设计，文献［16-19］采用均匀化方法分析了热弹性效应周期性材料的性能特征。更多关于多相材料渐进均匀化技术的前沿研究正在进行中^［20-21］，如文献［22-23］利用渐进均匀化技术研究了压电复合材料。

在多尺度拓扑优化过程中，渐进均匀化方法用等效模型表示多孔晶胞的力学性能，对结构复杂的周期性晶胞单元进行网格细化，当精度要求较高时计算成本也显著提高。图形处理单元（graphics processing unit，GPU）被广泛用于加速计算，尤其是用于超大规模数据计算^［24-25］。由于GPU具有支持并行计算所需大量线程的特殊体系架构，成为均匀化加速的强大工具。在均匀化研究领域，QUINTELA等^［26］用C实现了2D均匀化程序的串行版本，随后用OpenMP和CUDA实现了并行版本。为计算3D晶胞结构的弹性特性，QUINTELA等^［27］用OpenMP和统一计算设备架构（compute unified device architecture，CUDA）开发了并行版本均匀化程序，获得了较高的加速比。FRITZEN等^［28］在其提出的黏塑性材料混合计算均匀化方法基础上进行了扩展，为Nvidia GPU开发了高性能数值计算库，利用GPU提供的功能加速均匀化过程。另外，多尺度拓扑优化是一个迭代计算过程，在求解大规模问题时需消耗大量计算和内存资源。为求解更复杂、更大规模的问题，常用GPU进行并行计算。XIA等^［29］采用GPU和等几何分析（IGA）并行策略，提出基于水平集的拓扑优化方法，并比较了串行CPU、多线程并行CPU与GPU的效率，得到该并行策略的加速比达到了两个数量级。JESUS等^［30］将无矩阵迭代求解的细粒度GPU实例作为结构分析的求解工具，提出一种拓扑优化多粒度GPU的并行策略，并将其用于等值面提取和体积分数计算。HE等^［31］针对单个GPU分析大规模工程优化问题存在的效率低下和内存不足等问题，提出了一种基于多GPU平台的高效并行独立系数（IC）再分析方法，通过为每个GPU划分合理大小的矩阵和向量，实现良好的负载平衡和减少GPU之间的通信。DAVID等^［32］提出了一种基于分布式GPU计算的拓扑优化并行计算方法，用基于平滑聚合的代数多重网格（AMG）预处理的分布式共轭梯度求解器，利用多GPU平台计算求解，通过有限元分析（finite element analysis，FEA）获得线性方程组，并用结构化网格和非结构化网格对分布式GPU系统的性能与可扩展性进行了评估。

多孔材料特征复杂，需用多尺度拓扑优化方法，对普遍采用的渐进均匀化方法并行研究尚存在空白。当用多尺度拓扑对3D微结构模型进行尺度优化、形状优化时，求解弹性张量矩阵 $C^{H}$ 算法的时间复杂度为O（n³），n为微结构模型的离散程度。针对此问题，本文提出求解 $C^{H}$ 的高效GPU并行算法，步骤包括水平集初始化、大型稀疏刚度矩阵方程求解以及本构特性计算，为多尺度拓扑优化提供一种高效、可靠的计算方法，充分利用GPU的并行计算能力，大幅提升渐进均匀化算法的效率，可解决多尺度拓扑优化求解一系列多尺寸、多形状微结构单元 $C^{H}$ 矩阵效率低等问题。在模型构建层面，并行算法可增加模型精细化程度，为特征复杂的晶胞模型提供更大的设计空间；在总刚求解层面，刚度矩阵具有对称及正定特性，本文结合共轭梯度法研究GPU并行求解算法；在本构特性计算层面，本文算法支持多晶胞结构同时计算，充分考虑多尺度拓扑优化下晶胞结构的多样化个性。

1　基于均匀化方法的多尺度拓扑优化

1.1　多尺度几何模型构建

在多尺度拓扑优化问题中，宏观尺度与微观尺度相差多个数量级，需采取不同描述方法建立几何模型。在宏观尺度下，模型表示为几何空间中的连续区域，用设计域 $Ω$ 表示。设计域离散为有限个单元，本文以六面体单元为三维设计域有限单元模型，其内部结构表现为复杂多孔特征，适合渐进均匀化方法。为实现多尺度拓扑优化，需在微观尺度下进行多孔结构设计，本文采用基于网格线框模型生成微结构的方法^［13］，用水平集描述微结构模型，线框拓扑信息分别存放于结点矩阵和线框矩阵。结点矩阵大小为3×N（N为结点数），其列号代表线框结构中结点的编号，每列3行数据依次表示结点x坐标、y坐标和z坐标。由于两点确定一条线框，线框矩阵大小为2×M（M为线框数），每列依次存放线框的起、止结点编号。借助拓扑信息矩阵可自定义网格线框模型，表1和表2分别为结点矩阵和线框矩阵，线框模型可视化结果如图1所示。

表1 结点矩阵

Table 1 Node matrix

	2	3	4	5	6	7	8
1	1	0	0	1	0	1	1
2	0	1	0	0	1	1	1
3	0	0	1	1	1	0	1

新窗口打开| 下载CSV

表2 线框矩阵

Table 2 Wireframe matrix

	1	2	3	4	5	6	7	8		9	10	11	12
1	1	1	1	2	2	3	3	4		4	5	6	7
2	2	3	4	5	7	7	6	5		6	8	8	8

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 线框模型可视化

Fig.1 Visualization of wireframe model

一组节点以及节点间的连接关系表示微结构模型的基本结构特征，而其实体域范围由水平集初值描述，线框模型杆直径决定水平集函数值初始化。

1.2　多尺度分析模型构建

在多尺度结构拓扑优化问题中，基于微小应变与线弹性材料响应假设，在固定设计域 $Ω$ 内定义的结构位移场 $u$ 由静态平衡方程控制：

\begin{array}{l} d i v σ + b = 0, \\ σ = C ϵ, \\ ϵ = \frac{1}{2} (\nabla u + {(\nabla u)}^{T}), \end{array}\}

在

Ω 上

（1）

u = 0

，在

Γ_{e} 上

，

σ n = t ，

在

Γ_{n} 上

，

其中， $b$ 为体积力（考虑一般性，假定为0）， $ϵ$ 为无穷小应变张量， $σ$ 为与 $ϵ$ 相关的对称应力张量，可通过弹性张量 $C$ 计算得到，为得到微结构单元弹性张量 $C$ ，在边界 $\partial Ω$ 上应用基本自然边界， $Γ_{e}$ 和 $Γ_{n}$ 为在边界 $\partial Ω$ 上不相连的部分， $n$ 为 $\partial Ω$ 外表面法向量，在自由表面上， $t$ 为在 $Γ_{n}$ 上施加的指定牵引力，通常为0。

在宏观尺度上求解平衡方程式（1），需基于渐进均匀化方法获得微观尺度的有效信息，即均匀化单元弹性张量 $C$ 。渐进均匀化，可用等效模型表示微结构单元的力学性能，已被广泛用于多尺度拓扑优化设计^［33-34］。在渐进均匀化算法中，先建立相应的有限元方程并求解，得到单元位移与整体位移场，再计算均匀化单元弹性张量 $C$ 。均匀化弹性张量 $E_{i l}^{H}$ 的计算式为

E_{i j k l}^{H} = \frac{1}{|Ω|} \int_{Ω} E_{p q r s} (ε_{p q}^{0 (i j)} - ε_{p q}^{(i j)}) (ε_{r s}^{0 (i j)} - ε_{r s}^{(i j)}) d Ω ，

（2）

其中， $E_{p q r s}$ 表示局部变化弹性张量， $|Ω|$ 表示微结构单元体积， $ε_{p q}^{0 (i j)}$ 为给定的宏观应变场，而局部变化应变场 $ε_{p q}^{(i j)}$ 定义为

ε_{p q}^{(i j)} = ε_{p q} (X^{i j}) = \frac{1}{2} (X_{p, q}^{i j} + X_{q, p}^{i j})

，（3）

其中 $， X^{i j}$ 表示位移场，通过求解以下方程得到：

\int_{Ω} E_{i j p q} ε_{i j} (v) ε_{p q} (X^{k l}) d Ω = \int_{Ω} E_{i j p q} ε_{i j} (v) ε_{p q}^{0 (k l)} d V ， v \in Ω ，

（4）

其中， $v$ 为虚位移场。用文献［12］中提供的代码求解式（4）并计算二维多孔材料均匀化弹性张量。

1.3　多尺度拓扑优化方法

用六面体有限单元离散设计域，每个单元 $e$ 分配一个密度 $ρ_{e}$ ，取值为 $[0,1]$ ，其中，中间密度在理论上表现为单元体内所含实体材料的体积分数。在固定设计域 $Ω$ 内形成的密度场 $ρ$ 称为体积分数场，以避免与材料的质量密度混淆。由于线框模型可明确定义微结构，故多尺度设计在理论上具有可制造性，此外，将微观结构维度设置为一维，线框模型杆直径一致变化，所表征的微结构模型密度在区间 $[0,1]$ 内取值，微观尺度设计可视为尺寸优化。在设计域上用单一线框模型进行拓扑优化，以确保多尺度优化结构具有良好的连续性和可制造性。为计算任意中间密度微结构单元弹性张量 $C^{H}$ ，可预先计算密度梯度变化的单元弹性张量 $C_{i}^{H}$ ，然后基于线性插值计算任意密度的单元弹性张量 $C_{e}^{H}$ ，

C_{e}^{H} = β_{e} C_{i}^{H} + （ 1 - β_{e} ） C_{i + 1}^{H} ，

（5）

β_{e} = \frac{ρ_{i + 1} - ρ_{e}}{ρ_{i + 1} - ρ_{i}}

。（6）

密度梯度设置越小，基于线性插值计算的单元弹性张量越准确，但需求解更多方程（式（4）），这将消耗大量时间。为此提出GPU并行算法，以提高求解一系列多尺寸、多形状微结构单元矩阵 $C^{H}$ 的效率。

1.4　GPU并行架构

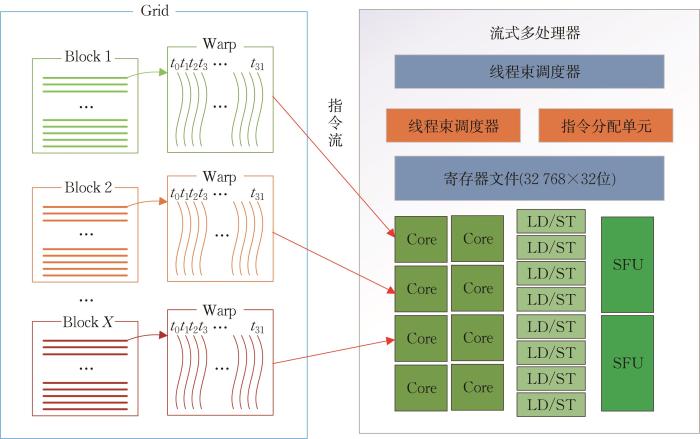
GPU具有并行计算大型数据的能力，自NVIDIA^［35］于2007年发布CUDA以来，GPU被广泛用于大规模科学计算。CUDA是一种异构计算平台，由CPU和GPU两种架构组成，其应用分为CPU主机端代码与GPU设备端代码，两者通过PCle总线进行信息交流^［36］。主机端代码主要负责设备的控制和数据传输，设备端代码定义功能函数并完成相应计算，此函数称为核函数。线程作为最小执行单元，在并行计算时，GPU将利用大量线程执行核函数^［37］。逻辑上将全部线程以一定数量各自归集到一起形成线程块，块中线程以线程束（32个线程）为单位在CUDA核心处理器上运行，如图2所示。流式多处理器（SM）作为GPU并行架构的组成单元，支持大量线程并发执行，而线程束正是SM的并发执行单元。在SM中，以单指令、多线程（SIMT）方式管理执行线程，线程束中的执行线程在同一时刻运行同一条指令^［38］。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 GPU并行架构

Fig.2 GPU parallel architecture

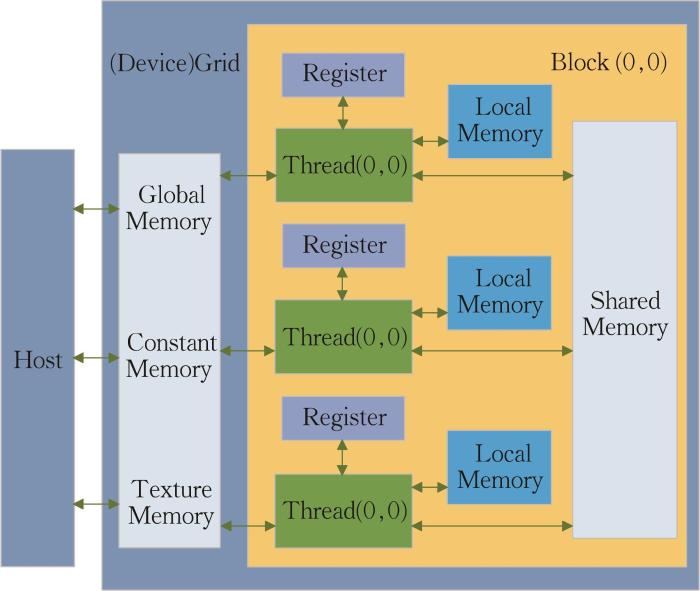
通过CUDA，运用合适的内存模型提升程序运行效率，其中寄存器内存访问速度最快，保证了常用变量的读写速度，每个线程拥有独立寄存器空间，线程间互不干扰。线程块中线程所使用的共享显存，其速度接近寄存器但存储空间更大，是提升程序效率的主要工具。全局显存存储空间大，但速度慢，主要存储设备端与主机端之间的传输数据，全局显存允许GPU所有线程对其进行读写。图3展示了本文并行算法中CUDA线程及内存的层次逻辑结构。首先，程序在CPU端申请主机内存并将程序复制到GPU端全局显存，当GPU完成并行计算后，将设备显存中的结果数据复制到主机内存。共享显存具有带宽高、延迟低的特点，其可见范围仅为线程块，合理利用共享显存可显著提高程序性能。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 CUDA线程及内存的层次逻辑结构

Fig.3 Logical structure of CUDA threads and memory hierarchy

2　构建微结构模型的并行策略

2.1　生成微结构模型

渐进均匀化分析初始步骤为生成微观尺度下的多孔结构模型，即微结构，宏观尺度下连续结构体将被离散为有限个微结构单元。为简化微结构模型获取过程并获得更高的模型精度，本文采用基于网格线框的水平集初始化算法，其中水平集初值由网格线框生成，将由水平集表示的几何模型作为均匀化模型的输入。微结构模型由水平集函数表示，定义为

\{\begin{matrix} φ (x) > 0, x \in Ω, \\ φ (x) = 0, x \in Γ, \\ φ (x) < 0, x \in \bar{D} / (Ω ⋃ Γ), \end{matrix}

（7）

其中 $， Ω$ 和 $Γ$ 分别表示微结构模型的固体区域和结构边界， $\bar{D}$ 为密度梯度微结构模型的唯一参考域。

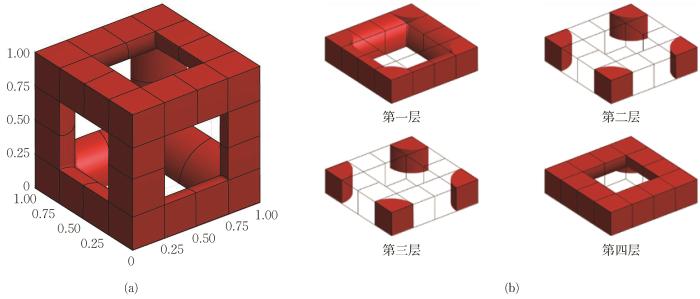
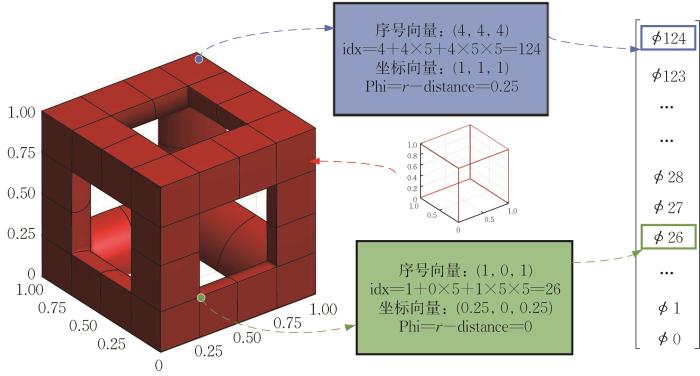
将水平集函数 $φ$ 作为符号距离函数， $x$ 为水平集离散网格点坐标向量。微结构设计域为无量纲、单位长度的立方体。将单位长度除以每个坐标轴方向上的离散网格点数量，得到相邻网格点间的相对距离。由离散网格点在各坐标轴上的序号，得到其在设计域内的坐标。如图4（a）所示，轴向离散网格点数为5，从原点开始均匀排列于立方体设计域内。图4（b）展示的为沿z轴的各层水平集离散网格单元，红色代表含有材料的微结构模型实体，网格单元的材料用量以及分布形式由单元结点上的水平集值φ插值决定。求水平集离散网格点与线框的最小距离，给定线框模型的支柱半径r，计算水平集值φ=r-d，得到水平集值3D逻辑矩阵：

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 水平集模型

Fig.4 Level set model

[\begin{matrix} 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \\ 0.25 & 0 & 0 & 0 & 0.25 \\ 0.25 & 0 & - 0.25 & 0 & 0.25 \\ 0.25 & 0 & 0 & 0 & 0.25 \\ 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \end{matrix}]

φ（：，：， 1）

[\begin{matrix} 0.25 & 0 & 0 & 0 & 0.25 \\ 0 & - 0.10 & - 0.10 & - 0.10 & 0 \\ 0 & - 0.10 & - 0.31 & - 0.10 & 0 \\ 0 & - 0.10 & - 0.10 & - 0.10 & 0 \\ 0.25 & 0 & 0 & 0 & 0.25 \end{matrix}]

φ（：，：， 2）

[\begin{matrix} 0.25 & 0 & - 0.25 & 0 & 0.25 \\ 0 & - 0.10 & - 0.31 & - 0.10 & 0 \\ - 0.25 & - 0.31 & - 0.46 & - 0.31 & - 0.25 \\ 0 & - 0.10 & - 0.31 & - 0.10 & 0 \\ 0.25 & 0 & - 0.25 & 0 & 0.25 \end{matrix}]

φ（：，：， 3）

[\begin{matrix} 0.25 & 0 & 0 & 0 & 0.25 \\ 0 & - 0.10 & - 0.10 & - 0.10 & 0 \\ 0 & - 0.10 & - 0.31 & - 0.10 & 0 \\ 0 & - 0.10 & - 0.10 & - 0.10 & 0 \\ 0.25 & 0 & 0 & 0 & 0.25 \end{matrix}]

φ（：，：， 4）

[\begin{matrix} 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \\ 0.25 & 0 & 0 & 0 & 0.25 \\ 0.25 & 0 & - 0.25 & 0 & 0.25 \\ 0.25 & 0 & 0 & 0 & 0.25 \\ 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \end{matrix}]

φ（：，：， 5）

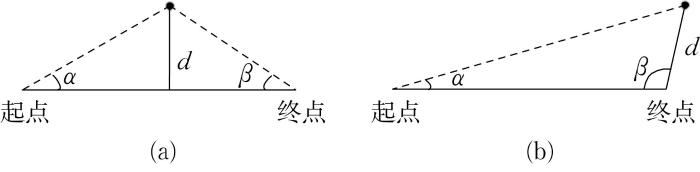
对设计域立方体进行网格离散，确定离散结点上的水平集值。由于水平集值φ=r-d，故只要确定水平集离散网格点与线框各线段的最小距离 $d$ 便能确定水平集值φ。φ为正，表示离散结点位于微结构模型内部，反之，位于微结构模型外部。在计算最小距离时，若离散结点与线框线段的起点夹角 $α$ 和终点夹角 $β$ 均小于90°，则最小距离d为结点到线段的垂直距离（图5（a））；若 $α$ 和 $β$ 其中之一大于90°，则最小距离d为结点到线段的起点或终点的直线距离（图5（b））。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 离散结点与线框的最小距离

Fig.5 Minimum distance between discrete nodes and wireframes

2.2　微结构模型初始化的并行策略

2.2.1　CUDA线程和内存的层次结构

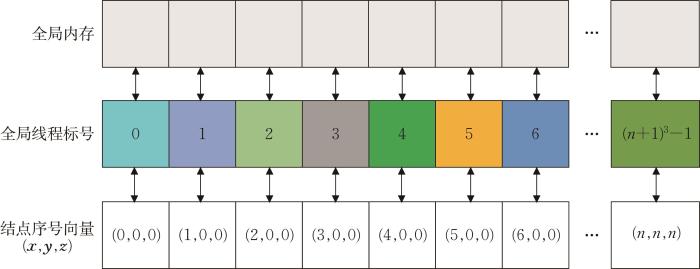
由分析水平集模型初始化过程，可知不同离散结点与线框的最小距离可并行计算，故用每条线程计算每个离散网格点上的水平集值。由于线程块以线程束为单位，因此CUDA处理器核心同一时刻执行相同指令，为避免线程块中多个线程占用一个核处理器，将线程数设置为32（线程束大小）的倍数。本文采用2D线程块模型，图6展示的为线程全局标号与离散网格结点序号的映射关系。线程块中的单个线程全局标号对应GPU全局显存中的数据索引值。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 线程全局标号与离散网格结点序号的映射关系

Fig.6 The mapping relationship between thread global labeling and discrete grid node numbering

2.2.2　水平集初始化并行策略

水平集初始化并行策略如表3所示。←表示寄存器或本地内存中的变量赋值操作，⇒/⇐表示全局内存的读/写操作。函数GetCoordinate（）可通过线程全局标号idx及离散网格尺寸size推导线程对应离散结点的位置向量 p。遍历线框模型中的线框，计算离散结点 p 与每段线框的最短距离distance。首先，取线框始末端的位置向量start P 与end P，用Norm（）函数计算向量的模长，用GetAngle（）函数分别计算图5中的夹角 $α$ 和 $β$ ，求得最短距离distance。用给定的线框模型支柱半径r，计算水平集值Phi=r-distance。将线程遍历得到的maxPhi赋值给全局水平集值数组Phi_idx，获取与全局标号idx对应的离散结点水平集值。并行计算水平集初值示例如图7所示。

表3 水平集初始化并行算法

Table 3 Level set initialization parallel algorithm

新窗口打开| 下载CSV

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 并行计算水平集初值示例

Fig.7 Example of initial values for parallel computing level sets

3　3D微结构弹性张量预计算并行算法

采用渐近均匀化方法计算多孔材料周期性微结构单元的弹性张量，通过大型稀疏矩阵的并行求解算法及均匀化本构矩阵的并行积分算法提升渐近均匀化方法的计算效率。

3.1　渐进均匀化过程整体方程的并行求解

在求解有限元整体平衡方程 $K x = f$ 时，若用直接法 $x = K \ f$ 求解，将消耗大量内存且计算量巨大^［39］。通常，用共轭梯度法（conjugate gradients，CG）求解大型稀疏矩阵方程，稀疏矩阵需满足对称及正定条件^［40］，而整体刚度矩阵 $K$ 恰好满足这一要求。共轭梯度法较预条件共轭梯度法（PCG）更适合并行计算，在多次迭代中获得一系列逐步逼近真实解的近似解，当近似解在允许误差范围内时，迭代结束。CG算法步骤如下：

Step 1 初始化解 $x_{0};$

Step 2 计算 $r_{0} = b - A x_{0}, p_{0} = r_{0};$

Step 3 对迭代次数 $k = 0, 1, 2, \dots$ ；

Step 4 得到 $α_{k} = \frac{r_{k}^{T} r_{k}}{p_{k}^{T} A p_{k}} ；$

Step 5 $x_{k + 1} = x_{k} + α_{k} p_{k} ；$

Step 6 $r_{k + 1} = r_{k} - α_{k} A p_{k} ；$

Step 7 $β_{k} = \frac{r_{k + 1}^{T} r_{k + 1}}{r_{k}^{T} r_{k}} ；$

Step 8 $p_{k + 1} = r_{k + 1} + β_{k} p_{k}$ 。

有限元法的整体刚度矩阵为稀疏矩阵，本文CG方法采用行压缩（compressed sparse row，CSR）方式存储稀疏矩阵 A，也适用于有限元法中非规则稀疏矩阵的压缩^［41］，如整体刚度矩阵。CSR格式将稀疏矩阵分为3个一维向量，分别为Val向量，记录非零元素值；Col_Val向量，记录非零元素对应的列号；Row_Val向量，记录矩阵每行中首个非零元素前的总非零元素个数。

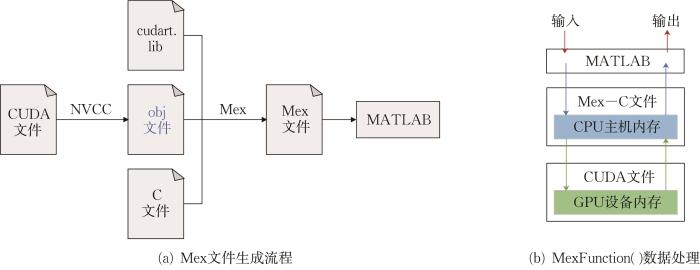
在渐进均匀化代码中，多处涉及大型稀疏矩阵方程的求解，为提升求解稀疏矩阵方程的效率，将预条件共轭梯度算法进行集成。本文联合Matlab， C与CUDA混合编程模式实现对稀疏矩阵方程的高效并行求解（图8）。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Matlab，C和CUDA混合编程模型

Fig.8 Mixed programming model of Matlab， C and CUDA

并行共轭梯度算法如表4所示。←表示寄存器或本地内存变量赋值操作，⇒/⇐表示全局内存读/写操作。其中，第1~6行为CG算法的准备工作，计算 $r_{0} = b - A x_{0}$ ；第7~25行为CG算法的迭代求解，用d_x⇐alpha*d_p+d_x语句完成近似解 $x$ 更新，当误差值 $r 小于 t o l * t o l$ 或迭代次数超过最大允许值时，循环结束。在共轭梯度并行算法中，函数cublasScopy（）可完成向量间拷贝，函数cublasSdot（）并行运算向量间点乘，如 $r_{k}^{T} r_{k}$ ，标量与向量之间的乘积由函数cublasSscal（）完成，函数cusparseSpMV（）可并行运算用CSR格式存储的稀疏矩阵与向量的乘积，如 $A p_{k}$ ，函数cublasSaxpy（）完成向量的更新，如 $x_{k + 1} = x_{k} + α_{k} p_{k}$ 。

表4 并行共轭梯度算法

Table 4 Parallel conjugate gradient algorithm

Segment 1-CG，共轭梯度算法

1： a=1

2： r0=0

3： d_Ax ⇐ matA*d_x----cusparseSpMV （）

4： d_r ⇐ -a*d_Ax+d_r----cublasSaxpy （）

5： r1←d_r.*d_r----cublasSdot （）

6： k=1

7： while r1>tol*tol && k<=max_iter // 条件判断

8： if k>1

9： beta=r1/r0；

10： d_p ⇐ beta*d_p----cublasSscal （）

11： d_p ⇐ a*d_r+d_p----cublasSaxpy （）

12： end

13： else

14： d_p ⇐ d_r----cublasScopy （）

15： end

16： d_Ax ⇐ mat A*d_p----cusparseSpMV （）

17： dot←d_p.*d_Ax----cublasSdot （）

18： alpha=r1/dot

19： alpha←numerator / denominator

20： d_x ⇐ alpha*d_p+d_x----cublasSaxpy （）

21： d_r ⇐ -alpha*d_p+d_r---cublasSaxpy （）

22： r0=r1；

23： r1←d_r.*d_r----cublasSdot （）

24： k++

25： end

新窗口打开| 下载CSV

3.2　均匀化本构矩阵的并行计算

将六面体单元作为渐进均匀化对象，由单位应变求微结构单元结点位移，由式（8）求在均匀应变下微结构单元中的离散结点位移场，该两组位移矩阵是计算本构矩阵 $C$ 的关键信息，矩阵 $C$ 的各元素由下式确定：

C_{i j}^{H} = \frac{1}{|Ω|} \sum_{(e)} \int_{Ω^{(e)}} (x_{(e)}^{0 (i)} - x_{(e)}^{(i)})^{T} k_{e} (x_{(e)}^{0 (j)} - x_{(e)}^{(j)}) d Ω^{(e)}

，（8）

其中， $x_{(e)}^{0 (i)}$ 表示对应于第 $i$ 个单位应变单元的位移， $x_{(e)}^{(i)}$ 表示离散结点位移场位移， $Ω$ 表示微结构单元体积。本文设计的核函数CUDA_CalSum（）负责 $计算 C_{i j}^{H}$ 各离散积分点数值，将离散积分点值累加获得最终数值积分值，即本构矩阵中的元素值 $C_{i j}^{H}$ 。

并行计算 $C^{H}$ 离散积分点值的算法如表5所示，其中，elem_N为微结构单元数，当微结构单元用于变密度法拓扑优化时，可设置密度等梯度变化系列微结构单元，同时计算多个单元本构矩阵。将数据从全局显存取存到CUDA线程的寄存器单元，可避免对全局显存多次读取，提升存储读取效率。通过拉梅常数将单元刚度矩阵分解为两部分， $C_{i j}^{H}$ 离散积分点值计算被分解，即sumAll ← Lambda/ d_Volume_{ele*blockN+idx}*sum_L + Mu/d_Volume_{ele*blockN+idx}*sum_M，其中，Lambda与Mu分别为拉梅第一、第二常数。本构矩阵并行算法如表6所示，每个CUDA线程负责组装一个完整单元本构矩阵 C 及离散积分点值累加。

表5 并行计算C^H离散积分点值算法

Table 5 Parallel computing C^H discrete integral point value algorithm

新窗口打开| 下载CSV

表6 并行计算本构矩阵算法

Table 6 Parallel computational constitutive matrix algorithm

新窗口打开| 下载CSV

4　实验验证与分析

4.1　实验条件

实验所用机器硬件配置：CPU为Intel Core i9-10900x（十核心/二十线程），主频3.70 GHz，随机存储器RAM为Tigo DDR4 2 666 MHz，内存64 GB，GPU为GeForce RTX 2080，拥有2 944个CUDA内核，其中每个SM的最大激活线程数为1 024，线程块中最大激活线程数为1 024，线程块最大尺寸为1 024×1 024×64，网格最大尺寸为（2³¹-1）×65 535×65 535。操作系统为Windows 10.1 64位，CPU代码的编译器为Mathworks MATLAB 2018a和Microsoft Visual Studio 2019，GPU代码的编译器为NVIDIA CUDA 11.0，实验所用并行算法的全部CUDA内核程序均由作者编写调试。

4.2　实验设计与数据

以悬臂梁为例，展示多尺度拓扑优化渐进均匀化GPU并行算法的加速效率。三维悬臂梁设计域如图9所示，梁的长、宽、高分别设为L，0.2L，L。高度L设为1，符合无量纲计算规则。在右端面下边缘向下施加竖向分布单位载荷F，左端面受约束。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 三维悬臂梁的设计域和边界条件

Fig.9 Design domain and boundary conditions of 3D cantilever beams

通过渐进均匀化过程计算微结构单元本构矩阵，其CPU串行算法基于Matlab编写实现。针对多尺度结构拓扑优化，主要计算环节为水平集初始化、大型稀疏刚度矩阵方程求解以及本构矩阵并行计算等。实验将微结构单元在轴向的水平集离散网格数作为自变量，称为分辨率。CPU串行算法与GPU并行算法分别在分辨率（自由度）为4³（192），8³（1 536），16³（12 288），32³（98 304），64³（786 432），128³（6 291 456）下执行相应计算环节。

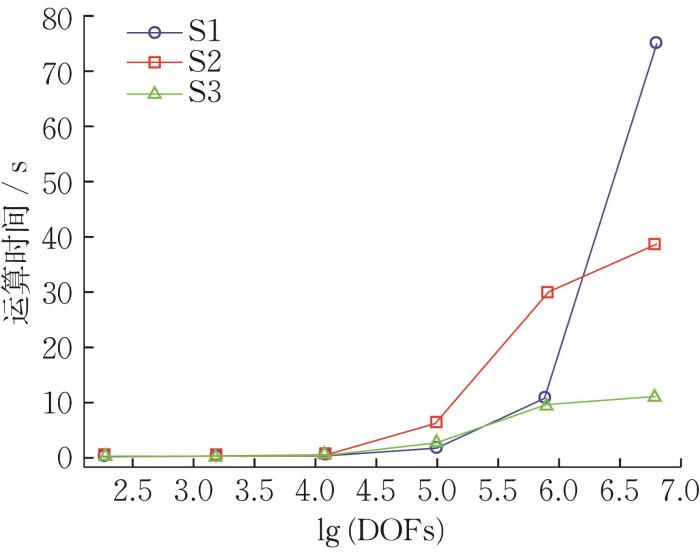
在不同分辨率下串行算法与并行算法完成各计算环节所需的平均时间如表7所示，其中S1，S2，S3分别代表水平集初始化、大型稀疏刚度矩阵方程求解以及本构矩阵并行计算。

表7 运行时间及加速比

Table 7 Running time and acceleration ratio

序号

分辨

率

自由

度数

步骤

运行时间/s

加速比

CPU_M

GPU_CUDA

4³

192

0.068

0.007

0.004

0.199

1.018

0.435

0.342

0.007

0.009

8³

1 536

0.076

0.098

0.045

0.179

1.016

0.418

0.425

0.097

0.108

16³

12 288

0.101

0.733

0.143

0.189

0.966

0.270

0.534

0.759

0.530

32³

98 304

0.347

9.434

1.464

0.190

1.454

0.517

1.826

6.488

2.832

64³

786 432

1.980

112.796

10.274

0.183

3.759

1.072

10.820

30.007

9.584

128³

6 291 456

14.421

1 397.177

77.820

0.192

36.116

6.897

75.109

38.686

11.283

新窗口打开| 下载CSV

加速比为原CPU串行算法的执行时间除以GPU并行算法执行时间得到的比值，即表7中的第5列数据除第6列数据得到第7列的GPU并行算法加速比。

由于微结构单元结构具有对称性，其在x，y，z方向上的性质是相同的。可通过对本构矩阵求逆，得到柔度矩阵 $S^{H}$ ：

S_{11}^{H} = \frac{1}{E_{x}}

，

S_{22}^{H} = \frac{1}{E_{y}}

，

S_{33}^{H} = \frac{1}{E_{z}}

，（9）

$其中， E_{x}$ ， $E_{y}$ ， $E_{z}$ 分别表示微结构单元各轴向杨氏模量，且 $E_{x}$ = $E_{y}$ = $E_{z}$ 。在不同分辨率下求得的杨氏模量如表8所示。CPU串行计算杨氏模量，数据均为double（双精度浮点）类型。GPU并行计算，为节省显存开销，同时降低主机向GPU传输数据的时间，使用了float（单精度浮点）类型，CPU与GPU计算结果并没有严格相等。经分析，GPU相较于CPU杨氏模量相对误差始终低于1×10^-2。随着分辨率的增加，微结构单元水平集模型更精细，杨氏模量逐渐收敛，趋于更精确的结果。当追求高准确度计算结果时，使用GPU并行算法更节省时间与资源。

表8 杨氏模量

Table 8 Young's modulus

自由度	杨氏模量/GPa		相对误差
自由度	CPU	GPU	相对误差
192	349.207	348.649	1.5×10^-3
1 536	330.442	329.913	1.6×10^-3
12 288	333.689	333.154	1.6×10^-3
98 304	303.242	302.756	1.6×10^-3
786 432	299.738	299.253	1.6×10^-3
6 291 456	300.135	297.207	9.0×10^-3

新窗口打开| 下载CSV

4.3　实验结果分析

在渐进均匀化过程中，水平集初始化、总刚度方程求解及本构矩阵并行计算等的运算时间变化情况如图10所示。当自由度较小时，即分辨率越小模型精度越低，GPU并行算法性能并不比CPU串行算法优越；当自由度逐渐增加时，GPU并行算法较CPU串行算法运算时间始终低一个水平，体现了GPU算法在面对大规模计算问题时的优越性。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 计算环节执行时间

Fig.10 Execution time of calculation phase

由图11可知，当自由度（分辨率）在192（4³）~98 304（32³）时，GPU并行算法的加速效率并不明显，当自由度大于98 304时，计算规模呈几何级增加，GPU并行算法的加速效率开始凸显，在大型稀疏刚度矩阵方程求解环节和本构矩阵并行计算环节，其加速比可达两个数量级。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 GPU/CPU加速比

Fig.11 Acceleration ratio of GPU/CPU

综上分析可知，当模型自由度（分辨率）较低时，不足以体现GPU并行计算的能力，两种算法效率相近；随着自由度（分辨率）的增加，CPU串行算法无法适应大规模计算要求，此时凭借GPU强大的并行计算能力令加速比保持递增趋势。

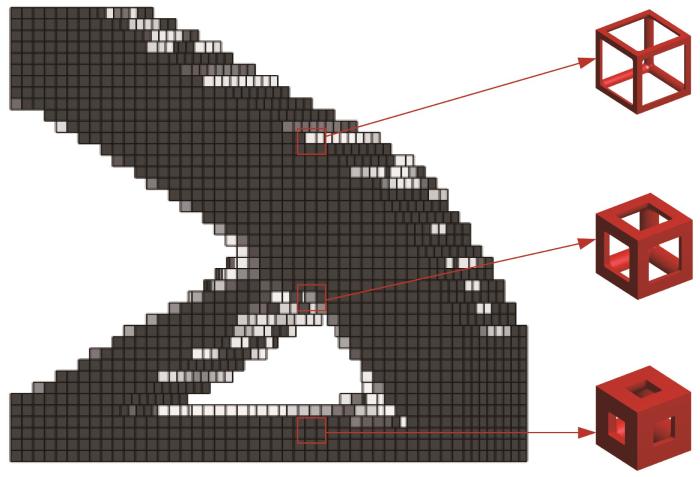
图12为悬臂梁多尺度拓扑优化结果，其中一系列密度梯度的单元具有相同的微结构和不同的体积。在多尺度拓扑优化中，每个梯度均需计算本构矩阵，基于渐进均匀化并行算法用GPU进行并行计算，可满足优化过程的算力要求。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 悬臂梁多尺度拓扑优化结果

Fig.12 Multiscale topology optimization results of cantilever beams

5　总结

基于渐进均匀化多尺度拓扑优化并行算法，研究了优化过程中水平集初始化、大型稀疏刚度矩阵方程求解以及本构矩阵并行计算等。实验结果表明，当计算规模较大时，GPU并行算法的加速比显著，尤其是大型稀疏刚度矩阵方程求解和本构矩阵并行计算环节，其加速比达几十倍。此外，两种算法得到的微结构单元杨氏模量值一致，验证了GPU并行算法的准确性。本文的并行算法可扩展至其他应用场景，但仍有待进一步完善，例如结合OpenMP， CUDA与MPI搭建多尺度结构拓扑优化CPU/GPU异构并行算法，以进一步提升结构优化设计效率。

http://dx.doi.org/10.3785/j.issn.1008-9497.2023.06.001

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SCHAEDLER

T A

， CARTER

W B

Architected cellular materials

［J］. Annual Review of Materials Research， 2016， 46： 187-210. DOI：10.1146/annurev-matsci-070115-031624