基于多因素融合的多级透平轴系校中优化方法研究

doi:10.3785/j.issn.1006-754X.2025.05.173

基于多因素融合的多级透平轴系校中优化方法研究

狄广强^,¹, 王一博², 孙朝阳¹, 于成海¹, 温建锋², 贾九红^,^,²

1.中国联合重型燃气轮机技术有限公司，上海 201306

2.华东理工大学机械与动力工程学院，上海 200237

Research on multi-stage turbine shafting alignment optimization method based on multi-factor fusion

DI Guangqiang^,¹, WANG Yibo², SUN Zhaoyang¹, YU Chenghai¹, WEN Jianfeng², JIA Jiuhong^,^,²

1.China United Heavy Duty Gas Turbine Technology Co. , Ltd. , Shanghai 201306, China

2.School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China

通讯作者: 贾九红（1978—），女，教授，博士生导师，博士，从事结构完整性等研究，E-mail: jhjia@ecust.edu.cn, https://orcid.org/0000-0002-0925-0562

收稿日期: 2025-05-20 修回日期: 2025-08-25

基金资助:

国家自然科学基金面上项目.  52575175
国家自然科学基金面上项目.  52475156
国家重点研发计划资助项目.  2023YFB3712100

Received: 2025-05-20 Revised: 2025-08-25

作者简介 About authors

狄广强（1993—），男，工程师，硕士，从事转子动力学研究，E-mail:diguangqiang@spic.com.cn , E-mail：diguangqiang@spic.com.cn

摘要

针对重型燃气轮机多级透平轴系校中难题，建立了融合轴承支反力和轴承间相对变位的优化校中方法，并进行了热态验证。首先，采用有限元软件ANSYS Workbench模拟轴系冷态变形，获得了关键轴承的支反力和垂直位移；其次，采用融合轴承支反力和轴承间相对变位的多参数优化方法，利用MATLAB软件计算得到最优解；接着，采用Fluent软件仿真分析进气蜗壳与轴系之间气流的分布，考虑了轴系在实际工作状态下的温度影响，来验证热态下最优解的有效性；最后，在冷态下将轴承5#下沉0.057 mm，对轴系进行了精调，并开展了热态下校中实验，结果表明轴系振动量符合指标要求，验证了校中方案的有效性。所提出的轴系校中优化方法考虑了轴系实际温度和复杂载荷，对于轴系的精调具有较好的指导意义。

关键词： 精调 ; 冷态校中 ; 有限元 ; 线性优化 ; 热态验证

Abstract

Aiming at the alignment problem of the multi-stage turbine shafting of heavy duty gas turbines, an optimization alignment method integrating the reaction force of bearing and relative displacement between bearings was established, and a verification in hot-state was conducted. Firstly, the finite element software ANSYS Workbench was used to simulate the deformation in cold-state of the shafting, and the reaction forces and vertical displacements of the key bearings were obtained. Secondly, a multi-parameter optimization method integrating reaction force of bearing and the relative displacement between bearings was adopted, and the optimal solution was calculated by using the MATLAB software. Then, the Fluent software was used to simulate and analyze the airflow distribution between the intake volute and the shafting, the temperature influence under the actual working state of the shafting was taken into account to verify the validity of the optimal solution in hot-state. Finally, the bearing 5# was lowered by 0.057 mm in cold-state, the shafting was precisely adjusted, and an alignment experiment in hot-state was conducted. The results showed that the vibration of the shafting met the index requirements, verifying the effectiveness of the alignment scheme. The proposed shafting alignment optimization method takes into account the actual temperature and complex loads of the shafting, and has a good guiding significance for the precise adjustment of the shafting.

Keywords： precision adjustment ; calibration in cold-state ; finite element ; linear optimization ; verification in hot-state

PDF (2204KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

狄广强, 王一博, 孙朝阳, 于成海, 温建锋, 贾九红. 基于多因素融合的多级透平轴系校中优化方法研究[J]. 工程设计学报, 2025, 32(6): 839-844 doi:10.3785/j.issn.1006-754X.2025.05.173

DI Guangqiang, WANG Yibo, SUN Zhaoyang, YU Chenghai, WEN Jianfeng, JIA Jiuhong. Research on multi-stage turbine shafting alignment optimization method based on multi-factor fusion[J]. Chinese Journal of Engineering Design, 2025, 32(6): 839-844 doi:10.3785/j.issn.1006-754X.2025.05.173

重型燃气轮机多级透平轴系不对中状态易引起轴承磨损加剧甚至损坏、减速箱齿轮啮合不良、轴系振动情况恶化等问题。轴系校中的质量是保证轴系安全性和可靠性的一个重要指标。因此，在实际工程中，通常需要先开展轴系的校中计算，为后续多级透平轴系的制造、安装和实验提供指导^[1-3]。

轴系校中常用的方法有三弯矩法和有限元法等^[4-6]。Qian等^[4]基于三弯矩方程，建立了轴系校中的数学模型，并将计算结果与现场实测的安装数据进行比较，验证了所提出的轴系校中计算方法的有效性和准确性，但是模型推导难度较大。王琴等^[5]针对小型船舶轴系，将三弯矩法与有限元法进行对比后发现，三弯矩法的计算速度较快，但对轴承支承的简化易导致支反力出现偏差，其仅适用于较简单的轴系。相较于建立数学模型^[7，8]，有限元法的使用更为灵活，应用更为广泛，尤其是结合功能强大的软件如ANSYS、ABAQUS等^[9，10]，可综合考虑轴系校中的多个影响因素，提高轴系校中质量，使得计算结果更加精确。Zhou等^[11-13]提出了矩阵位移法，构建了相应的数学模型，考虑了船体变形对轴系校中的影响，但未涉及多因素的融合。有限元法可以综合考虑多个因素的影响^[14-16]，如郭鹏等^[15]采用有限元法开展了融入轴承变位、转速等因素的轴系校中研究，为相关的研究提供了很好的借鉴。

本文的研究对象为重型燃气轮机多级透平综合性能试验台。其设计温度较高，而高温是引入轴系不平衡的关键因素之一^[14,17]。金尚崇等^[18]为了研究温度对轴系校中的影响，建立了考虑油膜力的热态校中模型，分析了热态下温度与载荷的耦合情况。此外，轴系校中多以轴承座为基准^[19-20]，轴承相对于轴承座有一定的游隙余量，会导致参考基准的物理位置存在不确定性。因此，亟须建立一种针对性较强的优化校中方法，针对多级透平综合性能试验台轴系复杂、轴承变位要求严格、目标工作温度较高等工况，以试验件转子中心线为基准，进行轴系对中精调。本研究首先采用有限元法，基于冷态校中计算结果，融合轴承支反力和轴承间相对变位等因素，进行轴系校中优化分析与计算；然后，对优化结果进行热态分析，来验证校中结果的可靠性。

1 轴系直线校中分析

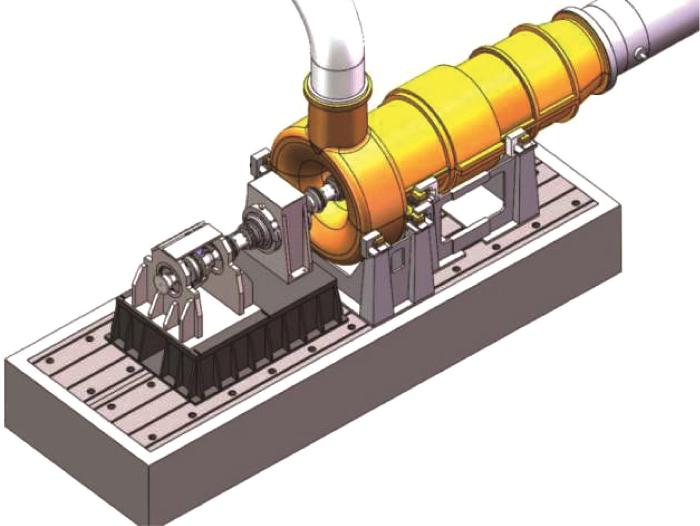
本文以某重型燃气轮机多级透平综合性能试验台为研究对象，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 重型燃气轮机多级透平综合性能试验台

Fig.1 Comprehensive performance test bench for multi-stage turbines of heavy duty gas turbine

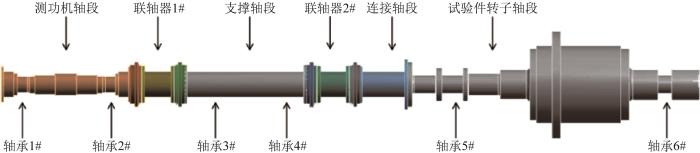
试验台轴系的关键部件有测功机轴段、联轴器1#（连接轴承座与水力测功机）、支撑轴段、联轴器2#（连接轴承座与连接轴段）、连接轴段、试验件转子轴段及轴承1#至轴承6#。采用SolidWorks软件建立轴系三维模型，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 轴系三维模型

Fig.2 Three-dimensional model of shafting

轴承的静态刚度如表1所示。轴承1#和轴承2#为滚动球轴承；轴承3#至轴承6#为滑动轴承，轴承内径为290 mm，轴承跨度为900 mm。

表1 轴承静态刚度

Table 1 Static stiffness of bearings

轴承编号	到左端的距离/mm	静态刚度/(10⁵ N/mm)
轴承编号	到左端的距离/mm	水平支承刚度	垂向支承刚度
1#	256.5	2.500	2.500
2#	1333.5	2.500	2.500
3#	2627.6	2.138	2.143
4#	3377.6	2.138	2.143
5#	5516.2	4.330	4.330
6#	8121.2	5.237	5.237

新窗口打开| 下载CSV

在仅考虑重力载荷的冷态工况下，分析透平轴系的位移。通过ANSYS Workbench软件求解，获得关键轴承冷态下的支反力与垂直位移。结果表明，最大位移发生在试验件转子轴段，这和实际情况吻合。提取轴承1#至轴承6#对应的支反力和垂直位移后发现，轴承5#的垂直位移最大，轴承4#与轴承5#之间的相对位移较大，导致该两轴承间的相对变位较大。

轴承间的相对变位 $\partial$ _i 为：

\partial_{i} = \frac{y_{i + 1} - y_{i}}{x_{i + 1} - x_{i}}

式中：x_i 为各轴承的轴向位移，y_i 为各轴承的垂直位移，i=1, 2, …, 5。

根据式(1)可算得轴承4#相对于轴承5#的变位为0.034 mm/100 mm，超过实际设计中的许用临界值0.030 mm/100 mm，其他轴承的相对变位均小于该许用值，所以本文将轴承5#的变位进行优化校中，以使轴系能平稳地工作。

2 轴系优化校中分析

2.1　优化校中的目标函数

由于轴承5#和轴承6#紧邻试验件转子，两者的支反力较大，在仅考虑重力载荷的冷态工况下通过ANSYS Workbench软件计算得到其支反力分别为31 785 N和35 742 N。轴承支反力过大易导致轴承接触应力超限及润滑油膜破裂，进而诱发振动加剧及早期失效等问题，因此将轴承5#和轴承6#的支反力作为优化目标。

在轴系校中过程中，通常会调整某个或某几个轴承的位置。如果其中某个轴承的位置发生变化，则往往会导致该轴承和其他轴承的负荷发生变化^[12]。

假设第j号轴承垂直位移的调整量为Δy_j，其他轴承的位置固定，则第j号轴承对第i号轴承的负荷影响系数A_ij 为：

A_{i j} = \frac{R_{0 i} - R_{i j}}{Δ y_{i}}

(2)

式中：R₀_i 为第i号轴承在校中基准状态下的负荷，R_ij 为第i号轴承在调整状态下的负荷。

轴承5#的支反力R₅为：

\begin{array}{l} R_{5} = R {}_{05}+ A_{51} y_{1} + A_{52} y_{2} + A_{53} y_{3} + A_{54} y_{4} + \\ A_{55} y_{5} + A_{56} y_{6} \end{array}

(3)

令：

\begin{array}{l} R'_{5} = A_{51} y_{1} + A_{52} y_{2} + A_{53} y_{3} + A_{54} y_{4} + \\ A_{55} y_{5} + A_{56} y_{6} \end{array}

(4)

则R₅可简化为：

R_{5} = R_{05} + R'_{5}

(5)

轴承6#的支反力R₆为：

\begin{array}{l} R_{6} = R_{06} + A_{61} y_{1} + A_{62} y_{2} + A_{63} y_{3} + A_{64} y_{4} + \\ A_{65} y_{5} + A_{66} y_{6} \end{array}

(6)

令：

\begin{array}{l} R'_{6} = A_{61} y_{1} + A_{62} y_{2} + A_{63} y_{3} + A_{64} y_{4} + \\ A_{65} y_{5} + A_{66} y_{6} \end{array}

(7)

则R₆可简化为：

R_{6} = R_{06} + R'_{6}

(8)

轴承5#、轴承6#的支反力之和R为：

R = R_{5} + R_{6} = R_{05} + R'_{5} + R_{06} + R'_{6}

(9)

当 $R'_{5}$ 和 $R'_{6}$ 取最小值时，R为最小值。

2.2　约束条件

根据轴系实际工作要求，设置以下约束条件^[18]。

1）相邻两轴承的相对变位不超过0.03 mm/100 mm，即：

\partial \leq 3 \times 10^{- 4}

(10)

2）轴承负荷不小于轴承相邻两跨距间所有重量总和的20%，即：

R_{0 i} \geq M_{i} \times 20 %

式中：M_i 为轴承相邻两跨距间的所有重量总和。

基于上述约束条件求解目标函数。利用MATLAB软件的“linprog”函数求解线性规划问题：

\{\begin{array}{l} m i n f \\ \begin{array}{l} s . t . A Y \leq b \\ A_{e q} Y = b_{e q} \\ Y_{1} \leq Y \leq Y_{u} \end{array} \end{array}

(11)

式中：f为目标函数； Y 为待优化的参数， Y_l为 Y 的下限， Y_u为 Y 的上限； A 为不等式约束矩阵， A_eq为等式约束矩阵； b 为不等式约束向量， b_eq为等式约束向量。

将轴承5#的支反力最小定义为目标函数Ⅰ，轴承5#和轴承6#的支反力之和最小定义为目标函数Ⅱ。将具体参数代入式(11)，则：

\{\begin{array}{l} m i n f_{1} = A_{55} y_{5}, m i n f_{2} = (A_{55} + A_{65}) y_{5} \\ s . t . - 0.655 \leq Δ y_{5} \leq 0.655 m m \\ y_{1} = y_{2} = y_{3} = y_{4} = y_{6} = 0 \\ - 3 \leq y_{5} \leq 3 m m \end{array}

(12)

式中：f₁为目标函数Ⅰ（R₅=R₀₅+A₅₅y₅）的线性项，f₂为目标函数Ⅱ（R₅+R₆=R₀₅+R₀₆+(A₅₅+A₆₅)y₅）的线性项；约束中Δy₅的上下限由许用相对变位推导而得；y₅的上下限参考轴系实际调整范围设定。

2.3　优化结果分析

目标函数Ⅰ中，以y₅为唯一优化变量，结合轴系校中参数，最优目标值为31 869 N，目标函数Ⅱ的最优目标值为67 608 N。分别在目标函数Ⅰ和目标函数Ⅱ的约束下进行优化校中计算，得到轴承5#的变位量相近，均约为-0.057 mm，说明两目标函数在该场景下具有一致性，即轴承5#下沉0.057 mm时，目标函数最优。

3 校中方案验证

为了验证上述冷态校中方案在实际工作条件下的有效性，本研究开展热态下校中仿真和实验，分析热态下轴承间的相对变位。

在热态下，轴系主要受到燃气、冷却气体以及外部环境温度的影响，采用Fluent软件分析轴系的温度分布，结合轴系实际额定载荷校验轴系相对变位。

3.1　温度载荷计算

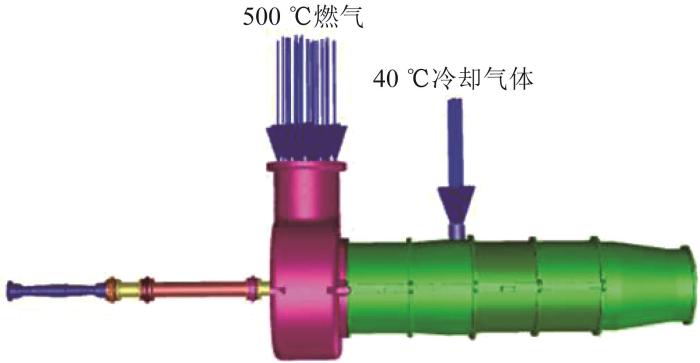
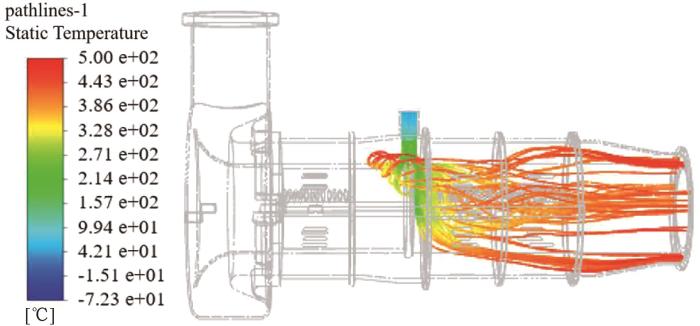
通过分析透平轴系的实际工况可知，轴系主要受到来自蜗壳进气口处的500 ℃燃气和来自叶片端的40 ℃冷却气体的交互作用。温度载荷加载方式如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 温度载荷施加方式

Fig.3 Application method of temperature load

在热态下，整个轴系的温度分布是由高温燃气与冷却气体相互作用得到的，因此采用Fluent软件分析进气蜗壳与轴系所围成空间的流固耦合，进而分析轴系的温度分布。首先，分析蜗壳进气即模型中设置的inlet_500燃气对整体模型的作用效果；其次，分析模型的inlet_40冷却气体对整体模型的作用效果。经过Fluent求解器求解，分别提取稳态工况下inlet_500和inlet_40作用下进气蜗壳与轴系的整体温度分布，如图4和图5所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

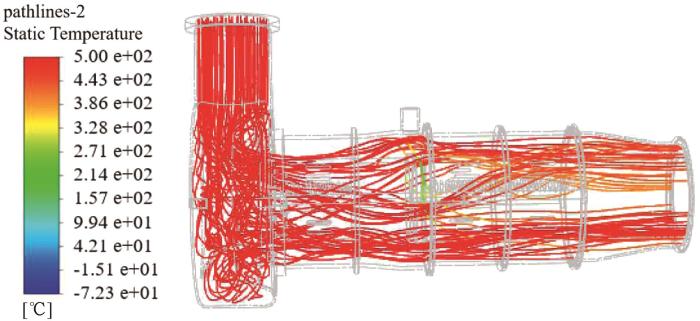
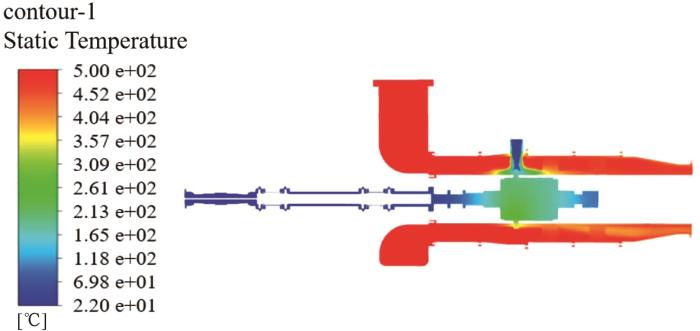
图4 inlet_500作用下的温度分布云图

Fig.4 Temperature distribution map under influence of inlet_50

图5

新窗口打开| 下载原图ZIP| 生成PPT

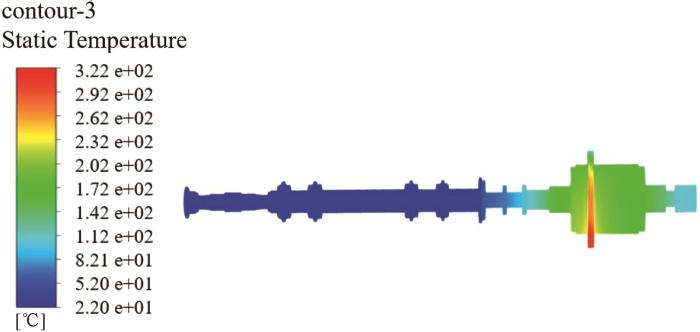
图5 inlet_40作用下的温度分布云图

Fig.5 Temperature distribution map under influence of inlet_40

燃气和冷却气体发生对流与热交换，使得整体模型的温度分布发生变化，直到趋于稳态。在稳态下提取温度场，得到整体模型的温度分布，如图6所示，可以很清晰地看出温度流场的分布。对整体模型进行设置，隐藏进气蜗壳模型，保留轴系模型，得到轴系的温度分布，如图7所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 整体模型温度分布云图

Fig.6 Temperature distribution map of overall model

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 轴系温度分布云图

Fig.7 Temperature distribution map of shafting

如图6所示，当500 ℃的燃气从蜗壳进气口处流入、40 ℃的冷却气体从叶片正上方注入时，在燃气和冷却气体的共同作用下，试验件转子的温度从高温降至低温，达到了冷却的效果。由于之前在对模型的处理中防止了燃气注入，轴系的其余部件均只受到来自叶片处的热传导及环境温度的热对流。由图7可知，轴系的最高温度在叶片处。可根据每一轴段的温度计算结果分析轴系在热态下的变形。

3.2　额定转速加载

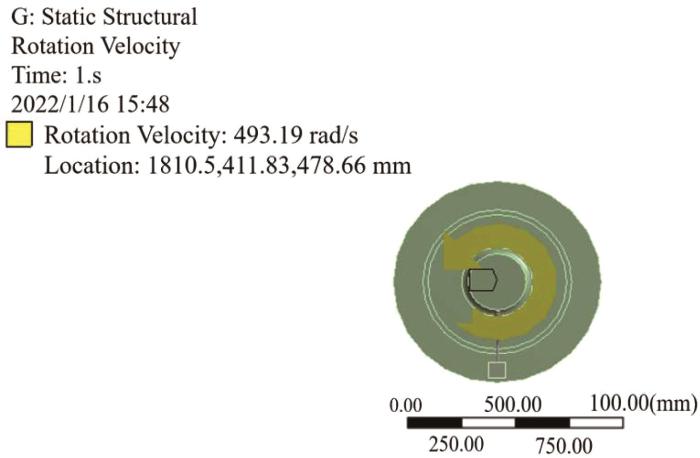
试验件转子在热态下正常工作时，转速是决定轴系动态特性的重要因素之一，所以在热态下验证校中方案时需要考虑转速的影响。根据实际工艺参数可知，所研究轴系的额定转速为3 364 r/min。轴系额定转速的施加如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 轴系额定转速的施加

Fig.8 Application of rated rotational speed of shafting

3.3　仿真结果分析

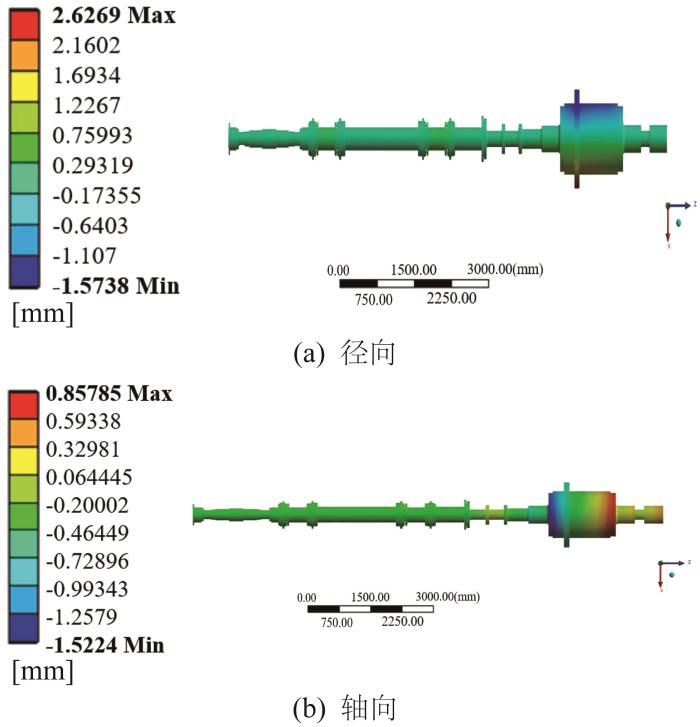
根据以上载荷，采用ANSYS Workbench软件求解热态下的轴系变形，得到轴系径向和轴向变形云图，如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 轴系变形云图

Fig.9 Deformation map of shafting

由图9(a)可知，轴系径向最大变形发生在试验件转子的叶片处，最大变形量为2.626 9 mm。原因是叶片处的温度最高，受热膨胀变形最严重。由图9(b)可知，轴系轴向最大变形发生在试验件转子中间轴段的两侧，最大变形量分别为1.522 4 mm和0.857 85 mm。原因是这两侧的温度梯度较大，导致变形较严重。

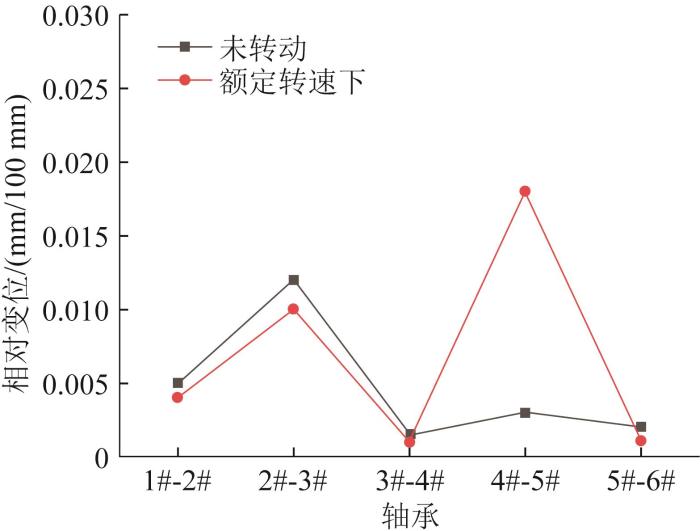
根据轴承1#至轴承6#的径向变形量，可算得校中优化后未转动和额定转速下每两个轴承间的相对变位，如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 校中优化后轴承间的相对变位

Fig.10 Relative displacement between bearings after alignment optimization

由图10可知，校中优化后未转动和额定转速下轴承间的相对变位均低于许用临界值。虽然额定转速下轴承4#-5#和轴承5#-6#的相对变位高于未转动时，但是整体的相对变位均低于许用临界值，故校中优化结果满足要求。

3.4　实验结果分析

基于上述优化参数对轴系进行实际精调后，在0~3 300 r/min的转速范围内开展了热态实验。结果表明，轴系振动峰值稳定控制在0.04 mm以内，振动量符合指标要求，验证了所提出的校中优化方案的有效性和可靠性。

4 结论

本研究针对多级透平综合性能试验台轴系校中难题，建立了融合轴承支反力和轴承间相对变位的多因素优化校中方法：通过ANSYS Workbench软件仿真分析了轴系冷态变形，获得了关键轴承的支反力和轴承间相对变位，并采用MATLAB软件求解最优调整参数，然后用Fluent软件模拟轴系实际热态工况，借助ANSYS Workbench验证了优化校中方案的有效性和可靠性，并进行了实验验证。主要研究结论如下：

1）冷态下的仿真结果显示，轴系最大变形位于试验件转子轴段，轴承4#与轴承5#的相对变位为0.034 mm/100 mm，超过3 $\times$ 10^-4的许用临界值，需要进行轴承预变位优化。

2）以轴承5#和轴承6#的支反力最小为优化目标，优化计算结果表明，当轴承5#下沉0.057 mm时，轴承4#与轴承5#的相对变位降至许用临界值以下，满足冷态下校中对轴承间相对变位与轴承负荷的约束要求。

3）在0~3 300 r/min的转速范围内开展了热态下校中优化方案的验证实验。结果表明，轴系振动峰值稳定控制在0.04 mm以内，振动量符合指标要求。

综上，本文提出的轴系校中优化方法考虑了轴系实际温度和复杂载荷，对于轴系的精调具有较好的指导意义。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SHIMOI

， TANAKA

A method for quantitatively analyzing the angle of direction for arbitral c-axis alignment with retardation measurements

［J］. Optics & Laser Technology， 2015， 65： 189-193.