空间望远镜焦平面基板结构热-力耦合双目标拓扑优化设计

doi:10.3785/j.issn.1006-754X.2025.05.135

空间望远镜焦平面基板结构热-力耦合双目标拓扑优化设计

曹雪虎^,^,, 纪敬虎^,

江苏大学机械工程学院，江苏镇江 212013

Dual-objective topology optimization design for focal plane substrate structure of space telescope with thermo-mechanical coupling

CAO Xuehu^,^,, JI Jinghu^,

School of Mechanical Engineering, Jiangsu University, Zhenjiang 212013, China

通讯作者: 纪敬虎（1985—），男，副教授，博士，从事机械系统摩擦动力学、人工智能、激光微纳制造技术等研究，E-mail: jijinghu@ujs.edu.cn

收稿日期: 2025-05-07 修回日期: 2025-07-02

基金资助:

国家自然科学基金资助项目. 52075225
江苏省高等学校自然科学基金资助项目. 24KJB460009

Received: 2025-05-07 Revised: 2025-07-02

作者简介 About authors

曹雪虎（1997—），男，硕士生，从事结构轻量化研究，E-mail:1436412487@qq.com，https://orcid.org/0009-0004-4697-588X , E-mail：1436412487@qq.com

摘要

针对空间望远镜焦平面基板结构刚度、热稳定性与轻量化的协同设计难题，通过拓扑优化方法对其进行优化设计。以某大型空间望远镜焦平面基板结构为优化对象，构建了以柔度最小化和温度梯度最小化为目标函数的拓扑优化数学模型，并采用层次分析法确定目标的权重系数。随后，使用COMSOL Multiphysics软件进行求解，得到了基板结构的拓扑优化结果。最后，基于优化结果对基板结构进行重构，并进行了有限元仿真验证。结果表明：与原始基板相比，优化后基板的质量减小了39.94%，最大位移减小了4.92%，基频达到801.2 Hz，满足设计要求，同时实现了轻量化目标。研究结果为其余工程结构的轻量化设计提供了参考。

关键词： 焦平面基板结构 ; 热-力耦合 ; 双目标拓扑优化 ; 层次分析法 ; 有限元仿真

Abstract

Aiming at the collaborative design challenge of stiffness, thermal stability and lightweight for the focal plane substrate structure in space telescopes, the topology optimization method is adopted to conduct optimization design. Taking the focal plane substrate structure of a large space telescope as the optimization object, a topological optimization mathematical model with dual objective functions of minimizing compliance and temperature gradient was established, and the analytic hierarchy process was employed to determine the weight coefficients of objectives. Subsequently, the COMSOL Multiphysics software was used for solution, and the topological optimization results of the substrate structure were obtained. Finally, the substrate structure was reconstructed based on the optimization results and validated through finite element simulation. The results demonstrated that compared with the original substrate, the optimized substrate achieved a 39.94% reduction in mass, a 4.92% decrease in maximum displacement, and a fundamental frequency of 801.2 Hz, thereby meeting design requirements and achieving the lightweight goal. The research results provide a reference for the lightweight design of other engineering structures.

Keywords： focal plane substrate structure ; thermo-mechanical coupling ; dual-objective topology optimization ; analytic hierarchy process ; finite element simulation

PDF (4504KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

曹雪虎, 纪敬虎. 空间望远镜焦平面基板结构热-力耦合双目标拓扑优化设计[J]. 工程设计学报, 2025, 32(6): 831-838 doi:10.3785/j.issn.1006-754X.2025.05.135

CAO Xuehu, JI Jinghu. Dual-objective topology optimization design for focal plane substrate structure of space telescope with thermo-mechanical coupling[J]. Chinese Journal of Engineering Design, 2025, 32(6): 831-838 doi:10.3785/j.issn.1006-754X.2025.05.135

空间望远镜作为人类探索宇宙的核心观测工具，正朝着大口径化方向快速发展^[1-2]。然而，随着口径的持续增大，望远镜整体结构的尺寸和质量也不断增大，这给系统设计、空间装配及运载发射等环节带来了严峻挑战。

焦平面是空间望远镜的关键组件，其表面安装了大量光学元件，承担着信息转换的重要功能^[3]。焦平面基板结构为这些光学元件提供稳定支撑，其稳定性直接影响最终的成像质量。因此，焦平面基板结构需满足多维度性能要求：首先，应具备卓越的刚度特性，既能维持光学元件的位形精度，又能确保发射阶段的结构基频满足动力学要求；其次，需具备有效的热控体系，可将温度梯度控制在较小范围内，避免热应力过大而引发变形；最后，必须实现轻量化设计，以降低发射成本^[4]。传统的经验设计方法在小口径望远镜焦平面基板结构的设计中尚可适用，但对于大口径望远镜，由于结构惯性载荷急剧增长，常规设计方法难以兼顾刚度、热稳定性与轻量化的多维需求。因此，需要引入一种新的设计方法，以实现大口径望远镜焦平面基板结构的多目标协同优化设计。

拓扑优化理论起源于Michell的桁架理论^[5]，经过数十年的发展，先后演变出均匀化法^[6]、变密度法^[7]、水平集法^[8]和渐进结构进化法^[9]等方法。在结构设计初期应用拓扑优化，优化空间大，且更易获得形状合理、布局紧凑的轻量化结构。例如：刘伟等^[10]分析了齿轮箱体的静动态特性并对其进行了多目标拓扑优化，改进后的箱体在质量减小11.2%的同时，最大应力下降了39.6%，位移减小了5.1%。韩博文等^[11]提出了基于折衷规划法与熵权-层次分析的多目标拓扑优化方法，并将其应用于机载雷达支架的轻量化设计与结构优化，优化后支架的质量减小了53.8%。沈保山等^[12]采用变密度拓扑优化法对转向摇臂支架进行了轻量化设计，减重比例高达54.8%。Zeng等^[13]受铸造约束的拓扑优化方法的启发，提出了一种适用于大口径空间望远镜反射镜结构设计的优化模型，该模型可同时优化加强筋的分布和高度，优化后反射镜的光学性能提升了62.5%。Mao等^[14]针对自主式水下航行器（autonomous underwater vehicle, AUV）的电池架在工作过程中面临的热-力耦合挑战（包括电池发热和载荷冲击），建立了热-固耦合拓扑优化模型，为AUV电池架的创新设计提供了理论支撑和优化方法。张小强等^[15]针对聚变堆偏滤器的W/Cu模块进行了拓扑优化设计，在10 MW/m²热负荷下，W/Cu模块的最高温度降低了108.5 K，界面热应力下降了264.2 MPa，冷却性能显著提升。田立勇等^[16]基于煤矿井下的复杂环境，通过对更换托辊机器人的履带式底盘进行动力学仿真和对其姿态调整机构进行拓扑优化，使横移平台的应力降低了13.71 MPa，质量减小了36.92%，从而显著提升了机器人的行驶稳定性与结构性能。

近年来，面向航空航天领域复杂热力环境下的多物理场耦合多目标拓扑优化研究不断深入，并取得了一系列重要进展。郭伟超等^[17]提出了一种宏微观并行的拓扑优化方法，并结合聚类算法划分微结构类型，解决了热-力耦合载荷下导弹导引头的轻量化与热防护一体化设计问题，优化后导引头的质量减小了50%。叶帅等^[18]结合拓扑优化与尺寸灵敏度分析，对星载临边光谱仪反射镜背部筋的构型进行了设计，并引入综合评价因子优化了柔性支撑结构，在重力载荷与热-力耦合工况下，实现了在保证反射镜面型精度满足使用要求的同时减重60%。朱兆基等^[19]提出了一种静-动-随机振动多工况优化流程，并结合柔度约束和固有频率最大化目标，对火箭发动机的承力结构进行了优化，使其质量减小了30%，一阶模态频率提升了35.4%，进而增强了发动机对振动环境的适应性。

尽管上述研究在热-力耦合多目标优化方面取得了显著成果，并逐渐应用于航空航天结构，但当前的拓扑优化研究主要集中在单物理场下多工况或者双物理场下单目标的结构优化上，无法满足空间望远镜焦平面基板结构对高刚度、低温度梯度和轻量化的多维要求。为此，本文针对大口径空间望远镜焦平面基板结构，构建其在热-力耦合作用下的双目标拓扑优化模型，并以柔度最小化与温度梯度最小化为目标进行协同优化，致力于开发出能够适应复杂工况的高性能轻量化基板结构。

1 空间望远镜焦平面基板结构的设计要求

初始的大口径空间望远镜焦平面基板结构如图1所示，其安装方式为：四周由螺栓固定，光学元件通过夹紧装置、定位装置等安装在中间凹槽内。针对航空航天领域的轻量化和高刚度要求，基板结构的材料选择TC4钛合金。TC4钛合金的密度为4.43 g/cm³，弹性模量为114 GPa，导热系数为8 W/(m·K)，屈服强度为860 MPa。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 初始空间望远镜焦平面基板结构示意

Fig.1 Schematic of original substrate structure of space telescope focal plane

空间望远镜焦平面基板结构所受的载荷除了自身重力外，还包括安装在凹槽内的光学元件以及其余装置所产生的压力；热量主要由光学元件工作时所产生。所设计的基板结构需满足以下要求：1）最大变形量不超过0.05 mm；2）最大von Mises应力不超过所用材料的屈服极限和抗拉极限；3）温度梯度小于0.05 K/mm；4）基频不低于120 Hz。

2 基板结构热-力耦合双目标拓扑优化设计

2.1　拓扑优化方法

连续体结构拓扑优化通常基于有限元离散化方法，通过引入材料分布表征函数来确定单元域的材料分布状态。其中：函数值为1表示实体材料，0表示空隙区域。现阶段，最常用的拓扑优化方法为固体各向同性材料惩罚模型（solid isotropic material with penalization, SIMP）。在SIMP中，将每个单元的材料视为多孔材料，以相对密度作为设计变量，并将单元的材料特性（如弹性模量）表示为相对密度的函数，数学表达式如下：

E_{i} = [\underset{̲}{ρ} + (\bar{ρ} - \underset{̲}{ρ}) ρ_{i}^{P}] E_{0}, i = 1, 2, \dots, N

(1)

式中：E_i 为单元i中材料的弹性模量； $\underset{̲}{ρ}$ 、 $\bar{ρ}$ 分别为计算过程中为避免奇异性而设置的下界和上界，取 $\underset{̲}{ρ}$ =0.001， $\bar{ρ}$ =1；ρ_i 为单元i中材料的相对密度；P为惩罚因子，对于实体，一般取P=3；E₀为给定各向同性材料的弹性模量；N为单元数量。

由式(1)可知，连续体结构的构型可用材料相对密度ρ_i 来描述，即ρ_i 可作为构型设计问题中的设计变量，表示为：

ρ = {(ρ_{1} ρ_{2} \dots ρ_{Ν})}^{T}

(2)

2.2　热-力耦合双目标拓扑优化数学模型

本文针对空间望远镜焦平面基板结构的热-力耦合拓扑优化问题，构建了综合考虑柔度最小化与温度梯度最小化的双目标优化模型。结合结构力学与热传导理论，建立如下目标函数：

Π = w \frac{φ}{φ_{0}} + (1 - w) \frac{ψ}{ψ_{0}}

(3)

式中：П为双目标函数；φ为基板结构的柔度；ψ为基板结构的温度梯度；w为目标的权重系数；φ₀和ψ₀分别为初始柔度和初始温度梯度，引入初始参数的目的是实现目标函数的无量纲化。

基板结构柔度的目标函数可表示为：

φ (ρ) = F^{T} U = U^{T} K U

(4)

式中： U 为位移矩阵； K 为刚度矩阵； F 为外载荷，包括机械载荷 F_m和热载荷 F_t。

对于基板结构的温度梯度，为了量化结构的导热均匀性，以温度梯度的积分作为目标函数，表示为：

ψ (ρ) = {\int_{Ω} ‖\nabla T (ρ)‖}^{2} d Ω = T^{T} K_{t} T

(5)

其中：

\nabla T = (\frac{\partial T}{\partial x}, \frac{\partial T}{\partial y}, \frac{\partial T}{\partial z})

式中： K_t为热刚度矩阵， $\nabla T$ 为温度梯度， T 为温度矩阵，Ω为设计域。

由于基板结构的材料是均匀的，因此可使用体积约束替代质量约束，体积约束定义如下：

V = f V_{0} = \sum_{i = 1}^{N} ρ_{i} v_{i}

(6)

式中：V为设计域的体积，f为优化体积比，V₀为整个设计域的初始体积，v_i 为优化后的单元体积。

结合式(3)至(6)，最终的拓扑优化数学模型可表示为：

\{\begin{array}{l} F i n d ρ_{i} (i = 1, 2, \dots, N) \\ M i n i m i z e Π = w \frac{φ}{φ_{0}} + (1 - w) \frac{ψ}{ψ_{0}} \\ \begin{array}{l} s . t . K U = F_{m} + F_{t} \\ \nabla \cdot (k (ρ) \nabla T) + q = 0 \\ V = f V_{0} = \sum_{i = 1}^{N} ρ_{i} v_{i} \\ 0 \leq ρ_{i} \leq 1 \end{array} \end{array}

(7)

式中：q为热源强度， $k (ρ)$ 为热导率。

2.3　双目标权重系数

在解决热-力耦合双目标拓扑优化问题时，目标权重系数的确定是关键环节。针对热力学与结构力学双场耦合的复杂场景，优化问题本质上属于典型的多属性决策问题，各目标函数之间既存在涉及能量传递的物理耦合关系，又表现出不同量纲与数量级的数学特性差异。为此，本文通过引入层次分析法来构建系统化的权重决策模型^[20]。

层次分析法由Saaty于20世纪70年代提出，其核心是通过层次分解原理、相对标度理论和排序合成法则^[21]，构建目标层—准则层—方案层的递阶模型^[22]。运用九级标度法将专家经验转化为判断矩阵，采用特征根算法计算权重系数，并通过随机一致性比率（C_R<0.1）来验证逻辑严谨性。层次分析法的本质是求解正互反矩阵的最大特征值及其归一化特征向量，利用方根法或和积法来实现多维指标的公度性处理。相较于传统赋权法，层次分析法的系统化数学处理机制既保留了决策者认知框架，又强化了复杂决策的结构化分析能力。

在层次分析法中，层次结构模型的科学构建是确定权重系数的基础。本文基于热-力耦合双目标拓扑优化的特性，构建了聚焦于结构柔度和温度梯度这2个关键因素的层次结构模型。

在完成层次结构模型构建后，着手构造判断矩阵。判断矩阵的构造是基于各因素间的相对重要性来实现的。在比较各因素重要性的过程中，采用1~9标度法进行赋值操作，具体赋值规则详见表1。

表1 标度法的赋值规则

Table 1 Assignment rule of scaling method

相对重要性^①	赋值
同等重要	1
稍微重要	3
明显重要	5
强烈重要	7
极端重要	9

① 相对重要性是指因素j相对于因素t的重要程度。

新窗口打开| 下载CSV

标度法为衡量各因素之间的相对重要性提供了一套标准化、可量化的方法。当对因素j和因素t进行比较时，若认为因素j相对于因素t的重要程度为a（a的取值依据1~9标度法确定），则判断矩阵中因素j与因素t对应的位置赋值a；同时，由于比较是相互的，则判断矩阵中因素t与因素j对应的位置赋值1/a。基于上述规则，对所有因素进行两两比较并完成赋值操作，即可构造完整的判断矩阵。

对于本文所研究的焦平面基板结构，柔度占主导地位，故柔度因素相对于温度梯度因素为极端重要，由此可得到表2所示的判断矩阵。

表2 判断矩阵

Table 2 Judgment matrix

因素	柔度	温度梯度
柔度	1	9
温度梯度	1/9	1

新窗口打开| 下载CSV

在层次分析法的理论架构内，当决策系统的维度n=2时，其判断矩阵具有内在的完全一致性。凭借相关的数学推导，可知一致性比率C_R=0恒成立，这是由正互反矩阵的特定结构属性决定的。设二维决策系统的判断矩阵 A 为：

A =

[\begin{matrix} 1 & a \\ \frac{1}{a} & 1 \end{matrix}]

(8)

判断矩阵 A 的特征方程可表示为：

λ^{2} - 2 λ = 0

(9)

式中：λ为特征值。

根据式(9)，解得最大特征值 $λ_{m a x} = 2$ 。

定义一致性指数C_I为：

C_{I} = (λ_{m a x} - n) / (n - 1)

(10)

由式(10)可知，只有n=2时才能确保分子项为0。特别地，Saaty所提出的一致性检验理论指出：当n≤2时，随机一致性指数R_I定义为0，故C_R=C_I/R_I的运算失去实际意义。因此，在双目标优化场景下，判断矩阵必然满足完全一致性条件，可省略常规的一致性校验流程。

通过几何平均法计算优化目标的权重系数，计算式如下：

w = \frac{\sqrt[]{1 \times a}}{\sqrt[]{1 \times a} + \sqrt[]{1 \times 1 / a}}

(11)

将极端重要对应的赋值代入式(11)，求解得到基板结构柔度的权重系数为0.9，温度梯度的权重系数为0.1。

3 基板结构拓扑优化与有限元分析

3.1　优化流程

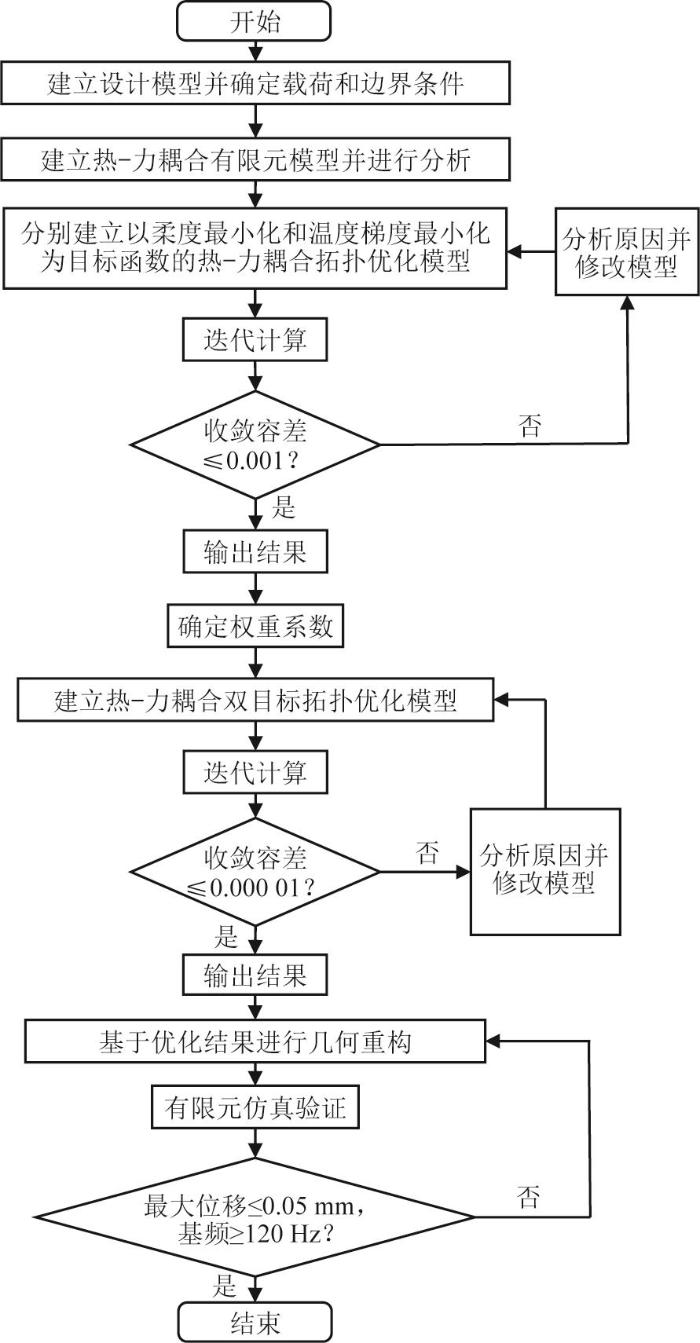
空间望远镜焦平面基板结构热-力耦合双目标拓扑优化设计流程遵循系统化实施路径：在预分析阶段，利用COMSOL Multiphysics软件建立热-力耦合有限元模型并定义设计域边界；随后，分别进行柔度最小化与温度梯度最小化的单目标拓扑优化，以获取各自的最优值作为后续双目标函数归一化处理的基准。接着，通过层次分析法确定柔度和温度梯度的权重系数，并采用SIMP变密度法进行迭代求解，以获得最优的材料分布；最后，对基板结构的拓扑构型进行几何重构，以提升后续的工艺可行性，并通过有限元仿真来验证其刚度、强度及温度均匀性等核心指标。具体优化流程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基板结构热-力耦合双目标拓扑优化流程

Fig.2 Dual-objective topology optimization flow of substrate structure with thermo-mechanical coupling

3.2　优化结果与几何重构

在开展热-力耦合双目标拓扑优化时，鉴于目标函数已进行归一化处理，为有效防止优化过程过早达到收敛状态，将收敛容差设为0.000 01，其余各项参数的设置均与单目标拓扑优化时保持一致。

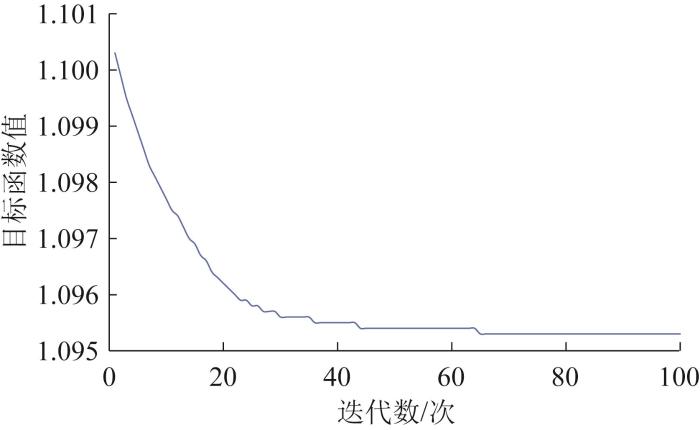
图3所示为基板结构拓扑优化目标函数随迭代次数的变化曲线。结果表明：在初始优化阶段（0~20次迭代），目标函数值呈急剧下降的趋势，反映出基板结构具有显著的可优化空间；从第20次迭代开始一直到第60次迭代期间，目标函数值虽仍持续下降，但下降速度明显减缓，这意味着优化过程正在逐步逼近最优解，相应的优化空间也逐渐变小；在第60次迭代后，目标函数值基本上保持不变，趋于稳定状态，这表明已十分接近最优解。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 基板结构拓扑优化目标函数的变化曲线

Fig.3 Variation curve of objective function for substrate structure topology optimization

图4所示为优化后基板结构的多切面单元密度分布云图。观察图4可知，基板结构各切面单元的密度呈现十分突出的两极分化趋势，大体朝着0和1的方向发展，中间密度的单元数量极少，这充分说明优化结果成功避免了大量中间密度单元的出现。结果表明，所构建的优化模型具有较高的可靠性与有效性。

图4

新窗口打开| 下载原图ZIP| 生成PPT

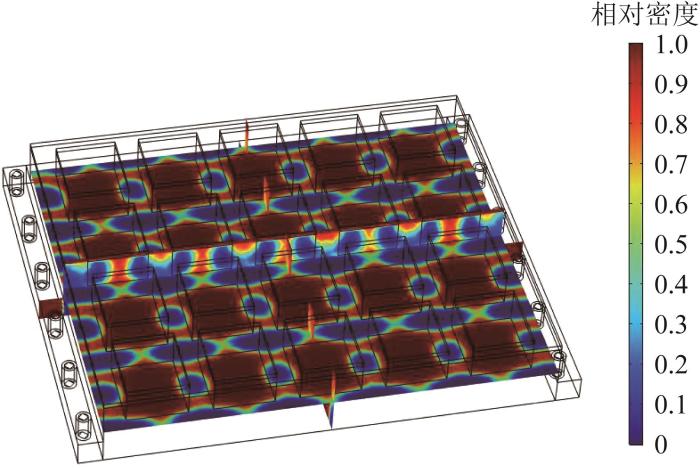
图4 优化后基板结构多切面单元密度分布云图

Fig.4 Cloud map of multi-slice element density distribution of substrate structure after optimization

综上，所构建的热-力耦合双目标拓扑优化模型具有优良的收敛特性与稳定性，收敛过程符合优化问题的典型特征，验证了该拓扑优化方法的工程适用性，实现了预期优化目标。

基于优化后基板结构的单元密度分布云图，结合工程制造可行性与装配适配性要求，对基板结构进行几何重构设计。重构后的基板结构如图5所示。从图5中可以看出，新基板底面形成规律性孔洞拓扑构型，功能槽周缘呈现支撑肋与镂空区域交替分布的结构特征。这种拓扑构型通过合理分配材料分布梯度，可显著改善结构应力分布的均匀性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 双目标优化重构后的基板结构

Fig.5 Substrate structure after dual-objective optimization and reconstruction

3.3　有限元仿真验证

为了验证新基板结构的性能，通过有限元仿真得到优化前后基板结构的位移分布云图、von Mises应力分布云图和热应变分布云图，如图6至图8所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

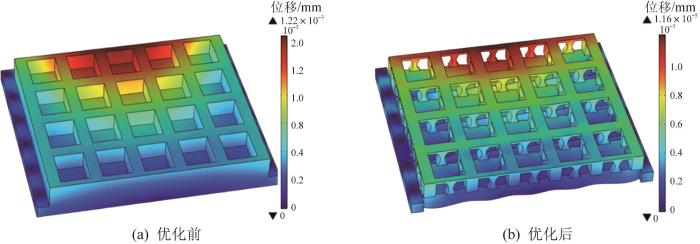
图6 优化前后基板结构的位移分布云图

Fig.6 Cloud maps of displacement distribution of substrate structure before and after optimization

图7

新窗口打开| 下载原图ZIP| 生成PPT

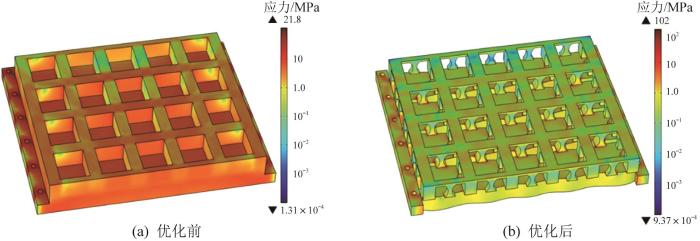
图7 优化前后基板结构的von Mises应力分布云图

Fig.7 Cloud maps of von Mises stress distribution of substrate structure before and after optimization

图8

新窗口打开| 下载原图ZIP| 生成PPT

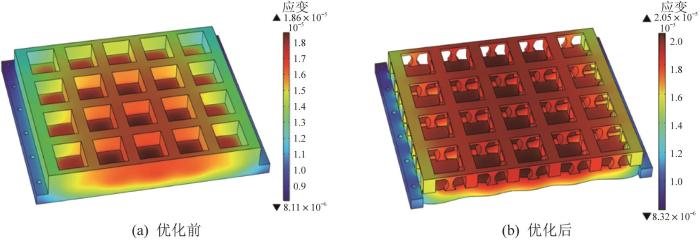
图8 优化前后基板结构的热应变分布云图

Fig.8 Cloud maps of thermal strain distribution of substrate structure before and after optimization

根据有限元仿真分析结果，导出优化前后基板结构在热-力耦合作用下各个性能指标的最大值，如表3所示。

表3 优化前后基板结构的性能对比

Table 3 Performance comparison of substrate structures before and after optimization

对比项

最大位移/10^-3mm

最大应力/MPa

最大热应变/10^-5

最大温度梯度/

(K/mm)

基频/Hz

质量/kg

变化幅度/%

-4.92

+367.89

+10.22

+22.67

-21.54

-39.94

优化前

1.22

21.8

1.86

0.034 4

1 021.1

3.220

优化后

1.16

102.0

2.05

0.042 2

801.2

1.934

新窗口打开| 下载CSV

从表3结果来看，优化后基板结构的最大位移为1.16×10^-3 mm，与优化前的1.22×10^-3 mm相比降低了4.92%。由图6可知，优化后的位移分布更加均匀且位移较大的区域明显减少，表明通过拓扑优化减少了局部应力集中，显著提高了基板结构的均匀性和稳定性。优化后基板结构的最大应力虽从21.8 MPa增大到102.0 MPa，但仍远小于TC4钛合金的屈服强度。优化后基板结构的最大热应变为2.05×10^-5，比优化前增大了10.22%，但仍小于5×10^-5的设计要求。

为进一步量化分析优化前后基板结构的性能，设定以下阈值：以最大位移的1/2为高位移阈值，最大应力的1/2为高应力阈值，最大热应变的7/10为高热应变阈值。通过计算可得，相比于优化前，优化后基板结构的高位移区域占比从27.0%降至19.5%，高应力区域占比从0.003 0%降至0.000 5%，高热应变区域占比从87.7%降至76.9%。定量分析结果表明，优化后基板结构的高值区域显著减小，且材料分布更均匀，这表明拓扑优化技术的应用显著改变了结构的力传递路径和散热路径，同时使变形量分布和应力分布更加合理，从而提高了结构的整体性能。

优化后基板结构的基频为801.2 Hz，相较于优化前的1 021.1 Hz有所降低，但远高于设计要求的120.0 Hz，且与其他组件的基频相差较大，可有效避免因共振而导致的结构破坏。

综上，优化后的基板结构满足设计要求，同时其质量减小了39.94%，实现了轻量化设计。采用3D打印技术制造优化后的新基板结构，如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 优化后基板结构的实物图

Fig.9 Actual image of optimized substrate structure

4 总结

本文对大口径空间望远镜焦平面基板结构进行了热-力耦合双目标拓扑优化，并通过有限元仿真对优化结果进行了验证，得到以下结论。

1）针对刚度、热稳定性与轻量化的协同设计难题，提出了一种热-力耦合双目标拓扑优化模型，并将其成功应用于空间望远镜焦平面基板结构的优化设计，获得了满足设计要求的拓扑构型。

2）根据拓扑优化结果，考虑加工性和装配性，对基板结构进行了几何重构，并对重构后的基板结构进行了有限元仿真。结果表明：优化后基板结构的质量为1.934 kg，相比于优化前减小了39.94%；最大位移为1.16×10^-3 mm，相比于优化前降低了4.92%；最大应力与最大热应变均满足设计要求。新基板结构在刚度性能、热稳定性满足设计要求的前提下，质量大幅减小，实现了轻量化目标。

3）通过3D打印技术制作了优化后的基板结构，验证了热-力耦合双目标拓扑优化设计方法的工程可行性，这可为其他类似航空航天结构的轻量化设计提供参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SAVITSKIĬ

A M

， SOKOLOV

I M

Questions of constructing lightened primary mirrors of space telescopes

［J］. Journal of Optical Technology， 2009， 76（10）： 666-669.