基于改进MOMVO算法的大荷载绝缘拉棒端头多目标优化

doi:10.3785/j.issn.1006-754X.2025.05.110

基于改进MOMVO算法的大荷载绝缘拉棒端头多目标优化

吴田^,¹^,², 吴滨帆^,^,¹^,², 邱中华³, 彭勇⁴, 朱祥⁴

1.三峡大学电气与新能源学院，湖北宜昌 443002

2.湖北省输电线路工程技术研究中心，湖北宜昌 443002

3.国网四川省电力公司超高压分公司，四川成都 610041

4.中国电力科学研究院有限公司，湖北武汉 430074

Multi-objective optimization of large-load insulating pull rod end based on improved MOMVO algorithm

WU Tian^,¹^,², WU Binfan^,^,¹^,², QIU Zhonghua³, PENG Yong⁴, ZHU Xiang⁴

1.College of Electrical Engineering and New Energy, China Three Gorges University, Yichang 443002, China

2.Hubei Transmission Line Engineering Technology Research Center, Yichang 443002, China

3.Extra High Voltage Company, State Grid Sichuan Electric Power Company, Chengdu 610041, China

4.China Electric Power Research Institute Limited, Wuhan 430074, China

通讯作者: 吴滨帆（2001—），男，硕士生，从事带电作业绝缘工器具优化设计研究，E-mail: 1044435906@qq.com，https://orcid.org/0009-0003-5666-0155

收稿日期: 2025-03-06 修回日期: 2025-04-27

基金资助:

国家自然科学基金资助项目. 51807110
国家电网公司科学技术项目. 5500-202455164A-1-1-ZN

Received: 2025-03-06 Revised: 2025-04-27

作者简介 About authors

吴　田（1983—），男，高级工程师，博士，从事带电作业、高电压与绝缘技术等研究，E-mail:wutian_08@163.com , E-mail：wutian_08@163.com

摘要

针对特高压大荷载绝缘拉棒笨重、使用不便的问题，提出了一种绝缘拉棒端头多目标优化方法，以减小质量和提升绝缘性能及机械性能。首先，建立绝缘拉棒的有限元仿真模型，分析了其端头的电场分布和机械特性。然后，基于最优拉丁超立方抽样试验设计方法和径向基神经网络，构建了绝缘拉棒端头质量、最大应力、最大形变量和最大电场强度的代理模型。在此基础上，采用MOMVO（multi-objective multi-verse optimization，多目标多元宇宙优化）算法开展了多目标优化设计。在优化过程中，结合Sine-Tent-Cosine混沌映射策略、正余弦算法以及自适应参数更新策略，以提高MOMVO算法的多目标优化性能。最后，通过仿真和试验来检验多目标优化方法的可行性。结果表明：改进MOMVO算法的优化性能优于传统的NSGA-II（non-dominated sorting genetic algorithm-Ⅱ，二代非支配排序遗传算法）和MOEA/D（multi-objective evolutionary algorithm based on decomposition，基于分解的多目标进化算法）等。相较于优化前，优化后绝缘拉棒端头的最大应力、最大形变量和最大电场强度分别下降了17.03%、6.85%和5.58%，质量减小了10.66%。研究结果为绝缘工器具的综合优化设计提供了参考。

关键词： 大荷载绝缘拉棒 ; 有限元仿真 ; 代理模型 ; 多目标优化 ; 多目标多元宇宙优化算法

Abstract

Aiming at the problems of excessive weight and inconvenient use of large-load insulating pull rods for ultra-high voltage, a multi-objective optimization method for the end of insulating pull rods is proposed to reduce weight and enhance insulation performance and mechanical properties. Firstly, a finite element simulation model of the insulating pull rod was established, and the electric field distribution and mechanical characteristics of its end were analyzed. Then, based on the optimal Latin hypercube sampling experimental design method and the radial basis function neural network, the surrogate models for the mass, maximum stress, maximum deformation and maximum electric field intensity of the insulating pull rod end were constructed. On this basis, the MOMVO (multi-objective multi-verse optimization) algorithm was utilized to conduct multi-objective optimization design. During the optimization process, the multi-objective optimization performance of the MOMVO algorithm was improved by combining the Sine-Tent-Cosine chaotic mapping strategy, the sine cosine algorithm, and the adaptive parameter update strategy. Finally, the feasibility of the multi-objective optimization design method was verified through simulation and tests. The results indicated that the optimization performance of the improved MOMVO algorithm was superior to that of the traditional NSGA-II (non-dominated sorting genetic algorithm-II) and MOEA/D (multi-objective evolutionary algorithm based on decomposition). Compared with before optimization, the maximum stress, maximum deformation and maximum electric field intensity of the optimized insulating pull rod end decreased by 17.03%, 6.85% and 5.58%, respectively, while the mass decreased by 10.66%. The research results provide reference for the comprehensive optimization design of insulating tools and equipment.

Keywords： large-load insulating pull rod ; finite element simulation ; surrogate model ; multi-objective optimization ; multi-objective multi-verse optimization algorithm

PDF (5684KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吴田, 吴滨帆, 邱中华, 彭勇, 朱祥. 基于改进MOMVO算法的大荷载绝缘拉棒端头多目标优化[J]. 工程设计学报, 2025, 32(5): 696-707 doi:10.3785/j.issn.1006-754X.2025.05.110

WU Tian, WU Binfan, QIU Zhonghua, PENG Yong, ZHU Xiang. Multi-objective optimization of large-load insulating pull rod end based on improved MOMVO algorithm[J]. Chinese Journal of Engineering Design, 2025, 32(5): 696-707 doi:10.3785/j.issn.1006-754X.2025.05.110

随着超高压和特高压输电线路的大规模投入使用，绝缘拉棒作为更换绝缘子串的承力工具，对带电作业技术的发展和电力系统的安全稳定运行具有重要意义。然而，电压等级的提高以及绝缘子串长、荷载大等特性^[1]，使得对绝缘拉棒机械性能和绝缘性能的要求越来越高，导致绝缘拉棒的长度和质量明显增大。因此，大荷载绝缘拉棒的优化设计成为当前带电作业工器具研制领域的主要趋势，这既能降低生产成本，又能提高带电作业安全性。

目前，绝缘承力工器具的优化设计方法主要分为3类。第1类是基于人机工程学、新型连接技术以及有限元分析法等^[2-4]对绝缘承力工器具进行结构优化设计。这类方法可以改善绝缘承力工器具的应力和电场分布特性，但在轻量化设计方面的提升空间有限，难以满足实际作业需求。第2类是采用新型的高性能纤维绝缘材料（如聚对苯撑苯并二噁唑纤维、芳纶纤维）替代环氧玻璃钢^[5-6]，这类方法可以有效减小绝缘承力工器具的整体质量，同时还能够提升其机械性能和电气性能。但该类方法在实际应用中存在一些问题：一是新型高性能纤维绝缘材料普遍存在价格昂贵、制造工艺复杂等问题；二是这类方法在带电作业领域的应用经验较少，特别是在突遇高湿度、降雨等恶劣作业环境下，难以保障作业安全。第3类是通过试错法、经验法和类比法等对绝缘承力工器具进行尺寸优化，该类方法可有效避免上述2类方法存在的问题，但这类方法仍停留在传统的人工经验驱动优化阶段，存在效率慢、精度低及难以满足多目标协同优化需求等局限性。因此，在现有尺寸优化方法的基础上，寻求绝缘承力工器具的新型智能化尺寸优化方法成为推动带电作业技术发展的关键。

多目标优化算法作为优化设计中的主流方法，已在工程领域得到了广泛应用。杜进桥等^[7]通过有限元分析法和二代非支配排序遗传算法（non-dominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ）建立了盆式绝缘子屏蔽罩绝缘特性的优化模型，以屏蔽罩凹面和表面的最大电场强度为目标，有效改善了其电场分布。张维凯等^[8]综合考虑结构变化对盆式绝缘子机械性能和绝缘性能的影响，构建了以应力和电场强度为目标的优化模型，在保证机械性能安全裕度的基础上改善了沿面电场分布情况。刘丰硕等^[9]为提高中频变压器的绝缘特性，考虑变压器的功率密度，以绝缘结构的体积和电场强度为目标，通过C-MOEA/D（constrained multi-objective evolutionary algorithm based on decomposition，基于分解的约束多目标进化算法）进行优化设计，实现了变压器的全局优化。综上所述，多目标优化算法在绝缘设备的优化设计中已取得较多研究成果。然而，对于带电作业工器具的优化设计，不仅要考虑其电气性能和机械性能，还要兼顾其质量和形状，且随着结构尺寸的变化，这几者之间通常存在相互矛盾和相互冲突的关系。

多目标优化算法和计算模型的有效结合是提升优化精度的重要手段之一。经典的多目标优化算法NSGA-Ⅱ^[10]和MOEA/D^[11]难以处理复杂的高维多目标优化问题：NSGA-Ⅱ容易因参数的最佳配置、目标优化冲突以及精英解过度占据种群等问题而造成优化解的多样性和收敛性变差；MOEA/D将多个目标分解后所生成的子问题数量庞大，导致计算负担较大，算法性能显著衰退。2017年，Mirjalili等^[12-13]在MVO（multi-verse optimization, 多元宇宙优化）算法的基础上开发了MOMVO（multi-objective MVO，多目标多元宇宙优化）算法，该算法具有较强的全局搜索能力，在处理复杂的高维多目标优化问题时具有显著优势。但是，在初始MOMVO算法的迭代过程中，由于虫洞存在概率线性单调递增、旅行距离率单调递减至零以及常规种群初始化等问题，其全局搜索和局部搜索相对不平衡^[14]，故需要对现存问题进行改进，以增强算法的适用性和鲁棒性。

基于此，本文以大荷载绝缘拉棒端头为研究对象，综合考虑其质量、应力、形变量以及电场强度与结构尺寸之间的相互影响，利用最优拉丁超立方抽样试验设计方法和径向基神经网络建立相应的多目标优化模型。随后，采用Sine-Tent-Cosine混沌映射策略改进MOMVO算法的种群初始化过程，利用正余弦算法改进其虫洞位置更新机制，并基于自适应参数更新策略改进正余弦算法和MOMVO算法中的关键参数，以实现多目标优化模型的求解。最后，通过仿真和试验来检验所提出的多目标优化方法的可行性和准确性。

1 大荷载绝缘拉棒计算模型的建立与分析

1.1　绝缘拉棒计算模型建立

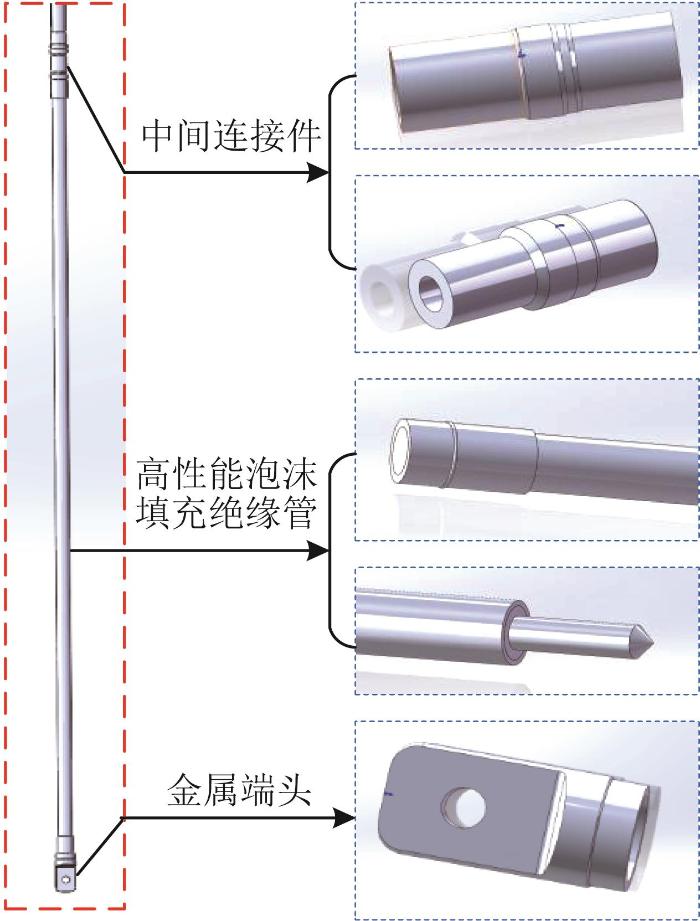
本文选取的绝缘拉棒为某厂家研制的1 000 kV大荷载硬质绝缘拉棒，其整体由金属端头、高性能泡沫填充绝缘管以及中间连接件三部分组成。该绝缘拉棒分为3节，各节通过内锥连接的方式相互连接，端头与绝缘管通过螺纹连接。利用SolidWorks软件构建整根绝缘拉棒的三维模型。限于篇幅，仅展示绝缘拉棒第1节的模型，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 绝缘拉棒三维模型（第1节）

Fig.1 Three-dimensional model of insulating pull rod (the first section)

绝缘拉棒金属端头的材料为40Cr；高性能泡沫填充绝缘管主要由泡沫管芯、环氧树脂玻璃钢和外部绝缘涂层三部分构成；中间连接件选用的材料为60Si₂Mn。各部件材料的相关参数^[15]如表1所示。

表1 绝缘拉棒各部件材料的相关参数

Table 1 Relevant parameters of materials for each component of insulating pull rod

材料	相对介电常数	密度/ (kg/m³)	杨氏模量/GPa	泊松比
40Cr	3	7 850	210	0.26
环氧树脂玻璃钢	5	1 780	35	0.30
泡沫管芯	3	45	0.015	0.30
环氧树脂	4	1 200	1	0.38
60Si₂Mn	1	7 850	205	0.30

新窗口打开| 下载CSV

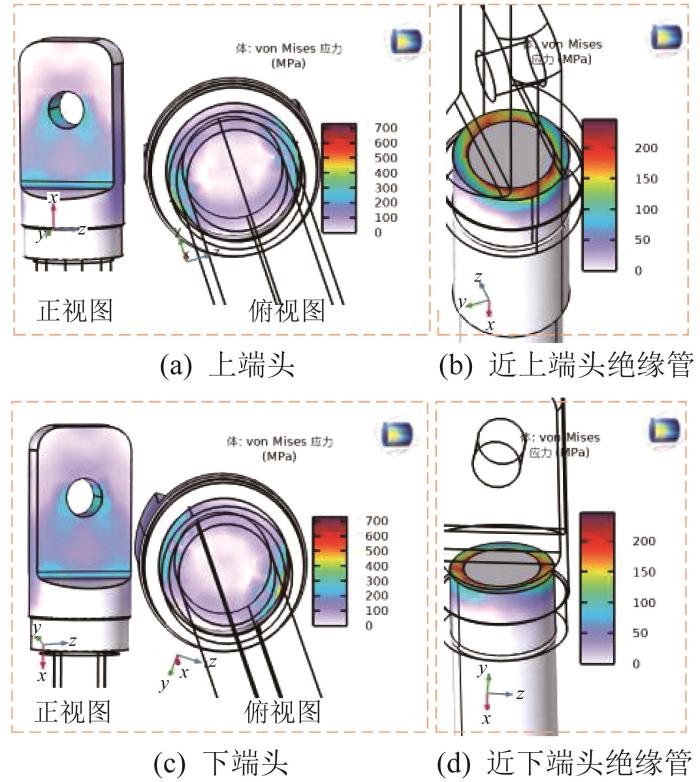
1.2　绝缘拉棒机械性能仿真分析

在开展绝缘拉棒机械性能仿真分析时，将在SolidWorks软件中构建的绝缘拉棒三维模型导入COMSOL软件以形成装配体，并设置接触对，在绝缘管的管芯处施加固定约束，在端头与绝缘管以及中间连接件之间设置刚性连接件以代替螺纹接触，上、下端头销控处分别施加沿x轴正、负方向的2.5倍额定荷载拉力^[16]，大小为250 kN。仿真模型采用自动划分网格方式^[17]，考虑到在利用极细网格进行应力分析时对计算资源的要求较高，本文选择的网格划分密度为“超细化”，最终划分得到的网格数量为94 134个。通过有限元仿真得到绝缘拉棒关键部件（端头和近端头绝缘管）的应力分布和形变量分布云图，分别如图2和图3所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 绝缘拉棒关键部件的应力分布云图

Fig.2 Cloud map of stress distribution of key components in insulating pull rod

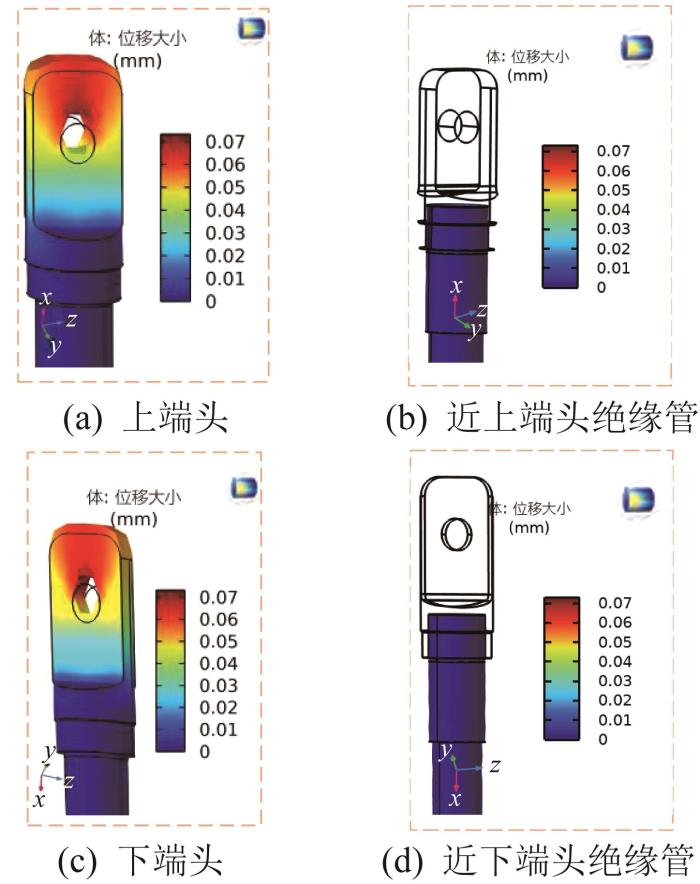
图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 绝缘拉棒关键部件的形变量分布云图

Fig.3 Cloud map of deformation distribution of key components in insulating pull rod

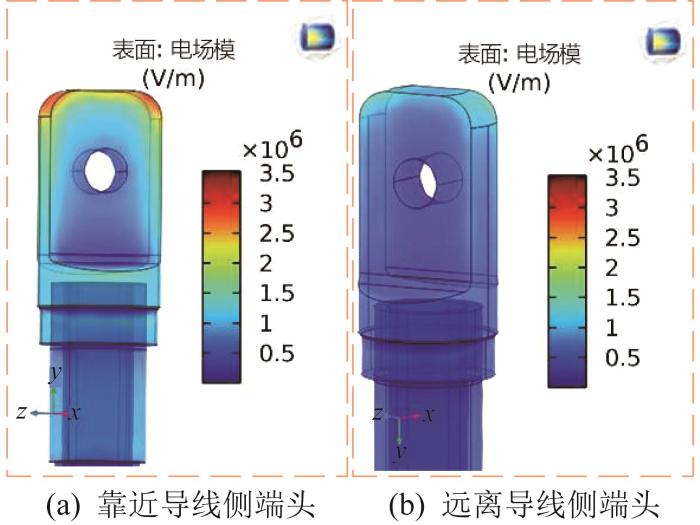
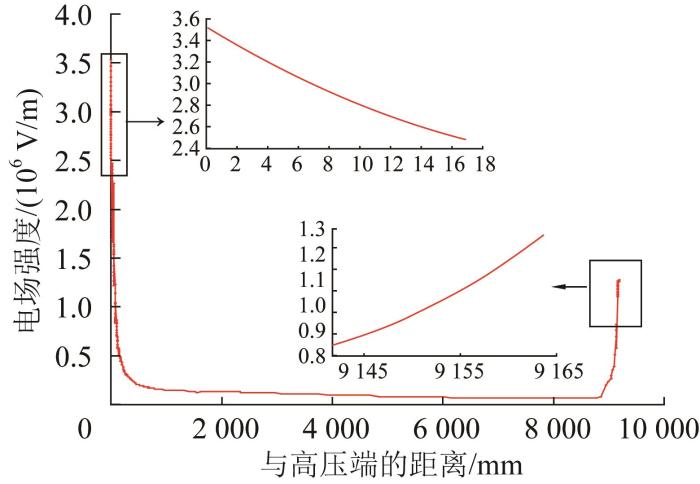
由图2可知，绝缘拉棒端头的最大应力集中在端头与绝缘管的螺纹连接处，大小为710.253 MPa，低于40Cr材料的最大屈服强度785 MPa；端头销控处应力为200~400 MPa；绝缘管与端头连接处的最大应力为230 MPa，绝缘管其余部分的应力较小，平均应力约为20 MPa，远低于环氧树脂玻璃钢的抗拉强度。由图3可知，端头销控处的形变量最大，约为0.073 24 mm，且越远离绝缘管的形变量越大，在销控附近形变量激增。因此，在设计绝缘拉棒端头时，需特别注意销控位置处的形变状况。

1.3　绝缘拉棒电场强度仿真分析

采用COMSOL软件对整根绝缘拉棒的电场强度进行计算。本文设置的电场环境为1 000 kV十分裂导线，空气域大小为50 m×50 m×50 m；为模拟导线无限长，两侧空气域不设置接地，其余空气域表面设置为接地，网格划分密度设置为“极细化”，最终划分得到的网格数量为14 342 708个。通过有限元仿真计算得到的绝缘拉棒端头表面的电场分布如图4所示，绝缘拉棒的轴向电场分布如图5所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 绝缘拉棒端头表面电场分布云图

Fig.4 Cloud map of electric field distribution on the surface of insulating pull rod end

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 绝缘拉棒的轴向电场分布

Fig.5 Axial electric field distribution of insulating pull rod

由图4和图5可以看出，绝缘拉棒电场分布情况为：两端端头的电场强度明显高于其他部分，靠近导线侧端头的最大电场强度为3.53×10⁶ V/m，远离导线侧端头的最大电场强度为1.28×10⁶ V/m；绝缘拉棒的轴向电场分布总体呈现出两端高、中部低的特征，高、低压端电场强度的变化比较明显，中部绝缘管的电场强度变化比较缓慢。同时，靠近导线侧的第1节绝缘管的电场强度比其他部分大且承受较大应力，易产生应变，进而形成缝隙，导致水汽侵入，电场强度畸变，造成局部放电^[18]，甚至引发带电作业事故。

综上，绝缘拉棒端头的最大应力接近40Cr的最大屈服强度，安全裕度较小。综合考虑端头结构对绝缘拉棒电气性能和形变量的影响，在对绝缘拉棒端头进行轻量化设计过程中，需兼顾机械性能和绝缘性能。

2 大荷载绝缘拉棒端头多目标优化设计

2.1　改进的MOMVO算法

2.1.1　算法描述

MOMVO算法为Mirjalili等^[12]结合多目标优化问题与宇宙演化过程所提出的一种群体智能优化算法，通过模拟宇宙间的引力与排斥交互机制来维持种群多样性，具有较强的全局搜索能力。然而，MOMVO算法的局部搜索能力较差，在处理复杂的高维多目标优化问题时计算速度缓慢，易陷入局部最优。鉴于此，为提升MOMVO算法的性能，本文主要针对其种群初始化、探索和开发阶段进行改进。

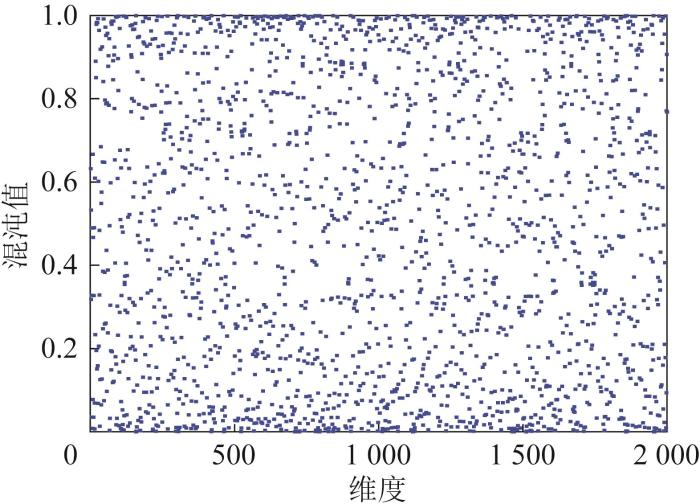
2.1.2　基于Sine-Tent-Cosine混沌映射策略的种群初始化

MOMVO算法的种群初始化过程极易出现分布不均匀现象，导致初始种群在搜索空间的某些区域过度集中，从而造成算法收敛速度缓慢、易陷入局部最优。

为此，本文引入Sine-Tent-Cosine混沌映射策略^[19]。将3种低维混沌复合，一方面可以克服低维混沌行为有限、序列分布不均匀等不足；另一方面能够避免高维混沌映射复杂程度高、难以实现的缺陷。Sine-Tent-Cosine混沌映射的具体公式如下：

x (n + 1) = \{\begin{array}{l} \begin{array}{l} c o s \{π [r s i n (π x (n)) + \\ 2 (1 - r) x (n) - 0.5]\}, x (n) < 0.5 \end{array} \\ \begin{array}{l} c o s \{π [r s i n (π x (n)) + \\ 2 (1 - r) (1 - x (n)) - 0.5]\}, 其他 \end{array} \end{array}

(1)

式中：x $(n)$ 为系统输入变量的混沌值；x $(n + 1)$ 为更新得到的混沌值；r为控制参数，r $\in$ [0, 1]；n为迭代步数。

当设定控制参数r=0.9时，所生成的2 000个混沌序列数值的分布如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Sine-Tent-Cosine混沌映射序列数值分布图

Fig.6 Distribution diagram of Sine-Tent-Cosine chaotic mapping sequence values

2.1.3　融合正余弦算法的虫洞位置更新机制

正余弦算法是Mirjalili^[20]在2016年受模拟数学中正余弦函数周期特性启发所提出的元启发式算法。为增强MOMVO算法的全局和局部搜索能力，以提升收敛效率和增加解的多样性，利用正余弦算法的位置更新机制改进MOMVO算法的虫洞位置更新机制，并去除传统虫洞机制中的旅行距离率T_DR，降低算法的复杂度。新的虫洞位置更新公式如式(2)和式(3)所示。

当r₂<W_EP时：

x_{i j} = \{\begin{array}{l} X_{j t} + k_{1} s i n k_{2} |k_{3} p_{j t} - X_{j t}|, r_{3} < 0.5 \\ X_{j t} - k_{1} c o s k_{2} |k_{3} p_{j t} - X_{j t}|, r_{3} \geq 0.5 \end{array}

(2)

当r₂≥W_EP时：

x_{i j} = x_{i j}

(3)

式中：x_ij 为第i个宇宙中的第j个物体；p_jt 为全局最优宇宙中的第j个物体；X_jt 为当前最优宇宙中的第j个物体；t为当前迭代次数；W_EP为虫洞存在概率；r₂、r₃为互不影响的随机数，取值范围在[0, 1]内；k₁为确定下一个位置区域（或移动方向）的振幅转换因子；k₂为朝最优解向外移动的距离，取值范围为[0, 2π]；k₃为最优解的随机权重，取值范围为[0, 2]。

2.1.4　自适应参数更新策略

1）改进振幅转换因子k₁。正余弦算法位置更新阶段的控制参数k₁为线性递减，这一方面会导致迭代初期的递减速率很快，造成全局搜索能力下降；另一方面会导致迭代后期的递减速率缓慢，造成收敛速度下降^[21-22]。为优化融合正余弦算法的MOMVO算法的探索阶段，本文结合指数函数特性设计了自适应参数更新策略，用于改进k₁，具体如下：

k_{1} = \{\begin{array}{l} 1 - δ {(\frac{t}{T})}^{β_{1}}, t < \frac{T}{2} \\ δ {(1 - \frac{t}{T})}^{β_{2}}, t \geq \frac{T}{2} \end{array}

(4)

式中：δ为幅值控制参数，取δ=1；β₁为前半段衰减速率调节参数，取β₁=3；β₂为后半段衰减速率调节参数，取β₂=0.5；T为最大迭代次数。

2）改进虫洞存在概率W_EP。传统MOMVO算法中的虫洞存在概率W_EP是决定虫洞机制启动的重要参数，W_EP通常为线性增长。为提高探索阶段的个体交互更新能力和开发阶段的精细搜索能力，引入自回归更新策略和动态调整参数λ，用于改进W_EP，具体如下：

W_{E P} (t + 1) = W_{E P} (t) + \frac{λ (W_{E P, m a x} - W_{E P, m i n})}{T}

(5)

其中：

λ = 1 + μ {(1 - \frac{t}{T})}^{τ}

式中：W_EP $(t + 1)$ 为更新后的虫洞存在概率；W_EP $(t)$ 为初始虫洞存在概率；W_{EP, max}和W_{EP, min}分别为虫洞存在概率的最大值和最小值；μ为动态调整增长率，取μ=4；τ为指数衰减参数，取τ =(e-1)/2。

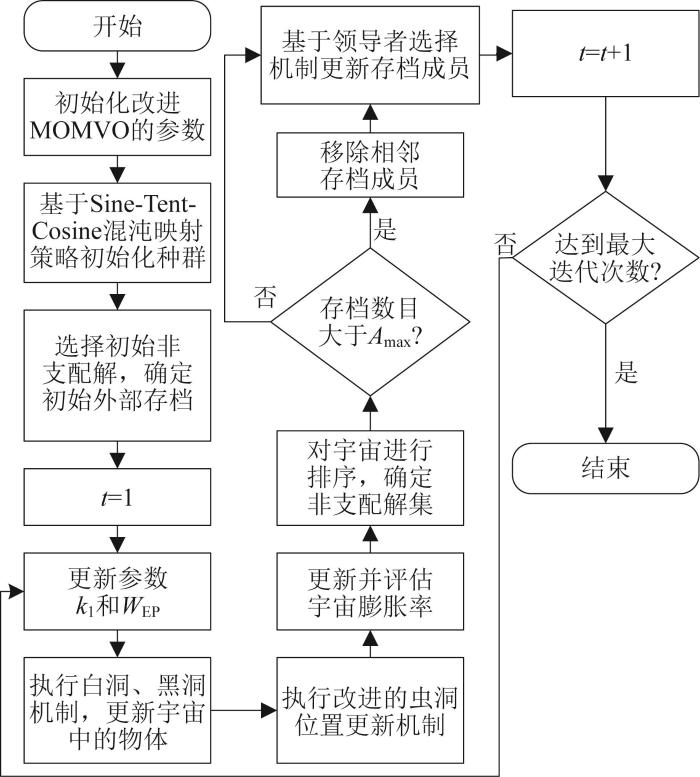
2.1.5　改进MOMVO算法的流程

本文所提出的改进MOMVO算法的基本流程如图7所示，具体步骤如下：

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 改进MOMVO算法的流程

Fig.7 Flow of improved MOMVO algorithm

步骤1：设置改进MOMVO算法的参数，包括变量数目d_im、变量上下界u_b和l_b、目标数量N_o、种群数量p_s、储存最优解的最大数量A_max及最大迭代次数T等。

步骤2：基于Sine-Tent-Cosine混沌映射策略得到的混沌序列，利用式(6)将混沌序列映射到初始多元宇宙种群中。

x_{i j} = x (n) \cdot (u_{b} - l_{b}) + l_{b}

(6)

步骤3：计算初始宇宙膨胀率，根据膨胀率进行排序，选择初始非支配解，并加入外部存档。

步骤4：开始迭代，根据式(4)和式(5)随迭代次数更新k₁和W_EP，根据式(7)执行白洞、黑洞机制，实现对宇宙中物体的更新。

x_{i j}^{} = \{\begin{array}{l} x_{k j}^{},_{}_{} r_{1} < N (U_{i}) \\ x_{i j}^{},_{}_{} r_{1} \geq N (U_{i}) \end{array}

(7)

式中：N $(U_{i})$ 为第i个宇宙的归一化膨胀率，U_i 为第i个宇宙的位置，r₁为[0, 1]内的随机数，x_kj 为根据轮盘赌机制得到的第k个宇宙中的第j个物体。

步骤5：根据改进后的虫洞位置更新策略，利用式(2)和式(3)执行虫洞机制，实现宇宙间物体的转移，提高解的质量。

步骤6：更新并评估所有宇宙的膨胀率，对宇宙排序，确定非支配解集，并保存到外部存档中。

步骤7：判断外部存档数量是否大于储存最优解的最大数量，若为小于，则根据式(8)所示的领导者选择机制将新产生的非支配解加入外部存档；否则，根据式(9)移除相邻的存档成员后再通过领导者选择机制将新产生的非支配解加入外部存档。

P_{h} = \frac{z}{N_{h}}

(8)

P_{h}^{'} = \frac{N_{h}}{z}

(9)

式中：P_h 为选择第h个解的概率， $P_{h}^{'}$ 为移除第h个解的概率，z为大于1的常数，N_h 为存档区域内第h个解附近的解数量。

步骤8：迭代次数加1，并判断是否达到最大迭代次数，若达到，则终止算法并输出Pareto前沿，即所有非支配解的集合；否则，返回步骤4。

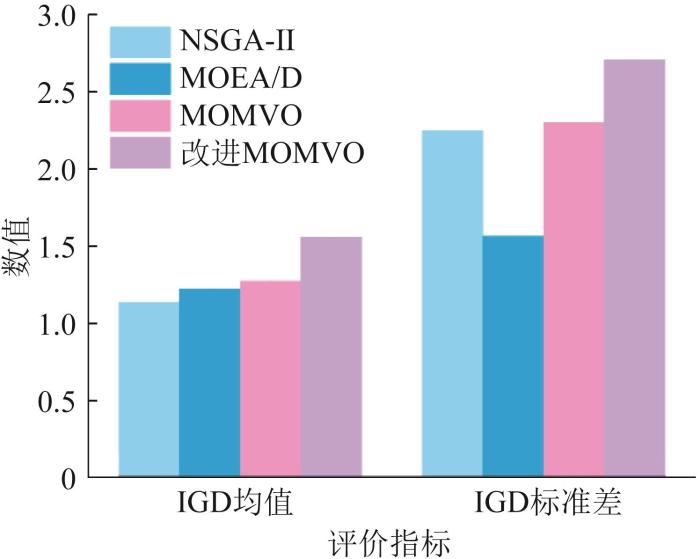
2.2　算法测试

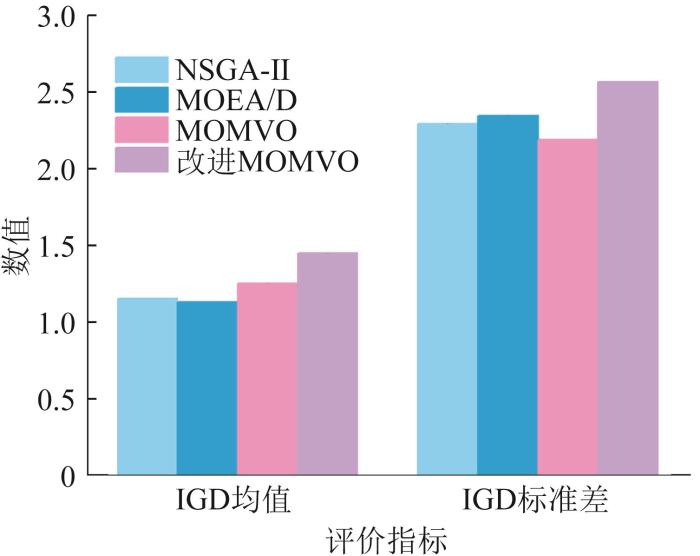
本文选取基准测试函数ZDT1、DTLZ2^[23]来验证改进MOMVO算法的性能。重复运行NSGA-II、MOEA/D、MOMVO算法和改进MOMVO算法各30次并进行对比分析。

为衡量上述多目标优化算法的收敛性和解均匀性，选择IGD（inverted generational distance，反世代距离）的均值和标准差作为评价指标：IGD的均值和标准差越小，说明算法得到的解集与真实Pareto前沿越接近，解集的空间分布均匀性越好，算法越稳定^[24-25]。ZDT1、DTLZ2基准函数下各算法的测试结果（IGD均值取负对数）分别如图8和图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 ZDT1基准函数下的测试结果

Fig.8 Test results under the ZDT1 benchmark function

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 DTLZ2基准函数下的测试结果

Fig.9 Test results under the DTLZ2 benchmark function

由图8和图9可知，改进MOMVO算法的IGD均值和IGD标准值皆为最优。由此说明，相较于NSGA-II、MOEA/D和MOMVO算法，改进MOMVO算法具备更好的收敛性，且其解集空间分布更为均匀。

2.3　目标函数及优化变量选取

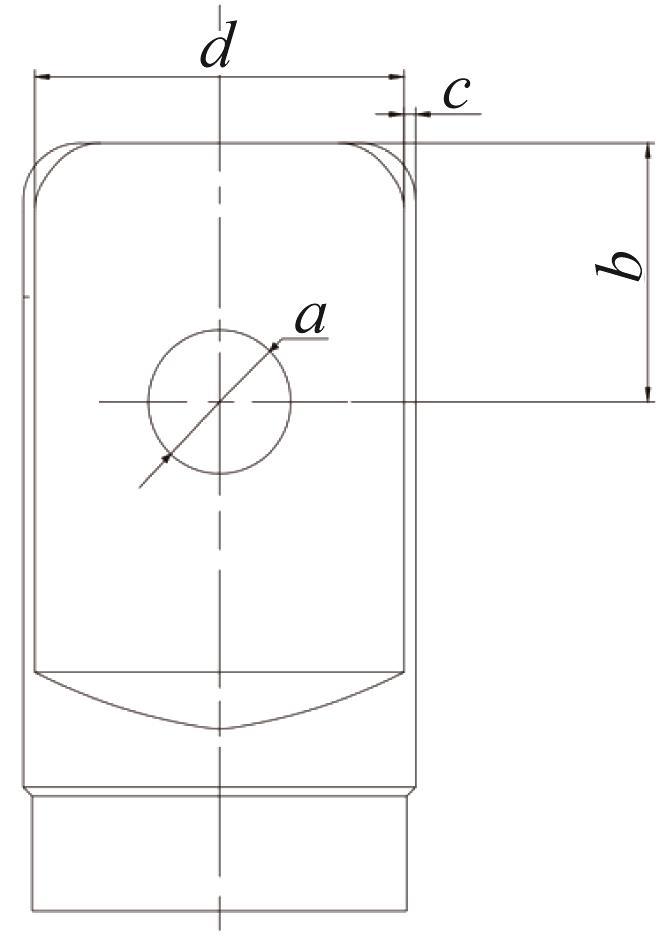
为提高大荷载绝缘拉棒的安全性和便捷性，本文选取绝缘拉棒端头的最大应力σ、最大形变量Δl、最大电场强度E_m和质量M作为优化目标。

经有限元仿真分析，选取端头销控直径a、端头销控位置b、端头厚度c、端头宽度d作为优化变量。绝缘拉棒端头关键优化部位如图10所示。4个优化变量的取值范围如表2所示。需要注意的是，在设计过程中，端头厚度与端头宽度之间须满足以下约束条件：

c < d - 30 m m

(10)

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 绝缘拉棒端头的关键优化部位

Fig.10 Key optimization position of insulating pull rod end

表2 绝缘拉棒端头优化变量的取值范围 (mm)

Table 2 Value range of optimization variables for insulating pull rod end

优化变量	初始值	最小值	最大值
端头销控直径a	25	20	50
端头销控位置b	45	40	55
端头厚度c	25	20	45
端头宽度d	69	65	88

新窗口打开| 下载CSV

2.4　试验设计

选择合适的试验设计方法是实现多目标优化的关键环节之一。目前，常用的试验设计方法包括全因素试验设计、D最优试验设计以及拉丁超立方抽样试验设计等。其中，拉丁超立方抽样是最常用的基础抽样方法，但其样本分布可能存在一定偏差。

相较于传统的拉丁超立方抽样，最优拉丁超立方抽样^[26]利用最小化协方差矩阵优化准则，确保了样本点在多维空间中的分布更加均匀，减少了抽样偏差，同时尽可能地填充参数空间，使得样本点分布更加合理。综合考虑数据抽取效率以及试验设计的可靠性，本文选取最优拉丁超立方抽样试验设计方法。

基于最优拉丁超立方抽样试验设计方法，在样本空间内抽取100个样本点，并通过SolidWorks软件建模以及COMSOL软件有限元仿真获取100组试验数据，部分试验结果如表3所示。

表3 绝缘拉棒端头优化试验设计方案及结果

Table 3 Experimental design schemes and results for optimization of insulating pull rod end

序号	端头销控直径/mm	端头销控位置/mm	端头厚度/mm	端头宽度/mm	最大应力/MPa	最大形变量/mm	最大电场强度/(V/m)	质量/kg
1	25.328 4	45.744 1	22.482 9	74.842 2	560.412 6	0.074 97	3.262 8×10⁶	1.914 1
2	48.409 8	50.433 9	24.995 9	78.322 2	641.152 7	0.103 39	3.072 5×10⁶	1.922 1
3	42.771 6	51.656 8	21.557 3	74.330 9	688.298 8	0.100 51	3.469 2×10⁶	1.689 0
4	30.338 3	54.915 4	24.331 6	68.048 9	828.042 9	0.072 24	4.097 1×10⁶	1.702 3
5	47.752 1	48.462 0	38.969 2	69.780 8	949.587 7	0.109 39	3.123 6×10⁶	2.055 4
6	20.976 0	45.323 4	35.807 3	74.946 5	445.974 3	0.047 17	2.991 2×10⁶	2.622 0
7	37.155 1	43.797 7	33.225 2	87.450 6	404.636 6	0.060 08	2.903 6×10⁶	2.915 7
8	35.612 2	46.921 3	39.328 7	76.167 5	409.427 9	0.052 30	2.769 8×10⁶	2.651 8
9	33.183 2	40.702 1	20.802 2	69.598 1	851.693 2	0.107 32	3.373 5×10⁶	1.578 9
10	21.563 1	54.180 5	39.683 4	87.257 6	314.102 7	0.035 60	2.806 8×10⁶	3.475 0
…	…	…	…	…	…	…	…	…
100	47.005 3	40.103 6	33.554 2	80.242 2	402.401 3	0.096 27	2.850 6×10⁶	2.404 2

新窗口打开| 下载CSV

2.5　代理模型建立

2.5.1　径向基神经网络

径向基神经网络是一种以径向基函数作为隐层激活函数的3层反馈网络，具有高度非线性映射能力、泛化能力及结构相对简单等优点，被广泛应用于工程优化。

考虑到本文优化目标与优化变量之间的关系较为复杂，利用径向基神经网络对试验数据进行拟合^[27]，建立优化目标与优化变量之间的数学模型。径向基神经网络的核心函数如下：

ϕ (‖x - c_{m}‖) = e x p (- \frac{{‖x - c_{m}‖}^{2}}{2 σ_{m}^{2}})

(11)

式中： $‖x - c_{m}‖$ 为输入点与第m个隐层节点对应的中心点之间的欧几里得距离，σ_m 为第m个隐层节点的径向基函数宽度， c_m 为第m个隐层节点的径向基函数中心向量。

输出层的加权求和计算公式如下：

y (x) = \sum_{m = 1}^{N_{1}} δ_{m} ϕ (‖x - c_{m}‖)

(12)

式中：N₁为隐层节点数，δ_m 为第m个隐层节点到输出层的权重系数。

2.5.2　代理模型

本文采用MATLAB软件工具箱中newrb函数构建和训练径向基神经网络代理模型。经多次试验，设置扩展常数为10，计算目标误差为0，最大神经元数量为80。

代理模型的拟合效果由复相关系数R确定：R越接近1，表明拟合效果越好^[28-29]。最终得到的绝缘拉棒端头的最大应力、最大形变量、最大电场强度和质量的拟合曲线如图11所示，对应的复相关系数R分别为0.984、0.999、0.970、0.999，均大于0.9，说明各代理模型的拟合效果良好，具有较高的可靠性。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 绝缘拉棒端头各优化目标的拟合曲线

Fig.11 Fitting curves of each optimization target of insulating pull rod end

2.6　优化结果与分析

基于MATLAB软件编写改进MOMVO算法程序，设置优化目标数量为4，种群数量为200，最大迭代次数为300。最终得到的绝缘拉棒端头多目标优化的Pareto前沿如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 绝缘拉棒端头多目标优化的Pareto前沿

Fig.12 Pareto frontier of multi-objective optimization for insulating pull rod end

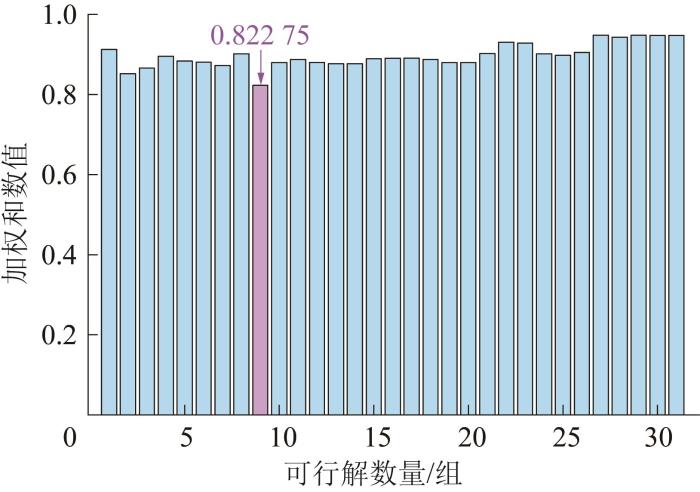
以优化前绝缘拉棒的仿真结果作为约束条件，从Pareto前沿中筛选可行Pareto前沿，共包含31组可行解。利用加权目标函数的方法，对可行解集进行归一化处理，并根据式(13)计算加权和数值，将加权和最小的组合作为最优解。

Z = \partial_{1} F_{1}^{*} + \partial_{2} F_{2}^{*} + \partial_{3} F_{3}^{*} + \partial_{4} F_{4}^{*}

(13)

式中： $F_{1}^{*}$ 、 $F_{2}^{*}$ 、 $F_{3}^{*}$ 、 $F_{4}^{*}$ 分别为绝缘拉棒端头的最大应力、最大形变量、最大电场强度和质量的归一化数值， $\partial_{1}$ 、 $\partial_{2}$ 、 $\partial_{3}$ 、 $\partial_{4}$ 分别为各优化目标的权重。

本文将绝缘拉棒端头质量作为第一优化目标，最大应力作为第二优化目标，最大电场强度作为第三优化目标，最大形变量作为第四优化目标，将权重 $\partial_{1}$ 、 $\partial_{2}$ 、 $\partial_{3}$ 、 $\partial_{4}$ 分别设定为0.25、0.20、0.20、0.35。各优化目标可行解的加权和数值如图13所示。优化后绝缘拉棒端头的尺寸参数如表4所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 绝缘拉棒端头多目标优化可行解的加权和数值

Fig.13 Weighted sum value of feasible solutions of multi-objective optimization for insulating pull rod end

表4 优化后绝缘拉棒端头的尺寸参数 (mm)

Table 4 Dimensional parameters of optimized insulating pull rod end

参数	数值
端头销控直径	27.311
端头销控位置	52.855
端头厚度	24.373
端头宽度	66.195

新窗口打开| 下载CSV

3 仿真试验与性能试验

3.1　仿真试验

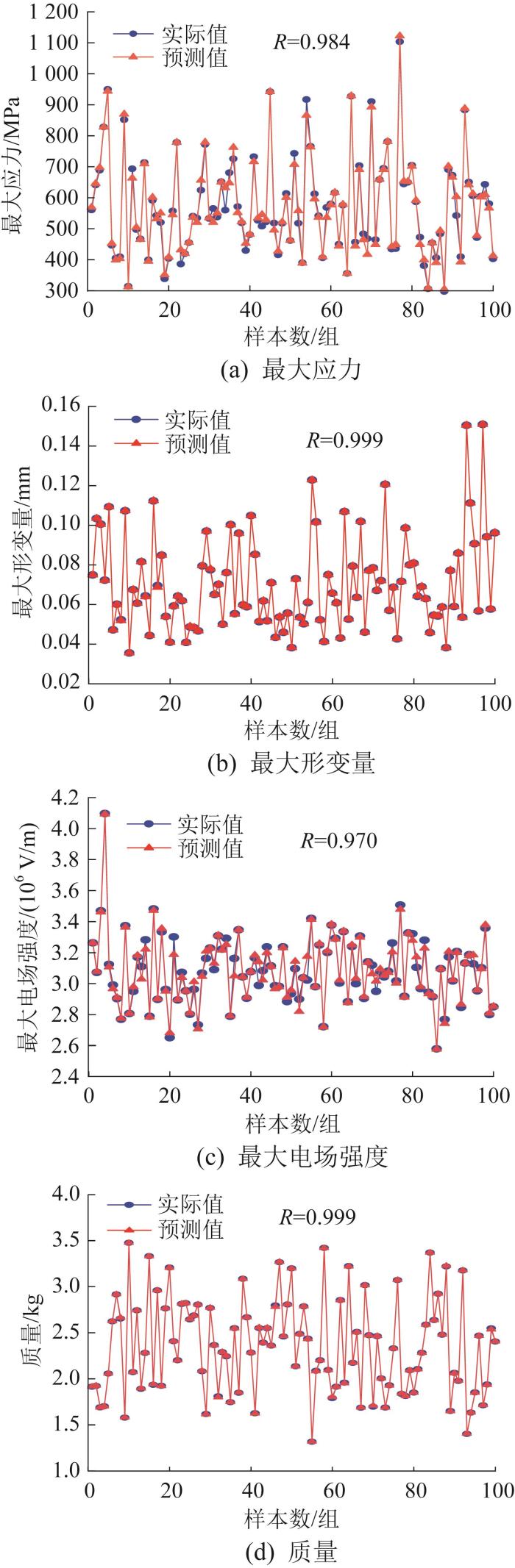
为验证上述绝缘拉棒端头优化方案的可行性与准确性，对优化后的绝缘拉棒开展仿真试验。优化后绝缘拉棒端头的性能参数和质量的预测值与仿真值如表5所示。经对比分析，优化后端头的最大应力、最大形变量、最大电场强度以及质量的预测值与仿真值的相对误差分别为0.67%、1.47%、0.90%、1.81%，均低于5%，验证了优化方案的可行性与准确性。

表5 优化后绝缘拉棒端头的性能参数与质量

Table 5 Performance parameters and quality of optimized insulating pull rod end

对比项	最大应力/MPa	最大形变量/mm	最大电场强度/(V/m)	质量/kg
预测值	593.235	0.067	3.306×10⁶	1.630
仿真值	589.302	0.068	3.336×10⁶	1.660

新窗口打开| 下载CSV

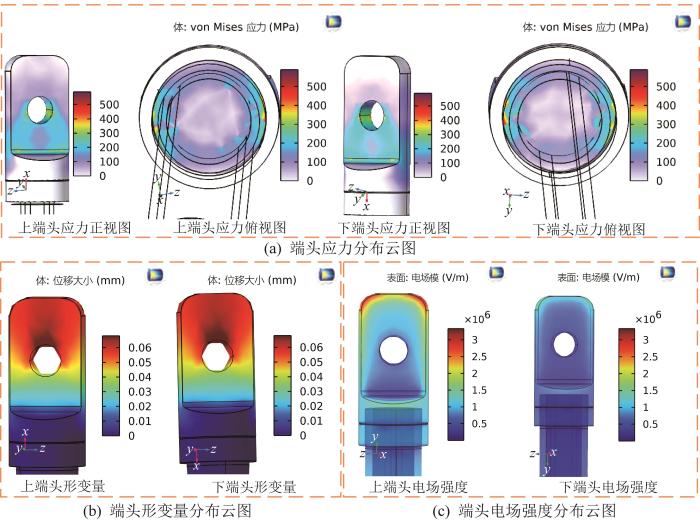
优化后绝缘拉棒端头的应力、形变量、电场强度仿真结果如图14所示。与优化前相比，端头的最大应力降低了17.03%，最大形变量降低了6.85%，最大电场强度降低了5.58%，质量减小了10.66%，符合预期设计目标。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 优化后绝缘拉棒端头的仿真结果

Fig.14 Simulation results of optimized insulating pull rod end

3.2　性能试验

根据DL/T 878—2021《带电作业用绝缘工具试验导则》的要求^[30]，对优化后的绝缘拉棒开展机械性能和电气性能试验，试验布置如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 绝缘拉棒性能试验布置

Fig.15 Performance test layout for insulating pull rod

在机械性能试验中，分别开展静、动荷载试验，在施加150 kN和250 kN的荷载后，绝缘拉棒未出现永久变形和损伤情况。在电气性能试验中，分别开展工频耐压试验和操作冲击耐压试验。在试验过程中，绝缘拉棒未出现闪络和击穿现象，且未发现放电痕迹。结果表明，所得的绝缘拉棒端头多目标优化方案满足带电作业工具设计导则，优化后的绝缘拉棒可应用于特高压带电作业场景。

4 结论

为减小大荷载绝缘拉棒的质量并提高其机械性能安全裕度，同时保证良好的绝缘性能，基于改进MOMVO算法提出了一种绝缘拉棒端头多目标优化方法，所做工作及相关结论如下。

1）将Sine-Tent-Cosine混沌映射策略、正余弦算法和自适应参数更新策略融合到MOMVO算法中，提出了一种改进的MOMVO算法。测试结果表明，改进MOMVO算法的性能显著优于NSGA-II、MOEA/D和MOMVO算法。

2）基于最优拉丁超立方抽样试验设计方法和径向基神经网络建立了绝缘拉棒端头最大应力、最大形变量、最大电场强度和质量的代理模型，各模型均具有较高的拟合度。

3）基于改进MOMVO算法有效地实现了绝缘拉棒端头机械性能、电气性能与质量的协同优化，在以减小端头质量作为核心目标的前提下实现了绝缘拉棒机械性能与电气性能的改善。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.110

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

胡毅，刘凯，刘庭，等.

超/特高压交直流输电线路带电作业

［J］. 高电压技术， 2012， 38（8）： 1809-1820.