精密磨床液体静压导轨承载特性分析与参数优化

doi:10.3785/j.issn.1006-754X.2025.05.120

精密磨床液体静压导轨承载特性分析与参数优化

张坤^,^,¹, 郭宏亮¹, 石有圣², 李洪凯¹, 赵栋杰^,¹

1.聊城大学机械与汽车工程学院，山东聊城 252000

2.聊城市科技信息研究中心，山东聊城 252000

Analysis of load-bearing characteristics and parameter optimization of hydrostatic guideway in precision grinding machine

ZHANG Kun^,^,¹, GUO Hongliang¹, SHI Yousheng², LI Hongkai¹, ZHAO Dongjie^,¹

1.School of Mechanical & Automotive Engineering, Liaocheng University, Liaocheng 252000, China

2.Liaocheng Science & Technology Information Research Center, Liaocheng 252000, China

通讯作者: 赵栋杰（1977—），男，副教授，博士，从事机器人技术与应用研究，E-mail: zhaodongjie@lcu.edu.cn

收稿日期: 2025-03-12 修回日期: 2025-04-14

基金资助:

山东省重点研发计划项目. 2017NC212010
山东省高校科研计划项目. J18KB009

First author contact: ZHANG K, GUO H L, SHI Y S, et al. Analysis of load-bearing characteristics and parameter optimization of hydrostatic guideway in precision grinding machine[J]. Chinese Journal of Engineering Design, 2025, 32(3): 393-402.

Received: 2025-03-12 Revised: 2025-04-14

作者简介 About authors

张　坤（1996—），男，硕士生，从事静压导轨设计与分析技术研究，E-mail:13563837199@163.com，https://orcid.org/0009-0003-2765-4987 , E-mail：13563837199@163.com

摘要

承载力和刚度是衡量液体静压导轨承载特性的关键性能指标，直接影响精密磨床的加工精度与稳定性。针对液体静压导轨对置油垫结构参数的交互作用机制不明确、现有研究多局限于单油垫分析的问题，以某型精密磨床的花岗岩液体静压导轨为研究对象，系统地开展了多参数耦合作用下的承载特性分析与参数优化。首先，基于流体力学理论构建了液体静压导轨承载特性的数学模型，并推导出对置油垫承载力与刚度的解析表达式。然后，通过单因素分析揭示了供油压力、油腔间隙、封油边宽度及小孔节流器直径对液体静压导轨承载特性的独立影响规律，发现供油压力和油腔间隙对承载力和刚度有显著影响。最后，采用BBD（Box-Behnken Design）法设计了27组试验，构建了二阶多项式回归模型，以解析多参数的交互作用机制，并基于响应面法开展了多目标优化，获得了设计参数的最优解集。结果表明：优化后液体静压导轨的承载力和刚度分别提升了24.99%和19.62%。研究结果为精密磨床液体静压导轨的承载性能提升和参数优化提供了一定的理论参考。

关键词： 液体静压导轨 ; 承载特性 ; 交互作用 ; 参数优化 ; 响应面法

Abstract

Load-bearing capacity and stiffness are key performance indicators for measuring the load-bearing characteristics of hydrostatic guideways, directly affecting the machining accuracy and stability of precision grinding machines. In response to the unclear interaction mechanism of the structural parameters of the opposed oil pads in hydrostatic guideways and the limitation of existing studies focusing on single oil pad analysis, taking the granite hydrostatic guideway of a certain type of precision grinding machine as the research object, the load-bearing characteristic analysis and parameter optimization under the coupling effect of multiple parameters were systematically carried out. Firstly, based on the theory of fluid mechanics, a mathematical model of the load-bearing characteristics of the hydrostatic guideway was established, and analytical expressions for the load-bearing capacity and stiffness of the opposed oil pads were derived. Then, through single-factor analysis, the independent influence laws of oil supply pressure, oil cavity clearance, oil seal edge width and orifice throttler diameter on the load-bearing characteristics of the hydrostatic guideway were revealed. It was found that the oil supply pressure and oil cavity clearance had a significant impact on the load-bearing capacity and stiffness. Finally, 27 groups of experiments were designed using the BBD (Box-Behnken Design) method, and a second-order polynomial regression model was constructed to analyze the interaction mechanism of multiple parameters. Meanwhile, the multi-objective optimization was carried out based on the response surface method, and the optimal solution set of the design parameters was obtained. The results showed that the load-bearing capacity and stiffness of the optimized hydrostatic guideway were improved by 24.99% and 19.62%, respectively. The research results provide a theoretical reference for the enhancement of the load-bearing performance and parameter optimization of hydrostatic guideways in precision grinding machines.

Keywords： hydrostatic guideway ; load-bearing characteristics ; interaction ; parameter optimization ; response surface method

PDF (4046KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张坤, 郭宏亮, 石有圣, 李洪凯, 赵栋杰. 精密磨床液体静压导轨承载特性分析与参数优化[J]. 工程设计学报, 2025, 32(3): 393-402 doi:10.3785/j.issn.1006-754X.2025.05.120

ZHANG Kun, GUO Hongliang, SHI Yousheng, LI Hongkai, ZHAO Dongjie. Analysis of load-bearing characteristics and parameter optimization of hydrostatic guideway in precision grinding machine[J]. Chinese Journal of Engineering Design, 2025, 32(3): 393-402 doi:10.3785/j.issn.1006-754X.2025.05.120

花岗岩液体静压导轨采用花岗岩作为导轨的基体材料，相比于传统的铸铁液体静压导轨，其具有运动精度高、运动稳定性好、摩擦阻力小、故障率低、承载特性好和精度保持性好等特点，近些年在精密磨床领域的应用越来越广泛。承载特性是液体静压导轨的关键性能指标，其受到供油压力、油腔间隙、封油边宽度及小孔节流器直径等设计参数的影响。研究上述设计参数对液体静压导轨承载特性的影响规律，确定设计参数的优化组合，对提升液体静压导轨的承载特性具有重要意义。

近年来，学者们针对油腔尺寸、油膜厚度、节流器孔径等参数对液体静压导轨承载特性的影响开展了广泛研究。高殿荣等^[1]分析了油腔数目对液体静压导轨承载力和刚度的影响，得到了油腔的最佳排列方式。彭冲^[2]对油腔封油面上单个油槽的位置、深度和宽度进行了分析，确定了油槽的最优匹配参数。董鹏程^[3]对液体静压导轨中单个油垫的静态特性进行了仿真分析，并对油膜厚度、节流孔直径和油腔深度进行了优化计算。仝志伟等^[4]研究了转台底部支承布局对液体静压导轨平面度误差的影响规律，并对转台底部支承布局进行了重构。张伟^[5]计算了不同工作载荷下液体静压导轨的承载力、油膜厚度和刚度。朴银川等^[6]建立了液体静压导轨模型，并对其静动态特性进行了仿真预测。Shen等^[7]研究了油膜厚度对液体静压轴承承载性能的影响，发现了油膜厚度与其动静态性能之间的联系。夏毅敏等^[8]分析了在较大油膜偏移量下节流器孔径、长度与液体静压导轨承载特性的关系。杨添任^[9]研究了油腔间隙与液体静压导轨承载特性之间的关系。

综上所述，现有关于液体静压导轨的研究主要针对单油垫，而对于在实际工况中应用更普遍的对置油垫液体静压导轨的分析不充分。为此，本文以某型精密磨床的花岗岩液体静压导轨（采用对置油垫）为研究对象，分析油腔间隙、供油压力、封油边宽度及小孔节流器直径等设计参数间的交互作用对其承载特性的影响规律，并在此基础上对设计参数进行优化，旨在为液体静压导轨的设计与优化提供理论支持。

1 设计参数对液体静压导轨承载特性的影响规律

1.1　液体静压导轨结构

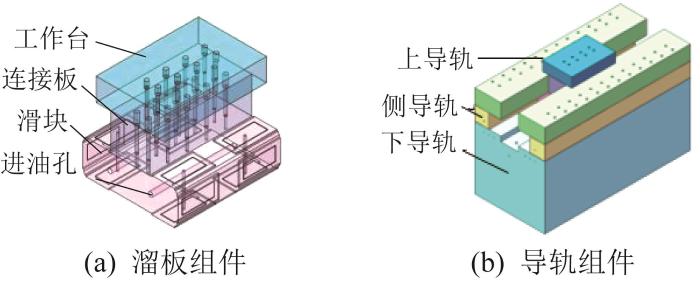
本文所研究的某型精密磨床的花岗岩液体静压导轨的结构如图1所示，主要由溜板组件和导轨组件两部分组成，溜板组件相对导轨组件水平滑动。溜板组件由工作台、连接板和滑块组成，滑块内设有互通的油路，由液压站通过进油孔为滑块供应液压油。导轨组件由上导轨、侧导轨和下导轨组成，下导轨设有回油槽，用于收集从油腔中溢流出的液压油，所收集的液压油经过滤系统处理后输送回液压站。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 花岗岩液体静压导轨结构

Fig.1 Structure of granite hydrostatic guideway

该液体静压导轨由6对等面积的矩形对置油垫支承。由进油孔输送的液压油会在滑块的油垫上形成油膜，从而对导轨起支承作用。液压油所在流道和油膜如图2(a)所示。从图2(a)中可以看出，滑块两侧各有2个矩形油垫对导轨进行左右支承，起到限位的作用；滑块上下各有4个矩形油垫对导轨进行支承，其中滑块下方的4个油垫为主油垫，即承载油垫。液体静压导轨采用小孔节流方式，小孔节流静压支承剖面如图2(b)所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

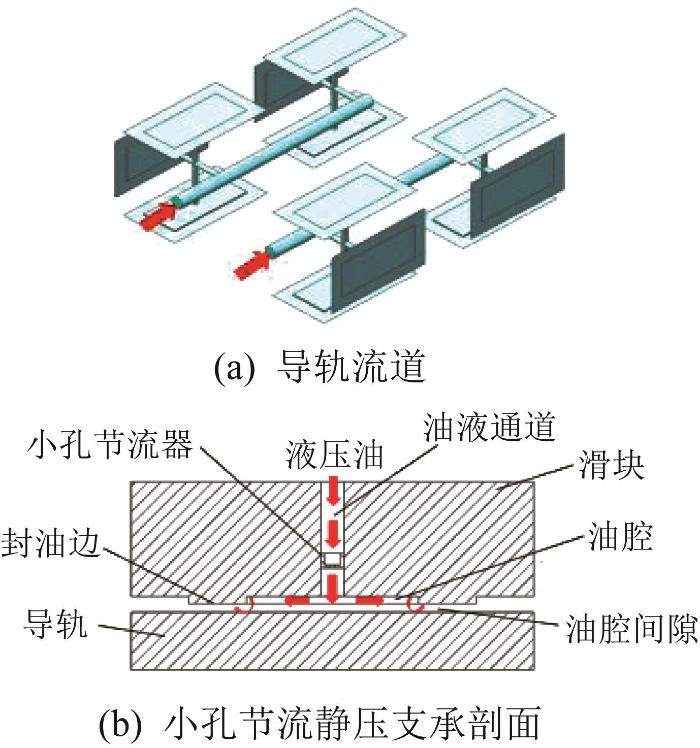
图2 液体静压导轨流道及其静压支承剖面示意图

Fig.2 Schematic diagram of hydrostatic guideway flow passage and its static pressure support cross-section

液体静压导轨的设计参数与液压油的性能参数如表1所示。

表1 液体静压导轨设计参数与液压油性能参数

Table 1 Design parameters of hydrostatic guideway and performance parameters of hydraulic oil

参数	数值
油垫宽度/mm	100
油垫长度/mm	180
封油边宽度/mm	20
小孔节流器直径/mm	0.16
油腔间隙/ $μ m$	40
初始油膜厚度/ $μ m$	20
供油压力/MPa	1.0
液压油密度/( $k g / m^{3}$ )	848.4
液压油动力黏度/( $N ∙ s / m^{2}$ )	0.019 259

新窗口打开| 下载CSV

1.2　液体静压导轨承载特性方程

由于花岗岩材料的密度远低于铸铁，在导轨结构及供油压力相同的情况下，花岗岩液体静压导轨比铸铁液体静压导轨具有更高的有效承载能力，且溜板组件尺寸越大，花岗岩液体静压导轨的优势越明显。此外，花岗岩液体静压导轨的低热膨胀特性可使其在20 ℃温升工况下的刚度衰减率控制在5%以内，而铸铁液体静压导轨会因热变形而导致刚度下降18%^[10]。

承载力和刚度是衡量液体静压导轨承载特性的核心性能指标，直接影响其稳定性、精度和使用寿命。在设计和分析液体静压导轨时，必须考虑承载力和刚度这2个关键特性。

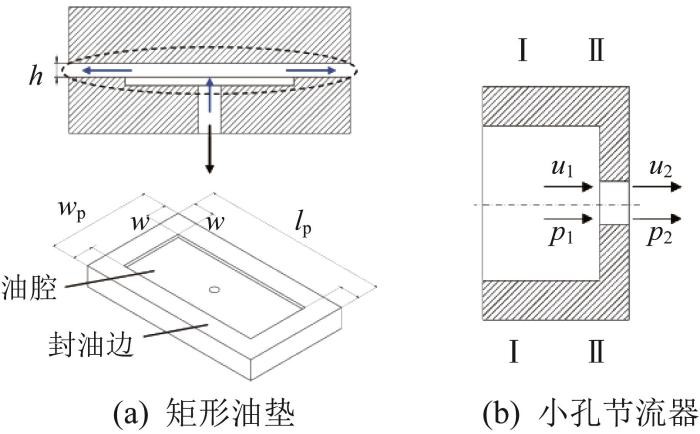
液体静压导轨中矩形油垫和小孔节流器的结构如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 矩形油垫和小孔节流器的结构示意图

Fig.3 Structure diagram of rectangular oil pad and orifice throttler

如图3(a)所示，矩形油垫可视为由4对平行板组成，液压油从中间流入并向四边流出。矩形油垫的液阻可表示为^[11]：

R_{h} = \frac{6 μ}{h^{3} K}

(1)

其中：

K = \frac{w_{p} - w}{w} + \frac{l_{p} - w}{w}

式中：R_h为油垫的液阻， $μ$ 为液压油动力黏度， $h$ 为油膜厚度，K为油腔的结构参数，w_p为油垫宽度，l_p为油垫长度，w为封油边宽度。

如图3(b)所示，小孔节流器可看作孔径大于孔长的薄壁小孔。小孔节流器的液阻可表示为^[10]：

R_{c} = \frac{2 \sqrt[]{2 ρ ∆ p}}{α π d^{2}}

(2)

式中：R_c为小孔节流器的液阻， $ρ$ 为液压油密度， $∆ p$ 为压降， $α$ 为流量系数（通常取0.6 $~$ 0.7），d为小孔节流器直径。

对于流动液体而言，其两端的压力差与液体流量和沿程路径相关。液体流动过程中的流量、压降、液阻之间的关系可通过类似于欧姆定律的公式来描述：

Q = \frac{∆ p}{R}

(3)

式中：Q为液体流量，R为流动液体的液阻。

在设计载荷的作用下，则有^[10]：

p = \frac{p_{s}}{1 + λ_{0}}

(4)

式中： $p$ 为油腔压力，p_s为供油压力， $λ_{0}$ 为初始液阻比。

在液压支承理论中，常引入液阻比来分析承载特性。小孔节流式油垫的初始液阻比 $λ_{0}$ 可表示为：

λ_{0} = \frac{8 ρ h_{0}^{6} p_{0} K^{2}}{36 π^{2} α^{2} d^{4} μ^{2}}

(5)

式中： $h_{0}$ 为初始油膜厚度，p₀为油腔的初始压力。

液体静压导轨采用闭式结构，则单个油垫的承载力可表示为：

W_{o i} = \frac{2 p_{s} A_{e}}{1 + \sqrt[]{1 + 4 J {(h_{i} / h_{0})}^{6}}}

(6)

其中：

J = λ_{0} (\begin{matrix} 1 + λ_{0} \end{matrix})

式中： $W_{o i}$ 为单个油垫的承载力（ $i = 1, 2$ ，表示上下2个对置油垫，1表示下油垫，2表示上油垫，下文同），J为液阻比参数， $h_{i}$ 为受载时的油膜厚度， $A_{e}$ 为有效承载面积。

对于选定的液压油和油腔结构，供油压力 $p_{s}$ 、有效承载面积 $A_{e}$ 、初始液阻比 $λ_{0}$ 、初始油膜厚度 $h_{0}$ 均为已知量，故单个油垫的承载力 $W_{o i}$ 为关于受载时油膜厚度 $h_{i}$ 的函数。

单个油垫的刚度可表示为其承载力对受载时油膜厚度的导数，即：

S_{o i} = - \frac{\partial W_{o i}}{\partial h_{i}} = \frac{24 p_{s} A_{e} {(h_{i} / h_{0})}^{5} J}{h_{0} \sqrt[]{1 + 4 J {(h_{i} / h_{0})}^{6}} {[1 + \sqrt[]{1 + 4 J {(h_{i} / h_{0})}^{6}}]}^{2}}

(7)

式中： $S_{o i}$ 为单个油垫的刚度。

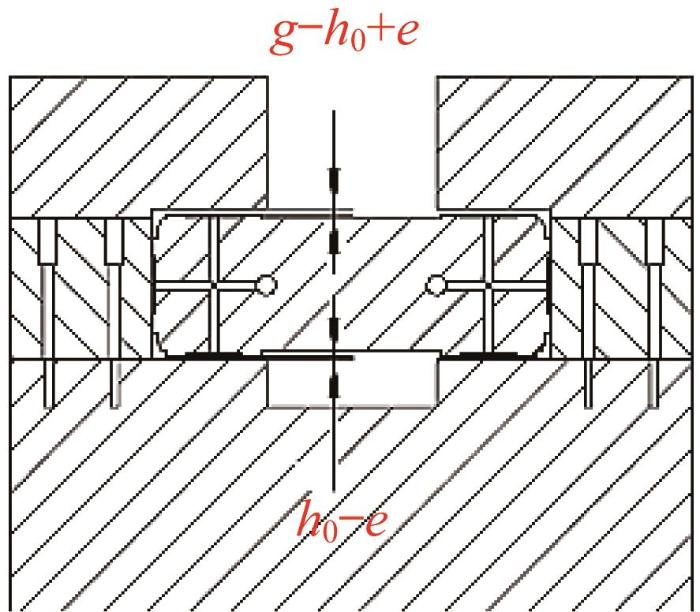
对于等面积的对置油垫，若忽略其自重，则可设无负载时上下油膜厚度分别为 $g - h_{0}$ 、 $h_{0}$ ，其中 $g$ 为油腔间隙（油腔间隙为滑块与上下油腔的间隙之和）。在外载荷和自重的合力W的作用下，油垫产生偏移量 $e$ （ $- h_{0} \leq e \leq h_{0}$ ），则上下油膜厚度 $h_{2}$ 、 $h_{1}$ 分别表示为：

h_{1} = h_{0} - e

(8)

h_{2} = g - h_{0} + e

(9)

采用闭式结构的液体静压导轨的受力如图4所示，则等面积对置油垫在产生偏移量 $e$ 时的承载力 $W_{o} (e)$ 和刚度 $S_{o} (e)$ 可表示为：

W_{o} (e) = W_{o 1} (e) - W_{o 2} (e)

(10)

S_{o} (e) = S_{o 1} (e) + S_{o 2} (e)

(11)

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 液体静压导轨受力示意图

Fig.4 Force diagram of hydrostatic guideway

1.3　设计参数对承载特性的影响规律

由上文分析可知，供油压力、油腔间隙、封油边宽度和小孔节流器直径等设计参数是影响液体静压导轨承载特性的主要因素。选取这些设计参数为研究对象，分析其对液体静压导轨承载力和刚度的影响规律。

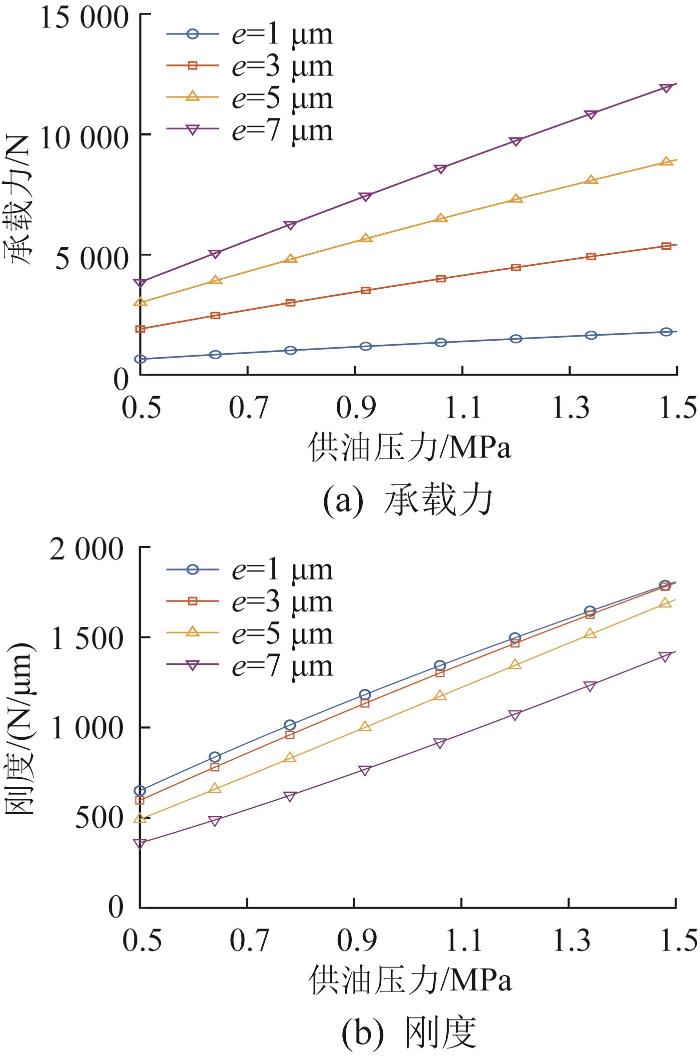
1.3.1　供油压力对承载特性的影响

在油垫偏移量e分别为1、3、5、7 $μ m$ 的条件下，液体静压导轨的承载力和刚度随供油压力（0.5~1.5 MPa）的变化规律如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 供油压力对液体静压导轨承载特性的影响

Fig.5 Influence of oil supply pressure on load-bearing characteristics of hydrostatic guideway

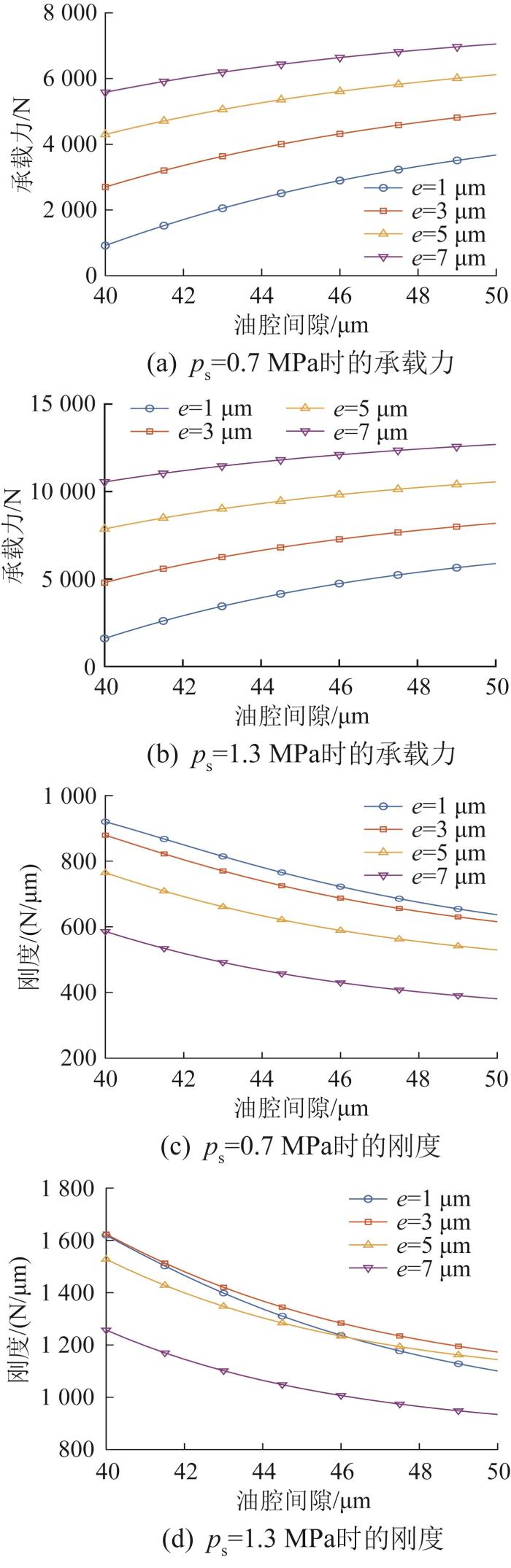
由图5可知，液体静压导轨的承载力和刚度均随供油压力的升高而增大。在实际应用中，需要考虑液阻比过大所导致的能量损失和系统效率降低问题，当初始液阻比接近0.707时，液体静压导轨系统的承载特性最优^[12-14]。由式(5)可知，初始液阻比随供油压力的升高而增大，当供油压力处于0.7~1.3 MPa时，初始液阻比能够保持在合适的范围内，此时承载力和刚度均处于较高水平。

1.3.2　油腔间隙对承载特性的影响

在供油压力p_s分别取0.7、1.3 MPa，油垫偏移量e分别为1、3、5、7 $μ m$ 的条件下，液体静压导轨的承载力和刚度随油腔间隙（40~50 $μ m$ ）的变化规律如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 油腔间隙对液体静压导轨承载特性的影响

Fig.6 Influence of oil cavity clearance on load-bearing characteristics of hydrostatic guideway

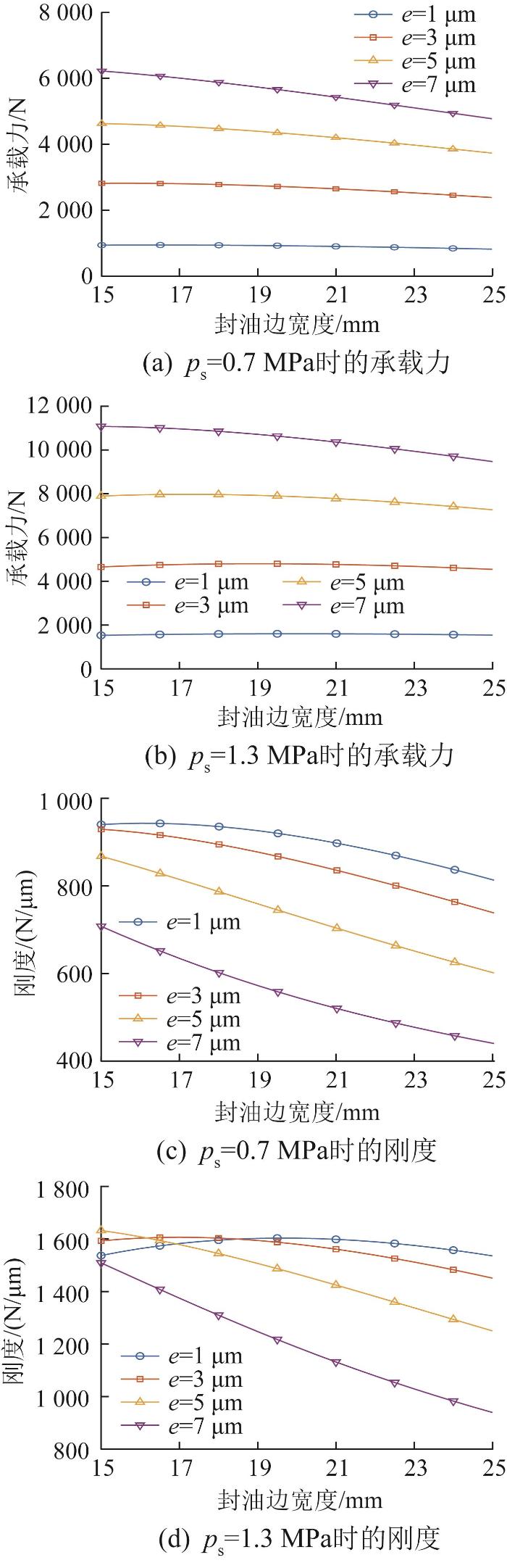
由图6可知，液体静压导轨的承载力随油腔间隙的增大而增大，但其增大速率随油腔间隙的增大而减缓；刚度随油腔间隙的增大而减小，表明适当减小油腔间隙有助于保持较高的刚度。当油腔间隙取45 $~$ 48 $μ m$ 时，承载力处于相对较高的水平；当油腔间隙取40 $~$ 45 $μ m$ 时，刚度可以维持在较高水平。综合考虑承载力和刚度，可获得较为理想的油腔间隙取值范围，为40 $~$ 45 $μ m$ 。在该取值范围内，尽管在刚度增大的过程中承载力会出现一定程度的减小，但刚度的增大幅度明显超过了承载力的减小幅度。

1.3.3　封油边宽度对承载特性的影响

在供油压力p_s分别取0.7、1.3 MPa，油垫偏移量e分别为1、3、5、7 $μ m$ 的条件下，液体静压导轨的承载力和刚度随封油边宽度（15~25 mm）的变化规律如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 封油边宽度对液体静压导轨承载特性的影响

Fig.7 Influence of oil seal edge width on load-bearing characteristics of hydrostatic guideway

由图7可知，液体静压导轨的承载力和刚度均随封油边宽度的增大而减小，且封油边宽度对刚度的影响更为显著。随着封油边宽度的增大，有效承载面积呈减小趋势，这直接导致了承载力和刚度的减小。尽管供油压力的升高可以部分抵消这种影响，但封油边宽度增大的影响仍占主导作用，致使承载力和刚度总体上呈减小趋势。综合考虑承载力和刚度，可获得较为理想的封油边宽度取值范围，为15~19 mm。在该取值范围内，承载力和刚度均能保持较高的水平，且减小趋势相对较缓。

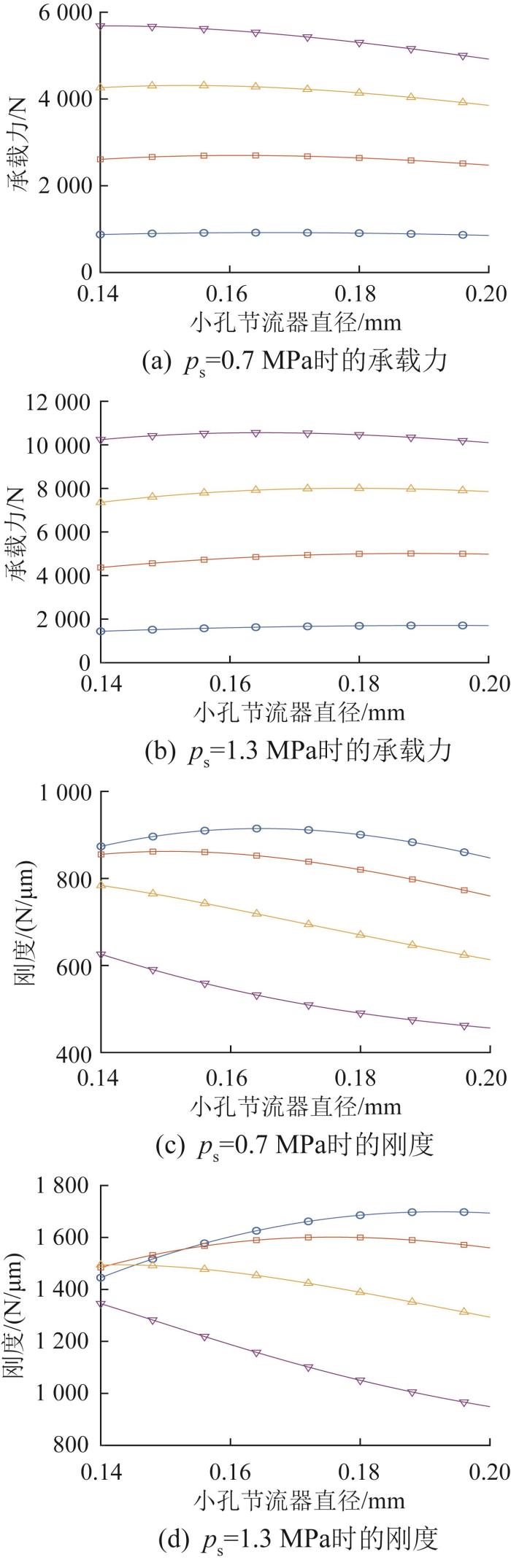
1.3.4　小孔节流器直径对承载特性的影响

在供油压力p_s分别取0.7、1.3 MPa，油垫偏移量e分别为1、3、5、7 $μ m$ 的条件下，液体静压导轨的承载力和刚度随小孔节流器直径（0.14~0.20 mm）的变化规律如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 小孔节流器直径对液体静压导轨承载特性的影响

Fig.8 Influence of orifice throttler diameter on load-bearing characteristics of hydrostatic guideway

由图8可知，液体静压导轨的承载力和刚度均随小孔节流器直径的增大呈先增大后减小的变化趋势，表明存在一个小孔节流器直径临界值，使得承载力和刚度达到峰值。综合考虑承载力和刚度，通过对比不同油垫偏移量对承载力和刚度的影响，发现在油垫偏移量较大的情况下，小孔节流器直径取0.15 $~$ 0.18 $m m$ 时能够实现较高的承载力和刚度。

通过上述单因素分析结果，可得到供油压力、油腔间隙、封油边宽度及小孔节流器直径这4个设计参数的最优取值范围，使得液体静压导轨在设计阶段的承载力和刚度取得较大值。各设计参数的具体取值范围如表2所示。

表2 液体静压导轨各设计参数的取值范围

Table 2 Value range of each design parameter of hydrostatic guideway

设计参数	取值范围
供油压力/MPa	0.7 $~$ 1.3
油腔间隙/ $μ m$	40 $~$ 45
封油边宽度/ $m m$	15 $~$ 19
小孔节流器直径/ $m m$	0.15 $~$ 0.18

新窗口打开| 下载CSV

2 基于响应面法的液体静压导轨设计参数优化

2.1　响应面法

响应面法在多因素分析中具有显著优势，该方法可通过较少的试验次数高效地寻找最优解，可视化复杂变量间关系，预测响应变量表现，并全面分析因素交互作用，适用于多因素、多响应复杂系统的优化设计。因此，本文采用响应面法，通过构建数学模型来拟合液体静压导轨设计参数与其承载力、刚度之间的映射关系，利用可视化的响应曲面定位优化区域，最终通过模型求解获得承载力、刚度的最优取值条件^[15-19]。

响应面分析基于Desigh-Expert 13软件开展，本文采用BBD（Box-Behnken Design）法进行试验设计。响应面模型采用二阶多项式回归模型，可表示为：

\hat{y} = β_{0} + \sum_{a = 1}^{m} β_{a} x_{a} + \sum_{a = 1}^{m} β_{a a} x_{a}^{2}

+ \sum_{a = 1}^{m} \sum_{b < a}^{m} β_{a b} x_{a} x_{b}

(12)

式中： $\hat{y}$ 为目标函数值， $β_{0}$ 为常数项， $β_{a}$ 、 $β_{a a}$ 、 $β_{a b}$ 分别为线性项、二次项和交互项的待定系数， $x_{a}$ 、 $x_{b}$ 为自变量，m为自变量个数。

2.2　试验设计

选取供油压力、油腔间隙、封油边宽度、小孔节流器直径作为影响因素（为方便表示，将各影响因素依次记为A、B、C、D）。根据表2中各影响因素的取值范围，进行四因素三水平试验设计，共设置27组试验，如表3所示。根据上述分析，响应目标函数为承载力和刚度，其数值分别由式(10)和式(11)计算得到。利用Desigh-Expert 13软件对表3中的试验数据进行多元回归拟合，得到承载力和刚度响应面模型的方差分析结果，如表4所示。

表3 液体静压导轨设计参数优化试验方案与结果

Table 3 Experimental schemes and results of design parameter optimization for hydrostatic guideway

序号	因素				承载力/N	刚度/ (N/μm)
序号	A/MPa	B/ $μ m$	C/mm	D/mm	承载力/N	刚度/ (N/μm)
1	1.3	43	15	0.16	7 101.58	1 113.78
2	1.0	43	17	0.16	6 348.41	1 232.36
3	1.0	45	19	0.16	6 348.41	1 232.36
4	1.0	43	19	0.15	7 376.28	1 272.81
5	0.7	43	17	0.15	4 625.09	867.84
6	1.0	45	17	0.18	4 540.32	814.65
7	1.0	40	19	0.16	5 278.16	1 098.28
8	0.7	43	19	0.16	7 587.19	1 595.22
9	1.0	43	19	0.18	7 972.81	1 578.69
10	1.0	43	15	0.15	6 348.41	1 232.36
11	0.7	43	15	0.16	5 700.58	1 137.06
12	0.7	45	17	0.16	7 110.58	1 168.43
13	1.0	40	15	0.16	6 665.54	1 227.99
14	1.3	45	17	0.16	4493.91	858.69
15	1.0	43	17	0.16	5 142.18	1 105.84
16	1.0	43	17	0.16	8 434.93	1 583.41
17	1.0	45	15	0.16	6 136.57	1 214.29
18	1.3	43	17	0.15	9 382.99	1 654.87
19	0.7	40	17	0.16	6 505.82	1 147.17
20	1.0	45	17	0.15	6 380.01	1 389.69
21	1.0	40	17	0.15	4 632.51	791.76
22	1.3	43	17	0.18	3 917.92	793.18
23	1.0	40	17	0.18	7 218.97	1 272.19
24	1.0	43	15	0.18	6 076.52	1 255.80
25	1.3	43	19	0.16	4 912.91	1 069.65
26	1.3	40	17	0.16	5 015.77	797.98
27	0.7	43	17	0.18	7 893.39	1 632.31

新窗口打开| 下载CSV

表4 承载力和刚度响应面模型的方差分析结果

Table 4 Variance analysis results of load-bearing capacity and stiffness response surface models

来源	承载力		刚度
来源	F值	P值^①	F值	P值^①
模型	1 404.95	$<$ 0.000 1	3 277.88	$<$ 0.000 1
A	1 681.06	$<$ 0.000 1	4 1591.77	$<$ 0.000 1
B	2 158.63	$<$ 0.000 1	2 096.13	$<$ 0.000 1
C	1.46	0.250 0	1 361.20	$<$ 0.000 1
D	4.75	$<$ 0.000 1	49.92	$<$ 0.000 1
AB	25.29	0.000 3	35.48	$<$ 0.000 1
AC	10.68	0.006 7	4.05	0.067 2
AD	61.86	$<$ 0.000 1	2.85	0.117 4
BC	2.95	0.111 8	0.741 6	0.406 0
BD	1.80	0.003 0	5.50	0.037 1
CD	18.16	0.001 1	24.37	0.000 3
$A^{2}$	14.11	0.002 7	1.70	0.216 2
$B^{2}$	111.07	$<$ 0.000 1	110.51	$<$ 0.000 1
$C^{2}$	5.77	0.033 3	2.45	0.143 1
$D^{2}$	1.69	0.218 3	68.98	$<$ 0.000 1
$r^{2}$	0.999 4		0.999 7
$r_{a d j}^{2}$	0.998 7		0.999 4
$r_{p r e}^{2}$	0.996 5		0.998 5

① P值小于0.05说明参数具有显著性。

新窗口打开| 下载CSV

由表4可知，承载力和刚度响应面模型的F值分别为1 404.95、3 277.88，且对应的P值均小于0.000 1，说明所构建的模型具有良好的适应性，可用于预测响应值；2个响应面模型的决定系数 $r^{2}$ 、校正系数 $r_{a d j}^{2}$ 、预测决定系数 $r_{p r e}^{2}$ 均大于0.99，说明所构建的模型较为准确。从P值可以看出，在单因素影响中，仅封油边宽度对承载力的影响不显著；在多因素交互影响中，AB、AC、AD、BD、CD、 $A^{2}$ 、 $B^{2}$ 、 $C^{2}$ 对承载力的影响显著，AB、BD、CD、 $B^{2}$ 、 $D^{2}$ 对刚度的影响显著。去除不显著的影响因素后，可得承载力与刚度的二次多项式回归拟合公式，分别为：

W_{o} = 7 226.91 + 1 885.01 A + 675.43 B + 299.26 D + 126.61 A B + 82.31 A C + 198.04 A D + 93.54 B D - 107.32 C D - 81.91 A^{2} - 229.81 B^{2} - 52.4 C^{2}

(13)

S_{o} = 1 093.56 + 356.62 A - 80.06 B - 64.51 C - 38.82 D - 18.04 A B - 7.1 B D - 14.95 C D + 27.57 B^{2} - 21.78 D^{2}

(14)

2.3　响应面分析

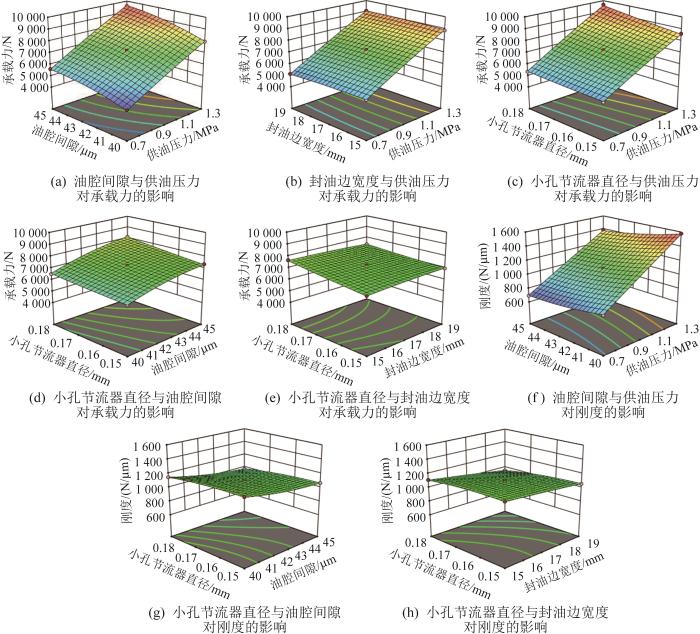
分析供油压力、油腔间隙、封油边宽度及小孔节流器直径这4个影响因素的两两交互作用（忽略影响不显著因素的交互作用）对液体静压导轨承载力和刚度的影响规律，并绘制相应的响应曲面，如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 设计参数对液体静压导轨承载特性的交互影响

Fig.9 Interaction influence of design parameters on load-bearing characteristics of hydrostatic guideway

当2个因素对液体静压导轨的承载力、刚度产生交互影响时，响应面呈曲面形态，观察其投影在平面上的等高线即可直观地判断各设计参数的优化区间。通过分析图9所示的响应面，可得到以下结论：承载力和刚度的峰值均集中在供油压力为1.0~1.2 $M P a$ 、油腔间隙为40~43 $μ m$ 、封油边宽度为15~17 $m m$ 、小孔节流器直径为0.17~0.18 $m m$ 的取值区间内；承载力随供油压力的升高而增大，当油腔间隙缩小时其提升作用更为明显；当封油边宽度减小且小孔节流器直径增大时，承载力增大较快，但两者超过特定取值范围后提升效果逐渐减弱；刚度的增大主要依赖供油压力的升高，油腔间隙变化仅在供油压力较高的条件下对刚度产生有限的影响；调整封油边宽度可显著提高刚度，而小孔节流器直径的增大对刚度的影响较小。

根据表4中的方差分析结果，采用标准化回归系数法计算各设计参数对液体静压导轨承载力和刚度的独立贡献率，如表5所示。基于对响应面和贡献率的分析可知，供油压力对承载力和刚度的影响最为显著，故赋予最高权重，为0.5；油腔间隙对承载力和刚度均有明显影响，但其影响程度小于供油压力，故赋予次高权重，为0.3；封油边宽度对承载力有一定的影响，但对刚度的影响较小，故赋予较低权重，为0.1；小孔节流器直径对承载力和刚度均有一定影响，但其影响程度较小，同样赋予较低权重，为0.1。

表5 各设计参数对承载力和刚度的贡献率 (%)

Table 5 Contribution rate of each design parameter to load-bearing capacity and stiffness

设计参数	承载力	刚度
供油压力	6.7	58.4
油腔间隙	22.1	25.3
封油边宽度	3.5	11.6
小孔节流器直径	11.7	4.7

新窗口打开| 下载CSV

2.4　优化结果

以承载力 $W_{o}$ 最大、刚度 $S_{o}$ 最大为优化目标，以供油压力A、油腔间隙B、封油边宽度C、小孔节流器直径D为设计变量，其权重分别设为0.5、0.3、0.1、0.1，建立优化数学模型：

\{\begin{array}{l} m a x W_{o} \\ m a x S_{o} \\ s . t . 0.7 \leq A \leq 1.3 M P a \\ 40 \leq B \leq 45 μ m \\ 15 \leq C \leq 19 m m \\ 0.15 \leq D \leq 0.18 m m \end{array}

(15)

基于Desigh-Expert 13软件中的多目标优化模块对上述优化数学模型进行求解，根据优化目标选取数值化解决方案中满足条件的设计点，取整后作为最终的优化结果。将各设计参数的优化结果代入式(10)和式(11)，计算对应的承载力和刚度并与优化前对比，结果如表6所示。

表6 优化前后液体静压导轨的承载特性对比

Table 6 Comparison of load-bearing characteristics of hydrostatic guideway before and after optimization

设计参数与性能参数	优化前	优化后
供油压力/MPa	1.0	1.1
油腔间隙/ $μ m$	40	41
封油边宽度/ $m m$	20	15
小孔节流器直径/ $m m$	0.16	0.18
承载力/N	6 140.52	7 675.36
刚度/( $N / μ m$ )	1 098.76	1 314.34

新窗口打开| 下载CSV

由表6可以得出，相较于优化前，优化后液体静压导轨的承载力提高了24.99%，刚度提高了19.62%，说明优化后的承载特性具有较大提升。

3 结论

1）以某型精密磨床的花岗岩液体静压导轨为研究对象，建立了其承载特性数学模型，并通过单因素分析确定了承载力和刚度最优时各设计参数的取值范围：供油压力为0.7 $~$ 1.3 MPa，油腔间隙为40 $~$ 45 $μ m$ ，封油边宽度为15 $~$ 19 $m m$ ，小孔节流器直径为0.15 $~$ 0.18 $m m$ 。

2）通过响应面分析研究了供油压力、油腔间隙、封油边宽度及小孔节流器直径对液体静压导轨承载特性的交互影响规律。结果表明：供油压力与其他3个因素均形成显著交互作用，且随着供油压力的升高，承载力和刚度均呈增大趋势，表明供油压力为影响承载特性的关键因素；油腔间隙与小孔节流器直径之间存在交互作用，同时减小油腔间隙和小孔节流器直径可在一定程度上提高承载力和刚度；当封油边宽度与其他因素形成交互作用时，增大封油边宽度对承载力的提升有一定作用，但对刚度的影响较小。基于各设计参数的独立贡献率，赋予供油压力（主导参数）、油腔间隙（次主导参数）、封油边宽度及小孔节流器直径的权重分别为0.5、0.3、0.1、0.1，形成多目标优化优先级体系，避免在优化过程中出现取值冲突的情况。

3）通过构建液体静压导轨承载力和刚度的响应面模型来优化设计参数，可简化计算过程，缩短设计周期。优化后液体静压导轨的承载力提高了24.99%，刚度提高了19.62%。研究结果为精密磨床液体静压导轨承载性能的提升提供了一定的参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

高殿荣，赵建华，张作超.

液体静压导轨单一导轨面内油腔数目的分析

［J］. 工程力学， 2013， 30（4）： 423-428， 441.