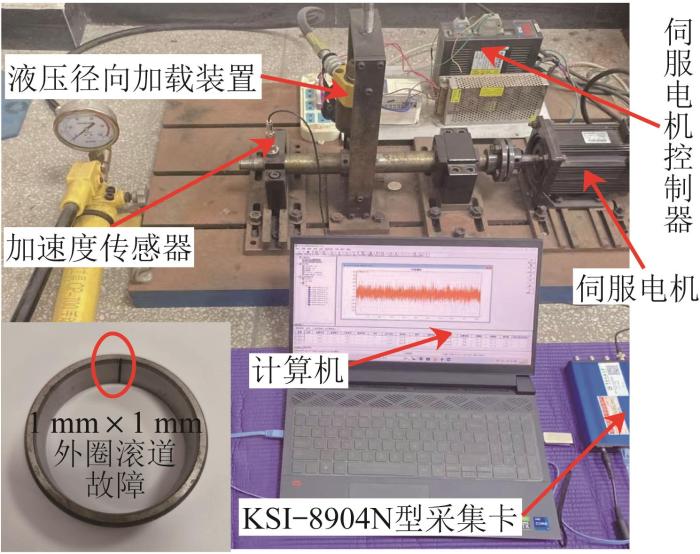
本文链接:
为了更好地预测滚道或滚动体故障导致的轴承振动特性,国内外学者对故障轴承的动力学进行了大量研究。如:曹宏瑞等[5]建立了中介轴承滚道表面剥落等局部损伤故障的动力学模型,将惯性力作为恒定激励,研究了不同磨损状态下轴承的振动响应;陈於学等[6]将轴承内外圈和滚动体早期缺陷的振动信号视为周期性脉冲,建立了滚动轴承早期缺陷振动的线性简化模型;牛蔺楷等[7]考虑了滚动轴承外圈故障的冲击力激励并进行定量计算,研究得出该冲击力的大小与接触载荷及轴承尺寸成正比;Pate等[8]将滚动体的位移激励视为半正弦位移激励,建立了存在单一缺陷和多缺陷的深沟球动力学模型;刘静等[9]建立了一种考虑滚动体与内外圈之间非理想Hertz线接触特性和时变位移激励的圆柱滚子轴承局部故障动力学模型,弥补了传统线接触经验公式无法顾及滚子和滚道曲率的不足;田晶等[10]将轴承故障的激励函数简化为时变半正弦位移激励函数,分析了故障宽度、径向载荷和转速比对故障特征参数的影响;李昊泽等[11]针对轴承外圈故障,引入与故障尺寸相关的时变位移激励函数和时变冲击力函数,研究了故障尺寸对轴承振动特性的影响规律;罗茂林等[12]用半正弦函数表示局部故障引起的位移激励,建立了考虑时变位移激励和冲击力的双冲击动力学模型;王凯等[13]建立了考虑时变刚度和缺陷本身的时变半正弦位移激励模型,研究了多种工况下复合故障对系统动力学的影响。基于上述文献可知,故障常用冲击力和位移模拟,其中位移大多采用半正弦函数来描述,而没有考虑故障边缘的接触变形。滚动体过故障期间会引起故障边缘的接触变形,采用单一的函数不能准确描述其振动特性。
为了准确获得滚动体过故障期间的位移激励,可采用分段函数来描述位移变化。如:张慧玲等[14]针对轴承内外圈点蚀故障,根据滚动体接触到的缺陷深度,建立了单个矩形函数、半正弦函数及分段半正弦函数,考虑了缺陷形状对时变位移的影响,并采用不同的分段函数描述位移激励;刘静宇等[15]提出了一种与滚动体实时位置相关且考虑了故障底部非规则形貌的时变位移激励函数,建立了滚动轴承外圈局部故障的四自由度动力学模型,分析了故障宽度对故障特征指标的影响;Liu等[16]根据局部故障球轴承中滚动体与滚道的接触数目,建立了不同的位移激励函数,研究了具有不同缺陷尺寸的滚动体与滚道之间的接触特性。上述分段位移函数用来描述滚动体与故障底部发生碰撞的情况,其中采用半正弦函数描述故障边缘的弹性变形,采用矩形函数描述滚动体与故障底部的接触变形,但未考虑故障边缘刚度变小的情况。
鉴于此,本文针对滚动体与故障底部不发生碰撞的情况,提出一种考虑外圈滚道故障边缘弹性变形的位移激励函数。采用反比例函数描述故障边缘的弹性变形,采用半正弦函数描述滚动体过故障期间的位移变化,并采用有限元分析法确定了不同故障宽度下分段位移激励函数的系数;在此基础上,以NU306局部故障轴承为研究对象,建立了故障动力学模型,对比分析了基于本文提出的分段位移激励函数与传统位移激励函数的轴承振动特性,以期为局部故障滚动轴承振动特性的深入研究提供一定的参考。
1 滚动轴承位移激励建模
1.1 位移激励函数
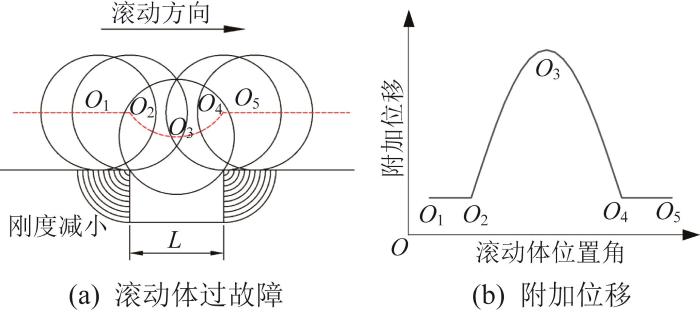
在传统的滚动轴承故障动力学建模中,滚动体过故障产生附加位移如图1所示。滚动体的圆心依次经过O1至O5,定义滚动体圆心从O1到O2为滚动体进故障前,从O2到O4为滚动体过故障期间,从O4到O5为滚动体出故障后。
图1
图1
传统滚动体过故障产生附加位移示意图
Fig.1
Schematic diagram of traditional additional displacement generated by rolling element through fault
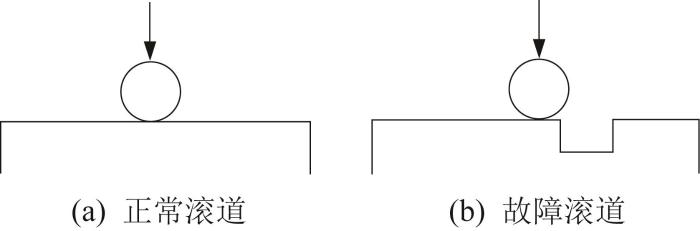
圆柱滚子轴承滚动体与滚道接触的等效模型如图2所示。滚动体与滚道之间的变形由接触变形和结构变形组成。滚动体过正常滚道时,由于滚道结构刚度较大,结构变形可以忽略;滚动体过故障滚道边缘时,结构变形较大,不可忽略。设滚动体与正常滚道之间的接触刚度为K11,接触变形为δ1;滚动体与故障滚道边缘的接触刚度为K21,接触变形为δ2,结构变形为δ3。
图2
图2
圆柱滚子轴承滚动体与滚道接触等效模型
Fig.2
Equivalent model for contact between roller and raceway of cylindrical roller bearing
根据Hertz接触理论,有:
式中:F为滚动体与外圈之间的接触力;K为滚动体与滚道之间的接触刚度;δ为滚动体与滚道之间的接触变形;n为接触变形系数,n=10/9。
由于δ2+δ3>δ1,在同等载荷作用下,由
图3
图3
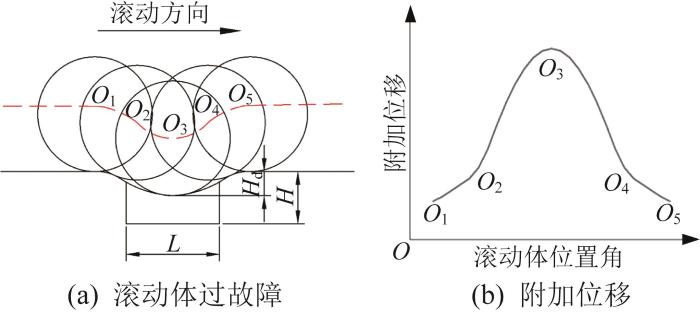
实际滚动体过故障产生附加位移示意图
Fig.3
Schematic diagram of actual additional displacement generated by rolling element through fault
滚动体过故障期间的下降深度Hd为:
式中:Dr为滚动体直径,L为故障宽度。
本文主要研究滚动体与故障底部不发生碰撞的情况,并将其定义为早期故障,即Hd<H,其中H为故障深度。
为了准确得到滚动体过故障期间的时变位移激励,本文采用有限元仿真方法获得滚动体过故障期间的附加位移,并通过MATLAB软件对附加位移进行曲线拟合。滚动体进故障前和出故障后的附加位移激励是由刚度弱化效应造成的,通过曲线拟合发现反比例函数更适合模拟该附加位移激励;滚动体过故障期间的位移激励由滚动体位移导致,目前大多采用正弦函数进行拟合[8]。经过多次拟合发现,上述拟合的拟合度较高且拟合效果良好。因此,本文采用上述方法,得出位移激励函数如下:
式中:mod函数为求余函数;α=2arcsin (L/Do),其中Do为轴承外圈滚道直径;θ0为滚动体初始位置角;θj 为滚动体位置角;A1至A8均为变量,其值与轴承运行工况及结构参数等有关[16]。
1.2 故障有限元模型
表1 NU306圆柱滚子轴承几何参数
Table 1
| 几何参数 | 数值 |
|---|---|
| 滚动体直径Dr/mm | 11 |
| 轴承节圆直径Dm/mm | 51.5 |
| 轴承内圈滚道直径Di/mm | 40.5 |
| 轴承外圈滚道直径Do/mm | 62.5 |
| 外圈厚度T/mm | 19 |
| 接触角β/(°) | 0 |
| 滚动体数量Z/个 | 12 |
| 滚动体与滚道之间的径向间隙ε1/mm | 0.01 |
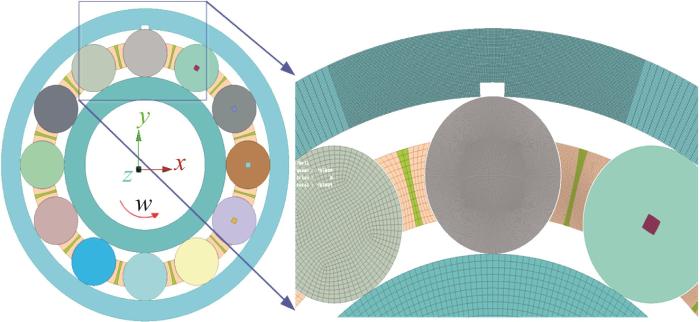
假设滚动轴承外圈故障为贯穿式矩形故障,其有限元模型如图4所示。故障宽度分别设为0.5、1、2 mm,深度为1 mm。
图4
图4
滚动轴承外圈故障有限元模型
Fig.4
Finite element model of rolling bearing outer ring fault
采用PLANE162单元对模型进行网格划分,以减少求解时间且具有较高的精度。本文研究的重点是滚动体过故障期间的运动行为,因此对故障区域和滚动体的网格进行细化。细化处的网格尺寸为0.1 mm,非细化处为0.5 mm,共划分为165 839个单元、168 698个节点。
在实际使用中,外圈通常与轴承座过盈配合。为了使所建立的模型更接近于轴承实际运行状态,对轴承外圈施加全约束。圆柱滚子轴承在运行时仅承受径向载荷,因此在轴承内圈y轴正方向施加3 000 N等效径向载荷,在内圈内表面节点逆时针方向施加2 100 r/min的转速。
为了提高计算结果的准确性,轴承内外圈和滚动体的材料选用GCr15钢,保持架选用黄铜,具体材料参数如表2所示。
表2 滚动轴承材料参数
Table 2
| 材料 | 密度/(kg/m3) | 弹性模量/GPa | 泊松比 |
|---|---|---|---|
| GCr15钢 | 7 830 | 206 | 0.3 |
| 黄铜 | 8 500 | 105 | 0.324 |
为了避免仿真时发生穿透现象,采用二维自动面-面接触。分别建立12个滚动体与内外圈及保持架的接触对,接触面的静摩擦因数为0.01,动摩擦因数为0.005。
1.3 分段位移激励函数系数的确定
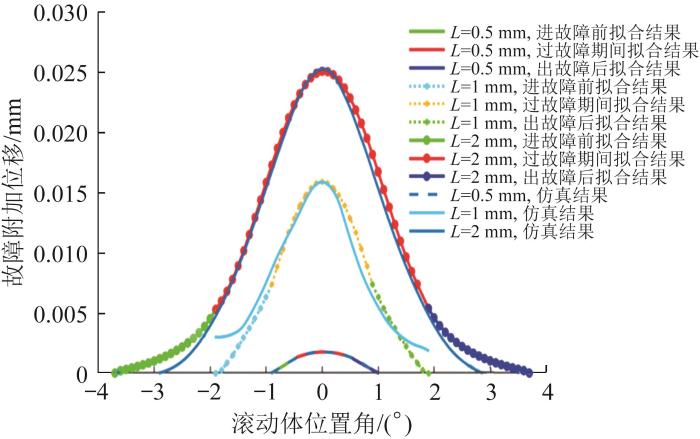
附加位移曲线可以反映滚动轴承内部的振动特性。为了减小附加位移的误差,将滚动体进故障前和出故障后产生的附加位移采用Custom Equations自定义反比例函数拟合,滚动体过故障期间产生的附加位移采用Sum of sin functions函数进行拟合,得到滚动体过故障产生的附加位移曲线,如图5所示。
图5
图5
滚动体过故障产生的附加位移曲线
Fig.5
Additional displacement curves of rolling element through fault
通过有限元仿真与函数拟合得到不同故障宽度下附加位移曲线的拟合度,如表3所示。由表可知,曲线拟合度较高,进一步说明了分段位移激励函数的有效性。
表3 附加位移曲线拟合度
Table 3
| 故障宽度/mm | 拟合度 | ||
|---|---|---|---|
| 反比例函数拟合(左) | 半正弦函数拟合 | 反比例函数拟合(右) | |
| 0.5 | 0.991 0 | 0.997 4 | 0.994 7 |
| 1 | 0.986 6 | 0.963 9 | 0.973 3 |
| 2 | 0.997 4 | 0.991 7 | 0.984 8 |
拟合得到不同故障宽度下分段位移激励函数的系数,如表4所示。由表可知:A1和A6为反比例函数的系数,其随着故障宽度的增大而减小,反比例函数曲线变得平滑;A2和A7也是反比例函数的系数,随着故障宽度的增大,A2减小,A7增大,附加位移产生变早,且持续时间变长;A3和A8为反比例函数的偏距,随着故障宽度的增大,其变化较小,说明故障宽度对其影响较小;A4为正弦函数的幅值,随着故障宽度的增大而增大,这是因为故障宽度越大,滚动体进入故障的深度越大,故障导致的附加位移幅值越大;A5为正弦函数的偏距,其与滚动体过故障期间的初始位移有关,随着故障宽度的增大而增大,说明过故障期间的初始位移随故障宽度的增大而增大。
表4 分段位移激励函数系数
Table 4
| 系数 | 数值 | ||
|---|---|---|---|
| L=0.5 mm | L=1 mm | L=2 mm | |
| A1 | |||
| A2 | 0.205 | 0.071 | |
| A3 | |||
| A4 | |||
| A5 | |||
| A6 | |||
| A7 | -0.117 | 0.007 | 0.089 |
| A8 | |||
用数学解析法计算滚动体过故障期间的函数系数A4和A5,并将A4和A5的计算结果与有限元仿真结果进行对比,来验证函数系数值的准确性。
在滚动体过故障期间,位移激励函数为:
文献[14]介绍的滚动体过故障期间的位移激励函数为:
式中:ϕ为滚子进故障后的滚动角度。
当L=1 mm,θj =0时,由
将上述结果代入
由
表5 系数 A4 和 A5 仿真值与计算值的对比
Table 5
| 系数 | 仿真值 | 计算值 | 相对误差/% |
|---|---|---|---|
| A4 | 8.800×10-6 | 8.76×10-6 | 0.45 |
| A5 | 7.100×10-6 | 7.14×10-6 | 0.56 |
2 滚动轴承动力学建模及振动特性分析
2.1 滚动轴承动力学建模
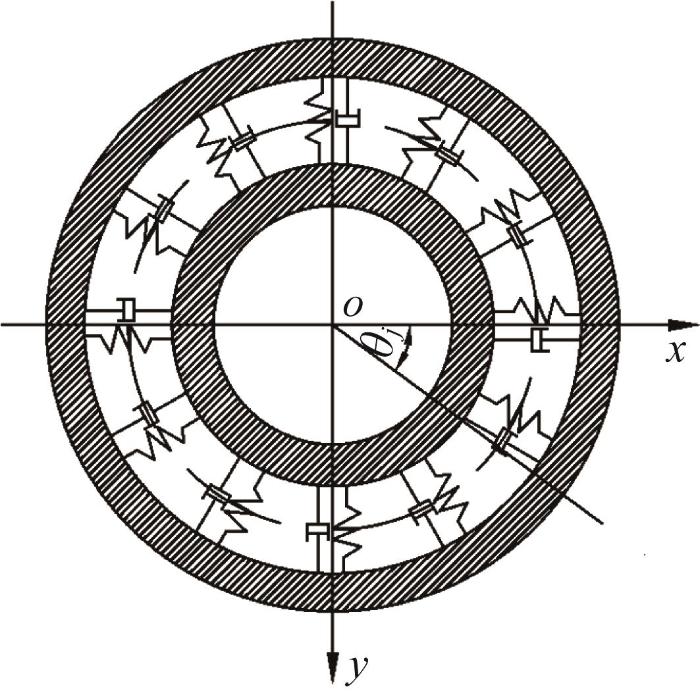
建立圆柱滚子轴承简化模型,如图6所示。为了研究滚动轴承的动力学特性,本文基于弹簧质量系统动力学模型,将滚动体视为非线性接触弹簧。
图6
根据Hertz接触理论,滚动体与外圈之间的接触力如
通过仿真可知,当轴承外圈发生故障时,接触力和接触变形都随着滚动体位置的变化而改变,此时滚动体与外圈之间的时变接触力Ft可表示为:
式中:Kt为滚动体与外圈之间的时变接触刚度;δt为滚动体与外圈之间的时变接触变形。
外圈故障的滚动轴承在x、y向的总接触力Fx、Fy 为:
式中:δj 为第j个滚动体的总接触变形,ςj 为第j个滚动体的载荷区系数,Kj 为第j个滚动体与滚道之间的时变接触刚度。
式中:K1为滚动体与故障单边接触时的接触刚度;K2为滚动体与故障双边接触时的接触刚度;Kn为滚动体与正常滚道之间的接触刚度,其值可根据文献[19]中接触刚度的计算方法计算得出。
将外圈故障轴承的时变位移激励引入正常轴承的动力学模型,得出外圈故障轴承的二自由度动力学方程:
式中:m为内圈和转轴的总质量,c为系统阻尼;wx、wy 分别为x、y向的径向载荷分量。
2.2 振动特性分析
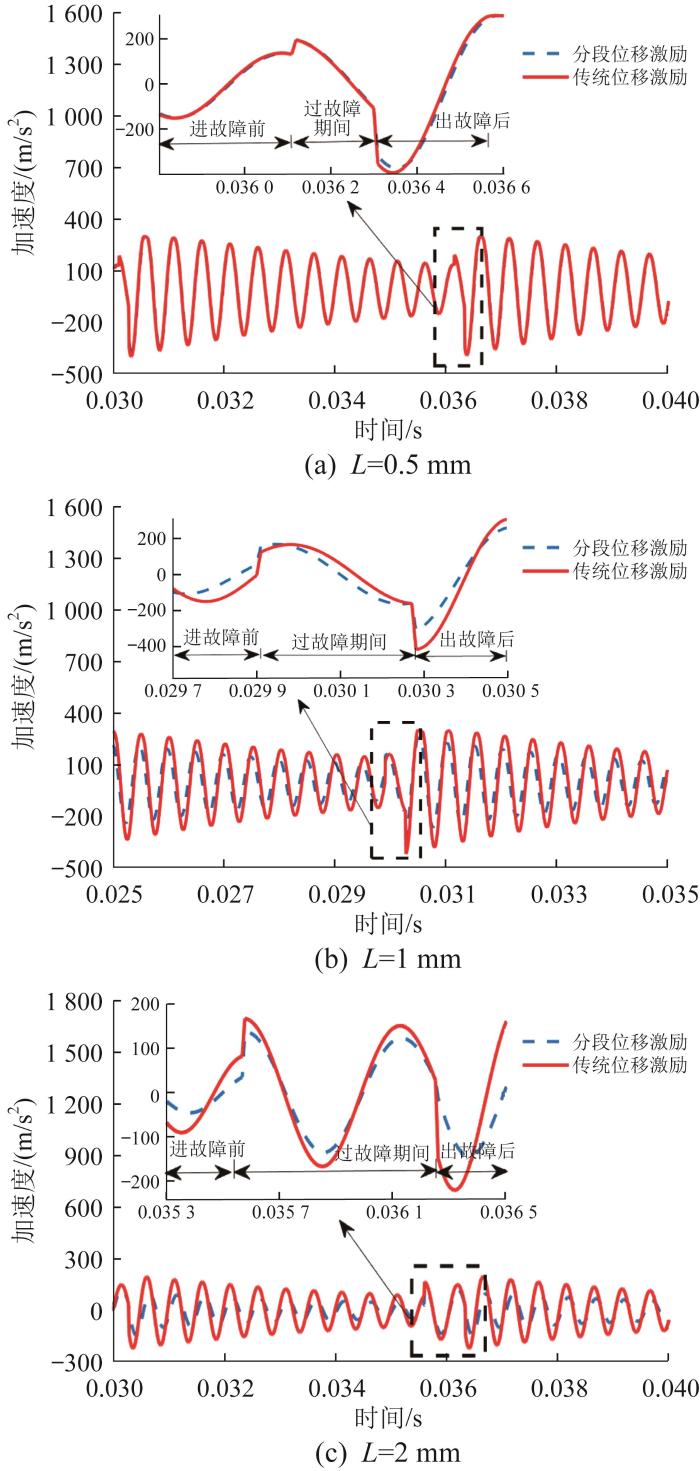
为了分析本文提出的分段位移激励函数的优越性,将分段位移激励函数模型与传统正弦位移激励函数模型进行对比,分析不同位移激励下轴承的振动特性,结果如图7所示。
图7
图7
不同位移激励下滚动轴承振动特性
Fig.7
Vibration characteristics of rolling bearing under different displacement excitations
由图7可知:在滚动体进故障前和出故障后这2个时间段内,分段位移激励下的振动响应曲线相比于传统位移激励下的平缓,这是因为滚动体在进故障前和出故障后的弹性变形对冲击有缓冲作用,缓解了系统的过刚度状况;在滚动体过故障期间,分段位移激励下的振动幅值比传统位移激励下的小,这是因为滚动体过故障期间的振动幅值受滚动体过故障期间初始状态(即滚动体进故障前的最终状态)的影响,而分段位移激励考虑了故障处的弹性变形。由图(a)可知,在外圈为小故障时,分段位移激励与传统位移激励下的振动响应曲线基本重合,这是因为小故障时滚道弹性变形较小。由图(b)和图(c)可知,中故障时的振动幅值比大故障时大,这是因为滚道出现大故障时的弹性变形较大,导致故障前后端圆弧面的曲率半径较大。
综上所述,在早期小故障时可选择传统半正弦位移激励模型或分段位移激励模型;发生中大型故障时,滚道的弹性变形较大,在进故障前与出故障后振动特性的差异较大,此时传统位移激励模型相对实际具有较大误差。
均方根值RMS、峰峰值PTP和峭度值Ku是分析轴承振动特征的常用时域指标。RMS用于评估振动信号的整体能量,以判断振动强度的大小;PTP用于描述振动信号正峰值与负峰值之差,以判断振幅是否超出阈值;Ku值可以反映振动中的冲击成分。为了更好地分析分段位移激励函数和传统位移激励函数反映的振动特性,对不同故障宽度下的位移激励模型进行分析,得到振动信号的时域指标值,如表6所示。
表6 不同故障宽度下振动信号的时域指标值
Table 6
| 时域指标 | 半正弦位移激励 | 分段位移激励 | ||||
|---|---|---|---|---|---|---|
L= 0.5 mm | L= 1 mm | L= 2 mm | L= 0.5 mm | L= 1 mm | L= 2 mm | |
| RMS/g | 168.1 | 181.4 | 118.5 | 167.5 | 141.3 | 91.8 |
| PTP/g | 775.5 | 771.6 | 771.6 | 775.5 | 826.83 | 841.6 |
| Ku | 2.1 | 1.9 | 2.5 | 2.1 | 2.3 | 6.0 |
由表6可知,在分段位移激励下,振动信号的均方根值较小,说明振动能量较小,故考虑故障边缘弹性变形可以降低振动能量,缓解系统过刚度状况。分段位移激励下的峰峰值较大,说明分段位移激励模型对故障振动信号更敏感。分段位移激励下的峭度值与正常峭度值相差较大,其更能反映大故障的发生。因此,分段位移激励函数相比传统半正弦位移激励函数具有一定的优越性。
3 模型验证
3.1 有限元模型验证
通过对比保持架转速的仿真值与理论值,来验证本文所建立的有限元模型的有效性。
保持架转速理论值ωm为:
式中:ni为内圈转速。
当ni=2 100 r/min时,代入轴承参数,可得ωm=86.47 rad/s。
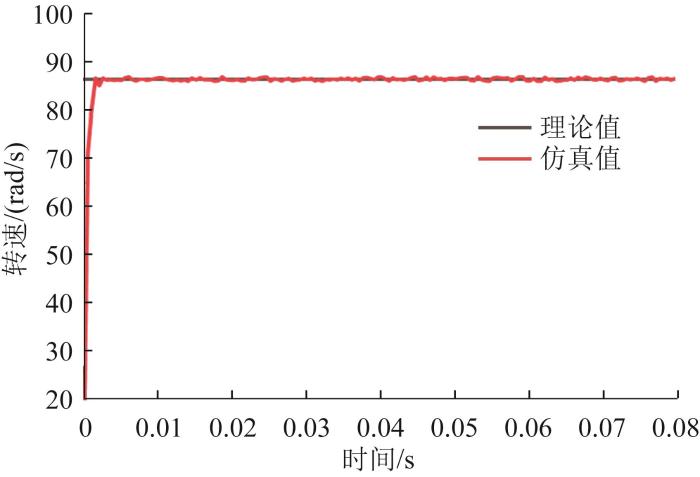
保持架转速仿真值与理论值的对比如图8所示。由图可知,转速仿真平均值为86.40 rad/s,与理论值的相对误差为2.2%。由于滚动体与保持架兜孔发生非连续碰撞,转速仿真值稳定后在理论值附近波动。
图8
图8
保持架转速仿真值与理论值的对比
Fig.8
Comparison between simulated value and theoretical value of cage speed
3.2 动力学模型验证
图9
图10
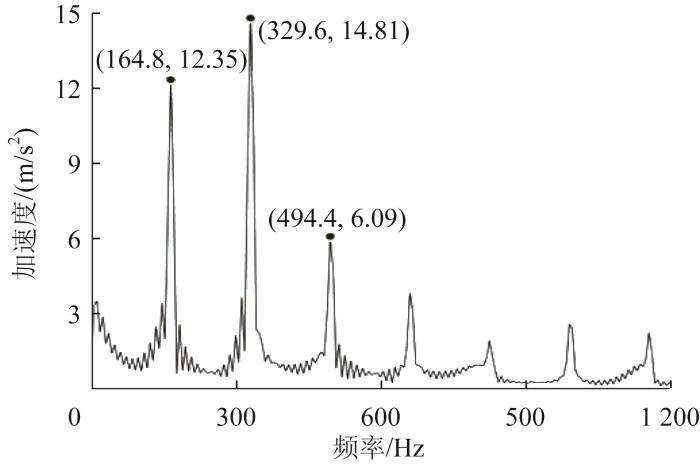
图10
测试得到的轴承振动信号频谱图
Fig.10
Spectrum diagram of bearing vibration signal obtained by test
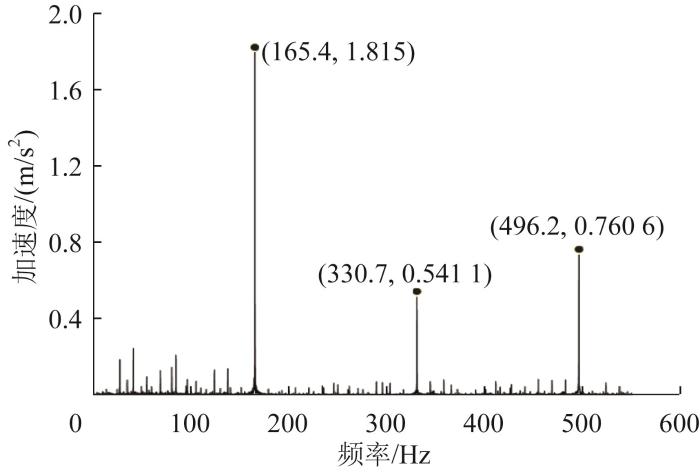
在转速为2 100 r/min、载荷为3 000 N的工况下进行动力学仿真,得到的轴承振动频谱特征如图11所示。由图可知,信号中存在明显的冲击成分,这是由位移激励和刚度激励同时作用造成的。动力学仿真得到的外圈故障特征频率为164.80 Hz。
图11
图11
动力学仿真得到的轴承振动信号频谱图
Fig.11
Spectrum diagram of bearing vibration signal obtained by dynamic simulation
滚动轴承外圈故障特征频率f的理论计算公式为:
将轴承参数代入
轴承外圈故障特征频率理论值、仿真值与实验值的对比如表7所示。由于理论计算时没有考虑时变刚度,仿真和实验中考虑了时变刚度,因此仿真和实验中滚动体过故障的时间会增加,其外圈故障特征频率值会比理论值小。由表可知,仿真值小于理论值,实验值大于理论值,这是因为在实验过程中存在测量误差,但仿真值相对理论值和实验值的误差均在-0.4%以内,故该动力学模型是有效的。
表7 轴承外圈故障特征频率理论值、仿真值与实验值的对比
Table 7
| 特征频率/Hz | 数值 | 仿真值相对实验值的误差/% | 仿真值相对理论值的误差/% |
|---|---|---|---|
| 理论值 | 165.15 | -0.36 | -0.21 |
| 仿真值 | 164.80 | ||
| 实验值 | 165.40 |
4 结 论
本文考虑了滚动轴承故障处的刚度变化,提出了一种新的分段位移激励模型。以NU306局部故障轴承为研究对象,建立了其有限元模型和动力学模型,获取了基于分段位移激励模型的振动响应。通过与传统位移激励下的振动特性的对比,得出如下结论:
1)在滚动体过故障的整个过程中,采用考虑滚道刚度变化的分段位移激励模型得到的振动响应曲线比采用传统位移激励模型的平缓。
2)在早期小故障时可选择传统半正弦位移激励模型或分段位移激励模型;在中大型故障时,分段位移激励模型更接近实际。
3)分段位移激励模型对故障信号更敏感,更能察觉出大故障的发生,相比于传统半正弦位移激励模型具有一定的优越性。
参考文献
滚动轴承表面损伤建模与冲击力的定量计算
[J].
Modeling of local surface defect in rolling bearing and quantitative calculation of impact force
[J].
A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races
[J].
基于非理想Hertz线接触特性的圆柱滚子轴承局部故障动力学建模
[J].
Dynamic modeling on localized defect of cylindrical roller bearing based on non-hertz line contact characteristics
[J].DOI:10.3901/jme.2014.01.091 [本文引用: 1]
中介轴承多点故障动力学建模和仿真分析
[J].
Dynamic modeling and simulation analysis of inter-shaft bearing with multi-point faults
[J].
考虑时变激励的滚动轴承局部故障动力学建模
[J].
Dynamic modeling of rolling bearing local fault considering time-varying excitation
[J].
考虑冲击力的球轴承外圈剥落缺陷双冲击现象动力学建模
[J].
Dynamic modeling of the dual-impulse behavior produced by a spall on the outer race of a ball bearing considering impact forces
[J].
A survey of condition monitoring and protection methods for medium-voltage induction motors
[J].
不同元件故障状态下滚动轴承的动态特性研究
[J].
Dynamic characteristics of compound fault in deep groove ball bearing
[J].
滚动轴承点蚀故障动力学建模与仿真
[J].
Dynamic modeling and simulation of rolling bearing with pitting failure
[J].
滚动轴承局部故障动力学建模与振动分析
[J].
Dynamic modeling and vibration characterization of rolling bearing with local fault
[J].
Vibration analysis of ball bearings with a localized defect applying piecewise response function
[J].
圆柱滚子轴承故障机理与振动特性分析
[D].
Fault mechanism and vibration characteristics analysis of cylindrical roller bearing
[D].
考虑滚动轴承故障处塑性变形的有限元建模与动力学特性分析
[J].
Finite element modeling and dynamic characteristics analysis with plastic deformation at rolling bearing failure considered
[J].
滚动轴承缺陷非线性激励机理与建模研究
[D].
Study on nonlinear excitation mechanism and modeling of rolling bearing defects
[D].DOI:10.3934/naco.2014.4.295 [本文引用: 1]
Research on dynamic characteristics of rolling bearing under different component fault conditions
[J].DOI:10.1088/1742-6596/2785/1/012053 [本文引用: 1]
基于同轴振动特征融合的滚动轴承故障诊断研究
[D].
Research on fault diagnosis of rolling bearing based on coaxial vibration feature fusion
[D].
Analyses of contact forces and vibration response for a defective rolling element bearing using an explicit dynamics finite element model
[J].
中介轴承故障动力学建模与振动特征分析
[J].
Dynamic modeling and vibration analysis for inter-shaft bearing fault
[J].DOI:10.3901/jme.2020.21.089 [本文引用: 1]