耦合焊接残余应力的横波可控震源振动器平板疲劳寿命预测

doi:10.3785/j.issn.1006-754X.2025.04.145

耦合焊接残余应力的横波可控震源振动器平板疲劳寿命预测

陈振^,¹^,²^,³, 陈能鹏^,^,², 冉庆杰², 王乔木², 魏超成², 鞠浩文²

1.页岩气评价与开采四川省重点实验室，四川成都 610500

2.西南石油大学机电工程学院，四川成都 610500

3.石油天然气装备技术四川省科技资源共享服务平台，四川成都 610500

Fatigue life prediction of sheer wave vibroseis vibrator baseplate coupled with welding residual stress

CHEN Zhen^,¹^,²^,³, CHEN Nengpeng^,^,², RAN Qingjie², WANG Qiaomu², WEI Chaocheng², JU Haowen²

1.Sichuan Key Laboratory of Shale Gas Evaluation and Exploitation, Chengdu 610500, China

2.School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China

3.Petroleum and Natural Gas Equipment Technology, Sichuan Province Science and Technology Resource Sharing Service Platform, Chengdu 610500, China

通讯作者: 陈能鹏（2000—），男，硕士生，从事往复式压缩机曲轴扭振研究，E-mail: 2624134676@qq.com，https://orcid.org/0009-0004-8169-4450

收稿日期: 2024-05-27 修回日期: 2024-07-10

基金资助:

四川省科技厅自然科学基金面上项目. 2024NSFSC0094

First author contact: CHEN Z, CHEN N P, RAN Q J, et al. Fatigue life prediction of sheer wave vibroseis vibrator baseplate coupled with welding residual stress[J]. Chinese Journal of Engineering Design, 2025, 32(1): 102-111.

Received: 2024-05-27 Revised: 2024-07-10

作者简介 About authors

陈　振（1985—），男，副教授，博士，从事机械装备结构可靠性及优化研究，E-mail:117976897@qq.com , E-mail：117976897@qq.com

摘要

振动器平板是耦合横波可控震源振动器与大地的关键媒介，而平板齿与平板的焊接部位在地震波激发工况下受力复杂，易发生疲劳失效，导致平板的使用寿命较低。针对传统结构疲劳寿命分析方法不考虑焊接残余应力的问题，采用等应变原理建立应力耦合准则，并对平板焊接焊缝危险部位开展焊接残余应力与工作载荷应力的耦合计算。随后，基于修正的S—N曲线和耦合应力谱，采用Miner准则分析平板在焊接残余应力与工作载荷应力耦合作用下的疲劳寿命。结果表明：在焊接残余应力与工作载荷应力的耦合作用下，平板发生疲劳破坏的工作寿命为8.69 a，与实际8 a工作寿命的相对误差为8.6%。耦合焊接残余应力的振动器平板疲劳寿命预测方法具有较高的精度和稳定性，可为横波可控震源的维护与优化提供新的思路与方法。

关键词： 横波可控震源 ; 振动器平板 ; 焊接残余应力 ; 工作载荷应力 ; 应力耦合 ; S—N曲线

Abstract

Vibrator baseplate is the key medium for coupling shear wave vibroseis vibrator with earth, while the welding part of baseplate teeth and baseplate is prone to fatigue failure due to complex force under the condition of seismic wave excitation, which leads to low service life of baseplate. In view of the problem that the welding residual stress was not considered in the traditional structure fatigue life analysis method, the stress coupling criterion was established by using the equal strain principle, and the coupling calculation of welding residual stress and working load stress was carried out for the dangerous parts of the baseplate welding seam. Then, based on the modified S-N curve and coupled stress spectrum, the Miner criterion was used to analyze the fatigue life of baseplate under the coupling of welding residual stress and working load stress. The results showed that the fatigue failure life of the baseplate under the coupling of welding residual stress and working load stress was 8.69 a, and the relative error with the actual working life of 8 a was 8.6%. The fatigue life prediction method of vibrator baseplate coupled with welding residual stress has high accuracy and stability, which can provide a new idea and method for the maintenance and optimization of shear wave vibroseis.

Keywords： sheer wave vibroseis ; vibrator baseplate ; welding residual stress ; working load stress ; stress coupling ; S-N curve

PDF (3889KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈振, 陈能鹏, 冉庆杰, 王乔木, 魏超成, 鞠浩文. 耦合焊接残余应力的横波可控震源振动器平板疲劳寿命预测[J]. 工程设计学报, 2025, 32(1): 102-111 doi:10.3785/j.issn.1006-754X.2025.04.145

CHEN Zhen, CHEN Nengpeng, RAN Qingjie, WANG Qiaomu, WEI Chaocheng, JU Haowen. Fatigue life prediction of sheer wave vibroseis vibrator baseplate coupled with welding residual stress[J]. Chinese Journal of Engineering Design, 2025, 32(1): 102-111 doi:10.3785/j.issn.1006-754X.2025.04.145

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.04.145

横波可控震源作为一种高效、环保、安全和低成本的地球物理勘探热点技术，能产生频率和幅值可控的连续横波信号。其中，振动器平板是耦合可控震源振动器与大地的关键媒介。在地震波激发工况下，振动器平板既要承受可控震源车主体的压重作用，又要承受来自振动器的变频交变激振力，尤其是平板与平板齿的焊接部位，因受到焊接残余应力的影响，此处的应力较为复杂。因此，平板与平板齿的焊接部位偶发无法预测的疲劳裂纹甚至断裂现象。有效预测振动器平板在横波勘探工况下的疲劳寿命，对于实现横波可控震源的预防性维护及降低施工现场事故发生率具有重要意义。然而，现有的振动器平板疲劳寿命预测方法未考虑焊接残余应力对焊缝区域的影响，预测误差较大。

研究表明，结构的疲劳寿命受焊接残余应力的影响^[1]。现阶段，针对焊接残余应力的研究主要集中在焊接顺序、焊接层间温度等焊接工艺参数对焊接残余应力分布和大小的影响方面^[2-5]。Fu等^[6]运用有限元分析和实验验证相结合的手段，分析了焊接顺序对T形接头焊接残余应力和变形的影响，结果表明：焊接顺序对焊接残余应力、结构变形具有显著影响。李琴等^[7]通过确定Q345钢平板焊接残余应力最小时的焊接工艺参数取值范围，实现了平板焊接速度和焊接层间温度的优化。Rybicki等^[8]分析了不同焊接速度对管道焊缝组织及其机械特性的影响，结果表明：焊缝中的结晶边界偏析度越高，焊接残余应力越大。魏崇一等^[9]通过分析焊接残余应力场，探讨了循环载荷下T形接头焊接残余应力的释放受载荷大小、应力比及方向的影响规律，结果表明：循环载荷为焊接残余应力激发、释放的关键因素。因此，在预测焊接结构的疲劳寿命时，须考虑载荷应力与焊接残余应力的耦合作用。王文静等^[10]根据焊缝的厚度效应，采用基于表面外推的热点应力法来校正S—N曲线（应力—寿命曲线），实现了薄板焊接结构疲劳可靠度的准确求解。Grbović等^[11]基于航空发动机的焊缝疲劳裂纹扩展规律，建立了一个用于计算焊缝疲劳寿命的扩展有限元预测模型。黄庆文等^[12]根据应力频谱，结合P—S—N曲线（P为存活率）和Miner疲劳累积损伤理论，对谐波减速器柔轮的疲劳寿命进行了预测，预测结果与国内谐波减速器的普遍寿命相近。范文学等^[13]运用S—N曲线对Q235B十字焊接接头进行了疲劳寿命预测，结果表明：其疲劳寿命基于不同的S—N曲线表现出巨大的差异性。由此可知，在对焊接结构进行疲劳寿命预测时，应修正S—N曲线。Sudret等^[14]在考虑S—N曲线不确定度的基础上，开展了核电厂关键零部件疲劳寿命的概率评估。Engesvik等^[15]同样在考虑了S—N曲线不确定度的基础上，对焊接接头的疲劳承载能力进行了概率分析。高会英等^[16]综合分析了各种不确定因素对焊接接头疲劳寿命的影响，并将多项式混沌理论应用于疲劳寿命的预测。魏国前等^[17]提出了一种焊接结构疲劳寿命预测方法，并针对多种焊接接头开展了二级变幅载荷谱的拉伸疲劳试验，分别采用Miner模型、M-H（Manson-Halford）模型和Pavlou方法估算了接头试件的疲劳寿命。张红卫等^[18]通过对比考虑焊接残余应力前后的桥壳疲劳寿命，发现考虑焊接残余应力后桥壳的疲劳循环次数下降且失效位置发生变化，由此验证了预测疲劳寿命时考虑焊接残余应力的必要性。

综上，为探究焊接残余应力对结构疲劳损伤的影响，国内外学者采用数值模拟与实验研究相结合的方法，系统地分析了不同焊接工艺参数（如焊接速度、焊接层间温度等）对焊接残余应力场的大小及分布的影响规律，并深入探讨了焊接残余应力与结构疲劳寿命的关联性。然而，目前有关耦合焊接残余应力的结构疲劳寿命预测方法仍存在很多空白。基于此，本文采用修正S—N曲线与Miner准则相结合的方法，开展耦合焊接残余应力的横波可控震源振动器平板疲劳寿命预测研究，旨在形成一种更加符合工程实际、计算精度和效率更高的疲劳寿命预测方法。

1 振动器平板焊接残余应力分析

1.1　焊接热源模型建立

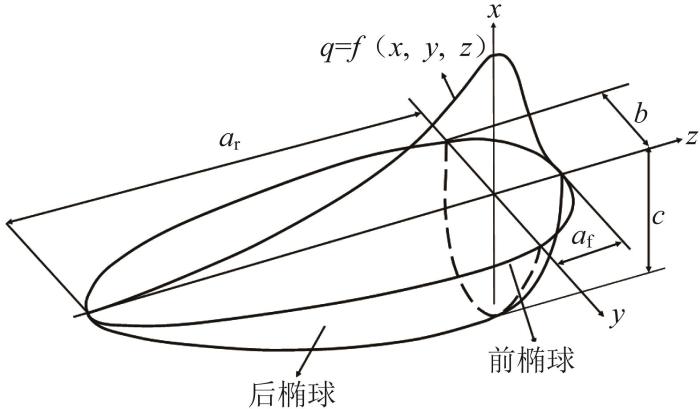
鉴于横波可控震源振动器平板与平板齿焊接时焊缝处形成的温度场与Goldak等^[19]提出的双椭球热源模型符合程度较高，本文采用双椭球热源模型来模拟焊缝温度场。该模型利用2个椭球体来描述热源的形状和热流分布，分别对应热源移动方向的前后部分，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双椭球热源模型

Fig.1 Double ellipsoid heat source model

根据图1，双椭球热源模型的数学参数表达式为：

\{\begin{matrix} q_{f} (x, y, z) = \frac{6 \sqrt[]{3} f_{f} Q}{a_{f} b c \sqrt[]{π}} e x p [- \frac{3 x^{2}}{c^{2}} - \frac{3 y^{2}}{b^{2}} - \frac{3 {(z - v t)}^{2}}{a_{f}^{2}}], y \geq 0 \\ q_{r} (x, y, z) = \frac{6 \sqrt[]{3} f_{r} Q}{a_{r} b c \sqrt[]{π}} e x p [- \frac{3 x^{2}}{c^{2}} - \frac{3 y^{2}}{b^{2}} - \frac{3 {(z - v t)}^{2}}{a_{r}^{2}}], y < 0 \end{matrix}

(1)

其中：

\{\begin{matrix} f_{f} + f_{r} = 2 \\ f_{f} = \frac{a_{f}}{a_{f} + a_{r}} \\ f_{r} = \frac{a_{r}}{a_{f} + a_{r}} \end{matrix}

式中： $q_{f}$ 、 $q_{r}$ 分别为前、后椭球热源模型内部的焊接热流密度； $f_{f}$ 、 $f_{r}$ 分别为总输入功率在熔池前后两部分的能量分布系数； $a_{f}$ 、 $a_{r}$ 分别为焊接方向前、后半轴的长度；b为焊缝宽度方向半轴长度；c为焊缝深度方向半轴长度；v为焊接速度；t为焊接时间； $Q$ 为有效热输入； $η$ 为焊接热效率，通常取0.65~0.90。

结合式(1)与现场工况，确定双椭球热源模型的参数，如表1所示。

表1 双椭球热源模型参数

Table 1 Parameters of double ellipsoid heat source model

参数	数值
$q_{f}$ /(W·mm^-3)	44.0
$q_{r}$ /(W·mm^-3)	36.7
$a_{f}$ /mm	3
$a_{r}$ /mm	6
b/mm	4
c/mm	2
Q/W	4 004

新窗口打开| 下载CSV

根据现场工况与双椭球热源模型的形状参数，在焊接有限元软件SYSWELD中建立振动器平板与平板齿的焊接热源模型，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 振动器平板与平板齿的焊接热源模型

Fig.2 Welding heat source model of vibrator baseplate and baseplate tooth

1.2　焊接模型构建及焊接工艺选取

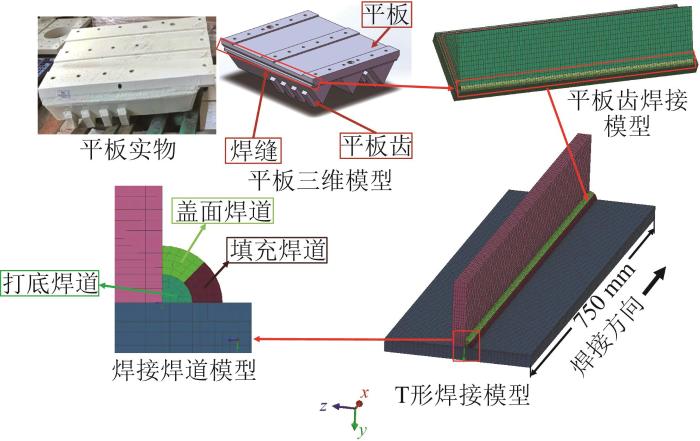
相关研究表明，焊件模型形状对焊接残余应力的影响较小^[20]。基于此，在确保计算精度的前提下，本文将振动器平板与平板齿的焊接模型简化为T形焊接模型。将T形焊接模型的两端固定，设置其母材材料为45钢，焊缝填充材料为ERNiCrMo-3镍铬钼焊丝，并输入焊接热源模型参数；采用以六面体为主的三维网格单元对焊接模型进行网格划分，如图3所示。最终划分得到的网格数量为256 315个。通过网格无关性验证后，进行后续的焊接数值模拟。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 振动器平板焊接模型及其网格划分

Fig.3 Welding model of vibrator baseplate and its mesh division

鉴于振动器平板材料为45钢且平板厚度达到52 mm，采用打底、填充、盖面三道焊接工序完成焊接。结合熔化极气体保护焊对振动器平板与平板齿的焊接过程进行模拟。首先，在平板与平板齿之间呈45°进行打底焊，以实现平板与平板齿的连接；待打底焊缝冷却至规定温度后，在平板与平板齿之间呈45°进行填充焊；最后，在相同位置处进行盖面焊，以保证平板与平板齿的焊接更为牢固。具体焊接工艺参数如表2所示^[21]。

表2 焊接工艺参数

Table 2 Welding process parameters

焊层	焊道数	焊接电压/V	焊接电流/A	焊接速度/（mm/s）
打底焊	1	28	231	8
填充焊	1	27	235	6
盖面焊	1	26	220	5

新窗口打开| 下载CSV

1.3　焊接残余应力分析

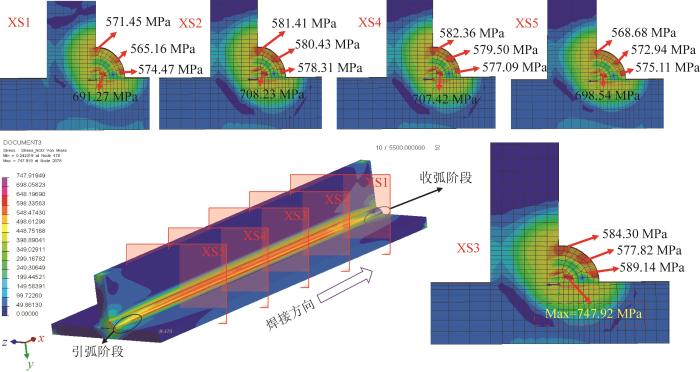
基于上文所构建的振动器平板焊接模型，利用SYSWELD软件对平板与平板齿的焊接过程进行数值模拟，计算得到振动器平板的焊接残余应力场分布云图，如图4所示。沿焊接方向等距选取5个截面，以分析沿焊缝垂直截面的焊接残余应力分布规律。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 振动器平板焊接残余应力场

Fig.4 Welding residual stress field of vibrator baseplate

从图4中可以看出，振动器平板的焊接残余应力主要集中在焊缝区域，其最大残余应力达到747.92 MPa，位于XS3截面的打底焊缝处，远高于平板母材45钢的屈服强度。尽管焊缝处平板母材的材料性质发生了变化，但焊接残余应力未超过ERNiCrMo-3镍铬钼焊丝的屈服强度，说明仍处于线弹性阶段。此外，由图4所示的5个焊缝垂直截面的焊接残余应力分布规律可知，yOz平面的焊接残余应力分布整体呈逐渐向外扩散的圆弧形；在打底焊缝处存在最大残余应力，填充焊缝、盖面焊缝以及其交界处的残余应力较大。

为了进一步分析振动器平板焊缝区域焊接残余应力的分布规律，以确定各向焊接残余应力的峰值，沿焊接方向提取平板沿x、y、z向的焊接残余应力，如图5所示。图中：XS1M~XS5M节点分别对应XS1~XS5截面焊接残余应力最大处，即危险节点。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 振动器平板沿焊接方向的焊接残余应力

Fig.5 Welding residual stress of vibrator baseplate along welding direction

由图5可知，焊缝区域各向焊接残余应力除了在引弧与收弧阶段表现为突变外，在距离起焊点70~680 mm的焊接段内基本呈平稳状态，属于焊接稳定阶段。但在距离起焊点300~370 mm的焊缝处，焊接残余应力出现了微小波动，分析原因如下：在焊接过程中，平板两端作为固定点，变形较小，而在距离起焊点300~370 mm的中间段存在较大变形。通常情况下，工件焊缝处的焊接残余应力由稳定阶段的焊接残余应力峰值来表征。由此可知，该振动器平板焊缝处的各向焊接残余应力分别为528.5，140.0，132.0 MPa。

2 振动器平板工作载荷应力分析

2.1　振动器平板-大地耦合模型构建

在可控震源激振过程中，大地可视为半无限空间体。根据横波可控震源的工作原理和设定的大地条件，对振动器平板作适当简化，并建立振动器平板-大地耦合模型，其中大地尺寸为10 m $\times$ 10 m×8 m。在横波可控震源激振时，振动器平板与大地均发生弹性变形，故将振动器平板与大地均设置为线弹性材料，其中平板为45钢，大地为硬质土。鉴于平板齿为不规则几何体，采用四面体网格进行划分，最小网格尺寸为2 mm，振动器平板其余部分的网格尺寸为5 mm；振动器平板与大地接触的近地表空间区域采用过渡四面体网格进行划分，网格最小尺寸为10 mm；大地其余部分采用过渡六面体网格进行划分，网格尺寸为20~50 mm。振动器平板-大地耦合模型的网格划分如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 振动器平板-大地耦合模型网格划分

Fig.6 Grid division of vibrator baseplate-earth coupling model

2.2　振动器平板工作载荷确定

横波可控震源振动器主要由箱体、活塞杆、重锤和平板等结构组成，如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 振动器结构示意

Fig.7 Structure schematic of vibrator

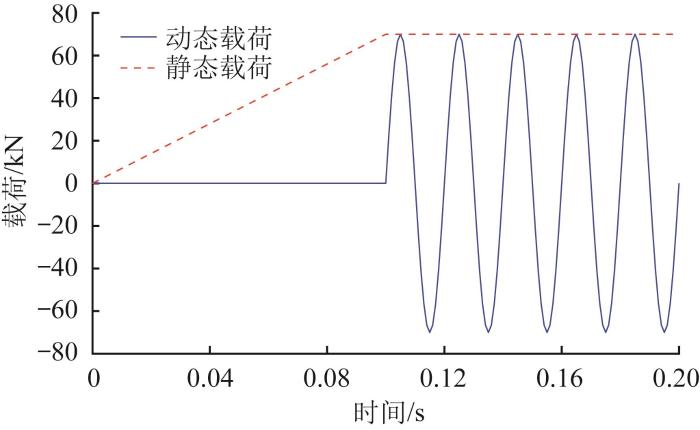
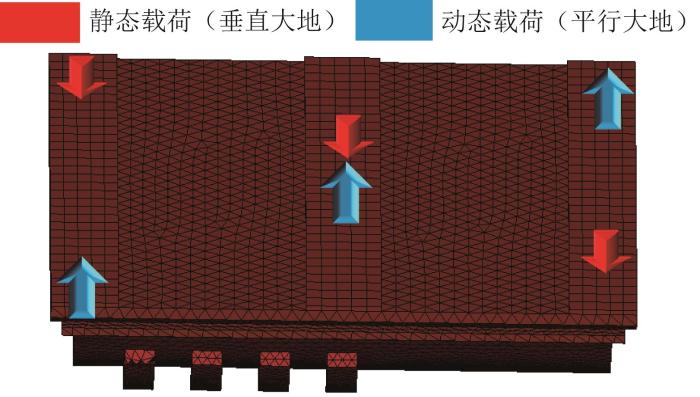
在横波可控震源工作时，振动器平板所受的载荷分别为垂直于大地方向的压重载荷和平行于大地方向的液压激振载荷。在静态工况下，振动器平板所受的载荷为震源车身自重，方向为指向地心，大小为280 kN（均匀加载到4块平板上），静态载荷施加过程持续时间为0.1 s；液压激振载荷为幅值、频率可控的动态载荷，本文以频率为50 Hz、幅值为280 kN的正弦信号模拟激振载荷，共加载5个周期。单块振动器平板所受的载荷随时间的变化曲线如图8所示，施加形式如图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 振动器平板所受载荷的变化曲线

Fig.8 Load variation curve of vibrator baseplate

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 振动器平板载荷施加形式

Fig.9 Application form of vibrator baseplate load

2.3　振动器平板的工作载荷应力分析

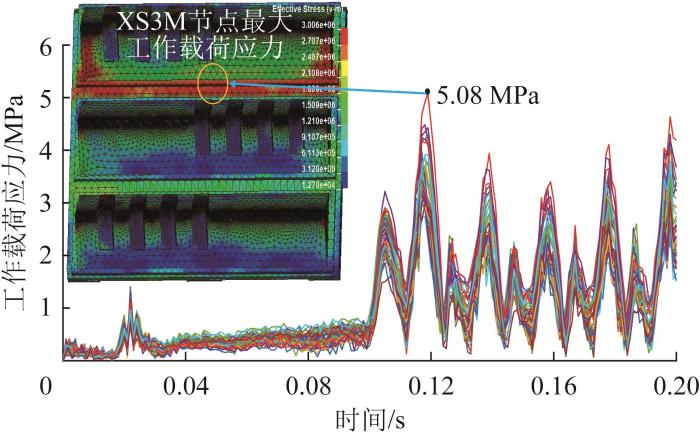
基于振动器平板-大地耦合模型开展有限元分析，得到振动器平板打底焊缝处各危险节点的工作载荷应力随时间的变化曲线，如图10所示。由图10可知，各节点处的工作载荷应力表现出相似的周期性波动，但各节点处的工作载荷应力峰值存在差异。其中，打底焊缝中段XS3M节点（距离起焊点352 mm）处的工作载荷应力在t=0.107 s时达到峰值，为5.08 MPa，为该焊缝上最危险的节点。XS3M节点处沿x、y、z向的工作载荷应力随时间的变化规律如图11所示。分解得到的各向工作载荷应力可为后续应力耦合与疲劳寿命预测提供计算基础。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 振动器平板打底焊缝处各危险节点的工作载荷应力

Fig.10 Working load stress of each dangerous node at the bottom weld of vibrator baseplate

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 振动器平板打底焊缝处XS3M节点的工作载荷应力

Fig.11 Working load stress of XS3M node at the bottom weld of vibrator baseplate

3 振动器平板的焊接残余应力与工作载荷应力耦合

3.1　焊接残余应力的等效计算

在焊接过程中，振动器平板焊缝处母材在焊接温度场的作用下发生了组织相变，导致材料性质发生了变化；同时，因外载荷引起的工作载荷应力由液压激振力控制，而焊接残余应力由位移或应变控制，两者的耦合并非简单的叠加关系^[22]。因此，在耦合焊接残余应力与工作载荷应力前，根据等应变公式(2)以及45钢的材料参数（弹性模量为2×10¹¹ Pa，泊松比为0.28），对振动器平板打底焊缝处的焊接残余应力进行等效计算，等效焊接残余应力沿焊接方向的变化规律如图12所示。

\{\begin{matrix} σ_{x}^{0} = \frac{υ E (ε_{y} + ε_{z})}{2 (1 - υ)} \\ σ_{y}^{0} = \frac{υ E (ε_{x} + ε_{z})}{2 (1 - υ)} \\ σ_{z}^{0} = \frac{υ E (ε_{x} + ε_{y})}{2 (1 - υ)} \end{matrix}

(2)

式中： $σ_{x}^{0} 、 σ_{y}^{0} 、 σ_{z}^{0}$ 分别为x、y、z向上的等效焊接残余应力， $ε_{x}$ 、 $ε_{y}$ 、 $ε_{z}$ 分别为x、y、z向上的应变， $E$ 为弹性模量， $υ$ 为泊松比。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 振动器平板沿焊接方向的等效焊接残余应力

Fig.12 Equivalent welding residual stress of vibrator baseplate along welding direction

由图12可知，振动器平板的等效焊接残余应力有所减小，但整体变化趋势与等效前相似，同样是距离起焊点352.4 mm的XS3M节点处的x、y、z向等效应力最大，分别为103.1，62.28，33.29 MPa。将该节点处的等效焊接残余应力与工作载荷应力进行耦合。

3.2　应力耦合准则的建立与运用

在对耦合焊接残余应力的振动器平板进行疲劳寿命预测时，平板的应力由两部分组成^[23-26]：

σ = σ^{0} + σ^{f}

(3)

式中： $σ$ 为耦合应力， $σ = {[σ_{x} σ_{y} σ_{z}]}^{T}$ ； $σ^{0}$ 为等效焊接残余应力， $σ^{0} = {[σ_{x}^{0} σ_{y}^{0} σ_{z}^{0}]}^{T}$ ， $σ^{0} = 0$ 表示区域内不存在焊接残余应力； $σ^{f}$ 为工作载荷应力， $σ^{f} = {[σ_{x}^{f} σ_{y}^{f} σ_{z}^{f}]}^{T}$ 。

基于式(3)所示耦合原则，将振动器平板的等效焊接残余应力和工作载荷应力进行耦合，并利用式(4)对3个方向上的耦合应力进行复合计算^[27]，得到最终的耦合应力 $σ_{c}$ ：

σ_{c} = \pm \sqrt[]{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2}}

(4)

以振动器平板打底焊缝处XS3M节点的应力耦合为例，联合式(3)和式(4)计算得到XS3M节点处的耦合应力 $σ_{c}$ 在5个激振周期内的变化曲线，结果如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 振动器平板XS3M节点处耦合应力的变化曲线

Fig.13 Coupling stress variation curve at XS3M node of vibrator baseplate

由图13可知，振动器平板的耦合应力呈现与工作载荷应力类似的正弦波动变化规律，各激振周期内耦合应力的峰值与幅值均为焊接残余应力起主导作用，耦合应力峰值为126.53 MPa，最大幅值为123.79 MPa。因此，在对振动器平板进行疲劳寿命预测时，可将该应力谱作为疲劳寿命预测的响应输入。

4 基于修正 S — N 曲线的振动器平板疲劳寿命预测

4.1　 S — N 曲线的建立与修正

本文采用S—N曲线对横波可控震源振动器平板进行疲劳寿命预测，S—N曲线的准确度直接影响平板疲劳寿命预测的精度和效率。S—N曲线表示最大应力S与循环次数N的关系曲线，即：

l g N = l g C - m l g S

(5)

式中：C、m为振动器平板材料常数。

针对横波可控震源振动器，全尺寸平板的S—N曲线通常难以采用试验方法直接获取，因此需对平板母材45钢的S—N曲线进行修正：

l g N = l g C - m l g σ_{- 1 D} - m l g K_{σ D}

(6)

其中：

K_{σ D} = \frac{K_{f}}{C_{D}} + \frac{1}{β} - 1

式中： $σ_{- 1 D}$ 为对称循环应力幅； $K_{σ D}$ 为修正系数，由平板的尺寸、粗糙度、应力集中系数确定； $C_{D}$ 为尺寸系数； $β$ 为表面状态系数； $K_{f}$ 为有效应力集中系数。

振动器平板S—N曲线的修正参数如表3所示。

表3 振动器平板 S — N 曲线的修正参数

Table 3 Modified parameters of S-N curve of vibrator baseplate

参数	数值	来源
尺寸系数C_D	0.782	《抗疲劳设计手册》^[28]
表面状态系数β	0.850	表面加工工艺采用粗车加工
有效应力集中系数 $K_{f}$	1.740	文献[29]中对应的材料应力集中系数确定方法

新窗口打开| 下载CSV

结合文献[30-31]，可得到常温条件下45钢的材料常数 $m = 7.314 4$ ，根据线性关系，反推得到C的值。综上，修正后的S—N曲线为：

l g N = 23.593 3 - m l g S - m l g 2.40

(7)

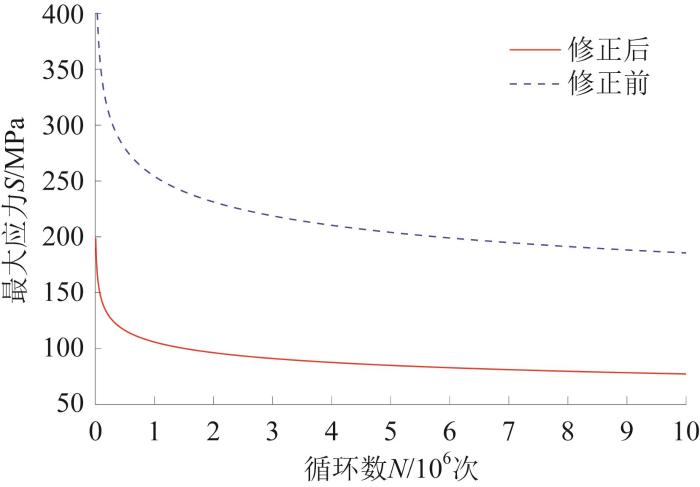
利用修正后的S—N曲线预测耦合焊接残余应力的振动器平板疲劳寿命，其中S为等效焊接残余应力与工作载荷应力的耦合应力，即σ_c。修正前后振动器平板的S—N曲线如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 修正前后振动器平板的 S — N 曲线

Fig.14 S-N curves of vibrator baseplate before and after correction

4.2　振动器平板疲劳寿命预测分析

1）Miner准则。

Miner准则指出，结构在循环载荷作用下的疲劳损伤量可线性累加，各个应力水平之间互不相关，且加载顺序对总损伤量没有影响。基于Miner准则，振动器平板在多级应力循环作用下的损伤量D可表示为：

D = \sum_{i = 1}^{M} \frac{n_{i}}{N_{i}}

(8)

式中： $n_{i}$ 为第i级应力作用下平板的实际循环次数， $N_{i}$ 为平板在第i级应力下的失效循环次数，M为应力水平级数。

为简化计算，假设各级应力仅施加一次，此时各级应力水平下的实际循环次数 $n_{i}$ =1。根据式(8)，可得振动器平板在多级应力循环作用下的循环次数 $N_{F}$ ：

N_{F} = \frac{1}{D}

(9)

2）疲劳寿命预测。

S—N曲线的修正是基于等幅载荷/应力开展的，故在利用Miner准则预测振动器平板在多级应力循环下的疲劳寿命前，需要对获得的耦合应力σ_c进行修正。选用Goodman公式对耦合应力σ_c进行修正，计算式如下：

\frac{S_{a}}{σ_{c}} + \frac{S_{m}}{S_{b}} = 1

(10)

式中： $S_{a}$ 为应力幅； $S_{m}$ 为平均应力； $S_{b}$ 为抗拉极限，本文取 $S_{b} =$ 600 MPa。

将修正后的耦合应力σ_c代入修正后的S—N曲线，计算得到振动器平板在各级应力水平下的循环次数，如表4所示。基于Miner准则，计算平板在多级应力水平下的疲劳损伤量。

表4 各级应力水平下振动器平板的疲劳损伤量

Table 4 Fatigue damage of vibrator baseplate under each stress level

应力水平/MPa	循环数/次	损伤量
122.74	3.41×10⁵	2.93×10^-6
112.53	6.43×10⁵	1.55×10^-6
86.83	4.29×10⁶	2.33×10^-7
82.27	6.36×10⁶	1.57×10^-7
112.15	6.60×10⁵	1.52×10^-6

新窗口打开| 下载CSV

根据表4，可得耦合焊接残余应力后振动器平板的总损伤量D $= 6.39 \times 10^{- 6}$ 。鉴于在进行疲劳寿命分析时加载了5个周期的循环载荷，故单个周期下振动器平板的平均累积损伤量 $\bar{D} = D / 5 = 1.28 \times 10^{- 6}$ 。由此可得，当发生疲劳破坏时，振动器平板的应力循环次数 $N_{F} = 1 / \bar{D} = 7.82 \times 10^{5}$ 次。在实际工况下，利用横波可控震源进行油气勘探时，每天约激振400次，每年平均工作7.5个月，则考虑焊接残余应力与工作载荷应力耦合作用下振动器平板的工作寿命为8.69 a，与现场实际工况下振动器平板的8 a工作寿命偏差较小，相对误差为8.6%。

仅以最危险节点为代表来计算振动器平板的疲劳寿命缺乏可靠性，为提升预测精度与稳定性，利用所提出的方法对振动器平板打底焊缝处其他4个危险节点（XS1M、XS2M、XS4M、XS5M）进行疲劳寿命预测（结果见表5），并计算了5个节点的平均疲劳寿命。

表5 振动器平板各危险节点的疲劳寿命

Table 5 Fatigue life of each dangerous node of vibrator baseplate

节点	应力循环数 N_F/次	平均累积损伤量D	疲劳寿命/a
XS1M	7.53×10⁵	1.33×10^-6	8.37
XS2M	7.57×10⁵	1.32×10^-6	8.41
XS3M	7.82×10⁵	1.28×10^-6	8.69
XS4M	7.33×10⁵	1.37×10^-6	8.14
XS5M	7.40×10⁵	1.35×10^-6	8.22

新窗口打开| 下载CSV

根据表5，可得振动器平板疲劳寿命的均值为8.366 a，与现场统计的平均工作寿命8 a的相对误差为4.58%，低于10%。此外，振动器平板疲劳寿命预测的标准差为0.189 7 a，小于0.4 a^[32]。由此说明，本文所提出的耦合焊接残余应力的疲劳寿命预测方法具有较高的精度和稳定性。

5 结论

本文开展了考虑焊接残余应力与工作载荷应力耦合作用的横波可控震源振动器平板疲劳寿命预测研究，主要工作及结论如下：

1）基于有限元仿真法对振动器平板的焊接残余应力分布规律进行了分析，得到了焊缝处的最大残余应力为747.92 MPa，由此确定了振动器平板的危险区域。

2）基于等应变原理建立了振动器平板焊接残余应力与工作载荷应力的耦合应力谱，耦合应力的变化规律与工作载荷应力相似，均呈5个周期的正弦波动；耦合应力各周期的峰值受焊接残余应力主导，耦合应力的峰值为126.53 MPa，最大幅值为123.79 MPa。

3）对振动器平板母材的S—N曲线进行了修正，并基于Miner准则分析得到耦合应力作用下振动器平板的疲劳寿命为8.69 a，与实际8 a工作寿命的相对误差为8.6%，低于10%。同时，对振动器平板其他危险节点进行了疲劳寿命分析。结果表明，预测结果的标准差为0.189 7 a，说明本文所提出的疲劳寿命预测方法的稳定性较高。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

RADAJ

. Design and analysis of fatigue resistant welded structures［M］. Cambridge： Abington Publishing， 1990.