基于Kriging模型的大型立式磨机选粉机结构优化设计研究

doi:10.3785/j.issn.1006-754X.2024.04.170

基于Kriging模型的大型立式磨机选粉机结构优化设计研究

李浩^,^,, 王颖, 马耀帅, 孙春亚, 黄荣杰, 王昊琪, 李琳利

郑州轻工业大学机电工程学院，河南郑州 450002

Research on structural optimization design for powder separator of large vertical mill based on Kriging model

LI Hao^,^,, WANG Ying, MA Yaoshuai, SUN Chunya, HUANG rongjie, WANG Haoqi, LI Linli

College of Mechanical and Electrical Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China

收稿日期: 2024-09-23 修回日期: 2024-10-24

基金资助:

国家自然科学基金面上项目.  52175256
河南省科技研发计划联合基金资助项目.  225200810029
河南省科技攻关重点项目.  242102221013

First author contact: LI H, WANG Y, MA Y S, et al. Research on structural optimization design for powder separator of large vertical mill based on Kriging model[J]. Chinese Journal of Engineering Design, 2024, 31(6): 801-809.

Received: 2024-09-23 Revised: 2024-10-24

作者简介 About authors

李浩（1981—），男，教授，博士生导师，博士，从事工业数字孪生、产品设计方法学、智能制造服务等研究，E-mail:lihao@zzuli.edu.cn,http://orcid.org/0000-0001-6841-5075 , E-mail：lihao@zzuli.edu.cn

摘要

大型立式磨机是一个结构复杂、运行参数多、监控与操作点多、多物理场的粉磨系统，其性能与结构有直接关系。基于NX二次开发的参数化设计方法，建立了LGM型大型立式磨机的计算流体动力学-离散相模型（computational fluid dynamics-discrete phase model, CFD-DPM），实现对其选粉机格栅结构的分析与设计，探讨转子叶片结构对立磨机工作性能的影响；提出了基于Kriging模型的选粉机结构优化设计方法，并在Isight平台进行优化验证。结果显示，在参数设计范围内适当减小选粉机转子叶片的腰部长度和头部长度，增大其厚度和倾角，可以有效提高转子扭矩和转子叶片间气流速度，优化后扭矩增大了2.91%，流速提高了9.76%，证明了所提出方法的有效性。研究结果为立式磨机的结构设计与优化提供了新的理论依据和实践指导，具有较高的科研参考价值和工业应用前景。

关键词： 立式磨机 ; 选粉机 ; Kriging代理模型 ; 优化设计 ; 转子叶片

Abstract

Large vertical mill is a grinding system with complex structure, multiple operating parameters, multiple monitoring and operating points, and multiple physical fields, and its performance is directly related to the structure. Based on the parametric design method of NX secondary development, CFD-DPM (computational fluid dynamics-discrete phase model) of LGM large vertical mill was established. The grating structure of the powder separator was analyzed and designed, and the influence of the rotor blade structure on the performance of the mill was discussed. A structure optimization design method for powder separator based on Kriging model was proposed and verified on Isight platform. The results showed that the rotor torque and the velocity of the airflow between rotor blades could be effectively improved by appropriately reducing the waist length and head length of the rotor blades and increasing their thickness and inclination angle within the parameter design range. The torque was increased by 2.91% and the flow rate by 9.76% after optimization, which proved the effectiveness of the proposed method. The research results provide a new theoretical basis and practical guidance for the structural design and optimization of vertical mill, and have high scientific research reference value and industrial application prospect.

Keywords： vertical grinder ; powder separator ; Kriging surrogate model ; optimal design ; rotor blade

PDF (3687KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李浩, 王颖, 马耀帅, 孙春亚, 黄荣杰, 王昊琪, 李琳利. 基于Kriging模型的大型立式磨机选粉机结构优化设计研究[J]. 工程设计学报, 2024, 31(6): 801-809 doi:10.3785/j.issn.1006-754X.2024.04.170

LI Hao, WANG Ying, MA Yaoshuai, SUN Chunya, HUANG rongjie, WANG Haoqi, LI Linli. Research on structural optimization design for powder separator of large vertical mill based on Kriging model[J]. Chinese Journal of Engineering Design, 2024, 31(6): 801-809 doi:10.3785/j.issn.1006-754X.2024.04.170

大型立式磨机（以下简称立磨机）是水泥生产及矿物等加工中不可或缺的干式粉碎设备，在建筑、化工、冶金等行业中发挥着重要作用。它由多个关键部件组成，包括磨盘、磨辊、选粉机、液压缸和减速机等，零部件众多，在运行过程中涉及机械、电子、液压和热力等多个系统，且须适应多变的工况条件，因此其设计是一种个性化定制设计^[1]。立磨机运行时，物料由喂料口下落到磨盘，电动机带动辊磨装置研磨物料；随着磨盘的转动，物料被甩到磨盘的边缘，由风机吹入选粉机内部的热风将物料从磨盘边缘带到立磨机上部；经过研磨而形成的粉末颗粒经过选粉机的筛选，细颗粒被吹出选粉机，粗颗粒则回落到磨盘上继续研磨。矿渣和煤渣等物料的磨粉过程至关重要，是实现高效、环保生产的关键环节^[2]。选粉机是成品质量的主要分级装置，通过导向叶片和转子叶片将固体颗粒分级，确保成品质量。因此，需优化导向叶片和转子叶片的设计，以满足不同细度的成品质量要求，并提高作业效率。选粉机的格栅结构会影响转子扭矩、流场，进而影响颗粒的产量、细度和生产能耗。本研究对立磨机选粉机的格栅结构进行分析，探讨其对转子扭矩和转子叶片间流场速度的影响，并基于此对选粉机结构进行多目标优化设计。

多目标优化是从一个问题的所有可行解中，依据特定指标选出最优解^[3]。求解多目标优化问题通常需要通过大量实验来确定设计变量与目标函数之间的关系。立磨机结构复杂，工况多变，在其优化设计过程中存在变量众多、目标函数计算困难和耗时等问题。为解决这些问题，可以构建黑箱模型^[4]，即创建一个简化的代理模型来模拟原模型，以减少计算量。这个代理模型应具有与原模型相似的输入输出关系，通过有限的样本点来预测原模型的响应，实现高效求解。采用代理模型进行多目标优化时，对代理模型的精度有很高的要求，而代理模型的精度与设计空间中采样点的个数和位置有关。典型的代理模型有多项式响应曲面、Kriging模型、径向基函数、支持向量回归模型和人工神经网络等^[5-6]。Zhang等^[7]选择了多个期望的局部极小值，根据代理模型的拟合质量将其分为局部和整体的极小值，并进一步进行全局空间探索，提出了一种基于Kriging模型的空间探索（Kriging-based space exploration, KSE）方法；王正平等^[8]对多项式响应面方法的特点进行了分析，将响应面近似方法应用于代理模型的构建，减少了计算量并保证了计算精度；王莉华等^[9]采用径向基函数法分析了时变的刚柔流耦合动力学问题，并考察了该方法用于求解耦合动力学问题的稳定性；丁春风等^[10]针对复杂工程系统中的稳健参数优化问题，提出了一种新的基于Kriging模型的序贯优化设计方法，该方法能以较少的加点次数获得较优的全局解，具有较强的全局寻优能力和稳健性；杨扬等^[11]基于序贯层次Kriging模型，对微型飞行器机身结构进行了设计优化；Wang等^[12]提出了一种自适应Kriging方法，为了有效地选择更多的样本点，进行Kriging模型更新，提出了一种新的学习函数用于选择代表性样本。

本文提出了一种基于Kriging模型的立磨机选粉机结构优化设计方法。首先，根据立磨机建模和数值模拟的要求，设计适用于立磨机多物理场耦合的仿真方案，确定优化设计变量和多个优化目标，建立目标函数计算模型；其次，采用随机试验设计（design of experiments，DOE）方法在参数设计范围内选取初始样本点，利用多物理场耦合仿真技术计算样本点的响应值，并利用样本点及其响应值构建代理模型；最后，将智能优化算法与代理模型相结合，不断进行更新与寻优直至得到最优解，从而实现立磨机选粉机结构的优化设计。

1 选粉机格栅结构的设计与分析

1.1　立磨机结构及模型

立磨机是一种基于智能制造的大型矿山装备。其内部结构复杂，多种结构协调工作，共同完成破碎、干燥、磨粉、分级输送等任务。立磨机的复杂性不仅体现在物理结构上，还体现在运行过程中。立磨机运行时磨盘内存在高速气流和固体粉末颗粒，属于气固两相耦合系统^[13]。选粉机高速转动进行筛粉，除气相流场中存在湍流现象之外，内部气流及颗粒不规则的运动状态也会使仿真计算的精度受到影响。基于立磨机的复杂构成，本文以LGM型立磨机为研究对象，采用UG NX和Visual Studio 2017软件对立磨机的流体域进行参数化建模^[14]；采用ICEM CFD前处理软件对立磨机流体域模型进行网格划分和网格质量检查^[15]。在对其流体域进行数值分析时，要对多相流的介质进行分析和处理。由于立磨机中颗粒的体积较小，采用保留颗粒流动特性的欧拉-拉格朗日（Eulerian-Lagrangian）模型建立计算流体动力学-离散相模型（computational fluid dynamics-discrete phase model, CFD-DPM）并模拟^[16-17]，以提升仿真计算的效率和精度。

网格划分是进行数值计算之前的必要步骤，网格质量对计算精度和计算时间有直接影响。在立磨机的选粉机、导流环、磨盘、磨辊等应力集中部位采用较密集的网格，在计算数据变化较小的部位如进风口、出料口、返料斗和壳体等采用较稀疏的网格。本研究以行列式2×2×2质量检查标准检查网格质量，发现其最小为0.58，满足了求解器要求。同时，对模型进行网格无关性验证。初步设定的网格数量为1 000万个，接下来依次生成数量为500万、250万、125万个的网格模型，利用这些模型在相同的条件下分别求解，得到的误差小于10%；随着网格数量增多，参数的解趋于定值，且解之间的误差逐渐减小。以上结果表明网格无关性验证已完成。最终，对根据实际产品构建的三维模型进行网格划分，网格数量约为460万个^[18]。LGM型立磨机的主要结构尺寸参数如表1所示。

表1 LGM型立磨机主要结构尺寸参数

Table 1 Main structural dimension parameters of LGM type vertical mill

结构尺寸参数	数值
转笼高度/m	2.45
转笼半径/m	2.05
转子切向夹角/(°)	90
转子数量/个	200
进风口面积/m²	4.68
风环水平入射夹角/(°)	65

新窗口打开| 下载CSV

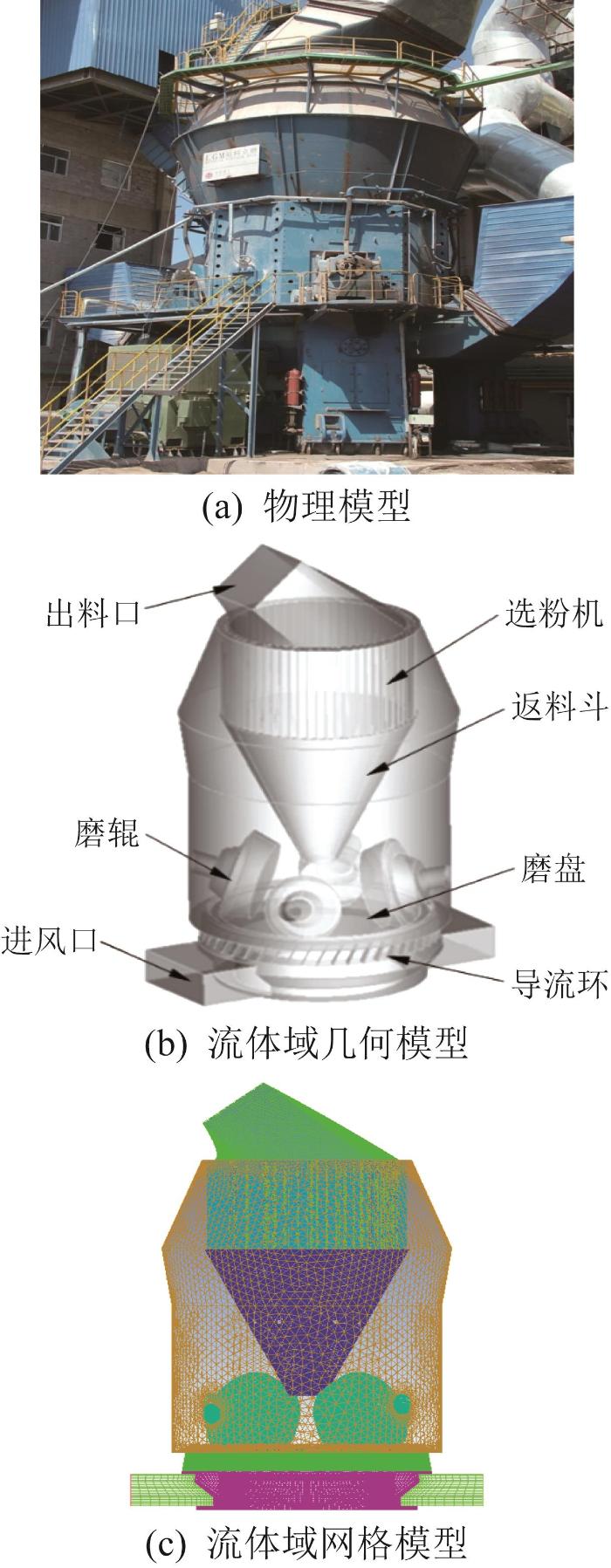
在建模时简化了立磨机部分结构，保留了其主体部分，主要包括选粉机、导流环、磨盘、磨辊、进风口、出料口、返料斗和壳体等。立磨机物理模型及在UG NX中创建的流体域几何模型、网格模型如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 立磨机物理模型及流体域几何模型和网格模型

Fig.1 Physical model, fluid domain geometry model and mesh model of vertical mill

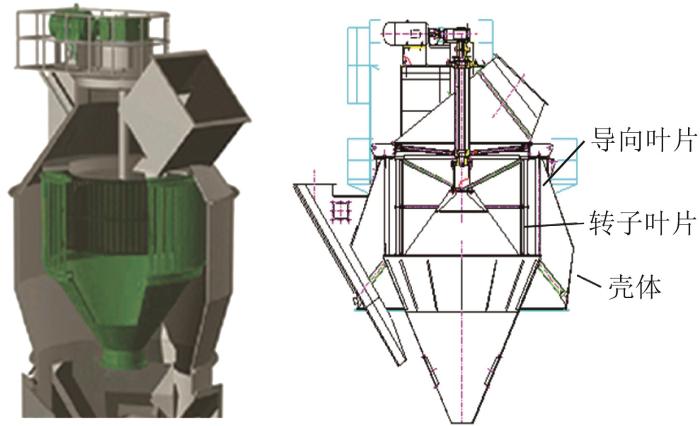
选粉机是立磨机的重要组成部分，位于立磨机上部区域，主要作用是对辊磨机构研磨后的粉末颗粒进行快速筛选，使粗颗粒回落，细颗粒筛出，防止细颗粒在立磨机内部堆积和粘附，影响立磨机的工作效率。选粉机的部件主要包括导向叶片、转子叶片和壳体等，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 选粉机结构示意图

Fig.2 Schematic diagram of structure of powder separator

物料颗粒进入选粉机后，即经过由转子叶片产生的旋转力场，其中涉及曳力和离心力的复杂作用。颗粒粒径不同，则受到这2种力影响的程度不同。对于粒径较大的粗颗粒，离心力占主导地位，导致其在转子叶片的外侧被甩出，随后与选粉机的导向叶片或壳体发生碰撞，被重新引导回落至磨盘上，再次接受磨辊的碾压和研磨，直至达到所要求的细度；对于细颗粒，由于其体积和质量均较小，离心力不足以克服气流的曳力，因此更容易被气流携带，穿过转子叶片的间隙，最终作为成品而被收集。

1.2　选粉机格栅结构设计

选粉机的转笼为格栅结构，如图3所示。格栅结构对转子扭矩和转子叶片间气流速度具有显著影响^[18]。转子叶片结构如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

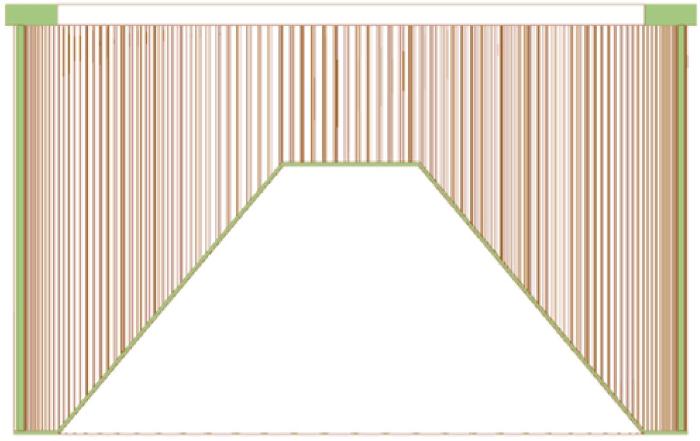
图3 选粉机转笼格栅结构示意

Fig.3 Schematic of gridiron of rotating cage of powder separator

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 转子叶片结构示意

Fig.4 Schematic of structure of rotor blade

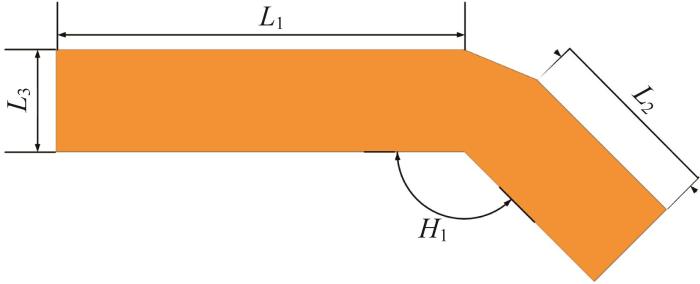
将转子叶片的腰部长度L₁、头部长度L₂、厚度L₃和倾角H₁作为设计变量，改变其值，分析转子叶片结构改变后对立磨机工作性能的影响。转子叶片结构参数的设计范围如表2所示。

表2 转子叶片结构参数设计范围

Table 2 Design range of structure parameters of rotor blade

设计变量	上限	下限
L₁/mm	25	45
L₂/mm	8	20
L₃/mm	6	12
H₁/(°)	110	180

新窗口打开| 下载CSV

1.3　选粉机格栅结构对立磨机工作性能的影响

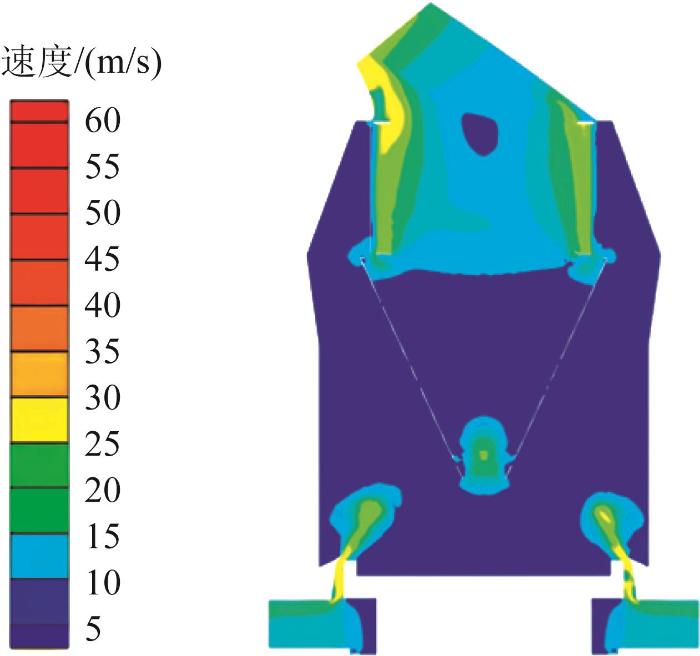
通过数值模拟，得到选粉机内部气流速度分布云图，如图5所示。由图可知，选粉机内部的气流速度不相同。特别在转子叶片的边缘区域，由于叶片的旋转作用，气流速度较高，形成了明显的高速流场区域，直接影响了颗粒的受力状况和运动轨迹，对于颗粒的分级起到了关键作用；在转子叶片的顶部和尾部区域，气流速度逐渐降低，这与叶片的形状和安装角度有关。通过调节叶片的结构参数值，可以改变气流速度的分布，从而优化分级效果。例如：增大叶片的倾角可以提高叶片顶部的气流速度，有助于细颗粒的收集；减小倾角则可能使高速气流集中在叶片中部，有利于粗颗粒的分离。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 选粉机内部气流速度分布云图

Fig.5 Velocity distribution cloud diagram of airflow inside powder separator

调节设计变量值，得到不同结构下转子叶片间气流速度云图。观察转子叶片顶端到尾端间的流速变化，以格栅中心为圆心，读取直径为3 950 mm处格栅的气流速度，则转子叶片间气流速度分布云图及其局部放大图如图6所示。不同结构下的扭矩和流速如表3所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

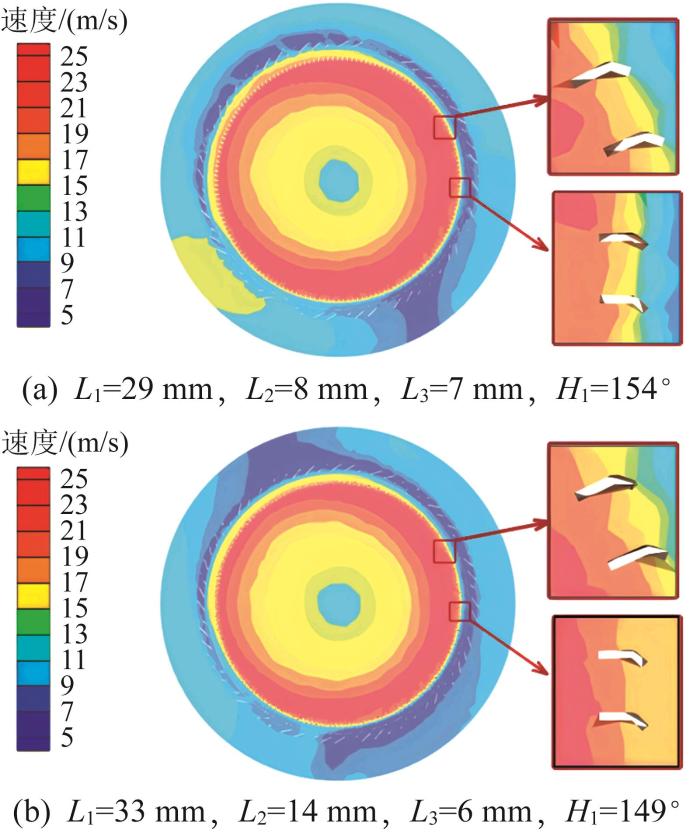
图6 不同结构下转子叶片间气流速度分布云图及其局部放大图

Fig.6 Velocity distribution cloud diagram and local magnification image of airflow between rotor blades under different structures

表3 不同结构下转子扭矩和转子叶片间气流速度

Table 3 Rotor torque and velocity of airflow between rotor blades under different structures

序号	结构参数	扭矩/(N·m)	流速/(m/s)
1	L₁=30 mm，L₂=17 mm， L₃=10 mm，H₁=124°	858.750	19.086
2	L₁=42 mm，L₂=18 mm， L₃=8 mm，H₁=134°	854.214	19.015
3	L₁=38 mm，L₂=16 mm， L₃=11 mm，H₁=168°	881.235	21.744
4	L₁=33 mm，L₂=14 mm， L₃=6 mm，H₁=149°	781.147	19.985
5	L₁=23 mm，L₂=15 mm， L₃=9 mm，H₁=169°	881.236	21.483
6	L₁=35 mm，L₂=12 mm， L₃=6 mm，H₁=129°	813.600	18.729
7	L₁=29 mm，L₂=8 mm， L₃=7 mm，H₁=154°	780.286	20.744
8	L₁=40 mm，L₂=14 mm， L₃=9 mm，H₁=140°	803.639	20.293
9	L₁=37 mm，L₂=19 mm， L₃=11 mm，H₁=160°	839.741	21.935

新窗口打开| 下载CSV

在一般情况下，增大L₁和L₂会导致叶片区域的气流速度提高，因为较长的叶片具有更大的阻力面积，从而加速了气流。同时，阻力面积的增大也在一定程度上导致转子扭矩增大。而由表3可知，在结构1和结构2中，L₃和H₁的变动幅度较小，L₁从30 mm大幅增加到42 mm，L₂从17 mm增加到18 mm，但流速和扭矩都略有减小。这表明各参数之间可能产生了协同或拮抗作用，导致在多参数作用下单一参数变化时得到了与预期不相符的结果。同时，参数对结果的影响可能是非线性的，且存在阈值，超过阈值后性能变化可能更加显著。

在一定范围内，流速的提高可以增大物料的通过量，从而增强选粉机的处理能力，使其在单位时间内处理更多的物料；扭矩的增大不仅能提高颗粒分级精度，还能缓减扭矩不足导致的设备疲劳和损坏，增强设备的稳定性和耐用性。然而，流速与扭矩随参数的变化趋势并不总是保持一致。例如，在结构6和结构7下，各参数的共同作用致使流速提高，而扭矩却减小了。因此在进行参数优化过程中，需要将流速和扭矩作为2个优化目标进行分析。

综上可知，各参数的共同作用对系统性能产生了复杂的影响。为了对转子叶片多个结构参数进行协同优化，而不是孤立地调整单个参数，需要针对该系统设计一种更准确高效的多参数优化方法，且对转子叶片结构参数的优化设计是针对多个目标的优化问题。

2 基于Kriging模型的选粉机结构优化设计方法

2.1　优化设计方法介绍

为了提高选粉机的分级效率，提升立磨机整体的运行性能，需对转子叶片的结构参数L₁、L₂、L₃、H₁进行优化。多目标优化的目标是最大化转子扭矩T和最大化气流速度v。为了实现这一目标，需要针对每个不同结构参数的组合进行独立的仿真计算，计算得到的扭矩和流速即为其响应值。基于这些数据，可构建优化模型，使模型能够预测不同结构参数下转子的扭矩和流速，在不进行昂贵和耗时的全尺度数值模拟的情况下，快速评估不同设计方案的优劣。

本文提出了一种基于Kriging模型和非支配排序遗传算法Ⅱ（non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ）的优化方法。利用遗传算法的全局搜索能力，结合Kriging模型来减少对原始模型的评估次数；同时，通过遗传算法的迭代过程，逐步改进代理模型，从而找到最优解。

2.2　Kriging模型

Kriging模型是一种无偏最优的插值近似模型，被广泛应用于低维贵重黑箱问题的处理，具有较好的非线性预测能力^[19]。该模型利用协方差函数对随机过程进行空间建模和预测，是一种方差最小的无偏估计模型。其利用随机过程来描述目标函数与设计变量之间的相互作用，并可以利用已知样本点目标值的线性组合来估计未知样本点的目标值。可以表示为：

\hat{y} (x) = f (x) + Z (x)

(1)

式中： $\hat{y} (x)$ 为未知样本点的目标值， $x 为$ $设计变量; f (x)$ 为 $x$ 的已知函数，表示全局近似模拟值； $Z (x)$ 为对数据观测及数据相关性量化后建立的均值为0、方差为 $σ^{2}$ 的随机过程模型。

$Z (x)$ 的协方差为：

c o v [Z (x_{i}), Z (x_{j})] = σ^{2} \prod_{k = 1}^{n} R_{k} (θ_{k}, d_{k})

(2)

式中： $θ_{k}$ 为模型的参数，k为变量数，k=1, 2, …, n； $d_{k}$ 为样本点间的 $k$ 维距离； $R_{k} (θ_{k}, d_{k})$ 为相关函数。

常用的相关函数主要有高斯函数、线性函数、指数函数和样条函数等。

将选粉机结构参数优化问题表示为如下的数学模型：

\{\begin{matrix} \begin{array}{l} m a x T & v \\ s . t . 25 \leq L_{1} \leq 45 m m \\ 8 \leq L_{2} \leq 20 m m \end{array} \\ \begin{array}{l} 6 \leq L_{3} \leq 12 m m \\ 10 ° \leq H_{1} \leq 180 ° \end{array} \end{matrix}

(3)

2.3　NSGA-Ⅱ

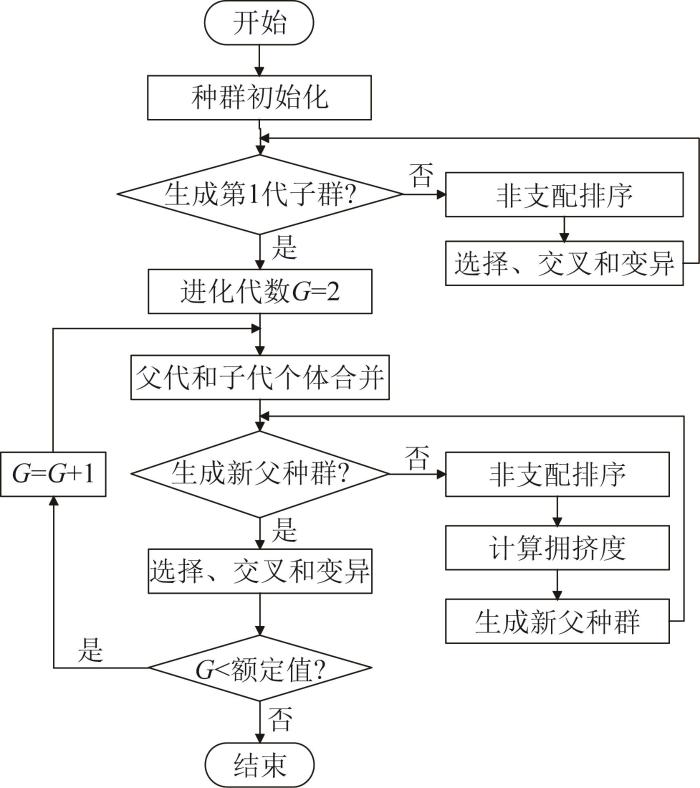
NSGA-Ⅱ是一种先进的遗传算法^[20]，在处理多目标优化问题中表现出卓越的效率和准确性。该算法的核心在于其独特的非支配排序机制，能够根据个体间的支配关系将种群划分为不同的层次，确保在优化过程中能同时考虑所有目标。此外，NSGA-Ⅱ中引入了拥挤距离的概念，通过计算个体间的相对距离，有效避免了优化过程中解的聚集现象，增强了算法的搜索能力。

NSGA-Ⅱ的流程框图如图7所示^[20]。其流程为：对种群进行初始化，对所有个体进行非支配排序，并设定相应的适应度值；采用选择、交叉和变异算子生成新一代种群，将其规模设定为N；将新生成的种群与原有种群合并，再次进行非支配排序，从而得到多个非支配集F(1), F(2), …, F(m)，并对每个非支配集的个体计算拥挤度，选择合适的个体组成新一代的父种群；如果F(1)的种群大小小于N，则向新父种群中添加下一支配集F(2)，直到种群大小大于N，并对最后添加的非支配集个体进行拥挤度排序，选取合适的个体，使新父种群的大小达到N，然后通过遗传算子产生新的子代种群。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 NSGA-II流程框图

Fig.7 Flow block diagram of NSGA-II

3 选粉机结构多目标优化分析

3.1　基于Isight多目标优化模型的建立

Isight软件是当前应用较为广泛的计算机辅助优化工具，提供了优化方法、试验设计、近似拟合、稳健性设计和质量设计等关键流程组件，集成了梯度优化算法、直接搜索方法、全局优化算法和多目标优化方法等多种优化策略，支持与多种主流的CAD、CFD、数值模拟、结构分析、成本分析和目标分析等软件的接口集成。用户可以根据自己的优化目标，组合流程组件、内置工具或调用外部程序来构建优化任务。Isight通过一个框架管理整个流程，协调不同软件工具来共同优化产品设计，同时提供数据分析、后处理功能以及根据优化结果自动生成报告的功能，支持多目标决策方案的比较，从而显著提升优化效率和优化结果的准确性^[22]。

在Isight平台上进行多目标优化的主要步骤包括^[23]：1）试验设计；2）创建代理模型；3）应用优化算法来获取目标函数的Pareto最优解集；4）验证优化算法的精确度和稳定性。选粉机结构参数优化设计的流程如图8所示。首先，通过数值分析确定选粉机的运行参数，包括设计目标、设计变量及其范围，并进行试验设计，对得到的样本点进行数值计算，获取各样本点的响应值；其次，基于样本点及其响应值构建代理模型，至模型精度符合要求后选择合适的智能算法对解集进行寻优；最后，根据优化结果再次进行数值模拟，以验证优化算法的可靠性。

图8

新窗口打开| 下载原图ZIP| 生成PPT

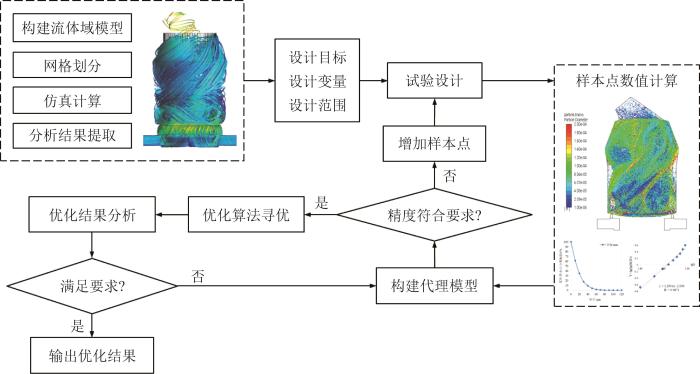
图8 选粉机结构参数优化设计流程框图

Fig.8 Flow block diagram of optimization design of structural parameters of powder separator

3.2　优化结果及参数灵敏度分析

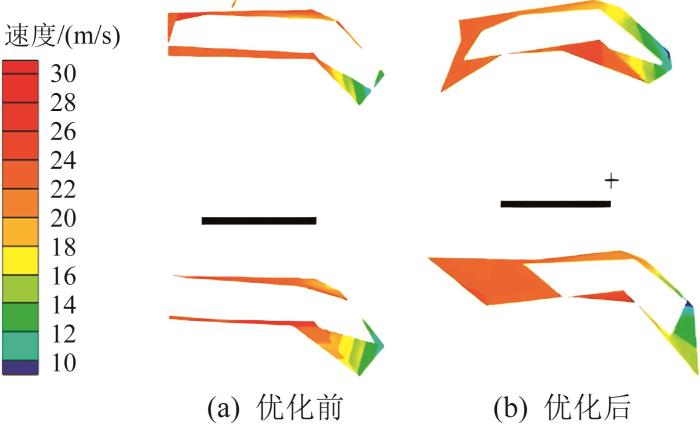
在Isight软件中选择NSGA-Ⅱ优化算法，设置算法的种群规模、进化代数、交叉概率分别为20，50，0.9，按照设定的参数，求解器共进行20×50=1 000次计算。根据优化结果进行仿真计算，得到气流速度分布云图，如图9所示。由图可知，优化后转子叶片阻力面积明显增大，气流速度显著提高。可见，该优化方案在一定程度上提升了选粉机的工作性能。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 优化前后转子叶片间气流速度分布云图

Fig.9 Velocity distribution cloud diagram of airflow between rotor blades before and after optimization

优化前后转子结构参数及转子扭矩和流速的对比如表4所示。由表可知，在设计范围内适当减小L₁、L₂，增大L₃、H₁，能有效提高扭矩和流速，优化后扭矩增大了2.91%，流速提高了9.76%。

表4 优化前后转子结构参数及转子扭矩和转子叶片间气流速度的对比

Table 4 Comparison of rotor structure parameters, rotor torque and velocity of airflow between rotor blades before and after optimization

比较项	优化前	优化后	变化量/%
L₁/mm	40	38	-5.00
L₂/mm	18	16	-11.11
L₃/mm	10	11	10.00
H₁/（°）	135	168	24.44
T/(N·m)	856.314	881.236	2.91
v/(m/s)	19.063	20.924	9.76

新窗口打开| 下载CSV

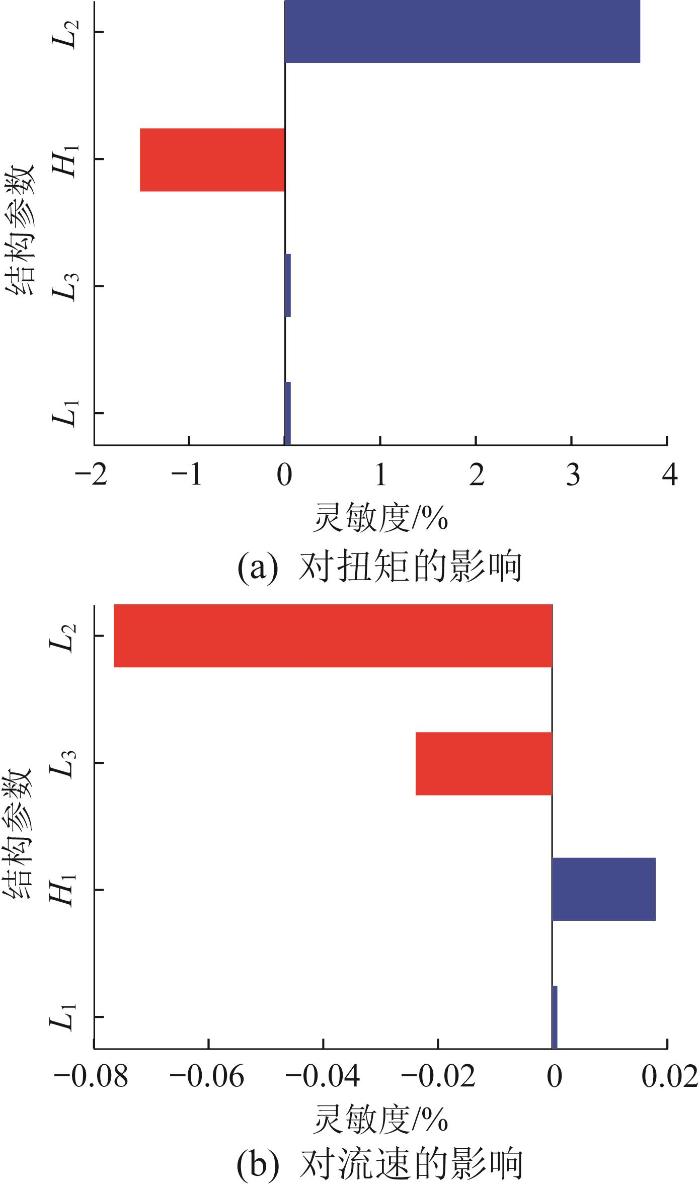
为了确定转子叶片结构参数对扭矩和流速的影响大小，确定影响较大的参数，对各参数进行灵敏度分析。根据已知参数、扭矩和流速的信息，利用Isight软件中的DOE模块对各参数进行灵敏度分析，结果如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 转子叶片结构参数灵敏度分析结果

Fig.10 Sensitivity analysis results of structure parameters of rotor blade

由图10可知：L₂、H₁对扭矩和流速的影响较大；L₂与扭矩呈正相关关系，与流速呈负相关关系；H₁与扭矩呈负相关关系，与流速呈正相关关系。即：随着H₁增大，扭矩减小，流速增大；随着L₂增大，扭矩增大，流速减小。

4 结论

本文以LGM型立磨机为数值模拟对象，采用UG NX、ICEM CFD软件进行三维建模和网格划分，采用Eulerian-Lagrangian方法构建多相流模型，对复杂颗粒-流体系统进行仿真分析。通过模拟试验，探讨了选粉机转子叶片腰部长度、头部长度、厚度和倾角等结构参数对转子扭矩和叶片间气流速度的影响。针对选粉机结构参数多目标优化问题，提出了基于Kriging模型的优化设计方法。采用NSGA-Ⅱ寻优及应用Kriging模型来求解最优解，并进行参数敏感性分析，识别对性能影响最大的参数。在Isight平台上进行优化验证，结果表明，采用该优化方法能够有效实现对选粉机转子叶片结构的优化，从而提高立磨机的工作性能。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

肖人彬

大规模个性化定制：大规模个性化的新发展

［J］. 计算机集成制造系统， 2023， 29（12）： 4215-4226.