本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.03.204

随着工业智能化的快速推进，对电机的性能要求不断提高。磁齿轮复合电机是一种新型的低速大转矩电机^[1]，其内、外转子之间通过磁力耦合作用实现无接触传动，并且可实现自减速。磁齿轮复合电机已广泛应用于机器人关节转动、船舶驱动等场合，具有广阔的应用前景。目前，针对磁齿轮复合电机拓扑结构的研究较多，而其控制大多采用简单的PI（proportional integral，比例积分）控制^[2]。传统的PI控制往往难以获得较好的控制效果，尤其是磁齿轮复合电机的双转子结构需要通过磁力耦合作用实现自减速和转矩传递，更加剧了控制系统的不稳定性。

蜻蜓算法（dragonfly algorithm，DA）是一种根据蜻蜓种群的行为特点开发的仿生算法^[3-4]，用于解决非线性、多极值、高维、复杂的全局优化问题。DA与神经网络^[5]、遗传算法^[6]、粒子群优化算法^[7]等相比，具有结构简单、参数少、搜索精度高、不易陷入局部最优等优点，较适合应用于磁齿轮复合电机的控制研究。

本文提出了一种磁齿轮复合电机控制方法，将改进的DA（improved DA，IDA）与PI控制相结合，实现PI参数的寻优整定。首先，根据电机的工作原理建立其矢量控制数学模型；其次，针对DA存在的收敛速度和收敛精度等方面的不足，通过引入Tent映射^[8]、改进权重系数和引入差分算法^[9]构建IDA；最后，基于Simulink平台搭建仿真控制系统，对PI、DA-PI和IDA-PI三种控制方法的控制效果进行仿真，并进行实验验证。

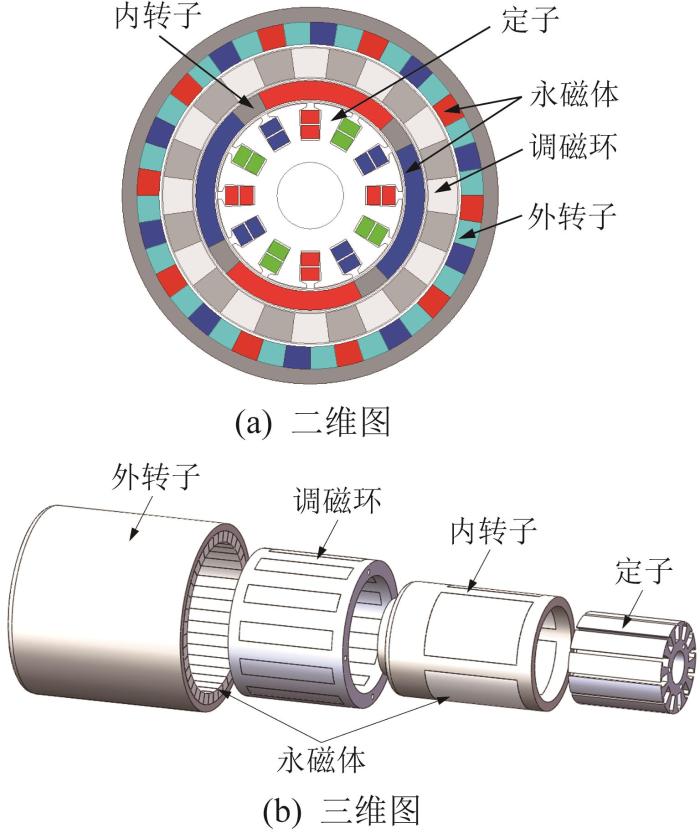
磁齿轮复合电机的结构如图1所示。其由内到外依次是电机定子、内转子、调磁环和外转子，其中：内转子内嵌径向充磁的永磁体；调磁环由非导磁材料PLA（poly lactic acid，聚乳酸）和导磁材料叠压硅钢片交替排列而成；外转子采用Halbach 型磁钢排列结构。

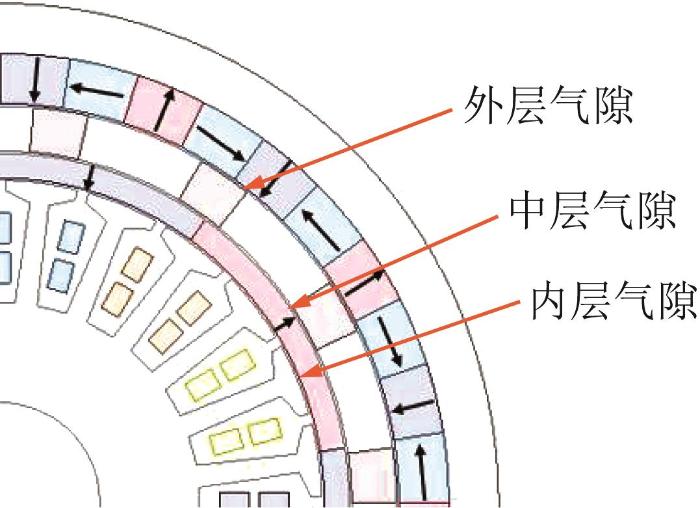
电机共有3层气隙磁场，如图2所示。Halbach 型磁钢排列结构比传统的径向充磁结构有更好的气隙磁场和转矩脉动，有利于提高电机的输出转矩^[10]。电机的内转子为高速转子，在电枢绕组的旋转磁场作用下旋转，内转子产生的旋转磁场经过调磁环调制后带动外转子转动，内、外转子的旋转方向相反；在电机运动过程中，调磁环处于固定状态。

由文献[11]可知，当内、外转子的极对数p₁、p₂和调磁环上的调磁块数N_s满足p₁+p₂=N_s时，磁齿轮的输出转矩最大，此时内、外转子与调磁环之间的传动关系可表示为:

式中：ω₁、ω₂、ω_s分别为内转子、外转子、调磁环的角速度。

由于调磁环是固定的，ω_s=0，因此通过式(1)可推导出电机的传动比为负的外、内转子极对数之比，表示为:

式中：G为传动比。

磁齿轮复合电机的主要参数如表1所示。

根据电机的工作原理，在建立电机矢量控制数学模型时作出以下假设：

1）电枢三相绕组完全对称，电枢电流对称；

2）忽略电机铁心饱和，不计涡流、磁滞损耗；

3）磁路是线性的，电枢绕组在电枢表面均匀分布，高速转子的磁场对称。

矢量控制是将ABC三相静止坐标系下的三相电压和电流通过坐标变换的方式转换为dq旋转坐标系下的电压和电流，实现解耦控制。磁齿轮复合电机是非线性、强耦合的电机，采用矢量控制比较适合。

磁齿轮复合电机内、外转子上的永磁体均会产生磁链，从而受到电磁转矩而进行传动。由式(2)可得：

式中：ω_m为合成磁链的电角速度，ω₁p₁、-ω₂p₂分别为内、外转子的电角速度。

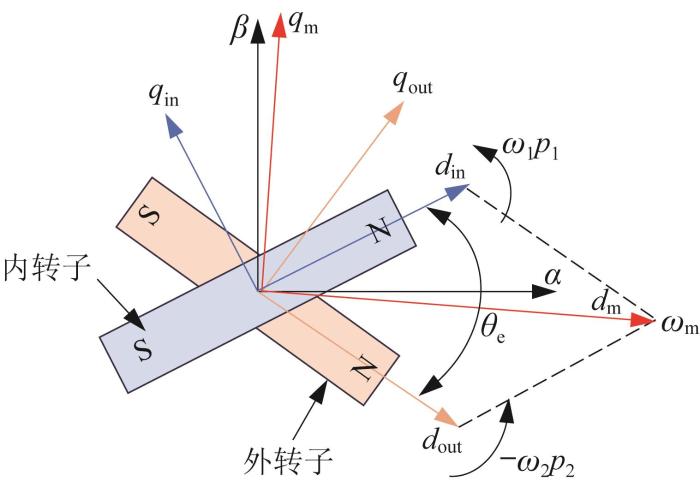
由此可知，内、外转子永磁体产生的磁链矢量的电角速度相同。根据文献[12]介绍的方法，建立dq坐标系，将内、外转子的磁链进行矢量合成，如图3所示。

dq坐标系下电机的电压方程为：

式中：R为电机线圈的电阻；u_d 、u_q，i_d 、i_q，Ψ_d 、Ψ_q 分别为定子的电压、电流、磁链在d、q轴的分量。

dq坐标系下电机的磁链方程为：

式中：Ψ₁、Ψ₂、Ψ_pm分别为内、外转子永磁体的磁链和合成磁场的磁链，L_d 、L_q 分别为定子电感在d、q轴的分量，θ_e为合成磁场的电角度。

电磁转矩方程为：

式中：T_E为电机的总电磁转矩；p_H为合成磁场的极对数，且p_H=p₁。

T_E为内、外转子合成磁场上的电磁转矩，因此内、外转子均受到电磁转矩的作用，故表示为：

式中：T_ei、T_eo分别为内、外转子受到的电磁转矩。

根据内、外转子磁链的合成关系，可推导出内、外转子所受电磁转矩的表达式为：

下面建立磁齿轮复合电机的运动方程。电机由双转子进行传动，因此将电机分为两部分：内转子和定子绕组为内电机部分，内转子、调磁环和外转子组成磁齿轮部分。内转子是内电机和磁齿轮的共用部分，受到电磁转矩和磁齿轮传动转矩T_pm的共同作用，则内电机的运动方程为：

磁齿轮的运动方程为：

式中：J₁、J₂分别为内、外转子的转动惯量，B₁、B₂分别为内、外转子的阻尼系数，T_L为负载。

由文献[13]可知，在磁齿轮传动过程中内转子受到的传动转矩是呈正弦函数变换的转矩，可表示为：

式中：T_m为传动转矩的峰值。

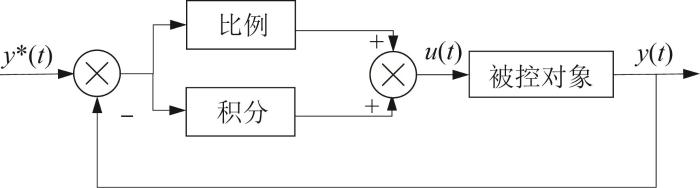
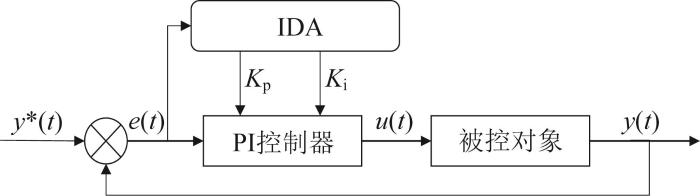
PI控制器广泛应用于电机控制领域，具有结构简单、易于实现的特点。PI控制框图如图4所示，可表示为：

式中：y*(t)、y(t)、u(t)分别为目标值、反馈值和PI控制器输出值，K_p、K_i分别为比例系数、积分系数，T_i为积分时间常数。

PI控制器的参数直接影响着控制系统的控制效果。常用试凑法确定PI参数，这不仅需要依靠经验，且效率和精度都较低，因此引入IDA来确定PI控制器的最佳参数。智能算法的引入不仅不需要参数调节的经验，而且可使PI参数的寻优效率、精度和可靠性都得到较大提升。针对DA在收敛速度、收敛精度等方面存在的不足，本文在算法寻优的前期、中期和后期分别进行改进。

蜻蜓的狩猎和迁徙行为分别对应DA的搜索阶段和开发阶段。蜻蜓群体中个体i的位置更新主要由分离向量 S_i 、对齐向量 A_i 、聚集向量 C_i 、觅食向量 F_i 和躲避天敌向量 E_i 这5个因素决定。DA寻优流程如下。

Step 1：确定蜻蜓的种群数目N、搜索空间维度D、最大迭代次数Q_max和待优化变量的范围[b_l, b_u]，进行随机初始化种群。

Step 2：通过目标函数计算适应度值，确定食物源和天敌的位置。

Step 3：更新蜻蜓的惯性权重w和5种行为权重s、a、c、f、e，计算5种行为因子S、A、C、F 和E。

Step 4：更新蜻蜓步长向量；查验更新后的蜻蜓个体是否在区间内，若发现其超出区间范围，进行纠错。

Step 5：判断是否满足输出条件。若满足，执行Step 6；否则，返回，执行Step 2。

Step 6：输出最优蜻蜓的位置向量。

通过引入Tent映射、改进权重系数和引入差分算法，对DA进行改进。

1）引入Tent映射。

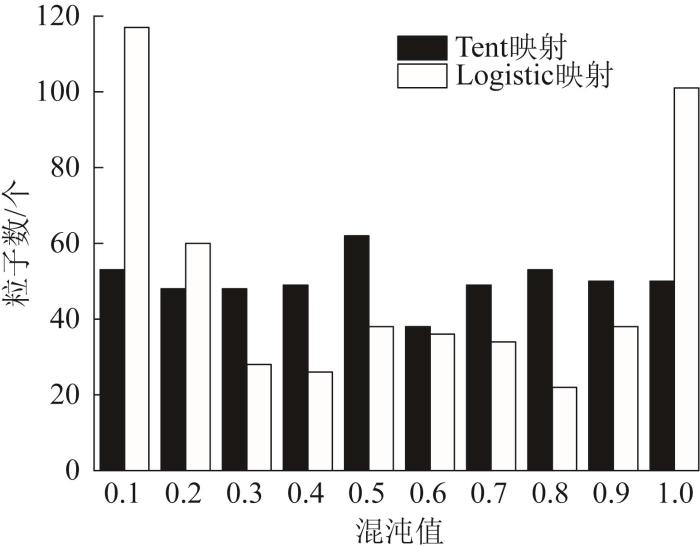
对于优化算法来说，初始种群直接影响着算法的收敛速度和收敛精度。随机初始化种群存在较大的随机性，无法实现对取值区间的较广覆盖，导致算法寻优前期收敛速度较慢，因此在种群初始化时引入混沌运动。混沌运动具有遍历性和随机性的特点，可以有效解决算法前期收敛速度慢的问题。在仿生算法中应用较多的是Logistics映射^[14]，但通过仿真发现，Tent映射拥有比Logistics映射更好的遍历性，且粒子的分布更加均匀。Logistic和Tent映射的混沌序列分布如图5所示。由图可知，在取值区间内Tent映射的粒子分布更为均匀，Logistics映射在[0, 0.1]和[0.9, 1]混沌值内分布的粒子更多，因此Logistics映射的均匀性较差，可能会影响算法寻优的速度和精度。因此，将Tent混沌映射引入DA。

Tent映射系数z表示为：

由于Tent映射存在一些容易造成混沌序列不稳定的周期点，引入一个随机变量来避开不稳定的周期点。改进后的表达式为：

式中：M为0到1的随机数。

2）改进惯性权重。

惯性权重是DA的一个重要参数，直接影响着算法步长的更新，其值代表了对前一次步长向量的继承比例。惯性权重越大，步长更新越大，从而可提高全局搜索的效率；反之，步长更新越小，则可以更好地进行局部开发。标准的惯性权重表示为：

式中：w_max、w_min分别为惯性权重的最大值和最小值，Q(i)为当前迭代次数。

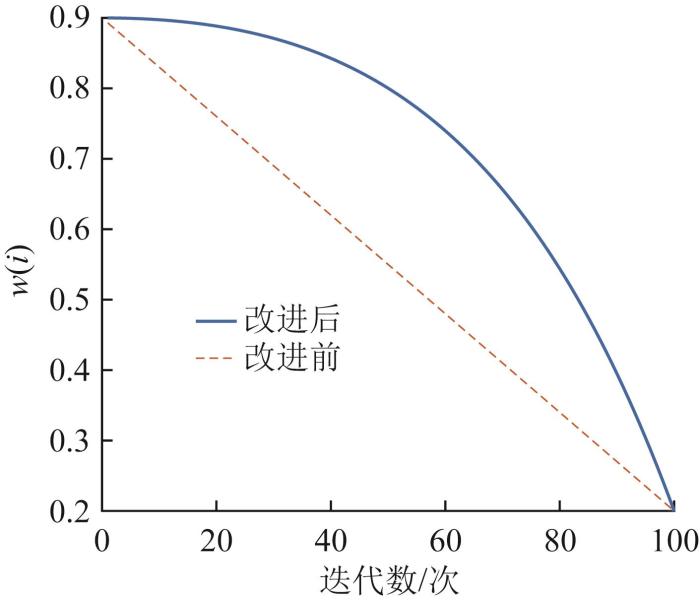
一般情况下，取w_max=0.9，w_min=0.2。改进前后惯性权重的调整过程如图6所示。在算法寻优过程中，全局搜索和局部开发的惯性权重改变率相同则表示全局搜索和局部开发的迭代次数相同，这样就有可能导致全局搜索的效果不佳，从而更容易陷入局部最优。在前期的全局搜索中，应有较大的惯性权重且改变率较小，以获取较长时间的大步长更新，进行快速全范围的全局搜索；在后期的局部开发中，加大惯性权重的改变率，以加快收敛速度。改进后惯性权重表示为：

3）引入差分进化算法。

差分进化算法是一种具有较强开发能力的优化算法，主要包括变异、交叉和选择三部分，具有收敛速度快和收敛精度高的特点。DA寻优后期存在活力不足的情况，因此引入差分优化算法。通过变异、交叉和选择产生新的蜻蜓个体，对比新旧蜻蜓个体的适应度值并保留最佳的下一代蜻蜓个体，从而增强算法的后期活力，提高算法的收敛速度和精度。

变异操作过程表示为：

式中：V_i^Q 为变异后的个体；X_r1^Q、X_r2^Q 和X_r3^Q 为第Q代种群中随机选取的个体；P∈[0 1]，为缩放因子。

交叉操作过表示为：

式中：C_i^Q 为交叉后的个体；H∈[0 1]，为交叉率。

选择操作过程表示为：

式中：G(C_i^Q+1 )和G(X_i^Q )分别为C_i^Q+1和X_i^Q 的适应度值。

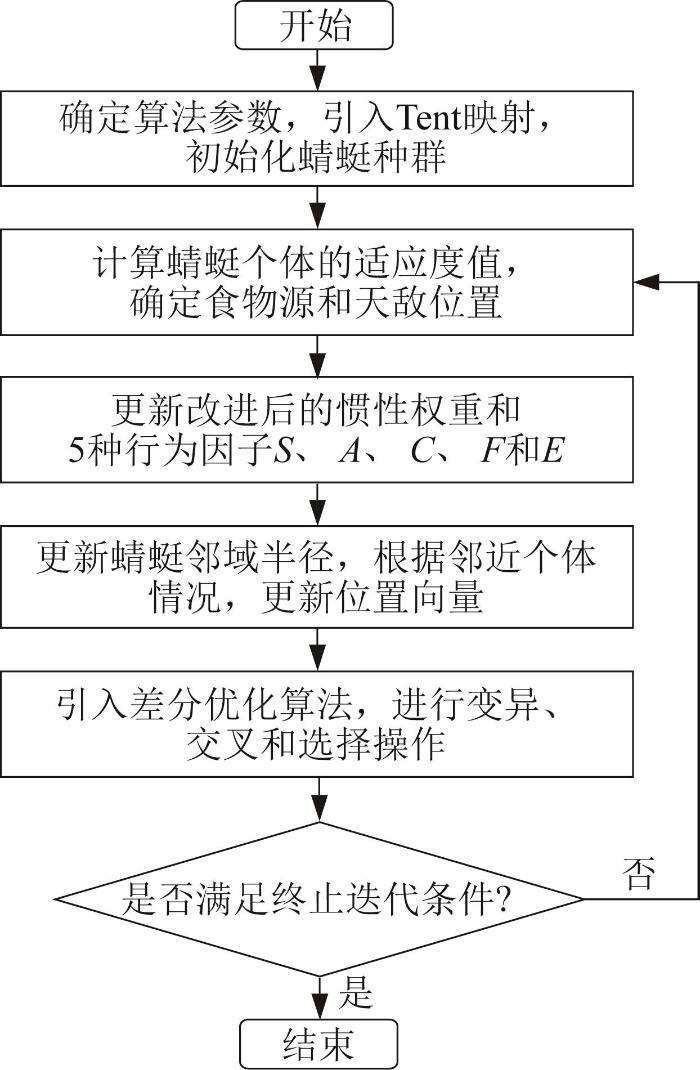
DA改进流程如图7所示。

磁齿轮复合电机具有强非线性和强耦合性的特点，且为双转子结构，因此本文采用IDA-PI控制器。控制器的结构如图8所示。

磁齿轮复合电机采用双闭环控制系统，电流环和转速环控制器的控制参数共有4个；采用IDA对参数进行整定，即寻找转速环和电流环控制器的最优参数组合K=（K_sp, K_si, K_ip, K_ii）。将这4个待优化参数看作IDA中蜻蜓种群在4维空间搜寻的最优个体的位置，最优个体则通过适应度函数值来评定，因此目标适应度函数的选择对于系统的控制性能至关重要。本文将一种基于ITAE（integrated time and absolute error，误差绝对值积分）的超调惩罚项作为适应度函数^[15-16]，以减小超调量，提升控制效果。适应度函数Y的表达式为：

式中：β为惩罚权重，常取β=15。

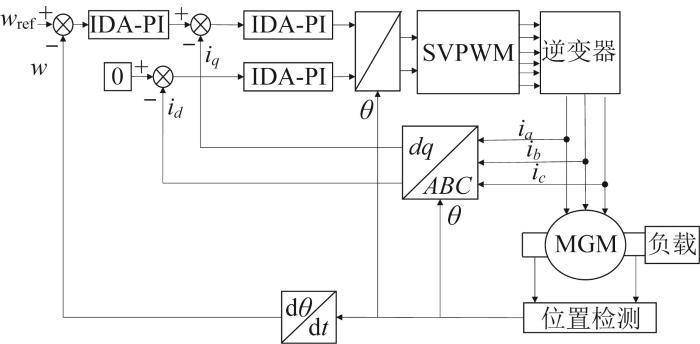
磁齿轮复合电机双闭环PI矢量控制框图如图9所示^[17-18]。采用IDA-PI对转速环和电流环控制器的参数进行整定与优化。

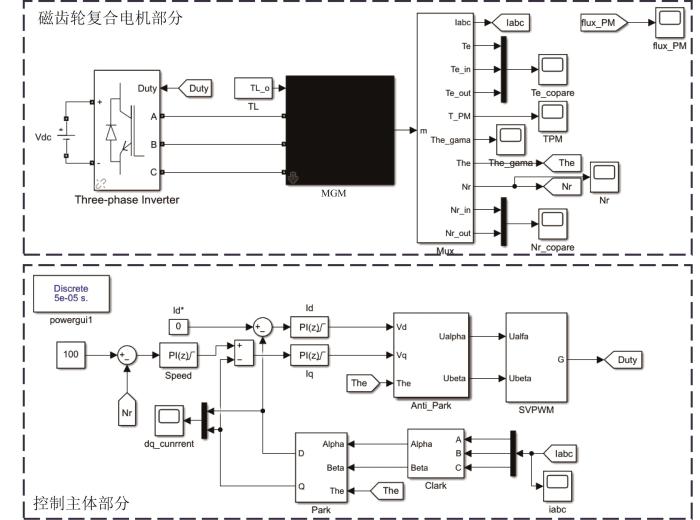
在Simulink中搭建磁齿轮复合电机矢量控制系统的仿真模型，如图10所示。仿真模型分为磁齿轮复合电机和控制主体两部分。

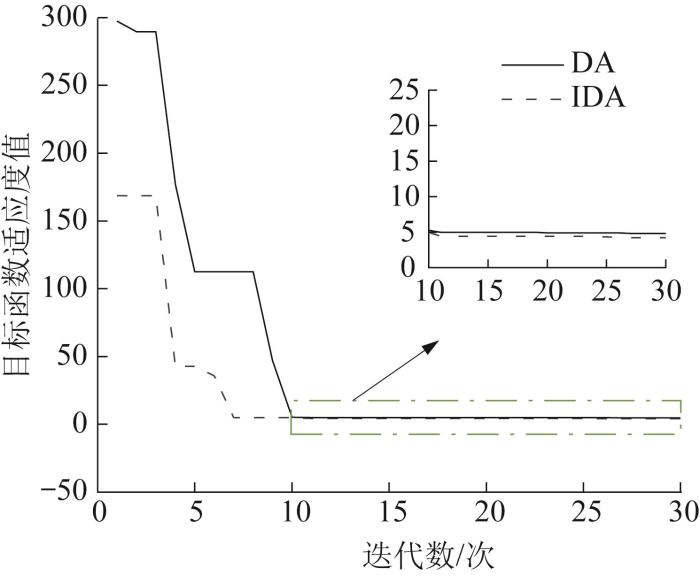
基于仿真模型对传统PI、DA-PI和IDA-PI控制的控制效果进行对比分析。仿真时间为2.5 s，电机外转子以100 r/min的输出转速空载启动，分别进行空载启动以及电机稳态运行后突加5 N负载的仿真实验；蜻蜓的种群数为30个，最大迭代数为30次，待优化参数的取值区间均为[0, 30]。DA和IDA目标函数值的收敛曲线如图11所示。由图可知：IDA迭代24次后收敛，最优目标函数适应度值为4.207 314；DA迭代26次后收敛，最优适应度值为4.807 340。因此，IDA的性能更为优越。

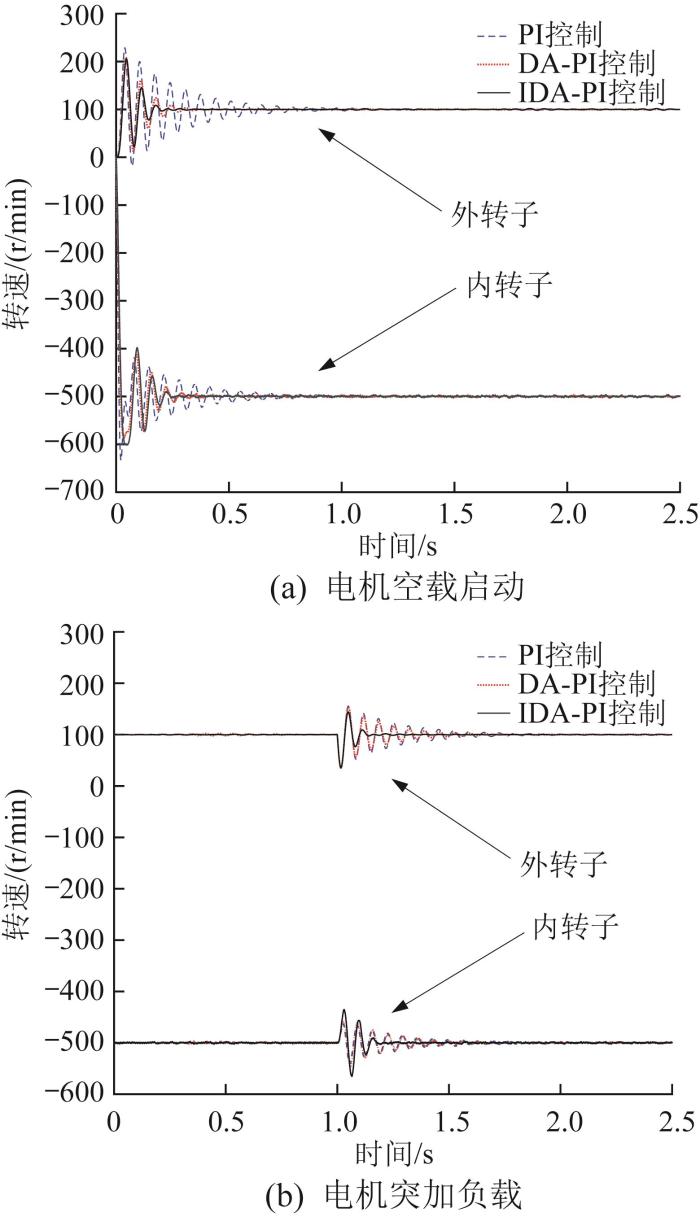
磁齿轮复合电机在PI、DA-PI和IDA-PI控制下的转速如图12所示。由图可知，内转子和外转子的稳态转速均在500 r/min和100 r/min左右，满足了电机的减速比设计要求。磁齿轮复合电机是双转子电机，外转子是电机的输出轴，内转子仅是运动传递过程中的过渡部分，因此电机控制效果主要看外转子的控制效果。同时，外转子在PI、DA-PI和IDA-PI控制下的最大转速分别为211.5，208.4，207 r/min；空载启动时，外转子转速误差在5%内的调节时间分别为0.997，0.357，0.267 s；突加负载时，外转子转速误差在5%以内的调节时间分别为0.859，0.531，0.147 s。可见，IDA-PI的控制效果最好，超调量最小，动态响应最快，调节时间最短。

所设计加工的磁齿轮复合电机样机如图13所示。

为了验证仿真结果的正确性，搭建了磁齿轮复合电机控制实验平台，如图14所示。实验平台主要包括电机样机、转矩/转速传感器、磁粉制动器、上位机、STM32F407开发板、驱动板和电源等。驱动板电源为驱动板提供48 V的电压，电机的U、V、W三相线连接在驱动板上；磁粉制动器为实验平台提供稳定的负载；转矩/转速传感器与开发板连接，开发板与上位机通过数据线进行通信，双闭环矢量控制程序通过Keil软件烧录至开发板。

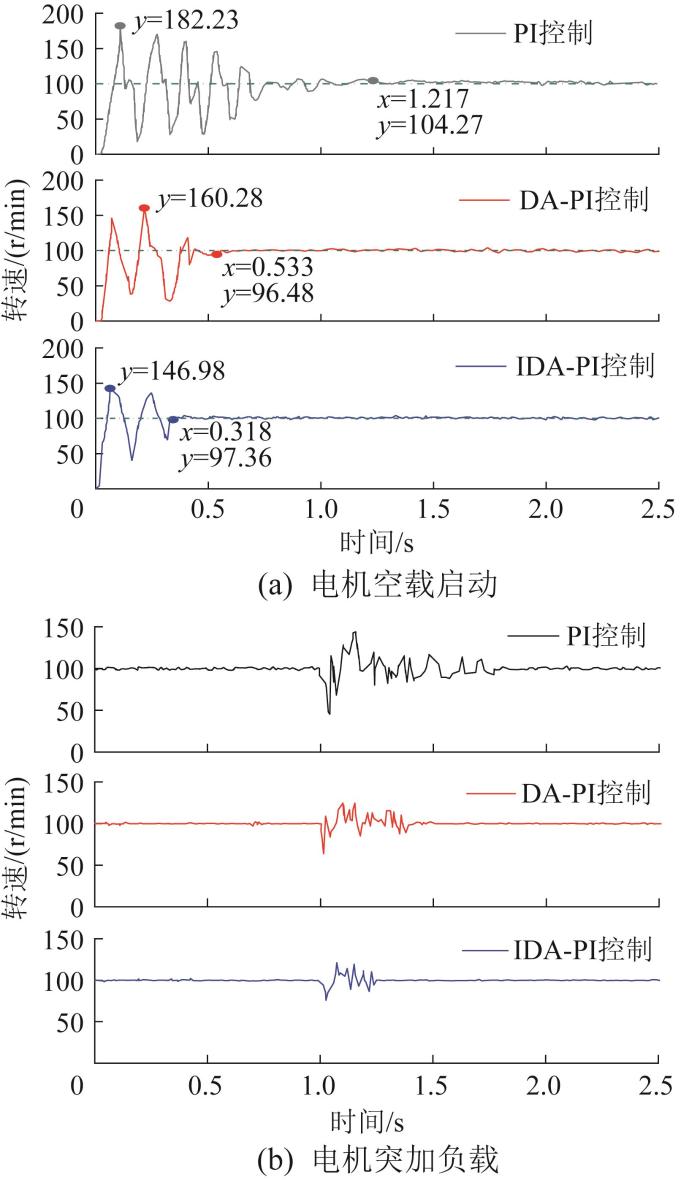
设置外转子的输出转速为100 r/min。通过传感器记录电机在空载启动和突加负载工况下的转速，结果如图15所示。

由图15可知，在PI、DA-PI和IDA-PI控制下，1.25 s后电机外转子的输出转速大致都为100 r/min。磁齿轮复合电机的减速传动是不同于传统减速器的非接触传动，其通过磁场产生的转矩传动，因此空载启动时转速会产生较大波动。空载启动时，在PI、DA-PI和IDA-PI控制下的最大转速分别为182.23，160.28，146.98 r/min，PI控制下的超调量最大，IDA-PI控制下的超调量最小；超调量测量值与仿真值相近，但小于仿真值；从电机启动到转速误差在5%内的调节时间分别为1.217，0.533，0.318 s，PI控制下的调节时间最长，IDA-PI控制下的调节时间最短。突加负载时，IDA-PI的控制效果最好，调节时间最短。调节时间的测量值与仿真值相近，但均比仿真值大，造成这一现象的原因可能是电机内、外转子的永磁体在粘贴时出现了偏心，以及在整体装配时安装精度不够，导致转子转动时出现偏心和摆动。实验结果与仿真结果总体上较一致，验证了IDA-PI控制是3种控制方法中控制效果最好的。

本文提出了一种磁齿轮复合电机的控制方法。首先，根据电机的双转子结构和工作原理，采用磁场矢量合成的方法将内、外转子永磁体产生的磁场进行合成，并建立了电机矢量控制数学模型；其次，将IDA与PI控制结合，实现了控制器参数的优化，降低了传统人工调试PI参数的难度，缩短了调节时间；最后，通过仿真和实验表明，在IDA-PI控制下，磁齿轮复合电机控制系统的超调量和稳态误差较小，系统的动态响应速度较快，验证了所提控制策略的有效性。本文研究为不同拓扑结构磁齿轮复合电机的控制提供了理论指导。