基于BP和HBP流变模型的磁流变阻尼器数值模拟与性能分析

doi:10.3785/j.issn.1006-754X.2024.03.185

基于BP和HBP流变模型的磁流变阻尼器数值模拟与性能分析

舒慧杰^,, 胡国良^,^,, 朱文才, 喻理梵, 李品烨

华东交通大学机电与车辆工程学院，江西南昌 330013

Numerical simulation and performance analysis of magnetorheological damper based on BP and HBP rheological models

SHU Huijie^,, HU Guoliang^,^,, ZHU Wencai, YU Lifan, LI Pinye

School of Mechatronics and Vehicle Engineering, East China Jiaotong University, Nanchang 330013, China

通讯作者: 胡国良（1973—），男，江西南昌人，教授，博士，从事磁流变智能器件及其结构等研究，E-mail: glhu@ecjtu.edu.cn, https://orcid.org/0000-0002-8621-2922

收稿日期: 2023-07-03 修回日期: 2023-08-04

基金资助:

国家自然科学基金资助项目.  52165004
江西省自然科学基金重点资助项目.  20212ACB204002
江西省国际科技合作重点项目.  20232BBH80010

Received: 2023-07-03 Revised: 2023-08-04

作者简介 About authors

舒慧杰（1998—），男，江西吉安人，硕士生，从事磁流变阻尼器结构设计及优化研究，E-mail:2627079815@qq.com , E-mail：2627079815@qq.com

摘要

针对传统本构模型表达磁流变液的流变特性精度不高的问题，采用MCR302流变仪对磁流变液的流变特性进行测试，获得了不同磁场下剪切应力与剪切速率之间的关系。利用遗传算法对Bingham-Papanastasiou（BP）模型和Herschel-Bulkley-Papanastasiou（HBP）模型进行参数辨识。利用辨识结果建立了仿真模型，对磁流变阻尼器的动态特性进行数值模拟。设计并加工了磁流变阻尼器，搭建了阻尼力测试平台进行阻尼力测试实验，并将实验结果与仿真结果进行对比。结果表明：HBP模型对磁流变液流变特性的辨识结果与实验结果吻合较好；2个模型对阻尼器动态特性的预测结果相差较大，仅对流速的预测一致性较好；基于HBP模型的阻尼力预测值与实验值较吻合。所提出的HBP模型表达磁流变液流变特性的精度较高，具有良好的实用价值。研究结果可以为振动控制领域磁流变阻尼器力学模型的选择提供参考。

关键词： 流变特性 ; 磁流变液 ; 数值模拟 ; 参数辨识

Abstract

To solve the problem that the traditional constitutive model was not accurate in expressing the rheological characteristics of magnetorheological (MR) fluid, the rheological characteristics of MR fluid were tested by using the MCR302 rheometer, and the relationship between shear stress and shear rate under different magnetic fields was obtained. Genetic algorithm was used to identify the parameters of Bingham-Papanastasiou (BP) model and Herschel-Bulkley-Papanastasiou (HBP) model. The simulation model was established based on the identification results, and the dynamic characteristics of the MR damper were simulated numerically. A MR damper was designed and processed, and a damping force test platform was built to test the damping force, and the experimental results were compared with the simulation results. The results showed that the identification results of the rheological characteristics of MR fluid by HBP model were in good agreement with the experimental results. The prediction results of the two models were quite different in the dynamic characteristics of the damper, but the prediction consistency of the flow rate was good. The predicted value of damping force based on HBP model was in good agreement with the experiment value. The proposed HBP model could express the rheological characteristics of MR fluid with high accuracy and had good practical value. The research results can provide reference for the selection of mechanical model of MR damper in vibration control field.

Keywords： rheological characteristic ; magnetorheological (MR) fluid ; numerical simulation ; parameter identification

PDF (4363KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

舒慧杰, 胡国良, 朱文才, 喻理梵, 李品烨. 基于BP和HBP流变模型的磁流变阻尼器数值模拟与性能分析[J]. 工程设计学报, 2024, 31(3): 402-408 doi:10.3785/j.issn.1006-754X.2024.03.185

SHU Huijie, HU Guoliang, ZHU Wencai, YU Lifan, LI Pinye. Numerical simulation and performance analysis of magnetorheological damper based on BP and HBP rheological models[J]. Chinese Journal of Engineering Design, 2024, 31(3): 402-408 doi:10.3785/j.issn.1006-754X.2024.03.185

磁流变（magnetorheological，MR）阻尼器是利用磁流变液的流变效应制作而成的智能减振装置。与普通液压减振器相比，磁流变阻尼器具有结构简单、响应速度快、输出阻尼力大及阻尼力连续可调等优点，在机械、汽车以及土木工程等领域的振动半主动控制中得到广泛应用^[1-5]。

磁流变液的流变特性通常采用流变仪进行测试，然后从测试数据中提取相关参数，用于定性分析磁流变液的流变行为或后续通过流变模型进行数值模拟。目前，国内外学者对磁流变液流变行为的预测模型展开了研究。传统的Bingham模型由于形式简单而被广泛利用。如：Hu等^[6]采用COMSOL多物理场仿真软件和Bingham模型对磁流变阻尼器进行了多物理场耦合建模及仿真；祝世兴等^[7]提出了一种改进Bingham模型，用于精确描述磁流变阻尼器力与速度之间的非线性关系；Pei等^[8]通过粒子模拟方法来探索流体微观结构的行为和流变特性，并建立了改进的本构模型来描述流体流变特性。

然而，Bingham模型中将流体剪切速率与剪切应力的关系假定为线性关系，而磁流变液在工作中存在剪切增稠与剪切稀化行为，为此有学者提出利用Herschel-Bulkley模型来描述磁流变液。如：Zhang等^[9]通过试验确定了Herschel-Bulkley模型的参数，给出的表达精度为0.931 2；Ouyang等^[10]、Guo等^[11]和Kemerli等^[12]采用Herschel-Bulkley模型表达磁流变液的流变特性，并对磁流变阻尼器中二维轴对称流动进行仿真分析，结果表明，采用Herschel-Bulkley模型所得到的流变特性的仿真结果较准确；吴俊岐等^[13]利用Herschel-Bulkley模型实现了牛顿流与黏塑性流的混合仿真计算；Elsaady等^[14]利用Herschel-Bulkley模型对磁流变阻尼器的动态滞回特性进行建模。然而，Herschel-Bulkley模型本质上是Bingham模型的衍生，仍存在预测结果不准确的问题。为此，Cvek^[15]、LÜ等^[16]和Wei等^[17]通过总结现有非常规黏塑性模型，提出了一种新的表达磁流变液流变特性的本构方程，并基于新模型重新构建了一系列用于预测磁流变阻尼器的物理模型。除此之外，Li等^[18]分析了温度对流变特性及其产生机理的影响，并结合纳维-斯托克斯方程和黏温方程，提出了一种新的带温度预测的本构模型。

本构模型仅仅用于对液体流动行为进行简化描述，并不能完全解释流体行为^[19]。Bingham模型简单地将黏弹性物质的流动行为分为纯弹性和纯黏性，假设当剪切应力超过屈服应力时，流体以恒定黏度流动，但模型在数值模拟过程中存在数值发散问题^[20]。Herschel-Bulkley模型虽然对数值发散问题进行了修正，但在极端剪切速率下得到的结果仍存在一定误差。

基于此，本文采用MCR302流变仪对选用的磁流变液样品的流变特性进行测试，应用Herschel-Bulkley-Papanastasiou（HBP）模型来对磁流变液的流变特性进行描述，并与Bingham-Papanastasiou（BP）模型进行对比分析；同时，设计了阻尼器，进行其力学性能测试，用于验证模型的有效性。

1 磁流变液流变特性的测试

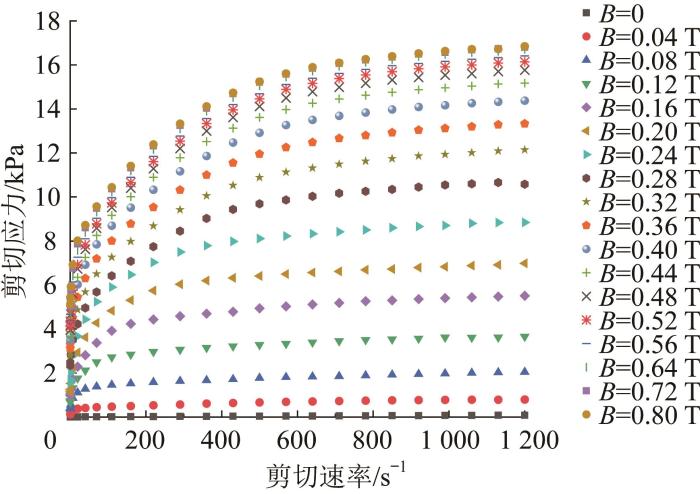
采用MCR302流变仪测试磁流变液的流变特性。设定测试电流从0增加到5 A，增量为0.25 A；随着测试电流增大，磁流变液的流变特性趋于稳定，因此当电流为3.5 A时将电流增量调整为0.5 A。电流为3.5 A和5 A时对应的磁感应强度B分别为0.56 T和0.80 T。设定剪切速率从0.01 s^-1增加到1 200 s^-1。磁流变液流变特性曲线如图1所示。由图可知：在相同的剪切速率下，剪切应力随着磁感应强度的增大而增大；当磁感应强度达到一定值时，剪切应力不再随磁感应强度的增大而明显变化，说明磁流变液在该磁场下趋于磁饱和。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 测试所得磁流变液流变特性曲线

Fig.1 Rheological characteristic curves of MR fluid obtained by test

2 模型参数辨识

根据采集的测试数据，利用遗传算法对BP和HBP模型的参数进行辨识。同时以均方根误差R_MSE最小作为优化目标，对辨识结果进行优化。

R_{M S E} = \sqrt[]{\frac{\sum_{i = 1}^{N} (τ_{i} - τ_{p})^{2}}{N - P}}

式中：τ_i 为测试得到的剪切应力，i为测试点的序号，i=1, 2, …, N；τ_p为预测的剪切应力；P为模型自由度。

2.1　BP模型参数辨识

BP模型的动力黏度μ_app定义如下：

μ_{a p p} = μ_{p} + \frac{τ_{y}}{\dot{γ}} [1 - e x p (- m_{p} \dot{γ})]

(2)

则：

τ = μ_{p} \dot{γ} + τ_{y} [1 - e x p (- m_{p} \dot{γ})]

(3)

式中：μ_p是零场黏度，设置为0.8 Pa·s；τ_y为屈服应力； $\dot{γ}$ 为剪切速率；τ为剪切应力；m_p为模型参数，用来控制黏度函数的平滑度。

方程(2)在屈服区成立，在未屈服区以牛顿流体的流动特性来表征磁流变液的流变特性。其中τ_y和m_p随着B的变化而变化。

测试及通过BP模型所得的磁流变液流变特性曲线如图2所示。由图可知：B>0.20 T时辨识结果较好，曲线穿过了大多数测试数据点；B≤0.20 T时，两者有一定误差。说明BP模型更适合于对屈服区的表达，对于非屈服区及小磁场下的屈服区，其表达不够精确。BP模型参数辨识结果如表1所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

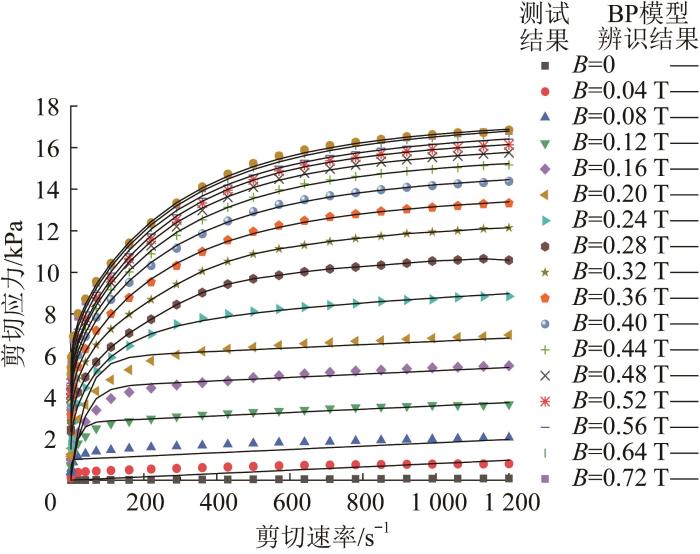
图2 测试及通过BP模型所得的磁流变液流变特性曲线

Fig.2 Rheological characteristic curves of MR fluid obtained by test and BP model

表1 BP模型参数辨识结果

Table 1 Identification result of BP model’s parameters

B/T	μ_p/(Pa·s)	τ_y/Pa	m_p/s
0	0.8	0	1.106 3
0.04	0.8	204.3	1.050 0
0.08	0.8	1 000.0	0.800 0
0.12	0.8	2 776.9	0.060 7
0.16	0.8	4 464.6	0.028 8
0.20	0.8	5 881.8	0.025 3
0.24	0.8	7 610.4	0.021 0
0.28	0.8	9 251.1	0.014 7
0.32	0.8	9 300.2	0.014 3
0.36	0.8	10 521	0.014 7
0.40	0.8	12 610	0.014 7
0.44	0.8	13 327	0.147 0
0.48	0.8	14 000	0.014 6
0.52	0.8	14 223	0.014 7
0.56	0.8	14 483	0.014 7
0.64	0.8	14 832	0.014 7
0.72	0.8	14 595	0.014 7

新窗口打开| 下载CSV

2.2　HBP模型参数辨识

HBP模型的动力黏度μ′_app定义如下：

μ_{a p p}^{'} = m {(\frac{\dot{γ}}{{\dot{γ}}_{r e f}})}^{n - 1} + \frac{τ_{y}}{\dot{γ}} [1 - e x p (- m_{p} \dot{γ})]

(4)

则：

τ = m {(\frac{\dot{γ}}{{\dot{γ}}_{r e f}})}^{n - 1} \dot{γ} + τ_{y} [1 - e x p (- m_{p} \dot{γ})]

(5)

式中：m为流体一致性系数，n为拟合指数，均为可以设置为任意值的标量，当n=1时为BP模型，该方程在屈服区和未屈服区均成立； ${\dot{γ}}_{r e f}$ 为参考剪切速率。

在进行求解计算时，设定 ${\dot{γ}}_{r e f} = 1$ ，则整理后得到:

τ = m {\dot{γ}}^{n} + τ_{y} [1 - e x p (- m_{p} \dot{γ})]

(6)

HBP模型涉及τ_y、m_p、m和n这4个参数，它们均随着B的变化而变化，因此其拟合曲线具有更高的拟合度。测试及通过HBP模型所得的磁流变液流变特性曲线如图3所示，HBP模型参数辨识结果如表2所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

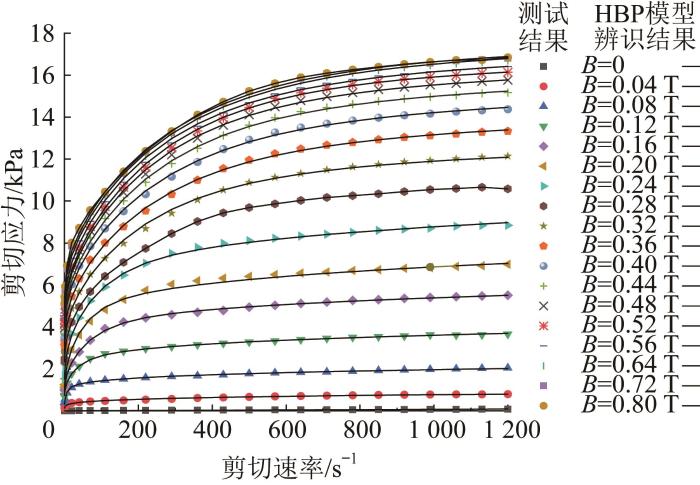
图3 测试及通过HBP模型所得的磁流变液流变特性曲线

Fig.3 Rheological characteristic curves of MR fluid obtained by test and HBP model

表2 HBP模型参数辨识结果

Table 2 Identification result of HBP model’s parameters

B/T	τ_y/Pa	m_p/s	m/(Pa·s)	n
0	0.938 4	1.001	0.119 5	0.920 5
0.04	100	0.500	120	0.249 2
0.08	393.3	0.114	438.8	0.184 7
0.12	1 000	0.030	740	0.181 8
0.16	1 773	0.014 1	1 142	0.165 5
0.20	2 500	0.011 34	1 508	0.152 9
0.24	3 400	0.008 79	1 885	0.149 7
0.28	4 175	0.005	2 595	0.129 2
0.32	4 800	0.004 2	3 050	0.124 6
0.36	5 400	0.003 7	3 500	0.118 4
0.40	5 800	0.003 7	3 900	0.114 2
0.44	6 050	0.003 65	4 250	0.110 4
0.48	6 350	0.003 65	4 582	0.103 0
0.52	6 550	0.003 65	4 800	0.099 37
0.56	6 800	0.003 6	5 000	0.094 09
0.64	7 000	0.003 6	5 400	0.084 48
0.72	7 150	0.003 6	5 652	0.077 46
0.80	7 256	0.003 6	5 750	0.073 57

新窗口打开| 下载CSV

3 模型验证

设计了一种阻尼力低于2 kN的磁流变阻尼器，同时，采用COMSOL软件对该阻尼器进行模拟，并分别用BP和HBP模型来描述磁流变液的流变特性。由于磁流变液会直接对磁场变化作出反应，选择将流变模型的参数定义为随磁场变化而变化，通过在COMSOL中定义插值函数的方式给出；将辨识出的不同磁场下的参数值作为插值点，得出每个参数随磁场的变化曲线。以阻尼器的输出阻尼力为性能指标，来分析并对比仿真与实验结果。为了防止阻尼器因结构复杂而降低加工和装配精度，影响实验结果，采用最简单的剪切阀式结构的阻尼器。

3.1　数值模拟

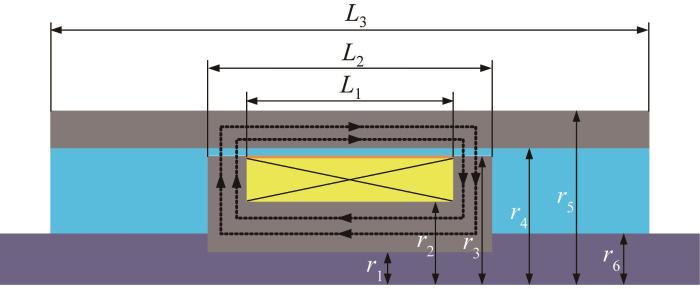
磁流变阻尼器的结构参数如表3所示，其参数化模型如图4所示。由于所用阻尼器的结构呈轴对称，为了减小计算量，采用二维轴对称模型进行模拟。

表3 磁流变阻尼器结构参数 (mm)

Table 3 Structural parameters of MR damper

符号	参数	数值
r₁	活塞头孔径	5.0
r₂	绕线架半径	13.0
r₃	活塞头半径	20.5
r₄	缸体内径	21.5
r₅	缸体外径	29.5
r₆	活塞杆外径	8.0
L₁	绕线槽宽	33.0
L₂	活塞头宽	45.0
L₃	缸体宽	95.0

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 磁流变阻尼器参数化模型

Fig.4 Parametric model of MR damper

磁流变阻尼器是一个磁场与流场耦合的系统。对该耦合系统施加振幅为5 mm、频率为1 Hz的正弦激励，振动时间为1 s；激励电流I分别设定为0，0.25，0.5，1.0，1.5 A，来模拟磁场作用下磁流变液的流场特性。

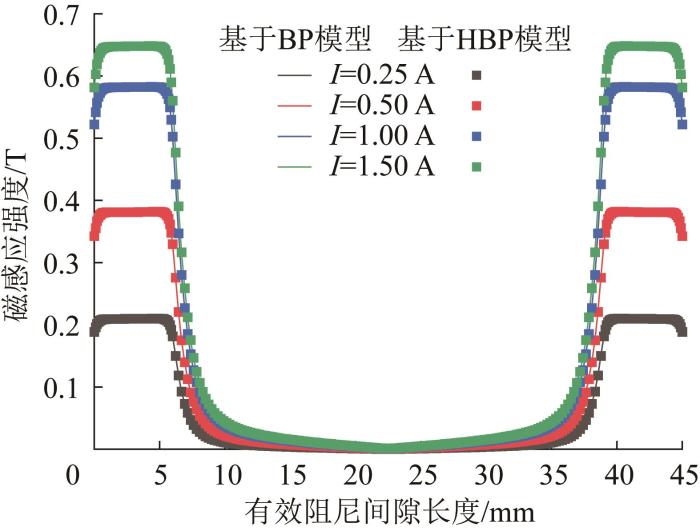
基于不同模型的有效阻尼间隙处的磁感应强度如图5所示。由图可知：磁感应强度随路径的变化曲线呈两端大、中间小，磁场分布满足了设计要求；在2种模型下阻尼器的磁场特性一致，这是由于材料的磁化模型是一致的。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于不同模型的有效阻尼间隙处的磁感应强度

Fig.5 Magnetic flux density at effective damping gap based on different models

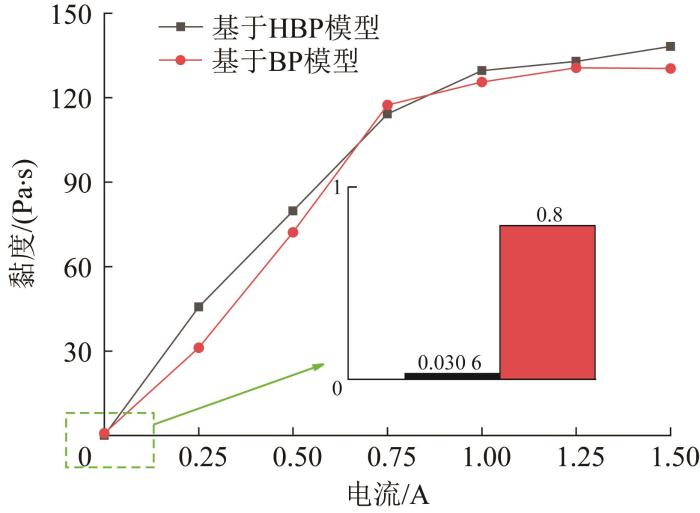
通过COMSOL的计算流体力学模块进行后处理，可求得不同电流下有效阻尼间隙处磁流变液的黏度平均值。磁流变液黏度随电流的变化曲线如图6所示。由图可知：零电流时基于BP模型的磁流变液的黏度大于HBP模型，而随着电流增大，两者的变化趋势一致；随着电流增大，磁流变液黏度均增大；当I>1.25Ａ时，基于BP模型的磁流变液的黏度基本不再发生变化，且在大电流下基于BP模型的黏度较小。这是由流体模型对流变仪测试数据的表达差异引起的，HBP模型与BP模型分别用4个参数与3个参数对测试数据进行表达，2个模型在数值模拟中存在差异。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 有效阻尼间隙处磁流变液黏度随电流的变化曲线

Fig.6 Variation curve of viscosity of MR fluid with current at effective damping gap

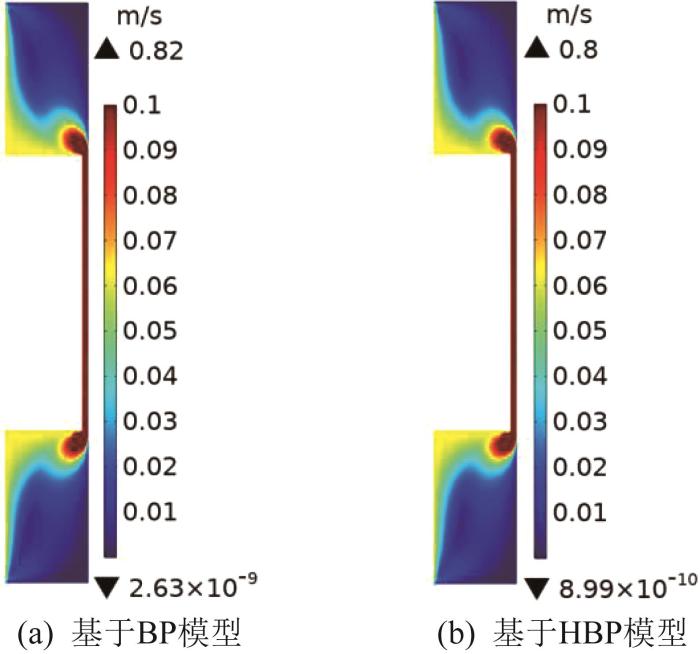
当激励电流为0.25 A、振动时间为1 s时流体区域的流速分布云图如图7所示。由图可知：最大流速较为接近，只相差0.02 m/s；流速的分布趋势一致。说明2种模型对流速的预测结果较一致。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 激励电流为0.25 A、振动时间为1 s时流体区域的流速分布云图

Fig.7 Distribution cloud diagram of flow velocity in fluid region with excitation current of 0.25 A and vibration time of 1 s

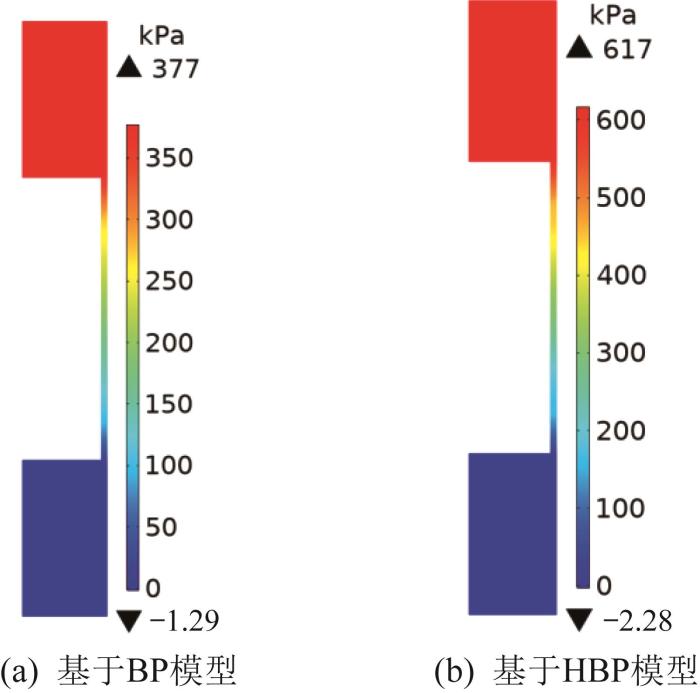
激励电流为0.25 A、振动时间为1 s时流体区域的压力分布云图如图8所示。由图可知，相较于HBP模型，基于BP模型的压力较小，且相差较为显著。为了更直观地比较两者之间的差异，在COMSOL后处理中定义一个积分器，对整个流体区域进行积分。定义下边界的压力为0，此时积分结果为上下腔体之间的压差。将压差乘以活塞头截面积，得出阻尼力值，如表4所示。由表可知，2种模型下阻尼力的仿真结果相差较大。这是由于出于单一变量原则，流变模型拟合了所有剪切速率下的测试数据点，BP模型在剪切速率过小及过大时存在一定误差，因此对整体辨识结果的准确性影响较大，进而影响数值模拟结果，而HBP模型本身是针对剪切增稠与剪切稀化的修正模型，因此对全局的数据表达较为理想。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 激励电流为0.25 A、振动时间为1 s时流体区域的压力分布云图

Fig.8 Distribution cloud diagram of pressure in fluid region with excitation current of 0.25 A and vibration time of 1 s

表4 激励电流为0.25 A、振动时间为1 s时阻尼力仿真结果

Table 4 Simulation results of damping force with excitation current of 0.25 A and vibration time of 1 s

I/A	基于BP模型的阻尼力/N	基于HBP模型的阻尼力/N
0	295.58	59.986
0.25	438.56	377.24
0.50	617.68	780.24
1.00	640.56	1 050.23
1.50	644.35	1 158.92

新窗口打开| 下载CSV

3.2　阻尼力测试实验

加工好的磁流变阻尼器实物如图9所示。其中，励磁线圈匝数为480。为了在实验过程中监测磁流变液的温度，在端盖上安装了温度传感器。为了保证实验中阻尼通道恒定，在励磁线圈上方涂上了环氧树脂，使活塞头外径恒定。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 磁流变阻尼器实物

Fig.9 Prototype of MR damper

为了分析不同激励电流对磁流变阻尼器输出阻尼力的影响，搭建了阻尼力测试平台，如图10所示。阻尼器的一端固定在测试平台的横梁上，另一端与激振平台的动力杆相连。激振平台的振动频率可以通过计算机程序设定并施加到阻尼器上。包括速度、位置和输出阻尼力在内的实时信号可以通过测试平台中内置的力和速度传感器反馈给计算机。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 阻尼力测试平台

Fig.10 Damping force test platform

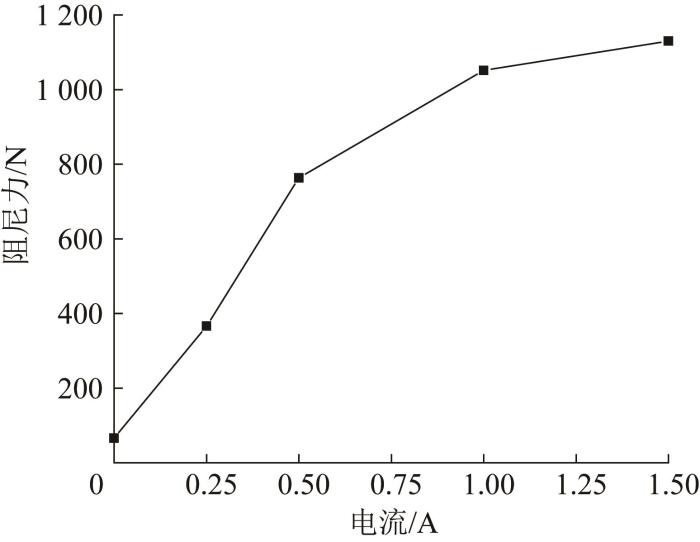
设置正弦激励的振幅和频率分别为5 mm和1 Hz，通过调节稳流器向阻尼器输出不同大小的励磁电流，测量不同激励电流下阻尼器的输出阻尼力。阻尼力随激励电流的变化曲线如图11所示。由图可知，随着励磁电流的增大，阻尼力也增大，当励磁电流为0，0.25，0.50，1.00，1.50 A时，阻尼力分别为65.6，365.8，763.1，1 051.1，1 130.5 N。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 阻尼力随激励电流的变化曲线

Fig.11 Variation curve of damping force with excitation current

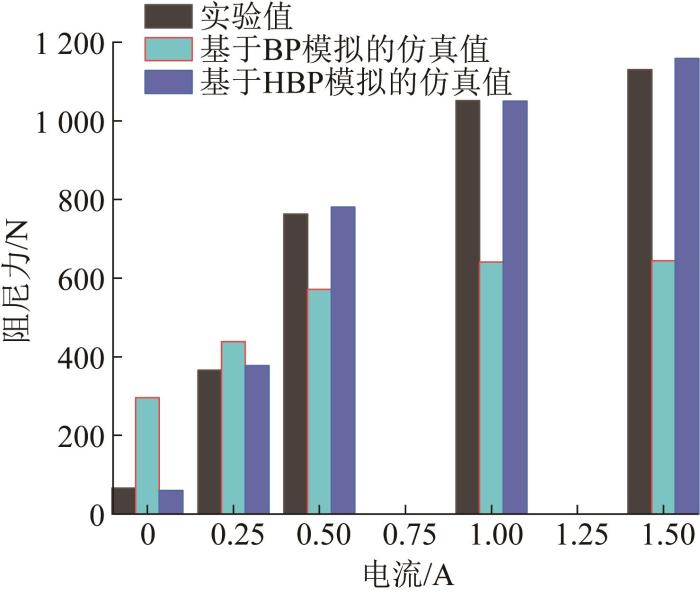
不同激励电流下阻尼力测试值与仿真值的对比如图12所示。由图可知：基于BP模型的阻尼力的仿真值与测试值相差较大；当电流为1.00，1.50 A时，基于BP模型的阻尼力仿真值基本不变，与实验结果不相符；基于HBP模型的阻尼力的仿真值与测试值较吻合，因此HBP模型对阻尼力的预测更为准确。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同激励电流下阻尼力测试值与仿真值的对比

Fig.12 Comparison between measured and simulated values of damping force under different excitation currents

4 结论

本文采用MCR302流变仪对磁流变液进行流变特性测试，利用测试数据，分别对BP和HBP模型进行参数辨识，并对模型进行了验证，得到以下结论:

1）HBP模型的辨识结果与实验结果吻合良好，验证了用HBP模型表达磁流变液的流变特性是合理的。

2）基于HBP模型的阻尼力预测值与实验值较吻合，HBP模型的精度更高，对磁流变液阻尼器阻尼力的预测更准确。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LIU

， YANG

， LIAO

A new method of parameters identification for magnetorheological damper model

［J］. Journal of Mechanical Engineering， 2018， 54（6）： 62-68.