基于3D-motif法的刮研表面形貌表征

doi:10.3785/j.issn.1006-754X.2024.03.199

基于3D-motif法的刮研表面形貌表征

杨春鹏^,, 王立华^,^,, 陈谢瑞, 蒋维

昆明理工大学机电工程学院，云南昆明 650500

Characterization of scraped surface morphology based on 3D-motif method

YANG Chunpeng^,, WANG Lihua^,^,, CHEN Xierui, JIANG Wei

Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China

通讯作者: 王立华（1974—），男，四川达县人，教授，博士，从事结合面特性研究，E-mail: kmwanglihua@163.com，https://orcid.org/0000-0002-7071-4565

收稿日期: 2023-08-30 修回日期: 2023-09-26

基金资助:

国家自然科学基金资助项目. 52265012

Received: 2023-08-30 Revised: 2023-09-26

作者简介 About authors

杨春鹏（1999—），男，吉林松原人，硕士生，从事表面微观形貌表征研究，E-mail:1289598373@qq.com , E-mail：1289598373@qq.com

摘要

针对刮研表面微观特性和功能机理研究中缺少表面形貌量化表征方法的问题，采用3D-motif法对刮研表面形貌进行表征。使用LI-3型接触式三维表面形貌测量仪对刮研表面进行测量，并利用三维点云数据生成刮研表面的二维灰度图像。然后，根据3D-motif法中集水盆地的定义，采用分水岭算法对刮研表面的灰度图像进行motif分割与合并。以不同精度等级的刮研表面的整体纹理区域motif分割结果为对象，定义了特征显著度并提取计算了刮研表面在2种不同面积尺度（25 mm²和0.25 mm²）上的深度、面积、方向角、各向异性率、扁平系数和特征显著度等6项motif参数。结合部分motif参数的分布情况和motif数量的变化趋势，从形貌特征的尺寸和形态两个方面对刮研表面进行了表征和分析，实现了以较少参数完整表征刮研表面的三维形貌。研究结果可为后续刮研表面微观特性的深入分析提供理论基础。

关键词： 刮研表面 ; 3D-motif法 ; 表面形貌 ; 分水岭算法

Abstract

In response to the lack of quantitative characterization methods of surface morphology in the study of microscopic properties and functional mechanism of scraped surfaces, the 3D-motif method was used to characterize the scraped surface morphology. The scraped surface was measured by using LI-3 contact three-dimensional surface morphology measuring instrument, and the two-dimensional grayscale image of the scraped surface was generated by three-dimensional point cloud data. Then, according to the definition of catchment basin in 3D-motif method, the motif segmentation and merging for the grayscale image of scraped surface were conducted by using watershed algorithm. Taking the overall texture region motif segmentation results of scraped surfaces with different precision levels as the object, the feature saliency was defined, and six motif parameters, including depth, area, direction angle, anisotropy rate, flatness coefficient and feature saliency, were extracted and calculated for the scraped surface on two different area scales (25 mm² and 0.25 mm²). Combined with the distribution of some motif parameters and the change trend of the number of motif, the scraped surface was characterized and analyzed from the dimension and morphology of the morphological features, achieving the complete characterization of the three-dimensional morphology of the scraped surface with fewer parameters. The results can provide a theoretical basis for further analysis of the microscopic properties of scraping surfaces.

Keywords： scraped surface ; 3D-motif method ; surface morphology ; watershed algorithm

PDF (4565KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨春鹏, 王立华, 陈谢瑞, 蒋维. 基于3D-motif法的刮研表面形貌表征[J]. 工程设计学报, 2024, 31(3): 368-376 doi:10.3785/j.issn.1006-754X.2024.03.199

YANG Chunpeng, WANG Lihua, CHEN Xierui, JIANG Wei. Characterization of scraped surface morphology based on 3D-motif method[J]. Chinese Journal of Engineering Design, 2024, 31(3): 368-376 doi:10.3785/j.issn.1006-754X.2024.03.199

刮研是一种平面光整加工的微量切削方法^[1]，具有对加工尺寸限制小、加工位置灵活以及刮研后表面润滑性能优异、配合刚度高、运行平稳和使用寿命长且易修复等特点^[2]。刮研表面大多应用于大型设备和高精度设备的滑动结合面，其质量直接影响设备的最终精度、配合性能和机械效率等。但是，现阶段的刮研加工主要依靠人工进行操作，自动化程度低，此外还缺乏对刮研表面微观机理的研究。

目前，针对刮研工艺的研究主要集中在改进具体类型零件的刮研方法和提高刮研自动化程度等方面。例如：孙雷雷^[3]对刮研表面的自动检测技术进行了研究；曹恒督等^[4]设计了一种可以自动识别研点的刮研机器人；Hsieh等^[5]对自动刮研机的结构及其制造工艺进行了设计与研究；刘伟等^[6]针对导轨研发了一套自动刮研系统。然而，上述研究缺乏对刮研表面表征方式和功能机理的理论分析，导致自动化刮研难以达到与手工刮研相同的加工精度。刮研表面的微观形貌与其功能机理关联紧密，对刮研表面形貌进行准确表征是实现刮研自动化与标准化的前提。

现有的加工表面形貌表征方法主要包括三维中面法、分形法和motif法。其中：三维中面法是二维轮廓法在三维尺度上的推广和完善^[7]，通过数学算法拟合得到具有代表性特征的三维中面^[8]，适用于表征具有各向同性的表面以及具有普遍性和确定性纹理的表面。但是，刮研表面的刮痕分布使得基于刮研表面形貌数据拟合的三维中面的可靠性较差，故难以用该方法来表征刮研表面的微观形貌。分形法是基于数学中的分形理论^[9]，适用于表征具有随机性、多尺度性和自相似性或自仿射性的表面^[10-11]，即具有分形特征的表面，而刮研表面不具有上述特点。motif法是一种基于包络制的表征方法，可根据加工表面特征设定符合实际的表征准则，通过以分水岭算法为代表的分割算法^[12-13]，不经过滤波直接从原始形貌数据中提取具有代表性的轮廓特征，不会丢失类似于刮研表面研点的重要轮廓信息，适用于表征刮研表面的微观形貌。

然而，目前针对刮研表面测量和表征的研究很少。Fan等^[14]在二维参数的基础上扩充了2个几何参数和1个功能性参数，在宏观尺度上实现了对刮研表面研点的统计学评价。此外，现有研究还缺乏能够表征刮痕形态等与刮研表面结构特征和功能特性直接相关的重要参数。因此，有必要对刮研表面的微观形貌进行全面的参数化表征，以形成有效的评价办法。

为了深入研究刮研表面的特性，笔者根据刮研表面特征，基于3D-motif法提出了特征显著度，并结合ISO 25178-2:2021^[15]中的motif参数，定义了包含特征显著度在内的一组motif表征参数。基于motif参数的平均值、分布情况以及合并后的motif数量，对刮研表面的微观形貌进行分析和表征，以形成有效且全面的表征体系，有助于后续对刮研表面开展定量的特性分析。

1 刮研表面测量实验

1.1　刮研表面制备

为了充分表征刮研表面的微观形貌，制备3组精度不同的刮研表面进行测量与分析。鉴于1级、3级和4级这3种精度等级的刮研表面在研点数量的要求上区别较大，且表面粗糙度参数的差异也较为明显，本文选用这3种精度的刮研表面进行对比分析。

3组刮研表面试件按工艺标准经不同程度刮研加工而成，分别达到1级、3级和4级精度，如图1所示。3组刮研表面试件的材料均为HT200，最终尺寸均为40 mm×40 mm×10 mm。各刮研表面可见呈网格状交错分布的刀痕，其他参数如表1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同精度的刮研表面试件

Fig.1 Scraped surface specimens with different precision

表1 不同精度刮研表面试件的特征参数

Table 1 Characteristic parameters of scraped surface specimens with different precision

刮研表面精度	粗糙度/μm	研点数/个	刀痕状态
1级	1.661 8	≥25	细密
3级	2.040 2	≥20	细密
4级	2.599 6	≥12	较为粗大

新窗口打开| 下载CSV

1.2　测量设备及数据采集

本文选择图2所示的LI-3型接触式三维表面形貌测量仪作为刮研表面形貌数据的测量设备，该设备利用激光干涉位移传感器测量探针接触位置的高度，并通过移动工作台来改变探针的测量位置，从而实现对刮研表面形貌数据的整体测量。LI-3型接触式三维表面形貌测量仪的量程大且分辨率较高，配置了分辨率为5 nm的传感器，其z向测量范围为0~4 mm；工作台的x、y向位移均为50 mm。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 LI-3型接触式三维表面形貌测量仪

Fig.2 LI-3 contact three-dimensional surface morphology measuring instrument

刮研表面形貌数据的测量和处理方案如下：

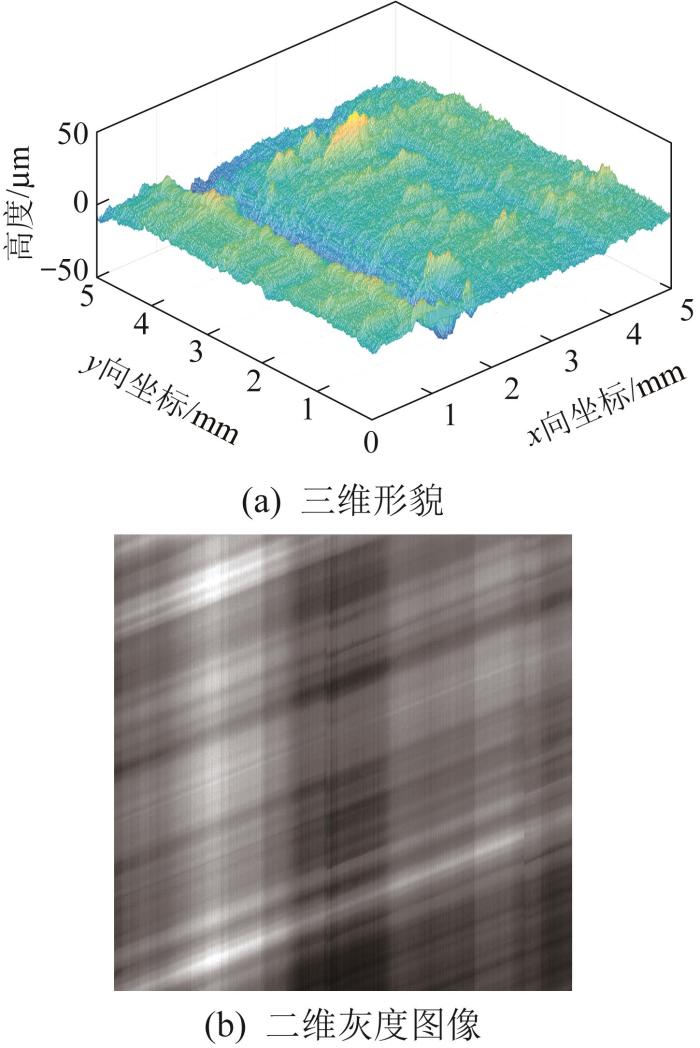
1）为了从不同面积尺度上进行分析，每组刮研表面均分别测量取样面积为25 mm²、取样间隔为10 μm和取样面积为0.25 mm²、取样间隔为1 μm的2组形貌数据；测量速度设为低速，测量结果以txt格式的单列点云数据（包含25万个测量点）输出。

2）将采集的点云数据导入MATLAB软件进行转换处理，以重构刮研表面的三维形貌，如图3(a)所示（以3级精度、25 mm²面积尺度的刮研表面为例）。随后，基于重构的三维形貌生成（500×500）像素的二维灰度图像^[16]，如图3(b)所示。其中，灰度值由高度转换确定，将测得的高度数据划分成256级灰度值，利用式(1)计算每个像素点的灰度值。最高点的灰度值为255，即纯白；最低点的灰度值为0，即纯黑。

G_{(i, j)} = \frac{255 \times (A_{(i, j)} - A_{m i n})}{A_{m a x} - A_{m i n}}

(1)

式中：G₍_i_,_j₎为像素点（i, j）的灰度值，A_（_i_,_j_）为像素点（i, j）的真实高度，A_max为真实高度的最大值，A_min为真实高度的最小值。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 刮研表面的三维形貌及二维灰度图像

Fig.3 Three-dimensional morphology and two-dimensional grayscale image of scraped surface

2 基于分水岭算法的3D-motif分割与合并

2.1　基于分水岭算法的3D-motif分割

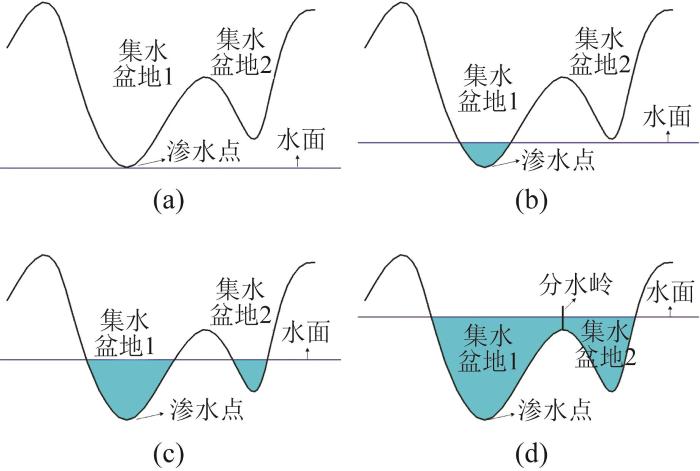
目前，2D-motif的定义已有统一规范的标准，但3D-motif的定义暂未统一。本文采用Barré等^[17-18]提出的3D-motif定义，即由一组分水岭包围的集水盆地为一个3D-motif，这种定义完全符合2D-motif定义的三维推广。在该定义中，一个3D-motif任意方向的铅垂面与该3D-motif的相交线均为一个标准的2D-motif。

根据上述3D-motif的定义，本文采用分水岭算法对刮研表面的灰度图像进行分割。分水岭算法将表面形貌看作由峰和谷组成的地貌，假定从表面最低点开始逐渐浸水直至淹没最高点，每个被峰包围的谷为一个集水盆地，在不同的集水盆地相互溢出接触点处建立堤坝；当整个浸水过程结束后，得到由堤坝集合而成的分水岭以及被分割出的集水盆地，该集水盆地即为3D-motif，如图4所示。分水岭算法的优势为分割彻底，且分割后不会遗失表面形貌中重要的结构特征，可充分保留显著的微观特征。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 分水岭算法的浸水过程

Fig.4 Immersion process of watershed algorithm

2.2　3D-motif的合并算法

原始分水岭算法为了进行彻底分割，保留了所有闭合的集水盆地，这会造成过分割现象，即会产生大量琐碎的过小3D-motif，如图5所示。这些琐碎的3D-motif虽符合集水盆地的标准，但因受到面积和高度的限制，无法作为具有代表性的特征。因此，须对原始分割得到的3D-motif进行合并，以得到足够大且具有代表性的3D-motif。这一合并过程需要在去除过多琐碎3D-motif的同时防止具有显著结构特征的3D-motif被合并，否则会导致表面的重要特征丢失，进而影响最终的分析精度。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 原始分水岭算法的过分割现象

Fig.5 Over-segmentation phenomenon of original watershed algorithm

本文先通过最小面积阈值法来去除过分割产生的琐碎3D-motif，然后遍历剩余的3D-motif，将不满足设定阈值的3D-motif按溢出顺序向相邻3D-motif进行深度合并。深度合并条件如下：

{\bar{z}}_{3} - m i n (z_{3}) \geq η m a x [({\bar{z}}_{1} - m i n (z_{1})), ({\bar{z}}_{2} - m i n (z_{2}))]

(2)

式中：z₁为被合并motif的高度；z₂为被合并motif的相邻motif的高度；z₃为合并后新motif的高度；z₁、z₂、z₃为对应的单个motif区域内的高度均值；η为深度条件系数，通常取1.1~1.3。

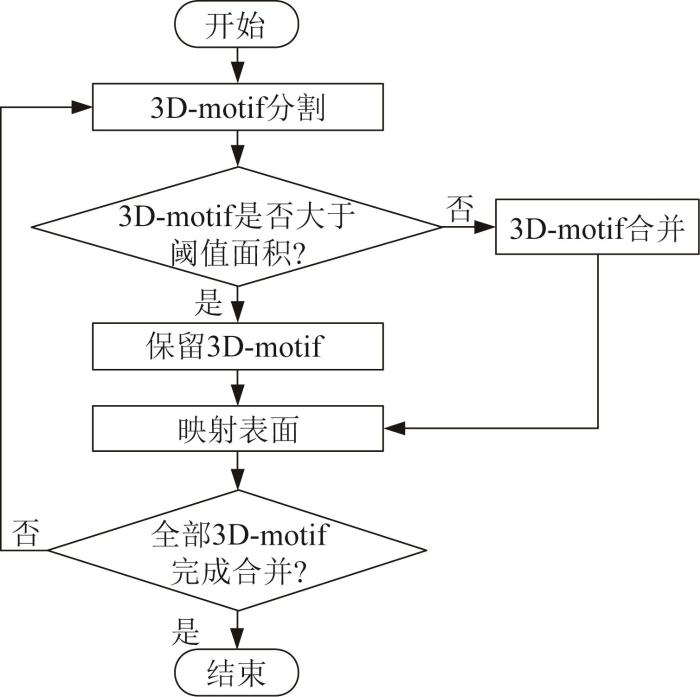
综上，3D-motif的合并流程如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 3D-motif的合并流程

Fig.6 Merging process of 3D-motif

按照图6所示的合并逻辑，将所有不符合面积要求的琐碎3D-motif进行循环合并，且依照深度原则，以避免损失显著的高度特征。最终得到的所有3D-motif均大于设定的面积阈值，避免了保留大量无意义的3D-motif。

此外，本文所使用的合并算法设置了原始表面的映射表面，映射表面只包含分水岭的分割信息，在得到符合条件的3D-motif后，对该motif区域内的元素进行统一赋值，这不会对原始表面信息产生影响，因此可在每次合并后再次调用分水岭算法重新进行分割循环，从而得到合适表征尺寸的3D-motif。

3 刮研表面形貌表征与结果分析

3.1　刮研表面形貌特征分析

刮研表面上最显著的结构特征为刮刀刮削形成的刮痕和研点，不同轮次的刮削成一定角度交错，最终形成网格状纹理。单次刮削的刮痕因刮刀和刮研手法不同而呈现出不同的规则形状，多为条形、燕尾形或“6”字形，但经多轮刮削和研磨后的刮痕大多呈不规则的多边形。由于下刀位置为上一次研磨后出现的研点处，而非对表面进行整体加工，因此最终刮研表面上的刮痕和研点的分布无特定规律。图7所示为经历2轮刮削和研磨的刮研表面的简化模型。其中：刮痕和研点的分布简化为均匀分布；考虑到研磨工序的影响，研点顶端简化为平整凸台。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 刮研表面简化模型

Fig.7 Simplified model of scraped surface

研点通常为一轮刮削和研磨后表面上相对较高的地方，其位置由研磨过程确定。研点处存在一定的塑性变形和表面硬化，其微观结构近似为面积较小的平整凸台。研点在摩擦过程中可减小实际接触面积，从而减小摩擦；研点在润滑过程中起油楔起升作用^[19]，在一定程度上减小了刮研表面润滑后的摩擦系数。当油膜较薄或润滑油为稀油液时，研点的油楔起升作用更为明显。当将刮痕简化为三角形沟槽且导轨上的研点与刮痕交替分布时，起升力的计算式如下：

W_{J} = \frac{n B μ {(L / n - 2 l)}^{3} Δ d}{d^{3}}

(3)

W_{D} = 0.133 \frac{μ v B l^{2} n}{d^{2} [1 + {(2 l / B)}^{2}]}

(4)

式中：W_J为静态起升力（即油膜斥力），W_D为动态起升力，B为刮痕宽度，μ为润滑油的动力黏度，n为研点数量，d为最小油膜厚度， $∆$ d为油膜厚度的变化率，L为导轨长度，l为刮痕长度，v为导轨运行速度。

由式(3)和式(4)可知，起升力与研点数量和刮痕形状相关，即研点数量和刮痕形状均会对刮研表面的润滑性能产生影响。数量恰当的研点和形状合适的刮痕会使润滑后的刮研表面运行更平稳，磨损量更小。

3.2　刮研表面形貌的3D-motif表征

利用motif法对加工表面形貌进行表征时需要定义相应的motif参数，以对motif进行评价。根据ISO 25178-2:2021中常用的motif参数，以及已有研究中集水盆地motif的常用参数，本文结合刮研表面具有复杂形状刮痕的特点，提出了一个新的motif参数——特征显著度k。计算单个motif向相邻符合条件的motif溢出的点与原motif最低点的高度差和距离，将这2个点的高度差与距离的比值定义为特征显著度k，以实现对表面形貌上的局部形态进行评价。特征显著度k的数值越大，则该区域在高度特征上相对周围环境越显著。

鉴于对刮研表面进行分割与合并后得到的3D-motif往往呈不规则形状，难以通过长度、宽度来表征刮研表面的形貌特征，因此本文结合各向异性率、面积参数与方向角对3D-motif的基本尺寸进行综合表征。该评价方法可直观体现motif尺寸参数对motif形态的影响。

结合5项常用的motif参数，本文最终定义以下6个motif参数来对刮研表面进行表征^[20-21]。

1）motif尺寸参数：深度h、面积S；

2）motif形态参数：方向角θ、各向异性率r、扁平系数f、特征显著度k。

其中，第p个motif的各向异性率r_p 、扁平系数f_p 的计算式如下：

r_{p} = \frac{(l_{p} - w_{p})}{l_{p}}

(5)

f_{p} = \sqrt[]{\frac{S_{p}}{π}} / h_{p}

(6)

式中：p为motif的位置编号，l_p 、w_p、S_p、h_p 分别为第p个motif的长度、宽度、面积和深度。

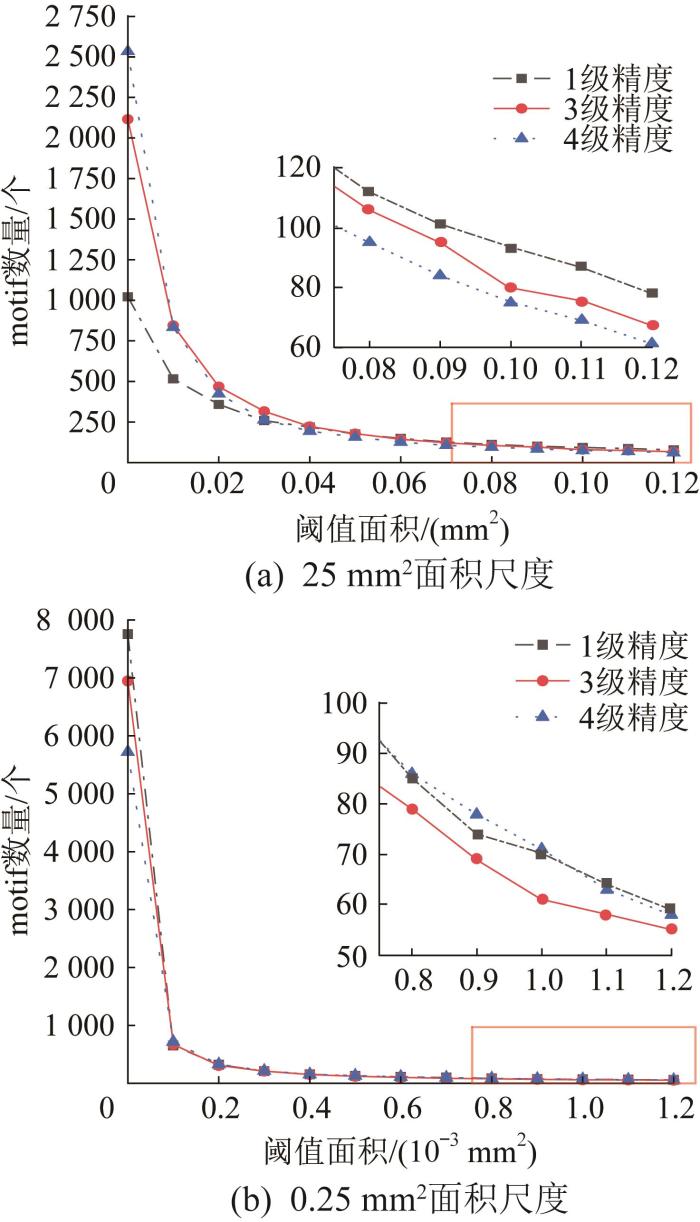
除了这6个参数外，本文还将结合合并后的motif数量及motif参数的分布情况，以实现从尺寸、形态、分布等多个方面对刮研表面的形貌特征进行综合评价。为了得到可以恰当表征刮研表面形貌的3D-motif，需要确定合适的motif面积阈值，以保证分割合并后得到的motif尺寸适用于表征刮研表面的形貌。设定多组面积阈值后，基于3D-motif法对不同面积尺度、不同精度的刮研表面的灰度图像进行分割与合并，得到阈值面积与合并后motif数量之间的关系，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 刮研表面motif数量与阈值面积的关系

Fig.8 Relationship between motif number and threshold area of scraped surface

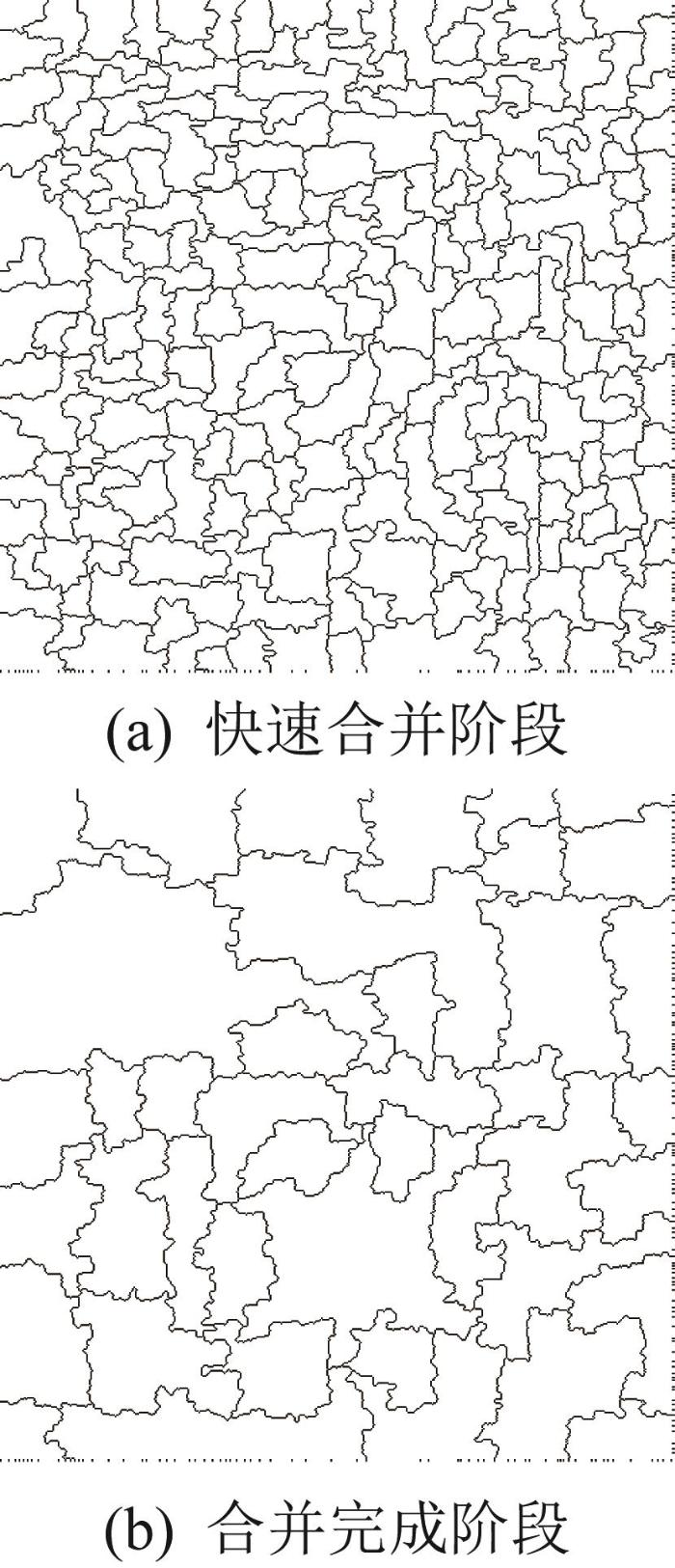
由图8(a)可知，对于3组25 mm²面积尺度的刮研表面，当阈值面积Δ≤0.04 mm²时，其motif数量随阈值面积的增大而显著减少，即处于快速合并阶段，如图9(a)所示。这是因为大量过分割得到的无意义motif被合并为包含显著特征点的较大motif；当Δ>0.04 mm²时，motif的合并基本发生在包含共同显著特征点的motif之间，故motif数量的减少速度明显降低；当Δ≥0.10 mm²时，motif数量随阈值面积增大的变化幅度已经很小，motif数量基本趋于稳定，即处于合并完成阶段，如图9(b)所示。当Δ=0.04 mm²时，单次合并时motif数量的变化幅度整体小于40%；当Δ=0.12 mm²时，单次合并时motif数量的变化幅度均低于15%，此时得到的motif数量已比较稳定，继续增大阈值面积对motif数量变化的影响较小，且保留的单个motif的尺寸已较大，可以表征局部的表面形貌。因此，针对25 mm²面积尺度的刮研表面，取Δ=0.04 mm²作为快速合并阶段的面积阈值，取Δ=0.12 mm²作为合并完成阶段的面积阈值^[21]。由图8(b)可知，在0.25 mm²面积尺度下，刮研表面的motif数量随阈值面积增大的变化趋势与25 mm²面积尺度的基本相同，均先经历快速合并阶段，即motif数量快速减少，之后再对不显著的特征区域进行合并，motif数量缓慢减少。按照与25 mm²面积尺度一样的判定条件，取单次合并时motif数量的变化幅度全部小于40%时的面积阈值，即Δ=0.4×10^-3 mm²作为快速合并阶段的面积阈值；取单次合并时motif数量的变化幅度均低于15%时的面积阈值，即Δ=1.0×10^-3 mm²作为合并完成阶段的面积阈值。此外，从图8中还可以看出，不同精度的刮研表面的motif数量在变化趋势上整体相同，但阈值面积较小时motif数量快速减少；随着阈值面积逐渐增大且接近快速合并阶段的阈值时，motif数量的减少幅度逐渐变缓，并在阈值面积接近合并完成阶段的阈值时基本稳定。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 刮研表面motif的不同合并阶段

Fig.9 Different merging stages of motif on scraped surface

3.3　刮研表面的motif参数分析

为观察分析刮研表面的整体纹理走向，选择阈值面积Δ=0.12 mm²时的3D-motif分割与合并结果作为25 mm²面积尺度刮研表面motif参数的提取对象，选择Δ=1.0×10^-3 mm²时的3D-motif分割与合并结果作为0.25 mm²面积尺度刮研表面motif参数的提取对象。3种精度的刮研表面在2种面积尺度下的motif参数均值分别如表2和表3所示。

表2 取 Δ=0.12 mm² 时刮研表面的motif参数均值（面积尺度为25 mm² ）

Table 2 Mean motif parameter value of scraped surface under Δ=0.12 mm² (with area scale of 25 mm²)

刮研精度	h/μm	S/mm²	θ/(°)	r	f	k
1级	15.178 8	0.307 5	87.4	0.841 4	2.061 2	0.283 8
3级	20.504 4	0.344 0	83.3	0.782 8	1.649 4	0.361 1
4级	28.281 9	0.359 3	88.1	0.786 5	1.297 6	0.394 6

新窗口打开| 下载CSV

表3 取 Δ=1.0×10^-³ mm² 时刮研表面的motif参数均值（面积尺度为0.25 mm² ）

Table 3 Mean motif parameter value of scraped surface under Δ=1.0×10^-3 mm² (with area scale of 0.25 mm²)

刮研精度	h/μm	S/mm²	θ/(°)	r	f	k
1级	5.398 7	0.003 4	118.1	0.821 8	6.132 6	0.099 3
3级	7.687 3	0.003 6	123.6	0.799 0	4.428 2	0.170 2
4级	12.293 0	0.003 4	115.7	0.830 5	2.672 3	0.217 8

新窗口打开| 下载CSV

由表2和表3可知，3种不同精度的刮研表面在深度h、方向角θ、扁平系数f、特征显著度k这4项motif参数上有明显差异，除θ外的其余3个参数的变化趋势呈一定规律。其中：h的平均值可以衡量一组刮研表面整体的深度水平，但是难以反映深度的波动情况和表面粗糙度；θ反映刮研表面的纹理走向，难以仅用均值进行评价。因此，有必要对这2项motif参数的分布情况进行分析。

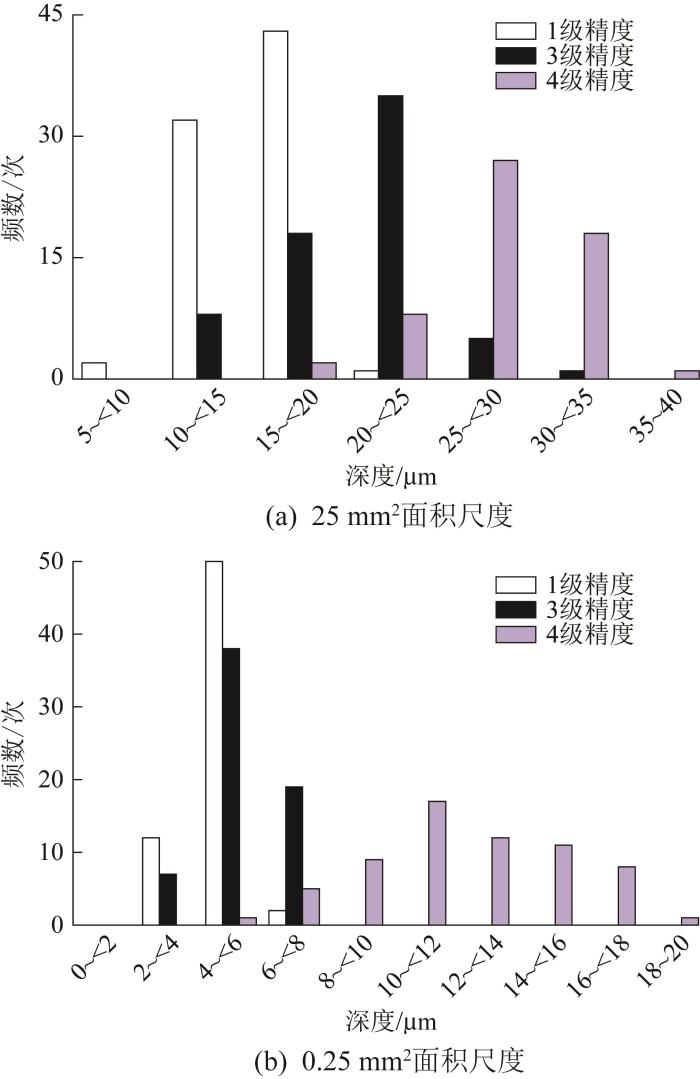
在2种不同面积尺度下，刮研表面的motif深度均值随精度的降低而逐渐增大，即单个显著区域的高度差增大，这与基于二维中线法测量得到的刮研表面粗糙度、微观不平度和微观不平度平均间距等参数的变化趋势相同，说明精度较高的刮研表面的平整度较优。这是因为精度高的刮研表面经过更多次的刮削和研磨，整体加工更细致均匀，研点处的形变量更大，使得高度较为显著的motif区域的平均显著度更小，即motif深度均值更小。从图10所示的刮研表面motif深度的分布情况可以看出，3种精度的刮研表面的motif深度在2种面积尺度下均接近正态分布，大多数motif的深度集中在各精度对应的motif深度均值附近。但随着刮研表面精度的降低，motif深度的分布范围逐渐增大，意味着表面粗糙度增大。由此可知，motif深度均值与刮研精度成反比，与表面粗糙度成正比。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 刮研表面motif深度的分布情况

Fig.10 Distribution of motif depth of scraped surface

精度不同的3组刮研表面的motif方向角均值基本一致。在25 mm²面积尺度下，3组刮研表面的motif方向角均值都接近90º，方向角主要集中在0º~20º和160º~180º这2个范围内，如图11(a)所示。虽然motif方向角均值接近90º，但刮研表面的实际纹理走向接近于沿0º横向发展，与最后一轮研磨加工后的刀痕方向接近。在0.25 mm²面积尺度下，3组刮研表面的motif方向角均值接近120º，分布上主要集中在100º~180º范围内，如图11(b)所示。由于涉及更微观的表面纹理，motif方向角与刮研表面刀痕形成时的加工角度相关且受到加工后金属表面的微观机理变化的影响。

图11

新窗口打开| 下载原图ZIP| 生成PPT

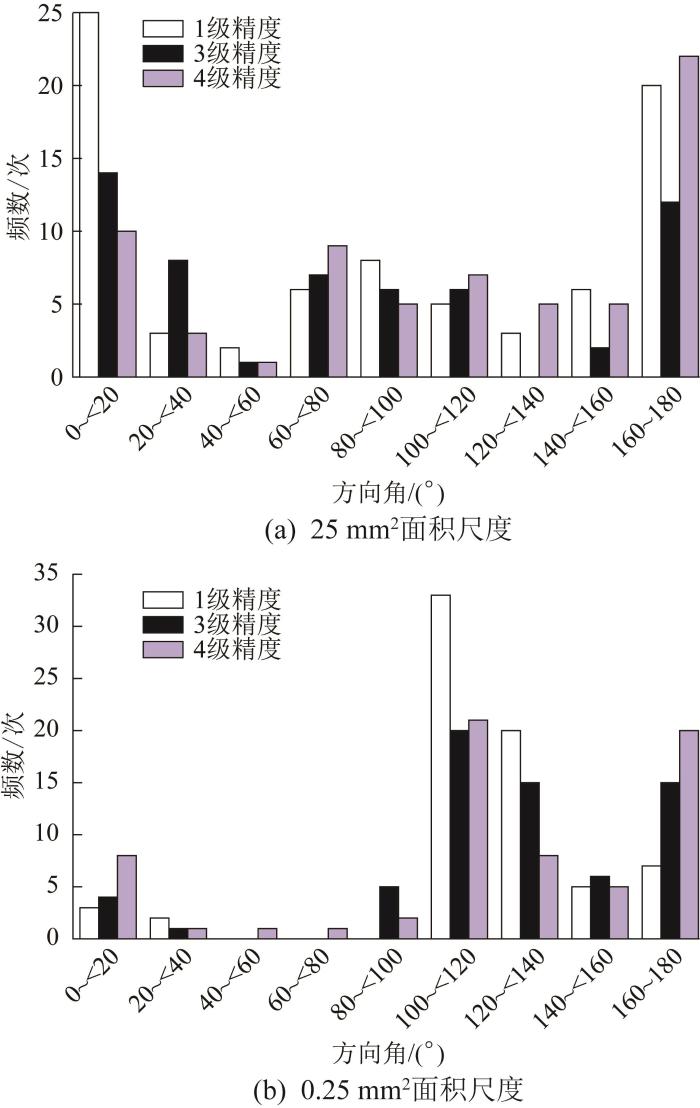
图11 刮研表面motif方向角的分布情况

Fig.11 Distribution of motif direction angle of scraped surface

对于其余的motif参数（面积S、各向异性率r、扁平系数f和特征显著度k），在25 mm²面积尺度下，刮研表面的motif面积均值随刮研精度的提高而减小；但在0.25 mm²面积尺度下，motif面积均值的变化无明显规律，整体变化趋势与motif数量的变化趋势相反。3组不同精度的刮研表面的motif各向异性率均值在2种面积尺度下的差异均不明显且无显著规律，其数值较接近1，说明motif的轮廓形态比较规则。在25 mm²和0.25 mm²面积尺度下，刮研表面motif的扁平系数和特征显著度的变化趋势为：随着刮研精度的提高，扁平系数均值增大，特征显著度均值减小，说明具有较为显著高度特征的局部区域相对于周围其他区域的显著程度降低，即motif形态更加扁平。

4 结论

本文以刮研表面为对象，采用分水岭算法对其灰度图像进行3D-motif分割与合并，并通过由6个motif参数构成的评价体系对刮研表面形貌进行表征与分析。主要结论如下：

1）刮研表面的研点经研磨后存在一定的塑性变形，其微观结构近似于面积较小的平整凸台。合适的研点数量与刮痕形状可以改善刮研表面的润滑性能。

2）不同精度刮研表面的motif深度、motif扁平系数、特征显著度的均值有明显差异，motif深度、特征显著度与刮研精度成反比，motif扁平系数与刮研精度成正比。

3）不同精度刮研表面的motif方向角均集中分布在最后一轮刮削方向上，motif深度的分布趋势在2种面积尺度上相同，分布范围随刮研精度的降低而增大。

本文定义了特征显著度，用于评价刮研表面局部区域高度特征点的形态，并尝试通过结合motif参数的均值与分布情况来综合表征刮研表面的微观形貌，可为刮研表面特性的分析和自动化刮研设备的研制提供参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张潮

刮研工艺介绍

［J］.机械制造，2004，42（1）：16-17. doi：10.3969/j.issn.1000-4998.2004.01.005

DOI:10.3969/j.issn.1000-4998.2004.01.005 [本文引用: 1]

ZHANG

Introduction of scraping technology

［J］. Machinery， 2004， 42（1）： 16-17.

DOI:10.3969/j.issn.1000-4998.2004.01.005 [本文引用: 1]

[2]

李小朋，孙雷雷，刘永红.

刮研加工自动化研究现状及发展分析

［J］.制造技术与机床，2012（7）：97-100. doi：10.3969/j.issn.1005-2402.2012.07.031

DOI:10.3969/j.issn.1005-2402.2012.07.031 [本文引用: 1]

X P

， SUN

L L

， LIU

Y H

Status of auto-scraping research and analysis of its development

［J］. Manufacturing Technology & Machine Tool， 2012（7）： 97-100.

DOI:10.3969/j.issn.1005-2402.2012.07.031 [本文引用: 1]

[3]

孙雷雷

刮研加工表面自动检测技术研究

［D］.青岛：中国石油大学（华东），2014.

[本文引用: 1]

SUN

L L

Research on automatic surface inspection technology for scraping workpiece

［D］. Qingdao： China University of Petroleum （East China）， 2014.

[本文引用: 1]

[4]

曹恒督，高志.

一种刮研机器人及其高点识别算法的设计

［J］.机械设计与制造，2021（10）：255-258，262. doi：10.3969/j.issn.1001-3997.2021.10.057

DOI:10.3969/j.issn.1001-3997.2021.10.057 [本文引用: 1]

CAO

H D

， GAO

Design of new auto-scraping robot and its high-points recognition algorithm

［J］. Machinery Design & Manufacture， 2021（10）： 255-258， 262.

DOI:10.3969/j.issn.1001-3997.2021.10.057 [本文引用: 1]

[5]

HSIEH

T H

， JYWE

W Y

， TSAI

Y C

， et al.

Design， manufacture， and development of a novel automatic scraping machine

［J］. The International Journal of Advanced Manufacturing Technology， 2017， 90（9）： 2617-2630.

[本文引用: 1]

[6]

刘伟，童慧芬，李梅，等.

导轨自动刮研系统的设计与研究

［J］.制造技术与机床，2014（1）：70-73. doi：10.3969/j.issn.1005-2402.2014.01.020

DOI:10.3969/j.issn.1005-2402.2014.01.020 [本文引用: 1]

LIU

， TONG

H F

， LI

， et al.

Design and research of automatic scraping system for guideway

［J］. Manufacturing Technology & Machine Tool， 2014（1）： 70-73.

DOI:10.3969/j.issn.1005-2402.2014.01.020 [本文引用: 1]

[7]

王犇

球头铣削表面形貌表征及摩擦磨损特性研究

［D］. 哈尔滨：哈尔滨理工大学，2021.

[本文引用: 1]

WANG

Study on surface topography characterization and friction and wear performance of ball-end milling

［D］. Harbin： Harbin University of Science and Technology， 2021.

[本文引用: 1]

[8]

TANG

C X

， TANG

， VAN WESTEN

C J

， et al.

Modeling landslide failure surfaces by polynomial surface fitting

［J］. Geomorphology， 2020， 368： 107358.

[本文引用: 1]

[9]

MANDELBROT

B B

. The fractal geometry of nature［M］. New York： W. H. Freeman and Company， 1982.

[本文引用: 1]

[10]

BROWN

C A

， CHARLES

P D

， JOHNSEN

W A

， et al.

Fractal analysis of topographic data by the patchwork method

［J］. Wear， 1993， 161（1/2）： 61-67.

[本文引用: 1]

[11]

张永芳，刘成，强程，等.

基于分块迭代函数系统的缸套表面织构的分形表征

［J］.中国表面工程，2022，35（1）： 220-230. doi：10.11933/j.issn.1007?9289.20210804001

DOI:10.11933/j.issn.1007?9289.20210804001 [本文引用: 1]

ZHANG

Y F

， LIU

， JIANG

， et al.

Fractal characterization on surface texture of cylinder liner based on partitioned iterated function system

［J］. China Surface Engineering， 2022， 35（1）： 220-230.

DOI:10.11933/j.issn.1007?9289.20210804001 [本文引用: 1]

[12]

JIANG

， SENIN

， SCOTT

P J

， et al.

Feature-based characterisation of surface topography and its application

［J］. CIRP Annals， 2021， 70（2）： 681-702.

[本文引用: 1]

[13]

VINCENT

， SOILLE

Watersheds in digital spaces： an efficient algorithm based on immersion simulations

［J］. IEEE Transactions on Pattern Analysis & Machine Intelligence， 1991， 13（6）： 583-598.

[本文引用: 1]

[14]

FAN

K C

， TORNG

， JYWE

， et al.

3-D measurement and evaluation of surface texture produced by scraping process

［J］. Measurement， 2012， 45（3）： 384-392.

[本文引用: 1]

[15]

International Organization for Standardization. Geometrical product specifications （GPS）： surface texture： areal. Part 2： terms， definitions and surface texture parameters：［S］. Geneve： International Organization for Standardization， 2021： 1-76.

[本文引用: 1]

[16]

万筱怡，刘小君，刘焜.

基于分水岭算法的3D-motif构造及其对表面形貌的表征

［J］.润滑与密封，2010，35（8）：31-35. doi：10.3969/j.issn.0254-0150.2010.08.009

DOI:10.3969/j.issn.0254-0150.2010.08.009 [本文引用: 1]

WAN

X Y

， LIU

X J

， LIU

3D-motif based on watershed algorithm and its application to the characterization of surface topography

［J］. Lubrication Engineering， 2010， 35（8）： 31-35.

DOI:10.3969/j.issn.0254-0150.2010.08.009 [本文引用: 1]

[17]

BARRÉ

， LOPEZ

Watershed lines and catchment basins： a new 3D-motif method

［J］. International Journal of Machine Tools and Manufacture， 2000， 40（8）： 1171-1184.

[本文引用: 1]

[18]

黄长辉，邹文栋，颜乐先，等.

一种3D-Motif方法对工件磨痕三维形貌的表征

［J］. 兵器装备工程学报，2010，31（2）：86-89. doi：10.3969/j.issn.1006-0707.2010.02.029

DOI:10.3969/j.issn.1006-0707.2010.02.029 [本文引用: 1]

HUANG

C H

， ZOU

W D

， YAN

L X

， et al.

Characterization of 3D morphology of grinding marks of workpieces by a 3D-Motif method

［J］. Journal of Ordnance Equipment Engineering， 2010， 31（2）： 86-89.

DOI:10.3969/j.issn.1006-0707.2010.02.029 [本文引用: 1]

[19]

金长善，于凤鸣.

关于导轨刮研表面润滑特性的分析

［J］. 设备维修，1984（6）：26-30.

[本文引用: 1]

JIN

C S

， YU

F M

Analysis of lubrication characteristics of scraping surface of guide rail

［J］. Plant Maintenance Engineering， 1984（6）： 26-30.

[本文引用: 1]

[20]

李志强

表面微观形貌的测量及其表征

［D］.重庆：重庆大学，2006.

[本文引用: 1]

Z Q

The survey and token of micro-scale surface

［D］. Chongqing： Chongqing University， 2006.

[本文引用: 1]

[21]

邹文栋，黄长辉，欧阳小琴，等.

合金韧窝断口微观形貌的扫描白光干涉三维检测重构及Motif表征

［J］.机械工程学报，2011，47（10）：8-13. doi：10.3901/jme.2011.10.008

DOI:10.3901/jme.2011.10.008 [本文引用: 2]

ZOU

W D

， HUANG

C H

， OUYANG

X Q

， et al.

Scanning white-light interferometric measurement 3D reconstruction and Motif evaluation of alloy dimple fracture microtopography

［J］. Journal of Mechanical Engineering， 2011， 47（10）： 8-13.

DOI:10.3901/jme.2011.10.008 [本文引用: 2]

刮研工艺介绍

2004

... 刮研是一种平面光整加工的微量切削方法^[1]，具有对加工尺寸限制小、加工位置灵活以及刮研后表面润滑性能优异、配合刚度高、运行平稳和使用寿命长且易修复等特点^[2].刮研表面大多应用于大型设备和高精度设备的滑动结合面，其质量直接影响设备的最终精度、配合性能和机械效率等.但是，现阶段的刮研加工主要依靠人工进行操作，自动化程度低，此外还缺乏对刮研表面微观机理的研究. ...

刮研工艺介绍

2004

刮研加工自动化研究现状及发展分析

2012

刮研加工自动化研究现状及发展分析

2012

刮研加工表面自动检测技术研究

2014

... 目前，针对刮研工艺的研究主要集中在改进具体类型零件的刮研方法和提高刮研自动化程度等方面.例如：孙雷雷^[3]对刮研表面的自动检测技术进行了研究；曹恒督等^[4]设计了一种可以自动识别研点的刮研机器人；Hsieh等^[5]对自动刮研机的结构及其制造工艺进行了设计与研究；刘伟等^[6]针对导轨研发了一套自动刮研系统.然而，上述研究缺乏对刮研表面表征方式和功能机理的理论分析，导致自动化刮研难以达到与手工刮研相同的加工精度.刮研表面的微观形貌与其功能机理关联紧密，对刮研表面形貌进行准确表征是实现刮研自动化与标准化的前提. ...

刮研加工表面自动检测技术研究

2014

一种刮研机器人及其高点识别算法的设计

2021

一种刮研机器人及其高点识别算法的设计

2021

Design， manufacture， and development of a novel automatic scraping machine

2017

导轨自动刮研系统的设计与研究

2014

导轨自动刮研系统的设计与研究

2014

球头铣削表面形貌表征及摩擦磨损特性研究

2021

... 现有的加工表面形貌表征方法主要包括三维中面法、分形法和motif法.其中：三维中面法是二维轮廓法在三维尺度上的推广和完善^[7]，通过数学算法拟合得到具有代表性特征的三维中面^[8]，适用于表征具有各向同性的表面以及具有普遍性和确定性纹理的表面.但是，刮研表面的刮痕分布使得基于刮研表面形貌数据拟合的三维中面的可靠性较差，故难以用该方法来表征刮研表面的微观形貌.分形法是基于数学中的分形理论^[9]，适用于表征具有随机性、多尺度性和自相似性或自仿射性的表面^[10-11]，即具有分形特征的表面，而刮研表面不具有上述特点.motif法是一种基于包络制的表征方法，可根据加工表面特征设定符合实际的表征准则，通过以分水岭算法为代表的分割算法^[12-13]，不经过滤波直接从原始形貌数据中提取具有代表性的轮廓特征，不会丢失类似于刮研表面研点的重要轮廓信息，适用于表征刮研表面的微观形貌. ...

球头铣削表面形貌表征及摩擦磨损特性研究

2021

Modeling landslide failure surfaces by polynomial surface fitting

2020

1982

Fractal analysis of topographic data by the patchwork method

1993

基于分块迭代函数系统的缸套表面织构的分形表征

2022

基于分块迭代函数系统的缸套表面织构的分形表征

2022

Feature-based characterisation of surface topography and its application

2021

Watersheds in digital spaces： an efficient algorithm based on immersion simulations

1991

3-D measurement and evaluation of surface texture produced by scraping process

2012

... 然而，目前针对刮研表面测量和表征的研究很少.Fan等^[14]在二维参数的基础上扩充了2个几何参数和1个功能性参数，在宏观尺度上实现了对刮研表面研点的统计学评价.此外，现有研究还缺乏能够表征刮痕形态等与刮研表面结构特征和功能特性直接相关的重要参数.因此，有必要对刮研表面的微观形貌进行全面的参数化表征，以形成有效的评价办法. ...

2021

... 为了深入研究刮研表面的特性，笔者根据刮研表面特征，基于3D-motif法提出了特征显著度，并结合ISO 25178-2:2021^[15]中的motif参数，定义了包含特征显著度在内的一组motif表征参数.基于motif参数的平均值、分布情况以及合并后的motif数量，对刮研表面的微观形貌进行分析和表征，以形成有效且全面的表征体系，有助于后续对刮研表面开展定量的特性分析. ...

基于分水岭算法的3D-motif构造及其对表面形貌的表征

2010

... 2）将采集的点云数据导入MATLAB软件进行转换处理，以重构刮研表面的三维形貌，如图3(a)所示（以3级精度、25 mm²面积尺度的刮研表面为例）.随后，基于重构的三维形貌生成（500×500）像素的二维灰度图像^[16]，如图3(b)所示.其中，灰度值由高度转换确定，将测得的高度数据划分成256级灰度值，利用式(1)计算每个像素点的灰度值.最高点的灰度值为255，即纯白；最低点的灰度值为0，即纯黑. ...

基于分水岭算法的3D-motif构造及其对表面形貌的表征

2010

Watershed lines and catchment basins： a new 3D-motif method

2000

... 目前，2D-motif的定义已有统一规范的标准，但3D-motif的定义暂未统一.本文采用Barré等^[17-18]提出的3D-motif定义，即由一组分水岭包围的集水盆地为一个3D-motif，这种定义完全符合2D-motif定义的三维推广.在该定义中，一个3D-motif任意方向的铅垂面与该3D-motif的相交线均为一个标准的2D-motif. ...

一种3D-Motif方法对工件磨痕三维形貌的表征

2010

一种3D-Motif方法对工件磨痕三维形貌的表征

2010

关于导轨刮研表面润滑特性的分析

1984

... 研点通常为一轮刮削和研磨后表面上相对较高的地方，其位置由研磨过程确定.研点处存在一定的塑性变形和表面硬化，其微观结构近似为面积较小的平整凸台.研点在摩擦过程中可减小实际接触面积，从而减小摩擦；研点在润滑过程中起油楔起升作用^[19]，在一定程度上减小了刮研表面润滑后的摩擦系数.当油膜较薄或润滑油为稀油液时，研点的油楔起升作用更为明显.当将刮痕简化为三角形沟槽且导轨上的研点与刮痕交替分布时，起升力的计算式如下： ...

关于导轨刮研表面润滑特性的分析

1984

表面微观形貌的测量及其表征

2006

... 结合5项常用的motif参数，本文最终定义以下6个motif参数来对刮研表面进行表征^[20-21]. ...

表面微观形貌的测量及其表征

2006

... 结合5项常用的motif参数，本文最终定义以下6个motif参数来对刮研表面进行表征^[20-21]. ...

合金韧窝断口微观形貌的扫描白光干涉三维检测重构及Motif表征

2011

... 结合5项常用的motif参数，本文最终定义以下6个motif参数来对刮研表面进行表征^[20-21]. ...

... 由图8(a)可知，对于3组25 mm²面积尺度的刮研表面，当阈值面积Δ≤0.04 mm²时，其motif数量随阈值面积的增大而显著减少，即处于快速合并阶段，如图9(a)所示.这是因为大量过分割得到的无意义motif被合并为包含显著特征点的较大motif；当Δ>0.04 mm²时，motif的合并基本发生在包含共同显著特征点的motif之间，故motif数量的减少速度明显降低；当Δ≥0.10 mm²时，motif数量随阈值面积增大的变化幅度已经很小，motif数量基本趋于稳定，即处于合并完成阶段，如图9(b)所示.当Δ=0.04 mm²时，单次合并时motif数量的变化幅度整体小于40%；当Δ=0.12 mm²时，单次合并时motif数量的变化幅度均低于15%，此时得到的motif数量已比较稳定，继续增大阈值面积对motif数量变化的影响较小，且保留的单个motif的尺寸已较大，可以表征局部的表面形貌.因此，针对25 mm²面积尺度的刮研表面，取Δ=0.04 mm²作为快速合并阶段的面积阈值，取Δ=0.12 mm²作为合并完成阶段的面积阈值^[21].由图8(b)可知，在0.25 mm²面积尺度下，刮研表面的motif数量随阈值面积增大的变化趋势与25 mm²面积尺度的基本相同，均先经历快速合并阶段，即motif数量快速减少，之后再对不显著的特征区域进行合并，motif数量缓慢减少.按照与25 mm²面积尺度一样的判定条件，取单次合并时motif数量的变化幅度全部小于40%时的面积阈值，即Δ=0.4×10^-3 mm²作为快速合并阶段的面积阈值；取单次合并时motif数量的变化幅度均低于15%时的面积阈值，即Δ=1.0×10^-3 mm²作为合并完成阶段的面积阈值.此外，从图8中还可以看出，不同精度的刮研表面的motif数量在变化趋势上整体相同，但阈值面积较小时motif数量快速减少；随着阈值面积逐渐增大且接近快速合并阶段的阈值时，motif数量的减少幅度逐渐变缓，并在阈值面积接近合并完成阶段的阈值时基本稳定. ...

合金韧窝断口微观形貌的扫描白光干涉三维检测重构及Motif表征

2011

... 结合5项常用的motif参数，本文最终定义以下6个motif参数来对刮研表面进行表征^[20-21]. ...

〈

〉