纤维增强复合材料多模式内聚断裂的相场模型

doi:10.3785/j.issn.1006-754X.2024.03.222

纤维增强复合材料多模式内聚断裂的相场模型

粟海波^,¹, 陈波潓¹, 吴熙²^,³, 王亮^,^,¹

1.上海交通大学船舶海洋与建筑工程学院，上海 200240

2.浙大城市学院工程学院，浙江杭州 310015

3.城市基础设施智能化浙江省工程研究中心，浙江杭州 310015

Phase-field model for multi-pattern cohesive fracture in fiber reinforced composite material

SU Haibo^,¹, CHEN Bohui¹, WU Xi²^,³, WANG Liang^,^,¹

1.School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China

2.School of Engineering, Hangzhou City University, Hangzhou 310015, China

3.Zhejiang Engineering Research Center of Intelligent Urban Infrastructure, Hangzhou 310015, China

通讯作者: 王亮（1987—），男，辽宁开原人，副教授，博士，从事复合材料力学与计算固体力学研究， E-mail: wang_liang@sjtu.edu.cn, http://orcid.org/0000-0002-1244-2557

收稿日期: 2023-12-13 修回日期: 2024-01-03

基金资助:

国家自然科学基金资助项目. 12102256
城市基础设施智能化浙江省工程研究中心开放基金资助项目. IUI2023-YB-07

Received: 2023-12-13 Revised: 2024-01-03

作者简介 About authors

粟海波（1999—），男，四川成都人，硕士生，从事复合材料相场模拟研究，E-mail:Harbour@sjtu.edu.cn , E-mail：Harbour@sjtu.edu.cn

摘要

经典的断裂相场法是基于脆性断裂理论建立的变分方法，因此其无法准确描述复合材料的准脆性断裂行为。基于此，提出了一种多相场模型来描述纤维增强复合材料的多模式内聚断裂行为。通过对各向异性相场驱动力和损伤本构关系的合理定义，提出了一种混合型内聚断裂相场模型，并通过推导得到了相应的演化方程与强度准则。采用该模型进行了3种复合材料板的裂纹扩展及失效仿真，结果表明，所提出的多相场模型能够有效模拟复合材料的多模式内聚断裂行为，具有较高的应用价值。

关键词： 复合材料 ; 相场模拟 ; 内聚断裂 ; 失效机理

Abstract

The classical fracture phase-field model is a variational method based on brittle fracture theory, which cannot accurately characterize the quasi-brittle fracture behavior of composite material. Based on this, a multi-phase-field model was proposed to describe the multi-pattern cohesive fracture behavior of fiber reinforced composites material. A hybrid cohesive fracture phase-field model was proposed by reasonably defining the phase-field driving force and the damage constitutive relationship for the anisotropic material, and the corresponding evolution equation and strength criterion were derived. The model was used to simulate the crack propagation and failure of three kinds of composite plates. The results showed that the proposed multi-phase-field model could effectively simulate the multi-pattern cohesive fracture behavior of composite material, and had high application value.

Keywords： composite materials ; phase-field modeling ; cohesive fracture ; failure mechanism

PDF (1761KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

粟海波, 陈波潓, 吴熙, 王亮. 纤维增强复合材料多模式内聚断裂的相场模型[J]. 工程设计学报, 2024, 31(3): 301-308 doi:10.3785/j.issn.1006-754X.2024.03.222

SU Haibo, CHEN Bohui, WU Xi, WANG Liang. Phase-field model for multi-pattern cohesive fracture in fiber reinforced composite material[J]. Chinese Journal of Engineering Design, 2024, 31(3): 301-308 doi:10.3785/j.issn.1006-754X.2024.03.222

纤维增强复合材料因其优良的力学性能，在航空航天器、车辆、船舶、建筑工程设备中得到广泛应用^[1-5]。相较于单组分材料，复合材料在材料特性、结构设计上的多变性，使得其在相同密度下具有更高的强度、刚度和韧性，但其损伤及失效机理更加复杂。对于常见的复合材料层合板，其损伤是由基体开裂、界面脱粘、分层、纤维断裂等多种因素相互作用而产生的，要精确地评估其损伤及失效行为相当困难。因此，开发先进有效的损伤及失效分析方法对复合材料的安全应用具有重要意义。

目前，材料的断裂分析主要基于断裂力学理论或损伤力学理论，相应的计算方法可分为非连续性方法^[6]和连续性方法^[7]两大类。非连续性方法用离散裂纹模型描述材料的开裂行为；连续性方法采用弥散裂纹模型，即通过引入损伤变量来表征材料的断裂过程。采用非连续性方法时需要显示、描述裂纹路径，存在裂纹跟踪、网格重划分等诸多困难；而基于损伤力学的连续性方法则存在损伤变量无直接的物理含义且可能存在网格依赖性等缺陷。最近20年间，断裂相场法作为新的材料断裂分析方法而受到了广泛关注。相场法仍采用弥散裂纹模型，但因基于断裂力学理论和损伤力学理论，而成为极具潜力的断裂分析方法之一。相场法基于Francfort等^[8]提出的能量变分原理，通过引入相场变量——序参量d将断裂面进行弥散化处理，将裂纹面断裂能转化为裂纹带的体积分，使得在数值计算上更容易实现。断裂相场法以断裂力学的能量法为基础，根据能量变分导出控制方程，从而驱动相场自发演化，因而不需要特意追踪和描述裂纹的扩展过程，这有效提高了断裂分析的便捷性和计算效率。

由于相场法的独特优势，其逐渐成为准确分析复合材料失效行为和机理的有效手段^[9]。如：2015年，Clayton等^[10]针对多晶体材料的破坏问题，提出了一种各向异性相场模型；Zhang等^[11-12]修改了结构张量的形式，将各向异性相场模型用于三维分析；Supriatna等^[13]基于木材结构，提出了新的各向异性混合模式的断裂失效相场模型，并进行了实验验证；Teichtmeister等^[14]引入了四阶结构张量，建立了四阶各向异性相场断裂模型，降低了对模型网格离散精度的要求，且使计算结果更容易收敛；Bleyer等^[15]建立了纤维复合材料的双相场模型，用于描述基体和纤维的断裂模式；Dean等^[16]基于Puck失效准则，提出了区分纤维和基体断裂的双相场损伤模型。

虽然相场模型的优势较为突出，但仍然存在一些固有缺陷。例如，经典相场模型的裂纹特征长度b对材料常数具有依存性，即b与材料强度相关。Amor等^[17]推导了b与临界应力 $σ_{c}$ 关系的解析表达式。Nguyen等^[18]利用这一关系，用材料强度 $σ_{m a x}$ 估计b，即 $b = 27 E G_{c} / (256 {σ_{m a x}}^{2})$ （式中：E为材料的弹性模量，G_c为材料断裂韧度），以接近材料本身的性质，此公式也被广泛利用^[11]。对于经典相场模型，裂纹特征长度与材料强度和断裂能的相关性，限制了其在复杂断裂问题中的准确应用。Wu^[19]提出了针对准脆性破坏的统一相场理论，建立了具有不同软化形式的统一内聚断裂相场模型，较好地解决了裂纹特征长度的非数值参数问题^[20]。统一内聚断裂相场模型中设有明确的材料强度及准脆性的断裂行为，裂纹特征长度不再由材料常数确定而作为数值参数存在。

本文针对纤维增强复合材料，提出了一种多相场内聚断裂分析模型。通过引入多相场变量，来准确描述复合材料的不同失效模式和机理；利用提出的相场分析方法，进行了单边缝复合材料开口板、含缺口变角度单层复合板、开孔复合材料层合板的裂纹扩展模拟，来证实所提出的相场模型在分析纤维增强复合材料复杂断裂失效中的优势和潜力。

1 纤维增强复合材料内聚断裂多相场模型

1.1　各向异性相场模型

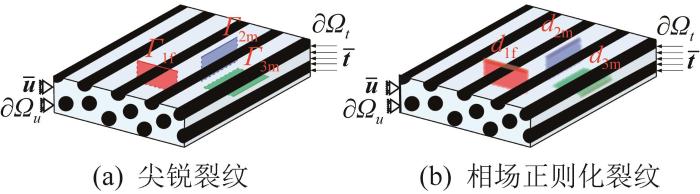
纤维增强复合材料的破坏模式包括纵向的纤维拉/压破坏、横向的基体拉/压破坏以及界面的分层破坏，且每种失效形式均存在不同程度的剪切耦合效应，因此属于混合模式的断裂失效。为了准确描述复合材料的不同失效模式，本文采用多相场模型。采用相场变量对材料内部的尖锐裂纹进行等效弥散化表征，即用相场变量d_1f表示纵向的纤维断裂裂纹 $Γ_{1 f}$ ，用d_2m、d_3m表示横向的基体开裂裂纹 $Γ_{2 m}$ 和 $Γ_{3 m}$ ，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 固体域内纤维和基体裂纹示意

Fig.1 Schematic of fiber and matrix cracks in solid domain

根据Francfort等^[8]提出的断裂变分原理，正则化后含裂纹弹性体系统的总能量泛函W由内部势能E′（包含弹性应变能 $ψ_{Ω}$ 和断裂表面能）和外力功P两部分构成：

W (u, d_{i}, \nabla d_{i}) = E' (u, d_{i}, \nabla d_{i}) + P (u)

(1)

E' (u) = \int_{Ω \ Γ} ψ_{Ω} (\nabla^{s y m} u, d_{i}) d Ω + \sum_{i = f, m} \int_{Ω} G_{c i}^{} γ_{i} (d_{i}, \nabla d_{i}) d Ω

(2)

P (u) = - \int_{Ω} f_{v} d Ω - \int_{\partial Ω_{t}} \bar{t} d \partial Ω

(3)

式中： u 为位移场； $\nabla^{s y m}$ 为对称哈密顿算子， $\nabla^{s y m} = (\nabla + \nabla^{T}) / 2$ ；下标i表示破坏类型，i=f表示纤维破坏，i=m表示基体破坏； $Ω$ 为实体域， $\partial Ω$ 为边界， $\partial Ω_{t}$ 为应力边界； $f_{v}$ 为体力； $\bar{t}$ 为力边界条件；γ_i 为各向异性的裂纹面密度函数。

γ_{i} (d_{i}, \nabla d_{i}) = \frac{1}{c_{0} b} [a (d_{i}) + b^{2} \nabla d_{i} \cdot M_{i} \nabla d_{i}]

(4)

式中：c₀为常数， $a (d_{i})$ 为裂纹几何函数， M_i 为在裂纹面密度泛函中引入的一个与纤维方向相关的结构张量^[11]。

根据变分原理，计算总能量泛函对于位移场及相场变量的变分，得：

\begin{array}{l} δ W = \sum_{i = f, m} \int_{Ω} \{\partial_{d_{i}} ψ_{Ω} + \frac{G_{c i}^{}}{c_{0} b} [a^{'} (d_{i}) - 2 b \nabla \cdot (M_{i} \nabla d_{i})]\} δ d_{i} d Ω + \sum_{i = f, m} \int_{\partial Ω} \frac{2 G_{c i}^{} b}{c_{0}} (M_{i} \nabla d_{i}) \cdot n δ d_{i} d \partial Ω + \\ \int_{Ω} (\nabla σ - f_{v}) δ u d Ω + \int_{\partial Ω_{t}} (n σ - \bar{t}) δ u d \partial Ω = 0 \end{array}

(5)

式中： n 为边界的外法向方向向量， $σ$ 为应力。

由此可以分别导出位移场和相场的控制方程。

对于位移场，其平衡方程和边界条件分别为：

\nabla σ + f_{v} = 0 i n Ω

(6)

n σ = \bar{t} o n \partial Ω_{t}, u = \bar{u} o n \partial Ω_{u}

(7)

式中： $\bar{u}$ 为位移边界条件， $\partial Ω_{u}$ 为位移边界。

对于相场，其控制方程和边界条件分别为：

\frac{\partial ψ}{G_{c i}^{} \partial d_{i}} - \frac{1}{c_{0} b} [a^{'} (d_{i}) - 2 b^{2} \nabla \cdot (M_{i} \nabla d_{i})] = 0 i n Ω

(8)

(M_{i} \nabla d_{i}) \cdot n = 0 o n \partial Ω

(9)

式(8)即为相场的演化方程，其中相场驱动力为：

D_{i}^{} = - \frac{\partial ψ}{G_{c i}^{} \partial d_{i}}

(10)

式(10)表示能量梯度驱动相场的演化。

基于Quintanas-Corominas等^[21]的研究，对于各向异性的弹性应变能，根据各部分能量对复合材料失效模式的贡献程度，可将其拆分为：

ψ_{Ω} (σ) = {(ϕ_{L}^{})}_{\pm} + ϕ_{I N} + {(ϕ_{T}^{})}_{\pm} + ϕ_{S T} + ϕ_{S L}

(11)

其中：

\begin{array}{l} {(ϕ_{L}^{})}_{\pm} = \frac{{〈{\bar{σ}}_{11}^{}〉}_{\pm}^{2}}{2 E_{1}} \\ ϕ_{I N} = - \frac{v_{12} {\bar{σ}}_{11} ({\bar{σ}}_{22} + {\bar{σ}}_{33})}{E_{1}} \\ {(ϕ_{T}^{})}_{\pm} = \frac{(1 - v_{23}) {〈{\bar{σ}}_{22} + {\bar{σ}}_{33}〉}_{\pm}^{2}}{4 E_{2}} \\ ϕ_{S T} = \frac{{\bar{τ}}_{23}^{2}}{2 G_{23}} \\ ϕ_{S L} = \frac{{\bar{τ}}_{12}^{2} + {\bar{τ}}_{13}^{2}}{2 G_{12}} \end{array}

式中： $\bar{σ}$ ₁₁、 $\bar{σ}$ ₂₂、 $\bar{σ}$ ₃₃为有效正应力分量； $\bar{τ}$ ₁₂、 $\bar{τ}$ ₁₃、 $\bar{τ}$ ₂₃为有效剪应力分量；E₁、E₂为杨氏模量；G₁₂、G₂₃为剪切模量；v₁₂、v₂₃为泊松比； ${〈x〉}_{\pm} = (x \pm | x |) / 2$ ，正负号表示材料的拉伸或压缩状态。

进一步将应变能拆分成主动（驱动裂纹扩展）部分的能量ψ_act和被动（不驱动裂纹扩展）部分的能量ψ_pas，相场退化函数作用于主动部分，则：

ψ_{Ω} = ψ_{a c t}^{} + ψ_{p a s}^{}

(12)

ψ_{p a s}^{} = {(ψ_{L}^{})}_{-} + ψ_{I N} + {(ψ_{T}^{})}_{-}

(13)

基于不同的断裂机理，采用相应的退化函数对相场驱动能量的不同部分进行退化，即纤维断裂、基体开裂和剪切破坏分别使用3种不同的退化函数，则：

\begin{array}{l} ψ_{a c t}^{} = g_{L} (d_{1 f}) \frac{{〈{\bar{σ}}_{11}^{}〉}_{+}^{2}}{2 E_{1}} + g_{S L} (d_{1 f}) g_{S L} (d_{3 m}) \frac{{\bar{τ}}_{13}^{2}}{2 G_{12}} + \\ g_{S L} (d_{1 f}) g_{S L} (d_{2 m}) \frac{{\bar{τ}}_{12}^{2}}{2 G_{12}} + g_{T} (d_{2 m}) \frac{{〈{\bar{σ}}_{22}^{}〉}_{+}^{2}}{2 E_{2}} + \\ g_{T} (d_{3 m}) \frac{{〈{\bar{σ}}_{33}^{}〉}_{+}^{2}}{2 E_{2}} + g_{S T} (d_{1 m}) g_{S T} (d_{2 m}) \frac{{\bar{τ}}_{23}^{2}}{2 G_{23}} \end{array}

(14)

式中：g_L、g_T、g_S_L、g_S_T分别为纵向纤维断裂、横向基体断裂、纵向纤维与基体剪切断裂、横向基体间剪切断裂等失效模式下的相场退化函数。

在本研究中，剪切损伤由纤维损伤和基体损伤来表征。这种能量分解考虑了不同断裂能对损伤模式的贡献，从而可以准确描述复合材料的失效行为。

基于Wu^[19]关于内聚力相场模型的研究，相场退化函数采用如下形式：

g (d) = \frac{1}{1 + ϕ (d)}

(15)

其中：

\begin{array}{l} ϕ (d) = a_{1} φ (d) \\ φ (d) = \frac{d (1 - 0.5 d)}{{(1 - d)}^{2}} \\ a_{1} = \frac{4 \hat{E} {\hat{G}}_{c}}{c_{0} b {\hat{f}}_{}^{2}} \end{array}

式中： $\hat{E} 、 {\hat{G}}_{c} 、 \hat{f}$ 分别为每种失效模式下的弹性模量、断裂韧度和材料强度。

1.2　复合材料损伤本构关系

本研究采用Hybrid相场模型^[22]，即材料的损伤本构关系及相场驱动力分别由不同的应变能泛函定义。其中材料损伤本构关系表示为：

σ = \frac{\partial Y^{*}}{\partial ε} = ℂ (d) : ε

(16)

式中：Y^*为含损伤应变能密度函数， $ℂ$ 为4阶损伤刚度张量， $ε$ 为应变，“：”表示张量的双点乘运算。

Y^{*} (ε, d) = \frac{1}{2} ε : ℂ (d) : ε

(17)

基于经典连续介质损伤力学理论，损伤刚度的矩阵形式 C 可以用相场退化函数定义为：

C (d) = [\begin{matrix} A & 0 \\ 0 & B \end{matrix}]

(18)

其中：

A = [\begin{matrix} g_{L} (d_{1 f}) C_{11} & g_{L} (d_{1 f}) g_{T} (d_{2 m}) C_{12} & g_{L} (d_{1 f}) g_{T} (d_{3 m}) C_{13} \\ g_{T} (d_{2 m}) C_{22} & g_{T} (d_{2 m}) g_{T} (d_{3 m}) C_{23} \\ s y m & g_{T} (d_{3 m}) C_{33} \end{matrix}]

\begin{array}{l} B = \\ [\begin{matrix} g_{S T} (d_{2 m}) g_{S T} (d_{3 m}) C_{44} \\ g_{S L} (d_{1 f}) g_{S L} (d_{3 m}) C_{55} \\ g_{S L} (d_{1 f}) g_{S L} (d_{2 m}) C_{66} \end{matrix}] \end{array}

式中：C_kl（k=1, 2, …, 6; l=1, 2, …, 6）为未损伤弹性刚度矩阵 C₀的分量。

对于二维问题，损伤刚度矩阵可以退化为：

C (d) = [\begin{matrix} g_{L} (d_{f}) C_{11} & g_{L} (d_{f}) g_{T} (d_{m}) C_{12} & 0 \\ g_{T} (d_{m}) C_{22} & 0 \\ s y m & g_{S L} (d_{f}) g_{S L} (d_{m}) C_{66} \end{matrix}]

2 相场演化方程与强度准则

基于上述复合材料损伤本构关系及相场退化函数的定义，可以得到不同失效模式下的相场驱动力D：

D_{1 f}^{} = - \frac{\partial_{d_{1 f}} g_{L}}{G_{L c}^{}} (ϕ_{L}^{})_{+} - \frac{\partial_{d_{1 f}} g_{S L}}{G_{S L c}^{}} ϕ_{S L}

D_{2 m}^{} = - \frac{\partial_{d_{2 m}} g_{T}}{G_{T c}^{}} (ϕ_{T}^{})_{+} - \frac{\partial_{d_{2 m}} g_{S T}}{G_{S T c}^{}} ϕ_{S T} - \frac{\partial_{d_{2 m}} g_{S L}}{G_{S L c}^{}} ϕ_{S L}

D_{3 m} = - \frac{\partial_{d_{3 m}} g_{T}}{G_{T c}^{}} (ϕ_{T}^{})_{+} - \frac{\partial_{d_{3 m}} g_{S T}}{G_{S T c}^{}} ϕ_{S T} - \frac{\partial_{d_{3 m}} g_{S L}}{G_{S L c}^{}} ϕ_{S L}

将式(11)代入相场驱动力，得到相场的演化方程：

\begin{array}{l} - \frac{{ϕ_{L}}^{'}}{G_{L c}^{}} \frac{{σ_{11}}^{2}}{2 E_{11}} - \frac{{ϕ_{S L}}^{'}}{G_{S L c}^{}} \frac{{τ_{12}}^{2} + {τ_{13}}^{2}}{2 G_{12}} - \\ \frac{1}{c_{0} b} [a^{'} (d_{1 f}) - 2 b^{2} \nabla \cdot (M_{1 f} \nabla d_{1 f})] = 0 \end{array}

\begin{array}{l} - \frac{{ϕ_{T}}^{'}}{G_{T c}^{}} \frac{{σ_{22}}^{2}}{2 E_{22}} - \frac{{ϕ_{S T}}^{'}}{G_{S T c}^{}} \frac{{τ_{23}}^{2}}{2 G_{23}} - \frac{{ϕ_{S L}}^{'}}{G_{S L c}^{}} \frac{{τ_{12}}^{2}}{2 G_{12}} - \\ \frac{1}{c_{0} b} [a^{'} (d_{2 m}) - 2 b^{2} \nabla \cdot (M_{2 m} \nabla d_{2 m})] = 0 \end{array}

\begin{array}{l} - \frac{{ϕ_{T}}^{'}}{G_{T c}^{}} \frac{{σ_{33}}^{2}}{2 E_{33}} - \frac{{ϕ_{S T}}^{'}}{G_{S T c}^{}} \frac{{τ_{23}}^{2}}{2 G_{23}} - \frac{{ϕ_{S L}}^{'}}{G_{S L c}^{}} \frac{{τ_{13}}^{2}}{2 G_{12}} - \\ \frac{1}{c_{0} b} [a^{'} (d_{3 m}) - 2 b^{2} \nabla \cdot (M_{3 m} \nabla d_{3 m})] = 0 \end{array}

式中： $σ$ ₁₁、 $σ$ ₂₂、 $σ$ ₃₃为名义正应力分量， $τ$ ₁₂、 $τ$ ₁₃、 $τ$ ₂₃为名义剪应力分量。

在损伤起始时，相场变量有边界条件 $d_{i} (x) = 0$ 和 $\nabla d_{i} (x) = 0$ ，据此可以得到内嵌的相场强度准则，即相场模型中不同模式下裂纹的起裂准则：

F_{1 f} = \frac{{σ_{11}}^{2}}{{X_{T}}^{2}} + \frac{{τ_{12}}^{2}}{{S_{L}}^{2}} + \frac{{τ_{13}}^{2}}{{S_{L}}^{2}} = 1

F_{2 m} = \frac{{σ_{22}}^{2}}{{Y_{T}}^{2}} + \frac{{τ_{23}}^{2}}{{S_{T}}^{2}} + \frac{{τ_{12}}^{2}}{{S_{L}}^{2}} = 1

F_{3 m} = \frac{{σ_{33}}^{2}}{{Y_{T}}^{2}} + \frac{{τ_{23}}^{2}}{{S_{T}}^{2}} + \frac{{τ_{13}}^{2}}{{S_{L}}^{2}} = 1

式中：X_T、Y_T分别为材料纵向和横向的拉伸强度，S_L、S_T分别为材料纵向和横向的剪切强度，F为失效模式因子。

对于二维问题，相场演化方程(22)至方程(24)对应退化为：

\begin{array}{l} ϕ_{L}^{'} \frac{σ_{11}^{2}}{2 E_{11} G_{L c}^{}} + ϕ_{T L}^{'} \frac{τ_{12}^{2}}{2 G_{12} G_{S L c}^{}} - \\ \frac{1}{c_{0} b} [a^{'} (d_{f}) - 2 b^{2} \nabla \cdot (M_{f} \nabla d_{f})] = 0 \end{array}

\begin{array}{l} ϕ_{T}^{'} \frac{σ_{22}^{2}}{2 E_{22} G_{T c}^{}} + ϕ_{T L}^{'} \frac{τ_{12}^{2}}{2 G_{12} G_{S L c}^{}} - \\ \frac{1}{c_{0} b} [a^{'} (d_{m}) - 2 b^{2} \nabla \cdot (M_{m} \nabla d_{m})] = 0 \end{array}

强度准则退化为：

F_{f} = \frac{{σ_{11}}^{2}}{{X_{T}}^{2}} + \frac{{τ_{12}}^{2}}{{S_{L}}^{2}} = 1

F_{m} = \frac{{σ_{22}}^{2}}{{Y_{T}}^{2}} + \frac{{τ_{12}}^{2}}{{S_{L}}^{2}} = 1

式(30)和式(31)即为复合材料Hahsin失效准则。

3 测试算例

通过Abaqus软件的用户自定义单元构建上述所建立的多相场模型。首先，模拟单边缝复合材料开口板的开裂行为，并与试验结果进行对比；其次，对含缺口变角度单层复合板进行裂纹扩展模拟，来验证相场模型捕捉各向异性材料复杂裂纹扩展的能力；最后，将相场模型与内聚力模型结合，来模拟开孔复合材料层合板的复杂断裂失效行为。

3.1　单边缝复合材料开口板裂纹测试

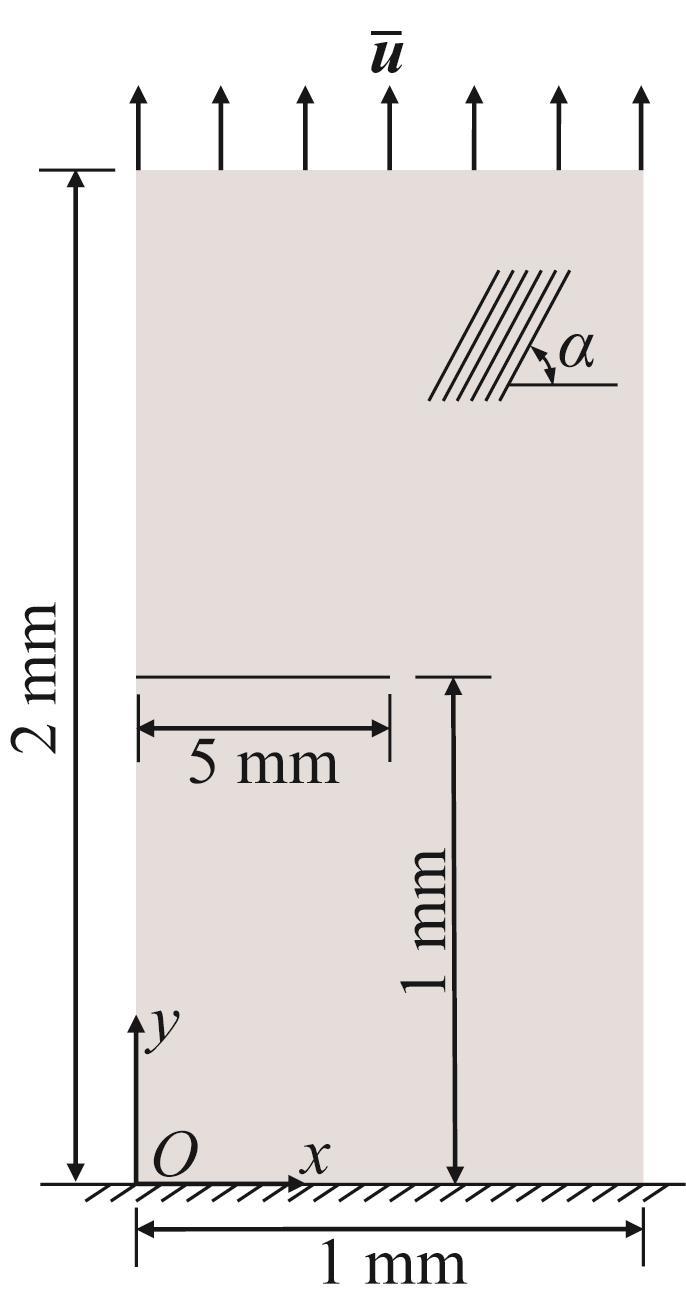
单边缝复合材料开口板的几何尺寸及开口位置如图2所示。平板采用单向铺层复合材料HTA/6376，材料特性参数如表1所示^[23]。纤维与水平方向的角度为 $α$ ，边界条件为两端拉伸。选取网格尺寸为0.002 mm，进行有限元离散；设置相场模型的裂纹特征长度b=0.02 mm，采用位移加载进行计算。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 单边缝复合材料开口板几何尺寸及开口位置示意

Fig.2 Schematic of geometric dimension and opening position of single edge notched composite specimen

表1 复合材料HTA/6376的特性参数

Table 1 Characteristic parameters of composite material HTA/6376

参数类型	参数	数值
弹性参数	E₁/GPa	114.8
	E₂/GPa	11.7
	G₁₂/GPa	9.66
	v₁₂	0.21
断裂参数	X_T/MPa	1 500
	Y_T/MPa	8.5
	S_L/MPa	120
	G_L/(N/mm)	106.3
	G_T/(N/mm)	0.277 4
	G_SL/(N/mm)	0.787 9

资料来源：文献[23]。

新窗口打开| 下载CSV

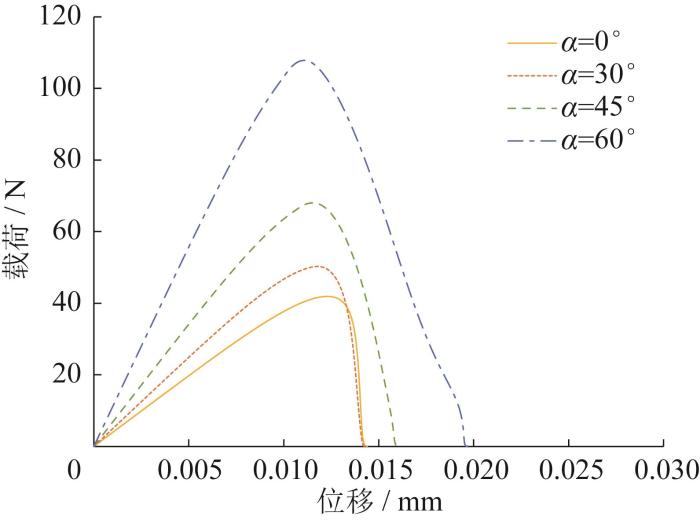
分别取 $α$ =0°，30°，45°，60°，90°，裂纹的相场模拟结果和试验结果^[23]如图3所示，相应的位移—载荷试验曲线如图4所示。由于 $α$ =90°时铺层单层板并未完全失效，故未绘制其位移—载荷曲线。由图可知，裂纹从初始裂缝的应力集中部位开始萌生并快速沿纤维方向扩展，这是由于引入的结构张量使得裂纹沿此方向扩展所需的能量最小。当 $α$ =30°，45°，60°时，纤维的倾斜使得复合材料板处于拉剪耦合状态，从而引起混合模式的断裂，即产生了I型和II型断裂的共同影响；当 $α$ =0°时，铺层单层板无拉剪耦合，属完全的基体I型断裂；当 $α$ =90°时，铺层单层板无拉剪耦合，但因存在初始缺陷而使左右两侧的应力状态不同，在右半部分的纤维在未断裂前一直受到左半部分产生的剪切力的作用，使得单层板裂纹由剪切产生的基体II型断裂主导，并沿着纤维方向扩展。需要指出的是，当 $α$ =90°时，如果继续对单层板施加载荷，可能会出现沿初始裂缝方向的纤维裂纹。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 单边缝复合材料开口板裂纹

Fig.3 Crack of single edge notched composite specimen

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 单边裂缝复合材料开口板位移—载荷试验曲线

Fig.4 Displacement-load test curves of single edge notched composite specimen

3.2　含缺口变角度单层复合板裂纹扩展模拟

对一含缺口变角度单层复合板进行裂纹扩展模拟。复合板的几何尺寸及施加在2个竖直边界上的边界条件如图5所示。复合板采用单向铺层的IM7/8552复合材料，材料特性常数如表2所示^[21]。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 含缺口变角度单层复合板的几何尺寸及边界条件示意

Fig.5 Schematic of geometric dimensions and boundary conditions of single-layer composite plate with variable angle of notch

表2 复合板材料IM7/8552的特性参数

Table 2 Characteristic parameters of composite plate material IM7/8552

参数类型	参数	数值
弹性参数	E₁/GPa	171
	E₂/GPa	9.08
	G₁₂/GPa	5.29
	v₁₂	0.32
断裂参数	X_T/MPa	2 325
	Y_T/MPa	62.3
	S_L/MPa	89.6
	G_L/(N/mm)	97.8
	G_T/(N/mm)	0.277
	G_SL/(N/mm)	0.788

资料来源：文献[21]。

新窗口打开| 下载CSV

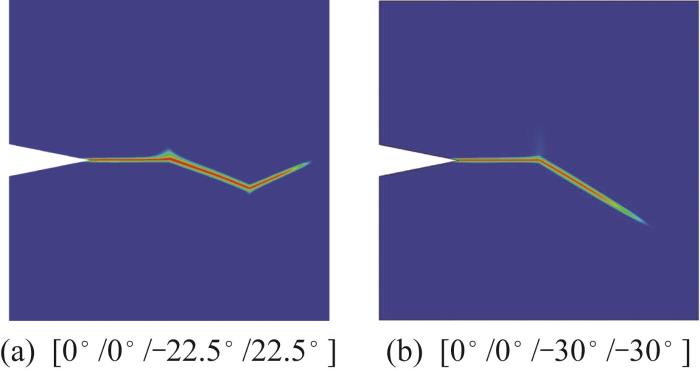
复合板为含初始缺口的1 mm×1 mm正方形板。板被分为4个区域，每个区域采用不同的纤维取向，即铺层角度[θ₁/θ₂/θ₃/θ₄]分别设置为[0°/-22.5°/0°/22.5°]、[0°/0°/-22.5°/22.5°]、[0°/0°/-30°/-30°]。板最左端的竖直边界上受到均匀的给定位移，右端的边界完全固定。选取网格尺寸为0.002 mm，特征长度为0.005 mm。

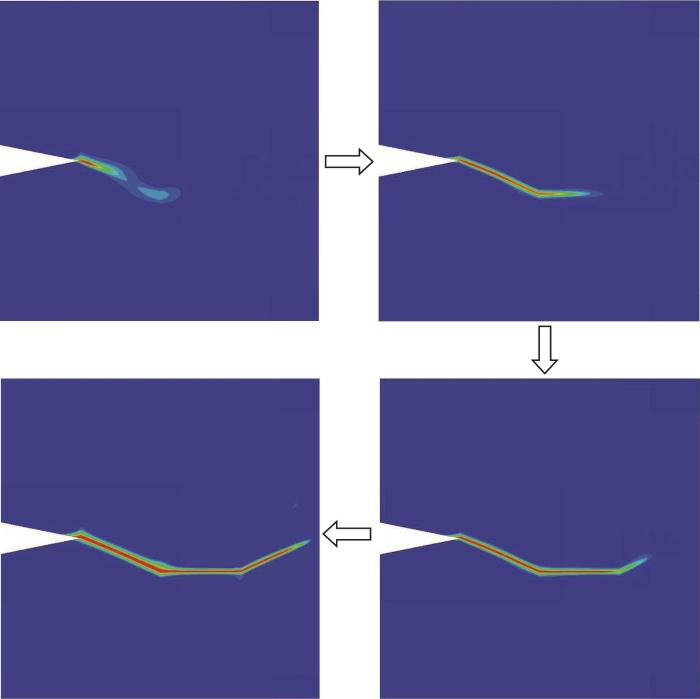
[0°/-22.5°/0°/22.5°]铺层复合板的裂纹扩展过程如图6中所示。由图可知，裂纹平行于纤维方向扩展。[0°/0°/-22.5°/22.5°]、[0°/0°/-30°/-30°]铺层复合板的失效模式如图7所示。由图可知，裂纹扩展路径仍然沿纤维方向。这是因为在裂纹扩展过程中，使基体开裂所需的能量低于使纤维断裂所需的能量，这验证了相场模型模拟各向异性断裂行为的准确性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 [0°/-22.5°/0°/22.5°]铺层复合板的裂纹扩展过程

Fig.6 Crack propagation process of laminated board [0°/-22.5°/0°/22.5°]

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 [0°/0°/-22.5°/22.5°]和[0°/0°/-30°/-30°] 铺层复合板失效模式

Fig.7 Failure patterns of laminated board [0°/0°/-22.5°/22.5°] and [0°/0°/-30°/-30°]

3.3　开孔复合材料层合板失效模拟

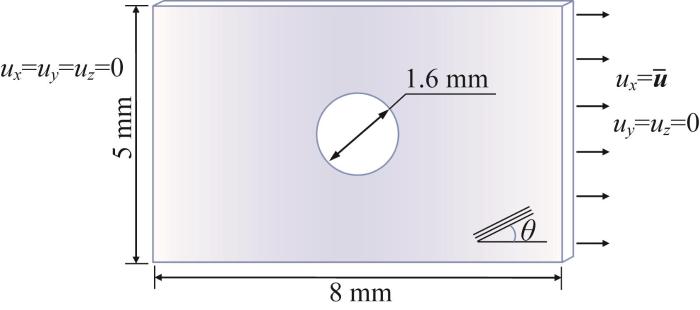
为了验证模型预测开孔复合材料层合板裂纹扩展而失效的能力，本文研究了不同铺层角度的开孔复合材料层合板的裂纹萌生与扩展行为。开孔板的几何尺寸及边界条件如图8所示，复合材料的特性参数如表3所示^[24]。进行相场模型与界面内聚力单元耦合建模，其中复合材料单层板采用多相场平面应力单元建模，在相邻层之间的界面插入三维内聚力单元进行建模，从而可同时顾及层内及层间的失效行为。采用147 456个平面应力单元和24 576个内聚力单元对模型进行有限元离散，设置内聚力单元层的厚度为0.25 mm，相场的特征长度为0.1 mm。为了较全面地分析不同铺层方向的开孔板的断裂特征，对[0°/90°]、[0°/-45°]、[45°/90°]三种交叉铺层复合材料开孔板进行拉伸模拟。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 开孔复合材料层合板的几何尺寸及边界条件示意

Fig.8 Schematic of geometric dimensions and boundary conditions of perforated composite laminates

表3 层合板材料IM7/855的特性常数

Table 3 Characteristic parameters of laminate material IM7/8552

参数类型	参数	数值
弹性参数	E₁/GPa	161
	E₂/GPa	11.4
	G₁₂/GPa	5.17
	v₁₂	0.32
断裂参数	X_T/MPa	2 806
	Y_T/MPa	60
	S_L/MPa	90
	G_L/(N/mm)	112.7
	G_T/(N/mm)	0.277
	G_SL/(N/mm)	0.63

资料来源：文献[24]。

新窗口打开| 下载CSV

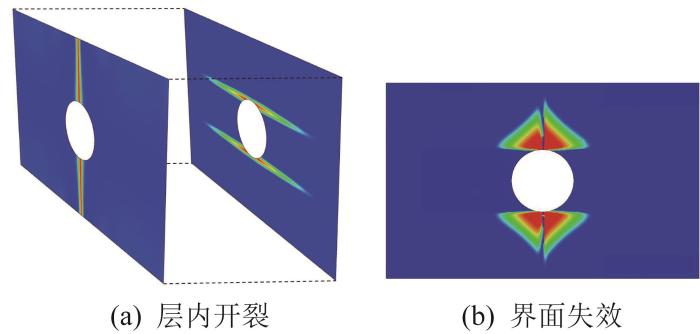
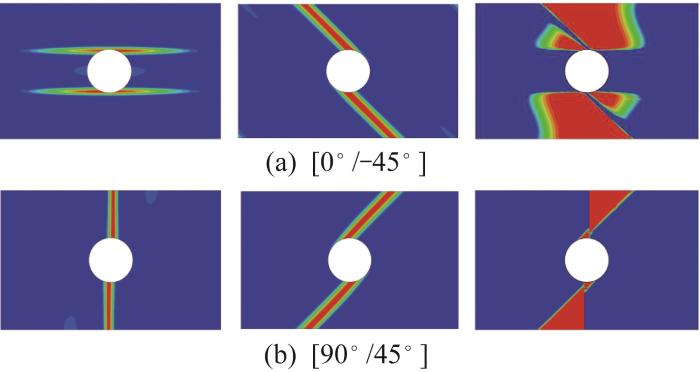
[0°/90°]复合材料开孔板的失效模式如图9所示。由图可知，每一层的基体裂纹都在圆孔周围开始萌生，并沿纤维方向往板边缘扩展。这些基体裂纹将引起界面处的剪切应力集中，导致产生由相邻层的基体裂纹引起的层间分层区。[0°/-45°]和[45°/90°]开孔板的多重失效模式如图10所示。其失效行为与[0°/90°]开孔板类似，应力集中引起基体开裂并导致分层断裂。由图10可知，这些分层断裂区域是由单层板的基体断裂形成的剪切区扩展而成。该算例验证了相场模型可以准确模拟由基体开裂引起的层间分层破坏行为。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 [0°/90°] 开孔复合材料层合板的失效模式

Fig.9 Failure pattern of perforated composite laminates [0°/90°]

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 [0°/-45°] 和 [90°/45°]开孔复合材料层合板的多重失效模式

Fig.10 Multiple failure pattern of perforated composite laminates

4 结论

本文提出了一种基于复合材料各向异性损伤机理的多相场分析模型。提出了混合相场公式，基于复合材料的不同损伤机理对各向异性的相场驱动力及其对应的相场退化函数进行了定义；对于材料损伤本构关系，则基于经典的各向异性损伤力学框架进行定义。基于上述定义，可以推导出不同失效模式下的相场演化方程与强度准则，从而得到等效的内聚断裂行为。针对复合材料层合板的层内失效与层间失效，进行相场模型与内聚力模型耦合建模，实现了复合材料的多模式断裂模拟。所提出的模型能有效捕捉复合材料层合板的复杂失效行为，如不同铺层角度下的裂纹扩展、层合板层内断裂及其引起的分层破坏等。仿真结果表明，此多相场模型可以合理预测与描述纤维增强复合材料的裂纹萌生及扩展过程。该模型顾及了基于失效模式的失效准则和等效的内聚断裂行为，因此在一定程度上可以替代经典的基于内聚力模型的数值计算方法。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

白翠平，马其华，周天俊.

车用CFRP油底壳的结构与制造工艺并行优化设计

［J］.工程设计学报，2020，27（5）：608-615. doi：10.3785/j.issn.1006-754X.2020.00.075

DOI:10.3785/j.issn.1006-754X.2020.00.075 [本文引用: 1]

BAI

C P

， MA

Q H

， ZHOU

T J

Concurred optimal design of structure and manufacturing process of CFRP oil pan for vehicles

［J］. Chinese Journal of Engineering Design， 2020， 27（5）： 608-615.

DOI:10.3785/j.issn.1006-754X.2020.00.075 [本文引用: 1]

[2]

郝春永，王栋亮，郑津洋，等.

铝内胆复合材料储氢瓶爆破压力与疲劳寿命关系研究

［J］.工程设计学报，2021，28（5）：594-601. doi：10.3785/j.issn.1006-754X.2021.00.072

DOI:10.3785/j.issn.1006-754X.2021.00.072

HAO

C Y

， WANG

D L

， ZHENG

J Y

， et al.

Research on the relationship between burst pressure and fatigue life of composite hydrogen storage tank with aluminum liner

［J］. Chinese Journal of Engineering Design， 2021， 28（5）： 594-601.

DOI:10.3785/j.issn.1006-754X.2021.00.072

[3]

李佳，宋梅利，冯君，等.

面向激光增材制造的仿生薄壁结构抗冲击研究

［J］.工程设计学报，2024，31（1）：67-73. doi：10.3785/j.issn.1006-754X.20224.03.317

DOI:10.3785/j.issn.1006-754X.20224.03.317

， SONG

M L

， FENG

， et al.

Study on impact resistance of bio-inspired thin-walled structure for laser additive manufacturing

［J］. Chinese Journal of Engineering Design， 2024， 31（1）： 67-73.

DOI:10.3785/j.issn.1006-754X.20224.03.317

[4]

郑传祥，王亮，魏双，等.

基于微观力学的复合材料气瓶爆破强度研究

［J］.工程设计学报，2016，23（5）：461-467. doi：10.3785/j.issn.1006-754X.2016.05.009

DOI:10.3785/j.issn.1006-754X.2016.05.009

ZHENG

C X

， WANG

， WEI

， et al.

Micromechanics-based burst failure analysis of composite vessel used for hydrogen storages

［J］. Chinese Journal of Engineering Design， 2016， 23（5）： 461-467.

DOI:10.3785/j.issn.1006-754X.2016.05.009

[5]

冯鹏

复合材料在土木工程中的发展与应用

［J］.玻璃钢/复合材料，2014（9）：99-104. doi：10.3969/j.issn.1003-0999.2014.09.013

DOI:10.3969/j.issn.1003-0999.2014.09.013 [本文引用: 1]

FENG

Development and application of composite in civil engineering

［J］. Fiber Reinforced Plastics/Composites， 2014 （9）： 99-104.

DOI:10.3969/j.issn.1003-0999.2014.09.013 [本文引用: 1]

[6]

NGO D， SCORDELIS

A C

Finite element analysis of reinforced concrete beams

［J］. ACI Journal Proceedings， 1967， 64（3）： 152-163.

[本文引用: 1]

[7]

RASHID

Y R

Ultimate strength analysis of prestressed concrete pressure vessels

［J］. Nuclear Engineering and Design， 1968， 7（4）： 334-344.

[本文引用: 1]

[8]

FRANCFORT

G A

， MARIGO

J J

Revisiting brittle fracture as an energy minimization problem

［J］. Journal of the Mechanics and Physics of Solids， 1998， 46（8）： 1319-1342.

[本文引用: 2]

[9]

彭帆，马玉娥，黄玮，等.

基于相场法的复合材料失效分析研究进展

［J］.复合材料学报，2023，40（5）：2495-2506.

[本文引用: 1]

PENG

， MA

Y E

， HUANG

， et al.

Failure analysis of composite materials based on phase field method： A review

［J］. Acta Materiae Compositae Sinica， 2023， 40（5）： 2495-2506.

[本文引用: 1]

[10]

CLAYTON

J D

， KNAP

Phase field modeling of directional fracture in anisotropic polycrystals

［J］. Computational Materials Science， 2015， 98： 158-169.

[本文引用: 1]

[11]

ZHANG

， HU

X F

， BUI

T Q

， et al.

Phase field modeling of fracture in fiber reinforced composite laminate

［J］. International Journal of Mechanical Sciences， 2019， 161-162： 105008. doi：10.1016/j.ijmecsci.2019. 07.007 .

DOI:10.1016/j.ijmecsci.2019. 07.007 [本文引用: 3]

[12]

张鹏

纤维增强复合材料破坏过程模拟的相场模型研究

［D］.大连：大连理工大学，2020.

[本文引用: 1]

ZHANG

Phase field modeling of fracture in fiber reinforced composite laminate

［D］. Dalian： Dalian University of Technology， 2020.

[本文引用: 1]

[13]

SUPRIATNA

， YIN

， KONOPKA

An anisotropic phase-field approach accounting for mixed fracture modes in wood structures within the representative crack element framework

［J］. Engineering Fracture Mechanics， 2022， 269： 108514.

[本文引用: 1]

[14]

TEICHTMEISTER

， KIENLE

， ALDAKHEEL

， et al.

Phase field modeling of fracture in anisotropic brittle solids

［J］. International Journal of Non-Linear Mechanics， 2017， 97： 1-21.

[本文引用: 1]

[15]

BLEYER

， ALESSI

Phase-field modeling of anisotropic brittle fracture including several damage mechanisms

［J］. Computer Methods in Applied Mechanics and Engineering， 2018， 336： 213-236.

[本文引用: 1]

[16]

DEAN

， KUMAR

P K A V

， REINOSO

， et al.

A multiphase-field fracture model for long fiber reinforced composites based on the Puck theory of failure

［J］. Composite Structures， 2020， 251： 112446.

[本文引用: 1]

[17]

AMOR

， MARIGO

J J

， MAURINI

Regularized formulation of the variational brittle fracture with unilateral contact： Numerical experiments

［J］. Journal of the Mechanics and Physics of Solids， 2009， 57（8）： 1209-1229.

[本文引用: 1]

[18]

NGUYEN

T T

， YVONNET

， BORNERT

， et al.

On the choice of parameters in the phase field method for simulating crack initiation with experimental validation

［J］. International Journal of Fracture， 2016， 197（2）： 213-226.

[本文引用: 1]

[19]

J Y

A unified phase-field theory for the mechanics of damage and quasi-brittle failure

［J］. Journal of the Mechanics and Physics of Solids， 2017， 103： 72-99.

[本文引用: 2]

[20]

J Y

， NGUYEN

V P

A length scale insensitive phase-field damage model for brittle fracture

［J］. Journal of the Mechanics and Physics of Solids， 2018， 119： 20-42.

[本文引用: 1]

[21]

QUINTANAS-COROMINAS

， REINOSO

， CASONI

， et al.

A phase field approach to simulate intralaminar and translaminar fracture in long fiber composite materials

［J］. Composite Structures， 2019， 220： 899-911.

[本文引用: 3]

[22]

AMBATI

， GERASIMOV

， DE LORENZIS

A review on phase-field models of brittle fracture and a new fast hybrid formulation

［J］. Computational Mechanics， 2015， 55（2）： 383-405.

[本文引用: 1]

[23]

CAHILL

L M A

， NATARAJAN

， BORDAS

S P A

， et al.

An experimental/numerical investigation into the main driving force for crack propagation in uni-directional fibre-reinforced composite laminae

［J］. Composite Structures， 2014， 107： 119-130.

[本文引用: 3]

[24]

HALLETT

S R

， GREEN

B G

， JIANG

W G

， et al.

An experimental and numerical investigation into the damage mechanisms in notched composites

［J］. Composites Part A： Applied Science and Manufacturing， 2009， 40（5）： 613-624.

[本文引用: 2]

车用CFRP油底壳的结构与制造工艺并行优化设计

2020

... 纤维增强复合材料因其优良的力学性能，在航空航天器、车辆、船舶、建筑工程设备中得到广泛应用^[1-5].相较于单组分材料，复合材料在材料特性、结构设计上的多变性，使得其在相同密度下具有更高的强度、刚度和韧性，但其损伤及失效机理更加复杂.对于常见的复合材料层合板，其损伤是由基体开裂、界面脱粘、分层、纤维断裂等多种因素相互作用而产生的，要精确地评估其损伤及失效行为相当困难.因此，开发先进有效的损伤及失效分析方法对复合材料的安全应用具有重要意义. ...

车用CFRP油底壳的结构与制造工艺并行优化设计

2020

铝内胆复合材料储氢瓶爆破压力与疲劳寿命关系研究

2021

铝内胆复合材料储氢瓶爆破压力与疲劳寿命关系研究

2021

面向激光增材制造的仿生薄壁结构抗冲击研究

2024

面向激光增材制造的仿生薄壁结构抗冲击研究

2024

基于微观力学的复合材料气瓶爆破强度研究

2016

基于微观力学的复合材料气瓶爆破强度研究

2016

复合材料在土木工程中的发展与应用

2014

复合材料在土木工程中的发展与应用

2014

Finite element analysis of reinforced concrete beams

1967

... 目前，材料的断裂分析主要基于断裂力学理论或损伤力学理论，相应的计算方法可分为非连续性方法^[6]和连续性方法^[7]两大类.非连续性方法用离散裂纹模型描述材料的开裂行为；连续性方法采用弥散裂纹模型，即通过引入损伤变量来表征材料的断裂过程.采用非连续性方法时需要显示、描述裂纹路径，存在裂纹跟踪、网格重划分等诸多困难；而基于损伤力学的连续性方法则存在损伤变量无直接的物理含义且可能存在网格依赖性等缺陷.最近20年间，断裂相场法作为新的材料断裂分析方法而受到了广泛关注.相场法仍采用弥散裂纹模型，但因基于断裂力学理论和损伤力学理论，而成为极具潜力的断裂分析方法之一.相场法基于Francfort等^[8]提出的能量变分原理，通过引入相场变量——序参量d将断裂面进行弥散化处理，将裂纹面断裂能转化为裂纹带的体积分，使得在数值计算上更容易实现.断裂相场法以断裂力学的能量法为基础，根据能量变分导出控制方程，从而驱动相场自发演化，因而不需要特意追踪和描述裂纹的扩展过程，这有效提高了断裂分析的便捷性和计算效率. ...

Ultimate strength analysis of prestressed concrete pressure vessels

1968

Revisiting brittle fracture as an energy minimization problem

1998

... 根据Francfort等^[8]提出的断裂变分原理，正则化后含裂纹弹性体系统的总能量泛函W由内部势能E′（包含弹性应变能

ψ_{Ω}

和断裂表面能）和外力功P两部分构成： ...

基于相场法的复合材料失效分析研究进展

2023

... 由于相场法的独特优势，其逐渐成为准确分析复合材料失效行为和机理的有效手段^[9].如：2015年，Clayton等^[10]针对多晶体材料的破坏问题，提出了一种各向异性相场模型；Zhang等^[11-12]修改了结构张量的形式，将各向异性相场模型用于三维分析；Supriatna等^[13]基于木材结构，提出了新的各向异性混合模式的断裂失效相场模型，并进行了实验验证；Teichtmeister等^[14]引入了四阶结构张量，建立了四阶各向异性相场断裂模型，降低了对模型网格离散精度的要求，且使计算结果更容易收敛；Bleyer等^[15]建立了纤维复合材料的双相场模型，用于描述基体和纤维的断裂模式；Dean等^[16]基于Puck失效准则，提出了区分纤维和基体断裂的双相场损伤模型. ...

基于相场法的复合材料失效分析研究进展

2023

Phase field modeling of directional fracture in anisotropic polycrystals

2015

Phase field modeling of fracture in fiber reinforced composite laminate

2019

... 虽然相场模型的优势较为突出，但仍然存在一些固有缺陷.例如，经典相场模型的裂纹特征长度b对材料常数具有依存性，即b与材料强度相关.Amor等^[17]推导了b与临界应力

σ_{c}

关系的解析表达式.Nguyen等^[18]利用这一关系，用材料强度

σ_{m a x}

估计b，即

b = 27 E G_{c} / (256 {σ_{m a x}}^{2})

（式中：E为材料的弹性模量，G_c为材料断裂韧度），以接近材料本身的性质，此公式也被广泛利用^[11].对于经典相场模型，裂纹特征长度与材料强度和断裂能的相关性，限制了其在复杂断裂问题中的准确应用.Wu^[19]提出了针对准脆性破坏的统一相场理论，建立了具有不同软化形式的统一内聚断裂相场模型，较好地解决了裂纹特征长度的非数值参数问题^[20].统一内聚断裂相场模型中设有明确的材料强度及准脆性的断裂行为，裂纹特征长度不再由材料常数确定而作为数值参数存在. ...

... 式中：c₀为常数，

a (d_{i})

为裂纹几何函数， M_i 为在裂纹面密度泛函中引入的一个与纤维方向相关的结构张量^[11]. ...

纤维增强复合材料破坏过程模拟的相场模型研究

2020

纤维增强复合材料破坏过程模拟的相场模型研究

2020

An anisotropic phase-field approach accounting for mixed fracture modes in wood structures within the representative crack element framework

2022

Phase field modeling of fracture in anisotropic brittle solids

2017

Phase-field modeling of anisotropic brittle fracture including several damage mechanisms

2018

A multiphase-field fracture model for long fiber reinforced composites based on the Puck theory of failure

2020

Regularized formulation of the variational brittle fracture with unilateral contact： Numerical experiments

2009

σ_{c}

关系的解析表达式.Nguyen等^[18]利用这一关系，用材料强度

σ_{m a x}

估计b，即

b = 27 E G_{c} / (256 {σ_{m a x}}^{2})

On the choice of parameters in the phase field method for simulating crack initiation with experimental validation

2016

σ_{c}

关系的解析表达式.Nguyen等^[18]利用这一关系，用材料强度

σ_{m a x}

估计b，即

b = 27 E G_{c} / (256 {σ_{m a x}}^{2})

A unified phase-field theory for the mechanics of damage and quasi-brittle failure

2017

σ_{c}

关系的解析表达式.Nguyen等^[18]利用这一关系，用材料强度

σ_{m a x}

估计b，即

b = 27 E G_{c} / (256 {σ_{m a x}}^{2})

... 基于Wu^[19]关于内聚力相场模型的研究，相场退化函数采用如下形式： ...

A length scale insensitive phase-field damage model for brittle fracture

2018

σ_{c}

关系的解析表达式.Nguyen等^[18]利用这一关系，用材料强度

σ_{m a x}

估计b，即

b = 27 E G_{c} / (256 {σ_{m a x}}^{2})

A phase field approach to simulate intralaminar and translaminar fracture in long fiber composite materials

2019

... 基于Quintanas-Corominas等^[21]的研究，对于各向异性的弹性应变能，根据各部分能量对复合材料失效模式的贡献程度，可将其拆分为： ...

... 对一含缺口变角度单层复合板进行裂纹扩展模拟.复合板的几何尺寸及施加在2个竖直边界上的边界条件如图5所示.复合板采用单向铺层的IM7/8552复合材料，材料特性常数如表2所示^[21]. ...

... 资料来源：文献[21]. ...

A review on phase-field models of brittle fracture and a new fast hybrid formulation

2015

... 本研究采用Hybrid相场模型^[22]，即材料的损伤本构关系及相场驱动力分别由不同的应变能泛函定义.其中材料损伤本构关系表示为： ...

An experimental/numerical investigation into the main driving force for crack propagation in uni-directional fibre-reinforced composite laminae

2014

... 单边缝复合材料开口板的几何尺寸及开口位置如图2所示.平板采用单向铺层复合材料HTA/6376，材料特性参数如表1所示^[23].纤维与水平方向的角度为

α

，边界条件为两端拉伸.选取网格尺寸为0.002 mm，进行有限元离散；设置相场模型的裂纹特征长度b=0.02 mm，采用位移加载进行计算. ...

... 资料来源：文献[23]. ...

... 分别取

α

=0°，30°，45°，60°，90°，裂纹的相场模拟结果和试验结果^[23]如图3所示，相应的位移—载荷试验曲线如图4所示.由于

α

=90°时铺层单层板并未完全失效，故未绘制其位移—载荷曲线.由图可知，裂纹从初始裂缝的应力集中部位开始萌生并快速沿纤维方向扩展，这是由于引入的结构张量使得裂纹沿此方向扩展所需的能量最小.当

α

=30°，45°，60°时，纤维的倾斜使得复合材料板处于拉剪耦合状态，从而引起混合模式的断裂，即产生了I型和II型断裂的共同影响；当

α

=0°时，铺层单层板无拉剪耦合，属完全的基体I型断裂；当

α

=90°时，铺层单层板无拉剪耦合，但因存在初始缺陷而使左右两侧的应力状态不同，在右半部分的纤维在未断裂前一直受到左半部分产生的剪切力的作用，使得单层板裂纹由剪切产生的基体II型断裂主导，并沿着纤维方向扩展.需要指出的是，当

α

=90°时，如果继续对单层板施加载荷，可能会出现沿初始裂缝方向的纤维裂纹. ...

An experimental and numerical investigation into the damage mechanisms in notched composites

2009

... 为了验证模型预测开孔复合材料层合板裂纹扩展而失效的能力，本文研究了不同铺层角度的开孔复合材料层合板的裂纹萌生与扩展行为.开孔板的几何尺寸及边界条件如图8所示，复合材料的特性参数如表3所示^[24].进行相场模型与界面内聚力单元耦合建模，其中复合材料单层板采用多相场平面应力单元建模，在相邻层之间的界面插入三维内聚力单元进行建模，从而可同时顾及层内及层间的失效行为.采用147 456个平面应力单元和24 576个内聚力单元对模型进行有限元离散，设置内聚力单元层的厚度为0.25 mm，相场的特征长度为0.1 mm.为了较全面地分析不同铺层方向的开孔板的断裂特征，对[0°/90°]、[0°/-45°]、[45°/90°]三种交叉铺层复合材料开孔板进行拉伸模拟. ...

... 资料来源：文献[24]. ...

〈

〉