铸铝一体化车门的多目标可靠性优化设计

doi:10.3785/j.issn.1006-754X.2024.03.159

铸铝一体化车门的多目标可靠性优化设计

吴勃夫^,, 吴姚烨^,^,, 贝璟, 吴宗扬, 孙亮

合肥工业大学汽车与交通工程学院，安徽合肥 230009

Multi-objective reliability optimization design for cast aluminum integrated car door

WU Bofu^,, WU Yaoye^,^,, BEI Jing, WU Zongyang, SUN Liang

School of Automotive and Transportation Engineering, Hefei University of Technology, Hefei 230009, China

通讯作者: 吴姚烨（1998—），男，江苏太仓人，硕士生，从事汽车轻量化研究，E-mail: wuyaoyee@163.com，https//orcid.org/0009-0002-2560-3919

收稿日期: 2023-04-26 修回日期: 2023-07-31

基金资助:

国家自然科学基金资助项目. 51875150

Received: 2023-04-26 Revised: 2023-07-31

作者简介 About authors

吴勃夫（1980—），男，安徽安庆人，讲师，博士，从事汽车空气动力学主、被动流动控制与汽车车身数字化制造研究，E-mail:bbfwu@163.com , E-mail：bbfwu@163.com

摘要

为提升车门的轻量化水平与性能，采用“材料—结构—性能”一体化集成方法设计铸铝一体化车门。基于构建的铸铝一体化车门有限元模型，以车门的厚度为设计变量，采用径向基函数（radial basis function, RBF）神经网络近似模型和二阶响应面近似模型并分别结合二代非支配排序遗传算法（non-dominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ）、多目标粒子群优化（multi-objective particle swarm optimization, MOPSO）算法以及多岛遗传算法（multi-island genetic algorithm, MIGA）对车门的下沉刚度工况位移、上扭转刚度工况位移、下扭转刚度工况位移、一阶弯曲模态频率、一阶扭转模态频率和质量进行确定性优化设计。在此基础上，考虑材料及加工制造等不确定性因素，对确定性优化解的质量水平进行6Sigma可靠性分析与优化。结果表明，二阶响应面近似模型与MOPSO算法的优化组合方案实现了车门的最佳轻量化，RBF神经网络近似模型与MOPSO算法的优化组合方案实现了车门下沉刚度工况位移的最小化。上述2种组合分别实现了车门轻量化与安全化的设计目标。研究结果可为车身零部件的优化设计提供参考。

关键词： 铸铝一体化车门 ; 轻量化 ; 径向基函数神经网络近似模型 ; 二阶响应面近似模型 ; 多目标粒子群优化算法 ; 6Sigma可靠性

Abstract

In order to improve the lightweight level and performance of the car door, the integrated method of "material-structure-performance" is adopted to design the cast aluminum integrated car door. Based on the constructed finite element model of the cast aluminum integrated car door, with the thickness of the car door as the design variable, the radial basis function (RBF) neural network approximation model and the second-order response surface approximation model were used in combination with the non-dominated sorting genetic algorithm-Ⅱ (NSGA-Ⅱ), multi-objective particle swarm optimization (MOPSO) algorithm and multi-island genetic algorithm (MIGA) to conduct the deterministic optimization design for the sinking stiffness condition displacement, upper torsional stiffness condition displacement, lower torsional stiffness condition displacement, first-order bending mode frequency, first-order torsional mode frequency and mass of the car door. On this basis, the 6Sigma reliability analysis and optimization for the quality level of the deterministic optimization solution were carried out considering the uncertainties of materials and manufacturing. The results showed the optimal combination of second-order response surface approximation model and MOPSO algorithm achieved the optimal lightweight of the car door, and the optimal combination of RBF neural network approximation model and MOPSO algorithm could minimize the the displacement of the car door under the sinking stiffness condition. The above two combinations achieved the design goals of lightweight and safety for the car door, respectively. The research results can provide reference for the optimization design of car parts.

Keywords： cast aluminum integrated car door ; lightweight ; radial basis function neural network approximation model ; second-order response surface approximation model ; multi-objective particle swarm optimization algorithm ; 6Sigma reliability

PDF (3215KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吴勃夫, 吴姚烨, 贝璟, 吴宗扬, 孙亮. 铸铝一体化车门的多目标可靠性优化设计[J]. 工程设计学报, 2024, 31(2): 188-200 doi:10.3785/j.issn.1006-754X.2024.03.159

WU Bofu, WU Yaoye, BEI Jing, WU Zongyang, SUN Liang. Multi-objective reliability optimization design for cast aluminum integrated car door[J]. Chinese Journal of Engineering Design, 2024, 31(2): 188-200 doi:10.3785/j.issn.1006-754X.2024.03.159

汽车轻量化是指通过采用轻量化材料或技术来实现车身减重，从而提高燃油经济性和减少CO₂的排放量^[1]。现阶段，向碳中和过渡的迫切需求加速了汽车轻量化技术的发展^[2]。汽车制造商正在积极研发和使用各种轻量化材料来替代传统的钢铁材料，如铝合金、镁合金和碳纤维增强塑料等。同时，汽车制造商也在不断研究和改进汽车制造技术，包括新的焊接技术、精密铸造和成型技术等，以实现更精细的车身设计和更高的制造精度。

车门是汽车的重要组成部件之一，其质量直接影响汽车的整体质量。对车门进行轻量化设计，可有效提升整车的轻量化水平。针对车门的轻量化设计，国内外学者开展了广泛研究。高云凯等^[3]构建了用于拼焊车门轻量化设计的Kriging与响应面近似模型，并采用二代非支配排序遗传算法（non-dominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ）寻求车门质量与下沉刚度的最优解。李军等^[4]构建了客车车门的径向基函数（radial basis function, RBF）神经网络近似模型，并采用多目标遗传算法实现了车门质量与一阶模态频率的最优目标。马彬彬等^[5]采用RBF神经网络近似模型，通过模拟退火优化算法，在满足车门侧向刚度和下沉刚度要求的条件下，实现了车门的轻量化设计。侯振方等^[6]将网格变形技术引入车门结构的多目标轻量化设计，通过构建Kriging近似模型并采用多目标遗传算法来进行车门质量和一阶模态频率的优化计算。方拓林等^[7]对整车碰撞模型进行了简化，并采用拉丁超立方试验设计方法和响应面近似模型，考虑车门的一阶模态频率、侧向刚度、下沉刚度和侧面碰撞性能，在车门质量不变的情况下，提升了各响应的最优性和车门结构的稳健性。陈静等^[8]运用Kriging方法和多目标粒子群优化（multi-objective particle swarm optimization, MOPSO）算法对碳纤维防撞梁的铺层厚度进行了优化，提高了防撞梁的低速碰撞性能。任明等^[9]运用Kriging方法构建了车架的NVH（noise, vibration, harshness，噪声、振动与声振粗糙度）、刚度与质量等性能参数的多目标优化近似模型，并采用模糊MOPSO算法实现了车架结构的轻量化。

然而，上述针对车门多目标优化的研究忽略了设计变量的不确定性，如材料特性、加工精度等，这可能会导致结构性能波动及确定性分析结果超出约束边界，从而降低最终方案的优化效果。此外，采用单一近似模型与单一优化算法所获得的优化结果为最优解的概率较低。

为此，笔者基于长安CS15汽车的钢制前车门开展内板与窗框一体化的铸铝车门模型的逆向设计，并分别建立原钢制车门和铸铝一体化车门的有限元模型，以分析车门的下沉刚度、上扭转刚度、下扭转刚度以及自由模态性能。然后，选取铸铝一体化车门的厚度为设计变量，运用最优拉丁超立方试验设计方法提取30组样本点，以构建RBF神经网络近似模型以及二阶响应面近似模型，再分别利用NSGA-Ⅱ、MOPSO算法和多岛遗传算法（multi-island genetic algorithm, MIGA）对车门的下沉刚度工况位移和质量进行确定性优化。最后，基于6Sigma可靠性标准对铸铝一体化车门进行可靠性分析，以获得最适合该车门多目标可靠性优化的设计方案。

1 铸铝一体化车门设计及其有限元模型构建

1.1　车门铸造工艺和材料选择

本文设计的铸铝一体化车门采用熔模精密铸造工艺进行生产。熔模精密铸造是一种高精度铸造工艺，也被称为失蜡铸造。熔模铸造的产品具有较高的尺寸和形状精度，适用于生产形状复杂、壁厚不均匀、内部空腔的产品。

车门的熔模铸造材料选用ZL201A铝合金，其材料性能参数如表1所示。

表1 ZL201A铝合金材料性能参数

Table 1 Material property parameters of ZL201A aluminum alloy

参数	数值
密度/(kg/m³)	2 800
弹性模量/GPa	69
泊松比	0.33
抗拉强度/MPa	≥390
伸长率/%	≥8

新窗口打开| 下载CSV

1.2　车门有限元模型构建

在建立车门有限元模型之前，需先建立车门的三维模型。在不改变原钢制车门边界条件的前提下，建立铸铝一体化车门的三维模型。相较于原钢制车门模型，铸铝一体化车门模型的组成部件显著减少，从钢制车门模型的18个组成部件减少为3个。部件的减少省去了多处焊接、铆接或胶粘工艺，使得车门结构简单且便于安装。

采用壳单元对车门三维模型进行离散化处理，以更准确、更高效地模拟车门的力学特性，同时能够节省建模时间和提高计算效率^[10]。在前处理软件HyperMesh中，构建钢制车门和铸铝一体化车门的有限元模型。考虑到仿真结果的精度，将网格单元尺寸设置为3 mm，焊点采用刚性单元模拟。钢制车门材料的密度为7 850 kg/m³，弹性模量为210 GPa，泊松比为0.7。

最终建立的钢制车门有限元模型如图1所示。其中，壳单元数量为302 247个，四边形单元数量为289 619个，三角形单元数量为12 628个，三角形单元所占比例为4.2%，小于8%，符合建模要求；焊点单元数量为969个，模型质量为17.46 kg。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 钢制车门有限元模型

Fig.1 Finite element model of steel car door

铸铝一体化车门有限元模型如图2所示。其中，壳单元数量为196 337个，四边形单元数量为191 947个，三角形单元数量为4 390个，三角形单元所占比例为2.2%，小于8%，符合建模要求；焊点单元数量为454个，模型质量为14.68 kg。铸铝一体化车门的窗框和内板通过共节点形成一体化模型，内板边缘设置胶粘面，内板周围设置5个螺栓连接凸台，外板对应位置处设置5个螺栓连接面；内板与外板通过螺栓连接与胶粘联合使用的方式进行装配。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 铸铝一体化车门有限元模型

Fig.2 Finite element model of cast aluminum integrated car door

2 铸铝一体化车门刚度分析

2.1　下沉刚度工况

车门的下沉刚度是指车门在自身重力和垂直方向载荷作用下抵抗变形的能力。下沉刚度直接影响车门与其侧围制件的间隙大小。在车辆行驶过程中，车门的下沉刚度能够有效防止车门因风力和路面颠簸等因素而产生过度振动和变形，从而提高车门的密封性和安全性。车门的下沉刚度可通过仿真模拟或实验测试来进行测量和评估。

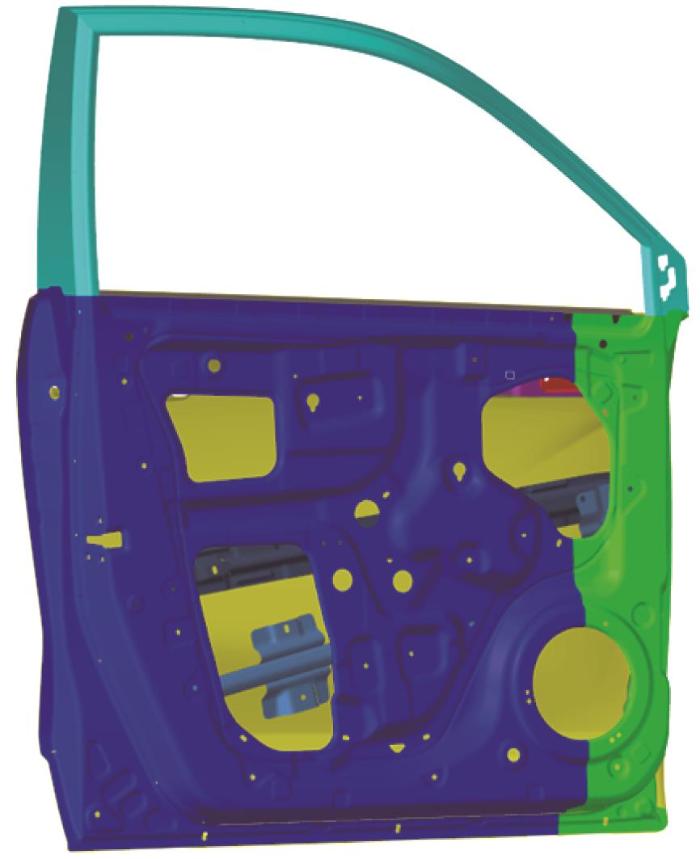
在下沉刚度工况中，约束铸铝一体化车门上下铰链螺栓孔位置的6个自由度和门锁位置沿竖直方向的自由度（即Z轴转动自由度），并在门锁位置处施加900 N竖直向下的下沉力F_Z，如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 铸铝一体化车门下沉刚度工况

Fig.3 Sinking stiffness condition of cast aluminum integrated car door

经OptiStruct软件求解可得，在铸铝一体化车门下沉刚度工况中，下沉力F_Z 加载点处的最大位移为3.773 mm，小于位移上限4.5 mm^[11]，满足设计要求。根据刚度计算公式K=F/d（其中K为刚度，F为外力，d为位移），求解得到铸铝一体化车门的下沉刚度为238.54 N/mm。

2.2　上扭转刚度工况

车门扭转刚度是指车门在平面内发生扭转变形时所产生的阻力。较高的扭转刚度能够有效防止车门在车辆行驶过程中发生过度扭转，从而保持车门的稳定性和密封性。此外，较高的车门扭转刚度还能提高车辆的安全性，减少车辆发生碰撞时车门的变形和损坏。

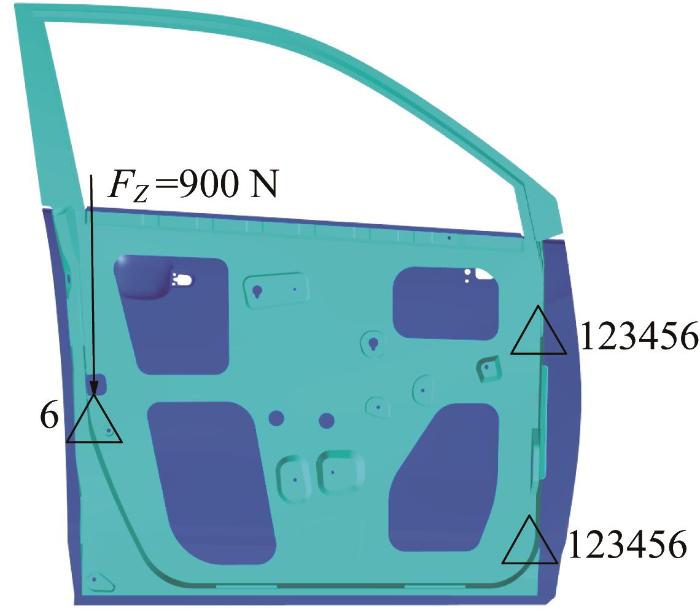
在上扭转刚度工况中，约束铸铝一体化车门上下铰链螺栓孔位置的6个自由度和门锁位置的3个平动自由度，并在窗框后下方位置处施加900 N垂直于表面的上扭转力F_U，F_U的方向为由车门内板指向外板，如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 铸铝一体化车门上扭转刚度工况

Fig.4 Upper torsional stiffness condition of cast aluminum integrated car door

经OptiStruct软件求解可得，在铸铝一体化车门上扭转刚度工况中，上扭转力F_U加载点处的最大位移为1.711 mm，小于位移上限6 mm^[12]，满足设计要求。根据刚度计算公式，求解得到铸铝一体化车门的上扭转刚度为526.01 N/mm。

2.3　下扭转刚度工况

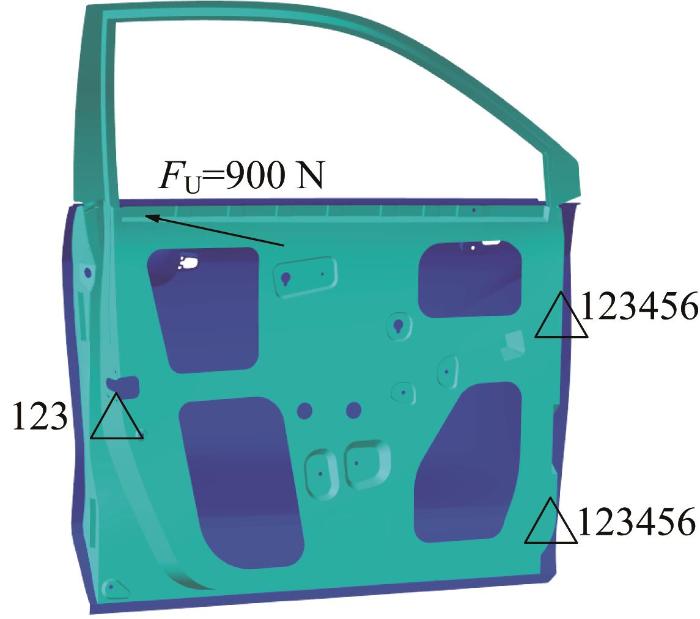
在下扭转刚度工况中，约束铸铝一体化车门上下铰链螺栓孔位置的6个自由度和门锁位置的3个平动自由度，并在车门内板后下方位置处施加900 N垂直于表面的下扭转力F_D，F_D的方向为由车门内板指向外板，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 车门下扭转刚度工况

Fig.5 Lower torsional stiffness condition of cast aluminum integrated car door

经OptiStruct软件求解，在铸铝一体化车门下扭转刚度工况中，下扭转力F_D加载点处的最大位移为0.618 mm，小于位移上限6 mm^[12]，满足设计要求。根据刚度计算公式，求解得到铸铝一体化车门的下扭转刚度为1 456.31 N/mm。

3 铸铝一体化车门模态仿真与试验分析

模态分析可有效反映物体的固有动态属性^[13]，通过对比模态仿真结果与试验结果的相对误差可以验证所构建的有限元模型的准确性。对铸铝一体化车门进行模态仿真与试验分析，以确定相应的模态参数，从而为其振动特性分析和结构动力特性的可靠性优化提供依据。

3.1　模态仿真

车门的振动特性主要由低阶模态决定，故在对铸铝一体化车门进行自由模态仿真时，将频率设置为0~100 Hz。由于最大的影响主要来自低频段，因此重点观察前2阶非零模态的频率^[14]。本文主要观察铸铝一体化车门的一阶弯曲模态频率与一阶扭转模态频率。铸铝一体化车门的模态仿真结果如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 铸铝一体化车门模态仿真结果

Fig.6 Modal simulation results of cast aluminum integrated car door

3.2　模态试验

模态试验设备包括DH8303动态信号测试系统、DHDAS动态信号采集分析软件、LC02力锤、BW1454加速度传感器和BNC（bayonet nut connector，刺刀螺母连接器）接口的信号转接线等。在开展模态试验时，铸铝一体化车门通过弹性绳悬挂的方式来近似模拟自由状态；在车门的外板与窗框处布置38个测点，如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 铸铝一体化车门模态试验测点布置

Fig.7 Modal test point arrangement for cast aluminum integrated car door

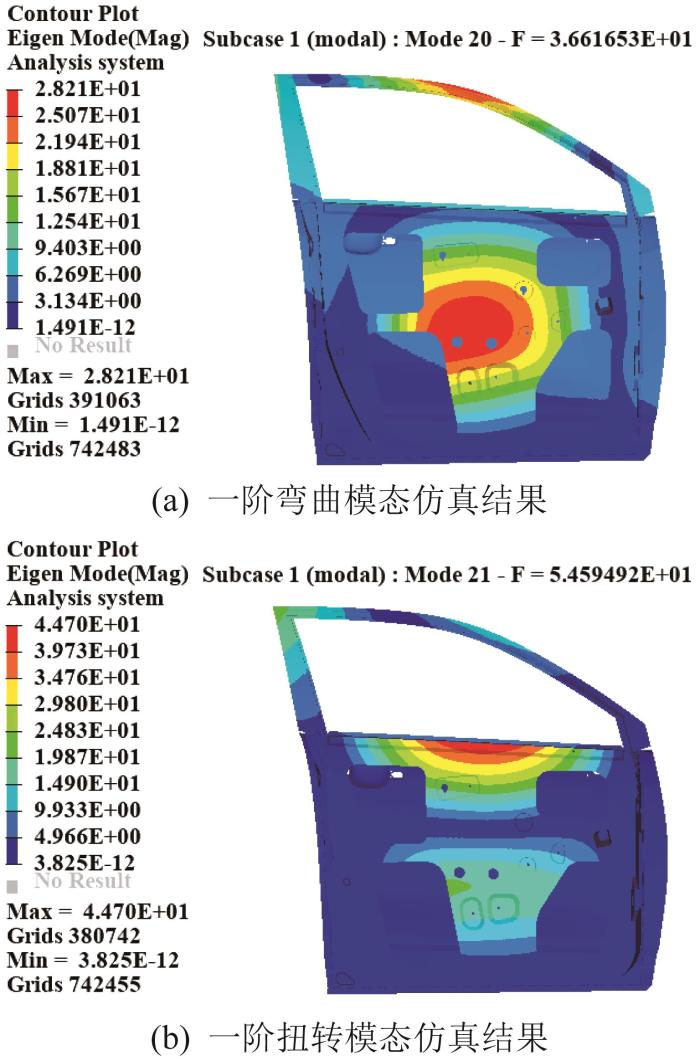
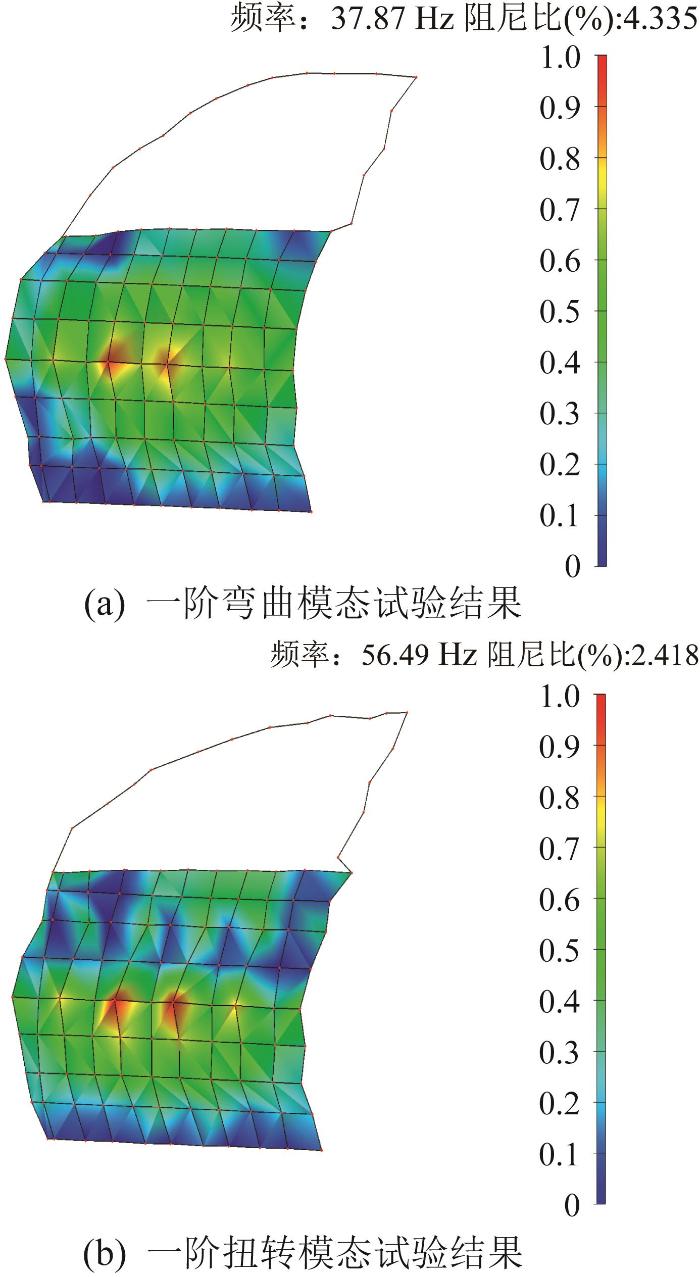
将铸铝一体化车门上38个测点的位置信息输入DHDAS动态信号采集分析软件并建立试验模型，以获得该车门的一阶弯曲模态与一阶扭转模态，结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 铸铝一体化车门模态试验结果

Fig.8 Modal test results of cast aluminum integrated car door

3.3　模态结果对比分析

铸铝一体化车门一阶弯曲模态频率、一阶扭转模态频率的仿真结果与试验结果的对比如表2所示。

表2 铸铝一体化车门模态仿真与试验结果对比

Table 2 Comparison of modal simulation and test results of cast aluminum integrated car door

模态	频率/Hz		相对误差/%
模态	仿真值	试验值	相对误差/%
一阶弯曲模态	36.62	37.87	3.4
一阶扭转模态	54.59	56.49	3.5

新窗口打开| 下载CSV

由表2可知，铸铝一体化车门一阶弯曲模态频率、一阶扭转模态频率的仿真值与试验值之间的相对误差控制在5%以内，验证了所构建的有限元模型的准确性。由于铸造工艺的限制，初次设计的铸铝一体化车门的内、外板及窗框的厚度均为3 mm，其一阶弯曲模态频率未达到设计所要求的40 Hz，因此须对该车门的模态性能进行优化。

4 铸铝一体化车门多目标确定性优化

4.1　最优拉丁超立方试验设计

最优拉丁超立方试验设计方法是基于拉丁超立方试验设计的改进方法。该方法可确保每个处理因素的不同水平的出现次数相等，以保证样本点更加均衡，从而降低了误差，提高了试验精度；同时，在保证试验结果可靠的前提下，能更好地探索处理因素之间的相互作用，从而提高试验效率和准确性^[15]。拉丁超立方试验设计方法与最优拉丁超立方试验设计方法的采样策略如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同拉丁超立方试验设计方法的采样策略

Fig.9 Sampling strategies of different Latin hypercube experimental design methods

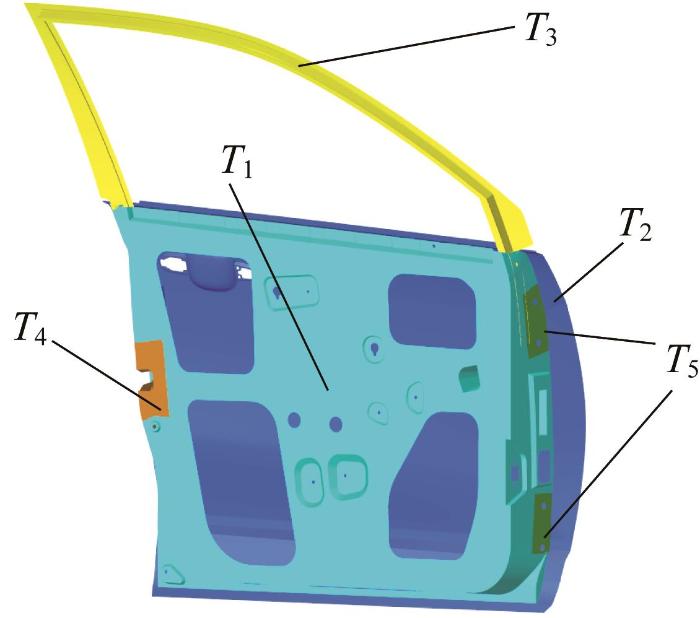
本文以铸铝一体化车门的内板厚度T₁、外板厚度T₂、窗框厚度T₃、门锁安装面厚度T₄及车门铰链安装面厚度T₅为设计变量（见图10，其中各部件厚度的取值范围均为2~4 mm），以一阶弯曲模态频率f₁、一阶扭转模态频率f₂、上扭转刚度工况位移d₂及下扭转刚度工况位移d₃为约束条件，以车门的质量m和下沉刚度工况位移d₁为优化目标，开展车门确定性优化设计。考虑到材料和加工制造的不确定性，通过获取所选铝合金的材料曲线来降低材料的不确定性，以使仿真结果与实际铸造部件的性能更加接近；同时，通过在工程图纸中添加CT7公差来控制铸造部件的各个尺寸，以减小加工制造带来的不确定性。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 铸铝一体化车门各部件厚度示意

Fig.10 Schematic of thickness of each component in cast aluminum integrated car door

采用最优拉丁超立方试验设计方法，获取30组设计变量样本点，并基于铸铝一体化车门的有限元模型，通过仿真分析获取车门的质量m、一阶弯曲模态频率f₁、一阶扭转模态频率f₂、下沉刚度工况位移d₁、上扭转刚度工况位移d₂和下扭转刚度工况位移d₃。铸铝一体化车门确定性优化的试验设计方案与结果如表3所示（限于篇幅，仅列举部分结果）。

表3 铸铝一体化车门确定性优化的试验设计方案与结果

Table 3 Experimental design scheme and results of deterministic optimization for cast aluminum integrated car door

试验编号	设计变量					m/kg	f₁/Hz	f₂/Hz	d₁/mm	d₂/mm	d₃/mm
试验编号	T₁/mm	T₂/mm	T₃/mm	T₄/mm	T₅/mm	m/kg	f₁/Hz	f₂/Hz	d₁/mm	d₂/mm	d₃/mm
1	2.069	3.862	2.828	3.103	3.448	12.90	25.72	46.06	2.073	3.145	1.301
2	2.207	3.172	2.276	3.241	2.276	11.49	27.17	47.50	3.588	2.860	1.174
3	3.448	2.276	3.241	4.000	3.103	15.83	37.35	58.59	1.857	1.378	0.460
4	3.034	3.793	2.345	3.862	2.966	13.63	34.36	54.94	2.252	1.616	0.604
5	2.483	2.345	2.000	2.483	3.172	10.97	29.55	50.20	4.699	2.448	0.951
︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙
28	2.000	2.966	3.586	2.552	2.483	14.05	24.82	45.34	2.295	2.426	1.416
29	3.655	4.000	2.897	2.690	3.241	16.19	38.58	60.32	1.281	1.199	0.444
30	3.586	3.724	3.655	3.793	2.759	17.75	38.11	59.71	1.009	1.214	0.426

新窗口打开| 下载CSV

4.2　近似模型构建

4.2.1　RBF神经网络近似模型

RBF神经网络是一种通过拟合离散多元数据来获取未知函数值的方法，其具有非线性逼近能力强、高效、模型简单以及适应性强等特点^[16]。

假设存在一组已知的输入值 $x_{1}, x_{2}, \dots,$ $x_{N}$ ， $x_{j} \in R$ ，对应的输出响应值为 $y_{1}, y_{2}, \dots, y_{N}$ ， $y_{j} \in R$ 。基于RBF神经网络近似模型，近似估计未知点的差值模型 $F (x)$ ：

F (x) = \sum_{j = 1}^{N} α_{j} h_{j} (x) + α_{N + 1}

(1)

其中：

h_{j} (x) = h ({‖x - x_{j}‖}^{c}), j = 1, 2, \dots, N

\sum_{j = 1}^{N} α_{j} = 0

式中： $h_{j} (x)$ 为一组RBF， $α_{j}$ 为RBF的差值系数， $‖x - x_{j}‖$ 为样本点和待测点之间的欧几里得距离；c为样条形状参数。

基于表3所示的试验数据和式(1)，构建铸铝一体化车门质量m、一阶弯曲模态频率f₁、一阶扭转模态频率f₂、下沉刚度工况位移d₁、上扭转刚度工况位移d₂和下扭转刚度工况位移d₃的RBF神经网络近似模型。

4.2.2　二阶响应面近似模型

响应面法能够对多变量优化系统进行有效的建模和分析。该方法通过回归拟合和绘制响应曲面等方式，快速获取各因素各水平对应的响应值，从而确定响应最优值及对应的试验条件。本文采用二阶响应面模型，其表达式为：

S (x) = P_{0} + \sum_{i = 1}^{n} P_{i} x_{i} + \sum_{i = 1}^{n} P_{i} x_{i}^{2} + \sum_{1 \leq i \leq l \leq n}^{n} P_{i l} x_{i} x_{l}

(2)

式中：P_i 为多项式系数，x_i 、x_l 为设计变量，n为设计变量个数。

基于表3所示的试验数据和式(2)，建立铸铝一体化车门质量m、一阶弯曲模态频率f₁、一阶扭转模态频率f₂、下沉刚度工况位移d₁、上扭转刚度工况位移d₂和下扭转刚度工况位移d₃的二阶响应面近似模型。限于篇幅以及考虑到确定性优化目标，仅给出铸铝一体化车门质量m和下沉刚度工况位移d₁的二阶响应面近似模型，具体如下：

\begin{array}{l} m = 0.078 78 + 1.937 4 T_{1} + 0.484 5 T_{2} + 2.351 5 T_{3} + \\ 0.041 0 T_{4} + 0.022 7 T_{5} + 0.000 2 T_{1}^{2} + 0.001 4 T_{2}^{2} + \\ 0.001 7 T_{3}^{2} + 0.001 1 T_{4}^{2} + 0.001 8 T_{5}^{2} - 1.983 0 T_{1} T_{2} + \\ 0.000 2 T_{1} T_{3} + 0.003 7 T_{1} T_{4} - 0.000 9 T_{1} T_{5} - \\ 0.001 7 T_{2} T_{3} - 0.001 4 T_{2} T_{4} + 0.000 8 T_{2} T_{5} + \\ 8.736 2 T_{3} T_{4} + 0.002 0 T_{3} T_{5} + 0.000 7 T_{4} T_{5} \end{array}

(3)

\begin{array}{l} d_{1} = 29.251 9 - 3.440 2 T_{1} - 0.323 7 T_{2} - 0.193 8 T_{3} - \\ 4.012 8 T_{4} - 5.750 0 T_{5} + 0.233 7 T_{1}^{2} - 0.027 0 T_{2}^{2} - \\ 0.032 3 T_{3}^{2} + 0.170 0 T_{4}^{2} + 0.302 3 T_{5}^{2} + 0.050 6 T_{1} T_{2} + \\ 0.055 6 T_{1} T_{3} + 0.091 1 T_{1} T_{4} + 0.203 6 T_{1} T_{5} + \\ 0.043 7 T_{2} T_{3} - 0.006 5 T_{2} T_{4} + 0.042 4 T_{2} T_{5} - \\ 0.003 6 T_{3} T_{4} - 0.010 9 T_{3} T_{5} + 0.635 8 T_{4} T_{5} \end{array}

(4)

4.3　近似模型精度分析

为了验证上文所构建的铸铝一体化车门各响应的RBF神经网络近似模型和二阶响应面近似模型的准确性，采用方差分析中的决定系数R²对各近似模型的精度进行评价，结果如表4所示。其中，R²越接近1，说明近似模型的精度越高。

表4 铸铝一体化车门各响应的近似模型的精度评价结果

Table 4 Accuracy evaluation results of approximation model of each response of cast aluminum integrated car door

响应	RBF神经网络近似模型	二阶响应面近似模型
d₁	0.974 86	0.931 54
d₂	0.980 79	0.979 53
d₃	0.970 83	0.961 69
f₁	0.999 21	0.999 93
f₂	0.999 43	0.999 50
m	0.999 11	0.999 98

新窗口打开| 下载CSV

由表4可知，铸铝一体化车门各响应的RBF神经网络近似模型与二阶响应面近似模型的R²均大于0.9且接近于1，说明所构建的近似模型满足精度要求，可作为优化模型。

4.4　确定性优化模型与优化算法

车门的质量与性能优化是一个典型的多目标优化问题。在提升车门轻量化水平和性能的过程中，须对其他性能参数的设计空间进行适当调整，即通过设置合理的约束条件来确保车门的各项性能均满足设计要求，从而实现车门整体性能的优化。根据上文确定的铸铝一体化车门的优化目标、设计变量、约束条件以及所构建的近似模型，建立其确定性优化数学模型：

\{\begin{array}{l} m i n_{} m \\ m i n_{} d_{1} \\ s . t ._{}_{}_{} d_{2} \leq 6 m m \\ \begin{matrix} _{}_{} d_{3} \leq 6 \end{matrix} m m \\ \begin{matrix} _{}_{} f_{1} \geq 40 \end{matrix} H z \\ \begin{matrix} _{}_{} f_{2} \geq 60 H z \end{matrix} \\ \begin{matrix} _{}_{} T_{i} \in [2, 4] \end{matrix} m m (i = 1, 2, \dots, 5) \end{array}

(5)

本文采用NSGA-II、MOPSO算法和MIGA对铸铝一体化车门的确定性优化数学模型进行优化求解。

NSGA-II是一种常用的多目标优化算法，其以NSGA为基础并引入了精英保持策略和拥挤度比较方法，加快了收敛速度并提高了全局搜索能力^[17]。本文中NSGA-II的参数设置如表5所示。

表5 NSGA-II的参数设置

Table 5 Parameter setting for NSGA-II

参数	数值
种群数/个	100
迭代数/次	50
交叉率	0.9
交叉分布指数	10
突变分布指数	20

新窗口打开| 下载CSV

MOPSO算法是基于PSO算法扩展而来的，该算法具有结构简单、易收敛和通用性强等特点。在MOPSO算法中，粒子通过在搜索空间中动态调整自身速度来达到移动至更好区域的目的；同时，每个粒子在多维搜索空间中移动时会根据自身与邻近粒子的距离来改变位置^[18]。本文中MOPSO算法的参数设置如表6所示。

表6 MOPSO算法的参数设置

Table 6 Parameter setting for MOPSO algorithm

参数	数值
迭代数/次	50
粒子数/个	100
惯性权重	0.9
全局增量	0.9
粒子增量	0.9

新窗口打开| 下载CSV

MIGA是基于并行分布遗传算法优化而来的。相较于传统的遗传算法，MIGA具有更强的求解能力和更高的计算效率^[19]。本文中MIGA的参数设置如表7所示。

表7 MIGA的参数设置

Table 7 Parameter setting for MIGA

参数	数值
种群数/个	50
岛屿数/个	10
迭代数/次	10
交叉率	1.0
变异率	0.01
迁移率	0.01

新窗口打开| 下载CSV

4.5　确定性优化结果分析

4.5.1　基于RBF神经网络近似模型的确定性优化结果

基于铸铝一体化车门各响应的RBF神经网络近似模型，分别采用3种优化算法对确定性优化模型进行迭代求解，获得对应的确定性优化结果并与原钢制车门各部件的厚度和性能参数进行对比，结果如表8所示。

表8 基于RBF神经网络近似模型的铸铝一体化车门确定性优化结果

Table 8 Deterministic optimization results of cast aluminum integrated car door based on RBF neural network approximation model

参数	初始值^1）	优化值
参数	初始值^1）	NSGA-Ⅱ	MOPSO	MIGA
T₁/mm	0.70	3.716 2	3.730 8	3.738 8
T₂/mm	1.40	2.000 6	2.000 0	2.003 7
T₃/mm	0.65	2.000 1	2.000 0	2.017 2
T₄/mm	0.70	3.999 1	3.990 8	3.980 5
T₅/mm	1.80	3.999 7	4.000 0	3.973 9
d₁/mm	4.402	1.843 5	1.837 9	1.866 9
d₂/mm	2.904	1.115 3	1.104 1	1.100 7
d₃/mm	1.443	0.352 1	0.347 9	0.347 1
f₁/Hz	49.22	40.00	40.11	40.17
f₂/Hz	75.53	61.21	61.33	61.41
m/kg	17.46	13.322	13.350	13.406

1）初始值为原钢制车门的参数值。

新窗口打开| 下载CSV

由表8可知，以RBF神经网络近似模型作为铸铝一体化车门的优化模型时，采用NSGA-II和MOPSO算法所获得的确定性优化结果比较接近，且基于这2种算法的车门轻量化效果优于基于MIGA的。

4.5.2　基于二阶响应面近似模型的确定性优化结果

基于铸铝一体化车门各响应的二阶响应面近似模型，分别采用3种优化算法对确定性优化模型进行迭代求解，获得对应的确定性优化结果并与原钢制车门各部件的厚度和性能参数进行对比，结果如表9所示。

表9 基于二阶响应面近似模型的铸铝一体化车门确定性优化结果

Table 9 Deterministic optimization results of cast aluminum integrated car door based on second-order response surface approximation model

参数	初始值^1）	优化值
参数	初始值^1）	NSGA-Ⅱ	MOPSO	MIGA
T₁/mm	0.70	3.726 8	3.722 8	3.747 0
T₂/mm	1.40	2.000 7	2.000 0	2.014 5
T₃/mm	0.65	2.000 0	2.000 0	2.007 9
T₄/mm	0.70	3.301 3	3.469 2	3.469 3
T₅/mm	1.80	3.994 1	3.948 8	3.982 5
d₁/mm	4.402	2.551 3	2.566 8	2.546 4
d₂/mm	2.904	1.172 1	1.170 3	1.160 2
d₃/mm	1.443	0.390 4	0.388 7	0.386 6
f₁/Hz	49.22	40.01	40.03	40.21
f₂/Hz	75.53	61.38	61.35	61.56
m/kg	17.46	13.302	13.302	13.376

1）初始值为原钢制车门的参数值。

新窗口打开| 下载CSV

由表9可知，以二阶响应面近似模型作为铸铝一体化车门的优化模型时，同样也是采用NSGA-II和MOPSO算法所获得的确定性优化结果比较接近，且基于这2种算法的车门轻量化效果优于基于MIGA的。

5 铸铝一体化车门多目标可靠性优化设计

5.1　基于6Sigma质量水平的可靠性分析

与传统的确定性优化相比，6Sigma可靠性优化增加了目标函数中目标的均方误差，以寻求最优解^[20-21]。可靠性优化的数学模型如下：

\{\begin{array}{l} m i n_{}_{}_{} y (f (x)) \\ s . t . P (g_{k} (x) \leq 0) \leq φ (- β_{t}), k = 1, 2, \dots, N_{1} \\ μ_{L} (x) \leq μ (x) \leq μ_{U} (x) \end{array}

(6)

式中： $y (f (x))$ 为目标函数， $P (g_{k} (x) \leq 0)$ 为失效概率分布函数， $g_{k} (x)$ 为约束函数， $φ (- β_{t})$ 为标准正态分布函数的累计分布函数， $β_{t}$ 为期望可靠度， $μ (x)$ 为随机设计变量的均值， $μ_{L} (x)$ 为随机设计变量的均值下限； $μ_{U} (x)$ 为随机设计变量的均值上限。

失效概率分布函数 $P (g_{k} (x) \leq 0)$ 能定义累计分布函数 $F (g_{k} (0))$ ，其表达式分别为：

P (g_{k} (x) \leq 0) = F (g_{k} (0)) \leq φ (- β_{t})

F (g_{k} (0)) = \int_{g_{k} (x) \leq 0} \dots \int f_{x} (x) d x

结构的失效概率 $P_{g}$ 和可靠度R的表达式如下：

P_{g} = φ (- β)

R = 1 - P_{g} = 1 - φ (- β)

在对结构进行确定性优化时，若设计变量受到不规则扰动，则确定性优化结果可能会产生较大误差，导致无法达到预期的优化效果或无法达到所要求的可靠性水平。而以低可靠性方案进行生产，可能会存在较高的质量风险。基于6Sigma可靠性标准，对上文的铸铝一体化车门确定性优化结果进行分析，其质量水平Q与可靠度R如表10所示。

表10 铸铝一体化车门确定性优化结果的质量水平与可靠度

Table 10 Quality level and reliability of deterministic optimization results of cast aluminum integrated car door

参数	RBF神经网络近似模型						二阶响应面近似模型
	NSGA-II		MOPSO		MIGA		NSGA-II		MOPSO		MIGA
	Q	R	Q	R	Q	R	Q	R	Q	R	Q	R
d₂/mm	8	1	8	1	8	1	8	1	8	1	8	1
d₃/mm	8	1	8	1	8	1	8	1	8	1	8	1
f₁/Hz	0.678	0.503	0.937	0.651	1.065	0.713	0.694	0.512	0.738	0.539	1.192	0.767
f₂/Hz	3.869	0.999	4.231	0.999	4.417	0.999	4.373	0.999	4.294	0.999	4.888	0.999

新窗口打开| 下载CSV

由表10可知，基于RBF神经网络近似模型与二阶响应面近似模型优化得到的铸铝一体化车门的一阶弯曲模态频率和一阶扭转模态频率的质量水平均不满足6Sigma可靠性标准。因此，需进一步使用6Sigma可靠性优化方法将铸铝一体化车门设计目标的标准差最小化并使其均值达到设定值，以降低车门各响应对设计变量的灵敏度，从而提高车门的可靠性。

5.2　铸铝一体化车门可靠性优化

基于6Sigma可靠性分析理论，建立铸铝一体化车门的可靠性优化数学模型：

\{\begin{array}{l} m i n_{}_{}_{} μ (m) + σ (m) \\ m i n_{}_{}_{} μ (d_{1}) + σ (d_{1}) \\ s . t . μ (d_{2}) + 6 σ (d_{2}) \leq 6 m m \\ μ (d_{3}) + 6 σ (d_{3}) \leq 6 m m \\ μ (f_{1}) + 6 σ (f_{1}) \geq 40 H z \\ μ (f_{2}) + 6 σ (f_{2}) \geq 60 H z \\ 2 \leq μ (T_{i}) + 6 σ (T_{i}) \leq 4 m m (i = 1, 2, \dots, 5) \end{array}

(7)

可靠性优化的目标为实现铸铝一体化车门质量和下沉刚度工况位移的最小化。经过6Sigma可靠性优化求解后，将Pareto解集中推荐的最优解输入铸铝一体化车门的有限元模型，通过仿真分析来验证可靠性优化结果的准确性。

5.2.1　基于RBF神经网络近似模型的可靠性优化结果

基于铸铝一体化车门各响应的RBF神经网络近似模型，分别采用3种优化算法对可靠性优化模型进行迭代求解，获得对应的可靠性优化结果并与原钢制车门各部件的厚度和性能参数进行对比，结果如表11所示。

表11 基于RBF神经网络近似模型的铸铝一体化车门可靠性优化结果

Table 11 Reliability optimization results of cast aluminum integrated car door based on RBF neural network approximation model

参数	初始值^1）	优化值
参数	初始值^1）	NSGA-Ⅱ	MOPSO	MIGA
T₁/mm	0.70	3.998 0	3.941 6	3.961 3
T₂/mm	1.40	2.135 1	2.000 0	2.066 5
T₃/mm	0.65	2.018 9	2.000 0	2.031 3
T₄/mm	0.70	3.968 8	4.000 0	3.948 0
T₅/mm	1.80	3.986 6	4.000 0	3.990 7
d₁/mm	4.402	1.696 6	1.680 1	1.744 4
d₂/mm	2.904	0.910 7	0.964 1	0.952 2
d₃/mm	1.443	0.276 2	0.278 8	0.280 1
f₁/Hz	49.22	42.45	42.31	42.35
f₂/Hz	75.53	64.18	63.91	63.98
m/kg	17.46	14.154	13.786	13.983

1）初始值为原钢制车门的参数值。

新窗口打开| 下载CSV

根据6Sigma可靠性标准，对基于RBF神经网络近似模型的铸铝一体化车门可靠性优化结果的质量水平Q与可靠度R进行分析，结果如表12所示。

表12 基于RBF神经网络近似模型的铸铝一体化车门可靠性优化结果的质量水平与可靠度

Table 12 Quality level and reliability of reliability optimization results of cast aluminum integrated car door based on RBF neural network approximation model

参数	NSGA-II		MOPSO		MIGA
参数	Q	R	Q	R	Q	R
d₂	8	1	8	1	8	1
d₃	8	1	8	1	8	1
f₁	7.57	1	6.17	1	6.55	1
f₂	8	1	8	1	8	1

新窗口打开| 下载CSV

由表12可知，与对应的确定性优化结果相比，经可靠性优化后铸铝一体化车门的一阶弯曲模态频率和一阶扭转模态频率的质量水平与可靠度均有所提高且达到了6Sigma水平。

由表11可知，利用RBF神经网络近似模型和MOPSO算法对铸铝一体化车门进行可靠性优化后，得到的车门质量和下沉刚度工况位移为3组优化方案中的最优值。对基于该组合获得的铸铝一体化车门可靠性优化结果进行仿真验证，结果如表13所示。

表13 基于RBF神经网络近似模型和MOPSO算法的铸铝一体化车门可靠性优化结果的仿真验证

Table 13 Simulation verification of reliability optimization results of cast aluminum integrated car door based on RBF neural network approximation model and MOPSO algorithm

参数	优化值	仿真值	相对误差/%
d₁/mm	1.680 1	1.650 0	1.8
d₂/mm	0.964 1	0.936 7	2.8
d₃/mm	0.278 8	0.282 4	1.3
f₁/Hz	42.31	41.76	1.3
f₂/Hz	63.91	63.21	1.1
m/kg	13.786	13.761	0.2

新窗口打开| 下载CSV

由表13可知，铸铝一体化车门的质量和各性能参数的优化值与仿真值的相对误差控制在5%以内，且通过仿真得到的车门结构的最大应力（317 MPa）小于材料的屈服强度，验证了RBF神经网络近似模型与MOPSO算法的优化组合方案的可行性。

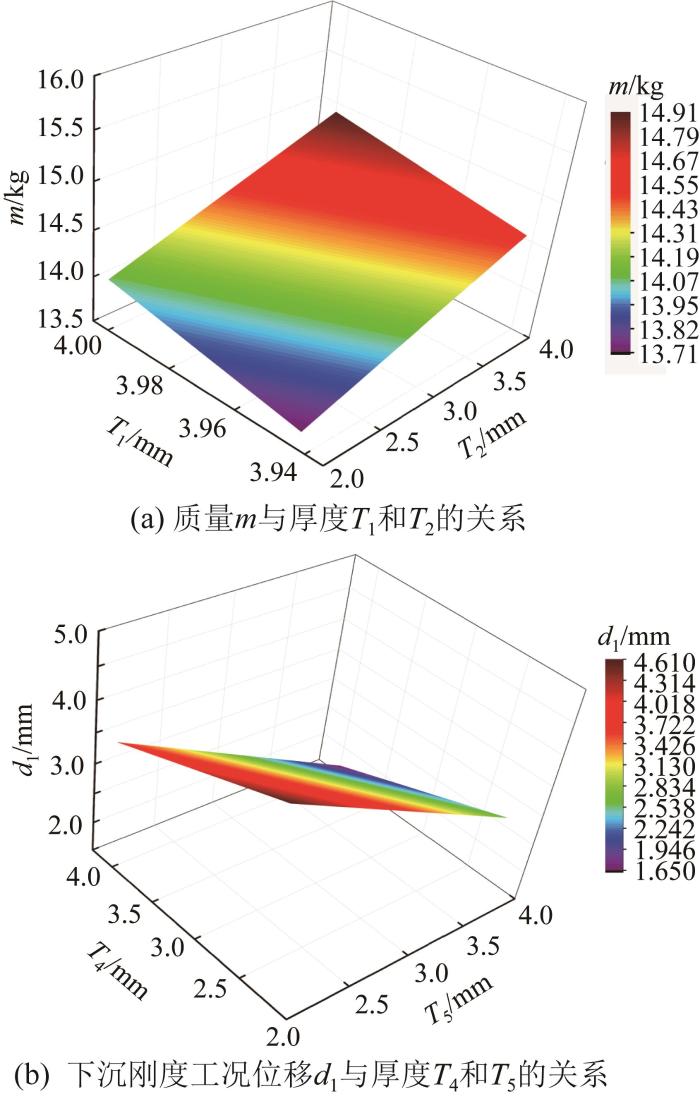
根据上述可靠性优化结果，绘制铸铝一体化车门的质量m与内板厚度T₁和外板厚度T₂的Plane函数拟合曲线，以及车门下沉刚度工况位移d₁与门锁安装面厚度T₄和铰链安装面厚度T₅的Plane函数拟合曲线，结果如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 基于RBF神经网络近似模型和MOPSO算法的铸铝一体化车门可靠性优化结果的拟合曲面

Fig.11 Fitting surfaces of reliability optimization results of cast aluminum integrated car door based on RBF neural network approximation model and MOPSO algorithm

由图11可知，铸铝一体化车门的质量m与厚度T₁和T₂呈线性关系，且m随T₁、T₂的增大而增大；下沉刚度工况位移d₁与厚度T₄和T₅同样呈线性关系，且d₁随T₄、T₅的增大而减小。

5.2.2　基于二阶响应面近似模型的可靠性优化结果

基于铸铝一体化车门各响应的二阶响应面近似模型，分别采用3种优化算法对可靠性优化模型进行迭代求解，获得对应的可靠性优化结果并与原钢制车门各部件的厚度和性能参数进行对比，结果如表14所示。

表14 基于二阶响应面近似模型的铸铝一体化车门可靠性优化结果

Table 14 Reliability optimization results of cast aluminum integrated car door based on second-order response surface approximation model

参数	初始值^1）	优化值
参数	初始值^1）	NSGA-Ⅱ	MOPSO	MIGA
T₁/mm	0.70	3.951 9	3.954 7	3.953 2
T₂/mm	1.40	2.040 7	2.000 0	2.007 9
T₃/mm	0.65	2.0013	2.000 0	2.033 3
T₄/mm	0.70	3.861 0	3.182 5	3.494 7
T₅/mm	1.80	3.670 3	3.900 8	3.993 2
d₁/mm	4.402	2.558 3	2.521 4	2.476 6
d₂/mm	2.904	1.110 9	1.112 0	1.101 7
d₃/mm	1.443	0.383 9	0.384 0	0.378 7
f₁/Hz	49.22	42.22	42.02	42.04
f₂/Hz	75.53	63.71	63.73	63.73
m/kg	17.46	13.894	13.851	13.924

1）初始值为原钢制车门的参数值。

新窗口打开| 下载CSV

根据6Sigma可靠性标准，对基于二阶响应面近似模型的铸铝一体化车门可靠性优化结果的质量水平Q与可靠度R进行分析，结果如表15所示。

表15 基于二阶响应面近似模型的铸铝一体化车门可靠性优化结果的质量水平与可靠度

Table 15 Quality level and reliability of reliability optimization results of cast aluminum integrated car door based on second-order response surface approximation model

参数	NSGA-II		MOPSO		MIGA
参数	Q	R	Q	R	Q	R
d₂	8	1	8	1	8	1
d₃	8	1	8	1	8	1
f₁	6.80	1	6.18	1	6.41	1
f₂	8	1	8	1	8	1

新窗口打开| 下载CSV

由表15可知，与对应的确定性优化结果相比，经可靠性优化后铸铝一体化车门的一阶弯曲模态频率和一阶扭转模态频率的质量水平与可靠度同样达到了6Sigma水平。

由表14可知，利用二阶响应面近似模型和MOPSO算法对铸铝一体化车门进行可靠性优化后，得到的车门质量为3组优化方案中的最优值。对基于该组合获得的铸铝一体化车门可靠性优化结果进行仿真验证，结果如表16所示。

表16 基于二阶响应面近似模型和MOPSO算法的铸铝一体化车门可靠性优化结果的仿真验证

Table 16 Simulation verification of reliability optimization results of cast aluminum integrated car door based on second-order response surface approximation model and MOPSO algorithm

参数	优化值	仿真值	相对误差/%
d₁/mm	2.521 4	2.526 4	0.2
d₂/mm	1.112 0	1.119 0	0.7
d₃/mm	0.384 0	0.388 4	1.1
f₁/Hz	42.02	41.66	0.9
f₂/Hz	63.73	63.35	0.6
m/kg	13.851	13.734	0.8

新窗口打开| 下载CSV

铸铝一体化车门的质量和各性能参数的优化值与仿真值的相对误差控制在5%以内，且通过仿真得到的车门结构的最大应力（336 MPa）小于材料的屈服强度，验证了二阶响应面近似模型和MOPSO算法的优化组合方案的可行性。

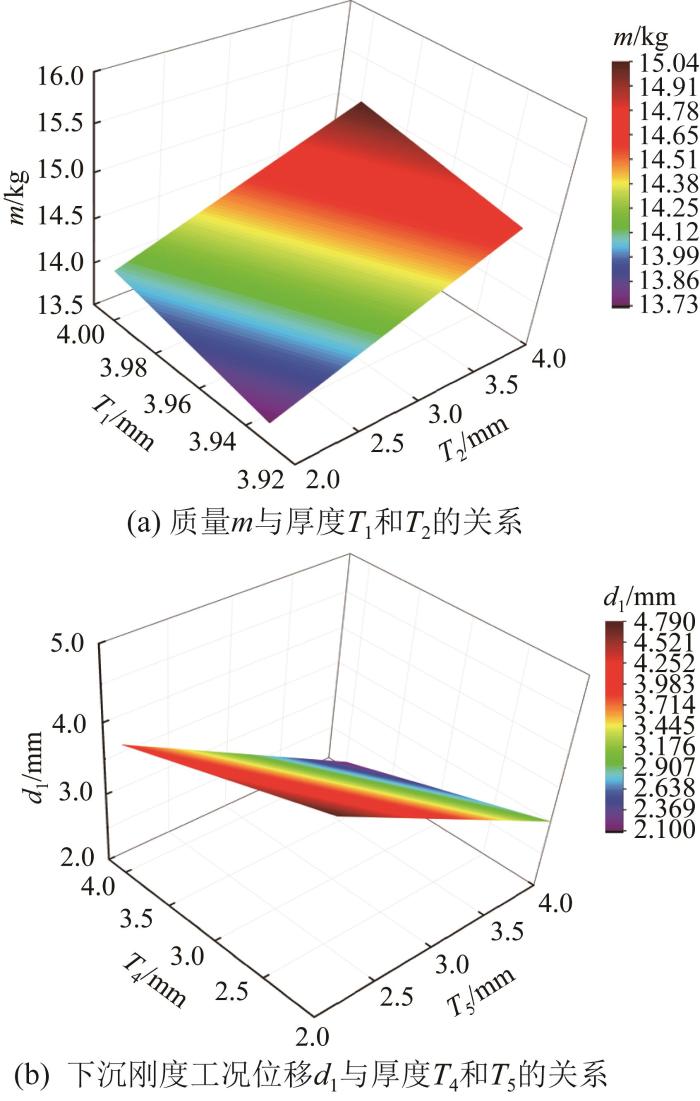
根据上述可靠性优化结果，绘制铸铝一体化车门的质量m与内板厚度T₁和外板厚度T₂的Plane函数拟合曲线，以及车门下沉刚度工况位移d₁与门锁安装面厚度T₄和铰链安装面厚度T₅的Plane函数拟合曲线，结果如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 基于二阶响应面近似模型和MOPSO算法的铸铝一体化车门可靠性优化结果的拟合曲面

Fig.12 Fitting surfaces of reliability optimization results of cast aluminum integrated car door based on second-order response surface approximation model and MOPSO algorithm

由图12可知，铸铝一体化车门的质量m与厚度T₁、T₂，以及下沉刚度工况位移d₁与厚度T₄、T₅均呈线性关系，其中m随T₁、T₂的增大而增大，d₁随T₄、T₅的增大而减小。

5.3　铸铝一体化车门可靠性优化结果分析

由上述6种方案的可靠性优化结果可知：二阶响应面近似模型与MOPSO算法的优化组合方案实现了铸铝一体化车门的最佳轻量化，在保证一阶弯曲模态频率大于40 Hz的前提下，车门的质量比钢制车门减小了21.3%，且下沉刚度工况位移减小了42.6%。当更注重下沉刚度工况位移的改善效果时，可采用RBF神经网络近似模型与MOPSO算法的优化组合方案。此时，铸铝一体化车门的下沉刚度工况位移比钢制车门减小了61.9%，且轻量化效果也较显著，优化后车门的质量相比于钢制车门减小了21.2%。

6 结论

本文基于长安CS15汽车的钢制车门，设计了铸铝一体化车门并对其进行多目标确定性优化和可靠性优化，最终实现了该车门的轻量化设计。主要研究工作及结论如下：

1）在保证车门整体尺寸与性能达到设计要求的前提下，基于熔模精密铸造设计了铸铝一体化车门，初步实现了车门的轻量化设计。

2）运用最优拉丁超立方试验设计方法提取了30组样本点，并构建了铸铝一体化车门刚度工况位移、模态频率和质量的高精度RBF神经网络近似模型与二阶响应面近似模型，并分别基于NSGA-Ⅱ、MOPSO算法和MIGA对铸铝一体化车门进行确定性优化。

3）对铸铝一体化车门的确定性优化解进行6Sigma可靠性优化与分析。结果表明：二阶响应面近似模型与MOPSO算法的优化组合方案实现了车门的最佳轻量化，RBF神经网络近似模型与MOPSO算法的优化组合方案实现了车门下沉刚度工况位移的最小化。这2种优化组合分别适用于车门的轻量化和安全化设计。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

徐建全，杨沿平.

纯电动汽车与传统汽车轻量化全生命周期多目标优化研究

［J］.汽车工程，2019，41（8）：885-891，914.