回转支承是兼有滚动轴承的回转支承特点和齿轮啮合传动特点的关键基础部件,能够同时承受径向、轴向负荷和倾覆力矩等联合载荷作用,具有复杂的动力学特性,且影响因素众多。回转支承作为关键的支承传动部件,具有结构紧凑、运动平稳、精度高及承载能力强等特点,在大型风电装备、工业机器人、工程机械和军事装备中得到广泛应用[1 ] 。回转支承的动态特性对高端装备系统的运行稳定性和可靠性有着重要的影响。回转支承的静、动力学研究还处于初级阶段,尤其是多因素影响下内齿式回转支承的多体接触动力学问题亟待深入研究。进一步开展基于动力学分析的多变量多目标优化设计研究对高性能回转支承的产品研发具有重要意义,同时为考虑回转支承动态性能的高端装备系统动力学研究奠定基础[2 ] 。
内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展。国内外学者对回转支承动态特性进行了一定的理论分析和实验研究。基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性。王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律。张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响。李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响。贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法。
由于内齿式回转支承内部相互作用关系复杂,影响因素较多,其动态特性研究还处于探索阶段,尤其是有关动态优化设计的研究还未见报道。作者考虑到钢球、4条套圈滚道与保持架的动态接触作用和小齿轮与内齿圈的动态啮合传动作用,建立了内齿式单排球式回转支承的参数化动力学模型,探讨关键设计参数对回转支承的动态特性影响,研究多变量多目标优化设计方法,为回转支承的动态设计与研发提供参考。
1 回转支承参数化多体动力学模型
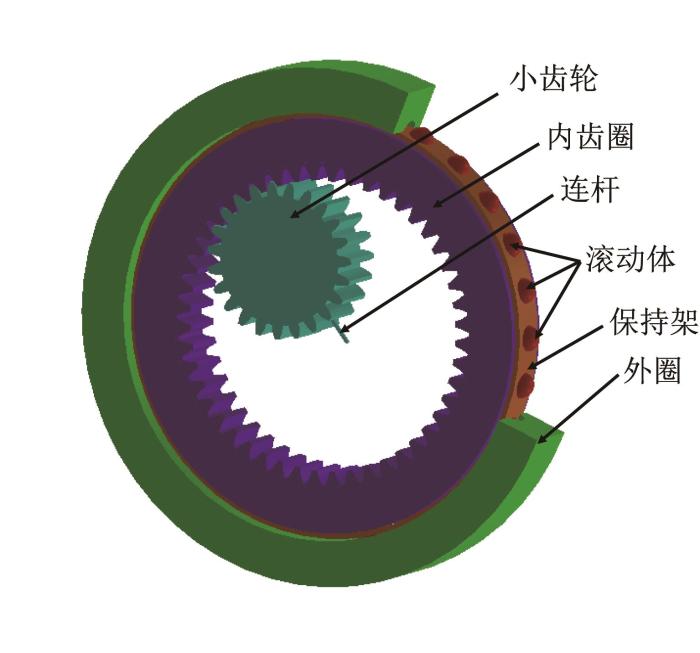
为了研究回转支承的动力学特性和动态优化设计,编制ADAMS参数化建模的宏命令程序,建立包含关键设计参数和力学参数的齿式回转支承参数化动力学模型。选取型号为013.25.400的回转支承,其内外圈、虚拟滚道及钢球的材料均为GCR15,保持架材料为黄铜。其主要结构参数如表1 所示。对小齿轮及内齿圈的齿数、模数、齿宽和轮齿啮合接触力学参数进行参数化描述,建立小齿轮与内齿轮啮合接触的参数化动力学模型。同时,对内外圈4条滚道的沟道直径,沟道曲率,钢球直径和个数,保持架内外径直径和兜孔孔径,钢球与套圈滚道、保持架兜孔的动态接触力学参数进行参数化建模,构建钢球与内外圈滚道和保持架动态接触的参数化动力学模型。所构建的回转支承参数化多体接触动力学模型如图1 所示。
图1
图1
回转支承参数化多体接触动力学模型
Fig.1
Dynamic model of parametric multi-body contact for slewing bearing
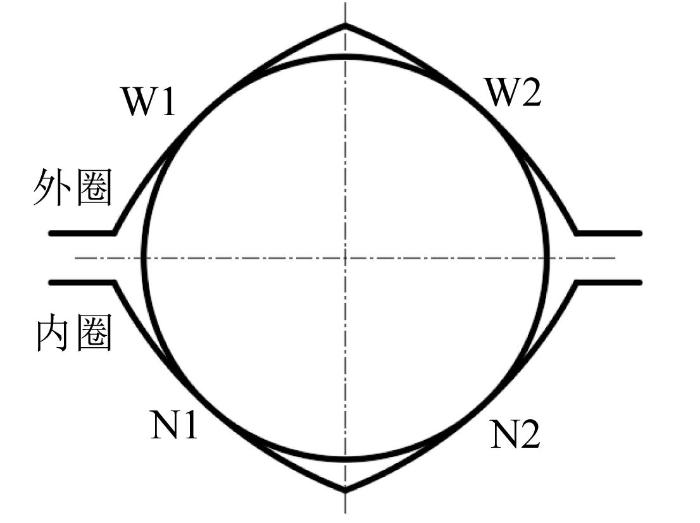
回转支承钢球与N1、N2、W1、W2这4条套圈滚道相互作用,形成了典型的四点交叉接触力学特征,4条套圈滚道如图2 所示。在各构件上添加相应的约束,并定义各构件的运动关系,采用冲击函数法来计算钢球与4条套圈滚道之间的动态接触力,则:
F n = K δ e + C v
式中:F n K δ e C v 为接触点法向相对速度。
图2
图2
N1 、N2 、W1 、W2 套圈滚道示意图
Fig.2
Schematic diagram of N1,N2,W1,W2 ring raceways
基于Hertz接触理论及钢球与内外圈滚道的接触刚度参数[17 ] ,采用ADAMS多体动力学仿真软件自带的step函数计算摩擦因数。钢球与滚道接触模型的参数如表2 所示。
采用ADAMS软件,编制宏命令程序,对回转支承各零部件的关键结构参数、约束类型、接触模型参数进行参数化设计,从而建立考虑钢球与4条套圈滚道、保持架兜孔的动态接触关系,小齿轮与内齿圈动态啮合关系的回转支承参数化多体接触动力学仿真模型。
沟道曲率半径会影响回转支承的承载能力,进而影响回转支承的使用寿命;在回转支承运转过程中,钢球与保持架的频繁碰撞与摩擦会导致保持架失效,因此合理选取保持架兜孔孔径能有效减弱保持架振动;初始接触角对钢球与套圈滚道间接触力的影响较大,合理的初始接触角能有效减小钢球与套圈滚道间的接触力;轮齿变位系数会影响齿轮与内齿圈的啮合特性,合理的轮齿变位系数能有效减小齿轮啮合力。由上可知,沟道曲率半径、保持架兜孔孔径、初始接触角和轮齿变位系数等设计参数对滚动轴承的回转支承力学特性和轮齿啮合传动特性有着重要影响,因此选取以上4个设计参数为设计变量,分别记为D 1 、D 2 、D 3 和D 4 。同时,在联合载荷作用下,钢球与套圈滚道的接触力、轮齿啮合力、运动齿圈的振动特性等是静动态力学性能、承载能力磨损和运动稳定性等高性能齿式回转支承的产品研发目标,故将目标函数f 1 ( x ) f 2 ( x ) f 3 ( x ) f 4 ( x )
2 不同参数对回转支承动态特性的影响
2.1 模型验证
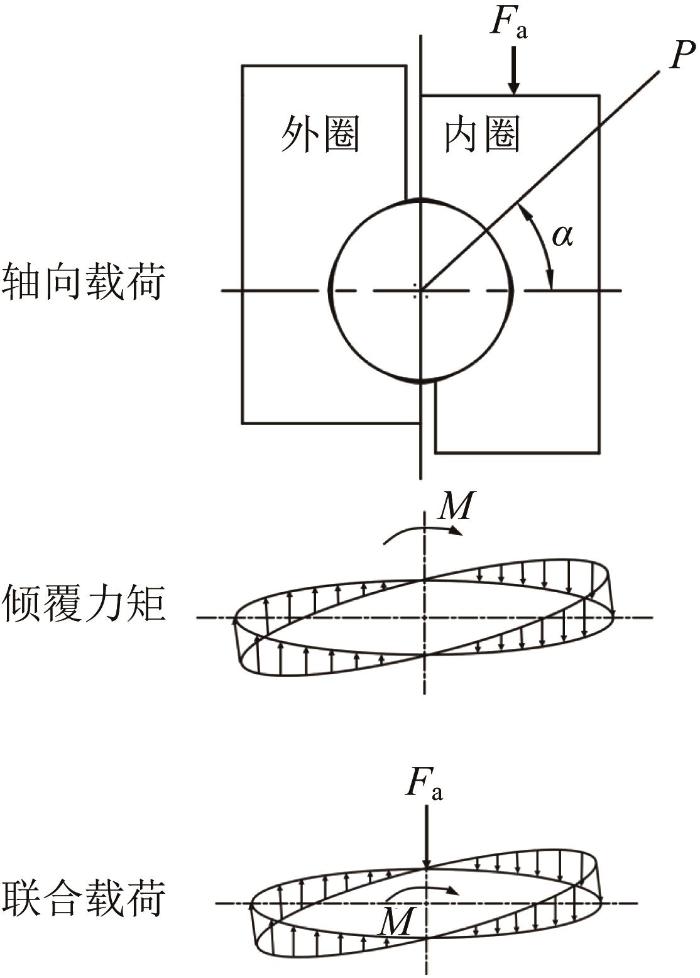
采用静力学平衡分析方法验证回转支承参数化多体接触动力学模型的准确性。在静力学仿真中,仅考虑钢球与套圈滚道之间发生接触变形,且转速为零,无轴向、径向间隙,其他均为刚体。采用静力学平衡理论时,作如下假设:1)忽略回转支承所有变形的影响,包括结构弹性变形和接触弹性变形;2)不考虑回转支承内部接触作用,仅考虑静力学平衡。不同载荷下钢球与套圈滚道间的受力如图3 所示。
图3
图3
不同载荷下钢球与套圈滚道间的受力示意图
Fig.3
Schematic diagram of force between steel ball and ring raceway under different loads
P 1 = F a n ⋅ s i n α (2)
P 2 = 4.37 M n D L s i n α (3)
P 1 = F a n ⋅ s i n α + 4.37 M n D L s i n α (4)
式中:P 1 P 2 P 3 F a α M
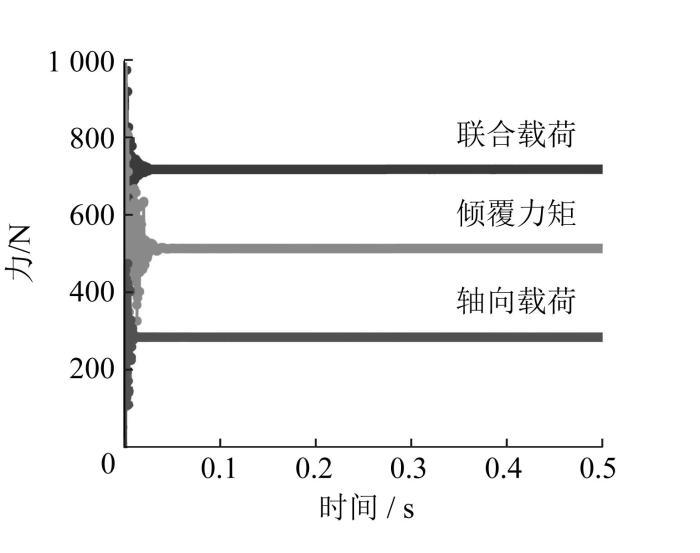
设置F a M 1 × 10 6 N ⋅ m m t =0.5 s,步长为1 000,进行仿真计算。
为了便于后续分析,对滚动体钢球进行编号,如图4 所示。1号钢球与N1滚道的接触力的仿真结果如图5 所示。由图4 可知,在初始阶段回转支承受载荷作用瞬间,受到的冲击较大,使得接触力有较大波动,然后接触力快速稳定在一个静力学平衡下的常数值。
图4
图4
滚动体钢球编号
Fig.4
Number of steel ball of rolling element
图5
图5
1 号钢球与N1 滚道的接触力仿真结果
Fig.5
Simulation results of contact force between No.1 steel ball and N1 raceway
将稳定后的仿真值与通过式(2)至式(4)算得的理论值及实际值进行对比,结果如表3 所示。由表3 可知,在不同载荷作用下,套圈滚道接触力仿真值、理论值、实际值之间存在一定的误差。由于理论计算是采用回转支承的整体静力学平衡计算公式,α 17 ],在倾覆力矩或联合载荷作用下,回转支承钢球与滚道之间的实际工作接触角通常在5°左右变化。理论值通常采用初始接触角来计算,计算结果偏大,在实际工程中能获得相对较大的安全系数。由此可知,所提出的回转支承参数化多体接触动力学模型具有较好的可靠性,相对误差在合理范围内,验证了模型的准确性,这为后续探讨关键设计参数对回转支承动态特性及动态优化设计奠定了基础。
2.2 单因素对回转支承多目标优化的影响
基于齿式回转支承参数化动力学模型,开展回转支承关键设计参数的单变量多目标优化分析,这是回转支承多变量多目标动态优化设计的重要环节。载荷条件不变,对回转支承施加驱动转速,以上述4个关键设计参数为变量,以回转支承动态性能参数为多目标函数,分析设计参数单变量变化对回转支承动态性能的影响规律。
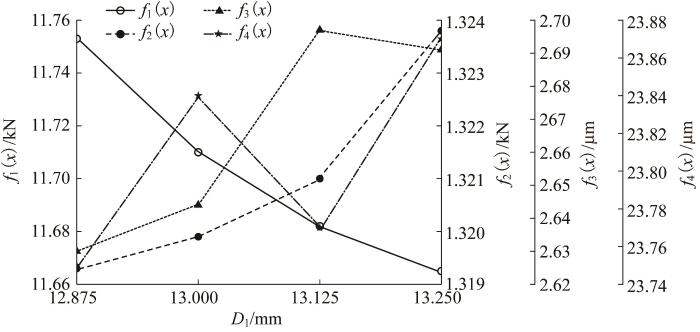
1)沟道曲率半径D 1 影响着钢球与套圈滚道的密合程度及接触点处的应力与接触变形,对钢球与滚道接触力影响较大[18 ] 。本文选取D 1 =12.875~13.250 mm,分析时在该范围内均匀取4个值。D 1 对回转支承动动态性能的影响如图6 所示。由图6 可知,随着D 1 增大,f 1 ( x ) f 2 ( x ) D 1 增大,钢球与滚道间的接触面积减小,在载荷不变的情况下,f 2 ( x ) D 1 =12.875 mm时,f 3 ( x ) f 4 ( x ) D 1 =12.875 mm。
图6
图6
D 1
Fig.6
Influence of D 1 on dynamic performance of slewing bearing
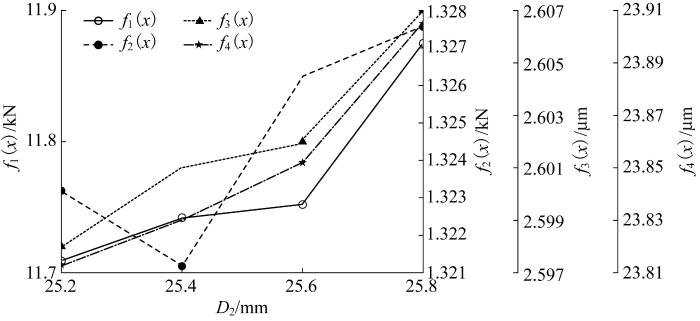
2)保持架将钢球分离,使得每个钢球与套圈始终保持在一起,引导钢球在滚道上运动,它对回转支承的稳定性有着重大影响。保持架的选型和结构设计还未有统一的参考标准。本文结合文献[12 ]的研究结果,选取保持架兜孔孔径D 2 =25.2~25.8 mm,分析时在该范围内均匀取4个值。D 2 对回转支承动态性能的影响如图7 所示。由图7 可知,随着D 2 增大,f 1 ( x ) f 3 ( x ) f 4 ( x ) D 2 >25.6 mm后,f 1 ( x ) f 3 ( x ) f 4 ( x ) D 2 过大导致滚动体在滚道运动的空间增大,加剧了内齿圈与保持架的冲击,使回转支承动态性能变差;当D 2 =225.4 mm时,f 2 ( x ) D 2 =25.2~25.4 mm。
图7
图7
D 2
Fig.7
Influence of D 2 on dynamic performance of slewing bearing
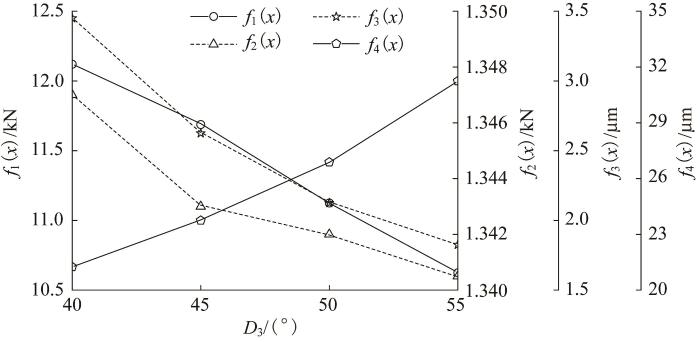
3)初始接触角D 3 直接影响回转支承的变形、受力和寿命等,是回转支承设计的重要参数。通过研究可知[20 ] ,当D 3 =40°~60°时,钢球与滚道接触力会发生显著变化。结合设计实际,选取D 3 =40°~55°,分析时在该范围内均匀取4个值。D 3 对回转支承动态性能的影响如图8 所示。由图8 可知,随着D 3 增大,f 1 ( x ) f 2 ( x ) f 3 ( x ) D 3 =55°时达到最小。说明当载荷条件不变时,增大D 3 可以显著提高回转支承的承载能力并降低轮齿啮合力,同时使内齿圈轴向偏移量变小;随着D 3 增大,钢球与滚道接触的椭圆区域趋向滚道边缘,加剧了内齿圈径向振动,使内齿圈径向位移增大。故考虑单因素对回转支承性能影响时,取D 3 =55°。
图8
图8
D 3
Fig.8
Influence of D 3 on dynamic performance of slewing bearing
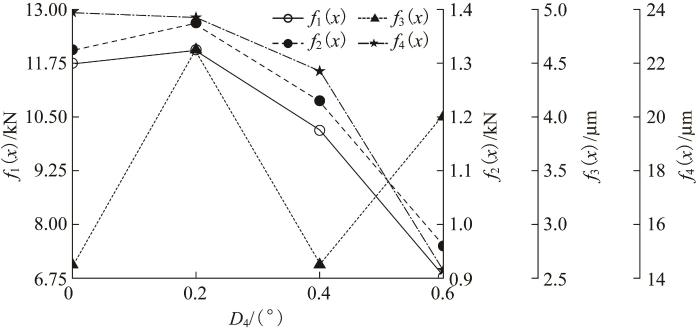
4)轮齿变位系数表征了轮齿的抗弯、抗断裂能力,对回转支承中齿轮的影响较大,进而影响回转支承的寿命。结合文献[14 ]的研究结果,选取D 4 =0~0.6,分析时在该范围内均匀取4个值。D 4 对回转支承动态性能的影响如图9 所示。由图9 可知,随着D 4 增大,f 1 ( x ) f 2 ( x ) D 4 =0.2时达到峰值,后迅速降低,在0.6时为最低点,说明在D 4 =0.2之后增大D 4 ,可显著提高回转支承的承载能力和降低齿轮啮合力;f 3 ( x ) f 4 ( x ) D 4 =0.6时达到最小,说明振动位移最小。故考虑单因素对回转支承性能影响时,取D 4 =0.6。
图9
图9
D 4
Fig.9
Influence of D 4 on dynamic performance of slewing bearing
3 回转支承多目标优化
D 1 、D 2 、D 3 、D 4 的初始设计值分别为13.0 mm,25.2 mm,45°,0。在上文单因素分析中,对每个单因素仅取4个值进行分析,其他3个参数则为初始设计值,这样得到的单因素最优的多参数组合不是最优组合。因此,需开展多因素对回转支承动态特性的影响分析。
试验设计(design of experiment, DOE)方法可以用来分析多个设计变量同时变化时对目标函数的影响规律。综合考虑D 1 、D 2 、D 3 、D 4 共同作用对回转支承动态特性的影响,在其取值范围内各均匀取4个值,得到256个组合。运用ADAMS的DOE模块对优化模型进行全因子试验设计,进行动态优化,得到最优的参数组合。基于全因子试验设计的全部仿真结果,得到各子目标函数取最优值时的设计变量组合,如表4 所示。
3.1 多目标优化模型的构建与求解
T ( X ) = m i n f 1 ( x ) , f 2 ( x ) , ⋯ , f i ( x ) T s . t . X ∈ S (5)
式中:f i ( x ) i =1, 2, …, 4;S
采用线性加权法来求解多目标优化模型。线性加权法是将f i ' ( x ) w i
F ( X ) = ∑ i = 1 n w i f i ' ( x ) (6)
式中:f i ' ( x ) f i ( x ) w i f i ' ( x )
3.2 统一量纲处理
在回转支承多目标优化中,各子目标函数的量纲不同。在构建新目标函数前,需对子目标函数值进行统一量纲处理。通过均值化处理,能够消除量纲和数量级的影响,不受某个异常目标函数值的波动而发生改变,保证了各子目标函数值的准确性;极小值化处理法能够体现各子目标函数值差异程度,可体现量纲后的各子目标函数对回转支承的重要程度影响。
f i ' ( x ) = f i ( x j ) f ¯ i ( x ) (7)
式中:f ¯ i ( x ) f i ' ( x ) j 为设计变量的组合数,j =1, 2, …, 256。
f i ' ( x ) = f i ( x j ) m i n f i ( x ) (8)
通过均值化和极小值化等统一量纲处理后,分别得到各子目标函数最优时其余子目标函数的无量纲数值,如表5 所示。
3.3 权系数的选取
权系数选取的合理性与准确性会直接影响评价结果的可靠性。根据第i [21 ] 。优化模型为:m i n f i ' ( x ) ; ( i = 1 , 2 , 3 , 4 )
f i ' ( x i ) = f i i ' (9)
δ i l = f i l ' - f i i ' ( l = 1 , 2 , ⋯ , 4 ) (10)
式中:f i l ' f i ' ( x ) x l
m i = 1 4 δ i l (11)
w i = m i ∑ i = 1 4 m i (12)
求得m i w i m i m 1 > m 2 > m 3 > m 4 w 1 > w 2 > w 3 > w 4 w i
F ( x ) = w 1 f 4 ' ( x ) + w 2 f 3 ' ( x ) + w 3 f 2 ' ( x ) + w 4 f 1 ' ( x ) (13)
结合表5 中的数据,通过式(9)至式(13)计算可得均值化、极小值化处理法下各子目标函数的权系数分别为:
w 1 = 0.520 19 , w 2 = 0.077 36 , w 3 = 0.414 73 , w 4 = 0.384 66
w 1 ' = 0.113 03 , w 2 ' = 0.056 70 , w 3 ' = 0.431 97 , w 4 ' = 0.398 30
将权系数进行排序,可得:w 3 > w 4 > w 1 > w 2 w 3 ' > w 4 ' > w 1 ' > w 2 ' 表5 中的无量纲函数值,则各目标子函数值均值化和极小值化后所构建的新的目标函数模型如式13所示。
3.4 优化结果的分析
通过上述对各子目标函数值采用不同方法进行统一量纲处理,运用排序法求解权系数,构建了多组新目标函数。对所构建的新目标函数进行相应的计算,得到回转支承最优设计变量组合,如表6 所示。
由表6 可知,采用不同方法进行统一量纲处理后,得到的最优参数均为:12.875 mm,25.2 mm,55°,0.6。将设计参数优化后各子目标函数值与各子目标函数初始值进行对比,并引入优化率,来评估优化效果[22 ] ,结果如表7 所示。
优化 率 = 原始 值 - 优化 值 原始 值 × 100 % (14)
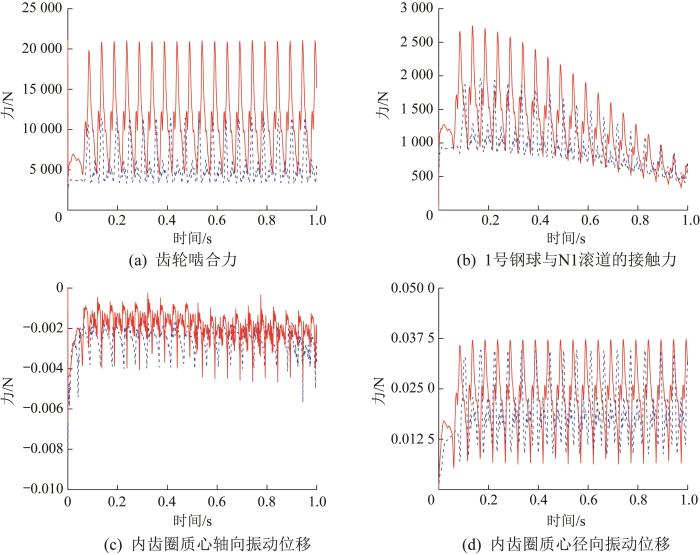
将优化后的设计参数值赋予回转支承参数化多体接触动力学模型,求解回转支承动态性能。优化前后回转支承动态性能的对比如图10 所示。由图10 可知,优化后各子目标函数值都有不同程度的减小,尤其是f 1 ( x ) f 2 ( x )
图10
图10
优化前后回转支承的动态特性曲线
Fig.10
Dynamic characteristic curves of slewing bearing before and after optimization
4 结 论
本文提出了基于参数化多体动力学分析的齿式回转支承多变量多目标优化设计方法。采用该方法,可以提高回转支承的动态性能,为回转支承动态优化设计提供参考。
1)通过建立回转支承参数化多体接触动力学模型,分析了沟道曲率半径、保持架兜孔孔径、初始接触角及轮齿变位系数对回转支承动态性能的影响。发现适当减小沟道曲率半径和保持架兜孔孔径,增大始接触角和轮齿变位系数,可增强套圈滚道的承载能力和减小齿轮啮合力,从而改善回转支承动态性能。
2)选取齿轮啮合力、1号钢球与内滚道的接触力及内齿圈质心轴向/径向振动位移最小作为优化设计目标,采用DOE方法,对关键设计参数进行全因子试验计算,结合线性加权法,构建并求解了多变量多目标优化模型,得到最优设计变量的参数组合,为高性能齿式回转支承的产品研发提供了参考数据。
3)根据多变量多目标优化结果,进行回转支承动力学分析。结果表明,回转支承内齿圈质心振动幅值和偏移量减小,齿轮啮合力和滚道接触力的振动幅值大幅度降低,内齿圈质心振动幅值和偏移量都减小,其动态性能得到明显改善。
参考文献
View Option
[1]
田贵 转盘轴承材料及其承载能力研究
[D]. 合肥 : 合肥工业大学 , 2016 : 1 -2 .
[本文引用: 1]
TIAN G Study on material and carrying capacity of slewing bearing
[D]. Hefei : Hefei University of Technology ,2016 : 1 -2 .
[本文引用: 1]
[2]
赵健 内齿式回转支承参数化分析与动态设计
[D]. 昆明 : 昆明理工大学 ,2021 : 2 -3 .
[本文引用: 1]
ZHAO J Parameterized analysis and dynamic design of internal gear slewing bearing
[D]. Kunming : Kunming University of Science and Technology , 2021 : 2 -3 .
[本文引用: 1]
[3]
GLODElŽ S POTOČNIK R FLAŠKER J Computational model for calculation of static capacity and lifetime of large slewing bearing's raceway
[J]. Mechanism and Machine Theory , 2012 , 47 : 16 -30 .
[本文引用: 1]
[4]
AMASORRAIN J SAGARTZAZU X DAMIÁND J Load distribution in a four contact-point slewing bearing
[J]. Mechanism and Machine Theory , 2003 , 38 (6 ): 479 -496 .
[本文引用: 1]
[6]
王艳霜 ,袁倩倩 负游隙对特大型双排四点接触球轴承载荷分布的影响
[J].机械工程学报 , 2012 , 48 (21 ): 110 -115 . doi:10.3901/jme.2012.21.110
DOI:10.3901/jme.2012.21.110
[本文引用: 1]
WANG Y S YUAN Q Q Influence of negative clearance on load distribution of large-size double row four-point-contact ball bearing
[J]. Journal of Mechanical Engineering , 2012 , 48 (21 ): 110 -115 .
DOI:10.3901/jme.2012.21.110
[本文引用: 1]
[7]
罗丫 ,杨本梦 ,涂文兵 滚动轴承保持架-滚动体接触动力学建模与接触特性
[J].航空动力学报 , 2022 , 38 (X ): 1 -9 .
[本文引用: 1]
LUO Y YANG B M TU W B Dynamic modeling of the contact between cage and rolling element in rolling bearing and contact characteristics
[J]. Journal of Aerospace Power , 2022 , 38 (X ): 1 -9 .
[本文引用: 1]
[8]
邱明 ,史鹏飞 ,成龙 ,等 四点接触球转盘轴承载荷分布的影响因素分析
[J]. 河南科技大学学报 , 2012 , 33 (5 ): 49 -53 , 3 .
[本文引用: 1]
QIU M SHI P F CHENG L et al Analysis of influencing factors on load distribution of four-point contact ball slewing bearings
[J]. Journal of Henan University of Science and Technology , 2012 , 33 (5 ): 49 -53 , 3 .
[本文引用: 1]
[9]
ZUPAN S PREBIL I Carrying angle and carrying capacity of a large single row ball bearing as a function of geometry parameters of the rolling contact and the supporting structure stiffness
[J]. Mechanism and Machine Theory , 2001 , 36 (10 ): 1087 -1103 .
[本文引用: 1]
[10]
姚廷强 ,王立华 ,刘孝保 ,等 变工况下角接触球轴承保持架稳定性分析
[J]. 振动与冲击 , 2016 , 35 (18 ): 172 -180 .
[本文引用: 1]
YAO T Q WANG L H LIU X B et al Dynamic stability analysis on the cage of ball bearing under varying working environment
[J]. Journal of Vibration and Shock , 2016 , 35 (18 ): 172 -180 .
[本文引用: 1]
[11]
王明凯 ,闫柯 ,马帅军 ,等 联合载荷作用下精密角接触球轴承动态特性演变规律
[J]. 航空动力学报 ,2022 , 37 (6 ): 1134 ⁃1149 .
[本文引用: 1]
WANG M K YAN K MA S J et al Evolutionary regularity of dynamic characteristics for precision angular contact ball bearing under combined loads
[J]. Journal of Aerospace Power , 2022 , 37 (6 ): 1134 -1149 .
[本文引用: 1]
[12]
张文虎 , 胡余生 , 邓四二 , 等 高速圆柱滚子轴承保持架振动特性研究
[J]. 航空动力学报 , 2019 , 38 (22 ): 85 -94 .
[本文引用: 2]
ZHANG W H HU Y S DENG S E et al Cage vibration behaviors of high-speed cylindrical roller bearings
[J]. Journal of Aerospace Power , 2019 , 38 (22 ): 85 ⁃94 .
[本文引用: 2]
[13]
李芃 ,王敏 ,戚晓利 ,等 单排球式回转支承动态力学性能的研究
[J].振动与冲击 , 2013 , 31 (14 ): 89 -93 .
[本文引用: 1]
LI P WANG M QI X L al at Dynamic mechanical properties of single-row bearings
[J]. Journal of Vibration and Shock , 2013 , 31 (14 ): 89 -93 .
[本文引用: 1]
[14]
张义民 ,杨健 ,胡鹏 ,等 考虑变位系数的直齿轮啮合特性分析
[J].东北大学学报 ,2013 , 34 (9 ): 1287 -1291 .
[本文引用: 2]
ZHANG Y M YANG J HU P al at Meshing characteristics analysis of spur gear pair considering modification coefficient
[J]. Journal of Northeastern University , 2013 , 34 (9 ): 1287 -1291 .
[本文引用: 2]
[15]
贾平 偏航变桨轴承力学特性分析及结构优化设计
[D]. 大连 : 大连理工大学 ,2012 .
[本文引用: 1]
JIA Ping Mechanical performance analysis and optimization design of yaw and pitch bearing
[D]. Dalian : Dalian University of Technology , 2012 .
[本文引用: 1]
[16]
RAO B R TIWARI R Optimum design of rolling element bearings using genetic algorithms
[J]. Mechanism and Machine Theory , 2006 , 42 (11 ): 233 -250 .
[本文引用: 1]
[18]
史朋飞 薄壁四点接触球转盘轴承的性能分析
[D]. 洛阳 :河南科技大学 , 2013 : 24 -26 .
[本文引用: 1]
SHI P F Analysis on performances of thin-walled four point-contact ball slewing bearing
[D]. LuoYang : Henna University of Science and Technology , 2013 : 24 -26 .
[本文引用: 1]
[19]
温保岗 , 王美令 , 乔留春 , 等 保持架间隙对角接触球轴承振动特性的影响
[J].轴承 , 2019 (7 ): 6 -9 .
WEN B G WANG M L QIAO L C et al Influence of cage clearance on vibration characteristics of angular contact ball bearings
[J]. Bearing , 2019 (7 ): 6 -9 .
[22]
饶江 基于Pareto最优的悬架参数多目标优化
[D]. 杭州 : 浙江大学 , 2010 .
[本文引用: 1]
RAO J Pareto-optimal of suspension parameters for multi-objective optimization
[D]. Hangzhou : Zhejiang University , 2010 .
[本文引用: 1]
转盘轴承材料及其承载能力研究
1
2016
... 回转支承是兼有滚动轴承的回转支承特点和齿轮啮合传动特点的关键基础部件,能够同时承受径向、轴向负荷和倾覆力矩等联合载荷作用,具有复杂的动力学特性,且影响因素众多.回转支承作为关键的支承传动部件,具有结构紧凑、运动平稳、精度高及承载能力强等特点,在大型风电装备、工业机器人、工程机械和军事装备中得到广泛应用[1 ] .回转支承的动态特性对高端装备系统的运行稳定性和可靠性有着重要的影响.回转支承的静、动力学研究还处于初级阶段,尤其是多因素影响下内齿式回转支承的多体接触动力学问题亟待深入研究.进一步开展基于动力学分析的多变量多目标优化设计研究对高性能回转支承的产品研发具有重要意义,同时为考虑回转支承动态性能的高端装备系统动力学研究奠定基础[2 ] . ...
转盘轴承材料及其承载能力研究
1
2016
... 回转支承是兼有滚动轴承的回转支承特点和齿轮啮合传动特点的关键基础部件,能够同时承受径向、轴向负荷和倾覆力矩等联合载荷作用,具有复杂的动力学特性,且影响因素众多.回转支承作为关键的支承传动部件,具有结构紧凑、运动平稳、精度高及承载能力强等特点,在大型风电装备、工业机器人、工程机械和军事装备中得到广泛应用[1 ] .回转支承的动态特性对高端装备系统的运行稳定性和可靠性有着重要的影响.回转支承的静、动力学研究还处于初级阶段,尤其是多因素影响下内齿式回转支承的多体接触动力学问题亟待深入研究.进一步开展基于动力学分析的多变量多目标优化设计研究对高性能回转支承的产品研发具有重要意义,同时为考虑回转支承动态性能的高端装备系统动力学研究奠定基础[2 ] . ...
内齿式回转支承参数化分析与动态设计
1
2021
... 回转支承是兼有滚动轴承的回转支承特点和齿轮啮合传动特点的关键基础部件,能够同时承受径向、轴向负荷和倾覆力矩等联合载荷作用,具有复杂的动力学特性,且影响因素众多.回转支承作为关键的支承传动部件,具有结构紧凑、运动平稳、精度高及承载能力强等特点,在大型风电装备、工业机器人、工程机械和军事装备中得到广泛应用[1 ] .回转支承的动态特性对高端装备系统的运行稳定性和可靠性有着重要的影响.回转支承的静、动力学研究还处于初级阶段,尤其是多因素影响下内齿式回转支承的多体接触动力学问题亟待深入研究.进一步开展基于动力学分析的多变量多目标优化设计研究对高性能回转支承的产品研发具有重要意义,同时为考虑回转支承动态性能的高端装备系统动力学研究奠定基础[2 ] . ...
内齿式回转支承参数化分析与动态设计
1
2021
... 回转支承是兼有滚动轴承的回转支承特点和齿轮啮合传动特点的关键基础部件,能够同时承受径向、轴向负荷和倾覆力矩等联合载荷作用,具有复杂的动力学特性,且影响因素众多.回转支承作为关键的支承传动部件,具有结构紧凑、运动平稳、精度高及承载能力强等特点,在大型风电装备、工业机器人、工程机械和军事装备中得到广泛应用[1 ] .回转支承的动态特性对高端装备系统的运行稳定性和可靠性有着重要的影响.回转支承的静、动力学研究还处于初级阶段,尤其是多因素影响下内齿式回转支承的多体接触动力学问题亟待深入研究.进一步开展基于动力学分析的多变量多目标优化设计研究对高性能回转支承的产品研发具有重要意义,同时为考虑回转支承动态性能的高端装备系统动力学研究奠定基础[2 ] . ...
Computational model for calculation of static capacity and lifetime of large slewing bearing's raceway
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
Load distribution in a four contact-point slewing bearing
1
2003
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
异形高耸塔机回转支承的接触动力学分析
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
异形高耸塔机回转支承的接触动力学分析
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
负游隙对特大型双排四点接触球轴承载荷分布的影响
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
负游隙对特大型双排四点接触球轴承载荷分布的影响
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
滚动轴承保持架-滚动体接触动力学建模与接触特性
1
2022
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
滚动轴承保持架-滚动体接触动力学建模与接触特性
1
2022
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
四点接触球转盘轴承载荷分布的影响因素分析
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
四点接触球转盘轴承载荷分布的影响因素分析
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
Carrying angle and carrying capacity of a large single row ball bearing as a function of geometry parameters of the rolling contact and the supporting structure stiffness
1
2001
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
变工况下角接触球轴承保持架稳定性分析
1
2016
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
变工况下角接触球轴承保持架稳定性分析
1
2016
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
联合载荷作用下精密角接触球轴承动态特性演变规律
1
2022
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
联合载荷作用下精密角接触球轴承动态特性演变规律
1
2022
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
高速圆柱滚子轴承保持架振动特性研究
2
2019
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
... 2)保持架将钢球分离,使得每个钢球与套圈始终保持在一起,引导钢球在滚道上运动,它对回转支承的稳定性有着重大影响.保持架的选型和结构设计还未有统一的参考标准.本文结合文献[12 ]的研究结果,选取保持架兜孔孔径D 2 =25.2~25.8 mm,分析时在该范围内均匀取4个值.D 2 对回转支承动态性能的影响如图7 所示.由图7 可知,随着D 2 增大,f 1 ( x ) f 3 ( x ) f 4 ( x ) D 2 >25.6 mm后,f 1 ( x ) f 3 ( x ) f 4 ( x ) D 2 过大导致滚动体在滚道运动的空间增大,加剧了内齿圈与保持架的冲击,使回转支承动态性能变差;当D 2 =225.4 mm时,f 2 ( x ) D 2 =25.2~25.4 mm. ...
高速圆柱滚子轴承保持架振动特性研究
2
2019
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
... 2)保持架将钢球分离,使得每个钢球与套圈始终保持在一起,引导钢球在滚道上运动,它对回转支承的稳定性有着重大影响.保持架的选型和结构设计还未有统一的参考标准.本文结合文献[12 ]的研究结果,选取保持架兜孔孔径D 2 =25.2~25.8 mm,分析时在该范围内均匀取4个值.D 2 对回转支承动态性能的影响如图7 所示.由图7 可知,随着D 2 增大,f 1 ( x ) f 3 ( x ) f 4 ( x ) D 2 >25.6 mm后,f 1 ( x ) f 3 ( x ) f 4 ( x ) D 2 过大导致滚动体在滚道运动的空间增大,加剧了内齿圈与保持架的冲击,使回转支承动态性能变差;当D 2 =225.4 mm时,f 2 ( x ) D 2 =25.2~25.4 mm. ...
单排球式回转支承动态力学性能的研究
1
2013
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
单排球式回转支承动态力学性能的研究
1
2013
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
考虑变位系数的直齿轮啮合特性分析
2
2013
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
... 4)轮齿变位系数表征了轮齿的抗弯、抗断裂能力,对回转支承中齿轮的影响较大,进而影响回转支承的寿命.结合文献[14 ]的研究结果,选取D 4 =0~0.6,分析时在该范围内均匀取4个值.D 4 对回转支承动态性能的影响如图9 所示.由图9 可知,随着D 4 增大,f 1 ( x ) f 2 ( x ) D 4 =0.2时达到峰值,后迅速降低,在0.6时为最低点,说明在D 4 =0.2之后增大D 4 ,可显著提高回转支承的承载能力和降低齿轮啮合力;f 3 ( x ) f 4 ( x ) D 4 =0.6时达到最小,说明振动位移最小.故考虑单因素对回转支承性能影响时,取D 4 =0.6. ...
考虑变位系数的直齿轮啮合特性分析
2
2013
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
... 4)轮齿变位系数表征了轮齿的抗弯、抗断裂能力,对回转支承中齿轮的影响较大,进而影响回转支承的寿命.结合文献[14 ]的研究结果,选取D 4 =0~0.6,分析时在该范围内均匀取4个值.D 4 对回转支承动态性能的影响如图9 所示.由图9 可知,随着D 4 增大,f 1 ( x ) f 2 ( x ) D 4 =0.2时达到峰值,后迅速降低,在0.6时为最低点,说明在D 4 =0.2之后增大D 4 ,可显著提高回转支承的承载能力和降低齿轮啮合力;f 3 ( x ) f 4 ( x ) D 4 =0.6时达到最小,说明振动位移最小.故考虑单因素对回转支承性能影响时,取D 4 =0.6. ...
偏航变桨轴承力学特性分析及结构优化设计
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
偏航变桨轴承力学特性分析及结构优化设计
1
2012
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
Optimum design of rolling element bearings using genetic algorithms
1
2006
... 内齿式回转支承由钢球、内外套圈(齿圈)和驱动齿轮等构成,其静、动态力学特性研究已取得一定进展.国内外学者对回转支承动态特性进行了一定的理论分析和实验研究.基于Hertz接触理论,Glodelž等[3 ] 提出了一种计算回转支承接触载荷和静承载力的计算方法,Amasorrain等[4 ] 推导了四点接触回转支承外加载荷与最大接触应力之间的关系;原思聪等[5 ] 基于多体系统学理论,建立了回转支承动力学模型,分析了回转过程中各位置角处的变形量与接触力的关系;王燕霜等[6 ] 建立双排四点球轴承接触载荷分布计算模型,分析了沟道曲率半径系数对双排四点接触球轴承对承载能力的影响;罗丫等[7 ] 采用非线性弹簧、阻尼单元模拟保持架与滚动体之间的碰撞,并考虑碰撞接触及兜孔间隙,建立滚动轴承动力学分析模型,研究了保持架与钢球接触力以及载荷的影响关系;邱明等[8 ] 建立了单个钢球-滚道接触模型,分析了初始接触角及沟道曲率半径对支承承载能力的影响;Zupan等[9 ] 开发了单排四点接触球转盘滚道接触压力分布求解模型,考虑了沟道曲率中心偏移量、接触角、游隙等影响因素,分析了回转支承接触点和结构弹性变形的影响规律;姚廷强[10 ] 等考虑钢球、套圈和保持架的三维动态接触关系,建立了角接触球轴承多体接触动力学模型,分析了在变载荷下的球轴承动力学特性和保持架的运动稳定性.王明凯等[11 ] 建立了精密轴承拟静力学分析模型,分析了接触角与接触力的关系,揭示了复杂联合载荷作用下回转支承动态特性演变的规律.张文虎等[12 ] 基于滚动轴承动力学理论,建立了高速圆柱滚子轴承动力学模型,分析了保持架对回转支承振动特性的影响.李芃等[13 ] 应用ANSYS/LS-DYNA软件建立了回转支承的多体接触有限元模型,采用显示动力学有限元算法,得出了回转支承运转过程中滚动体与滚道动力学响应特征;张义民等[14 ] 采用显示动力学的方法,分析了轮齿变位系数对齿轮啮合特性的影响.贾平[15 ] 建立了偏航、变桨轴承力学模型,分析了接触角、游隙、沟道曲率半径等结构参数对回转支承的力学性能的影响,并对结构参数进行了优化;Rao[16 ] 考虑节圆直径、钢球直径和数目、沟道曲率半径,提出了一种基于遗传算法的非线性滚动轴承优化方法. ...
风力发电机变桨轴承的力学性能分析
2
2015
... 基于Hertz接触理论及钢球与内外圈滚道的接触刚度参数[17 ] ,采用ADAMS多体动力学仿真软件自带的step函数计算摩擦因数.钢球与滚道接触模型的参数如表2 所示. ...
... 将稳定后的仿真值与通过式(2) 至式(4) 算得的理论值及实际值进行对比,结果如表3 所示.由表3 可知,在不同载荷作用下,套圈滚道接触力仿真值、理论值、实际值之间存在一定的误差.由于理论计算是采用回转支承的整体静力学平衡计算公式,α 17 ],在倾覆力矩或联合载荷作用下,回转支承钢球与滚道之间的实际工作接触角通常在5°左右变化.理论值通常采用初始接触角来计算,计算结果偏大,在实际工程中能获得相对较大的安全系数.由此可知,所提出的回转支承参数化多体接触动力学模型具有较好的可靠性,相对误差在合理范围内,验证了模型的准确性,这为后续探讨关键设计参数对回转支承动态特性及动态优化设计奠定了基础. ...
风力发电机变桨轴承的力学性能分析
2
2015
... 基于Hertz接触理论及钢球与内外圈滚道的接触刚度参数[17 ] ,采用ADAMS多体动力学仿真软件自带的step函数计算摩擦因数.钢球与滚道接触模型的参数如表2 所示. ...
... 将稳定后的仿真值与通过式(2) 至式(4) 算得的理论值及实际值进行对比,结果如表3 所示.由表3 可知,在不同载荷作用下,套圈滚道接触力仿真值、理论值、实际值之间存在一定的误差.由于理论计算是采用回转支承的整体静力学平衡计算公式,α 17 ],在倾覆力矩或联合载荷作用下,回转支承钢球与滚道之间的实际工作接触角通常在5°左右变化.理论值通常采用初始接触角来计算,计算结果偏大,在实际工程中能获得相对较大的安全系数.由此可知,所提出的回转支承参数化多体接触动力学模型具有较好的可靠性,相对误差在合理范围内,验证了模型的准确性,这为后续探讨关键设计参数对回转支承动态特性及动态优化设计奠定了基础. ...
薄壁四点接触球转盘轴承的性能分析
1
2013
... 1)沟道曲率半径D 1 影响着钢球与套圈滚道的密合程度及接触点处的应力与接触变形,对钢球与滚道接触力影响较大[18 ] .本文选取D 1 =12.875~13.250 mm,分析时在该范围内均匀取4个值.D 1 对回转支承动动态性能的影响如图6 所示.由图6 可知,随着D 1 增大,f 1 ( x ) f 2 ( x ) D 1 增大,钢球与滚道间的接触面积减小,在载荷不变的情况下,f 2 ( x ) D 1 =12.875 mm时,f 3 ( x ) f 4 ( x ) D 1 =12.875 mm. ...
薄壁四点接触球转盘轴承的性能分析
1
2013
... 1)沟道曲率半径D 1 影响着钢球与套圈滚道的密合程度及接触点处的应力与接触变形,对钢球与滚道接触力影响较大[18 ] .本文选取D 1 =12.875~13.250 mm,分析时在该范围内均匀取4个值.D 1 对回转支承动动态性能的影响如图6 所示.由图6 可知,随着D 1 增大,f 1 ( x ) f 2 ( x ) D 1 增大,钢球与滚道间的接触面积减小,在载荷不变的情况下,f 2 ( x ) D 1 =12.875 mm时,f 3 ( x ) f 4 ( x ) D 1 =12.875 mm. ...
风力发电机变桨轴承的力学性能分析
1
2015
... 3)初始接触角D 3 直接影响回转支承的变形、受力和寿命等,是回转支承设计的重要参数.通过研究可知[20 ] ,当D 3 =40°~60°时,钢球与滚道接触力会发生显著变化.结合设计实际,选取D 3 =40°~55°,分析时在该范围内均匀取4个值.D 3 对回转支承动态性能的影响如图8 所示.由图8 可知,随着D 3 增大,f 1 ( x ) f 2 ( x ) f 3 ( x ) D 3 =55°时达到最小.说明当载荷条件不变时,增大D 3 可以显著提高回转支承的承载能力并降低轮齿啮合力,同时使内齿圈轴向偏移量变小;随着D 3 增大,钢球与滚道接触的椭圆区域趋向滚道边缘,加剧了内齿圈径向振动,使内齿圈径向位移增大.故考虑单因素对回转支承性能影响时,取D 3 =55°. ...
风力发电机变桨轴承的力学性能分析
1
2015
... 3)初始接触角D 3 直接影响回转支承的变形、受力和寿命等,是回转支承设计的重要参数.通过研究可知[20 ] ,当D 3 =40°~60°时,钢球与滚道接触力会发生显著变化.结合设计实际,选取D 3 =40°~55°,分析时在该范围内均匀取4个值.D 3 对回转支承动态性能的影响如图8 所示.由图8 可知,随着D 3 增大,f 1 ( x ) f 2 ( x ) f 3 ( x ) D 3 =55°时达到最小.说明当载荷条件不变时,增大D 3 可以显著提高回转支承的承载能力并降低轮齿啮合力,同时使内齿圈轴向偏移量变小;随着D 3 增大,钢球与滚道接触的椭圆区域趋向滚道边缘,加剧了内齿圈径向振动,使内齿圈径向位移增大.故考虑单因素对回转支承性能影响时,取D 3 =55°. ...
水资源系统多目标综合评估模型与方法
1
2009
... 权系数选取的合理性与准确性会直接影响评价结果的可靠性.根据第i [21 ] .优化模型为:m i n f i ' ( x ) ; ( i = 1 , 2 , 3 , 4 )
水资源系统多目标综合评估模型与方法
1
2009
... 权系数选取的合理性与准确性会直接影响评价结果的可靠性.根据第i [21 ] .优化模型为:m i n f i ' ( x ) ; ( i = 1 , 2 , 3 , 4 )
基于Pareto最优的悬架参数多目标优化
1
2010
... 由表6 可知,采用不同方法进行统一量纲处理后,得到的最优参数均为:12.875 mm,25.2 mm,55°,0.6.将设计参数优化后各子目标函数值与各子目标函数初始值进行对比,并引入优化率,来评估优化效果[22 ] ,结果如表7 所示. ...
基于Pareto最优的悬架参数多目标优化
1
2010
... 由表6 可知,采用不同方法进行统一量纲处理后,得到的最优参数均为:12.875 mm,25.2 mm,55°,0.6.将设计参数优化后各子目标函数值与各子目标函数初始值进行对比,并引入优化率,来评估优化效果[22 ] ,结果如表7 所示. ...