融合多主体需求频率特征的复杂产品全生命周期价值链协同设计

doi:10.3785/j.issn.1006-754X.2023.03.207

融合多主体需求频率特征的复杂产品全生命周期价值链协同设计

何州^,¹^,², 王阳³, 蒋翔宇⁴, 洪兆溪^,^,⁴^,⁵, 何利力³, 冯毅雄⁴^,⁶

1.浙江工商大学萨塞克斯人工智能学院，浙江杭州 310012

2.杭州州力数据科技有限公司，浙江杭州 310019

3.浙江理工大学计算机科学与技术学院，浙江杭州 310018

4.浙江大学流体动力基础件与机电系统全国重点实验室，浙江杭州 310058

5.浙江大学宁波科创中心，浙江宁波 315100

6.贵州大学省部共建公共大数据国家重点实验室，贵州贵阳 550025

Collaborative design of complex product lifecycle value chain by fusing multi-agent demand frequency characteristics

HE Zhou^,¹^,², WANG Yang³, JIANG Xiangyu⁴, HONG Zhaoxi^,^,⁴^,⁵, HE Lili³, FENG Yixiong⁴^,⁶

1.Sussex Artificial Intelligence Institute, Zhejiang Gongshang University, Hangzhou 310012, China

2.Hangzhou Zhouli Data Technology Co. , Ltd. , Hangzhou 310019, China

3.School of Computer Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China

4.State Key Laboratory of Fundamental Components of Fluid Power and Mechatronic systems, Zhejiang University, Hangzhou 310058, China

5.Ningbo Innovation Center, Zhejiang University, Ningbo 315100, China

6.State Key Laboratory of Public Big Data, Guizhou University, Guiyang 550025, China

通讯作者: 洪兆溪（1990—），女，浙江杭州人，助理研究员，博士，从事智能设计及不确定性优化决策研究，E-mail: hzhx@zju.edu.cn, http://orcid.org/0000-0001-8407-0951

收稿日期: 2023-10-13 修回日期: 2023-11-15

基金资助:

浙江省重点研发计划项目. 2022C01238. 2023C01214

Received: 2023-10-13 Revised: 2023-11-15

作者简介 About authors

何州（1995—），男，浙江杭州人，工程师，硕士，从事价值链及人工智能技术研究，E-mail:zh277@sussex.ac.uk , E-mail：zh277@sussex.ac.uk

摘要

高周转率和短保质期的复杂产品具有较高订单频率的特征。传统的价值链设计大多基于复杂产品订单数据的时序和销量对销售周期的影响，忽略了其订单频率中蕴含的细节信息，因而难以准确捕捉多主体间快速变化的供需关系。为了解决这一问题，提出了一种融合多主体需求频率特征的复杂产品全生命周期价值链协同设计方法。首先，采用门控卷积的频率序列提取方法识别多主体需求；其次，将基于频率分段的Transformer时序预测模型融合于订单频率信息，根据改进的时序-频率多头自注意力（seq-fre multi-head attention）结构建立全生命周期价值链，不同分段的时序和频率特征对应不同的注意力头，以实现多段时序和频率特征的融合；最后，将新型价值链协同设计方法应用于某复杂产品多主体需求预测问题，进行实验验证。研究表明，所提出的融合需求频率特征的价值链协同设计方法预测准确度较高，具有很好的应用前景。

关键词： 价值链 ; 协同设计 ; 时序预测 ; Transformer ; 频率特征

Abstract

Complex products with high turnover and short shelf life are characterized by a higher order frequency. Traditional value chain design is mostly based on the time series of order data of complex products and the impact of sales volume on sales cycle, while ignoring the detail information contained in the order frequency, which is difficult to accurately capture the rapidly changing supply and demand relationship between multi-agents. In order to solve this problem, a collaborative design method of complex product lifecycle value chain fusing multi-agent demand frequency characteristics was proposed. Firstly, the frequency sequence extraction method of gated convolution was used to identify the multi-agent requirement; Secondly, the Transformer time series prediction model based on frequency segmentation was integrated into the order frequency information, and the lifecycle value chain was built according to the improved time series frequency multi-head self-attention (seq-fre multi-head attention) structure. The time series and frequency characteristics of different segments corresponded to different attention heads to realize the fusion of multi-stage time series and frequency features; Finally, the new value chain collaborative design method was applied to the multi-agent demand prediction problem of a complex product, and experimental verification was carried out. The result showed that the proposed value chain collaborative design method fusing demand frequency features has high prediction accuracy and good application prospects.

Keywords： value chain ; collaborative design ; time series prediction ; Transformer ; frequency feature

PDF (3642KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

何州, 王阳, 蒋翔宇, 洪兆溪, 何利力, 冯毅雄. 融合多主体需求频率特征的复杂产品全生命周期价值链协同设计[J]. 工程设计学报, 2024, 31(1): 1-9 doi:10.3785/j.issn.1006-754X.2023.03.207

HE Zhou, WANG Yang, JIANG Xiangyu, HONG Zhaoxi, HE Lili, FENG Yixiong. Collaborative design of complex product lifecycle value chain by fusing multi-agent demand frequency characteristics[J]. Chinese Journal of Engineering Design, 2024, 31(1): 1-9 doi:10.3785/j.issn.1006-754X.2023.03.207

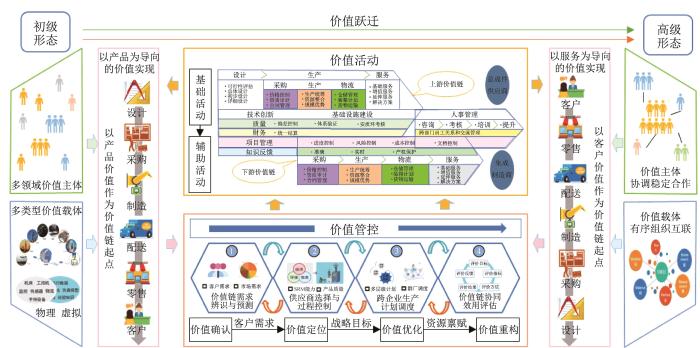
目前，制造业正面临从技术驱动到服务驱动，再到价值驱动的升级转变。将价值链协同与产品全生命周期融合，成为“工业5.0”时代复杂产品设计、制造和运维的重点。虽然复杂产品制造企业尝试利用数字化、自动化和网络化的先进技术打破产业上下游的业务、资源和信息孤岛，但受到客户需求个性化、市场环境动态化和生产系统集成化发展的影响，仍缺乏有效的产品全生命周期价值链协同设计方法，面临着生产管控效率低、协调互动困难、综合效能差等巨大挑战。复杂产品制造企业价值链演进升级的基本路径如图1所示。通过对企业生产运营的基础活动（如设计、生产、服务等）和辅助活动（如技术创新、基础设施建设等）的系统性价值分析，挖掘产品全生命周期价值链协同设计的原理与演化及决策机制，实现复杂产品制造企业价值链从“产品价值”到“客户价值”的形式跃迁。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 复杂产品制造企业价值链演进升级的基本路径

Fig.1 Basic path of value chain evolution and upgrading for complex product manufacturing enterprise

随着大数据技术的迅速发展，复杂产品的订单数据资源得以有效保留。这些数据资源的背后蕴含了产品价值链上多主体的市场营销信息，而大多数企业往往无法高效率、低成本地运用销售数据来辅助商业决策。如何利用这些销售数据指导企业的生产决策，仍是企业面临的重要课题。通常来讲，复杂产品的销量与天气、交通运输量等相似，是一个时间序列的预测问题^[1]。

时序预测的主要方法分为以下3种：数学统计方法、传统机器学习方法和深度学习方法。传统的数学统计方法主要采用统计学知识对数据时序中蕴含的发展过程、方向和趋势进行建模并预测，其常见的模型有移动平均（moving average）模型^[2]和自回归（auto regressive）模型^[3]等。然而，其较低的表达能力导致不能处理复杂数据中的宏观趋势预测问题和非线性关系，因此预测准确率不高。传统机器学习方法包括支持向量机^[4]、贝叶斯网络等^[5]，其克服了数学统计方法的缺点，在时序预测中取得了良好效果。但由于复杂产品销售数据具有季节性、动态性、周期性的特点及行业本身的特殊特征，序列数据往往存在很多干扰项，使得传统机器学习方法较难进行精准的预测。

深度学习方法可以将有效特征从大量原始数据中抽取出来，因此通过深度学习方法建立的模型的实用性和准确度较高。循环神经网络（recursive neural network，RNN）^[6]具有较强记忆性、参数共享且图灵完备（Turing completeness），在对序列数据的非线性特征进行学习时具有一定优势。RNN多用于自然语言处理领域，也被用于时序预测领域^[7]。基于双阶段注意力机制的RNN模型是经典的时序预测模型^[8]，其加入了注意力机制，编码时自适应选择相关程度高的序列信息，解码时考虑了编码阶段所有时间步的隐状态而非传统方法中的定长向量，解决了长期依赖问题^[9]。长短期记忆（long short-term memory，LSTM）网络^[10-11]是一类特殊的RNN，改善了RNN的长期依赖问题，解决了RNN训练中的梯度问题。LSTM网络能通过隐状态长期保留时序信息，常用于单变量和多变量序列数据的分析和预测^[12]。门控循环单元（gated recurrent unit, GRU）^[13]是简化版的LSTM网络，它将输入门和遗忘门结合在一起，形成一个更新门。GRU比LSTM网络的参数少，大大降低了复杂度。2017年提出的Transformer模型^[14]对长期预测的效果较好，虽然模型较为复杂，但对序列数据中的长期依赖关系拥有比LSTM网络更强大的建模能力，更加适用于时序建模。

尽管针对长时序列预测已经有了很多研究，但是针对复杂产品的长时段销量预测仍存在以下问题：1）在对原始数据的处理中，未考虑复杂产品高周转率和短保质期所带来的高订单频率的问题；2）传统的模型更多考虑了订单数据的时序和销量对销售周期的影响，而忽略了订单频率中蕴含的细节信息。为了解决以上问题，本文从长时序列预测的视角，运用深度学习理论，提出了一种基于订单时序和订单频率的改进注意力机制方法，并结合Transformer模型设计了时序-频率分解模型。

1 基于频率分段的时序预测模型的构建

Transformer模型基于编码器-解码器结构，其特点是能够有效地捕捉长期依赖关系，并利用多头自注意力机制挖掘序列数据的内在关联性^[15]。相比于LSTM等序列模型，Transformer模型可以一次性输入时间序列并进行并行计算，从而大大缩短计算时间，并且能够对长期和短期时序特征进行建模。

复杂产品制造企业的订单数据具有特殊性，其高周转率和短保质期带来了较高的订单频率，而Transfomer模型只考虑了订单数据的时序和销量对销售周期的影响，忽略了订单频率中蕴含的细节信息。针对这一问题，作者采用基于门控卷积的频率分段序列提取方法并改进了原始的Transformer输入编码，提出了基于改进编码的时序-频率多头自注意力（seq-fre multi-head attention）结构，用于序列间依赖关系的建模，并将改进的模型命名为SFTransformer模型。

1.1　时序-频率序列提取与输入编码

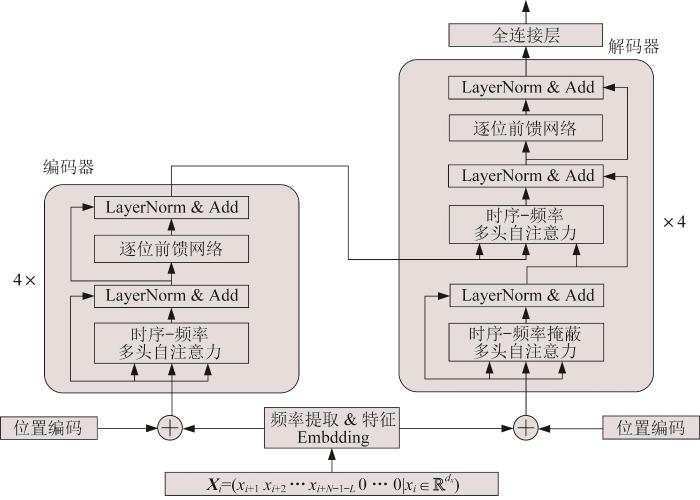
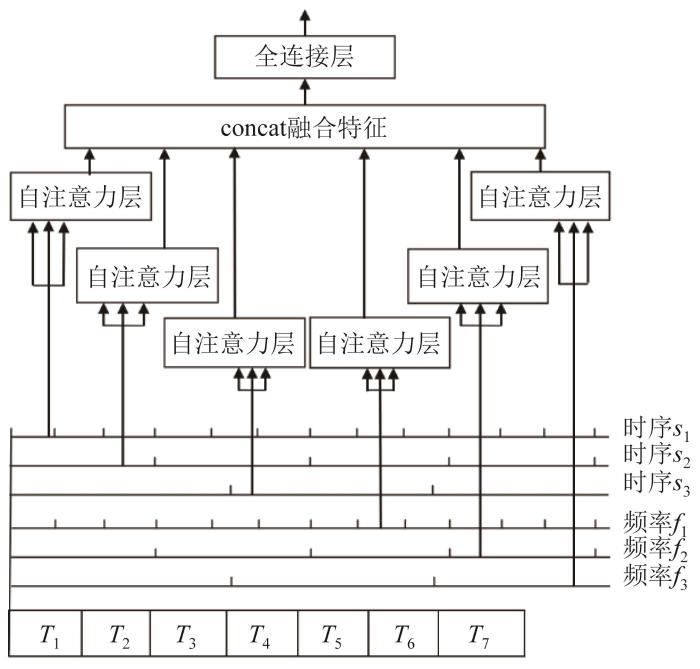
SFTransformer模型包含4层编码器-解码器架构，如图2所示。编码器由4个相同的层叠加而成，每层都有2个子层，第1个子层是时序-频率多头自注意力模块，第2个子层是基于位置的前馈网络（position-wise feed-forward network）。具体来说，在计算编码器的自注意力时，查询、键和值都来自前一个编码器层的输出。解码器同样包含4个相同的层，每层包含1个带掩蔽操作的时序-频率多头自注意力模块，经过层归一化（LayerNorm）和残差连接（Add）处理后进入一个逐位前馈网络，随后再次经过LayerNorm和Add处理，获得该层的输出并设为下一层的输入，最终经由全连接层输出最终结果。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 SFTransformer模型结构

Fig.2 Structure of SFTransformer model

在上述过程中，将时序数据融合并输入SFTransformer模型，建立更大范围的位置相关性。通过离散频率编码使模型在自注意力的计算过程中能够访问不确定距离的上下文关系。向量长度可学习，因此在自注意力计算过程中对输入矩阵进行逐层折叠的同时，能够保持上下文关系的信息不丢失，以此可以得到更加准确的预测效果。

本文提出的复杂产品销量预测问题定义为：设滑动窗口定长为N；预测步长为L；模型输入的第i个序列为连续时间序列 X_i， $X_{i} = (x_{i + 1} x_{i + 2} \dots x_{i + N - 1 - L} 0 \dots 0 | x_{i} \in R^{d_{x}})$ ，输出结果为预测的相应序列 Y_i， $Y_{i} = (y_{i + 1} y_{i + 2} \dots y_{i + N - 1} | y_{i} \in R^{d_{y}})$ ，其中， $d_{x}$ 为输入的隐藏维度， $d_{y}$ 为输出的隐藏维度， $R$ 为实数集。

复杂产品的高周转率和短保质期带来了较高的订单频率，而传统模型更多考虑的是订单数据的时序和销量对销售周期的影响，忽略了订单频率中蕴含的细节信息。为了提取数据集中的频率信息，采取一维门控卷积操作来提取频率序列数据。一维门控卷积操作一般运用在序列数据上，不同大小的卷积操作代表着序列对不同频率的依赖^[16]。

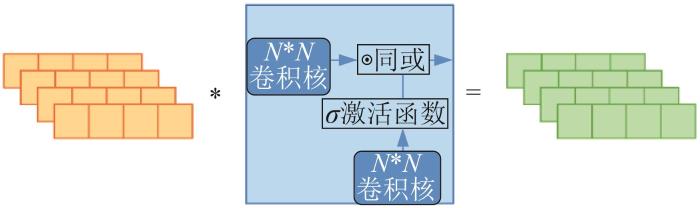
为了获取不同分段的销量和频率的有效信息，SFTransformer模型先将输入的自变量 $X_{i}$ 转换为嵌入输入层。已知预处理后频率序列数据的维数为12，一维门控卷积层的输出维度为 $d_{m o d e l}$ 。将原本的12个有效特征数据依次复制一遍，使其成为一个24维的向量，即 $d_{m o d e l}$ =24维，并在进行频率序列卷积时屏蔽销量序列而形成序列 $X^{F}$ ，在进行销量序列卷积时屏蔽频率序列而形成序列 $X^{T}$ 。

采用3个一维卷积核，分别为 $(k_{1}, v_{1})$ ， $(k_{2}, v_{2})$ ， $(k_{3}, v_{3})$ ，核大小依次为1, 3, 5。一维门控卷积的结构如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 一维门控卷积结构

Fig.3 Structure of one-dimensional gated convolution

最后，将卷积后的数据进行concat操作，获得时序嵌入序列 T 和频率嵌入序列 $F$ ，其中 $: T_{l} \in R^{24}, F_{l} \in R^{24}$ ，l=1, 2, 3。其运算过程如下：

T_{1} (i) = \sum_{m} X^{T} (m + i) k_{1} (m) ⊙ σ (\sum_{m} X^{T} (m + i) v_{1} (m))

(1)

T_{2} (i) = \sum_{m} X^{T} (m + i) k_{2} (m) ⊙ σ (\sum_{m} X^{T} (m + i) v_{2} (m))

(2)

T_{3} (i) = \sum_{m} X^{T} (m + i) k_{3} (m) ⊙ σ (\sum_{m} X^{T} (m + i) v_{3} (m))

(3)

F_{1} (i) = \sum_{m} X^{F} (m + i) k_{1} (m) ⊙ σ (\sum_{m} X^{F} (m + i) v_{1} (m))

(4)

F_{2} (i) = \sum_{m} X^{F} (m + i) k_{2} (m) ⊙ σ (\sum_{m} X^{F} (m + i) v_{2} (m))

(5)

F_{3} (i) = \sum_{m} X^{F} (m + i) k_{3} (m) ⊙ σ (\sum_{m} X^{F} (m + i) v_{3} (m))

(6)

式中： $m$ 为连续时间序列跨度， $m = 1, \dots, N - 1 - L$ ； $σ$ 为激活函数的常系数。

通过多个卷积函数运算和拼接操作后，模型获得不同周期的时间序列信息和频率序列信息。

在Transformer模型中，编码器的输入由两部分组成，分别是词编码矩阵 I （ $I \in R^{n \times d_{x}}$ ）和位置编码矩阵 P （ $P \in R^{n \times d_{x}})$ ，其中 $n$ 为时间段数。 P 表示每个观察点在时间窗口中的位置信息，即先后顺序。由于自注意力模块在计算注意力分布时只能给出输出向量与输入向量之间的权重关系，不能给出序列节点在时间窗口中的位置信息，因此有必要在输入中引入 P 进行位置嵌入。对于每个观察点而言，位置不是由1个数字表示的，而是由多维向量构成。 P 的维度与观察点的嵌入维度相等，2k表示偶数位置，2k+1表示奇数位置，p_os表示观察点在输入序列中的位置，0≤p_os<L/2，则：

\{\begin{array}{l} P_{2 k} = s i n [\frac{p_{o s}}{{(2 L)}^{2 k / d_{m o d e l}}}] \\ P_{2 k + 1} = c o s [\frac{p_{o s}}{{(2 L)}^{2 k / d_{m o d e l}}}] \end{array}

(7)

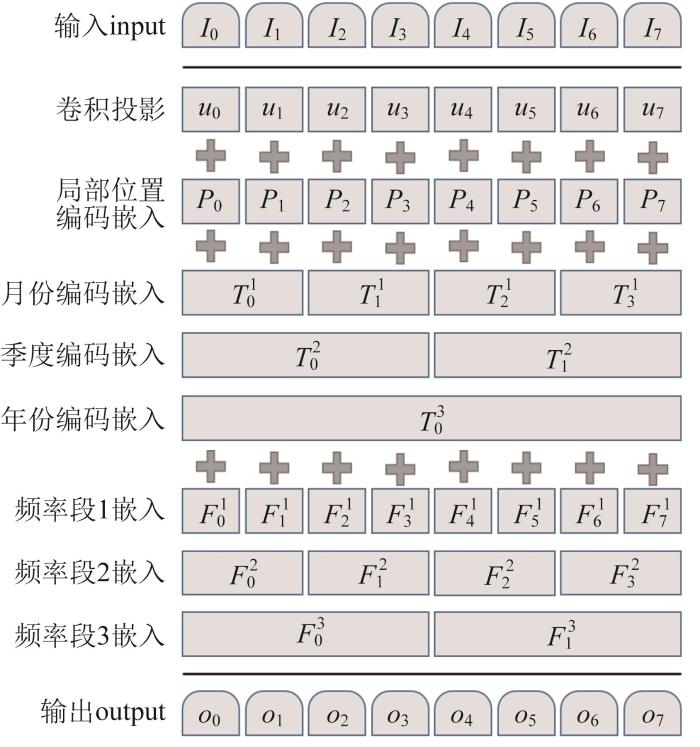
除了位置编码，编码层注意力输入的特征序列还包括时间序列信息和频率序列信息。考虑到时间特征和频率特征在实际应用中的有效性，采用时间序列数据，提取时间戳中的月位置嵌入、季度位置嵌入以及时间段内的订单频率嵌入，将这些编码为叠加的位置编码，共同构成可学习的嵌入^[17]。所提出的位置嵌入方法主要由以下4个部分构成：1）销量经过卷积得到的标量；2）sin函数固定的局部位置编码；3）由数据段对应时刻的月份、季度、年度得到的全局位置编码 T；4）订单频率标记的频率等级位置编码 F。

对上述4个主要部分进行叠加，作为时序和频率嵌入信息输入模型，使网络能有效捕捉时间帧之间的局部和全局相关性。其公式如下：

X_{i} = X_{t} + P_{(L \times (t - 1) + i)} + \sum_{p} {[T_{(L \times (t - 1) + i)}]}_{p} + \sum_{q} {[F_{(L \times (t - 1) + i)}]}_{q}

(8)

式中： $X_{t}$ 为时间窗口中长度为L的销量序列，t为时间窗口序列数， $p$ 为全局时间戳的数目， $q$ 为离散的频率段数， $i \in [1, 6]$ 。

将带有特征指标的销量时间序列作为模型的输入，并将周期信息注入输入的时间序列，供模型学习相关事件知识。

将前一个时间窗口的所有特征与其在不同时间戳尺度的时刻数据相加，构成新的特征数据序列并将它输入网络，使模型学习历史数据中的模式，从而帮助预测下一个时间窗口。采用上述方法对特征进行周期性增强后，模型得以测量输入信号间的时延相似度，并对多个相似的历史子序列进行聚合后输出。特征数据序列输入网络如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 特征数据序列输入网络

Fig.4 Input network for feature data sequences

1.2　基于时序-频率自注意力机制的编码器结构

编码完成后，为了确保序列中每一条信息的长度都相同，需要对数据进行特征缩放，如式(9)所示。

X_{i} = R e L U (I_{i} \times W_{i n} + b_{i n})

(9)

式中： $W_{i n}$ 为特征缩放层的权重矩阵， $I_{i}$ 为输入特征， $b_{i n}$ 为需要训练的参数。

经过缩放后的特征被送入自注意力机制层并由其完成对输入特征的编码。在编码层的时序-频率多头自注意力模块结构如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 时序-频率多头自注意力模块结构

Fig.5 Structure of timing-frequency multi-head self-attention module

该时序-频率自注意力模块结构的 Q 、 K 、 V 矩阵均由被调整后的输入序列构成，即：

\{\begin{array}{l} \begin{matrix} q_{i} = W_{i}^{q} \cdot X_{i} \\ k_{i} = W_{i}^{k} \cdot X_{i} \\ v_{i} = W_{i}^{v} \cdot X_{i} \end{matrix} \\ i = 1, 2, \dots, t \end{array}

(10)

定义6个映射矩阵 $W_{i}^{q} \in R^{24 \times 36}$ ，每个映射矩阵将原始的 Q 序列映射到36维空间，形成6个 $q_{i}$ 的新序列；定义6个映射矩阵 $W_{i}^{k} \in R^{24 \times 36}$ ，每个映射矩阵将原始的 K 序列映射到36维空间，形成6个 $k_{i}$ 的新序列；定义6个映射矩阵 $W_{i}^{v} \in R^{24 \times 36}$ ，每个映射矩阵将原始的 V 序列映射到36维空间，形成6个 $v_{i}$ 的新序列。

对每个注意力头( $q_{i}$ , $k_{i}$ , $v_{i}$ )进行一次自注意力运算，得到结果 $h_{i}$ 。将所有注意力头的输出 $h_{i}$ 进行拼接，并使用矩阵 $W_{0} = R^{24 \times 24}$ 映射出拼接结果 $H_{o u t}$ 。其流程如下：

h_{i} = a t t e n t i o n (W_{i}^{q} q, W_{i}^{k} k, W_{i}^{v} v)

(11)

a t t e n t i o n (Q, K, V) = s o f t m a x (\frac{Q K^{T}}{\sqrt[]{d_{x}}}) V

(12)

H_{o u t} = c o n c a t (h_{1}, \dots, h_{6}) W_{0}

(13)

基于上述分析可知， Q 、 K 、 V 三个矩阵的维度均为24×36维。但是在实际建模过程中，由于订单数据集在各个区间中的数量并不统一，特别是数据集中的最后一个批次，其输入数据样本数通常不足。为了保证 Q 、 K 、 V 维度的一致性，需要对输入数据执行掩码操作，用0填充所有新的样本观测值，以确保每个批次的样本个数都为24。

得到自注意力层后，下一步操作是层归一化（LayerNorm）与残差连接（Add）。通过对层激活值的归一化，可以加速模型的训练过程，使其更快地收敛，避免梯度消失问题。记层归一化结果为 $L_{N}$ ，其具体表示为：

L_{N} = L a y e r N o r m a l i z a t i o n (H_{o u t} + X_{i})

(14)

接下来是一个基于位置的全连接前馈神经网络。全连接前馈神经网络包含2次ReLU激活函数的线性变换， $F_{1}$ 为一次激活函数， $F_{2}$ 为二次激活函数，分别用来增强模型非线性以及调整输出的大小，使其输入、输出一致。

F_{1} = R e L U (x W_{1} + b_{1})

(15)

F_{2} = R e L U (F_{1} W_{2} + b_{2})

(16)

X_{o u t} = L a y e r N o r m a l i z a t i o n (F_{2} + L_{N})

(17)

式中： $x \in R^{1 \times 36}$ ，为前馈神经网络子层的单一样本行向量输入；矩阵 $W_{1} \in R^{36 \times 36} 、 W_{2} \in R^{36 \times 36}$ 及行向量 $b_{1} \in R^{1 \times 36} 、 b_{2} \in R^{1 \times 36}$ 均为需要训练的参数。

由式(4)至式(6)可得单个样本的输出 $X_{o u t} \in R^{1 \times 36}$ ，将24个样本的结果行向量拼接，可得到一个24×36型的矩阵，其与输入数据一致，可作为编码器下一层的输入使用。

综上所述，可以构建出SFTransformer模型的编码器结构。SFTransformer模型的编码模块中连接了4个编码器。通过使用多个编码器，可以使模型更有效地处理输入数据并生成更准确的输出。

1.3　基于时序-频率自注意力机制的解码器结构

原始的Transformer模型用于解决NLP（neuro-linguistic programming，神经语言程序学）问题，采用了双向注意力机制，而时间序列具有单向性。为了解决这个问题，需要在解码器第1层自注意力模块使用掩码机制，以屏蔽来自后续时间步的信息，可以表示为：

H_{m a s k} = s o f t m a x (\frac{Q_{i} \times K_{i}^{T}}{\sqrt[]{d_{x}}} \cdot [\begin{matrix} 1 & \dots & 0 \\ ⋮ & ⋮ \\ 1 & \dots & 1 \end{matrix}]) \times V_{i}

(18)

解码器第1层自注意力模块的输入来自上一层的输出，并附带了掩码机制。将式(18)中 $Q_{i}$ × $K_{i}^{T}$ 构成的输入调整矩阵点乘下三角矩阵，使得调整矩阵中所有在预测时间步之后的值全部置为0，仅保留当前时间步之前的值，以保证时间序列的单向性。这样的输入确保第1层注意力模块在解码时无法获取之后时间步的信息。

解码器第2层自注意力模块的输入来自两部分：第1部分来自上一层解码器的输出，但仅作为该层的查询矩阵 Q 使用；第2部分来自编码器的输出，这部分输入跳过了解码器的第1子层，直接输入第2个子层中，作为该层的键值矩阵 K 和 V。

由上可得，解码阶段的每个时间步都会输出一个输出序列的元素，接下来的每个时间步都重复这个过程。每个时间步的输出在下一个时间步被提供给解码器，最后部分是输出预测结果，通过解码器得到一个最终向量。经过线性层、全连接层和Softmax函数对向量进行计算，假设预测步长L=4，则编码器层输出序列 $X_{o u t} = (x_{o u t 1} x_{o u t 2} \dots {x_{o u t}}_{(s + 4)})$ ，其中s为序列数。三步时间独立线性层有3个矩阵 $W_{i} \in R^{24 \times 4}$ ，截取 $X_{o u t}$ 后面的4个输出，有预测输出 ${X'}_{o u t} = ({x_{o u t}}_{(s + 1)} {x_{o u t}}_{(s + 2)} {x_{o u t}}_{(s + 3)} {x_{o u t}}_{(s + 4)})$ 。然后按照时间顺序和矩阵 $W_{i}$ 进行运算，生成预测输出 $\hat{Y} = ({\hat{y}}_{s + 1} {\hat{y}}_{s + 2} {\hat{y}}_{s + 3} {\hat{y}}_{s + 4})$ 。具体过程如下：

{\hat{y}}_{s + 1} = l i n e a r ({x_{o u t}}_{(s + 1)}, W_{1})

(19)

{\hat{y}}_{s + 2} = l i n e a r ({x_{o u t}}_{(s + 2)}, W_{2})

(20)

{\hat{y}}_{s + 3} = l i n e a r ({x_{o u t}}_{(s + 3)}, W_{3})

(21)

{\hat{y}}_{s + 4} = l i n e a r ({x_{o u t}}_{(s + 4)}, W_{4})

(22)

模型在训练过程中采用均方误差（mean-square error, MSE）函数作为损失函数。将时间序列输入网络，将得到的预测评分与真实评分进行比较，计算损失。损失从解码器输出并反向传播到整个模型。

2 实验分析

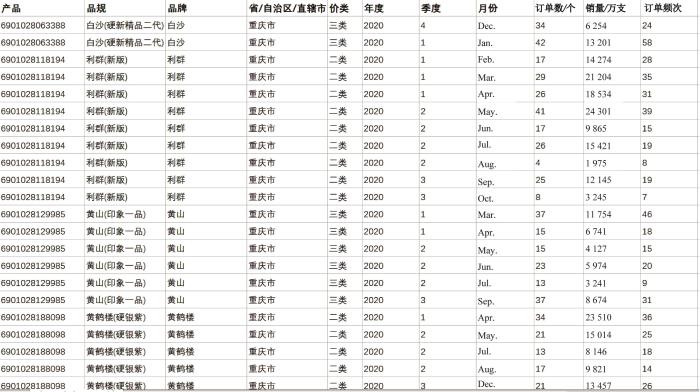
实验数据来源于某复杂产品制造企业的销售数据。收集了各产品2017—2020年的销售数据，其中2017—2019年的销量数据作为模型训练集，2020年的销量数据作为模型测试集。由经过特征筛选的产品品规、品牌、归属省份、所属价类、月订单数、月销量、月订单频次等数据构成销量预测的数据集。企业部分销售数据如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 某复杂产品制造企业销售数据集

Fig.6 Sales dataset of a complex product manufacturing enterprise

为了保证实验的准确性，在数据集中删除了2017—2019年过少的销售量，例如删除了月订单数低于3次、月销量低于5万支的数据。经过数据筛选，得到了591个产品序列、408 241条订单数据，将它作为输入数据。由于数据之间的结构不同，原始特征数据的量纲相差较大，在将数据输入模型前对原始数据进行标准化和归一化处理，以消除量纲对模型分析的影响。

实验环境中，CPU（central processing unit，中央处理器）采用AMD Ryzen 9 5900HX with Radeon Graphics，GPU（graphics processing unit，图形处理器）采用NVIDIA GTX3070 8G，内存为32G，开发环境为Pytorch 1.13.0+cu116，采用Jupyter notebook平台。

实验中，分别用均方误差E_SM、平均绝对误差E_MA、均方根误差E_RSM来评估模型的性能^[18-20]。E_SM、E_MA、E_RSM的值越小，代表模型的预测性能越好。

设置输入样本的步长为36，每个数据集的预测长度分为4和12两组。SFTransformer模型参数设置如表1所示。

表1 SFTransformer模型参数设置

Table 1 SFTransformer model parameter settings

参数	量值
batchSize	32
学习率	0.000 5
训练数	200轮
多头注意力	6个
隐藏数	16层
Dropout	0.05
优化器	Adam

新窗口打开| 下载CSV

实验中选取VAR（vector autoregressive，向量自回归）模型、LSTM模型、Transformer模型等3个常用的时间序列预测模型来与本文提出的SFTransformer模型作对比实验。SFTransformer模型与以上3个模型预测性能的对比如表2所示。由表可知，SFTransformer模型具有更稳定的长期预测性能。通过关注时序与频率特征，可以关注到其他模型无法关注到的订单频率信息，有较好的预测性能。SFTransformer模型的预测误差大大小于VAR模型和LSTM模型，并小幅小于Transformer模型，充分说明了时序-频率自注意力机制在时间序列预测问题上的优越性。

表2 不同模型预测性能的对比

Table 2 Comparison of prediction performance of different models

预测长度	评价指标	VAR模型	LSTM模型	Transformer模型	SFTransformer模型
4	E_SM	0.191	0.175	0.098	0.084
	E_MA	0.201	0.197	0.115	0.102
	E_RSM	0.437	0.418	0.313	0.290
12	E_SM	0.397	0.356	0.198	0.165
	E_MA	0.409	0.388	0.225	0.201
	E_RSM	0.730	0.596	0.445	0.406

新窗口打开| 下载CSV

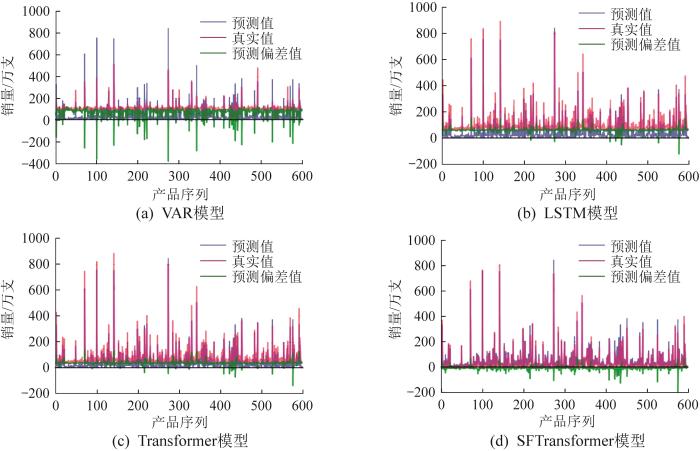
VAR模型、LSTM模型、Transformer模型和SFTransformer模型对产品销量的预测结果如图7所示。由图可知：SFTransformer模型的预测偏差极小，预测值与真实值很接近；Transformer模型的预测偏差较小，可以较好地预测销量趋势；LSTM模型的预测值大部分离容错区间较远；VAR模型在此类问题上无法预测相关趋势，预测值与真实值出现了极大的偏离。可见，SFTransformer模型对复杂产品订单长时间序列预测的结果好于Transformer模型。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 各模型对产品销量的预测结果

Fig.7 Prediction results of product sales volume by each model

3 结论

本文介绍了融合多主体需求频率特征的复杂产品全生命周期价值链协同设计方法。基于Transformer模型，构建了基于改进注意力机制的价值链高频需求预测模型——SFTransformer模型。以复杂产品全生命周期价值链中的订单需求为预测目标，在SFTransformer模型中设计了时序-频率多头自注意力机制。该机制将基于时序的订单数据的不同订单频率分别对应不同的注意力头来关注订单数据的时序特征和频率特征，结合了Embedding输入处理和Transformer模型结构。利用SFTransformer模型对实际的企业订单数据进行了预测，取得了较好效果，表明SFTransformer模型在一定程度上提升了预测准确率，说明融合多主体需求频率特征的复杂产品全生命周期价值链协同设计方法是有效的。

在数字经济时代，随着制造行业业务模式的增加，复杂产品价值链上业务数据的复杂度不断提高。本文针对复杂产品全生命周期价值链上多主体业务进行研究，挖掘数据中蕴含的价值。数据是分析问题的前提，数据集成与融合效果的好坏会直接影响后续工作的展开。因此，在后续的研究中，需要综合考虑数据来源及特征优化等相关问题，以确保数据集的准确性和高相关性。此外，企业在进行产品开发中会遇到很多复杂场景，因此，在后续的研究中，应该考虑融合多种预测模型的价值链协同设计，为实现复杂产品价值最大化提供更多的参考和指导，从而为企业的提效增益助力。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨海民，潘志松，白玮.

时间序列预测方法综述

［J］.计算机科学，2019，46（1）：21-28. doi：10.11896/j.issn.1002-137X.2019.01.004

DOI:10.11896/j.issn.1002-137X.2019.01.004 [本文引用: 1]

YANG

H M

， PAN

Z S

， BAI

Review of time series prediction methods

［J］. Computer Science， 2019， 46（1）： 21-28.

DOI:10.11896/j.issn.1002-137X.2019.01.004 [本文引用: 1]

[2]

王静，曹春正.

基于贝叶斯分层自回归时空模型的北京PM_2.5预测

［J］.南京信息工程大学学报（自然科学版），2023，15（1）：34-41.