经过不断的创新与发展,螺杆钻具已成为应用最广泛的井下动力钻具之一,对矿产资源的勘探与开发至关重要。螺杆马达是螺杆钻具的动力总成,通过定、转子之间形成的容积腔推动转子转动来带动钻头破碎岩石。螺杆马达作为螺杆钻具的核心部件,其在高温、高压、高应力环境下的工作性能决定了螺杆钻具的使用效果[1 -3 ] 。提高螺杆马达的机械性能可显著提高钻井效率和降低钻井成本。截面线型及其基本参数的选取是螺杆马达设计中的关键环节,良好的截面线型可以改善螺杆马达定、转子的接触情况和降低定子衬套的损坏概率。寻找最优截面线型以提高螺杆马达的工作性能一直是螺杆钻具行业的研究热点。
苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型。Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑。张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系。万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差。赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性。
目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良。此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证。螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响。内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] 。目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法。而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用。为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题。
为此,笔者拟采用显式非线性瞬态动力学方法来分析螺杆马达在不同负载工况下的工作性能,并提出可优化密封性能(尤其是转子齿顶和齿根过渡段的密封性能)的类圆弧新线型。同时,在相同负载工况下,对类圆弧线型螺杆马达与短幅内摆线螺杆马达进行效率、密封腔稳定性和可靠性的对比,并采用数值模拟和整机实验相结合的方法对类圆弧线型的可行性进行验证,旨在为螺杆马达线型设计提供参考和依据。
1 螺杆马达工作性能评价
1.1 效率评价
螺杆马达的效率由机械效率和容积效率两部分组成。机械效率是衡量螺杆马达有效做功程度的指标,机械效率越高,说明螺杆马达在较大负载工况下的扭矩输出越稳定。较高的机械效率是螺杆钻具设计者所追求的目标之一。但在实际应用中,任何一种机械能输出装置都存在一定的输出损耗。螺杆马达的扭矩损耗主要由以下几部分组成:因转子行星运动而产生的橡胶形变所造成的扭矩消耗,钻井液黏性剪切力所造成的扭矩消耗,定、转子之间的摩擦作用所引起的扭矩损失以及因钻井液压差作用而产生的径向载荷所引起的扭矩损失等。由于螺杆马达是负载决定输出的容积式机械,当已知加载的恒定负载扭矩M L 时,通过计算理论输出扭矩M T 即可得到机械效率[16 ] 。螺杆马达机械效率η m 的计算式如下:
η m = M L M T (1)
容积效率是评价螺杆马达总体密封性能的重要参数。螺杆马达容积效率η v 的计算式如下:
η v = n n T (2)
n T = 60 Q q (3)
式中:n 为螺杆马达的实际转速;n T Q 为螺杆马达的流量;q 为螺杆马达的每转排量。
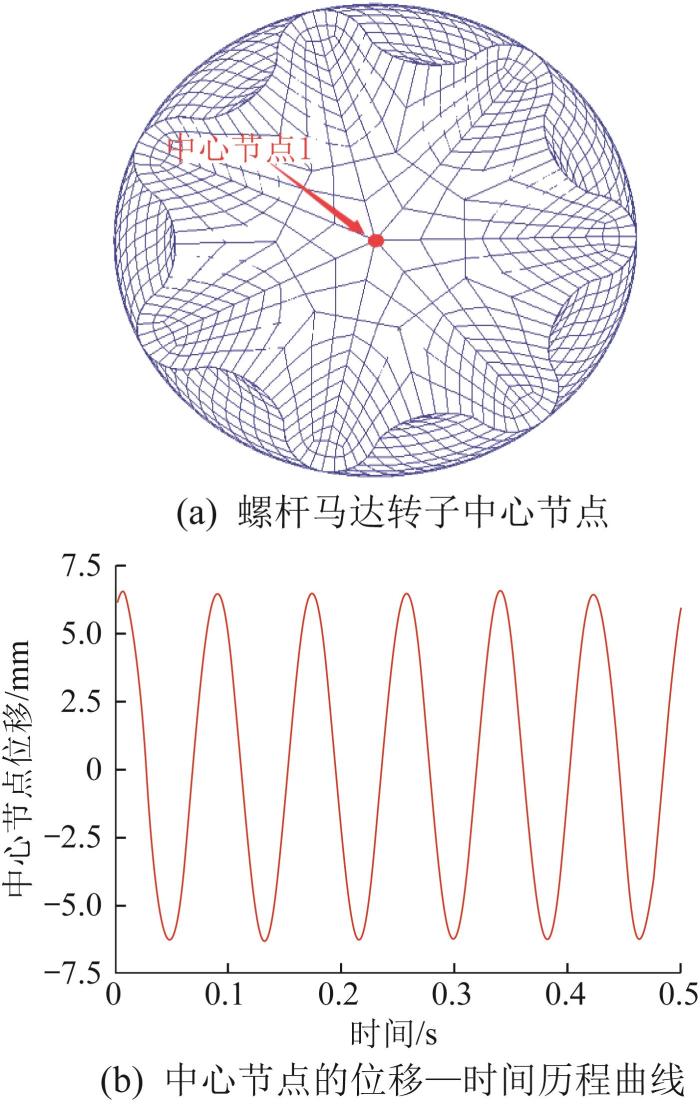
本文采用不可压缩流体模型与速度流场边界[17 ] 对螺杆马达的容积效率进行仿真计算。在仿真过程中,给定螺杆马达的流量Q ,已知螺杆马达的每转排量q ,利用式(3)计算得到螺杆马达的理论转速n T 图1 (a)所示仿真模型中螺杆马达转子中心节点1的位移,并输出其时间历程曲线,如图1 (b)所示;通过计算相同工况下相邻波峰与波谷之间的时间长度来计算螺杆马达的实际转速。令相邻波峰与波谷之间的时间间隔为t 0 N ,则螺杆马达的实际转速如式(4)所示,结合式(2)即可计算得到螺杆马达的容积效率[16 ] ,如式(5)所示。
n = 30 N + 1 t 0 (4)
η v = n n T = q 2 t 0 N + 1 Q (5)
图1
图1
螺杆马达转子中心节点及其位移—时间历程曲线
Fig.1
Screw motor rotor center node and its displacement‒time history curve
螺杆马达的总效率为容积效率与机械效率的乘积。结合上文公式,即可计算得到螺杆马达在某具体负载扭矩下的总效率η :
η = η m η v
1.2 密封腔性能评价
一个性能优异的螺杆马达在满足理论密封[16 ] 的同时,还必须保证其密封腔的可靠性与稳定性。螺杆马达的密封腔及其受力情况如图2 所示。由图可以看出,螺杆马达内含有多个螺旋状密封腔,相邻密封腔之间被由定、转子形成的接触带隔离开;一个完整的密封腔包含上、下2条接触带。目前应用广泛的密封接触理论[18 ] 认为:当一条接触带左右两端充满液体且压力分别为p 1 、p 2 时,只要其上、下两端的接触力F t 和F b 均大于0 N,就表明该时刻定、转子之间紧密接触,即不发生泄漏;同时,接触力不为0 N的接触带越长,密封越可靠。螺杆马达的密封腔除了要保证密封的可靠性外,还须保证密封的稳定性。在螺杆马达密封腔的推移过程中,接触力是动态变化的,接触力波动越小,说明接触越稳定,即密封腔的稳定性越好。通过仿真分析发现,在通入流体的初始阶段,由于流场紊乱,接触带的接触情况存在波动,故本文将密封腔向下推移0.15个导程时的接触力与初始时刻接触力的差值的平均值及均方差作为密封腔稳定性的量化评价指标。
图2
图2
螺杆马达密封腔及其受力示意
Fig.2
Sealing cavity of screw motor and its force diagram
2 短幅内摆线螺杆马达有限元仿真分析
2.1 短幅内摆线螺杆马达的结构参数
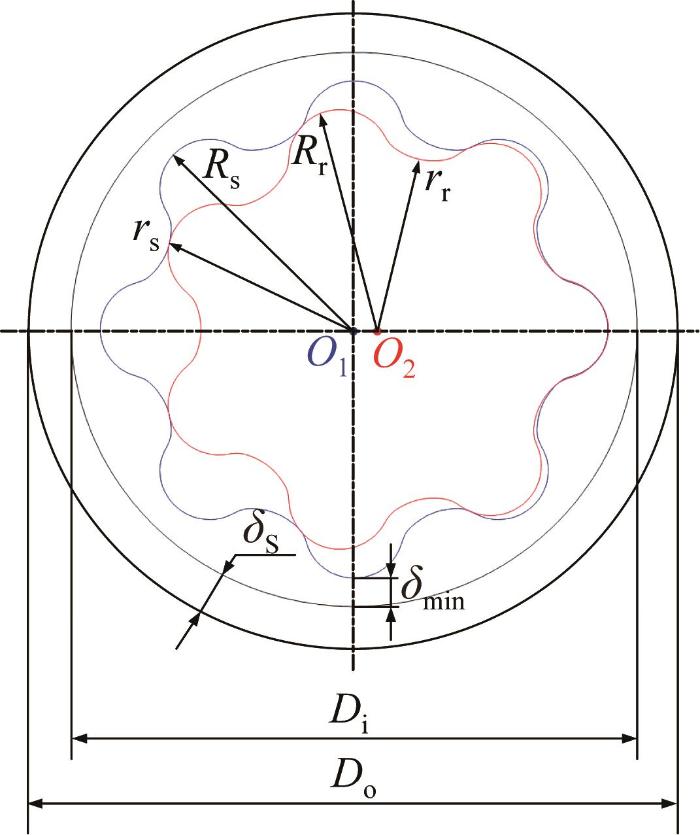
由于外摆线螺杆马达存在比较严重的打扣现象,很少在实际工程中使用,因此本文选择在实际工程中应用最为广泛的短幅内摆线螺杆马达为研究对象。所选择的短幅内摆线螺杆马达(7/8头螺杆马达)的流量为30.78 L/s,变幅系数为0.95,导程为914.4 mm,过盈量为0.2 mm,其二维截面参数和结构参数分别如图3 和表1 所示。
图3
图3
短幅内摆线螺杆马达截面参数示意
Fig.3
Schematic diagram of cross-sectional parameters of short-amplitude endocycloid screw motor
2.2 短幅内摆线螺杆马达有限元模型及仿真结果
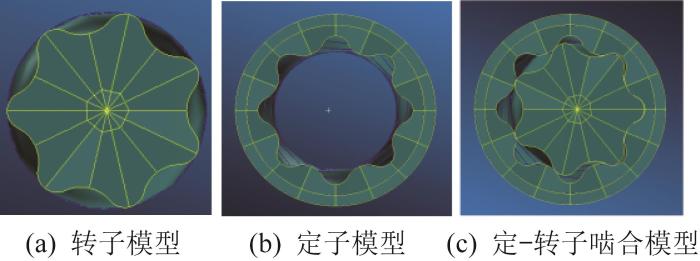
为分析短幅内摆线螺杆马达的工作性能,基于流固耦合方法建立其三维有限元模型[19 -22 ] ,如图4 所示。其中:转子材料采用镀铬合金,在建模过程中将其视为刚体;定子材料采用硬度为85,橡胶本构参数C 01 =2.23 MPa、C 10 =-0.03 MPa的丁晴橡胶。在螺杆马达实际工作过程中,转子在自转的同时绕定子中心作行星运动,故在仿真过程中,约束定子的所有自由度,约束转子的轴向自由度;将仿真时长设为0.5 s。为模拟螺杆马达在不同工况下的工作性能,在第0.18,0.26,0.34,0.42秒时分别对其施加200,400,600,800 N·m的负载扭矩。
图4
图4
短幅内摆线螺杆马达三维有限元模型
Fig.4
Three-dimensional finite element model of short-amplitude endocycloid screw motor
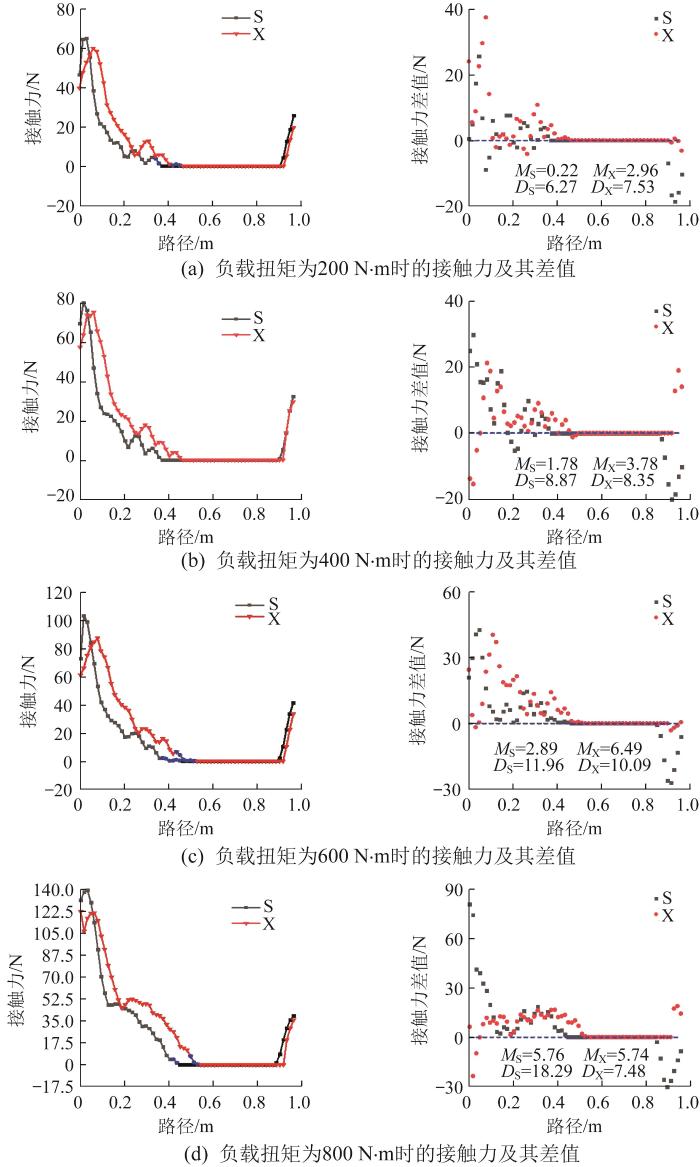
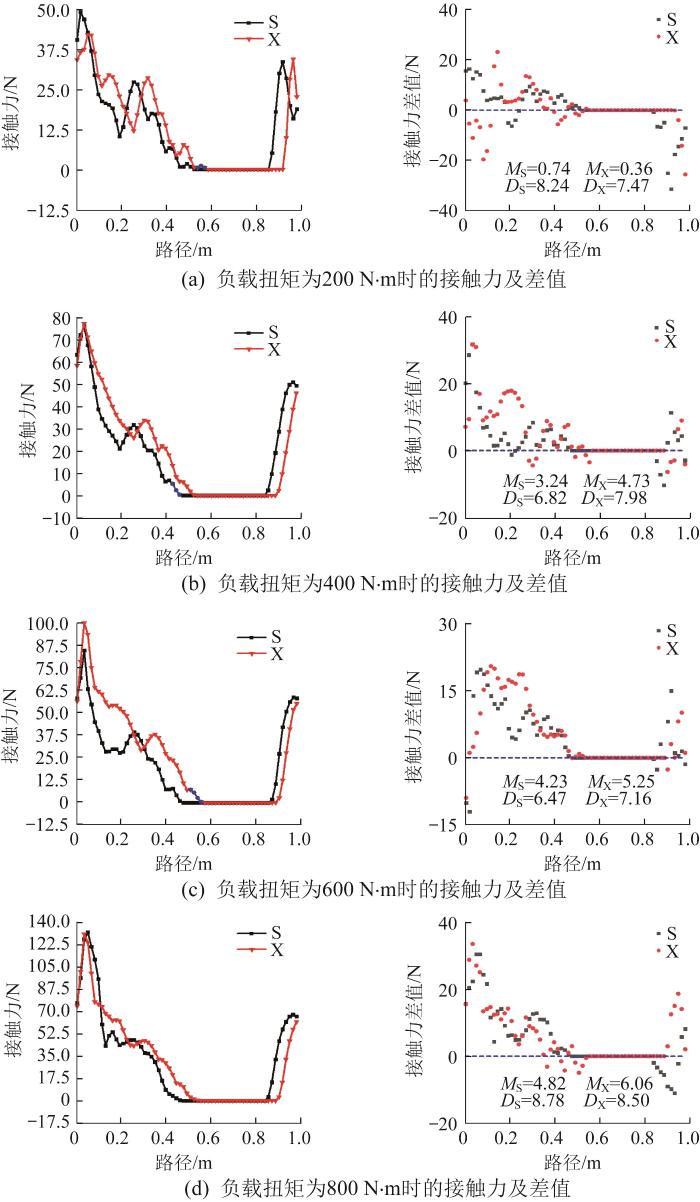
不同负载扭矩下短幅内摆线螺杆马达的接触力及其差值的仿真结果如图5 所示。图中:S表示密封腔上方接触带,X表示密封腔下方接触带,下文同。通过采集密封腔向下推移0.15个导程的接触力数据,整理得到不同负载扭矩下密封腔接触带的接触力并与初始时刻的接触力比较,得到接触力差值。其中:用M X 表示下接触带接触力差值的平均值,用M S 表示上接触带接触力差值的平均值,用D X 表示下接触带接触力差值的均方差,用D S 表示上接触带接触力差值的均方差。
图5
图5
不同负载扭矩下短幅内摆线螺杆马达的接触力及其差值
Fig.5
Contact force and its difference of short-amplitude endocycloid screw motor under different load torques
由图5 可知:对于短幅内摆线螺杆马达,随着负载扭矩的增大,其密封腔接触带的接触力峰值增大。当负载扭矩为200 N·m时,接触力峰值为65 N左右;当负载扭矩为800 N·m时,接触力峰值增大到140 N左右。由此说明,接触力峰值与负载扭矩呈正相关。在定、转子啮合过程中,接触力过大会导致定、转子的接触摩擦力增大,进而导致扭矩消耗增长,在交变载荷的影响下螺杆马达更容易磨损。此外,通过分析接触力差值的均方差发现:随着负载扭矩的增大,接触力差值的均方差在总体上呈增大趋势,表明密封腔的稳定性逐渐降低,即密封腔的失稳风险增大。因此,在实际应用中,应该合理控制负载扭矩,以防因过载而导致螺杆马达快速磨损。
不同负载扭矩下短幅内摆线螺杆马达工作性能的仿真结果如表2 所示。通过分析表2 仿真结果可以发现,随着负载扭矩的增大,短幅内摆线螺杆马达的实际转速并没有大幅度下降,说明该螺杆马达具有良好的转速硬特性[22 ] ;该螺杆马达出入口两端的压差呈现逐级递增的趋势,其容积效率相对稳定,但机械效率明显提高,总效率逐步提高,说明其具有良好的过载能力。
3 类圆弧线型螺杆马达的设计与分析
3.1 类圆弧线型螺杆马达设计
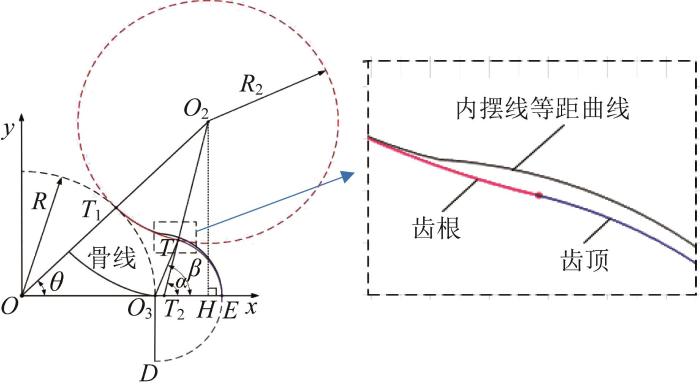
螺杆马达在井下有多种失效形式,其中最多见的是定、转子之间的磨损失效[18 -19 ] 。过大的接触力会加剧螺杆马达定、转子之间的磨损,导致接触情况较差,而过小的接触力又可能会导致密封腔的密封性能下降。因此,在保证螺杆马达转子齿顶和齿根的良好密封性能的前提下,应尽可能减小其密封腔接触带的接触力,以提高耐磨损能力。为了兼顾螺杆马达密封腔的良好密封性能和接触可靠性,提出了一种类圆弧线型螺杆马达,其截面线型如图6 所示。该截面线型是以短幅内摆线转子骨线为基准,分别用椭圆弧、圆弧代替短幅内摆线转子齿顶、齿根的等距曲线。
图6
图6
螺杆马达类圆弧线型示意
Fig.6
Schematic diagram of quasi circular-arc contour-pattern for screw motor
通过观察转子齿顶和齿根的局部放大图可以发现,相较于短幅内摆线螺杆马达,类圆弧线型螺杆马达定、转子的齿根和齿顶连接处的过渡段更加光滑,连接处曲率更小,且不会出现最大综合曲率为+∞的情况,因此其密封腔接触带的接触力也更小。
x = a c o s t y = b s i n t (6)
式中:a 为长半轴O 3 E 的长度,a =2e ;b 为短半轴O 3 D 的长度,b <a 。
齿根处的圆弧T 1 O 2 T 的半径为R 2 ,其中点T 为椭圆弧与圆弧的切点。由椭圆性质可知,只有椭圆端点的法线经过椭圆的中心。过点T 作椭圆弧法线并与x 轴交于点T 2 ,定义切点T 2 处的法向角为α ,方向角为β 。由椭圆性质可得:
t a n α = a b t a n t t a n β = b a t a n t (7)
l 1 = a 2 - b 2 a c o s t (8)
l 2 = b 4 c o s 2 t a 2 + b 2 s i n 2 t (9)
式中:l 1 、l 2 分别为线段O 3 T 2 、TT 2 的长度。
R + R 2 s i n θ 2 + ( R + R 2 ) c o s θ - R - a 2 - b 2 a c o s t 2 = b 4 c o s 2 t a 2 + b 2 s i n 2 t + R 2 2 (10)
∠ O O 2 T 2 = a r c s i n R + a 2 - b 2 a c o s t s i n t R + R 2 b 2 a 2 c o s 2 t + s i n 2 t (11)
θ R 2 = a r c t a n a t a n t b - a r c s i n R + a 2 - b 2 a c o s t s i n t R + R 2 b 2 a 2 c o s 2 t + s i n 2 t (12)
联立式(10)至式(12),可得R 2
R + R 2 s i n θ R 2 2 + R + R 2 c o s θ R 2 - R - a 2 - b 2 a c o s t 2 = b 4 c o s 2 t a 2 + b 2 s i n 2 t + R 2 2
E ( φ , k ) = ∫ 0 φ 1 - k 2 s i n 2 φ d φ (13)
L = ∫ 0 t a 2 s i n 2 t + b 2 c o s 2 t t d t (14)
L = - ∫ π 2 φ a 2 c o s 2 φ + b 2 s i n 2 φ φ d φ = a E π 2 , f - a E ( φ , f )
采用上述方法得到转子线型后,采用包络方法得到其共轭曲线,即可获得螺杆马达的类圆弧截面线型。以7/8头螺杆马达为例,其类圆弧线型如图7 所示。
图7
图7
7/8头螺杆马达类圆弧线型
Fig.7
Quasi circular-arc contour-pattern of 7/8 head screw motor
3.2 类圆弧线型螺杆马达有限元仿真分析
为了验证所设计的类圆弧线型的合理性,对类圆弧线型螺杆马达进行有限元仿真分析。在结构参数和边界条件设置上,类圆弧线型螺杆马达三维有限元模型与短幅内摆线螺杆马达三维有限元模型相同。不同负载扭矩下类圆弧线型螺杆马达的接触力及其差值的仿真结果如图8 所示。
图8
图8
不同负载扭矩下类圆弧线型螺杆马达的接触力及其差值
Fig.8
Contact force and its difference of screw motor with quasi circular-arc contour-pattern under different load torques
由图8 所示的接触力曲线可知:与短幅内摆线螺杆马达一样,类圆弧线型螺杆马达的接触力峰值与负载扭矩呈正相关,但在相同负载扭矩下,其接触力峰值低于前者,说明类圆弧线型螺杆马达具有更好的接触性能,即在同等工况下具有更好的耐磨性。此外,在接触力曲线的中间位置出现了一个“驼峰”,使得接触力减缓下降。虽然短幅内摆线螺杆马达的接触力曲线中也出现了驼峰,但是其出现驼峰的接触带长度比类圆弧线型螺杆马达的要短,说明类圆弧线型减缓接触力下降的效果更好,即类圆弧线型螺杆马达具有更加优异的过载能力。
从图8 所示的类圆弧线型螺杆马达密封腔上、下接触带的接触力差值可以看出,随着负载扭矩的增大,接触力差值的平均值有所增大,但其均方差并无太大波动,说明类圆弧线型螺杆马达的成腔稳定性更好,对负载表现出较好的适应性。此外,类圆弧线型螺杆马达接触力差值的均方差随负载扭矩增大的变化较小,在负载扭矩为800 N·m时,D S 与D X 值分别为8.78 N和8.50 N,而短幅内摆线螺杆马达的D S 与D X 值分别为18.29 N和7.48 N,说明前者在高负载扭矩下的成腔稳定性优于后者。
类圆弧线型螺杆马达工作性能的仿真结果如表3 所示。对比表2 和表3 可以发现:当负载扭矩小于400 N·m时,短幅内摆线螺杆马达的效率高于类圆弧线型螺杆马达;但当负载扭矩大于400 N·m时,类圆弧线型螺杆马达的效率更高。这进一步说明类圆弧线型螺杆马达具有更高的过载能力。
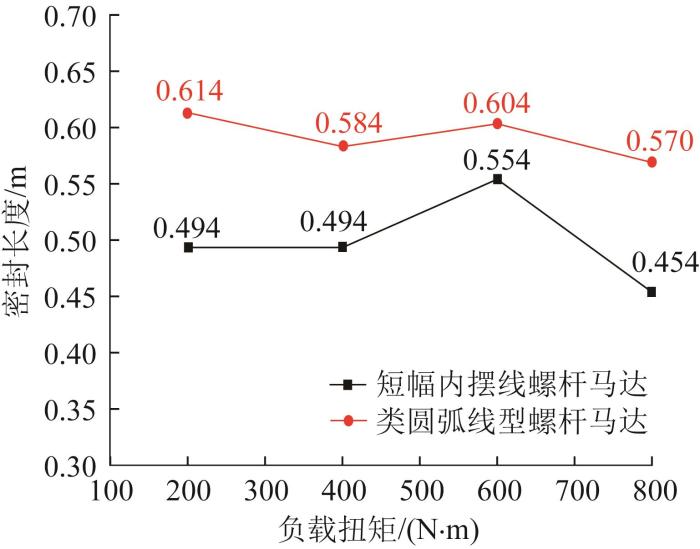
根据前文提出的密封可靠性评价准则,对比短幅内摆线螺杆马达和类圆弧线型螺杆马达的密封长度随负载扭矩的变化情况,结果如图9 所示。由图可知,随着负载扭矩的增大,2种螺杆马达的密封长度均呈振荡下降的趋势,但在相同负载扭矩下,类圆弧线型螺杆马达的密封长度更长,说明其密封可靠性更好。
图9
图9
不同螺杆马达的密封长度对比
Fig.9
Comparison of sealing length for different screw motors
3.3 类圆弧线型螺杆马达工作性能实验验证
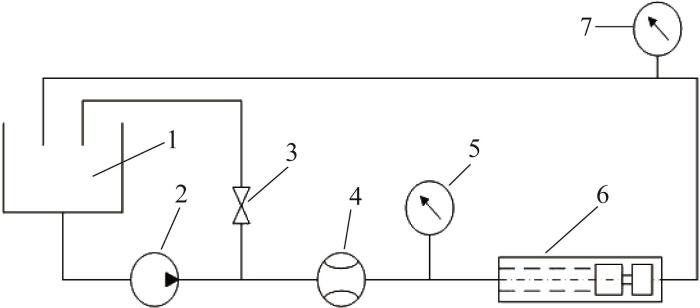
为了验证所设计的类圆弧线型螺杆马达的可行性,基于图10 所示的实验原理,利用图11 所示的实验台架对螺杆马达的工作性能进行测试。通过采集数据并整理得到类圆弧线型螺杆马达工作性能实验结果,如表4 所示。
图10
图10
螺杆马达工作性能测试实验原理
1—供液箱;2—供液泵;3—旁路调节阀;4—流量计;
5—入口压力表;6—被测螺杆马达;7—出口压力表。
Fig.10
Experimental principle of working performance testing for screw motor
图11
图11
螺杆马达工作性能测试实验台架
Fig.11
Working performance testing experimental bench for screw motor
通过对比表3 和表4 的数据可以发现:1)在相同的负载扭矩下,类圆弧线型螺杆马达工作性能的仿真结果与实验结果的误差较小,验证了仿真结果的准确性;2)随着负载扭矩的增大,类圆弧线型螺杆马达的实际转速(实验值比仿真值高5%左右)未出现大幅下降的情况,即未因负载扭矩增大而发生失速现象,说明其具有较好的转速硬特性;3)对比类圆弧线型螺杆马达总效率的实验值与仿真值可以发现,总效率与负载扭矩呈正相关,且实验效率高于仿真效率,但两者的相对误差不大且在合理范围内,说明所设计的类圆弧线型是合理的。研究结果可为后续其他线型螺杆马达的设计提供参考。
4 结 论
本文设计了一种类圆弧线型螺杆马达,并与短幅内摆线螺杆马达进行了对比。通过分析可以发现:1)类圆弧线型螺杆马达的实际转速较低,更符合当今低速大扭矩的钻井需要;2)在相同负载工况下,类圆弧线型螺杆马达密封腔接触带的接触力在保证良好密封前提下较小,说明该螺杆马达的接触性能及抗磨损能力较强,且工作寿命较长;3)类圆弧线型螺杆马达的密封长度更长,即密封可靠性较好;4)类圆弧线型螺杆马达密封腔接触带接触力差值的均方差较小,说明密封腔稳定性较好。
综上所述,相较于传统的短幅内摆线螺杆马达,类圆弧线型螺杆马达整体性能更加优异,更加符合当前实际工程需要。
参考文献
View Option
[1]
韩传军 ,张杰 ,刘洋 常规螺杆钻具定子衬套的热力耦合分析
[J].中南大学学报(自然科学版) ,2013 ,44 (6 ):2311 -2317 .
[本文引用: 1]
HAN C J ZHANG J LIU Y Thermal-structure coupling analysis for general stator lining of PDM
[J]. Journal of Central South University (Science and Technology) , 2013 , 44 (6 ): 2311 -2317 .
[本文引用: 1]
[2]
LIU H HAO Z X WANG L G et al Current technical status and development trend of artificial lift
[J]. Acta Petrolei Sinica , 2015 , 36 (11 ): 1441 -1448 .
DOI:10.7623/syxb201511014
[3]
孟凡林 新型型线单螺杆钻具的设计研究
[D].青岛 :中国石油大学(华东) ,2016 :1 -6 .
[本文引用: 1]
MENG F L Research and design of single screw drilling tool based on new molded lines
[D]. Qingdao : China University of Petroleum (East China) , 2016 : 1 -6 .
[本文引用: 1]
[4]
苏义脑 ,谢竹庄 螺杆钻具马达线型分析基础及研究方法
[J].石油机械 ,1985 ,13 (6 ):10 -20 ,9 .
[本文引用: 1]
SU Y N XIE Z Z Basic research on the contour-pattern of downhole drilling screw motors
[J]. China Petroleum Machinery , 1985 , 13 (6 ): 10 -20 , 9 .
[本文引用: 1]
[6]
CHOI T H KIM M S LEE G S et al Design of rotor for internal gear pump using cycloid and circular-arc curves
[J]. Journal of Mechanical Design , 2012 , 134 (1 ): 011005 .
[本文引用: 1]
[9]
[本文引用: 1]
WAN B L CAO Y D On assessment index and optimum parameters selection of curtate endocycloid isometric conjugate contour-pattern of hydraulic machinery
[J]. China Petroleum Machinery , 1989 , 17 (3 ): 1-11, 5 -6 .
DOI:10.1007/BF02943119
[本文引用: 1]
[10]
赵娜 螺杆钻具马达线型优化设计方法的研究
[D].沈阳 :沈阳工业大学 ,2016 :2 -16 .
[本文引用: 1]
ZHAO N Screw drill motor linear optimization design method research
[D]. Shenyang : Shenyang University of Technology , 2016 : 2 -16 .
[本文引用: 1]
[11]
路玥 螺杆马达转子的线型分析
[D].西安 :西安石油大学 ,2010 :2 -9 .
LU Y Profile analysis of screw motor’s rotor
[D]. Xi’an : Xi’an Shiyou University , 2010 : 2 -9 .
[12]
童华 ,陈国银 ,祝效华 谐壁厚螺杆钻具橡胶衬套线型设计与仿真分析
[J].系统仿真学报 ,2018 ,30 (2 ):647 -653 .
[本文引用: 1]
TONG H CHEN G Y ZHU X H Linear design and simulation analysis for harmonic-distance rubber bushing of PDM
[J]. Journal of System Simulation , 2018 , 30 (2 ): 647 -653 .
[本文引用: 1]
[15]
苏义脑 螺杆钻具研究及应用 [M].北京 :石油工业出版社 ,2001 :2 -47 .
[本文引用: 1]
SU Y N Research and application of screw drilling tools [M]. Beijing : Petroleum Industry Press , 2001 : 2 -47 .
[本文引用: 1]
[16]
张聪 螺杆马达啮合仿真模型与应用研究
[D].成都 :西南石油大学 ,2016 :1 -23 .
[本文引用: 3]
ZHANG C Research on meshing simulation model and application of screw motor
[D]. Chengdu : Southwest Petroleum University , 2016 : 1 -23 .
[本文引用: 3]
[17]
王勇帅 不可压缩流体流动及其耦合问题的时空有限元算法
[D].上海 :华东师范大学 ,2021 :1 -7 .
[本文引用: 1]
WANG Y S Timespace finite element methods for the incompressible fluid flows and their coupling problems
[D]. Shanghai : East China Normal University , 2021 : 1 -7 .
[本文引用: 1]
[18]
柳欢欢 基于流固耦合的螺杆马达动态仿真
[D].武汉 :华中科技大学 ,2017 :11 -29 .
[本文引用: 2]
LIU H H Dynamic simulation of positive displacement motor based on fluid-structure interaction
[D]. Wuhan : Huazhong University of Science and Technology , 2017 : 11 -29 .
[本文引用: 2]
[19]
单永平 螺杆马达流固耦合动态仿真及正交数值试验研究
[D].武汉 :华中科技大学 ,2019 :34 -45 .
[本文引用: 2]
SHAN Y P Fluid-structure coupling simulation and orthogonal numerical experiment of positive displacement motor
[D]. Wuhan : Huazhong University of Science and Technology , 2019 : 34 -45 .
[本文引用: 2]
[20]
郑道宽 螺杆马达的流固耦合仿真
[D].武汉 :华中科技大学 ,2015 :23 -31 .
ZHENG D K Fluid-solid coupling simulation of positive displacement motor
[D]. Wuhan : Huazhong University of Science and Technology , 2015 : 23 -31 .
[21]
黄晓霞 螺杆马达(PDM)流-固耦合动态仿真
[D].武汉 :华中科技大学 ,2013 :12 -32 .
HUANG X X Fluid-structure coupling dynamic simulation of positive displacement motor (PDM)
[D]. Wuhan : Huazhong University of Science and Technology , 2013 : 12 -32 .
[22]
王竹溪 ,郭敦仁 特殊函数概论 [M].北京 :北京大学出版社 ,2000 :520 -559 .
[本文引用: 3]
WANG Z X GUO D R Introduction to special functions [M]. Beijing : Peking University Press , 2000 : 520 -559 .
[本文引用: 3]
[23]
[本文引用: 1]
LIU S S LIU S D Special functions [M]. Beijing : China Meteorological Press , 1988 : 656 -745 .
DOI:10.1002/qj.49711448413
[本文引用: 1]
常规螺杆钻具定子衬套的热力耦合分析
1
2013
... 经过不断的创新与发展,螺杆钻具已成为应用最广泛的井下动力钻具之一,对矿产资源的勘探与开发至关重要.螺杆马达是螺杆钻具的动力总成,通过定、转子之间形成的容积腔推动转子转动来带动钻头破碎岩石.螺杆马达作为螺杆钻具的核心部件,其在高温、高压、高应力环境下的工作性能决定了螺杆钻具的使用效果[1 -3 ] .提高螺杆马达的机械性能可显著提高钻井效率和降低钻井成本.截面线型及其基本参数的选取是螺杆马达设计中的关键环节,良好的截面线型可以改善螺杆马达定、转子的接触情况和降低定子衬套的损坏概率.寻找最优截面线型以提高螺杆马达的工作性能一直是螺杆钻具行业的研究热点. ...
常规螺杆钻具定子衬套的热力耦合分析
1
2013
... 经过不断的创新与发展,螺杆钻具已成为应用最广泛的井下动力钻具之一,对矿产资源的勘探与开发至关重要.螺杆马达是螺杆钻具的动力总成,通过定、转子之间形成的容积腔推动转子转动来带动钻头破碎岩石.螺杆马达作为螺杆钻具的核心部件,其在高温、高压、高应力环境下的工作性能决定了螺杆钻具的使用效果[1 -3 ] .提高螺杆马达的机械性能可显著提高钻井效率和降低钻井成本.截面线型及其基本参数的选取是螺杆马达设计中的关键环节,良好的截面线型可以改善螺杆马达定、转子的接触情况和降低定子衬套的损坏概率.寻找最优截面线型以提高螺杆马达的工作性能一直是螺杆钻具行业的研究热点. ...
新型型线单螺杆钻具的设计研究
1
2016
... 经过不断的创新与发展,螺杆钻具已成为应用最广泛的井下动力钻具之一,对矿产资源的勘探与开发至关重要.螺杆马达是螺杆钻具的动力总成,通过定、转子之间形成的容积腔推动转子转动来带动钻头破碎岩石.螺杆马达作为螺杆钻具的核心部件,其在高温、高压、高应力环境下的工作性能决定了螺杆钻具的使用效果[1 -3 ] .提高螺杆马达的机械性能可显著提高钻井效率和降低钻井成本.截面线型及其基本参数的选取是螺杆马达设计中的关键环节,良好的截面线型可以改善螺杆马达定、转子的接触情况和降低定子衬套的损坏概率.寻找最优截面线型以提高螺杆马达的工作性能一直是螺杆钻具行业的研究热点. ...
新型型线单螺杆钻具的设计研究
1
2016
... 经过不断的创新与发展,螺杆钻具已成为应用最广泛的井下动力钻具之一,对矿产资源的勘探与开发至关重要.螺杆马达是螺杆钻具的动力总成,通过定、转子之间形成的容积腔推动转子转动来带动钻头破碎岩石.螺杆马达作为螺杆钻具的核心部件,其在高温、高压、高应力环境下的工作性能决定了螺杆钻具的使用效果[1 -3 ] .提高螺杆马达的机械性能可显著提高钻井效率和降低钻井成本.截面线型及其基本参数的选取是螺杆马达设计中的关键环节,良好的截面线型可以改善螺杆马达定、转子的接触情况和降低定子衬套的损坏概率.寻找最优截面线型以提高螺杆马达的工作性能一直是螺杆钻具行业的研究热点. ...
螺杆钻具马达线型分析基础及研究方法
1
1985
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
螺杆钻具马达线型分析基础及研究方法
1
1985
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
单螺杆马达的普遍线型
1
1997
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
单螺杆马达的普遍线型
1
1997
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
Design of rotor for internal gear pump using cycloid and circular-arc curves
1
2012
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
螺杆马达线型仿真计算及实现
1
2017
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
螺杆马达线型仿真计算及实现
1
2017
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
准等壁厚螺杆钻具马达断面型线设计
1
2014
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
准等壁厚螺杆钻具马达断面型线设计
1
2014
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
短幅外摆线等距线型单螺杆式水力机械的评价指标及其参数的优选
1
1989
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
短幅外摆线等距线型单螺杆式水力机械的评价指标及其参数的优选
1
1989
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
螺杆钻具马达线型优化设计方法的研究
1
2016
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
螺杆钻具马达线型优化设计方法的研究
1
2016
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
谐壁厚螺杆钻具橡胶衬套线型设计与仿真分析
1
2018
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
谐壁厚螺杆钻具橡胶衬套线型设计与仿真分析
1
2018
... 苏义脑等[4 -5 ] 从实现螺杆马达定、转子良好接触的角度出发,提出了渐开线线型、圆弧线型以及椭圆弧线型等新截面线型.Choi等[6 ] 通过对内外摆线连接处的曲率进行优化,使得螺杆马达转子的线型更加光滑.张强等[7 -8 ] 从二维啮合的角度出发,采用有限元软件对螺杆马达的过盈量、定子衬套类型和截面线型参数等进行了优化,并建立了螺杆马达优良转子参数评价体系.万邦烈等[9 ] 指出螺杆马达定、转子在啮合时的综合曲率可以表征定-转子共轭幅的接触情况:综合曲率越小,接触越好,反之越差.赵娜等[10 -12 ] 采用三次样条函数等方法对螺杆马达的线型进行了优化设计,并采用仿真模拟验证了优化方法的可行性. ...
螺杆钻具定转子热力耦合行为
1
2016
... 目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良.此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证.螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响.内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] .目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法.而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用.为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题. ...
螺杆钻具定转子热力耦合行为
1
2016
... 目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良.此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证.螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响.内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] .目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法.而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用.为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题. ...
连续油管钻磨工艺螺杆马达特性分析及现场应用
1
2014
... 目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良.此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证.螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响.内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] .目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法.而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用.为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题. ...
连续油管钻磨工艺螺杆马达特性分析及现场应用
1
2014
... 目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良.此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证.螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响.内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] .目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法.而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用.为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题. ...
1
2001
... 目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良.此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证.螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响.内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] .目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法.而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用.为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题. ...
1
2001
... 目前,普遍采用的螺杆马达截面线型主要为普通内摆线和短幅内摆线的外等距线型,但无论等距半径系数取多小,都会造成打扣现象[13 -14 ] ,这种现象会导致定、转子接触不良.此外,现有的螺杆马达截面线型设计方法大多是根据经验提出的,并没有进行实验验证.螺杆马达的截面线型对其总效率、密封腔的稳定性和可靠性有至关重要的影响.内摆线等距线型螺杆马达由于转子齿根和齿顶过渡段的形状较为突出,在啮合过程中往往会产生较高的接触力和应力集中,从而导致定子磨损失效[15 ] .目前,螺杆马达的截面线型设计以理想运动工况下二维截面线型过盈量设计为主,是一种静力学分析方法.而在实际情况下,螺杆马达的工作性能表现为三维动力学行为,其定、转子在交变载荷的影响下相互作用.为了获得更优的螺杆马达截面线型,应从二维静力学分析过渡到三维动力学分析,而从二维过渡到三维存在以下难点:定子橡胶衬套表现出高度非线性,定、转子接触非线性以及流固耦合等问题. ...
螺杆马达啮合仿真模型与应用研究
3
2016
... 螺杆马达的效率由机械效率和容积效率两部分组成.机械效率是衡量螺杆马达有效做功程度的指标,机械效率越高,说明螺杆马达在较大负载工况下的扭矩输出越稳定.较高的机械效率是螺杆钻具设计者所追求的目标之一.但在实际应用中,任何一种机械能输出装置都存在一定的输出损耗.螺杆马达的扭矩损耗主要由以下几部分组成:因转子行星运动而产生的橡胶形变所造成的扭矩消耗,钻井液黏性剪切力所造成的扭矩消耗,定、转子之间的摩擦作用所引起的扭矩损失以及因钻井液压差作用而产生的径向载荷所引起的扭矩损失等.由于螺杆马达是负载决定输出的容积式机械,当已知加载的恒定负载扭矩M L 时,通过计算理论输出扭矩M T 即可得到机械效率[16 ] .螺杆马达机械效率η m 的计算式如下: ...
... 本文采用不可压缩流体模型与速度流场边界[17 ] 对螺杆马达的容积效率进行仿真计算.在仿真过程中,给定螺杆马达的流量Q ,已知螺杆马达的每转排量q ,利用式(3) 计算得到螺杆马达的理论转速n T . 螺杆马达的实际转速采取如下方式获得:追踪图1 (a)所示仿真模型中螺杆马达转子中心节点1的位移,并输出其时间历程曲线,如图1 (b)所示;通过计算相同工况下相邻波峰与波谷之间的时间长度来计算螺杆马达的实际转速.令相邻波峰与波谷之间的时间间隔为t 0 N ,则螺杆马达的实际转速如式(4) 所示,结合式(2) 即可计算得到螺杆马达的容积效率[16 ] ,如式(5) 所示. ...
... 一个性能优异的螺杆马达在满足理论密封[16 ] 的同时,还必须保证其密封腔的可靠性与稳定性.螺杆马达的密封腔及其受力情况如图2 所示.由图可以看出,螺杆马达内含有多个螺旋状密封腔,相邻密封腔之间被由定、转子形成的接触带隔离开;一个完整的密封腔包含上、下2条接触带.目前应用广泛的密封接触理论[18 ] 认为:当一条接触带左右两端充满液体且压力分别为p 1 、p 2 时,只要其上、下两端的接触力F t 和F b 均大于0 N,就表明该时刻定、转子之间紧密接触,即不发生泄漏;同时,接触力不为0 N的接触带越长,密封越可靠.螺杆马达的密封腔除了要保证密封的可靠性外,还须保证密封的稳定性.在螺杆马达密封腔的推移过程中,接触力是动态变化的,接触力波动越小,说明接触越稳定,即密封腔的稳定性越好.通过仿真分析发现,在通入流体的初始阶段,由于流场紊乱,接触带的接触情况存在波动,故本文将密封腔向下推移0.15个导程时的接触力与初始时刻接触力的差值的平均值及均方差作为密封腔稳定性的量化评价指标. ...
螺杆马达啮合仿真模型与应用研究
3
2016
... 螺杆马达的效率由机械效率和容积效率两部分组成.机械效率是衡量螺杆马达有效做功程度的指标,机械效率越高,说明螺杆马达在较大负载工况下的扭矩输出越稳定.较高的机械效率是螺杆钻具设计者所追求的目标之一.但在实际应用中,任何一种机械能输出装置都存在一定的输出损耗.螺杆马达的扭矩损耗主要由以下几部分组成:因转子行星运动而产生的橡胶形变所造成的扭矩消耗,钻井液黏性剪切力所造成的扭矩消耗,定、转子之间的摩擦作用所引起的扭矩损失以及因钻井液压差作用而产生的径向载荷所引起的扭矩损失等.由于螺杆马达是负载决定输出的容积式机械,当已知加载的恒定负载扭矩M L 时,通过计算理论输出扭矩M T 即可得到机械效率[16 ] .螺杆马达机械效率η m 的计算式如下: ...
... 本文采用不可压缩流体模型与速度流场边界[17 ] 对螺杆马达的容积效率进行仿真计算.在仿真过程中,给定螺杆马达的流量Q ,已知螺杆马达的每转排量q ,利用式(3) 计算得到螺杆马达的理论转速n T . 螺杆马达的实际转速采取如下方式获得:追踪图1 (a)所示仿真模型中螺杆马达转子中心节点1的位移,并输出其时间历程曲线,如图1 (b)所示;通过计算相同工况下相邻波峰与波谷之间的时间长度来计算螺杆马达的实际转速.令相邻波峰与波谷之间的时间间隔为t 0 N ,则螺杆马达的实际转速如式(4) 所示,结合式(2) 即可计算得到螺杆马达的容积效率[16 ] ,如式(5) 所示. ...
... 一个性能优异的螺杆马达在满足理论密封[16 ] 的同时,还必须保证其密封腔的可靠性与稳定性.螺杆马达的密封腔及其受力情况如图2 所示.由图可以看出,螺杆马达内含有多个螺旋状密封腔,相邻密封腔之间被由定、转子形成的接触带隔离开;一个完整的密封腔包含上、下2条接触带.目前应用广泛的密封接触理论[18 ] 认为:当一条接触带左右两端充满液体且压力分别为p 1 、p 2 时,只要其上、下两端的接触力F t 和F b 均大于0 N,就表明该时刻定、转子之间紧密接触,即不发生泄漏;同时,接触力不为0 N的接触带越长,密封越可靠.螺杆马达的密封腔除了要保证密封的可靠性外,还须保证密封的稳定性.在螺杆马达密封腔的推移过程中,接触力是动态变化的,接触力波动越小,说明接触越稳定,即密封腔的稳定性越好.通过仿真分析发现,在通入流体的初始阶段,由于流场紊乱,接触带的接触情况存在波动,故本文将密封腔向下推移0.15个导程时的接触力与初始时刻接触力的差值的平均值及均方差作为密封腔稳定性的量化评价指标. ...
不可压缩流体流动及其耦合问题的时空有限元算法
1
2021
... 本文采用不可压缩流体模型与速度流场边界[17 ] 对螺杆马达的容积效率进行仿真计算.在仿真过程中,给定螺杆马达的流量Q ,已知螺杆马达的每转排量q ,利用式(3) 计算得到螺杆马达的理论转速n T . 螺杆马达的实际转速采取如下方式获得:追踪图1 (a)所示仿真模型中螺杆马达转子中心节点1的位移,并输出其时间历程曲线,如图1 (b)所示;通过计算相同工况下相邻波峰与波谷之间的时间长度来计算螺杆马达的实际转速.令相邻波峰与波谷之间的时间间隔为t 0 N ,则螺杆马达的实际转速如式(4) 所示,结合式(2) 即可计算得到螺杆马达的容积效率[16 ] ,如式(5) 所示. ...
不可压缩流体流动及其耦合问题的时空有限元算法
1
2021
... 本文采用不可压缩流体模型与速度流场边界[17 ] 对螺杆马达的容积效率进行仿真计算.在仿真过程中,给定螺杆马达的流量Q ,已知螺杆马达的每转排量q ,利用式(3) 计算得到螺杆马达的理论转速n T . 螺杆马达的实际转速采取如下方式获得:追踪图1 (a)所示仿真模型中螺杆马达转子中心节点1的位移,并输出其时间历程曲线,如图1 (b)所示;通过计算相同工况下相邻波峰与波谷之间的时间长度来计算螺杆马达的实际转速.令相邻波峰与波谷之间的时间间隔为t 0 N ,则螺杆马达的实际转速如式(4) 所示,结合式(2) 即可计算得到螺杆马达的容积效率[16 ] ,如式(5) 所示. ...
基于流固耦合的螺杆马达动态仿真
2
2017
... 一个性能优异的螺杆马达在满足理论密封[16 ] 的同时,还必须保证其密封腔的可靠性与稳定性.螺杆马达的密封腔及其受力情况如图2 所示.由图可以看出,螺杆马达内含有多个螺旋状密封腔,相邻密封腔之间被由定、转子形成的接触带隔离开;一个完整的密封腔包含上、下2条接触带.目前应用广泛的密封接触理论[18 ] 认为:当一条接触带左右两端充满液体且压力分别为p 1 、p 2 时,只要其上、下两端的接触力F t 和F b 均大于0 N,就表明该时刻定、转子之间紧密接触,即不发生泄漏;同时,接触力不为0 N的接触带越长,密封越可靠.螺杆马达的密封腔除了要保证密封的可靠性外,还须保证密封的稳定性.在螺杆马达密封腔的推移过程中,接触力是动态变化的,接触力波动越小,说明接触越稳定,即密封腔的稳定性越好.通过仿真分析发现,在通入流体的初始阶段,由于流场紊乱,接触带的接触情况存在波动,故本文将密封腔向下推移0.15个导程时的接触力与初始时刻接触力的差值的平均值及均方差作为密封腔稳定性的量化评价指标. ...
... 螺杆马达在井下有多种失效形式,其中最多见的是定、转子之间的磨损失效[18 -19 ] .过大的接触力会加剧螺杆马达定、转子之间的磨损,导致接触情况较差,而过小的接触力又可能会导致密封腔的密封性能下降.因此,在保证螺杆马达转子齿顶和齿根的良好密封性能的前提下,应尽可能减小其密封腔接触带的接触力,以提高耐磨损能力.为了兼顾螺杆马达密封腔的良好密封性能和接触可靠性,提出了一种类圆弧线型螺杆马达,其截面线型如图6 所示.该截面线型是以短幅内摆线转子骨线为基准,分别用椭圆弧、圆弧代替短幅内摆线转子齿顶、齿根的等距曲线. ...
基于流固耦合的螺杆马达动态仿真
2
2017
... 一个性能优异的螺杆马达在满足理论密封[16 ] 的同时,还必须保证其密封腔的可靠性与稳定性.螺杆马达的密封腔及其受力情况如图2 所示.由图可以看出,螺杆马达内含有多个螺旋状密封腔,相邻密封腔之间被由定、转子形成的接触带隔离开;一个完整的密封腔包含上、下2条接触带.目前应用广泛的密封接触理论[18 ] 认为:当一条接触带左右两端充满液体且压力分别为p 1 、p 2 时,只要其上、下两端的接触力F t 和F b 均大于0 N,就表明该时刻定、转子之间紧密接触,即不发生泄漏;同时,接触力不为0 N的接触带越长,密封越可靠.螺杆马达的密封腔除了要保证密封的可靠性外,还须保证密封的稳定性.在螺杆马达密封腔的推移过程中,接触力是动态变化的,接触力波动越小,说明接触越稳定,即密封腔的稳定性越好.通过仿真分析发现,在通入流体的初始阶段,由于流场紊乱,接触带的接触情况存在波动,故本文将密封腔向下推移0.15个导程时的接触力与初始时刻接触力的差值的平均值及均方差作为密封腔稳定性的量化评价指标. ...
... 螺杆马达在井下有多种失效形式,其中最多见的是定、转子之间的磨损失效[18 -19 ] .过大的接触力会加剧螺杆马达定、转子之间的磨损,导致接触情况较差,而过小的接触力又可能会导致密封腔的密封性能下降.因此,在保证螺杆马达转子齿顶和齿根的良好密封性能的前提下,应尽可能减小其密封腔接触带的接触力,以提高耐磨损能力.为了兼顾螺杆马达密封腔的良好密封性能和接触可靠性,提出了一种类圆弧线型螺杆马达,其截面线型如图6 所示.该截面线型是以短幅内摆线转子骨线为基准,分别用椭圆弧、圆弧代替短幅内摆线转子齿顶、齿根的等距曲线. ...
螺杆马达流固耦合动态仿真及正交数值试验研究
2
2019
... 为分析短幅内摆线螺杆马达的工作性能,基于流固耦合方法建立其三维有限元模型[19 -22 ] ,如图4 所示.其中:转子材料采用镀铬合金,在建模过程中将其视为刚体;定子材料采用硬度为85,橡胶本构参数C 01 =2.23 MPa、C 10 =-0.03 MPa的丁晴橡胶.在螺杆马达实际工作过程中,转子在自转的同时绕定子中心作行星运动,故在仿真过程中,约束定子的所有自由度,约束转子的轴向自由度;将仿真时长设为0.5 s.为模拟螺杆马达在不同工况下的工作性能,在第0.18,0.26,0.34,0.42秒时分别对其施加200,400,600,800 N·m的负载扭矩. ...
... 螺杆马达在井下有多种失效形式,其中最多见的是定、转子之间的磨损失效[18 -19 ] .过大的接触力会加剧螺杆马达定、转子之间的磨损,导致接触情况较差,而过小的接触力又可能会导致密封腔的密封性能下降.因此,在保证螺杆马达转子齿顶和齿根的良好密封性能的前提下,应尽可能减小其密封腔接触带的接触力,以提高耐磨损能力.为了兼顾螺杆马达密封腔的良好密封性能和接触可靠性,提出了一种类圆弧线型螺杆马达,其截面线型如图6 所示.该截面线型是以短幅内摆线转子骨线为基准,分别用椭圆弧、圆弧代替短幅内摆线转子齿顶、齿根的等距曲线. ...
螺杆马达流固耦合动态仿真及正交数值试验研究
2
2019
... 为分析短幅内摆线螺杆马达的工作性能,基于流固耦合方法建立其三维有限元模型[19 -22 ] ,如图4 所示.其中:转子材料采用镀铬合金,在建模过程中将其视为刚体;定子材料采用硬度为85,橡胶本构参数C 01 =2.23 MPa、C 10 =-0.03 MPa的丁晴橡胶.在螺杆马达实际工作过程中,转子在自转的同时绕定子中心作行星运动,故在仿真过程中,约束定子的所有自由度,约束转子的轴向自由度;将仿真时长设为0.5 s.为模拟螺杆马达在不同工况下的工作性能,在第0.18,0.26,0.34,0.42秒时分别对其施加200,400,600,800 N·m的负载扭矩. ...
... 螺杆马达在井下有多种失效形式,其中最多见的是定、转子之间的磨损失效[18 -19 ] .过大的接触力会加剧螺杆马达定、转子之间的磨损,导致接触情况较差,而过小的接触力又可能会导致密封腔的密封性能下降.因此,在保证螺杆马达转子齿顶和齿根的良好密封性能的前提下,应尽可能减小其密封腔接触带的接触力,以提高耐磨损能力.为了兼顾螺杆马达密封腔的良好密封性能和接触可靠性,提出了一种类圆弧线型螺杆马达,其截面线型如图6 所示.该截面线型是以短幅内摆线转子骨线为基准,分别用椭圆弧、圆弧代替短幅内摆线转子齿顶、齿根的等距曲线. ...
螺杆马达(PDM)流-固耦合动态仿真
0
2013
螺杆马达(PDM)流-固耦合动态仿真
0
2013
3
2000
... 为分析短幅内摆线螺杆马达的工作性能,基于流固耦合方法建立其三维有限元模型[19 -22 ] ,如图4 所示.其中:转子材料采用镀铬合金,在建模过程中将其视为刚体;定子材料采用硬度为85,橡胶本构参数C 01 =2.23 MPa、C 10 =-0.03 MPa的丁晴橡胶.在螺杆马达实际工作过程中,转子在自转的同时绕定子中心作行星运动,故在仿真过程中,约束定子的所有自由度,约束转子的轴向自由度;将仿真时长设为0.5 s.为模拟螺杆马达在不同工况下的工作性能,在第0.18,0.26,0.34,0.42秒时分别对其施加200,400,600,800 N·m的负载扭矩. ...
... 不同负载扭矩下短幅内摆线螺杆马达工作性能的仿真结果如表2 所示.通过分析表2 仿真结果可以发现,随着负载扭矩的增大,短幅内摆线螺杆马达的实际转速并没有大幅度下降,说明该螺杆马达具有良好的转速硬特性[22 ] ;该螺杆马达出入口两端的压差呈现逐级递增的趋势,其容积效率相对稳定,但机械效率明显提高,总效率逐步提高,说明其具有良好的过载能力. ...
... 第二类椭圆积分[22 -23 ] 的标准形式为: ...
3
2000
... 为分析短幅内摆线螺杆马达的工作性能,基于流固耦合方法建立其三维有限元模型[19 -22 ] ,如图4 所示.其中:转子材料采用镀铬合金,在建模过程中将其视为刚体;定子材料采用硬度为85,橡胶本构参数C 01 =2.23 MPa、C 10 =-0.03 MPa的丁晴橡胶.在螺杆马达实际工作过程中,转子在自转的同时绕定子中心作行星运动,故在仿真过程中,约束定子的所有自由度,约束转子的轴向自由度;将仿真时长设为0.5 s.为模拟螺杆马达在不同工况下的工作性能,在第0.18,0.26,0.34,0.42秒时分别对其施加200,400,600,800 N·m的负载扭矩. ...
... 不同负载扭矩下短幅内摆线螺杆马达工作性能的仿真结果如表2 所示.通过分析表2 仿真结果可以发现,随着负载扭矩的增大,短幅内摆线螺杆马达的实际转速并没有大幅度下降,说明该螺杆马达具有良好的转速硬特性[22 ] ;该螺杆马达出入口两端的压差呈现逐级递增的趋势,其容积效率相对稳定,但机械效率明显提高,总效率逐步提高,说明其具有良好的过载能力. ...
... 第二类椭圆积分[22 -23 ] 的标准形式为: ...
1
1988
... 第二类椭圆积分[22 -23 ] 的标准形式为: ...
1
1988
... 第二类椭圆积分[22 -23 ] 的标准形式为: ...