超深水打桩锤系统的可靠性分析与分配研究

doi:10.3785/j.issn.1006-754X.2023.00.053

超深水打桩锤系统的可靠性分析与分配研究

李江昊^,^,¹, 肖文生¹, 于文太², 王鸿雁^,^,³, 刘顺庆², 孙友福¹

1.中国石油大学（华东）海洋物探及勘探开发装备国家工程研究中心，山东青岛 266555

2.海洋石油工程股份有限公司安装事业部，天津 300450

3.青岛科技大学机电工程学院，山东青岛 266061

Reliability analysis and allocation research of ultra-deep water pile hammer system

LI Jianghao^,^,¹, XIAO Wensheng¹, YU Wentai², WANG Hongyan^,^,³, LIU Shunqing², SUN Youfu¹

1.National Engineering Research Center for Marine Geophysical Prospecting and Exploration and Development Equipment, China University of Petroleum (East China), Qingdao 266555, China

2.Installation Division, Offshore Petroleum Engineering Co. , Ltd. , Tianjin 300450, China

3.School of Mechanical and Electrical Engineering, Qingdao University of Science and Technology, Qingdao 266061, China

通讯作者: 王鸿雁（1983—），女，山东青岛人，副教授，博士，从事海洋油气装备技术研究，E-mail: wanghy0546@163.com，https://orcid.org/0000-0001-9774-6690

收稿日期: 2023-02-01 修回日期: 2023-03-10

基金资助:

工业和信息化部高技术船舶科研项目. CH02N20

Received: 2023-02-01 Revised: 2023-03-10

作者简介 About authors

李江昊（1997—），男，山东济南人，硕士生，从事超深水打桩锤系统可靠性研究，E-mail:375359564@qq.com，https://orcid.org/0009-0007-6927-2177 , E-mail：375359564@qq.com

摘要

超深水打桩锤系统的性能直接影响大型海洋油气平台的建设进度。为深入研究超深水打桩锤系统的故障机理，对系统进行可靠性分析与分配研究。首先，对超深水打桩锤系统进行故障模式与影响分析（failure mode and effect analysis, FMEA），并基于FMEA结果提出了一种改进的危害性分析（criticality analysis, CA）方法。然后，运用改进的AGREE（advisory group on reliability of electronic equipment，电子设备可靠性咨询组）分配法及基于FMECA（failure mode, effect and criticality analysis，故障模式、影响与危害性分析）的可靠性分配方法，对超深水打桩锤系统的子系统和零部件依次进行可靠性分配研究。最后，在MATLAB App Designer开发环境下对超深水打桩锤系统的CA及可靠性分配过程进行可视化界面设计。结果表明，超深水打桩锤系统共有27种故障模式，钢桩等9个零部件为系统薄弱环节；经一、二次可靠性分配后，系统可靠度分别为0.999 063 22，0.999 063 27。超深水打桩锤系统的可靠性研究识别了系统的薄弱环节，为其国产化设计提供了一定的理论指导。

关键词： 超深水打桩锤系统 ; 故障模式、影响与危害性分析 ; AGREE分配法 ; 可靠性分配 ; 可视化界面

Abstract

The performance of ultra-deep water pile hammer system directly affects the construction progress of large offshore oil and gas platforms. In order to conduct in-depth research on the failure mechanism of ultra-deep water pile hammer system, the reliability analysis and allocation research for the system was carried out. Firstly, the failure mode and effect analysis (FMEA) was conducted on the ultra-deep water pile hammer system, and an improved criticality analysis (CA) method was proposed based on the FMEA results. Then, using the improved AGREE (advisory group on reliability of electronic equipment) allocation method and reliability allocation method based on FMECA (failure mode, effect and criticality analysis), the reliability allocation research was carried out successively for subsystems and components of the ultra-deep water pile hammer system. Finally, the visual interface of the CA and reliability allocation process of ultra-deep water pile hammer system was designed in the MATLAB App Designer development environment. The results showed that there were a total of 27 failure modes in the ultra-deep water pile hammer system, and 9 components such as steel piles were weak links in the system; the system reliability after primary and secondary reliability allocation was 0.999 063 22 and 0.999 063 27, respectively. The reliability study of the ultra-deep water pile hammer system has identified the weak links of the system, which can provide certain theoretical guidance for its domestic design.

Keywords： ultra-deep water pile hammer system ; failure mode, effect and criticality analysis ; AGREE allocation method ; reliability allocation ; visual interface

PDF (3572KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李江昊, 肖文生, 于文太, 王鸿雁, 刘顺庆, 孙友福. 超深水打桩锤系统的可靠性分析与分配研究. 工程设计学报[J], 2023, 30(4): 485-494 doi:10.3785/j.issn.1006-754X.2023.00.053

LI Jianghao, XIAO Wensheng, YU Wentai, WANG Hongyan, LIU Shunqing, SUN Youfu. Reliability analysis and allocation research of ultra-deep water pile hammer system. Chinese Journal of Engineering Design[J], 2023, 30(4): 485-494 doi:10.3785/j.issn.1006-754X.2023.00.053

随着陆上石油与天然气资源的短缺，我国逐步将油气资源的开发重心转移到南海领域。在开采海洋油气资源的过程中，须建造TLP（tension leg platform，张力腿平台）、FPSO（floating production storage and offloading，浮式生产储油船）等大型深海油气平台，这些平台需要通过海底锚或锚泊线固定在井口区域，而海底锚与锚泊线则需要超深水打桩锤系统将锚桩打入海床。

超深水打桩锤系统长期在高压、高腐蚀的恶劣海洋环境中工作，且在深海打桩作业中会产生巨大的打击能量，一旦发生故障，极易造成巨额经济损失、海洋生态环境严重污染等后果。在实际工程应用中，要求超深水打桩锤系统有极高的可靠性，因此对超深水打桩锤系统进行可靠性分析与分配研究是十分有必要的。毕宇^[1]对MENCK MHU系列液压锤锤体的减震环进行了故障分析，并改进了柱塞润滑性和密封性以及减震环充气阀的结构。Guo等人^[2]对液压打桩锤的主控阀进行了稳健型设计，提高了主控阀的可靠度及抗干扰能力。Luo等人^[3]将固定权重的故障模式、影响与危害性分析（failure mode，effect and criticality analysis, FMECA）与决策试验/评估实验室方法相结合，并将其应用于智能船舶定位系统的可靠性分析，为智能船舶定位系统的设备安全性设计提供了一定的参考。Kadir^[4]提出了一种基于层次分析法（analytic hierarchy process, AHP）和数据包络分析（data envelopment analysis, DEA）的混合可靠性分配方法，有效提高了舰载系统的可靠性，并通过舵机系统实例研究验证了AHP-DEA可靠性分配方法的适用性。吴红秋等人^[5]基于改进的AGREE（advisory group on reliability of electronic equipment，电子设备可靠性咨询组）分配法对航空发动机的静叶调节机构进行了可靠性分配，并验证了该分配方法的合理性。杨超等人^[6]基于可靠性模糊综合分配方法对船舰装备进行了可靠性分配，研究结果具有较好的工程实践指导意义。上述文献为超深水打桩锤系统及其零部件的可靠性分析奠定了一定的基础。

然而，目前国内外有关液压打桩锤的可靠性研究局限于液压打桩锤单个零部件的可靠性分析，缺乏对液压打桩锤整体的可靠性研究。此外，现有的系统可靠性研究方法虽比较成熟，但是缺乏针对超深水打桩锤系统的系统性可靠性研究。

为解决上述问题，笔者在综合考虑超深水打桩锤系统可靠性影响因素的基础上，采用改进的FMECA与多种可靠性分配法相结合的分析方法对该系统开展可靠性研究，旨在为其可靠性分配分析奠定研究基础。

1 超深水打桩锤系统

超深水打桩锤系统是一套包含机械、液压、控制和通信等关键技术的高集成深海工程装备，其结构精密且复杂程度极高，涉及机械工程学、地质学和液压动力学等多个学科。超深水打桩锤系统的主要作用是通过冲击将钢桩贯入海床，其应用场景如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 超深水打桩锤系统应用场景

Fig.1 Application scenario of ultra-deep water pile hammer system

综合考虑超深水打桩锤系统的结构和功能，将其划分为液压系统、气压系统、电控系统、机械系统和动力系统等5个子系统。各子系统的主要功能如下：

1）液压系统的主要功能为传递动力和运动，并在深海打桩作业的各个阶段实现能量转换。

2）气压系统作为辅助系统，可以减小锤芯的运动阻力，并实现桩锤的非触水打击。

3）电控系统作为中枢系统，能够利用中央控制系统的人机交互界面读取运行数据，并对整个超深水打桩锤系统进行实时控制，从而确保深水打桩作业的顺利进行。

4）机械系统的结构强度直接影响整个超深水打桩锤系统的可靠性，其主要应用于减震、传递动力、支承零部件并直接参与深水打桩作业。

5）动力系统作为能源系统，通过发电机组供电，经过一系列的能量传递及能量转换，最终为超深水打桩锤系统的平稳运行提供动力。

2 基于FMECA的超深水打桩锤系统分析

2.1　故障模式统计

FMECA是由故障模式与影响分析（failure mode and effect analysis, FMEA）和危害性分析（criticality analysis, CA）两部分组成的一种提高系统可靠性的设计分析方法，主要用于分析系统每一种故障模式的影响及危害性，并提出针对性的改进措施^[7-9]。

我国对陆用打桩锤的研究比较成熟，并在水下液压打桩锤应用领域也积累了丰富的作业经验。如：中国海洋石油集团有限公司在中国南海陵水17-2油气田开发项目中曾租赁MENCK超深水打桩锤系统；中机锻压江苏股份有限公司一直致力于液压打桩锤的研发。参考上述2家公司记录的超深水打桩锤系统的可靠性数据以及挪威船级社发布的第6版OREDA（offshore reliability data，海上设备可靠性数据）手册^[10]，统计该系统的常见故障模式，如表1所示。

表1 超深水打桩锤系统常见故障模式

Table 1 Common failure modes of ultra-deep water pile hammer system

故障模式	故障代号	故障模式	故障代号
泄漏（液体）	LK(LIQ)	振动/噪声	VIB/N
泄漏（气体）	LEAK(G)	控制/信号失效	CTRL/SIG F
输出不稳定	UO	高温/声音异常	HT/CAC
输入不稳定	UI	锈蚀	C
磨损	ABW	性能改变	CAPCHG
变形	Dept.	堵塞	PLU
裂纹	Crack	杂质过多	SI
松脱	S	摩擦	FRICT
断裂	FRF	动作异常	ABAC
疲劳失效	FF	线路异常	ABLN
短路	SC	功能失效	MPFF
断路	OC	不能满足工作需求	FTF
打开/锁紧失效	OPN/L F	其他轻微故障	OTHSLTFLT
综合因素/常见失效	COMF

新窗口打开| 下载CSV

结合表1以及超深水打桩锤系统的可靠性数据，统计并绘制其子系统故障模式的三维饼状图，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

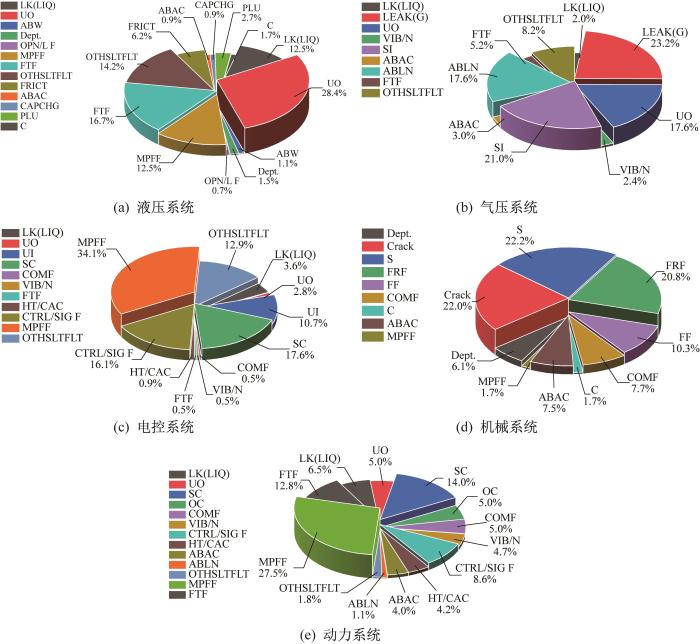
图2 超深水打桩锤系统故障模式统计结果

Fig.2 Statistical results of failure modes of ultra-deep water pile hammer system

2.2　故障模式与影响分析

FMEA是指对系统的子系统或零部件的故障模式及其可能产生的影响进行分析归纳，以便采取针对性的预防措施^[11]。采用故障严酷度来表示故障模式对系统影响的严重程度。基于Q/320621ZJ001—2019、GB/T 7826—2012和IEC 60812:2006，结合超深水打桩锤系统的基本结构和工作特性，制定FMEA的故障严酷度评价准则^[12]，如表2所示。

表2 超深水打桩锤系统故障严酷度评价准则

Table 2 Evaluation criteria for the severity of failures in ultra-deep water pile hammer system

严酷度等级	故障类型	分级标准
1	微小故障	系统功能稍有退化，对人员、财产、生态环境不构成危害，完成作业后检修、维护即可
2	临界故障	系统功能退化或作业误差较大，对人员、财产、生态环境不构成危害
3	较严重故障	系统短时间内停机，对人员、财产、生态环境构成较大危害
4	严重故障	系统丧失部分功能且长时间停机，对人员、财产、生态环境构成严重危害
5	灾难性故障	系统丧失功能，甚至造成机毁人亡、巨额财产损失及不可恢复的海洋环境污染

新窗口打开| 下载CSV

基于表2，对超深水打桩锤系统进行多因素故障模式分析，总结如下：整个系统共有30个主要零部件，99种故障模式，200种失效原因，针对各失效原因共提出192种处理方案或预防措施；故障严酷度为5级的故障模式有9种，4级的故障模式有15种，3级的故障模式有29种，2级的故障模式有29种，1级的故障模式有17种。

2.3　危害性分析

CA是指依据各故障模式的发生概率及严重程度等因素对系统的综合影响对各故障模式进行全面评价。鉴于故障模式危害度与产品危害度定量分析法的分析结果准确，且现有的超深水打桩锤系统可靠性数据较为丰富，本文采用故障模式危害度与产品危害度定量分析法对该系统进行危害度分析。传统的CA法针对故障模式危害度与产品危害度进行分析，两者的关系如下：

C_{r} = \sum_{i = 1}^{n} C_{m i} = \sum_{i = 1}^{n} λ_{p} α_{i} β_{i} t

(1)

式中：n为零部件在某一严酷度下的故障模式总数；C_r为零部件在某一严酷度下的危害度；C_m_i 为零部件第i种故障模式的危害度；λ_p为零部件各故障模式的发生率；α_i 为零部件第i种故障模式的发生率与零部件所有故障模式的发生率之和的百分比；β_i 为零部件第i种故障模式导致系统故障的条件概率，0≤β_i ≤1，任一故障模式的发生都会导致系统故障，因此β_i 均取1；t为零部件的平均工作时间。

传统CA法的分析结果为零部件在某一严酷度下的危害度，缺乏对零部件危害度的综合评价，即对零部件的可靠性分析比较片面。为解决上述问题，提出了一种以零部件危害度为分析目标的改进CA法，零部件危害度的计算公式如下：

C_{p} = \sum_{i = 1}^{k} C_{v i} = \sum_{i = 1}^{k} λ_{p} α_{i} β_{i} s_{i} t

(2)

式中：C_p为零部件的危害度；C_v_i 为改进后零部件第i种故障模式的危害度；k为零部件故障模式的总数；s_i 为零部件第i种故障模式的严酷度。

结合式(2)，通过MATLAB软件对超深水打桩锤系统的零部件进行危害度分析，结果如表3所示（由于包含所有数据的表格冗长，本文仅展示部分数据）。

表3 超深水打桩锤系统零部件危害度分析结果（部分）

Table 3 Criticality analysis results of components of ultra-deep water pile hammer system（part）

零部件	故障模式	λ_p/10^-6h^-1	α_i /%	s_i	t/h	C_p
电液换向阀	泄漏（液体）	0.03	0.74	3	43 800	0.481 500 089
	不能满足工作需求	0.58	14.29	3
	打开/锁紧失效	0.03	0.74	3
	高/低输出	3.30	81.28	4
	堵塞	0.12	2.96	4
其他液压阀组	异常磨损	0.20	6.83	3	43 800	0.236 231 488
	不能按需关闭	0.14	4.78	3
	不能满足工作需求	2.27	77.47	3
	打开/锁紧失效	0.10	3.41	2
	堵塞	0.22	7.51	3
液压缸	油管变形	0.16	4.36	2	70 080	0.201 032 214
	拉缸	1.15	31.34	3
	导向套锈蚀	0.15	4.09	2
	活塞杆不能动作	0.17	4.63	3
	缓冲装置故障	0.87	23.71	3
	外泄漏	1.17	31.88	3

新窗口打开| 下载CSV

结合表3可知，危害度较大的零部件依次是钢桩、锤头（锤芯）、砧铁、变压器、电液换向阀、锤芯悬吊单元、发电机组和液压泵等。针对危害度较大的零部件，应分别在研发设计、生产制造、投入使用前和投入使用等阶段采取优化结构、改善热处理工艺、制定风险紧急预案和重点防护并实时监测等措施来降低其危害度，从而提高超深水打桩锤系统的可靠性与可用度。

3 超深水打桩锤系统可靠性分配

3.1　可靠性分配基本理论

可靠性分配是指在工程规定的约束条件下，将系统的可靠性指标自上而下地依次分配给下级组成单元，直至确定各子系统、零部件的可靠性指标，同时保证整个系统的可靠性满足工程要求。可靠性分配的实质是对方程(3)进行求解^[13]：

\{\begin{matrix} R_{s} (R_{1}, R_{2}, \dots, R_{f}, \dots, R_{m}) \geq R_{s}^{*} \\ g_{r} (R_{1}, R_{2}, \dots, R_{f}, \dots, R_{m}) < g_{r}^{*} \end{matrix}

(3)

式中：R_s为实际的系统可靠性指标； $R_{s}^{*}$ 为规定的系统可靠性指标； $g_{r}^{}$ 为实际的系统可靠性约束条件； $g_{r}^{*}$ 为规定的系统可靠性约束条件，例如成本、体积和质量等限制因素。

可靠性分配方法较多，按照有无约束条件可以分为有约束分配法和无约束分配法。由于有约束分配法的操作难度较高，且超深水打桩锤系统的可靠性分配着重考虑系统可靠性，分析时可以忽略其他影响因素，因此本文采用无约束分配法对超深水打桩锤系统进行可靠性分配研究。

3.2　子系统可靠性分配

对超深水打桩锤系统进行故障树分析，得到系统可靠度为0.999 851 33，经可靠性维护后超深水打桩锤系统的稳态可用度已达0.999 914 34^[14]，且国内某型号水下液压打桩锤的无故障时间约为7 000 h。由于可靠性分配过程会受到分配方法、主观性等因素的干扰，因此初步设计超深水打桩锤系统的规定可靠度为0.999 8，不可靠度（即失效率）为0.000 2，且允许分配后的系统可靠度存在±0.1%的误差。

超深水打桩锤系统被划分为五大子系统，各子系统承担的功能不同，其复杂度和重要度也不尽相同。鉴于AGREE分配法的理论比较成熟，适用于常规复杂系统的可靠性分配，且该方法考虑了子系统的复杂度、重要度与系统失效的关系^[15]，本文采用AGREE分配法对超深水打桩锤系统的可靠性指标进行一次分配，具体如下：

R_{j} (t) = 1 - \frac{1 - {(R_{s} (t))}^{c_{j}}}{W_{j}}

(4)

其中：

\{\begin{matrix} c_{j} = \frac{n_{j}}{\sum_{j = 1}^{e} n_{j}} = \frac{n_{j}}{N} \\ W_{j} = \frac{N_{j}}{r_{j}} \end{matrix}

(5)

式中：R_j $(t)$ 为分配后第j个子系统的可靠度；R_s $(t)$ 为系统规定的可靠度；c_j 为第j个子系统的复杂度；W_j 为第j个子系统的重要度；n_j 为第j个子系统中零部件的数量；N为整个系统的关键零部件数量；e为子系统数量；N_j 为第j个子系统故障后引起系统发生故障的次数；r_j 为第j个子系统发生故障的次数。

对超深水打桩锤系统的5个子系统进行可靠性建模^[16]，其可靠性框图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 超深水打桩锤子系统可靠性框图

Fig.3 Reliability block diagram of ultra-deep water pile hammer subsystem

由图3可知，超深水打桩锤系统的各子系统均为串联关系，任一子系统发生故障均会导致系统故障^[17]。由式(5)可知，传统AGREE分配法将子系统的重要度定义为子系统发生故障后引起系统故障的次数与子系统发生故障的次数之比，因此各子系统的重要度均为1，失去了重要性对比的意义。而在实际应用工程中，子系统的重要度应考虑失效率、故障风险程度和平均工作时间等多重因素。为使基于AGREE分配法的可靠性分配结果更具有参考性，基于零部件的危害度分析结果对子系统的重要度进行修正，提出了一种改进的AGREE分配法，修正后的重要度表示为：

{W_{j}^{*}}^{2} = \frac{\sum_{v = 1}^{n_{j}} \sum_{i = 1}^{k} λ_{p} α_{i} β_{i} s_{i} t}{\sum_{v = 1}^{N} \sum_{i = 1}^{k} λ_{p} α_{i} β_{i} s_{i} t} = \frac{\sum_{v = 1}^{n_{j}} C_{p v}}{\sum_{v = 1}^{N} C_{p v}} = \frac{C_{θ j}}{\sum_{j = 1}^{e} C_{θ j}} = \frac{C_{θ j}}{C_{θ}}

(6)

式中： $W_{j}^{*}$ 为第j个子系统的修正重要度；C_p_v 为第v个零部件的危害度； $C_{θ j}$ 为第j个子系统的危害度； $C_{θ}$ 为整体系统的危害度。

传统AGREE分配法和改进AGREE分配法的各项基本参数如表4所示。

表4 AGREE分配法的基本参数

Table 4 Basic parameters of AGREE allocation method

子系统	零部件数量/个	复杂度	危害度	重要度
子系统	零部件数量/个	复杂度	危害度	传统方法	改进方法
合计	30	1	16.760 461 35
液压系统	7	0.233 3	1.211 855 80	1	0.268 894 85
气压系统	5	0.166 7	0.141 661 43	1	0.091 935 41
电控系统	7	0.233 3	1.217 747 68	1	0.269 547 73
机械系统	6	0.200 0	13.635 796 18	1	0.901 980 74
动力系统	5	0.166 7	0.553 400 26	1	0.181 709 11

新窗口打开| 下载CSV

根据式(4)至式(6)，对超深水打桩锤系统的可靠性指标进行分配，基于传统AGREE分配法和改进AGREE分配法的可靠性分配结果如表5所示。表中：可靠性分配的预计数据源自项目的合作单位及OREDA手册。

表5 超深水打桩锤子系统可靠性分配结果

Table 5 Reliability allocation results of ultra-deep water pile hammer subsystem

子系统	传统AGREE分配法		改进AGREE分配法		预计数据
子系统	可靠度	失效率	可靠度	失效率	可靠度	失效率
液压系统	0.999 953 33	0.000 046 67	0.999 826 44	0.000 173 56	0.999 981 400 2	0.000 018 599 8
气压系统	0.999 966 66	0.000 033 34	0.999 637 40	0.000 362 60	0.999 994 990 0	0.000 005 010 0
电控系统	0.999 953 33	0.000 046 67	0.999 826 86	0.000 173 14	0.999 974 890 3	0.000 025 109 7
机械系统	0.999 960 00	0.000 040 00	0.999 955 65	0.000 044 35	0.999 922 752 8	0.000 077 247 2
动力系统	0.999 966 66	0.000 033 34	0.999 816 54	0.000 183 46	0.999 977 290 2	0.000 022 709 8

新窗口打开| 下载CSV

为更加直观地比较传统AGREE分配法与改进AGREE分配法的优劣，对基于不同分配法得到的超深水打桩锤子系统的可靠度进行对比，结果如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基于不同AGREE分配法的超深水打桩锤子系统可靠度对比

Fig.4 Comparison of reliability of ultra-deep water pile hammer subsystem based on different AGREE allocation methods

根据表4、表5和图4，以动力系统与气压系统为例，动力系统与气压系统发生故障后对整个超深水打桩锤系统的危害性显然不同，故动力系统的可靠度不应与气压系统一致。但经传统AGREE分配法分配后两者的可靠度相同，并未体现子系统故障危害度的差异，违背了可靠性分配原则^[18]，而基于改进AGREE分配法的各子系统的可靠度均小于传统方法，经改进方法分配后超深水打桩锤系统的可靠度为0.999 063 22，失效率为0.000 936 78，与规定可靠度的相对误差为0.073 69%，在允许的分配误差范围内。改进AGREE分配法在满足系统初步设计的可靠性指标前提下在一定范围内降低了系统可靠度，这在一定程度上降低了超深水打桩锤系统的研制成本。此外，改进AGREE分配法考虑了子系统的工作时间、危害度等影响因素，使子系统的可靠性分配结果更具有合理性，可为超深水打桩锤系统的国产化研发设计提供一定的理论指导。

3.3　零部件可靠性分配

在超深水打桩锤系统的运行过程中，若某子系统中的任一关键零部件失效（规定功能无法实现），则可认为该子系统失效，进而导致整个系统失效。因此，考虑到整个超深水打桩锤系统的安全性，须对系统中各关键零部件的可靠性指标进行科学分配，并根据分配结果对系统进行国产化设计。

由可靠性分配原则可知，在实际工程应用中对零部件进行可靠性分配时，应综合考虑零部件的工作时间、维修时间和危害度等有关因素。传统的基于故障树的可靠性分配法针对不同层级的事件采用不同的可靠性分配方法^[19]，故障树分析中的次级、中级事件一般为系统的组成零部件。而AHP则考虑了零部件的故障发生率、危害度、维修性等关键影响因素，通过归一化后权重向量对次级、中级事件进行可靠性分配。鉴于AHP与CA法的影响因素基本一致，参考基于AHP的可靠性分配方法，提出了一种基于FMECA的可靠性分配方法，为复杂系统关键零部件的可靠性分配提供了一种新的思路，具体分配方式如下：

P_{j v} = \frac{P_{j} / ω_{j v}}{\sum_{v = 1}^{n_{j}} (1 / ω_{j v})}

(7)

其中：

ω_{j} = [\frac{C_{p 1}}{\sum_{v = 1}^{n_{j}} C_{p v}} \dots \frac{C_{p v}}{\sum_{v = 1}^{n_{j}} C_{p v}} \dots \frac{C_{p n_{j}}}{\sum_{v = 1}^{n_{j}} C_{p v}}]

式中：P_j 为第j个子系统的失效率；P_jv 为第j个子系统中第v个零部件的失效率；ω_jv 为归一化处理后第j个子系统中第v个零部件相对该子系统的权重； ω_j 为归一化处理后第j个子系统中各零部件相对该子系统的权重向量。

基于对超深水打桩锤系统的危害度分析，利用式(7)计算得到其子系统中各关键零部件的可靠性指标，如表6所示。

表6 超深水打桩锤系统零部件可靠性分配结果

Table 6 Reliability allocation results of components of ultra-deep water pile hammer system

子系统	零部件	危害度	权重	失效率	可靠度
液压系统	电液换向阀	0.481 500 089	0.397 324 572	0.000 000 57	0.999 999 43
	其他阀组	0.236 231 488	0.194 933 661	0.000 001 16	0.999 998 84
	液压缸	0.201 032 214	0.165 887 900	0.000 001 36	0.999 998 64
	液压泵	0.274 127 586	0.226 204 789	0.000 001 00	0.999 999 00
	液压油	0.002 978 400	0.002 457 718	0.000 091 89	0.999 908 11
	油箱	0.010 730 027	0.008 854 211	0.000 025 51	0.999 974 49
	蓄能器	0.005 256 000	0.004 337 150	0.000 052 07	0.999 947 93
气压系统	空压机	0.077 528 475	0.547 280 069	0.000 004 63	0.999 995 37
	空气过滤器	0.004 077 639	0.028 784 399	0.000 087 95	0.999 912 05
	油雾器	0.002 340 492	0.016 521 731	0.000 153 23	0.999 846 77
	油压缓冲器	0.003 253 714	0.022 968 243	0.000 110 22	0.999 889 78
	气动阀组	0.054 461 106	0.384 445 558	0.000 006 58	0.999 993 42
电控系统	变压器	0.754 532 522	0.619 613 190	0.000 001 60	0.999 998 40
	可编程逻辑控制器	0.116 946 000	0.096 034 673	0.000 010 35	0.999 989 65
	以太网交换机	0.100 740 000	0.082 726 498	0.000 012 01	0.999 987 99
	断路器	0.031 536 000	0.025 896 991	0.000 038 37	0.999 961 63
	继电器	0.019 146 702	0.015 723 045	0.000 063 20	0.999 936 80
	电磁先导阀	0.030 044 091	0.024 671 852	0.000 040 27	0.999 959 73
	各类传感器	0.164 802 360	0.135 333 750	0.000 007 34	0.999 992 66
机械系统	锤头（锤芯）	1.199 456 633	0.088 258 652	0.000 001 15	0.999 998 85
	砧铁	1.035 610 776	0.076 202 514	0.000 001 34	0.999 998 66
	钢桩	10.737 918 915	0.790 119 645	0.000 000 13	0.999 999 87
	桩帽	0.166 440 000	0.012 247 021	0.000 008 31	0.999 991 69
	锤芯悬吊单元	0.450 817 858	0.033 172 168	0.000 003 07	0.999 996 93
	减震环	0.045 552 000	0.076 052 806	0.000 030 36	0.999 969 64
动力系统	深水电机	0.109 965 513	0.183 596 458	0.000 021 23	0.999 978 77
	压力补偿器	0.030 222 000	0.050 458 112	0.000 077 24	0.999 922 76
	绞车	0.075 435 340	0.125 945 498	0.000 030 94	0.999 969 06
	动态脐带缆	0.050 840 595	0.084 882 550	0.000 045 91	0.999 954 09
	发电机组	0.286 936 809	0.479 064 576	0.000 008 14	0.999 991 86

新窗口打开| 下载CSV

分析表6可得，二次分配后超深水打桩锤系统的可靠度为0.999 063 27，失效率为0.000 936 73，与规定可靠度的相对误差为0.073 68%，在允许的分配误差范围内；钢桩、电液换向阀、液压泵、其他阀组、锤头（锤芯）、砧铁等零部件被分配的可靠度较高，验证了前文超深水打桩锤系统的FMECA结论。在超深水打桩锤系统的早期研发阶段，应对上述关键零部件进行更为可靠的结构设计，确保从源头上降低系统失效风险。

综上，基于FMECA对超深水打桩锤系统的零部件进行可靠性分配，确保危害度较高的零部件能够被分配到较高的可靠度，符合可靠性分配原则。实际算例验证了所提出方法的可行性，可为其他复杂系统的零部件可靠性分配提供一定的借鉴。

3.4　可视化界面设计

为实现超深水打桩锤系统的CA和可靠性分配过程的直观、简洁展示，基于人机交互技术，在MATLAB App Designer开发环境下设计可视化界面^[20-21]，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

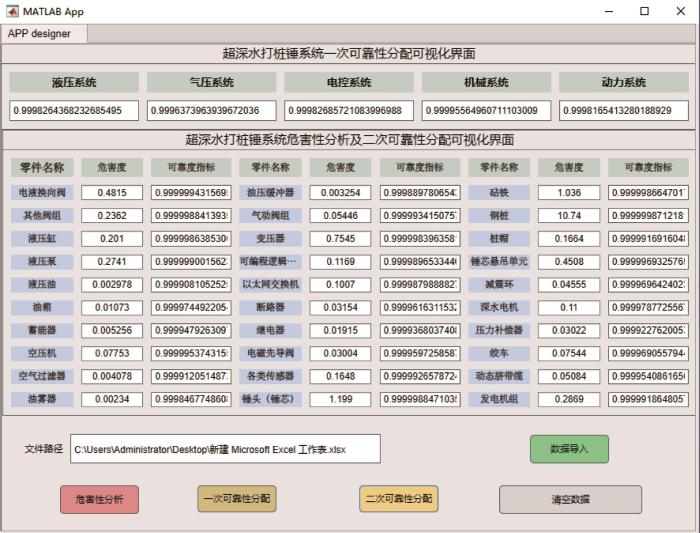
图5 超深水打桩锤系统的CA及可靠性分配可视化界面

Fig.5 Visual interface for CA and reliability allocation of ultra-deep water pile hammer system

超深水打桩锤系统的CA及可靠性分配可视化界面主要包含数据导入模块、CA模块、一次可靠性分配模块和二次可靠性分配模块等。数据导入模块的功能是读取CA所需的各项基本数据；CA模块的功能是对系统零部件进行危害度分析；一次可靠性分配模块的功能是基于AGREE分配法对子系统进行可靠性分配；二次可靠性分配模块的功能是基于FMECA结果对系统零部件进行可靠性分配。

4 结束语

基于改进的FMECA，结合多种可靠性分配方法对超深水打桩锤系统进行了可靠性研究，并在MATLAB App Designer开发环境下开发了可视化界面，现总结如下。

1）针对超深水打桩锤系统进行了FMECA，统计了其各个子系统的潜在故障模式并绘制了三维饼状图。通过利用改进的CA法对系统进行定量分析得到：钢桩、锤头（锤芯）和砧铁等9个零部件的危害度较大。同时，确定了各零部件故障对超深水打桩锤系统的影响程度，为系统零部件的可靠性优化设计提供了方向。

2）建立了超深水打桩锤子系统的可靠性框图，并基于改进的AGREE分配法对子系统进行可靠性分配，一次分配后整个系统的可靠度为0.999 063 22；综合考虑失效率、维修时间等影响因素，基于FMECA结果将子系统的可靠性指标分配给各零部件，二次分配后整个系统的可靠度为0.999 063 27。结果表明：钢桩、电液换向阀等零部件被分配的可靠度较高，与超深水打桩锤系统的CA结果一致。

3）基于人机交互技术，在MATLAB App Designer开发环境下对超深水打桩锤系统的CA及可靠性分配过程进行了可视化界面设计。

在后续研究中，将针对超深水打桩锤系统风险度较高的零部件进行可靠性优化设计，以期提高整体系统的可靠度及稳态可用度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

毕宇

海上风电单桩施工液压锤减震环故障分析及改进措施

［J］.船舶工程，2021，43（）：87-89，100.