进给系统热变形对机床运动重复性误差的影响研究

doi:10.3785/j.issn.1006-754X.2023.00.055

进给系统热变形对机床运动重复性误差的影响研究

孙光明^,^,¹^,², 杨景景¹, 陈思奇¹, 赵坚^,^,¹, 张贺帅²

1.天津城建大学控制与机械工程学院，天津 300384

2.天津大学机构理论与装备设计教育部重点实验室，天津 300072

Research on the effect of thermal deformation of feed system on the motion repeatability errors of machine tool

SUN Guangming^,^,¹^,², YANG Jingjing¹, CHEN Siqi¹, ZHAO Jian^,^,¹, ZHANG Heshuai²

1.School of Control and Mechanical Engineering, Tianjin Chengjian University, Tianjin 300384, China

2.Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education, Tianjin University, Tianjin 300072, China

通讯作者: 赵坚（1966—），女，山西太原人，教授，博士，从事机电系统一体化设计、机械创新设计和智能制造等研究，E-mail: zhaojiantcu@163.com, https://orcid.org/0000-0001-5966-0917

收稿日期: 2023-03-03 修回日期: 2023-03-31

基金资助:

天津市自然科学基金青年项目. 22JCQNJC01000
天津市企业科技特派员项目. 22YDTPJC00260

Received: 2023-03-03 Revised: 2023-03-31

作者简介 About authors

孙光明（1987—），男，河南驻马店人，讲师，博士，从事精密机床误差测量、分析与补偿技术研究，E-mail:gmsun@tju.edu.cn,https://orcid.org/0000-0002-0961-9964 , E-mail：gmsun@tju.edu.cn

摘要

为了分析进给系统热变形对机床运动重复性误差的影响，提出了一种基于分层模型-移动热源的进给系统热变形建模方法。将进给系统分为丝杠层和工作台层，将移动结合面等效为弹簧。采用实体单元和接触单元建立了有限元模型，在丝杠和导轨上施加移动热源，获得进给系统的温度场和热变形。在此基础上，分析了工作台进给速度、轴承预紧力矩和滑块支撑距离对机床运动重复性误差的影响，并进行了实验验证。研究表明，工作台进给速度和轴承预紧力距对机床运动重复性误差的影响较大，滑块支撑距离对机床运动重复性误差的影响较小。研究结果为在机床设计和装配中减小机床运动重复性误差提供了依据。

关键词： 进给系统 ; 热变形 ; 移动热载荷 ; 运动重复性误差

Abstract

In order to analyze the effect of thermal deformation of feed system on the motion repeatability errors of machine tool, a modeling method for thermal deformation of feed system based on a layered model-moving heat source was proposed. The feed system was divided into a screw layer and worktable layer, and the moving joint surface was equivalent to a spring. The finite element model was established by using solid element and contact element. The temperature field and thermal deformation of the feed system were obtained by applying moving heat source to the screw and guide rail. On this basis, the effect of worktable feed speed, bearing preload torque, and slider support distance on the motion repeatability errors of machine tool was analyzed and verified by experiments. The research showed that the worktable feed speed and bearing preload torque had a significant impact on the motion repeatability errors of machine tool, while the slider support distance had a relatively small impact on the motion repeatability errors of machine tool. The research results provide a basis for reducing the motion repeatability errors of machine tool in machine tool design and assembly.

Keywords： feed system ; thermal deformation ; move thermal load ; motion repeatability error

PDF (8499KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙光明, 杨景景, 陈思奇, 赵坚, 张贺帅. 进给系统热变形对机床运动重复性误差的影响研究. 工程设计学报[J], 2023, 30(4): 456-466 doi:10.3785/j.issn.1006-754X.2023.00.055

SUN Guangming, YANG Jingjing, CHEN Siqi, ZHAO Jian, ZHANG Heshuai. Research on the effect of thermal deformation of feed system on the motion repeatability errors of machine tool. Chinese Journal of Engineering Design[J], 2023, 30(4): 456-466 doi:10.3785/j.issn.1006-754X.2023.00.055

运动重复性误差影响着机床的加工精度和零件加工的一致性。它属于不可补偿误差，无法用误差补偿来进行抑制，只能通过装配误差的控制、装配精度的提高来达到抑制的目的。Sun等^[1]系统地分析了机床重复定位误差的影响因素，定性地研究了导轨装配误差、丝杠装配误差、滚珠丝杠预紧力、滑块间距等7个因素对重复定位误差的影响规律，研究结果表明，导轨装配误差和滚珠丝杠预紧力对重复定位误差有着显著影响。Cho等^[2]分析了偏摆角误差对机床运动重复性误差的影响，提出通过减小偏摆角误差来减小重复性误差。然而，以上研究均未涉及机床热变形对其运动重复性误差影响的分析。

机床热变形引起的机床误差可占机床总误差的70%^[3]。研究人员采用了多种技术模拟机床热特性来分析热变形对定位误差的影响。这些技术分为基于经验和基于原理两类。基于经验的模型主要用来研究机床热误差的补偿，采用算法建立热误差与测点温度之间的关系。多元回归法^[4-5]、神经网络算法^[6-8]、灰色模型优化算法^[9-10]和支持向量机^[11-12]等在机床热误差分析与建模中具有良好的应用。冯文龙等^[13]提出了一种基于热特性分析的误差建模方法，提高了数控机床的加工精度，误差补偿后机床的定位精度提高了90%以上。基于原理的模型主要用来研究热误差预测，其研究的重点是如何在精确边界条件下得到精确的模型。Kim等^[14]利用双线性元的有限元方法分析了滚珠丝杠副的温度分布，并建立了有限元模型。张庆锋等^[15]利用ANSYS软件预测了机床热误差，分析了整机温度场、热变形，并验证了温度场仿真结果的可靠性。Gomez-Acedo等^[16]提出了一种利用有限元模型来分析大型机床热特性的方法。采用有限元分析方法进行电主轴热特性的研究也给技术人员带来了参考^[17-20]。

上述研究主要集中于热变形导致的定位误差的建模和补偿，对于热变形对运动重复性误差影响的研究较少。因此，本文提出了一种基于分层模型-移动热源加载方式的精密机床直线进给系统热误差建模方法，分析进给系统热变形对机床运动重复性误差的影响。

1 基于分层模型-移动热源的进给系统热变形仿真

1.1　进给系统分层模型

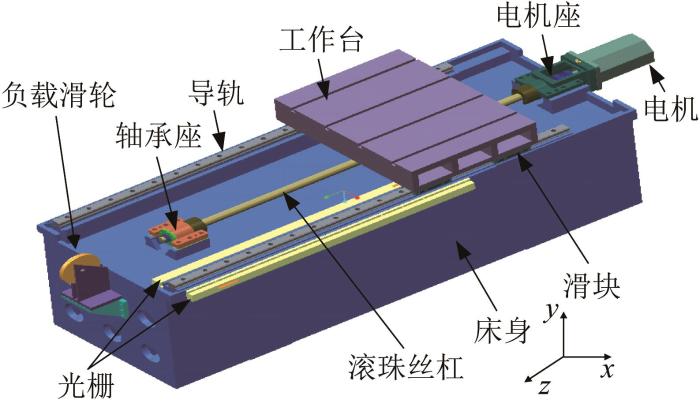
精密机床直线进给系统的结构如图1所示，其由床身、滚珠丝杠、导轨和工作台等组成。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 精密机床直线进给系统的结构

Fig.1 Structure of linear feed system of precision machine tool

将进给系统分层处理为丝杠层和工作台层，如图2所示。丝杠层主要包括滚珠丝杠、导轨、电机和轴承；工作台层主要包括工作台、滑块和螺母。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 进给系统分层模型

Fig.2 Layered model of feed system

1.2　进给系统有限元模型

进给系统存在2个移动结合面，分别是滚珠丝杠螺母副和导轨滑块副。为了精确模拟进给系统热变形，须对其进行等效刚度处理。

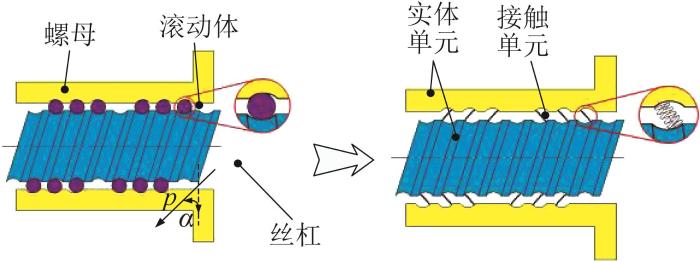
1）滚珠丝杠螺母副等效刚度处理。

滚珠丝杠螺母副等效刚度处理如图3所示。将滚珠丝杠螺母副离散成实体单元和接触单元，忽略滚珠质量，将其等效为弹簧，弹簧刚度为k_Ball，弹簧沿丝杠和螺母之间的共同接触线对齐布置。弹簧长度等于滚珠的直径。将滚珠等效为6列弹簧，每列含有4个弹簧，这4个弹簧在圆周方向均匀排列。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 滚珠丝杠螺母副等效刚度处理

Fig.3 Equivalent stiffness treatment of ball screw nut pair

2）导轨滑块副等效刚度处理。

导轨滑块副有限元模型如图4所示。将导轨与滑块之间的滚动体等效为弹簧，其中每排有26个弹簧。将等效弹簧单元的端点与滚道接触面建立耦合约束，并通过节点载荷施加在滚道面上。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 导轨滑块副有限元模型

Fig.4 Finite element model of guide rail slider pair

对进给系统的倒角、凹槽等部分进行简化，得到其有限元模型，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 进给系统有限元模型

Fig.5 Finite element model of feed system

1.3　机床热边界条件

受机床内部热源的影响，机床温度会发生变化，从而引起机床热变形^[21]。机床内部热源主要有进给系统的滚珠丝杠、导轨、电机、轴承、滑块和螺母，传热方式有热传导和热对流。在环境温度为20 ℃、进给速度为6 m/min、轴承预紧力矩为100 N∙m、滑块支撑距离为345 mm的工况下分析机床热边界条件，如表1所示。

表1 机床热边界条件分析

Table 1 Analysis of thermal boundary conditions for machine tool

边界条件	计算公式	字符意义	计算结果
轴承生热率q₁^[22]	$q_{1} = \frac{0.104 7 n_{1} (M_{1} + M_{2})}{V}$ $M_{1} = \{\begin{matrix} 10^{- 7} f_{0} {(v n)}^{\frac{2}{3}} d_{m}^{3} (v n_{1} > 2 000 m m^{2} / s \cdot r / m i n) \\ 160 \times 10^{- 7} f_{0} d_{m}^{3} (v n_{1} < 2 000 m m^{2} / s \cdot r / m i n) \end{matrix}$ $M_{2} = f_{1} F_{β} d_{m}$	n₁为轴承转速；M₁为轴承所受的黏性摩擦力矩；M₂为轴承所受的机械摩擦力矩；V为热源体积；ƒ₀为取决于润滑类型和轴承参数的常数；ν为润滑剂运动黏度；d_m为轴承中径；ƒ₁为与载荷和轴承结构相关的系数；F_β 为轴承摩擦力矩的计算载荷	1 510 520 W/m³
滚珠丝杠与螺母间的热流密度q₂^[23]	$q_{2} = \frac{0.104 7 n_{2} (0.94 M_{p} + M_{d})}{A_{2}}$ $M_{d} = \frac{F_{α} P_{h}}{2 π η_{1}} (1 - {η_{1}}^{2})$ $M_{p} = \frac{F_{p} P_{h}}{2 π η_{1}} (1 - {η_{1}}^{2})$	n₂为丝杠转速；M_p为滚珠螺旋阻力矩；M_d为驱动力矩；Α₂为丝杠与螺母的接触面积；F_α 为丝杠的轴向载荷；Ρ_h为丝杠的导程；η₁为丝杠的传动效率；F_p为丝杠的轴向预紧力	10 300 W/m²
电机热流密度q₃^[24]	$q_{3} = \frac{M_{t} \cdot n_{3}}{9 550 \cdot A_{3}} (1 - η_{2})$	M_t为电机输出扭矩；n₃为电机转速；η₂为电机机械效率；A₃为电机表面积	1 500 W/m²
导轨与滑块间的热流密度q₄^[24]	$q_{4} = \frac{μ W g v_{0}}{J \cdot A_{4}}$	μ为导轨与滑块间的动摩擦因数；W为施加在摩擦面上的力；g为重力加速度，取9.8 m/s²；J为热功当量，取4.2 J/cal；ν₀为滑动速度；A₄为导轨与滑块的摩擦面积	580 W/m²
自然对流换热系数 h₁^[25]	$h_{1} = \frac{N u \cdot κ}{L}$ $N u = C {(G r \cdot P r)}^{n}$ $G r = \frac{L^{3} g a_{v} Δ T}{v^{2}}$ $P r = \frac{c_{p} ρ v}{k}$	Nu为努塞尔数；κ为流体的热传导系数；L为定型尺寸；Gr为格拉晓夫数；Pr为普朗特系数；a_v为关于流体体积的膨胀系数；∆T为试验台表面与液体之间的温度差；c_p为流体的等压比热容；ρ为流体密度；C, n为常数，与液体的流动状态和发生导热表面的形状有关	轴承座表面、电机座表面： 55 W/（m²·℃）
强迫对流换热系数 h₂^[25]	$h_{2} = \frac{N u \cdot κ}{L}$ $N u = R e^{\frac{2}{3}} \cdot P r^{\frac{2}{3}} (R e < 4.3 \times 10^{5}, 0.7 < P r < 670)$ $R e = \frac{ω \times d_{0}}{v_{f}}$	Re为雷诺数；ω为角速度；d₀为公称直径；v_f为空气的运动黏度	丝杠螺母座表面： 230 W/（m²·℃）；丝杠表面： 650 W/（m²·℃）

新窗口打开| 下载CSV

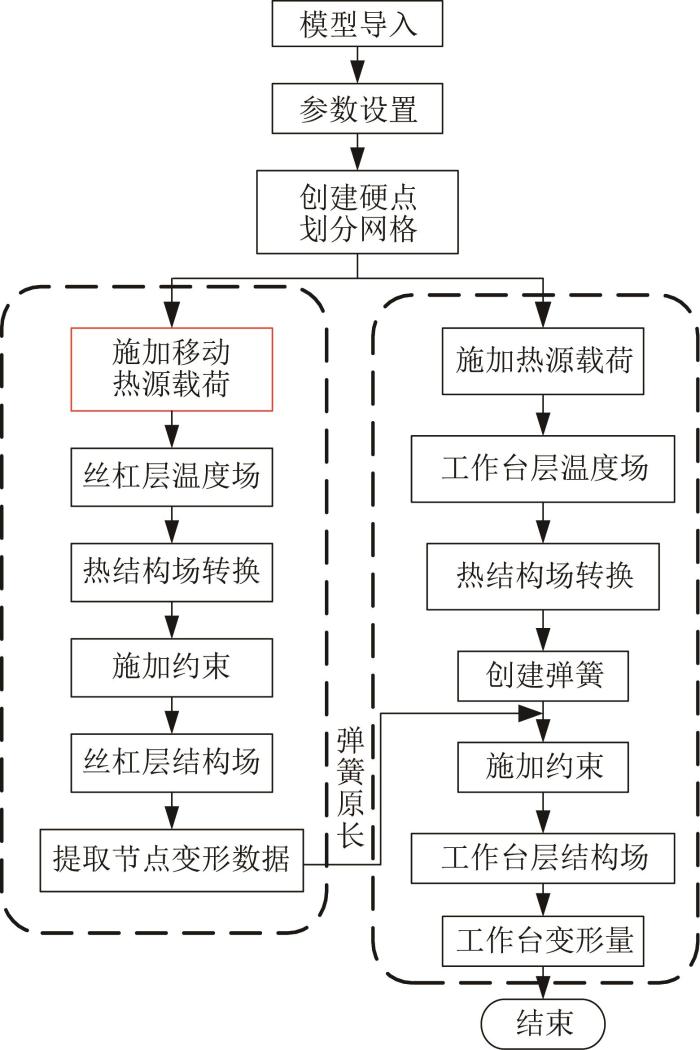
1.4　移动热源施加及分层仿真流程

在工作台作往复直线运动时，丝杠和滑块会发生空间位移。丝杠和滑块的移动会产生大量摩擦热，这些移动热源随着时间和空间的变化而变化，这给进给系统热变形的精确模拟带来了困难。将热边界条件中的热流密度当作载荷施加到仿真模拟中，可以获得热变形^[26]。运用ADPL（ANSYS parametric design language，ANSYS参数化设计语言）施加载荷，当丝杠和滑块每次移动时，将之前区域的热流密度移除，加载对流系数，而在当前区域处删除对流系数，加载移动热源的热流密度。

采用热-结构耦合的方法进行有限元仿真分析。采用丝杠层和工作台层分层仿真，在丝杠和导轨上施加移动热源，在轴承处施加固定热源。分层仿真流程如图6所示。首先仿真计算丝杠层中丝杠和导轨的热变形，其次提取弹簧位置的变形数据，最后将丝杠和导轨的热变形作为载荷用于工作台层的运动误差仿真中，提取其变形量，进行运动误差和运动重复性误差计算。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 基于分层-移动热源的进给系统分层仿真流程

Fig.6 Flow of layered simulation of feed system based on layered-moving heat source

1.5　有限元仿真结果

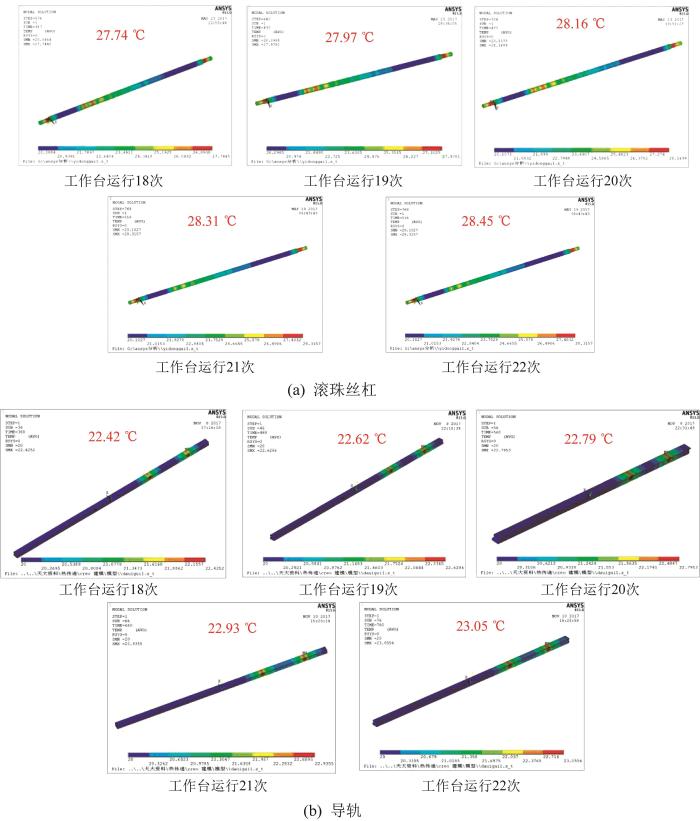
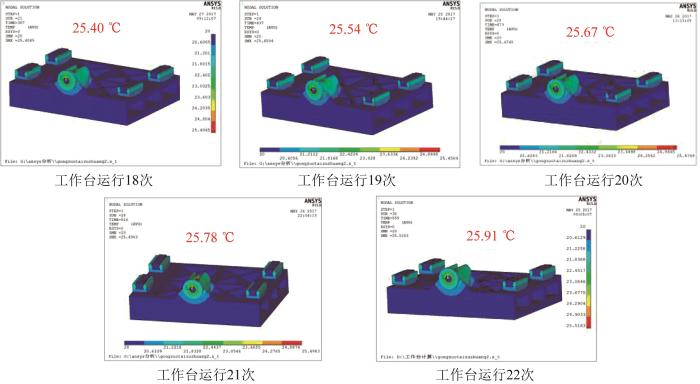
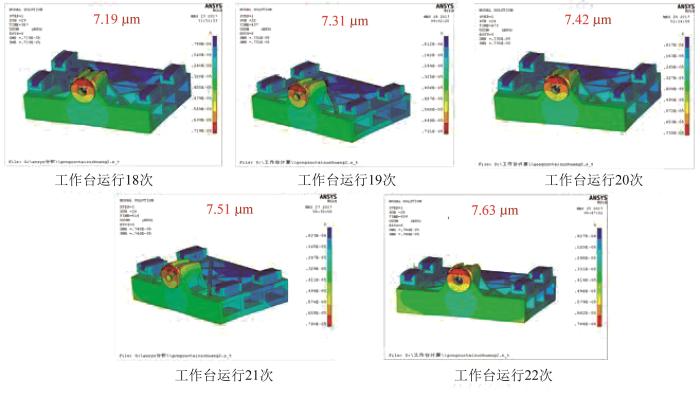
仿真时，工作台运行18~22次时进给系统的温度变化较大，引起的热变形变化较大，因此选取工作台运行18~22次时的结果进行分析。

丝杠层的温度场如图7所示。由图可知：工作台运行18次后，滚珠丝杠的最高温度为27.74 ℃，导轨的最高温度为22.42 ℃；运行22次后，丝杠最高温度上升了0.71 ℃，导轨最高温度上升了0.63 ℃。丝杠层的温度场、丝杠层的温度均随工作台运行次数的增加而变化。以温度场为基础开展结构场仿真，结果如图8所示。由图可知：丝杠和导轨的最大热变形随着工作台运行次数的增加而分别增加了1.08 μm和0.75 μm。这是因为工作台在运动时反复对丝杠和导轨进行摩擦，前一次摩擦产生的热量还未消散，再次的摩擦使摩擦位置的温度继续上升，热变形增大。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 丝杠层温度场

Fig.7 Temperature field of screw layer

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 丝杠层结构场

Fig.8 Structure field of screw layer

工作台的温度场如图9所示。由图可知：工作台的最高温度由运行18次时的25.40 ℃上升至22次时的25.91 ℃，温度随着其运行次数的增加而升高。工作台的结构场如图10所示。由图可知：其最大热变形由运行18次时的7.19 μm增加至22次时的7.63 μm，也随着工作台运行次数的增加而增大。工作台层的变形呈左右对称。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 工作台温度场

Fig.9 Temperature field of worktable

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 工作台结构场

Fig.10 Structure field of worktable

2 工作台运动重复性误差计算与分析

2.1　工作台运动误差计算

选取工作台表面的4个角和工作台中央共5个区域（P1至P5），分别在每个区域选取5个点来计算各个区域的运动误差。工作台运动误差包括3项移动误差和3项转角误差。工作台沿z向运动时，其运动误差为：

δ_{z} (z) = Δ z_{5}

(1)

δ_{y} (z) = \frac{(y_{2} + y_{4}) - (y_{1} + y_{3})}{2}

(2)

δ_{x} (z) = \frac{(x_{2} + x_{1}) - (x_{3} + x_{4})}{2}

(3)

ε_{z} (z) = \frac{(y_{2} + y_{4}) - (y_{1} + y_{3})}{2 L_{1}}

(4)

ε_{x} (z) = \frac{(y_{2} + y_{1}) - (y_{3} + y_{4})}{2 L_{2}}

(5)

ε_{y} (z) = \frac{(x_{3} + x_{4}) - (x_{2} + x_{1})}{2 L_{2}}

(6)

式中：δ_z (z)为线性位移误差；δ_y (z)为y向直线度误差；δ_x (z)为x向直线度误差；ε_z (z)为倾斜角误差；ε_x (z)为俯仰角误差；ε_y (z)为偏摆角误差；L₁为每个区域中点1与点2之间的距离；L₂为每个区域中点1与点3之间的距离。

z_{i j}

↑ = δ_{z} (z) + \frac{1}{2} L_{h} \cdot ε_{x} (z) + \frac{1}{2} L_{v} \cdot ε_{y} (z)

(7)

式中：z_ij $↑$ 为位置偏差，即实际位置与目标位置的偏差， $↑$ 表示从机床正方向测量；L_h为两滑块之间的水平距离；L_v为工作台竖直高度。

由式(7)可知，位置偏差受δ_z (z)、ε_x (z)和ε_y (z)的影响。根据方差的性质可知，位置偏差的方差受δ_z (z)、ε_x (z)和ε_y (z)的方差影响，δ_z (z)、ε_x (z)和ε_y (z)的方差越小，重复性误差越小，工作台运行平稳性越高。

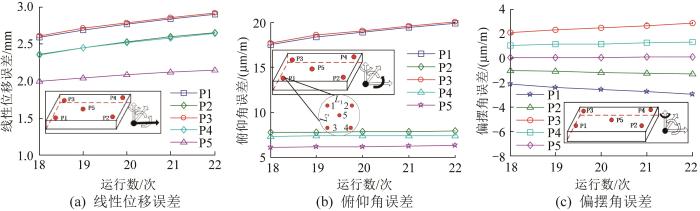
热变形会使工作台发生位置偏差，导致机床每次运动到同一位置时运动误差产生变化。为了分析热变形对运动重复性误差的影响，对机床同一位置不同时间的运动状态进行分析。分别计算P1至P5区域的线性位移误差、俯仰角误差和偏摆角误差，结果如图11所示。由图可知，线性位移误差最大值约为2.8 μm，俯仰角误差最大值约为20 μm/m，偏摆角误差最大值约为3 μm/m。随着工作台运行次数的增加，3项误差基本呈逐渐增大。这是因为，随着工作台运行次数的增加，丝杠的温度越来越高，丝杠的热变形越来越大，从而导致工作台线性位移误差、俯仰角误差和偏摆角误差增大。P1和P3的线性位移误差和俯仰角误差大于其余3处，这是因为P1和P3位于丝杠、螺母与工作台连接位置的上方，温度较高，热变形较大。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 工作台运动误差仿真结果

Fig.11 Simulation results of worktable motion errors

2.2　工作台运动重复性误差计算

按照ISO 230-6标准中的方法，计算P1至P5的运动重复性误差，结果如表2所示。由表可知：在所测量的5个区域中，P1的俯仰角重复性误差最大，为11.00 μm/m；P1和P3的各重复性误差比较接近；P5的线性位移重复性误差和偏摆角重复性误差最小。这是因为P1和P3离丝杠、螺母等热源较近，运动误差及其变化较大，而P5位于热源对称的工作台中央，热变形较小，运动误差及其变化较小，重复性性误差也较小。

表2 工作台运动重复性误差

Table 2 Motion repeatability error of worktable

区域	线性位移重复性误差/μm	偏摆角重复性误差/(μm/m)	俯仰角重复性误差/(μm/m)
P1	1.48	3.72	11.00
P2	1.39	1.54	0.83
P3	1.46	2.14	10.85
P4	1.33	1.24	0.80
P5	0.71	0.52	1.05

新窗口打开| 下载CSV

2.3　运动重复性误差影响因素分析

工作台进给速度、轴承预紧力矩和滑块支撑距离等对工作台热源点的热量生成有重要影响，这些因素若不加以控制，它们引起的热变形将会加大机床运动重复性误差。

第1节的仿真结果是以6 m/min的工作台进给速度、100 N∙m的轴承预紧力矩和345 mm的滑块支撑距离为初始条件进行仿真而得到的。以此条件为基准，采用单因素分析法来逐一研究工作台进给速度、轴承预紧力矩和滑块支撑距离对机床运动重复性误差的影响规律。取工作台表面热变形最大的P1区域来进行分析。

2.3.1　工作台进给速度对运动重复性误差的影响

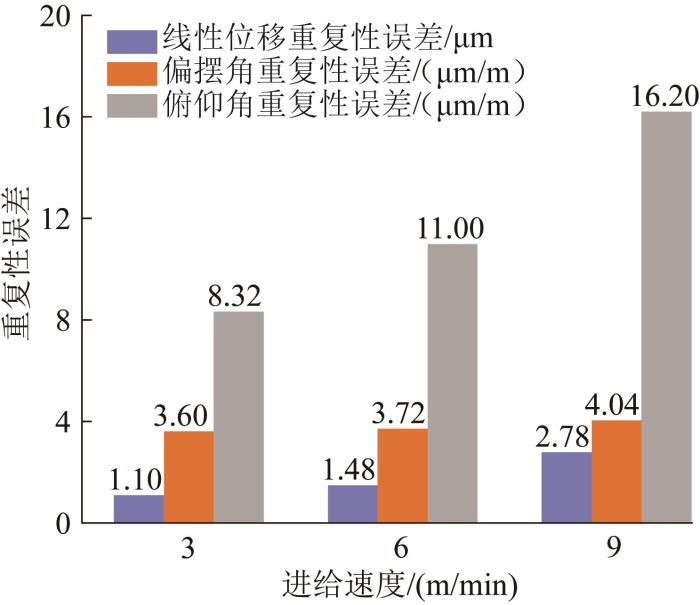
保持轴承预紧力矩和滑块支撑距离不变，只改变工作台进给速度。分析工作台进给速度分别为3，6，9 m/min时其对机床运动重复性误差的影响，结果如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同工作台进给速度下机床运动重复性误差仿真结果

Fig.12 Simulation results of motion repeatability errors of machine tool under different worktable feed speeds

由图12可知，随着工作台进给速度的提高，线性位移重复性误差从1.10 μm增加到2.78 μm，偏摆角重复性误差从3.60 μm/m增加到4.04 μm/m，俯仰角重复性误差从8.32 μm/m增加到16.20 μm/m。3项误差均随着工作台进给速度的提高而增大，说明机床在运行过程中不宜选用较高的进给速度。

2.3.2　轴承预紧力矩对运动重复性误差的影响

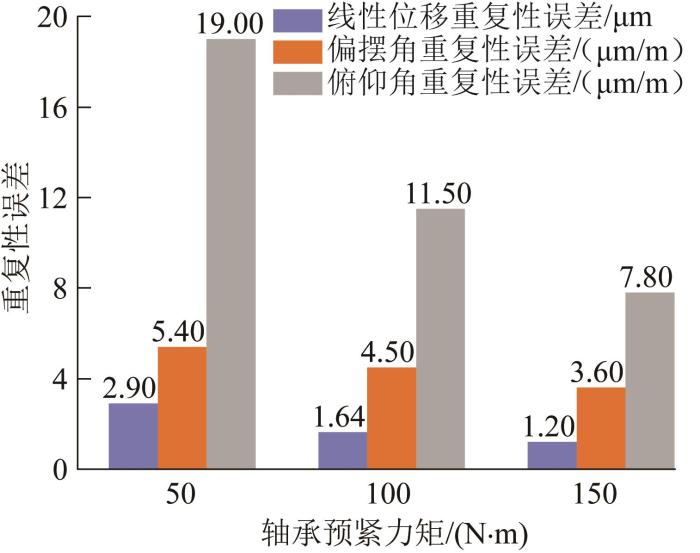
保持工作台进给速度和滑块支撑距离不变，只改变轴承预紧力距。分析轴承预紧力矩分别为50，100，150 N∙m时其对机床运动重复性误差的影响，结果如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同轴承预紧力矩下机床运动重复性误差仿真结果

Fig.13 Simulation results of motion repeatability errors of machine tool under different bearing preload torques

由图13可知，随着轴承预紧力矩的增大，线性位移重复性误差从2.60 μm减小到1.09 μm，偏摆角重复性误差从4.32 μm/m减小到3.44 μm/m，俯仰角重复性误差从16.20 μm/m减小到5.84 μm/m。3类误差均随着轴承预紧力矩的增大而大幅度减小，说明在装配过程中可以通过提高轴承预紧力距来减小机床的运动重复性误差，进而提高机床运动的稳定性。

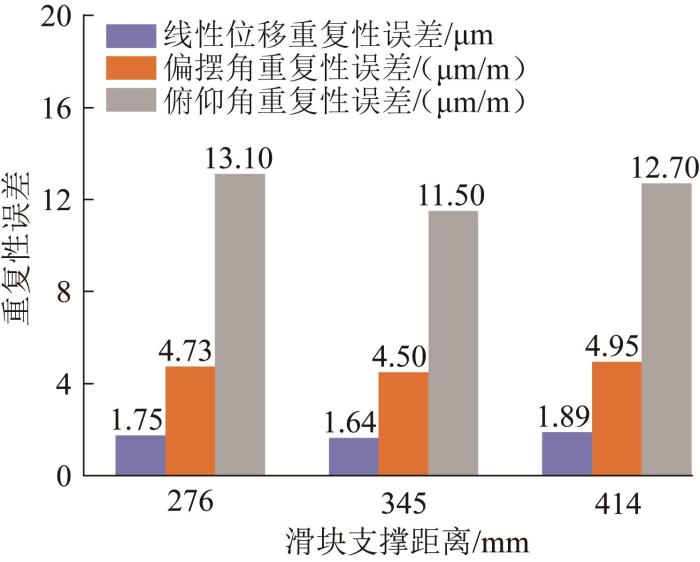
2.3.3　滑块支撑距离对运动重复性误差的影响

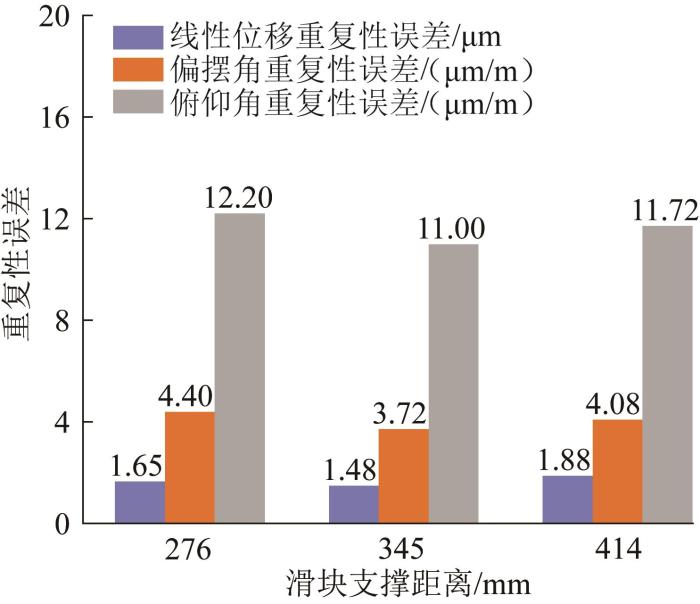
保持工作台进给速度和轴承预紧力矩不变，只改变滑块支撑距离。分析滑块支撑距离分别为276，345，414 mm时其对机床运动重复性误差的影响，结果如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同滑块支撑距离下机床运动重复性误差仿真结果

Fig.14 Simulation results of motion repeatability errors of machine tool under different slider support distances

由图14可知，随着滑块支撑距离的增大，各重复性误差先减小后略增大，变化幅值较小，说明滑块支撑距离对机床的运动重复性误差影响较小，但也应选取合适的滑块支撑距离。

3 实验验证

在单轴重复定位实验平台上进行实验，来验证仿真结果的正确性。用激光干涉仪测量机床的运动误差和运动重复性误差，采集工作台运行的误差数据，并对热变形最大区域P1的运动重复性误差进行详细分析。实验设计与仿真分析时相同，分别分析工作台进给速度、轴承预紧力矩、滑块支撑距离对机床运动重复性误差的影响。机床运动重复性误差测试实验的现场如图15所示。不同工作台进给速度、轴承预紧力矩、滑块支撑距离下机床运动重复性误差的实验结果如图16至如18所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 机床运动重复性误差测试实验现场

Fig.15 Site of the test experiment of motion repeatability errors of machine tool

图16

新窗口打开| 下载原图ZIP| 生成PPT

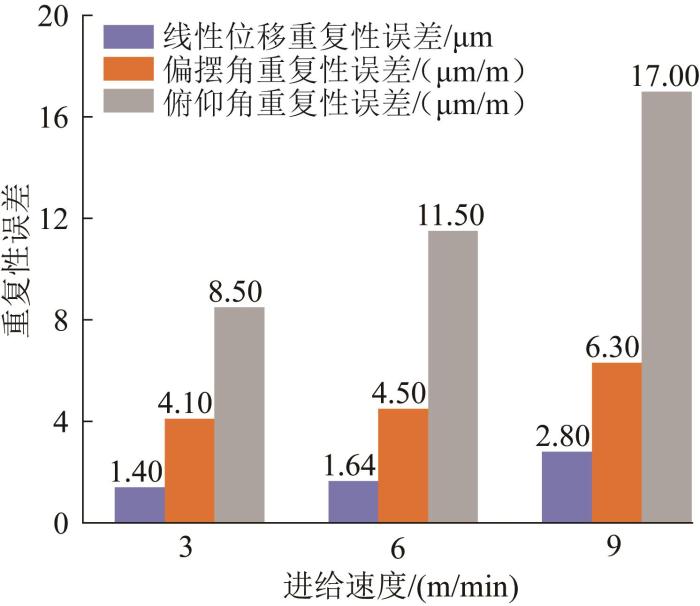
图16 不同工作台进给速度下机床运动重复性误差实验结果

Fig.16 Experimental results of motion repeatability errors of machine tool under different worktable feed speeds

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 不同轴承预紧力矩下机床运动重复性误差实验结果

Fig.17 Experimental results of motion repeatability errors of machine tool under different bearing preloading torques

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 不同滑块支撑距离下机床运动重复性误差实验结果

Fig.18 Experimental results of motion repeatability errors of machine tool under different slider support distances

对比实验结果与有限元仿真结果可知，实验结果与仿真结果基本一致，验证了仿真模型的准确性。

4 结语

本文研究了进给系统热变形对机床运动重复性误差的影响。提出了基于移动热源加载的分层仿真方法，探究了在不同因素作用下进给系统热变形对机床运动重复性误差的影响，并进行了实验验证。仿真和实验结果为在机床设计和装配中减小机床运动重复性误差提供了可靠的依据。根据仿真和实验结果，得到了如下结论：

1）工作台进给速度和轴承预紧力距对机床运动重复性误差的影响较大，滑块支撑距离对机床运动重复性误差的影响较小。

2）为了获得高精度的加工质量，在设计和装配机床的过程中，应采取较小的进给速度、较高的轴承预紧力矩，滑块支撑距离须调整适当，以减小进给系统热变形和机床运动重复性误差。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SUN

G M

， HE

G Y

， ZHANG

D W

， et al.

Experimental study on the repeatability of positioning of linear axes of machine tools

［J］. Proceedings of the Institution of Mechanical Engineers， Part B： Journal of Engineering Manufacture， 2020， 234（4）： 739-751.

[本文引用: 1]

[2]

CHO

D H

， KWON

H C

， KIM

K H

Improvement of position repeatability of a linear stage with yaw minimization

［J］. Applied Sciences， 2022， 12（2）： 657-657.

[本文引用: 1]

[3]

RAMESH

， MANNAN

M A

， POO

A N

Error compensation in machine tools： A review

［J］. International Journal of Machine Tools and Manufacture， 2000， 40（9）： 1235-1256.

[本文引用: 1]

[4]

LIU

J L

， MA

， WANG

S L

Data-driven thermally-induced error compensation method of high-speed and precision five-axis machine tools

［J］. Mechanical Systems and Signal Processing， 2020， 143： 106538. doi：10.1016/j.ymssp.2019.106538

[本文引用: 1]

[5]

孙志超，陶涛，黄晓勇，等.

车床主轴与进给轴耦合热误差建模及补偿研究

［J］.西安交通大学学报，2015，49（7）：105-112. doi：10.7652/xjtuxb201507018

[本文引用: 1]

SUN

Z C

， TAO

， HUANG

X Y

， et al.

Modeling and compensation of coupled thermal error of spindle and feed shafts

［J］. Journal of Xi'an Jiaotong University， 2015， 49（7）： 105-112.

DOI:10.7652/xjtuxb201507018 [本文引用: 1]

[6]

李彬，张云，王立平，等.

基于遗传算法优化小波神经网络数控机床热误差建模

［J］.机械工程学报， 2019，55（21）：215-220. doi：10.3901/JME.2019.21.215

[本文引用: 1]

， ZHANG

， WANG

L P

， et al.

Modeling for CNC machine tool thermal error based on genetic algorithm optimization wavelet neural networks

［J］. Journal of Mechanical Engineering， 2019， 55（21）： 215-220.

DOI:10.3901/JME.2019.21.215 [本文引用: 1]

[7]

， ZHAO

， MEI

X S

， et al.

Thermal error compensation of high-speed spindle system based on a modified BP neural network

［J］. The International Journal of Advanced Manufacturing Technology， 2017， 89（9/12）： 3071-3085.

[8]

YANG

， NI

Dynamic neural network modeling for nonlinear， nonstationary machine tool thermally induced error

［J］. International Journal of Machine Tools and Manufacture， 2004， 45（4）： 455-465.

[本文引用: 1]

[9]

张毅，杨建国.

基于灰色理论预处理的神经网络机床热误差建模

［J］.机械工程学报，2011，47（7）：134-139. doi：10.3901/jme.2011.07.134

[本文引用: 1]

ZHANG

， YANG

J G

Modeling for machine tool thermal error based on grey model preprocessing neural network

［J］. Journal of Mechanical Engineering， 2011， 47（7）： 134-139.

DOI:10.3901/jme.2011.07.134 [本文引用: 1]

[10]

鞠萍华，黄洛.

基于灰色GM（1，4）模型的数控机床热误差补偿技术

［J］.重庆大学学报，2017，40（10）：23-29. doi：10.11835/j.issn.1000-582X.2017.10.003

[本文引用: 1]

P H

， HUANG

Thermal error compensation technology of CNC machine tools based on Grey Model （1，4）

［J］. Journal of Chongqing University （Natural Science Edition）， 2017， 40（10）： 23-29.

DOI:10.11835/j.issn.1000-582X.2017.10.003 [本文引用: 1]

[11]

LEI

M H

， YANG

， WANG

， et al.

Semi-supervised modeling and compensation for the thermal error of precision feed axes

［J］. The International Journal of Advanced Manufacturing Technology， 2019， 104（9/12）： 4629-4640.

[本文引用: 1]

[12]

黄智，贾臻杰，邓涛，等.

基于支持向量机的静压转台热误差补偿

［J］.浙江大学学报（工学版），2019，53（8）：1594-1601.

[本文引用: 1]

HUANG

， JIA

Z J

， DENG

， et al.

Thermal error compensation of static pressure turntable based on support vector machine

［J］. Journal of Zhejiang University （Engineering Science）， 2019， 53（8）： 1594-1601.

[本文引用: 1]

[13]

冯文龙，黄奕乔，拓占宇，等.

基于温度积分方法的大型数控机床光栅定位热误差建模及实时补偿

［J］.上海交通大学学报，2016，50（5）：710-715.

[本文引用: 1]

FENG

W L

， HUANG

Y Q

， TUO

Z Y

， et al.

Modeling of thermally induced grating positioning error of large machine tools based on temperature integral method and reat-time compensation

［J］. Journal of Shanghai Jiaotong University， 2016， 50（5）： 710-715.

[本文引用: 1]

[14]

KIM

S K

， CHO

D W

Real-time estimation of temperature distribution in a ball-screw system

［J］. International Journal of Machine Tools and Manufacture， 1997， 37（4）： 451-464.

[本文引用: 1]

[15]

张庆锋，高翔.

基于ANSYS的高速精密冲床热-结构耦合分析

［J］.机床与液压，2016，44（18）：42-47.

DOI:10.3969/j.issn.1001-3881.2016.18.008 [本文引用: 1]

ZHANG

Q F

， GAO

Thermal-structure coupling analysis for high-speed precision press based on ANSYS

［J］. Machine Tool and Hydraulics， 2016， 44（18）： 42-47. doi：10.3969/j.issn.1001-3881.2016.18.008

[本文引用: 1]

[16]

GOMEZ-ACEDO

， OLARRA

， DE LOPEZ N la calle.

A method for thermal characterization and modeling of large gantry-type machine tools

［J］. The International Journal of Advanced Manufacturing Technology， 2012， 62（9/12）： 875-886.

[本文引用: 1]

[17]

任朝晖，李炎臻，刘杨.

高速电主轴热力学分析的仿真研究

［J］.机床与液压，2018，46（1）：121-125. doi：10.3969/j.issn.1001-3881.2018.01.025

[本文引用: 1]

REN

Z H

， LI

Y Z

， LIU

High-speed spindle thermodynamic analysis and simulation research

［J］. Machine Tool and Hydraulics， 2018， 46（1）：121-125.

DOI:10.3969/j.issn.1001-3881.2018.01.025 [本文引用: 1]

[18]

于慎波，杨成玉，赵海宁，等.

高速永磁同步电主轴的热态特性研究

［J］.重型机械，2017（5）：26-30.

S B

， YANG

C Y

， ZHAO

H N

， et al.

Research on thermal characteristics for high speed permanent magnetic synchronous motorized spindle

［J］. Heavy Machinery， 2017（5）： 26-30.

[19]

高帅，何毅斌，王彦伟，等.

影响高速电主轴热学特性的有限元优化分析

［J］.制造技术与机床，2018（11）：36-38，43.

GAO

， HE

Y B

， WANG

Y W

， et al.

Finite element analysis of thermal characteristics affecting high speed spindle

［J］. Manufacturing Technology & Machine Tool， 2018（11）： 36-38， 43.

[20]

， YANG

， ZHAO

， et al.

Simulation and experimental study on the thermally induced deformations of high-speed spindle system

［J］. Applied Thermal Engineering， 2015， 86： 251-268.

[本文引用: 1]

[21]

刘阔，韩伟，王永青，等.

数控机床进给轴热误差补偿技术研究综述

［J］.机械工程学报，2021，57（3）：156-173. doi：10.3901/jme.2021.03.156

[本文引用: 1]

LIU

， HAN

， WANG

Y Q

， et al.

Review on thermal error compensation for feed axes of CNC machine tools

［J］. Journal of Mechanical Engineering， 2021， 57（3）： 156-173.

DOI:10.3901/jme.2021.03.156 [本文引用: 1]

[22]

付振彪，王太勇，张雷，等.

滚珠丝杠进给系统动力学建模与动态特性分析

［J］.振动与冲击，2019，38（16）：56-62.

[本文引用: 1]

Z B

， WANG

T Y

， ZHANG

， et al.

Dynamic modeling and vibration analysis of ball screw feed driving systems

［J］.Journal of Vibration and Shock，2019，38（16）：56-62.

[本文引用: 1]

[23]

ROY

， SAHA

S K

Thermal and friction characteristics of laminar flow through a circular duct having helical screw-tape with oblique teeth inserts and wire coil inserts

［J］. Experimental Thermal & Fluid Science， 2015， 68： 733-743.

[本文引用: 1]

[24]

高卫国，王伟松，张大卫，等.

考虑结构热变形的机床进给系统热误差研究

［J］.工程设计学报，2019，26（1）：29-38. doi：10.3785/j.issn.1006-754X.2019.01.006

[本文引用: 2]

GAO

W G

， WANG

W S

， ZHANG

D W

， et al.

Research on thermal error of machine tool feed system considering structural thermal deformation

［J］.Chinese Journal of Engineering Design， 2019， 26（1）： 29-38.

DOI:10.3785/j.issn.1006-754X.2019.01.006 [本文引用: 2]

[25]

杨金玉

卧式加工中心热特性分析与工作空间热误差建模方法

［D］. 天津：天津大学， 2015.

[本文引用: 2]

YANG

J Y

Methods on thermal analysis and thermal error modeling in working space of horizontal machine tools

［D］. Tianjin： Tianjin University， 2015.

[本文引用: 2]

[26]

杨海栗，田建平，胡勇，等.

龙门加工中心丝杠组件热态性能与温度场实验研究

［J］.组合机床与自动化加工技术，2015（1）：4-8.

[本文引用: 1]

YANG

H L

， TIAN

J P

， HU

， et al.

The thermal properties and temperature field experimental study for ball screw system of gantry type machining center

［J］. Modular Machine Tool & Automatic Manufacturing Technique， 2015（1）： 4-8.

[本文引用: 1]

Experimental study on the repeatability of positioning of linear axes of machine tools

2020

... 运动重复性误差影响着机床的加工精度和零件加工的一致性.它属于不可补偿误差，无法用误差补偿来进行抑制，只能通过装配误差的控制、装配精度的提高来达到抑制的目的.Sun等^[1]系统地分析了机床重复定位误差的影响因素，定性地研究了导轨装配误差、丝杠装配误差、滚珠丝杠预紧力、滑块间距等7个因素对重复定位误差的影响规律，研究结果表明，导轨装配误差和滚珠丝杠预紧力对重复定位误差有着显著影响.Cho等^[2]分析了偏摆角误差对机床运动重复性误差的影响，提出通过减小偏摆角误差来减小重复性误差.然而，以上研究均未涉及机床热变形对其运动重复性误差影响的分析. ...

Improvement of position repeatability of a linear stage with yaw minimization

2022

Error compensation in machine tools： A review

2000

... 机床热变形引起的机床误差可占机床总误差的70%^[3].研究人员采用了多种技术模拟机床热特性来分析热变形对定位误差的影响.这些技术分为基于经验和基于原理两类.基于经验的模型主要用来研究机床热误差的补偿，采用算法建立热误差与测点温度之间的关系.多元回归法^[4-5]、神经网络算法^[6-8]、灰色模型优化算法^[9-10]和支持向量机^[11-12]等在机床热误差分析与建模中具有良好的应用.冯文龙等^[13]提出了一种基于热特性分析的误差建模方法，提高了数控机床的加工精度，误差补偿后机床的定位精度提高了90%以上.基于原理的模型主要用来研究热误差预测，其研究的重点是如何在精确边界条件下得到精确的模型.Kim等^[14]利用双线性元的有限元方法分析了滚珠丝杠副的温度分布，并建立了有限元模型.张庆锋等^[15]利用ANSYS软件预测了机床热误差，分析了整机温度场、热变形，并验证了温度场仿真结果的可靠性.Gomez-Acedo等^[16]提出了一种利用有限元模型来分析大型机床热特性的方法.采用有限元分析方法进行电主轴热特性的研究也给技术人员带来了参考^[17-20]. ...

Data-driven thermally-induced error compensation method of high-speed and precision five-axis machine tools

2020

车床主轴与进给轴耦合热误差建模及补偿研究

2015

车床主轴与进给轴耦合热误差建模及补偿研究

2015

基于遗传算法优化小波神经网络数控机床热误差建模

2019

基于遗传算法优化小波神经网络数控机床热误差建模

2019

Thermal error compensation of high-speed spindle system based on a modified BP neural network

2017

Dynamic neural network modeling for nonlinear， nonstationary machine tool thermally induced error

2004

基于灰色理论预处理的神经网络机床热误差建模

2011

基于灰色理论预处理的神经网络机床热误差建模

2011

基于灰色GM（1，4）模型的数控机床热误差补偿技术

2017

基于灰色GM（1，4）模型的数控机床热误差补偿技术

2017

Semi-supervised modeling and compensation for the thermal error of precision feed axes

2019

基于支持向量机的静压转台热误差补偿

2019

基于支持向量机的静压转台热误差补偿

2019

基于温度积分方法的大型数控机床光栅定位热误差建模及实时补偿

2016

基于温度积分方法的大型数控机床光栅定位热误差建模及实时补偿

2016

Real-time estimation of temperature distribution in a ball-screw system

1997

基于ANSYS的高速精密冲床热-结构耦合分析

2016

基于ANSYS的高速精密冲床热-结构耦合分析

2016

A method for thermal characterization and modeling of large gantry-type machine tools

2012

高速电主轴热力学分析的仿真研究

2018

高速电主轴热力学分析的仿真研究

2018

高速永磁同步电主轴的热态特性研究

2017

高速永磁同步电主轴的热态特性研究

2017

影响高速电主轴热学特性的有限元优化分析

2018

影响高速电主轴热学特性的有限元优化分析

2018

Simulation and experimental study on the thermally induced deformations of high-speed spindle system

2015

数控机床进给轴热误差补偿技术研究综述

2021

... 受机床内部热源的影响，机床温度会发生变化，从而引起机床热变形^[21].机床内部热源主要有进给系统的滚珠丝杠、导轨、电机、轴承、滑块和螺母，传热方式有热传导和热对流.在环境温度为20 ℃、进给速度为6 m/min、轴承预紧力矩为100 N∙m、滑块支撑距离为345 mm的工况下分析机床热边界条件，如表1所示. ...

数控机床进给轴热误差补偿技术研究综述

2021

滚珠丝杠进给系统动力学建模与动态特性分析

2019

... Analysis of thermal boundary conditions for machine tool

Table 1

边界条件

计算公式

字符意义

计算结果

轴承生热率q₁^[22]

$q_{1} = \frac{0.104 7 n_{1} (M_{1} + M_{2})}{V}$ ...

滚珠丝杠进给系统动力学建模与动态特性分析

2019

... Analysis of thermal boundary conditions for machine tool

Table 1

边界条件

计算公式

字符意义

计算结果

轴承生热率q₁^[22]

$q_{1} = \frac{0.104 7 n_{1} (M_{1} + M_{2})}{V}$ ...

Thermal and friction characteristics of laminar flow through a circular duct having helical screw-tape with oblique teeth inserts and wire coil inserts

2015

... 热流密度q₂^[23] ...

考虑结构热变形的机床进给系统热误差研究

2019

...

M_{p} = \frac{F_{p} P_{h}}{2 π η_{1}} (1 - {η_{1}}^{2})

n₂为丝杠转速；M_p为滚珠螺旋阻力矩；M_d为驱动力矩；Α₂为丝杠与螺母的接触面积；F_α 为丝杠的轴向载荷；Ρ_h为丝杠的导程；η₁为丝杠的传动效率；F_p为丝杠的轴向预紧力

10 300 W/m²

电机热流密度q₃^[24]

q_{3} = \frac{M_{t} \cdot n_{3}}{9 550 \cdot A_{3}} (1 - η_{2})

M_t为电机输出扭矩；n₃为电机转速；η₂为电机机械效率；A₃为电机表面积

1 500 W/m²

导轨与滑块间的 ...

... 热流密度q₄^[24] ...

考虑结构热变形的机床进给系统热误差研究

2019

...

M_{p} = \frac{F_{p} P_{h}}{2 π η_{1}} (1 - {η_{1}}^{2})

10 300 W/m²

电机热流密度q₃^[24]

q_{3} = \frac{M_{t} \cdot n_{3}}{9 550 \cdot A_{3}} (1 - η_{2})

M_t为电机输出扭矩；n₃为电机转速；η₂为电机机械效率；A₃为电机表面积

1 500 W/m²

导轨与滑块间的 ...

... 热流密度q₄^[24] ...

卧式加工中心热特性分析与工作空间热误差建模方法

2015

... h₁^[25] ...

... h₂^[25] ...

卧式加工中心热特性分析与工作空间热误差建模方法

2015

... h₁^[25] ...

... h₂^[25] ...

龙门加工中心丝杠组件热态性能与温度场实验研究

2015

... 在工作台作往复直线运动时，丝杠和滑块会发生空间位移.丝杠和滑块的移动会产生大量摩擦热，这些移动热源随着时间和空间的变化而变化，这给进给系统热变形的精确模拟带来了困难.将热边界条件中的热流密度当作载荷施加到仿真模拟中，可以获得热变形^[26].运用ADPL（ANSYS parametric design language，ANSYS参数化设计语言）施加载荷，当丝杠和滑块每次移动时，将之前区域的热流密度移除，加载对流系数，而在当前区域处删除对流系数，加载移动热源的热流密度. ...

龙门加工中心丝杠组件热态性能与温度场实验研究

2015

〈

〉