电连接器在各类武器、航天等装备中广泛应用,是实现系统内各零部件之间电能、电信号传输的基础元件。在装备长期贮存过程中,任何一个电连接器失效都有可能会导致后续的工作任务失败[1 ] 。因此,定量地设计和评估电连接器的可靠性对装备的定寿和延寿至关重要。
在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] 。按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] 。相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用。接触件结构参数的改变会对电连接器的接触可靠性产生影响。据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响。陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布。Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性。Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法。综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用。然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律。
为此,笔者拟从线簧孔式接触件的结构出发,揭示线簧丝倾角改变时接触件的失效机理;在此基础上,建立线簧孔式电连接器的贮存可靠性统计模型及其贮存寿命与线簧丝倾角的数学模型;最后,通过恒定应力加速退化试验得到不同线簧丝倾角下线簧孔式接触件的性能退化数据,以量化线簧孔式电连接器贮存寿命与线簧丝倾角之间的数学关系。
1 贮存寿命与线簧丝倾角的数学模型构建
1.1 线簧孔式接触件的结构
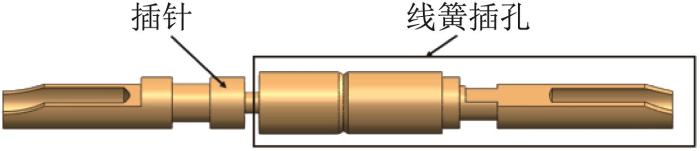
线簧孔式电连接器由线簧孔式接触件、绝缘件、密封件及壳体四大部分组成[10 ] 。其中,线簧孔式接触件包含两部分:线簧插孔和与之配合的插针,其结构如图1 所示。
图1
图1
线簧孔式接触件结构示意
Fig.1
Schematic diagram of wire spring hole contact structure
线簧插孔由前套、后套、内套以及线簧丝四部分组成。多根线簧丝按照单叶回转双曲面的直母线排列方式,均匀地分布在内套上并与内套的中心线形成一定角度,如图2 所示;前套和后套起固定线簧丝的作用,并分别与内套压接配合。
图2
图2
插针和线簧插孔内部接触示意
Fig.2
Schematic diagram of internal contact between pin and wire spring socket
图3 所示为线簧丝包络面示意,其中线簧丝与内套中心线的夹角θ λ 图3 可知,线簧丝倾角改变会使喉圆半径发生变化,而喉圆半径决定了线簧丝的形变量,从而影响线簧丝与插针之间的接触压力。
图3
图3
线簧丝包络面示意
Fig.3
Schematic diagram of wire spring envelope surface
1.2 线簧丝倾角改变时的失效机理分析
在贮存环境下,线簧孔式电连接器的接触失效机理主要为接触件基底材料铜的氧化腐蚀[11 -12 ] 。接触件的表面通常会进行镀金处理,由于镀层较薄且往往存在孔隙,使得部分基底材料铜暴露在空气中;同时,基底材料中的Cu+ 也会通过快速扩散通道(如晶体缺陷等)扩散至镀层表面[13 ] ,而Cu+ 对空气中的氧有强烈的亲和力,易发生反应,生成腐蚀物Cu2 O,且Cu2 O的增长速度与Cu+ 的扩散速率有关。随着Cu+ 的不断扩散,Cu2 O的厚度逐渐增大,接触件的接触电阻随之增大,直至超过失效阈值而发生接触失效。
从微观层面来看,Cu+ 的扩散需要克服能量势垒,克服能量势垒所消耗的能量即为离子间的扩散激活能Δ E J ,该应力的存在会使克服能量势垒所消耗的能量增大[14 ] 。根据空位扩散机制,可认为单个Cu+ 在挤压应力J d 2 ,单次扩散的位移为d ,则Cu+ 进行一次扩散所做的功为Jd 3 ,因此在挤压应力J 下的扩散激活能为Δ E - J d 3 J [15 ] 。由上文分析可知,线簧丝倾角增大会导致线簧丝与插针之间的接触压力增大,故Cu+ 单次扩散时所做的功Jd 3 也将增大,使得扩散激活能增大,导致单位时间内扩散至表面的Cu+ 数量减少,腐蚀物Cu2 O的增长速度减慢,从而延长了线簧孔式接触件的贮存寿命。
1.3 贮存可靠性统计模型
接触件电阻r 由体电阻r v 和接触电阻r t (包括收缩电阻r c 和膜层电阻r f )组成。由电接触理论[16 ] 可得,单根线簧丝与插针接触产生的收缩电阻r c0 和膜层电阻r f0 分别为:
r c 0 = ρ 1 + ρ 2 4 π H F r f 0 = ρ m H F (1)
式中:ρ 1 ρ 2 H F ρ m
在1对线簧孔式接触件中,每根线簧丝均按单叶回转双曲面的直母线方式排列,且线簧丝之间相互独立,可认为每根线簧丝与插针的接触情况相同,即收缩电阻与膜层电阻分别相同;电信号通过多根线簧丝传递至插针,因此多根线簧丝与插针之间的接触电阻为并联关系。现将线簧孔式接触件中所有线簧丝与插针接触产生的收缩电阻和膜层电阻分别看成一个整体,则接触件电阻可表示为:
r = r v + ρ 1 + ρ 2 4 n π H F + ρ m H n F (2)
ρ m = A e x p - Δ E β k T 0 t β (3)
式中:A β k T 0 t 为时间。
由失效机理分析可知,存在外部挤压应力时的扩散激活能为Δ E - J d 3 式(3)可以修正为:
ρ m = A e x p - Δ E - J d 3 β k T 0 t β (4)
r = r v + ρ 1 + ρ 2 4 n π H F + H A e x p - Δ E - J d 3 β k T 0 t β n F (5)
r = r 0 + α t β (6)
r 0 = r v + ρ 1 + ρ 2 4 n π H F
α = H A e x p - Δ E - J d 3 β k T 0 n F
式中:r 0 为体电阻与收缩电阻之和;α
记A 1 = H A / n F Q = Δ E - J d 3 β α
l n α = l n A 1 - Q k T 0 (7)
当温度一定时,Q / k T 0 A 1 l n A 1 l n α l n α ~ N μ l n α , σ l n α 2 μ l n α σ l n α α
μ l n α = μ l n A 1 - Q k T 0 = z 1 + z 2 1 000 T + 273.15 (8)
z 1 = μ l n A 1
z 2 = - Q 1 000 k
式中:z 1 z 2 T
记t r t D t e (即寿命)可表示为:
t e = i n f t : r ( t ) ≥ D ; t ≥ 0 (9)
由于膜层电阻退化率α G t
G t = P t e ≤ t = Φ l n t - l n D - r 0 - μ l n α / β σ l n α / β (10)
电连接器中单对接触件发生失效即可能会导致电信号传递失败,因此电连接器的整体寿命取决于最先发生失效的单对接触件的寿命。从功能上来看,电连接器是由一系列接触件组成的串联系统,其寿命分布为最小极值问题[2 ] 。因此,在同一线簧丝倾角下,具有g R t
R t = 1 - G t g = 1 - Φ l n t - l n D - r 0 - μ l n α / β σ l n α / β g (11)
1.4 贮存寿命与线簧丝倾角的数学模型
由式(11)可得,线簧孔式电连接器的贮存寿命t r
t r = e x p Φ - 1 1 - R 1 / g σ l n α β D - r 0 1 β e x p - μ l n α β (12)
在线簧孔式电连接器的加工制造过程中,误差不可避免,因此其材料硬度H F 式(7)取均值,可得:
μ l n α = μ l n A + μ l n H - μ l n n F - Q k T 0 (13)
t r = e x p Φ - 1 1 - R 1 / g σ l n α - μ l n H - μ l n A β D - r 0 1 β e x p μ l n n F β e x p Q β k T 0 (14)
由失效机理分析可知,同一线簧丝倾角下的挤压应力J J μ F μ S J = μ F / μ S
Q = Δ E - μ F d 3 μ S β (15)
μ l n n F = ∑ i = 1 m l n n F i m (16)
F i = μ F + x i
式中:m 为线簧孔式电连接器中线簧丝的总数量;Fi 为第i xi 为由加工制造误差导致的接触压力Fi 与接触压力均值μ F
e x p μ l n n F β = ∏ i = 1 m ( μ F + x i ) 1 m β n 1 β (17)
t r = e x p Φ - 1 1 - R 1 / g σ l n α - μ l n A - μ l n H β + Δ E k T 0 n D - r 0 ∏ i = 1 m μ F + x i 1 m 1 β e x p - μ F d 3 μ S k T 0 (18)
由文献[4 , 7 ]可知,在工程实际应用中常用的线簧丝倾角范围(7 ° ∼ 10 °
μ F = a θ + b (19)
将式(19)代入式(18),则式(18)中最后一项可拆解为2项,将与线簧丝倾角无关项与式(18)中的第1项进行合并同类项,则可得:
t r = e x p Φ - 1 1 - R 1 / g σ l n α - μ l n A - μ l n H β + Δ E μ S - b d 3 μ S k T 0 n D - r 0 ∏ i = 1 m a θ + b + x i 1 m 1 β e x p - a d 3 θ μ S k T 0 (20)
式(20)即为线簧孔式电连接器的贮存寿命与线簧丝倾角的数学模型。但由于指数部分引起的变化远远大于幂函数部分引起的变化,为了简化模型,将幂函数部分视为与线簧丝倾角无关的一个常数,令:
K 1 = e x p Φ - 1 1 - R 1 / g σ l n α - μ l n A - μ l n H β + Δ E μ S - b d 3 μ S k T 0 n D - r 0 ∏ i = 1 m a θ + b + x i 1 m 1 β
K 2 = - a d 3 μ S k T 0
由此可得,在工程实际应用中常用的线簧丝倾角范围(7 ° ∼ 10 °
t r = K 1 e x p K 2 θ (21)
2 恒定应力加速退化试验
为了量化线簧孔式电连接器贮存寿命与线簧丝倾角之间的数学关系,并验证所构建数学模型的准确性,开展线簧孔式接触件的恒定应力加速退化试验。试验条件和方法如下。
1)线簧丝倾角水平。根据工程实际应用中线簧孔式电连接器的线簧丝倾角使用范围,选择7°,8°,9°,10°四种线簧丝倾角水平。
2)温度应力水平。以温度应力水平提高不改变线簧孔式电连接器失效机理为前提,得到线簧孔式接触件在158 ℃下未出现除接触失效外的失效情况。参考前期经验,选取4组温度应力水平,最高温度T 4 =158 ℃,最低温度T 1 =105 ℃;按照温度应力水平等间隔的原则[17 ] ,确定中间温度T 2 =120 ℃,T 3 =140 ℃。
3)试验样本量。为了保证试验结果的一般性,同时为了提高寿命评估结果的准确性,在温度T 1 下每个线簧丝倾角水平均选取20对接触件,在温度T 2 、T 3 、T 4 下每个线簧丝倾角水平均各选取15对接触件。
4)测试间隔和截尾时间。通过对线簧孔式接触件进行摸底试验后可知,在12 h的测试间隔下,158 ℃下线簧孔式接触件样品的接触电阻退化趋势明显。基于10 ℃法则[18 ] ,圆整后确定在105,120,140 ℃下的测试间隔分别为120,72,24 h。根据前期其他型号电连接器的试验数据,确定截尾时间为1 500 h。
5)失效判据。由文献[19 ]可知,直径为1 mm的线簧孔式接触件的电阻不得大于5 m Ω 5 m Ω
6)测量方法。由于线簧孔式接触件的电阻较小,若选择常规的电阻测量仪,则测量结果在很大程度上会受到连接导线电阻的影响。因此,本文选择采用“开尔文四端线法”作为测量方法。线簧孔式接触件电阻测量现场如图4 所示。
图4
图4
线簧孔式接触件电阻测量现场
Fig.4
Resistance measurement site of wire spring hole contact
最终的线簧孔式接触件恒定应力加速退化试验方案如表1 所示。
3 试验数据统计与分析
3.1 接触件电阻测量结果
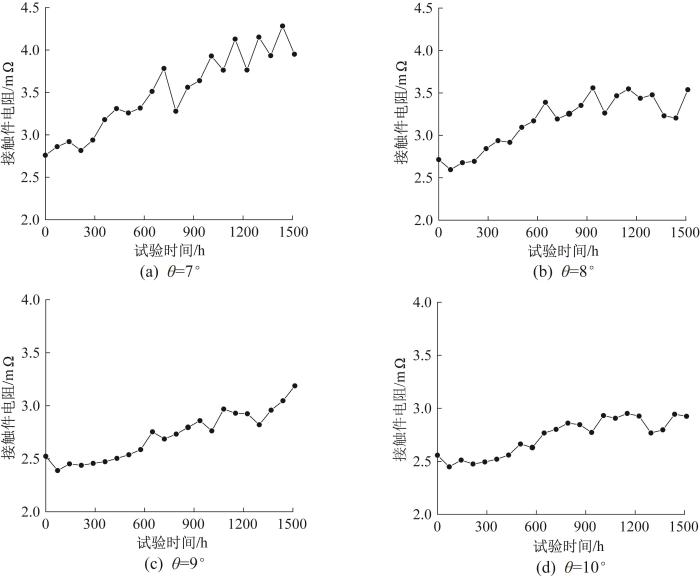
按照表1 拟定的试验方案,定时测量记录每对线簧孔式接触件的电阻,并对不同温度、不同线簧丝倾角下的线簧孔式接触件的性能退化数据求平均值。以120 ℃为例,计算得到不同线簧丝倾角下线簧孔式接触件的平均性能退化曲线,结果如图5 所示。由图5 可以发现,线簧孔式接触件的电阻随着试验时间的增加整体呈上升趋势,且随着线簧丝倾角的增大,接触件电阻的增大速率变小。
图5
图5
120 ℃下不同线簧丝倾角下线簧孔式接触件的平均性能退化曲线
Fig.5
Average performance degradation curves of wire spring hole contact under different wire spring inclination angles at 120 ℃
3.2 贮存可靠性统计模型检验
为了检验所构建的线簧孔式电连接器贮存可靠性统计模型的准确性,需要对膜层电阻退化率α χ δ ε φ γ φ φ = 1 , 2 , ⋯ , 4 T 下、第γ γ = 1 , 2 , ⋯ , 4 θ 下第δ δ = 1 , 2 , ⋅ ⋅ ⋅ , l φ γ l φ γ φ T 下第γ θ 对应的接触件数量)线簧孔式接触件的第ε ε = 1 , 2 , ⋅ ⋅ ⋅ , h φ γ h φ γ φ T 下第γ θ 对应的总测量次数)测量的电阻值。利用式(6),通过最小二乘法对第φ T 下第γ θ 对应的第δ P 值如表2 所示。
由表2 可知,不同温度和不同线簧丝倾角下线簧孔式接触件的膜层电阻退化率对数正态分布检验的P 值均大于0.05,由此可认为膜层电阻退化率服从对数正态分布,即线簧孔式电连接器的贮存可靠性统计模型可用式(11)来描述。
3.3 性能退化模型的参数估计
根据上文建立的线簧孔式接触件的性能退化模型(6),利用不同试验条件下的接触件电阻测量值,通过最小二乘法求出第γ [20 ] 。
由于在测量过程中线簧孔式接触件的电阻与理论值之间存在随机误差κ δ ε φ γ κ δ ε φ γ ∼ N 0 , σ κ δ ε φ γ 2 式(6)可知,χ δ ε φ γ t = f z 1 , z 2 , β , σ l n α
L = ∏ φ = 1 4 ∏ δ = 1 l φ γ ∏ ε = 1 h φ γ 1 2 π σ κ δ ε φ γ e x p - x δ ε φ γ - r δ ε φ γ 2 2 σ κ δ ε φ γ 2 1 l n α δ φ γ 2 π σ l n α γ e x p - l n α δ φ γ - μ l n α δ φ γ 2 2 σ l n α γ 2 (22)
令f 1 z 1 , z 2 , β , σ l n α = - l n L 式(22)进行最优化寻解,即可得到性能退化模型参数的极大似然估计值,计算结果如表3 所示。
3.4 贮存寿命与线簧丝倾角的数学模型求解
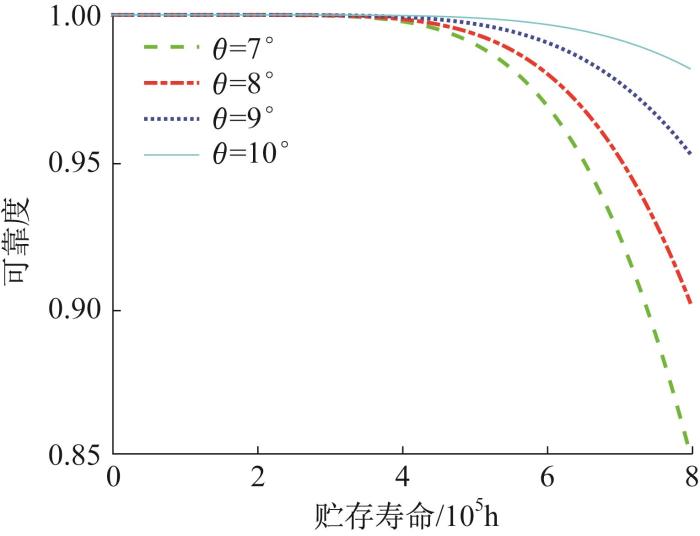
假设常应力下的温度为25 ℃,由加速因子不变原则[21 ] 可知,在失效机理不变的情况下,参数σ l n α β 表3 中的数据代入式(8)和式(11),即可得到各个线簧丝倾角水平下的线簧孔式电连接器的贮存可靠度函数。利用MATLAB软件编程得到常温(25 ℃)下线簧丝倾角不同时线簧孔式电连接器的可靠度曲线,结果如图6 所示。根据图6 ,不难发现随着线簧丝倾角的增大,同一可靠度下线簧孔式电连接器的贮存寿命增大。
图6
图6
不同线簧丝倾角下线簧孔式电连接器的可靠度曲线
Fig.6
Reliability curves of wire spring hole electrical connector under different wire spring inclination angles
将表3 中的数据代入式(12),即可得到可靠度R = 0.99 表4 所示。
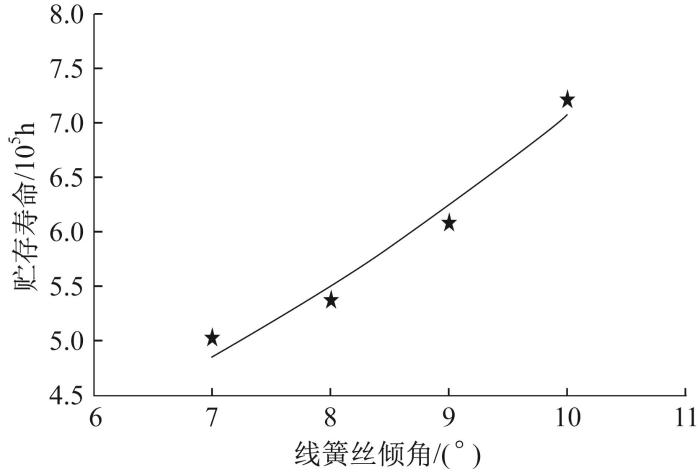
根据式(21),利用表4 数据进行最小二乘拟合,结果如图7 所示,可得K 1 = 201 597 K 2 = 0.125 6 0.968 1 7 ° ∼ 10 ° R = 0.99 t r = 201 597 e x p 0.125 6 θ
图7
图7
线簧孔式电连接器贮存寿命与线簧丝倾角的拟合曲线
Fig.7
Fitting curves between storage life and wire spring inclination angle of wire spring hole electrical connector
4 结 论
1)基于线簧丝倾角改变时线簧孔式接触件的失效机理,建立了线簧孔式电连接器的贮存可靠性统计模型及其贮存寿命与线簧丝倾角的数学模型。结果表明,贮存寿命与线簧丝倾角之间服从指数变化规律。
2)设计了不同线簧丝倾角下的线簧孔式接触件恒定应力加速退化试验方案,结果验证了所构建的线簧孔式电连接器贮存可靠性统计模型的准确性,且电连接器的贮存可靠性随线簧丝倾角的增大而增大。通过试验数据量化得到了线簧孔式电连接器贮存寿命与线簧丝倾角的函数关系式,其拟合精度较高,验证了所构建数学模型的准确性。
3)不同线簧丝倾角下线簧孔式电连接器的可靠性评估结果可为后续的电连接器可靠性增长设计提供一定的理论基础和参考。
参考文献
View Option
[1]
[本文引用: 1]
WANG S J CHEN W H QIAN P et al Reliability design model of aerospace electrical connector
[J]. Journal of Mechanical Engineering , 2017 , 53 (10 ): 180 -186 .
DOI:10.3901/jme.2017.10.180
[本文引用: 1]
[2]
陈文华 航天电连接器可靠性试验和分析的研究
[D].杭州 :浙江大学 ,1997 :9 -17 .
[本文引用: 2]
CHEN W H Study on reliability test and analysis of aerospace electrical connectors
[D]. Hangzhou : Zhejiang University , 1997 : 9 -17 .
[本文引用: 2]
[4]
关凌宇 线簧连接器的特性研究
[D].北京 :北京邮电大学 ,2018 :14 -29 .
[本文引用: 2]
GUAN L Y Research on the characteristics of wire spring connector
[D]. Beijing : Beijing University of Posts and Telecommunications , 2018 : 14 -29 .
[本文引用: 2]
[7]
[本文引用: 2]
LING S Q XU L FU R et al Optimization method of quality consistency for insertion force of electrical contact based on robust design principle
[J]. Journal of Mechanical Engineering , 2017 , 53 (4 ): 190 -197 .
DOI:10.3901/jme.2017.04.190
[本文引用: 2]
[8]
ZHOU Y L GUAN L Y NAN T Effect of structural design of hyperbolic wire spring connector on reliability of electrical contacts
[C]// The 2nd International Conference on Reliability Systems Engineering , Beijing : IEEE , 2017 : 329 -334 .
[本文引用: 1]
[9]
LING S XU L LI D et al Fretting wear reliability assessment methodology of gold-plated electrical connectors considering manufacture parameters distribution
[J]. Microelectronics Reliability , 2020 , 114 : 113787 .
[本文引用: 1]
[10]
魏宇杰 线簧孔式电连接器接触可靠性设计建模与试验评估
[D].杭州 :浙江理工大学 ,2020 :19 -21 .
[本文引用: 2]
WEI Y J The contact reliability design modeling and test evaluation of wire spring-type electrical connector
[D]. Hangzhou : Zhejiang Sci-Tech University , 2020 : 19 -21 .
[本文引用: 2]
[11]
CHEN W H LIU J GAO L et al Step-stress accelerated degradation test modeling and statistical analysis methods
[J]. Chinese Journal of Mechanical Engineering , 2013 , 26 (6 ): 1154 -1159 .
[本文引用: 1]
[12]
CHEN W H LIU J GAO L et al Accelerated degradation reliability modeling and test data statistical analysis of aerospace electrical connector
[J]. Chinese Journal of Mechanical Engineering , 2011 , 24 (6 ): 957 -962 .
[本文引用: 1]
[13]
戚正风 固态金属中的扩散与相变 [M].北京 :机械工业出版社 ,1998 :80 -105 .
[本文引用: 1]
QI Z F Diffusion and phase transition in solid metals [M]. Beijing : China Machine Press , 1998 : 80 -105 .
[本文引用: 1]
[15]
GALVELE J R A stress corrosion cracking mechanism based on surface mobility
[J]. Corrosion Science , 1987 , 27 (1 ): 1 -33 .
[本文引用: 1]
[16]
郭凤仪 ,陈忠华 电接触理论及其应用技术 [M].北京 :中国电力出版社 ,2008 :5 -12 .
[本文引用: 1]
GUO F Y CHEN Z H Electrical contact theory and its application technology [M]. Beijing : China Electric Power Press , 2008 : 5 -12 .
[本文引用: 1]
[17]
中华人民共和国第四机械工业部 恒定应力寿命试验和加速寿命试验方法总则 : [S].北京 :中国标准出版社 ,1981 :5 -12 .
[本文引用: 1]
The Fourth Ministry of Machinery Industry of the People's Republic of China General method for constant stress life test and accelerated life test : [S]. Beijing : China Standard Press , 1981 : 5 -12 .
[本文引用: 1]
[18]
盐见弘 失效物理基础 [M].北京 :科学出版社 ,1982 :2 -180 .
[本文引用: 1]
YAN J H Physics of failure [M]. Beijing : Science Press , 1982 : 2 -180 .
[本文引用: 1]
[19]
中国航空工业总公司第三○一所 J系列矩形线簧电连接器 : [S].北京 :中国标准出版社 ,1996 :1 -9 .
[本文引用: 1]
[301]
Institute of China National Aviation Industry Corporation. J series rectangular wire spring electric connector : [S]. Beijing : China Standard Press , 1996 : 1 -9 .
[21]
盖炳良 ,滕克难 ,王浩伟 ,等 基于加速因子不变原则的加速度计可靠性分析
[J].中国惯性技术学报 ,2018 ,26 (6 ):835 -840 .
[本文引用: 1]
GAI B L TENG K N WANG H W et al Reliability analysis for accelerometers based on invariant principle of acceleration factor
[J]. Journal of Chinese Inertial Technology , 2018 , 26 (6 ): 835 -840 .
[本文引用: 1]
航天电连接器的可靠性设计建模
1
2017
... 电连接器在各类武器、航天等装备中广泛应用,是实现系统内各零部件之间电能、电信号传输的基础元件.在装备长期贮存过程中,任何一个电连接器失效都有可能会导致后续的工作任务失败[1 ] .因此,定量地设计和评估电连接器的可靠性对装备的定寿和延寿至关重要. ...
航天电连接器的可靠性设计建模
1
2017
... 电连接器在各类武器、航天等装备中广泛应用,是实现系统内各零部件之间电能、电信号传输的基础元件.在装备长期贮存过程中,任何一个电连接器失效都有可能会导致后续的工作任务失败[1 ] .因此,定量地设计和评估电连接器的可靠性对装备的定寿和延寿至关重要. ...
航天电连接器可靠性试验和分析的研究
2
1997
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
... 电连接器中单对接触件发生失效即可能会导致电信号传递失败,因此电连接器的整体寿命取决于最先发生失效的单对接触件的寿命.从功能上来看,电连接器是由一系列接触件组成的串联系统,其寿命分布为最小极值问题[2 ] .因此,在同一线簧丝倾角下,具有g R t
航天电连接器可靠性试验和分析的研究
2
1997
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
... 电连接器中单对接触件发生失效即可能会导致电信号传递失败,因此电连接器的整体寿命取决于最先发生失效的单对接触件的寿命.从功能上来看,电连接器是由一系列接触件组成的串联系统,其寿命分布为最小极值问题[2 ] .因此,在同一线簧丝倾角下,具有g R t
军用电连接器接触件的技术集成创新
1
2014
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
军用电连接器接触件的技术集成创新
1
2014
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
线簧连接器的特性研究
2
2018
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
... 由文献[4 , 7 ]可知,在工程实际应用中常用的线簧丝倾角范围(7 ° ∼ 10 °
线簧连接器的特性研究
2
2018
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
... 由文献[4 , 7 ]可知,在工程实际应用中常用的线簧丝倾角范围(7 ° ∼ 10 °
双曲线插孔的力学研究
1
2017
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
双曲线插孔的力学研究
1
2017
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
弹性接触件双曲线插孔的力学分析
1
2016
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
弹性接触件双曲线插孔的力学分析
1
2016
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
基于稳健性设计原理的接触件插拔力质量一致性优化方法
2
2017
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
... 由文献[4 , 7 ]可知,在工程实际应用中常用的线簧丝倾角范围(7 ° ∼ 10 °
基于稳健性设计原理的接触件插拔力质量一致性优化方法
2
2017
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
... 由文献[4 , 7 ]可知,在工程实际应用中常用的线簧丝倾角范围(7 ° ∼ 10 °
Effect of structural design of hyperbolic wire spring connector on reliability of electrical contacts
1
2017
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
Fretting wear reliability assessment methodology of gold-plated electrical connectors considering manufacture parameters distribution
1
2020
... 在长期贮存过程中,电连接器的主要失效模式为接触失效[2 ] .按接触件的种类划分,电连接器可以分为线簧孔式、绞线式、开槽收口式、冠簧孔式和方形簧片式[3 ] .相比于其他类型的接触件,线簧孔式接触件具有较低的接触电阻、良好的接触可靠性等优点,其在武器装备中被广泛应用.接触件结构参数的改变会对电连接器的接触可靠性产生影响.据研究[4 ] ,在与线簧丝相关的结构参数中,线簧丝倾角对接触件的可靠性有显著影响.陈原等[5 ] 和袁越锦等[6 ] 通过理论计算和有限元仿真分析了线簧丝倾角等设计参数对线簧孔式接触件插拔力的影响规律;凌三强等[7 ] 基于稳健性设计原理,研究了包括线簧丝倾角在内的结构参数的最优组合,优化了线簧孔式接触件插拔力的质量特性分布.Zhou等[8 ] 对线簧孔式接触件进行了力学计算和有限元分析,通过对比接触压力及其极限范围来评估该接触件的可靠性.Ling等[9 ] 研究了线簧孔式接触件的结构设计参数分布对电连接器在微动磨损下的接触可靠性的影响,并给出了微动磨损下的可靠性评估方法.综上所述,线簧丝倾角是线簧孔式接触件的重要设计参数之一,合理地选择线簧丝倾角对接触件的接触可靠性起关键作用.然而,现有文献局限于线簧丝倾角对线簧孔式电连接器接触可靠性影响的定性研究,暂未给出线簧丝倾角对线簧孔式电连接器贮存寿命的影响规律. ...
线簧孔式电连接器接触可靠性设计建模与试验评估
2
2020
... 线簧孔式电连接器由线簧孔式接触件、绝缘件、密封件及壳体四大部分组成[10 ] .其中,线簧孔式接触件包含两部分:线簧插孔和与之配合的插针,其结构如图1 所示. ...
... 结合文献[10 ],膜层电阻率ρ m
线簧孔式电连接器接触可靠性设计建模与试验评估
2
2020
... 线簧孔式电连接器由线簧孔式接触件、绝缘件、密封件及壳体四大部分组成[10 ] .其中,线簧孔式接触件包含两部分:线簧插孔和与之配合的插针,其结构如图1 所示. ...
... 结合文献[10 ],膜层电阻率ρ m
Step-stress accelerated degradation test modeling and statistical analysis methods
1
2013
... 在贮存环境下,线簧孔式电连接器的接触失效机理主要为接触件基底材料铜的氧化腐蚀[11 -12 ] .接触件的表面通常会进行镀金处理,由于镀层较薄且往往存在孔隙,使得部分基底材料铜暴露在空气中;同时,基底材料中的Cu+ 也会通过快速扩散通道(如晶体缺陷等)扩散至镀层表面[13 ] ,而Cu+ 对空气中的氧有强烈的亲和力,易发生反应,生成腐蚀物Cu2 O,且Cu2 O的增长速度与Cu+ 的扩散速率有关.随着Cu+ 的不断扩散,Cu2 O的厚度逐渐增大,接触件的接触电阻随之增大,直至超过失效阈值而发生接触失效. ...
Accelerated degradation reliability modeling and test data statistical analysis of aerospace electrical connector
1
2011
... 在贮存环境下,线簧孔式电连接器的接触失效机理主要为接触件基底材料铜的氧化腐蚀[11 -12 ] .接触件的表面通常会进行镀金处理,由于镀层较薄且往往存在孔隙,使得部分基底材料铜暴露在空气中;同时,基底材料中的Cu+ 也会通过快速扩散通道(如晶体缺陷等)扩散至镀层表面[13 ] ,而Cu+ 对空气中的氧有强烈的亲和力,易发生反应,生成腐蚀物Cu2 O,且Cu2 O的增长速度与Cu+ 的扩散速率有关.随着Cu+ 的不断扩散,Cu2 O的厚度逐渐增大,接触件的接触电阻随之增大,直至超过失效阈值而发生接触失效. ...
1
1998
... 在贮存环境下,线簧孔式电连接器的接触失效机理主要为接触件基底材料铜的氧化腐蚀[11 -12 ] .接触件的表面通常会进行镀金处理,由于镀层较薄且往往存在孔隙,使得部分基底材料铜暴露在空气中;同时,基底材料中的Cu+ 也会通过快速扩散通道(如晶体缺陷等)扩散至镀层表面[13 ] ,而Cu+ 对空气中的氧有强烈的亲和力,易发生反应,生成腐蚀物Cu2 O,且Cu2 O的增长速度与Cu+ 的扩散速率有关.随着Cu+ 的不断扩散,Cu2 O的厚度逐渐增大,接触件的接触电阻随之增大,直至超过失效阈值而发生接触失效. ...
1
1998
... 在贮存环境下,线簧孔式电连接器的接触失效机理主要为接触件基底材料铜的氧化腐蚀[11 -12 ] .接触件的表面通常会进行镀金处理,由于镀层较薄且往往存在孔隙,使得部分基底材料铜暴露在空气中;同时,基底材料中的Cu+ 也会通过快速扩散通道(如晶体缺陷等)扩散至镀层表面[13 ] ,而Cu+ 对空气中的氧有强烈的亲和力,易发生反应,生成腐蚀物Cu2 O,且Cu2 O的增长速度与Cu+ 的扩散速率有关.随着Cu+ 的不断扩散,Cu2 O的厚度逐渐增大,接触件的接触电阻随之增大,直至超过失效阈值而发生接触失效. ...
电磁继电器贮存期接触电阻增长的动力学模型
1
2012
... 从微观层面来看,Cu+ 的扩散需要克服能量势垒,克服能量势垒所消耗的能量即为离子间的扩散激活能Δ E . 接触件插合时所产生的接触压力会在其接触表面形成一个挤压应力J ,该应力的存在会使克服能量势垒所消耗的能量增大[14 ] .根据空位扩散机制,可认为单个Cu+ 在挤压应力J d 2 ,单次扩散的位移为d ,则Cu+ 进行一次扩散所做的功为Jd 3 ,因此在挤压应力J 下的扩散激活能为Δ E - J d 3 J [15 ] .由上文分析可知,线簧丝倾角增大会导致线簧丝与插针之间的接触压力增大,故Cu+ 单次扩散时所做的功Jd 3 也将增大,使得扩散激活能增大,导致单位时间内扩散至表面的Cu+ 数量减少,腐蚀物Cu2 O的增长速度减慢,从而延长了线簧孔式接触件的贮存寿命. ...
电磁继电器贮存期接触电阻增长的动力学模型
1
2012
... 从微观层面来看,Cu+ 的扩散需要克服能量势垒,克服能量势垒所消耗的能量即为离子间的扩散激活能Δ E . 接触件插合时所产生的接触压力会在其接触表面形成一个挤压应力J ,该应力的存在会使克服能量势垒所消耗的能量增大[14 ] .根据空位扩散机制,可认为单个Cu+ 在挤压应力J d 2 ,单次扩散的位移为d ,则Cu+ 进行一次扩散所做的功为Jd 3 ,因此在挤压应力J 下的扩散激活能为Δ E - J d 3 J [15 ] .由上文分析可知,线簧丝倾角增大会导致线簧丝与插针之间的接触压力增大,故Cu+ 单次扩散时所做的功Jd 3 也将增大,使得扩散激活能增大,导致单位时间内扩散至表面的Cu+ 数量减少,腐蚀物Cu2 O的增长速度减慢,从而延长了线簧孔式接触件的贮存寿命. ...
A stress corrosion cracking mechanism based on surface mobility
1
1987
... 从微观层面来看,Cu+ 的扩散需要克服能量势垒,克服能量势垒所消耗的能量即为离子间的扩散激活能Δ E . 接触件插合时所产生的接触压力会在其接触表面形成一个挤压应力J ,该应力的存在会使克服能量势垒所消耗的能量增大[14 ] .根据空位扩散机制,可认为单个Cu+ 在挤压应力J d 2 ,单次扩散的位移为d ,则Cu+ 进行一次扩散所做的功为Jd 3 ,因此在挤压应力J 下的扩散激活能为Δ E - J d 3 J [15 ] .由上文分析可知,线簧丝倾角增大会导致线簧丝与插针之间的接触压力增大,故Cu+ 单次扩散时所做的功Jd 3 也将增大,使得扩散激活能增大,导致单位时间内扩散至表面的Cu+ 数量减少,腐蚀物Cu2 O的增长速度减慢,从而延长了线簧孔式接触件的贮存寿命. ...
1
2008
... 接触件电阻r 由体电阻r v 和接触电阻r t (包括收缩电阻r c 和膜层电阻r f )组成.由电接触理论[16 ] 可得,单根线簧丝与插针接触产生的收缩电阻r c0 和膜层电阻r f0 分别为: ...
1
2008
... 接触件电阻r 由体电阻r v 和接触电阻r t (包括收缩电阻r c 和膜层电阻r f )组成.由电接触理论[16 ] 可得,单根线簧丝与插针接触产生的收缩电阻r c0 和膜层电阻r f0 分别为: ...
1
1981
... 2)温度应力水平.以温度应力水平提高不改变线簧孔式电连接器失效机理为前提,得到线簧孔式接触件在158 ℃下未出现除接触失效外的失效情况.参考前期经验,选取4组温度应力水平,最高温度T 4 =158 ℃,最低温度T 1 =105 ℃;按照温度应力水平等间隔的原则[17 ] ,确定中间温度T 2 =120 ℃,T 3 =140 ℃. ...
1
1981
... 2)温度应力水平.以温度应力水平提高不改变线簧孔式电连接器失效机理为前提,得到线簧孔式接触件在158 ℃下未出现除接触失效外的失效情况.参考前期经验,选取4组温度应力水平,最高温度T 4 =158 ℃,最低温度T 1 =105 ℃;按照温度应力水平等间隔的原则[17 ] ,确定中间温度T 2 =120 ℃,T 3 =140 ℃. ...
1
1982
... 4)测试间隔和截尾时间.通过对线簧孔式接触件进行摸底试验后可知,在12 h的测试间隔下,158 ℃下线簧孔式接触件样品的接触电阻退化趋势明显.基于10 ℃法则[18 ] ,圆整后确定在105,120,140 ℃下的测试间隔分别为120,72,24 h.根据前期其他型号电连接器的试验数据,确定截尾时间为1 500 h. ...
1
1982
... 4)测试间隔和截尾时间.通过对线簧孔式接触件进行摸底试验后可知,在12 h的测试间隔下,158 ℃下线簧孔式接触件样品的接触电阻退化趋势明显.基于10 ℃法则[18 ] ,圆整后确定在105,120,140 ℃下的测试间隔分别为120,72,24 h.根据前期其他型号电连接器的试验数据,确定截尾时间为1 500 h. ...
1
1996
... 5)失效判据.由文献[19 ]可知,直径为1 mm的线簧孔式接触件的电阻不得大于5 m Ω 5 m Ω . ...
机电产品加速贮存试验与寿命评估方法研究
1
2021
... 根据上文建立的线簧孔式接触件的性能退化模型(6),利用不同试验条件下的接触件电阻测量值,通过最小二乘法求出第γ [20 ] . ...
机电产品加速贮存试验与寿命评估方法研究
1
2021
... 根据上文建立的线簧孔式接触件的性能退化模型(6),利用不同试验条件下的接触件电阻测量值,通过最小二乘法求出第γ [20 ] . ...
基于加速因子不变原则的加速度计可靠性分析
1
2018
... 假设常应力下的温度为25 ℃,由加速因子不变原则[21 ] 可知,在失效机理不变的情况下,参数σ l n α β 表3 中的数据代入式(8) 和式(11) ,即可得到各个线簧丝倾角水平下的线簧孔式电连接器的贮存可靠度函数.利用MATLAB软件编程得到常温(25 ℃)下线簧丝倾角不同时线簧孔式电连接器的可靠度曲线,结果如图6 所示.根据图6 ,不难发现随着线簧丝倾角的增大,同一可靠度下线簧孔式电连接器的贮存寿命增大. ...
基于加速因子不变原则的加速度计可靠性分析
1
2018
... 假设常应力下的温度为25 ℃,由加速因子不变原则[21 ] 可知,在失效机理不变的情况下,参数σ l n α β 表3 中的数据代入式(8) 和式(11) ,即可得到各个线簧丝倾角水平下的线簧孔式电连接器的贮存可靠度函数.利用MATLAB软件编程得到常温(25 ℃)下线簧丝倾角不同时线簧孔式电连接器的可靠度曲线,结果如图6 所示.根据图6 ,不难发现随着线簧丝倾角的增大,同一可靠度下线簧孔式电连接器的贮存寿命增大. ...