计算模型对空气静压轴承特性分析有效性的影响

doi:10.3785/j.issn.1006-754X.2023.00.010

计算模型对空气静压轴承特性分析有效性的影响

辛晓承^,^,¹, 龙威^,¹, 高浩¹, 王萍¹, 雷基林²

1.昆明理工大学机电工程学院，云南昆明 650500

2.昆明理工大学云南省内燃机重点实验室，云南昆明 650500

Effect of calculation model on effectiveness of characteristics analysis of aerostatic bearings

XIN Xiaocheng^,^,¹, LONG Wei^,¹, GAO Hao¹, WANG Ping¹, LEI Jilin²

1.Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China

2.Yunnan Province Key Laboratory of Internal Combustion Engines, Kunming University of Science and Technology, Kunming 650500, China

通讯作者: 龙威（1981—），女，河北张家口人，教授，博士，从事气体润滑研究，E-mail: daifor@163.com

收稿日期: 2022-06-08 修回日期: 2022-08-22

基金资助:

国家自然科学基金资助项目. 51766006
云南省万人计划资助项目. YNWR-QNBJ-2018-162

Received: 2022-06-08 Revised: 2022-08-22

作者简介 About authors

辛晓承（1998—），男，云南昭通人，硕士生，从事空气静压轴承研究，E-mail:xiao_cheng_xin@163.com，https://orcid.org/0000-0003-2270-3594 , E-mail：xiao_cheng_xin@163.com

摘要

空气静压轴承具有精度高、摩擦小和寿命长的特点，被广泛应用于航空航天等领域。不同空气静压轴承气膜的承载面积和厚度的差距悬殊，导致气膜内部的流场极为复杂，传统的基于层流假设的N-S（Navier-Stokes）方程已无法精确预测该轴承的工作特性。为此，以圆盘形中心供气小孔节流空气静压轴承为研究对象，基于气体润滑和湍流理论建立其气膜流场数学模型，分析了气膜流场内湍流斑形成涡旋后的发展运动以及向平滑层流过渡的过程。在相同工况下，针对气膜厚度较小（<10 μm）时的特征流场采用k-ɛ模型，针对气膜厚度中等（10~20 μm）时的特征流场采用大涡模拟（large eddy simulation, LES）模型，针对气膜厚度较大（20~30 μm）时的特征流场采用“k-ɛ模型+层流模型”。然后，设计并搭建空气静压轴承静态特性测试实验台，以验证所采用计算模型的准确性。结果表明：根据不同工况选择适宜的计算模型，可提高空气静压轴承气膜流场的计算精度。当气膜厚度小于10 μm时，气腔内湍动程度较大，宜采用k-ɛ模型进行描述；当气膜厚度增大到10~20 μm时，气腔内大涡旋以一定速度沿半径方向扩散并输运能量，宜采用LES模型进行描述；当气膜厚度增大至20~30 μm时，气膜的容性效应增强，使得气腔内后半部分呈现层流特征，宜采用混合计算模型进行描述。研究结果为不同工况下空气静压轴承的设计提供了参考数据，准确选择计算模型有利于缩短研发周期。

关键词： 空气静压轴承 ; 湍流理论 ; k-ɛ模型 ; 大涡模拟（LES）模型 ; 混合计算模型

Abstract

Aerostatic bearings have the characteristics of high precision, low friction and long life, which are widely used in aerospace and other fields. The bearing area and thickness of gas film of different aerostatic bearings are very different, resulting in extremely complex flow field inside the gas film. However, the traditional N-S (Navier-Stokes) equation based on the laminar flow hypothesis can not accurately predict the working characteristics of the bearing. Therefore, taking the disk-shaped center air supply orifice throttle aerostatic bearing as the research object, a mathematical model of its gas film flow field was established based on the gas lubrication and turbulence theory, and the development motion of turbulent spots in the gas film flow field after forming vortices and the transition process to smooth laminar flow were analyzed. Under the same operating conditions, the k-ɛ model was adopted for the characteristic flow field when the gas film thicknss was smaller (<10 μm), the large eddy simulation (LES) model was adopted for the characteristic flow field when the gas film thickness was medium (10‒20 μm), and the k-ɛ model and the laminar flow model were adopted for the characteristic flow field when the gas film thicknss was larger (20‒30 μm). Then, the static characteristics test platform of aerostatic bearing was designed and built to verify the accuracy of the calculation model. The results showed that selecting appropriate calculation model according to different operating conditions could improve the calculation accuracy of gas film flow field of aerostatic bearings. When the gas film thickness was less than 10 μm, the turbulence in the gas cavity was relatively large, and it was appropriate to describe it using the k-ɛ model. When the gas film thickness increased to 10‒20 μm, the large vortices in the gas cavity diffused and transported energy along the radius at a certain speed, which should be described by the LES model. When the gas film thickness increased to 20‒30 μm, the capacitance effect of the gas film increased, which made the rear half of the gas cavity present laminar flow characteristics, and the hybrid calculation model should be used to describe it. The research results provide reference data for the design of aerostatic bearings under different operating conditions, and the accurate selection of calculation model is conducive to shortening the development cycle.

Keywords： aerostatic bearing ; turbulence theory ; k-ɛ model ; large eddy simulation (LES) model ; hybrid calculation model

PDF (4364KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

辛晓承, 龙威, 高浩, 王萍, 雷基林. 计算模型对空气静压轴承特性分析有效性的影响. 工程设计学报[J], 2023, 30(2): 226-236 doi:10.3785/j.issn.1006-754X.2023.00.010

XIN Xiaocheng, LONG Wei, GAO Hao, WANG Ping, LEI Jilin. Effect of calculation model on effectiveness of characteristics analysis of aerostatic bearings. Chinese Journal of Engineering Design[J], 2023, 30(2): 226-236 doi:10.3785/j.issn.1006-754X.2023.00.010

空气静压轴承因具有精度高、摩擦小等优点而被广泛应用于航空航天、医疗卫生和精密制造等领域^[1-3]。尤其是在航空航天领域内，空气静压轴承作为航空发动机的重要部件，决定了发动机运行的安全性。因此，准确分析和描述空气静压轴承的工作特性极为重要。

空气静压轴承主要依靠自身表面与支承平台表面之间形成稳定气膜来提供足够的承载力和支承刚度。根据流体润滑原理，高压气体在通过节流器进入气膜的过程中，不仅流动方向和流速发生了改变，流动状态和能量输运过程也有剧烈的变化^[4-5]。由于现有观测手段的限制，轴承气膜内部的流场特性仍无法通过可视化实验来准确描述。目前，在实验中主要通过测量静态特性（静承载力、静刚度和耗气量）和动态特性（动刚度、微振动的时/频域特性）来评价轴承的工作特性。因此，国内外学者在研究轴承气膜流场变化时主要借助基于流体力学和气体润滑理论的数值计算方法。传统的计算方法通常不考虑轴承供气孔附近的复杂流动，而是以气膜承载表面为主要研究对象。同时，由于气膜厚度通常为微米级，可忽略气膜厚度方向上的压力梯度变化，并假设工作介质为理想气体，即认为气膜流场是完全发展的层流，通过联立气膜流场的运动方程、连续性方程和状态方程，考虑气体的黏性系数和边界条件，最终推导得到雷诺方程作为描述气膜流场的控制方程^[6-7]。相较于各种工程算法，这种将气膜流场简化为平滑层流的计算方法的推导过程较为严谨，且与实验结果的一致性较高。因此，在对计算精度要求不高的情况下，该方法基本可以满足要求^[8-10]。但随着计算机科学的发展和精密/超精密制造技术要求的提高，极小厚度气膜（<5 μm）下空气静压轴承的承载力和刚度的计算值与理论值存在巨大偏差^[11]，同时伴随着轴承微幅自激振动现象的发现^[12]，学者们意识到供气孔附近的复杂流动虽作用范围小，但是影响范围巨大。因此，有必要采用新的计算模型对轴承气膜内部的流场变化和能量输运特征进行完整、准确的分析和描述。

Chen等^[13]率先提出采用完全稳态N-S（Navier-Stokes）方程求解空气静压轴承气膜流场的方法，明确指出气腔内流体状态的复杂性不容忽视。张小青等^[14]将广义雷诺方程与运动学方程进行时域耦合，并采用直接数值模拟方法进行联立求解，获得了任意时刻下螺旋槽推力轴承-转子系统中微转子的瞬态位移和速度响应。Li等^[15]采用大涡模拟（large eddy simulation, LES）方法分析了空气静压轴承的时变流场。Dong等^[16]通过求解流-固耦合控制方程，分析了空气静压轴承的静承载力和其气膜的压力分布。陈东菊等^[17]将流量因子引入雷诺方程，推导出考虑可压缩气体稀薄效应的雷诺方程，利用该方程计算得到的刚度与实验值仅相差20%左右。Zhou等^[18]提出了一种混合求解方法：将空气静压轴承供气孔附近的气腔定义为内区，采用N-S方程求解；将其他部分定义为外区，采用雷诺方程求解。Gao等^[19]建立了Mobius公式并对单进气口空气静压轴承的性能进行了研究，发现利用该公式分析矩形空气静压轴承的性能非常有效。Zhang等^[20]采用分离变量方法研究了空气静压轴承承载力的影响因素。王伟等^[21]采用LES模型研究了空气静压轴承内部气容对微观流场的影响。

综上所述，基于现有的研究方法和手段，业内学者已基本达成了空气静压轴承气膜内不是平滑层流的统一观点，但是对于如何准确描述供气孔附近的复杂流动尚存在分歧。笔者的课题组前期根据空气静压轴承供气孔的实际特征，按照冲击射流的基本原理对供气孔和气腔区进行了严格的数学描述^[5]。但是，经过节流的压力气体在进入气腔后再沿半径方向发展扩散时，其动力学特征十分复杂，既与轴承的工作参数（供气压力、气膜厚度等）有关，又受到轴承结构参数（气腔的形状、尺寸等）的影响。对于这类非线性极强的瞬态非定常流动，采用直接数值模拟方法显然是无法满足要求的，而在采用非直接数值模拟方法对其进行分析描述时，是选择雷诺应力模型还是涡黏模型极为重要。因此，笔者以已有的实验结论为基础，通过分析不同工况下空气静压轴承气膜流场的特征以及根据气膜流场的流线特征、涡量特征及其内部湍动能的变化规律，给出相应的计算模型，并进一步分析这些计算模型的适用条件和误差。

1 空气静压轴承气膜流场数学模型

1.1　空气静压轴承工作原理

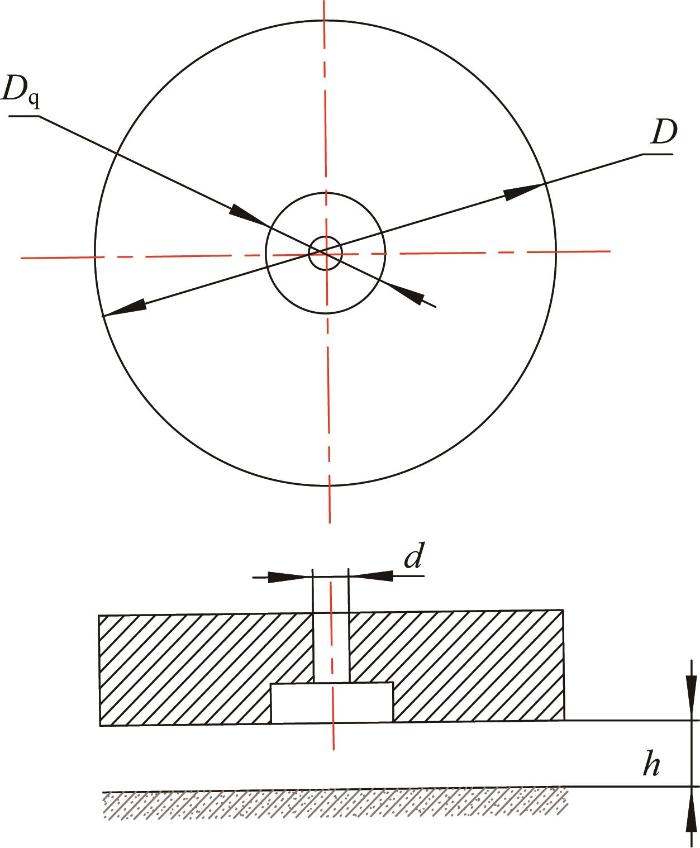
本文选择中心供气的圆盘形小孔节流空气静压轴承（见图1）为研究对象，其结构尺寸和工作参数如表1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 空气静压轴承结构示意

Fig.1 Structure diagram of aerostatic bearing

表1 空气静压轴承的结构尺寸和工作参数

Table 1 Structure dimensions and working parameters of aerostatic bearing

参数	数值
轴承直径D/mm	100
气腔直径D_q/mm	3
供气孔直径d/mm	0.2
气膜厚度h/μm	5~30
供气压力p_s/MPa	0.2~0.6

新窗口打开| 下载CSV

如图1所示，高压气体从供气孔进入空气静压轴承后，在压力能的作用下，轴承与支承平台之间形成厚度为h的气膜，经过小孔节流器的气体在冲击支承平台的过程中形成了湍流斑，从而引起切向扰动，形成湍流。由于气腔形状和尺寸的限制，一部分流场以分岔流的形式促成一系列小尺度的局部对流，很快耗散掉湍动能；一部分流场在内部剪切流的作用下形成奇特波状的湍流斑并进一步向下游输运扩散；还有一部分流场虽然在供气孔出口处的高压区呈现一定的非线性湍动特征，但是在轴承结构尺寸和工作参数的共同制约下快速完成混沌的无序行为，过渡为平滑稳定的层流并沿径向均匀地向外流出，形成稳定的气膜。

1.2　气膜流场控制方程

由于湍流流动极为复杂，多年来相关学者对湍流过程的数学描述基本都是从N-S方程出发的。完整的N-S方程可描述非定常三维可压缩黏性流动，整个流动过程满足以下3个方程。

1）连续性方程：

\frac{\partial ρ}{\partial t} + \nabla (ρ V) = 0

(1)

2）动量方程：

\{\begin{array}{l} \frac{\partial (ρ u)}{\partial t} + \nabla (ρ u V) = - \frac{\partial P}{\partial x} + \frac{\partial τ_{x x}}{\partial x} + \frac{\partial τ_{y x}}{\partial y} + \frac{\partial τ_{z x}}{\partial z} + ρ f_{x} \\ \frac{\partial (ρ v)}{\partial t} + \nabla (ρ v V) = - \frac{\partial P}{\partial y} + \frac{\partial τ_{x y}}{\partial x} + \frac{\partial τ_{y y}}{\partial y} + \frac{\partial τ_{z y}}{\partial z} + ρ f_{y} \\ \frac{\partial (ρ w)}{\partial t} + \nabla (ρ w V) = - \frac{\partial P}{\partial z} + \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + \frac{\partial τ_{z z}}{\partial z} + ρ f_{z} \end{array}

(2)

3）能量方程：

\begin{array}{l} \frac{\partial}{\partial t} [ρ (e + \frac{V^{2}}{2})] + \nabla [ρ (e + \frac{V^{2}}{2}) V] = \\ ρ \dot{q} + \frac{\partial}{\partial x} (k_{c} \frac{\partial T}{\partial x}) + \frac{\partial}{\partial y} (k_{c} \frac{\partial T}{\partial y}) + \frac{\partial}{\partial z} (k_{c} \frac{\partial T}{\partial z}) - \\ \frac{\partial (u ρ)}{\partial x} - \frac{\partial (v ρ)}{\partial y} - \frac{\partial (w ρ)}{\partial z} + \frac{\partial (u τ_{x x})}{\partial x} + \\ \frac{\partial (u τ_{y x})}{\partial y} + \frac{\partial (u τ_{z x})}{\partial z} + \frac{\partial (v τ_{x y})}{\partial x} + \frac{\partial (v τ_{y y})}{\partial y} + \\ \frac{\partial (v τ_{z y})}{\partial z} + \frac{\partial (w τ_{x z})}{\partial x} + \frac{\partial (w τ_{y z})}{\partial y} + \frac{\partial (w τ_{z z})}{\partial z} + ρ f V \end{array}

(3)

式中：ρ为流体密度；t为时间； $\nabla$ 为哈密顿算子；V为单位时间内流过流体微元的体积；u、v、w分别为流体在x、y、z方向上的速度；τ_xx、τ_xy、τ_xz 等分别为流体剪应力在微元各表面上的分量；f_x、f_y、f_z 分别为流体在x、y、z方向上所受的外力；P为流体微元的压力；e为流体的单位质量总能量； $\dot{q}$ 为单位体积流体的热量变化速率；k_c为流体传热系数；T为温度；f为流体所受外力。

但是，从数学角度出发，完整N-S方程的求解还存在2个难题：一个是关于解的存在性，N-S方程虽可很好地预测流体的运动，并可借助计算机得到很多近似解，但在数学上仍缺乏这些解存在的证明；另一个是解是否有边界，即是否会出现奇点或无穷大现象，暂未得到严谨的数学证明。由于N-S方程求解困难，目前计算流体领域采用的计算模型均是根据不同工况对完整N-S方程进行简化后推导得到的。其中，最为经典的是雷诺时均方程，用于描述湍流平均运动：

\frac{\partial (ρ {\bar{u}}_{i})}{\partial t} + \frac{\partial (ρ {\bar{u}}_{i} {\bar{u}}_{j})}{\partial x_{j}} = - \frac{\partial \bar{P}}{\partial x_{j}} + \frac{\partial}{\partial x_{j}} (μ \frac{\partial {\bar{u}}_{i}}{\partial x_{j}} - ρ \bar{u_{i}^{'} u_{j}^{'}})

(4)

式中： ${\bar{u}}_{i} 、 {\bar{u}}_{j}$ 分别为 $Δ t$ 时间内初始、终止时刻流体的时均速度； $x_{i} 、 x_{j}$ 分别为 $Δ t$ 时间内初始、终止时刻的方向； $- ρ \bar{u_{i}^{'} u_{j}^{'}}$ 为表征流场中局部湍动的湍流应力项（即雷诺应力项）。

对于三维流动而言，除了雷诺时均方程外，还会引入与其他变量 $ϕ$ 相关的方程，这2个方程共包括5个时均量（ $\bar{u} 、 \bar{v} 、 \bar{w} 、 \bar{P} 、 \bar{ϕ}$ ）和9个速度脉动值乘积的时均项（ $\bar{u_{i}^{'} u_{j}^{'}} 、 \bar{u_{j}^{'} ϕ_{}^{'}}$ ，i, j=1, 2, 3）。同时，为了表征雷诺应力项对流场的影响，常采用湍流黏性系数的函数来表示雷诺应力项：

- ρ \bar{u_{i}^{'} u_{j}^{'}} = - P_{t} δ_{i, j} + μ_{t} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) - \frac{2}{3} μ_{t} δ_{i, j} d i v V

(5)

其中：

P_{t} = \frac{1}{3} ρ (\bar{{u^{'}}^{2}} + \bar{{v^{'}}^{2}} + \bar{{w^{'}}^{2}}) = ρ k

k = \frac{1}{3} (\bar{{u^{'}}^{2}} + \bar{{v^{'}}^{2}} + \bar{{w^{'}}^{2}})

式中： $P_{t}$ 为湍流脉动造成的压力； $δ_{i, j}$ 为克罗内克算子；k为单位质量流体的湍动能； $μ_{t}$ 为湍流黏性系数，用于表征由流体分子扩散造成的迁移特性，根据流体的流动状态和空间位置取不同的值。

当流场中有明显的旋流和由应力驱动的二次流时，若只求解湍动能 $k$ ，则会忽视湍流脉动的各向异性，此时需考虑湍动能的耗散作用和流体的压缩作用。根据混合长度理论，不可压缩流体的雷诺应力输运方程可表示为：

\frac{\partial \bar{u_{i}^{'} u_{j}^{'}}}{\partial t} + {\bar{u}}_{k} \frac{\partial \bar{u_{i}^{'} u_{j}^{'}}}{\partial x_{k}} = \frac{D (\bar{u_{i}^{'} u_{j}^{'}})}{D t} = P_{i, j} + π_{i, j} + D_{i, j} - ε_{i, j}

(6)

其中：

ε_{i, j} = ν \bar{(\frac{\partial u_{i}^{'}}{\partial x_{k}}) (\frac{\partial u_{j}^{'}}{\partial x_{k}})}

式中： $u_{k}$ 为湍流瞬时速度；D( )/Dt为随体导数； $P_{i, j}$ 为应力产生项，是雷诺应力和平均运动速度梯度的乘积； $π_{i, j}$ 为压力应变再分配项，是脉动压强和脉动速度变形张量的平均值； $D_{i, j}$ 为雷诺应力扩散项，它包含与压力、速度相关的扩散作用，不规则流动所携带脉动动能形成的扩散作用以及由流体分子自身黏性形成的湍动能扩散作用； $ε_{i, j}$ 为湍动能耗散项，表征小尺度涡耗散时机械能转化为热能的速率。

在混合长度理论中，湍流黏性系数 $μ_{t}$ 与流体微元集合位置和时均速度有关，而与湍流特性参数无关，这极大地忽视了湍流脉动造成的黏性过程与流体分子扩散作用形成的黏性过程。因此，有必要考虑湍流脉动的特征速度和特征尺度。采用湍动能的平方根来表征湍流脉动速度，则湍流黏性系数 $μ_{t}$ 可表示为：

μ_{t} = c_{μ}^{'} ρ l \sqrt[]{k}

(7)

式中： $c_{μ}^{'}$ 为经验系数；l为湍流脉动的特征尺度。

进一步对雷诺应力输运方程进行收缩运算并简化，可得湍动能方程，即k方程：

\begin{array}{l} ρ \frac{\partial k}{\partial t} + ρ μ_{j} \frac{\partial k}{\partial x_{j}} = \\ \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{k}}) \frac{\partial k}{\partial x_{j}}] + μ_{t} \frac{\partial u_{i}}{\partial x_{j}} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) - c_{D} ρ \frac{k^{\frac{3}{2}}}{l} \end{array}

(8)

式中：流体分子黏性系数； $σ_{k}$ 为湍动能的普朗特数， $σ_{k} \approx 1$ ；c_D为经验系数。

根据周培源教授提出的能量耗散率 $ε$ 、湍动能k和湍流脉动特征尺度l的关系，可得 $ε$ 方程：

\begin{array}{l} ρ \frac{\partial ε}{\partial t} + ρ u_{k} \frac{\partial ε}{\partial x_{k}} = \\ \frac{\partial}{\partial x_{k}} [(μ + \frac{μ_{t}}{σ_{ε}}) \frac{\partial ε}{\partial x_{k}}] + \frac{c_{1}}{k} μ_{t} \frac{\partial u_{i}}{\partial u_{j}} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) - c_{2} ρ \frac{ε^{2}}{k} \end{array}

(9)

式中：c₁、c₂为经验系数。

鉴于本文研究的流场是空气静压轴承表面与支承平台表面之间的微米级气膜流场，该流场中湍动能的耗散主要是由上下壁面的约束导致的。基于上述分析，本文对3种气膜厚度下的流场特征进行研究。

1）当气膜流场内湍流是大量无规则的小尺度涡旋或是较大涡旋向小尺度涡旋传递能量时，采用k-ɛ模型进行描述，此时控制方程包括连续性方程、动量方程、k方程和 $ε$ 方程。

2）随着气膜厚度增大，因受几何结构和边界条件的影响，气膜流场内的涡旋达到平均流动特征尺度时，流场内的动量、能量、质量和其他标量主要由大涡旋输运，此时小尺度涡旋不仅具有各向同性，而且受几何结构和边界条件的影响较小。因此，气膜流场不能再用k-ɛ模型来描述了，而是应当忽略波数空间内小于给定物理宽度的小涡旋，直接用大涡旋的控制方程来描述，即LES模型：

\{\begin{array}{l} \frac{\partial ρ}{\partial t} + \frac{\partial ρ {\tilde{u}}_{i}}{\partial x_{i}} = 0 \\ \frac{\partial}{\partial t} (ρ {\tilde{u}}_{i}) + \frac{\partial}{\partial x_{j}} (ρ {\tilde{u}}_{i} {\tilde{u}}_{j}) = \frac{\partial}{\partial x_{i}} (μ \frac{\partial {\tilde{u}}_{i}}{\partial x_{j}}) - \frac{\partial \tilde{P}}{\partial x_{i}} - \frac{\partial τ_{i j}}{\partial x_{j}} \end{array}

(10)

其中：

τ_{i j} = ρ \tilde{u_{i} u_{j}} - ρ {\tilde{u}}_{i} {\tilde{u}}_{j}

式中：带波浪线的变量表示过滤的变量； $τ_{i j}$ 为亚网格应力。

由于该控制方程不易得到解析解，本文采用基于有限元法的ANSYS Fluent软件进行数值求解，并对照实验结果，分析LES模型描述气膜厚度中等时气膜流场的有效性。

3）当气膜厚度进一步增大时，从供气孔进入气腔的高压气体会先在供气孔附近形成充分发展的湍流，而后逐渐过渡为层流。根据文献[18]，此时应对气膜流场进行分区计算，即采用混合计算模型（k-ɛ模型+层流模型）：针对湍流区域，采用k-ɛ模型；针对层流区域，采用层流模型，并以湍流区域出口的压力值作为层流区域入口的压力值。

2 空气静压轴承气膜流场特性分析

空气静压轴承气膜厚度通常在几十微米内，且轴承表面和支承平台表面均采用非透明材料，因此无法对气膜流场开展可视化观测。为了验证本文理论分析的有效性，首先，利用数值计算方法分析不同工况下轴承气膜流场的特征，并通过云图和流线图进行可视化展示；然后，通过实验测试轴承承载力和刚度的变化规律，以验证数值计算结果的准确性。

对于图1所示的空气静压轴承，其工作介质空气的密度为1.225 kg/m³，动力黏度为1.79 $\times$ 10^-5 $N \cdot s / m^{3}$ ；供气孔入口压力均匀分布，供气压力为0.2~0.6 MPa；气膜流场出口压力为标况大气压，不计壁面粗糙影响，且壁面绝热无速度滑移，考虑局部湍流的影响。在ANSYS Fluent软件中选择k-ɛ模型和 LES模型进行计算时，压力-速度耦合器选择SIMPLE（semi-implicit method for pressure linked equations，压力耦合方程组的半隐式方法）算法；密度、湍动能、耗散率均采用二阶迎风格式；残差小于10^-6时计算结果收敛。

2.1　数值计算的网格无关性验证

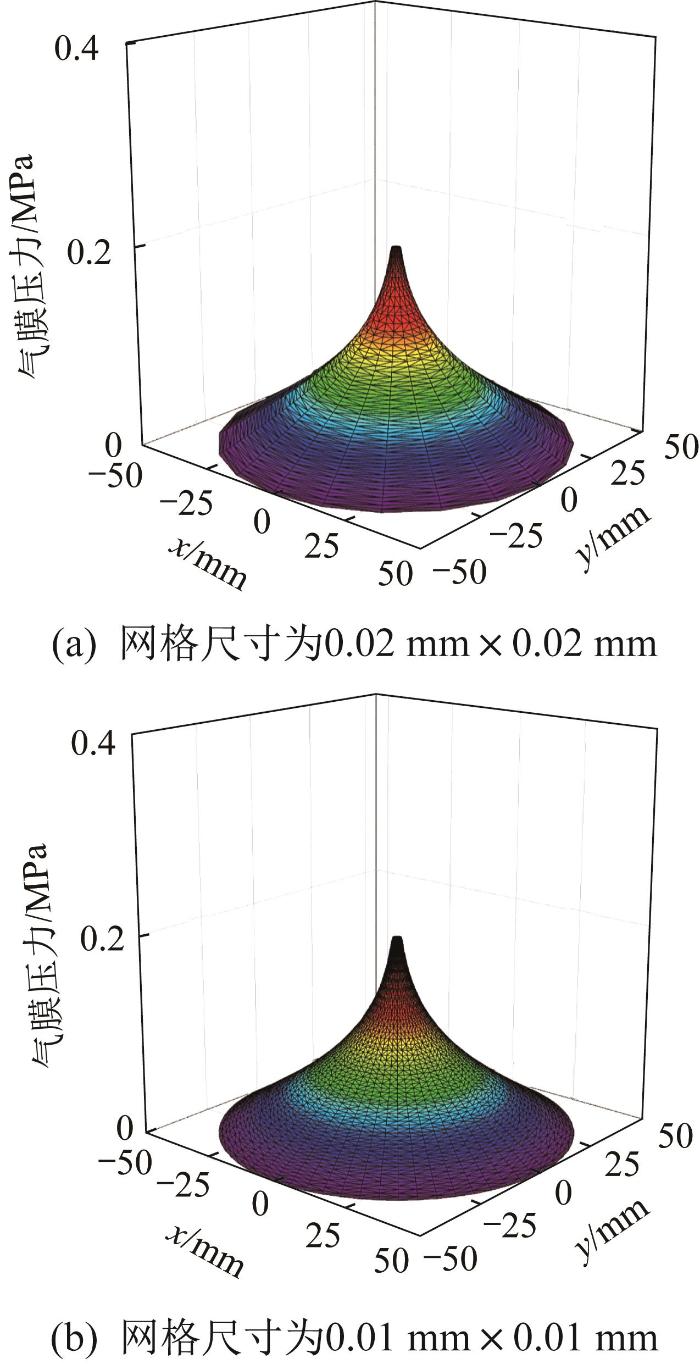
为保证数值计算结果的有效性，开展网格无关性验证。采用双倍网格加密的方法，分别计算供气压力为0.2 MPa、气膜厚度为5 μm的条件下，最大面网格尺寸为0.02 mm×0.02 mm和0.01 mm×0.01 mm时空气静压轴承气膜流场的压力分布情况，结果如图2所示。通过对比可知，基于2种网格尺寸计算得到的空气静压轴承的承载力的相对误差小于0.05%，说明网格尺寸继续变小并不能大幅提高计算精度，且会增大计算量，故本文选择0.02 mm×0.02 mm的网格尺寸进行数值计算，较为经济有效。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 气膜流场特性数值计算的网格无关性验证结果

Fig.2 Grid independence verification results of numerical calculation of gas film flow field characteristics

2.2　轴承的静态特性分析

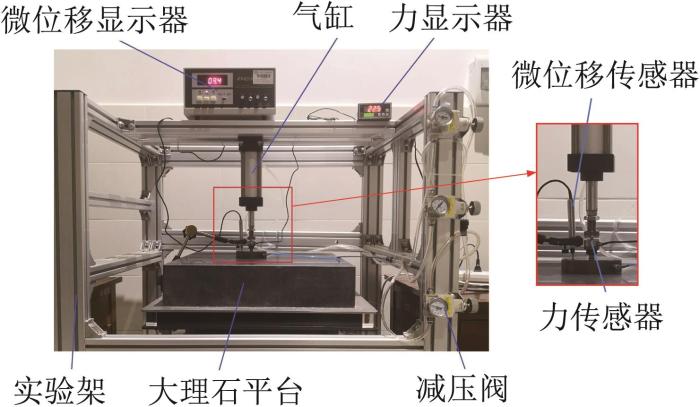
为保证空气静压轴承具有较高的承载能力，气膜厚度h≤30 μm。结合该轴承的设计使用要求，选择气膜厚度h=5，15，25 μm（分别对应气膜厚度较小、中等和较大的情况）进行分析。搭建如图3所示的实验台，对空气静压轴承的静态特性进行测试。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 空气静压轴承静态特性测试实验台

Fig.3 Test bench for static characteristics of aerostatic bearing

如图3所示，空气静压轴承水平放置在00级大理石平台上；DGS-C微位移显示器、XMT808-I压力显示器、IR2020-02减压阀和气缸等均被固定在实验架上；GD1X018微位移传感器由固定于大理石平台一侧的磁力表座固定，JHBM-H3-500KG力传感器固定在气缸出杆头部处。当气缸入口的供气压力大于气缸出口时，气缸出杆头部会向空气静压轴承传递均匀、稳定的垂直方向的力。通过调节气缸的入口压力和出口压力来保证所需的气膜厚度。每次实验重复5组，并求算术平均值，得到不同供气压力和不同气膜厚度下轴承的承载力和耗气量。

2.2.1　承载力

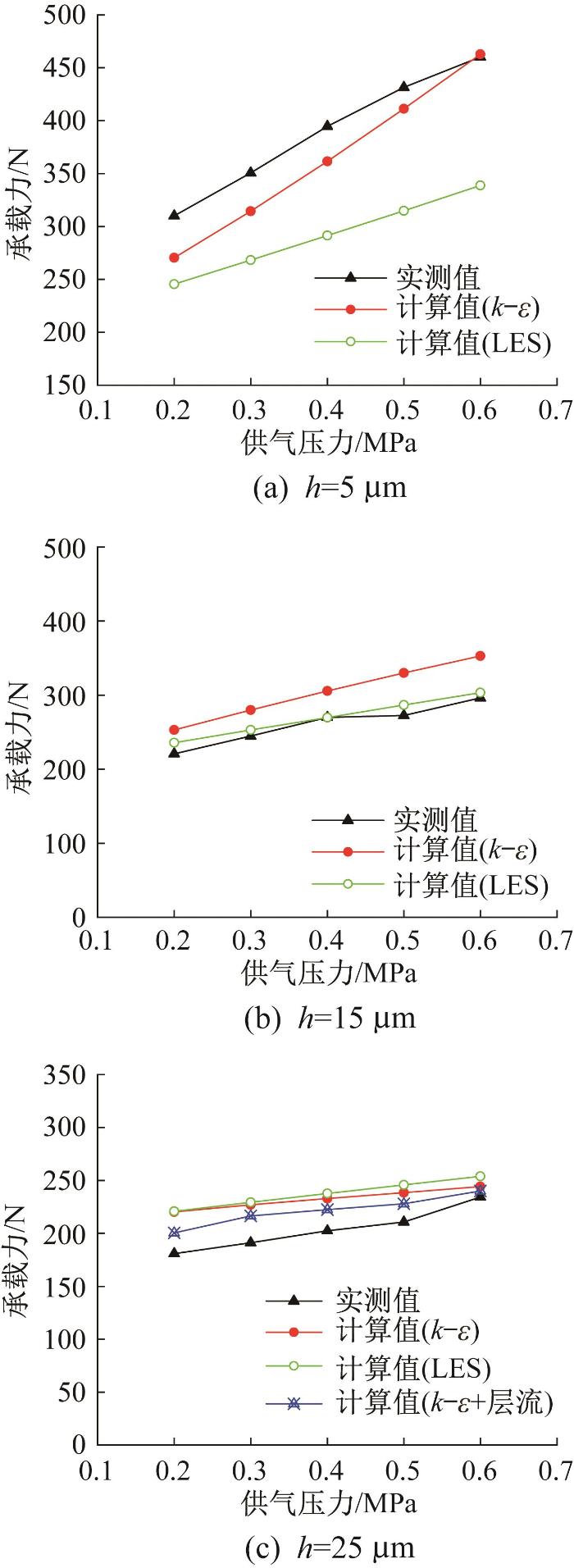
分别采用k-ɛ湍流模型和LES模型对气膜厚度h=5，15，25 μm时空气静压轴承的承载力进行数值计算，并与实验结果进行对比。图4所示为不同气膜厚度下空气静压轴承的承载力随供气压力的变化曲线。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同气膜厚度下空气静压轴承的承载力

Fig.4 Bearing capacity of aerostatic bearing under different gas film thicknesses

由图4(a)可知，当气膜厚度为5 μm时，空气静压轴承承载力的计算值与实测值均随供气压力的增大而增大，且变化规律基本一致，但基于k-ε模型的计算结果与实验结果的偏差更小，供气压力为0.6 MPa时两者的相对偏差小于1%。这是因为当气膜厚度为微米级时，上下壁面对气膜的强约束加快了流场内部的能量耗散，供气孔出口的压力气体在气腔内直接呈大雷诺数湍流，在气源压力的持续作用下，气膜流场内的涡旋呈大量无规律的耗散涡。由图4(b)可知，当气膜厚度为15 μm时，承载力的计算值与实测值均随供气压力的增大而增大，且变化规律基本一致，基于LES模型的计算结果与实验结果的偏差更小。这是因为随着气膜厚度的增大，气流通过时的阻力减小，使得进入气腔的气体在流动方向改变后仍保持一定动能，在大理石平台的冲击反射作用下气流折叠卷夹形成强度较大的涡旋，在气腔内沿流动方向扩散并输运能量。由图4(c)可知，当气膜厚度为25 μm时，采用k-ε模型和LES模型计算得到的承载力较为接近，仅在供气压力较大（0.6 MPa）时，基于k-ε模型的承载力计算值与实测承载力更接近。根据陈学东教授提出的混合分区数值计算方法^[18]，本文采用k-ε模型+层流模型进一步计算了25 μm气膜厚度下承载力随供气压力的变化情况，发现此时的承载力计算结果比单独使用k-ε模型或LES模型时更接近实测承载力。这不仅验证了混合分区数值计算方法的合理性，还证明了传统算法将气膜流场近似为层流模型的有效性。

进一步分析气膜厚度较小（5 μm）时基于k-ε模型计算得到的空气静压轴承气膜流场（稳态）的流线特征和涡量特征，结果如图5所示。由图5(a)可知，当气体通过供气孔进入气腔时，5 μm气膜厚度下的气膜流场中产生了一系列形态不规则和强度不同的涡旋。中间主涡旋的流速约为32 m/s，两侧伴生涡旋的流速约为15 m/s，但主涡旋表面流态极不稳定，说明此时流场内的湍流以杂乱无章的小尺度涡旋为主。由图5(b)可知，整个高压区呈现破碎且分散的涡量分布特征，再次验证了较小厚度下气膜流场中存在大量不规则涡旋并快速耗散由气源提供的压力能。这从原理上解释了k-ε模型能合理描述较小气膜厚度下的气膜流场特征。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 气膜厚度为5 μm时的气膜流场特征

Fig.5 Characteristics of gas film flow field with gas film thickness of 5 μm

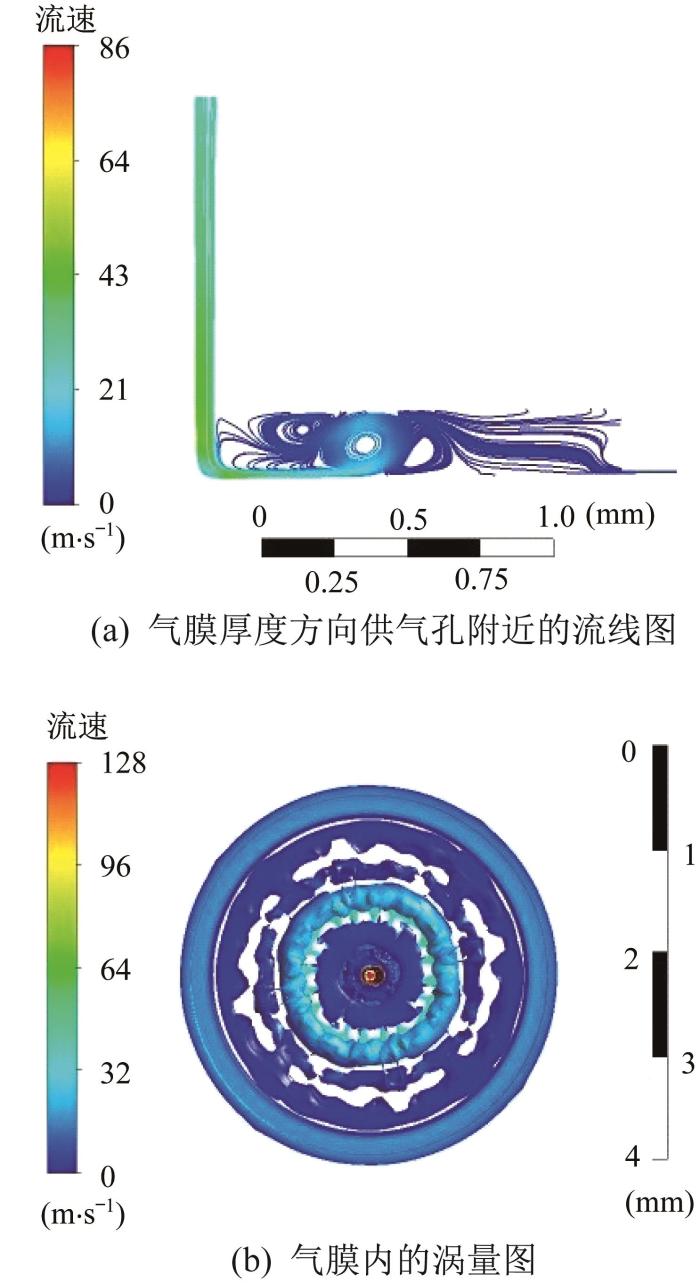
当气膜厚度逐渐增大至中等（15 μm）时，基于LES模型分析气膜流场（稳态）的流线特征和涡量特征，结果如图6所示。由图6(a)可知，当气体通过供气孔进入气腔时，气膜流场中出现了一个流速约为50 m/s的大涡旋，并在其下游伴生了一个流速不足20 m/s的小涡旋。2个涡旋的表面光滑，且大涡旋距离供气孔较远，说明大涡旋是以一定流速沿半径方向向外扩散并输运能量的，而伴生的小涡旋则被抑制，无法进一步破碎成更多、更小的湍流斑。由图6(b)可知，气膜流场内呈现比较集中的涡量，靠近供气孔附近的涡量较强且分布范围较广，即使是通过气腔外缘后仍保持较大的涡强。这说明气腔内主要以规律且较为集中的大涡旋为主，气源提供的压力能未被充分耗散，而是以湍动能的形式在气腔内沿流动方向扩散传递。这从原理上解释了LES模型能对中等气膜厚度下的气膜流场特征进行合理描述。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 气膜厚度为15 μm时的气膜流场特征

Fig.6 Characteristics of gas film flow field with gas film thickness of 15 μm

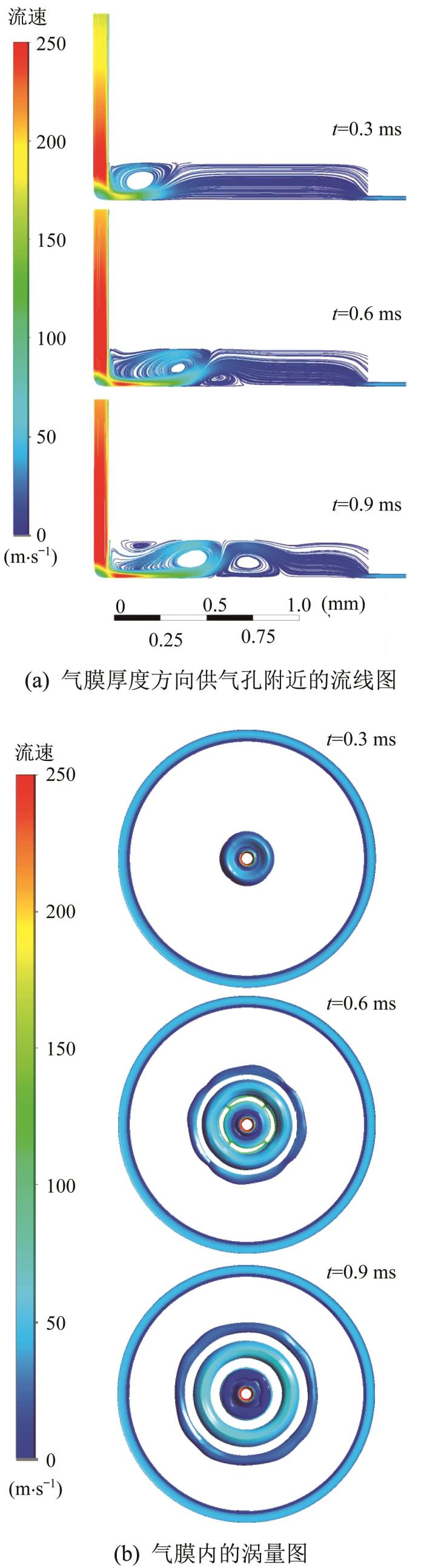
最后，分析基于k-ε模型+层流模型计算得到的气膜厚度较大（25 μm）时气膜流场（瞬态）的流线特征和涡量特征，结果如图7所示。由图7(a)可知，当气体通过供气孔进入气腔时，靠近供气孔附近出现了一个流速约为90 m/s的大涡旋，大涡旋能量衰减后出现了2个流速不足10 m/s的小涡旋，随后气流近似平直流线向下游流动，直到离开气腔边缘时因受变截面的影响流速稍有回升。结果说明，当气膜厚度进一步增大时，气膜的容性效应增强，虽然高压气流冲击大理石平台时会形成强度较大的涡旋，但由于较大气膜厚度（25 μm）下气膜流场内部的气体总量增大，大涡旋向下游移动时受到气腔内原有大量气体的阻碍，为克服下游气体的惯性力，大涡旋需要消耗自身动能来驱动下游流速较慢的气体，从而破碎成一定数量的小涡旋。随着动能耗尽，大涡旋逐渐衰退为以惯性力为主的层流。由图7(b)可知，在供气孔中心相对较小的范围内集中了高强度的湍动能，其在扩散较短距离后便迅速耗散，此后在气腔内几乎看不到涡量特征，即此时湍动能几乎被耗尽，流场近似退化为无旋流动。这既符合流体动力学的基本原理，又说明了传统的气体润滑理论在采用层流假设时限制气膜厚度是合理且必要的。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 气膜厚度为25 μm时的气膜流场特征

Fig.7 Characteristics of gas film flow field with gas film thickness of 25 μm

2.2.2　耗气量

采用不同计算模型对不同气膜厚度下空气静压轴承的耗气量进行计算，并与实验结果进行比较，结果如图8所示。由图可知，随着供气压力的增大，耗气量的计算值和实测值均逐渐增大；当气膜厚度为5 μm时，基于k-ε模型的计算结果与实验结果的偏差较小；当气膜厚度为15 μm时，基于LES模型的计算结果与实验结果较接近；当气膜厚度为25 μm时，基于k-ε模型+层流模型的混合计算结果更接近实验结果。综上所述，针对空气静压轴承耗气量这一静态特性，3种计算模型能对应不同气膜厚度工况进行准确计算。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同气膜厚度下空气静压轴承的耗气量

Fig.8 Air consumption of aerostatic bearing under different gas film thicknesses

2.2.3　静刚度

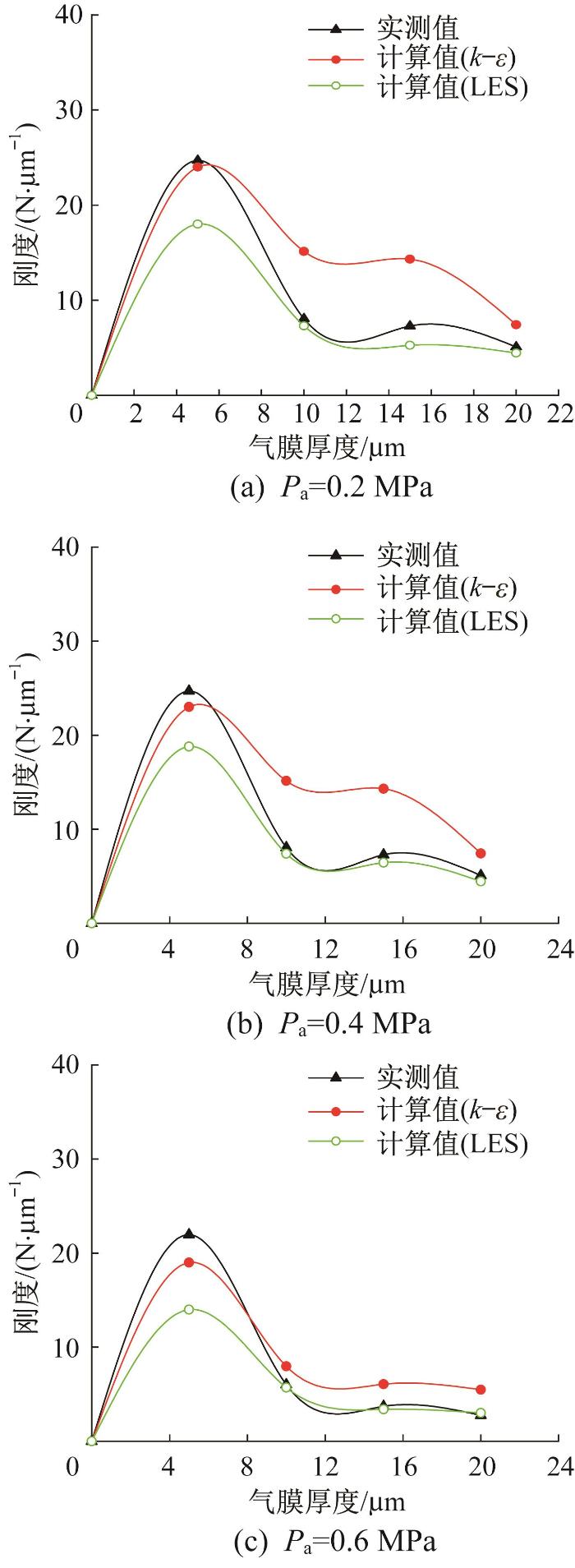
为验证上述计算模型的分析结果对不同初始能量下气膜流场的适用性，进一步分析不同供气压力（P_a=0.2，0.4，0.6 MPa）下空气静压轴承的静刚度，结果如图9所示，由图可知，当供气压力分别为0.2，0.4，0.6 MPa时，采用k-ε模型和LES模型计算得到的静刚度与实测静刚度在气膜厚度较小（h<5 μm）时呈现较好的一致性；随着气膜厚度的逐渐增大，供气压力较大时三者的吻合较好，但供气压力较小时三者的偏差较明显；当气膜厚度大于10 μm，静刚度的计算值与实测值均呈现较大偏差，相较而言，采用LES模型计算得到的静刚度与实测静刚度相差较小。因此，在设计空气静压轴承时，一定要根据实际工况选择适宜的计算模型，才能保证轴承在后续使用过程中安全、可靠。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同供气压力下空气静压轴承的静刚度

Fig.9 Static stiffness of aerostatic bearing under different air supply pressures

3 结论

1）基于气体润滑理论和湍流理论，对空气静压轴承气膜流场控制方程中的雷诺应力项进行讨论，明确了不同工况下气膜流场的控制方程。当气膜厚度较小（<10 μm）时，气腔内湍动程度较大，大量不规则的小涡旋迅速耗散入口处的能量，此时宜采用k-ε模型进行描述；当气膜厚度中等（10~20 μm）时，气膜流场内气阻减小，供气孔出口射流形成的大涡旋在气腔内沿半径方向扩散并输运能量，此时宜采用LES模型进行描述；当气膜厚度较大（20~30 μm）时，气膜的容性效应增强，在大涡旋驱动作用下，下游大量低速气体的能量被快速耗散，导致气腔内后半部分呈现层流特征，此时宜采用k-ε模型+层流模型的混合计算模型进行描述。

2）采用数值计算和实验测试相结合的方法，验证了不同气膜厚度下空气静压轴承气膜流场计算模型的合理性和有效性。当气膜厚度为5 μm时，采用k-ε模型的计算结果与实验结果的偏差最小；当气膜厚度为15 μm时，采用LES模型的计算结果更接近实验结果；当气膜厚度为25 μm时，采用k-ε模型和LES模型的计算结果接近，而采用k-ε模型+层流模型的计算结果与实验结果的吻合更好。此外，还通过非定常流场内流线和涡量随时间的演化特征来分析和解释选择3种计算模型的依据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李海月，程泽，赵丹妮，等.

基于悬吊法和气浮法的多自由度微重力模拟展开试验系统研究

［J］.工程设计学报，2020，27（4）：508-515. doi：10.3785/j.issn.1006-754X.2020.00.055