工程设计学报

工程设计学报, 2023, 30(2): 144-153 doi: 10.3785/j.issn.1006-754X.2023.00.025

设计基础理论与方法

基于多判别条件的储罐内爆弱顶性能评价分析

丁宇奇,,, 杨超梁, 芦烨,,, 杨明, 张佳贺, 刘凯, 卢宏

东北石油大学 机械科学与工程学院，黑龙江 大庆 163318

Evaluation and analysis of implosion weak roof performance of storage tank based on multiple discriminant conditions

DING Yuqi,,, YANG Chaoliang, LU Ye,,, YANG Ming, ZHANG Jiahe, LIU Kai, LU Hong

College of Mechanical Science and Engineering, Northeast Petroleum University, Daqing 163318, China

通讯作者: 芦 烨（1985—），女，黑龙江哈尔滨人，讲师，博士，从事油气储运装备强度评定与优化分析研究，E-mail: luye_nepu@163.com，https://orcid.org/0000-0002-6281-9105

收稿日期: 2022-08-25   修回日期: 2022-11-10  

基金资助: 国家自然科学基金资助项目.  51604080
黑龙江省博士后科研启动基金资助项目.  LBH-Q20082
黑龙江省自然科学基金资助项目.  LH2022A003

Received: 2022-08-25   Revised: 2022-11-10  

作者简介 About authors

丁宇奇（1982—），男，黑龙江肇东人，教授，博士，从事油气储运装备强度评定与优化分析研究，E-mail:jslx2004@163.com，https://orcid.org/0000-0002-6100-8423 , E-mail：jslx2004@163.com

摘要

储罐在偶发爆炸载荷作用下易发生结构破坏，致使罐内储液流出，从而造成巨大的经济损失，但采用弱顶设计的储罐在此类事故发生时能减少损失。为此，以立式拱顶储罐为研究对象，综合考虑储罐破坏过程中内部压力、应力以及裂纹扩展等因素，建立了基于多判别条件的储罐内爆弱顶性能评价方法。同时，通过数值模拟手段，采用CEL（coupled Euler-Lagrange, 耦合欧拉-拉格朗日）流固耦合算法建立了储罐内爆三维有限元模型，对内爆载荷作用下储罐的破坏过程及不同影响因素下储罐的弱顶性能开展研究。计算结果表明：在基于压力和应力的弱顶性能评价中，储罐在90°，135°，180°位置处的峰值压力比大于1，满足弱顶要求；在基于结构断裂的弱顶性能评价中，由于裂纹延伸到液位以下，2条裂纹分别穿过液位1.99 m和5.21 m，储罐不具备弱顶性能。随着储罐容积的增加、液位的升高，储罐的弱顶性能增强。根据计算所得结果，采取在液位以上设置防护圈的方法对储罐进行优化，使得非弱顶储罐满足弱顶结构设计要求。所建立的储罐弱顶性能评价条件可为储罐的弱顶设计及分析提供参考。

关键词： 储罐 ; 内爆 ; 结构破坏 ; 裂纹 ; 弱顶

Abstract

Storage tanks are prone to structural failure under occasional explosive loads, resulting in the outflow of liquid inside the tank and causing huge economic losses. However, storage tanks designed with weak roofs can reduce losses in such accidents. Therefore, taking the vertical vault storage tank as the research object, taking into account factors such as internal pressure, stress and crack propagation during the tank failure process, a method for evaluating the implosion weak roof performance of storage tank based on multiple discriminant conditions was established. Meanwhile, by means of numerical simulation, a three-dimensional finite element model of storage tank implosion was established using the CEL (coupled Euler-Lagrange) fluid-structure coupling algorithm. The failure process of storage tank under implosion load and the weak roof performance of storage tank under different influencing factors were studied. The calculation results showed that in the evaluation of weak roof performance based on pressure and stress, the peak pressure ratios of the storage tank at positions of 90°, 135° and 180° were greater than 1, meeting the requirements of weak roof; in the evaluation of weak roof performance based on structural fracture, due to the extension of cracks below the liquid level, two cracks passed through the liquid level of 1.99 m and 5.21 m, respectively, and the storage tank did not have weak roof performance. As the volume and liquid level of the storage tank increased, the weak roof performance of storage tank increased. Based on the calculated results, the method of setting a protective ring above the liquid level was adopted to optimize the storage tank, so that the non-weak roof storage tank met the design requirements of the weak roof structure. The established evaluation conditions for the weak roof performance of storage tanks can provide reference for the design and analysis of the weak roof of storage tanks.

Keywords： storage tank ; implosion ; structural failure ; crack ; weak roof

PDF (4732KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

丁宇奇, 杨超梁, 芦烨, 杨明, 张佳贺, 刘凯, 卢宏. 基于多判别条件的储罐内爆弱顶性能评价分析. 工程设计学报[J], 2023, 30(2): 144-153 doi:10.3785/j.issn.1006-754X.2023.00.025

DING Yuqi, YANG Chaoliang, LU Ye, YANG Ming, ZHANG Jiahe, LIU Kai, LU Hong. Evaluation and analysis of implosion weak roof performance of storage tank based on multiple discriminant conditions. Chinese Journal of Engineering Design[J], 2023, 30(2): 144-153 doi:10.3785/j.issn.1006-754X.2023.00.025

大型储罐通常存储易燃、易爆、易挥发的物料，挥发气体与空气混合后易发生爆炸，而爆炸产生的巨大能量会导致储罐自身结构发生破坏。若液位以下的罐壁结构发生破坏，储罐内燃烧的液体就会流出，从而形成流淌火。为了降低储罐在爆炸过程中造成的危害以及减少经济损失，研究储罐的弱顶性能和对非弱顶储罐进行优化设计尤为重要。

在储罐弱顶结构评价方面，刘巨保及其研究团队[1-3]通过引入储罐顶壁连接处与底壁连接处的破坏压力比k，建立了弱顶结构评价条件：若在空罐和半罐液位时k>1.5、满罐液位时k>2.5，则为弱顶储罐。李成兵等[4]、万昊天[5]参考国内外标准，认为储罐弱顶结构需满足焊脚高度足够小、罐顶坡度足够小和顶壁连接处有效连接面积足够小等条件。刘博等[6]通过对相关公式进行修正推导，提出储罐罐顶破坏压力与罐底提离压力的比值应小于1，同时需保证抗压环材料的屈服强度不小于220 MPa。在非弱顶储罐优化方面，丁明旭等[7]通过对储罐的破坏强度进行理论分析，提出在储罐顶壁连接处采用低强度钢可实现非弱顶储罐的优化。万昊天等[8]设计了一种弱壁结构，并通过实验手段进行了验证，得出弱壁结构可以提升非弱顶储罐的弱顶性能。刘巨保等[9]引入破坏压力比进行了弱顶连接结构评价，并通过数值模拟方法得出：a型抗压环的弱顶系数（2.069）最大，弱顶效果最好。丁宇奇等[10]以3 000 m3立式拱顶储罐为研究对象，从弱顶结构的要求入手，通过建立储罐数值模型优化了焊角尺寸、罐顶坡度和抗压环截面积等，有效提升了储罐的弱顶性能。此外，学者们还提出了其他的储罐弱顶优化方法，例如在储罐罐顶与包边角钢连接处采用强度较低的焊缝或单边焊缝[11-12]、在储罐底壁连接处增设加强筋或地脚螺栓[13-15]以及增大储罐罐顶曲率半径[16]等。

综上所述，现有研究主要从单一破坏压力角度来评价储罐的弱顶性能，并以此为依据对储罐进行优化，尚未建立综合考虑多种影响因素和实际破坏行为的储罐弱顶性能判别条件。为此，笔者以立式拱顶储罐为研究对象，结合爆炸载荷在罐内气体-储罐-罐内液体多相耦合界面处的传递过程，通过综合考虑储罐破坏过程中内部压力、应力及裂纹扩展等因素建立多判别条件，并基于三维有限元模型对内爆载荷作用下储罐的弱顶性能进行评价；同时，采用设置防护圈的方法对不具备弱顶性能的储罐进行弱顶优化设计。

1 基于多判别条件的储罐内爆弱顶性能评价方法

1.1　内爆载荷作用下储罐的破坏过程分析

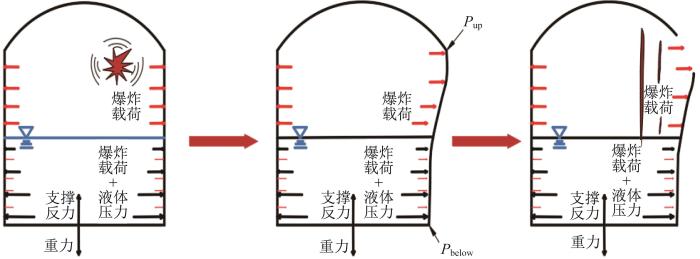
立式拱顶储罐在内爆载荷作用下的结构破坏过程如图1所示。储罐内部爆炸时产生的冲击波分别通过罐内气体-储罐耦合界面及罐内液体-储罐耦合界面传向储罐，导致储罐发生变形破坏；液位以下的罐壁受到液体的压力载荷，且压力载荷随着液体深度的增加而增大；整个储罐还承受自身的重力作用和地面的支撑反力。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   内爆载荷作用下储罐结构破坏示意

Fig.1   Schematic diagram of structural failure of storage tank under implosion load


当储罐内部产生爆炸冲击波后，冲击波分别沿储罐的径向和轴向向前传播，传到罐体时会发生反射，反射波向内传播发生叠加作用，在多次反射之后，储罐内压力逐渐趋于均匀[17-19]。总体来看，爆炸冲击波先与爆心在水平面上的投影点相接触，而后到达与起爆位置相近的顶壁连接处，最后到达罐底。虽然爆炸压力在传播过程中会衰减，但由于反射的增长效应，最大压力除了可能出现在起爆位置齐平处外，还可能出现在顶壁连接处或底壁连接处。

随着爆炸压力的传播，储罐内各部分的应力同步增大，当增大到一定程度并超过屈服极限时，储罐会发生破坏，其破坏形式表现为出现裂纹、破口和碎片等。由于顶壁连接处为储罐的易损位置[20]且压力聚集时间较长，破坏往往最先发生在顶壁连接处，表现形式为出现破口；罐壁处破坏形式表现为出现裂纹、破口和碎片等。虽然在储罐破坏过程中伴随着罐内载荷的泄漏，但在整个过程中，裂纹和破口仍会不断扩大，直到罐内载荷恢复正常水平。此时，破坏位置可能会扩展到液位以下，也可能在液位以上停止扩展。

在储罐内爆破坏的整个过程中，峰值压力、应力的大小及其出现的位置和时间决定了储罐的破坏位置。但即使储罐某一位置因较大的压力、应力而发生了破坏，罐内储液也有可能不会流出，这是因为罐内液体是否流出取决于破坏是否发生在液位以下。因此，当对储罐弱顶性能进行评价时，不仅要从罐内压力、应力的角度进行判断，还要从储罐实际破坏情况的角度进行判断。为此，建立了综合考虑压力、应力以及裂纹扩展等多个影响因素的储罐弱顶性能判别条件。

1.2　基于多影响因素的储罐弱顶性能判别条件

储罐弱顶设计的主要目的是控制储罐失效时最先发生破坏的位置在罐顶，从而避免液体流出。通过对内爆载荷作用下储罐破坏过程的分析，可以初步得到储罐在内爆过程中的罐内压力、应力分布情况。若要判断储罐是否为弱顶结构，则可根据储罐各部位的压力、应力以及破坏产生的裂纹这几方面进行判别。本文建立的储罐弱顶性能判别方法如下。

1）第1条判别条件：基于压力和应力的储罐弱顶性能判别条件。

①对于在储罐同一母线、不同高度处的各点，根据所有液位以上观测点的峰值压力Pup与液位以下观测点的峰值压力Pbelow的比值kP 来进行判别：若kP >1，则储罐具备弱顶性能；反之，储罐不具备弱顶性能。

②当峰值压力的比值满足弱顶条件时，根据液位以上观测点峰值压力的出现时间tup与液位以下观测点峰值压力的出现时间tbelow的比值kt 来进行判别：若kt <1，即峰值压力大的观测点先出现峰值压力，则储罐具备弱顶性能；若kt >1，即峰值压力小的观测点先出现峰值压力，则需从应力角度进行进一步判别。

③当峰值压力出现时间的比值kt >1，即不满足满足弱顶条件时，提取峰值压力小的观测点在峰值出现时刻的应力，若该应力小于内聚强度[21]，则储罐不会发生破坏，即具备弱顶性能；若该时刻的应力大于内聚强度，储罐可能会产生裂纹，则需通过第2条判别条件来判断储罐是否具备弱顶性能。

2）第2条判别条件：基于结构破坏的储罐弱顶性能判别条件。

①若裂纹初始发生在液位以下，则储罐不具备弱顶性能。

②若裂纹初始发生在液位以上，且裂纹停止扩展时下端点在液位以上，则储罐具备弱顶性能。

③若裂纹初始发生在液位以上，且裂纹停止扩展时下端点在液位以下，则储罐不具备弱顶性能。

只有同时满足以上所有条件，储罐才满足弱顶结构的要求，即具备弱顶性能。

2 内爆载荷作用下储罐的弱顶性能评价

2.1　储罐内爆三维有限元模型的建立

2.1.1　储罐几何模型的简化

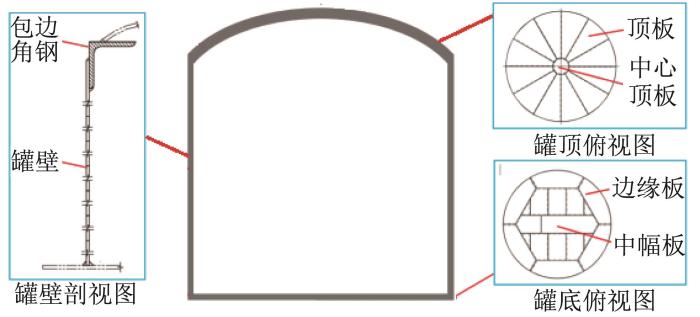
立式拱顶储罐由罐底、筒形罐壁和罐顶组成，如图2所示。其中：罐底由钢板拼接而成，中部钢板为中幅板，周边为边缘板；罐壁由多圈钢板焊接而成；罐顶由多对扇形板焊接而成，罐顶内侧采用型材制成加强肋，整个罐顶与罐壁板上的包边角钢焊接成一体。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   立式拱顶储罐结构示意

Fig.2   Structure diagram of vertical vault storage tank


由于真实储罐的结构非常复杂，在保证对计算分析影响不大的情况下，分别对储罐的灌顶、罐壁以及罐底结构进行适当简化。在灌顶结构简化方面，根据《立式圆筒形钢制焊接油罐设计规范》（GB 50341—2014）[22]，将顶板、中心顶板、连接板进行当量等效，即简化为等壁厚的薄壳结构；对于罐壁，忽略焊缝以及包边角钢的影响；将罐底直接简化成等厚薄壳结构。本文以1 000，3 000，5 000 m3的储罐为例进行分析，其内径为10.8~20.0 m，罐壁高度为12.48~17.82 m，壁板厚度为0.006~0.013 m，罐顶厚度为0.013 1~0.015 5 m。

2.1.2　储罐内爆三维有限元模型

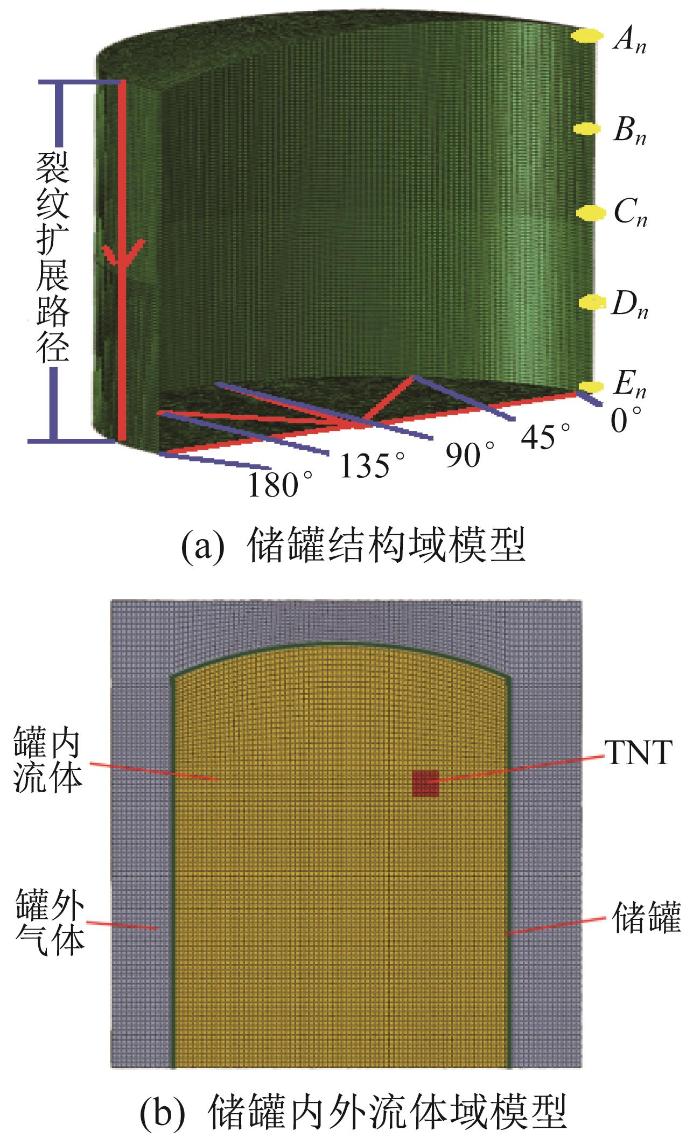
考虑到储罐内爆破坏属于三维空间问题，其结构域及内外流体域模型采用实体单元进行离散。其中：储罐结构采用拉格朗日网格进行描述；罐内气体燃爆载荷采用TNT当量法进行模拟[23]，TNT炸药与流体采用欧拉网格进行描述。为了保证储罐结构响应以及压力传递均在流体域内进行，建立包含储罐的罐外空气域，并通过CEL（coupled Euler-Lagrange，耦合欧拉-拉格朗日）流固耦合算法[24]对不同相之间的耦合关系进行描述，其中流体和储罐结构之间采用通用接触算法，以达到计算中自动追踪结构与流体之间耦合接触面的目的。储罐材料采用Q235B钢，内外气体均设置为理想气体。由于在高速剧烈载荷下，储罐材料表现出应变率强化效应，因此材料模型采用Johnson-Cook强化模型[25-26]来描述。同时，为了在数值模拟过程中实现储罐在内爆载荷作用下的断裂破坏，插入与储罐材料力学性能相同的黏结单元[27]，并参考文献[21]，将黏结单元的内聚强度设为517 MPa。鉴于储罐结构的对称性，本文仅建立了1/2模型，故储罐结构和流体域的对称面上均需要施加对称约束；对于储罐结构，在罐底施加全约束；对于罐外空气域的外部边界，均设置为无反射边界条件。储罐结构域及内外流体域有限元模型分别如图3(a)和图3(b)所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   储罐内爆三维有限元模型

Fig.3   Three-dimensional finite element model of storage tank implosion


根据上文建立的弱顶性能评价方法，先通过不同位置处的压力和应力对储罐的弱顶性能进行判断，再通过裂纹状态进行进一步判断。为此，从罐顶出发，沿罐体0°，45°，90°，135°，180°五个角度各引一条母线，在母线上选取不同高度处的压力和应力进行观测；同时，沿母线方向对不同时刻的裂纹情况进行观测，观测点及路径如图3(a)所示。图中：An 为罐顶与罐壁连接处，Bn 为罐壁与起爆位置齐平处，Cn 为液位高度处，Dn 为1/2液位高度处，En 为罐壁与罐底连接处，其中n=1, 2, …, 5，表示5个不同的环向角度（0°，45°，90°，135°，180°）。

2.2　储罐的弱顶性能分析
2.2.1　基于压力和应力的弱顶性能分析

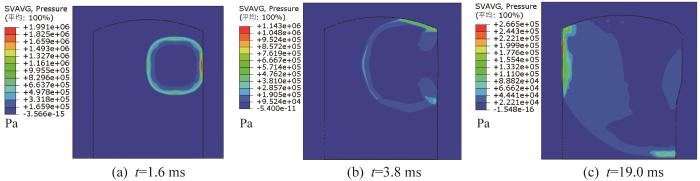
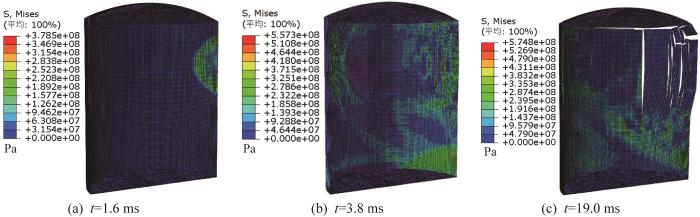
以半罐（液位高度为5.75 m）状态下1 000 m3的储罐为例，分析其内部产生的爆炸压力对弱顶性能的影响。通过有限元分析可得，在爆炸冲击波传播到罐壁、罐顶、罐底时刻（分别对应t=1.6，3.8，19.0 ms）储罐内的压力分布如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同时刻储罐内压力分布云图

Fig.4   Cloud chart of pressure distribution of storage tank at different times


由图4可知，在t=1.6 ms时，爆炸冲击波传播到罐壁并与罐壁发生碰撞，最大压力1 991 kPa出现在右侧罐壁与起爆位置齐平处附近；在t=3.8 ms时，爆炸冲击波传播到罐顶，压力在储罐右侧的顶壁连接处聚集，最大压力1 143 kPa出现在右侧顶壁连接处；在t=19.0 ms时，爆炸冲击波传播到右侧罐底，最大压力为266.5 kPa。

基于上文的第1条判别条件，提取各观测点的峰值压力、峰值压力出现时间并计算相应比值，对储罐的弱顶性能进行评价，结果如表1所示。

表1   储罐各观测点的峰值压力及其出现时间的比值

Table 1  Ratio of peak pressure and its occurrence time at each observation point of storage tank

观测点环向角度
0°(n=1)45°(n=2)90°(n=3)135°(n=4)180°(n=5)
压力比时间比压力比时间比压力比时间比压力比时间比压力比时间比
An /Bn0.212.000.581.582.851.322.741.012.751.12
An /Cn1.420.891.240.943.110.932.710.853.540.86
An /Dn5.820.333.510.474.350.623.130.664.040.71
An /En4.760.164.370.264.400.462.780.423.480.48
Bn /Cn6.660.442.150.591.090.701.020.841.290.77
Bn /Dn27.470.166.030.301.520.471.160.651.470.63
Bn /En22.440.087.540.161.550.341.030.431.260.43

新窗口打开| 下载CSV


从表1中各观测点的峰值压力比可知，A1点与B1点以及A2点与B2点的峰值压力比均小于1。由此说明，对于峰值压力比，在0°和45°位置处，An /Bn 不满足峰值压力比大于1的弱顶条件。除了以上不满足弱顶条件的位置，对于峰值压力比大于1但峰值压力出现时间比大于1的位置，还应进一步判断。在储罐的90°，135°，180°位置处，An 点与Bn 点的峰值压力出现时间比大于1，说明Bn 点比An 点先出现峰值压力，若压力峰值时刻Bn 点处的应力超过内聚强度517 MPa，则认为储罐是不安全的，即有可能会在Bn 点处发生破坏，故峰值压力比大于1没有意义，不能判定储罐为弱顶结构。为了进一步描述爆炸冲击波传播到罐壁、罐顶、罐底时刻储罐的应力变化情况，提取各对应时刻储罐的应力分布云图，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同时刻储罐内应力分布云图

Fig.5   Cloud chart of stress distribution of storage tank at different times


对比图4和图5可知，在t=1.6 ms时，由于爆炸冲击波传播到与起爆位置齐平的罐壁处，使得压力增大，进而导致此处应力增大，此时储罐最大应力为378 MPa；在t=3.8 ms时，压力已聚集到右侧顶壁连接处，导致此处产生应力，同时导致其与起爆位置齐平处出现1块应力较大的条状区域，该区域内某些位置的最大应力为557 MPa，已超过内聚强度517 MPa，说明该位置不再安全；在t=19.0 ms时，随着罐内压力的传递，储罐顶壁连接处及罐壁某些位置处的最大应力远超517 MPa，说明储罐结构已经发生了破坏。为了分析峰值压力比大于1且峰值压力出现时间比大于1的位置的弱顶性能，提取压力峰值时刻储罐各观测点的应力，结果如表2所示。

表2   储罐各观测点的峰值压力出现时间及对应应力

Table 2  Peak pressure occurrence time and corresponding stress at each observation point of storage tank

观测点环向角度
0°(n=1)45°(n=2)90°(n=3)135°(n=4)180°(n=5)
时间/ms应力/MPa时间/ms应力/MPa时间/ms应力/MPa时间/ms应力/MPa时间/ms应力/MPa
An3.243.26.043.413.2216.018.2212.020.6198.0
Bn1.6143.03.827.010.079.018.0139.018.4176.0
Cn3.684.56.475.914.256.921.4154.024.0183.0
Dn9.851.512.820.921.2105.027.688.529.038.1
En20.483.423.474.829.0167.043.073.843.030.3

新窗口打开| 下载CSV


从表2中的数据可知，在压力峰值时刻，储罐90°，135°，180°位置对应的Bn 点的应力分别为79，139，176 MPa，没有达到内聚强度517 MPa，故从应力上判断储罐结构不会发生破坏。由此说明，在90°，135°，180°位置处，储罐结构满足弱顶条件。

综上，结合表1和表2中的数据可知，在第1条判别条件下，液位以上观测点与液位以下观测点的峰值压力比均大于1，且液位以上观测点与液位以下观测点的峰值压力出现时间比均小于1。由此可得：在基于压力和应力的弱顶性能评价中，储罐满足弱顶条件。

2.2.2　基于结构破坏的弱顶性能分析

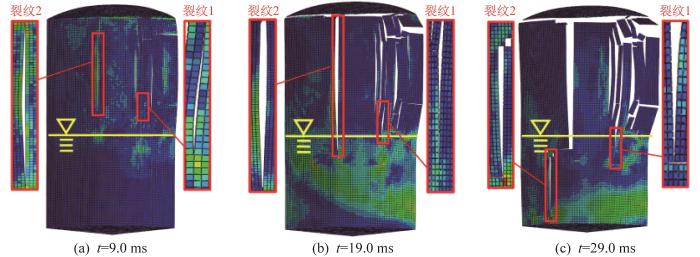
在储罐结构破坏过程中，由于受到爆炸压力的持续作用，使得应力持续增大。当应力增大到一定程度并超过内聚强度时，黏结单元消失，储罐结构发生破坏，破坏以裂纹的形式出现。本节基于结构破坏所产生的裂纹对储罐的弱顶性能进行分析。由于裂纹在初始发生时刻很微小，为了观察裂纹的出现顺序及其长度，对裂纹进行放大处理。不同时刻储罐裂纹的扩展情况如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同时刻储罐裂纹扩展情况

Fig.6   Crack propagation of storage tank at different times


从图6中可以看出，在t=9.0 ms时，储罐开始产生裂纹，且位于液位以上；在t=19.0 ms时，随着爆炸压力的传递，液位以上已充满压力，在压力载荷的作用下裂纹1和裂纹2继续向下扩展，裂纹1临近液位、裂纹2穿过液位；在t=29.0 ms时，裂纹1和裂纹2不再继续扩展，裂纹1扩展到液位以下，裂纹2已临近罐底。裂纹在初始发生时刻、穿过液位时刻和终止时刻的长度如表3所示。

表3   不同时刻裂纹的长度

Table 3  Crack lengths at different times

裂纹初始出现时刻穿过液位时刻终止时刻
时刻/ms端点高度①/m长度/m时刻/ms高度/m长度/m时刻/ms高度/m长度/m
裂纹1（30°）8.49.92（上）1.9716.412.48（上）6.6723.212.488.74
7.95（下）5.72（下）3.76
裂纹2（60°）9.09.89（上）1.5016.212.37（上）6.6624.412.4811.96
8.93（下）5.71（下）0.54

①端点高度为裂纹上、下端点距离罐底的高度。

新窗口打开| 下载CSV


由表3可知，由于裂纹1更靠近起爆位置，该位置在爆炸载荷产生的瞬间所承受的压力更大，故裂纹1最先出现；随着储罐的破坏以及爆炸载荷的传播，裂纹1附近压力的下降速度大于裂纹2附近。相比之下，裂纹2下端点的压力始终保持在较高的水平，故裂纹2的扩展时间较长。因此，在终止时刻，裂纹2的长度大于裂纹1。其中，裂纹1在t=8.4 ms时出现在液位以上，在t=16.4 ms时刚好穿过液位，在t=23.2 ms时停止扩展，此时其下端点距离罐底3.76 m。裂纹1的总长度为8.74 m，穿过液位1.99 m。裂纹2在t=9.0 ms时出现，在t=16.2 ms时刚好穿过液位，在t=24.4 ms时停止扩展，此时其下端点距离罐底0.54 m。裂纹2的总长度为11.96 m，穿过液位5.21 m。由于2条裂纹均穿过液位，基于第2条判别条件，该储罐不具备弱顶性能。

3 不同影响因素下储罐的内爆弱顶性能评价

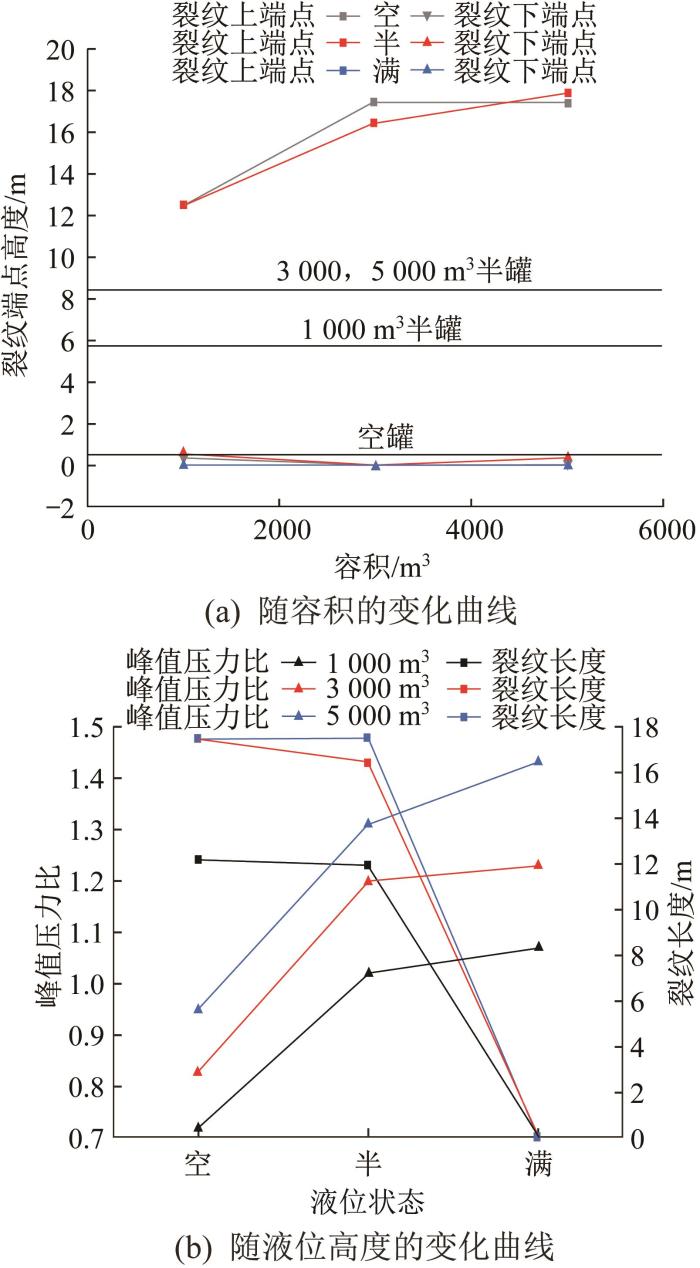
为了得到储罐容积与液位对其内爆破坏与弱顶性能的影响，分别选取1 000，3 000，5 000 m3容积下空罐（0.50 m）、半罐（1 000 m3为5.75 m，3 000 m3、5 000 m3为8.40 m）、满罐（1 000 m3为11.50 m，3 000 m3、5 000 m3为16.80 m）液位状态的储罐进行对比分析。结合本文建立的弱顶性能判别条件，基于第1条判别条件，不对最小峰值压力比小于1处的峰值压力出现时间比以及应力（除An /Bn 外）进行分析，以及不对最小峰值压力比大于1但峰值压力出现时间比小于1处的应力（除An /Bn 外）进行分析；基于第2条判断条件，仅对产生裂纹的储罐进行分析。不同影响因素下储罐的弱顶性能评价结果如表4所示。储罐弱顶性能随容积、液位高度的变化曲线如图7所示。

表4   不同影响因素下储罐的弱顶性能评价结果

Table 4  Evaluation results of weak roof performance of storage tank under different influencing factors

判别条件评价指标容积/m3
1 0003 0005 000
空半满空半满空半满

第1条

判别条件

最小峰值压力比（除An /Bn 外）0.721.021.070.831.201.230.951.311.43
峰值压力出现时间比—0.840.92—0.611.02—0.440.97
应力/MPa—————320———
是否具备弱顶性能否是是否是是否是是

第2条

判别条件

裂纹上端点高度/m12.4812.48017.5016.47017.4617.840
裂纹下端点高度/m0.320.54000000.330
裂纹长度/m12.1611.96—17.5016.47—17.4617.51—
液位高度/m0.505.75—0.508.40—0.508.40—
裂纹下端点与液位高度差值/m-0.18-5.21—-0.50-8.40—-0.50-8.07—
是否具备弱顶性能否否是否否是否否是
基于多判别条件的弱顶性能评价结果否否是否否是否否是

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   储罐弱顶性能随容积与液位高度的变化曲线

Fig.7   Changing curves of weak roof performance of storage tank with volume and liquid level-height


结合表4和图7可以看出，随着储罐容积的增大和液位的升高，最小峰值压力比（除An /Bn 外）逐渐增大；在空罐状态下，3种容积储罐的最小峰值压力比（除An /Bn 外）均小于1，不满足弱顶条件。基于第1条弱顶性能判别条件可知：在半罐和满罐状态下，3种容积储罐的最小峰值压力比（除An /Bn 外）均大于1，对于峰值压力比大于1且峰值压力出现时间比大于1的位置，储罐的最大应力小于内聚强度，满足弱顶条件。基于第2条弱顶性能判别条件可知：3种容积储罐在空罐、半罐状态下均产生了裂纹且均扩展到液位以下；随着液位的升高，裂纹长度逐渐变短；满罐状态下储罐未产生裂纹。综上，根据基于多判别条件的弱顶性能评价方法，随着储罐容积的增大、液位的升高，储罐的弱顶性能增强，但仅在满罐状态下具备弱顶性能。

4 储罐弱顶优化设计与分析

4.1　储罐弱顶优化设计方案

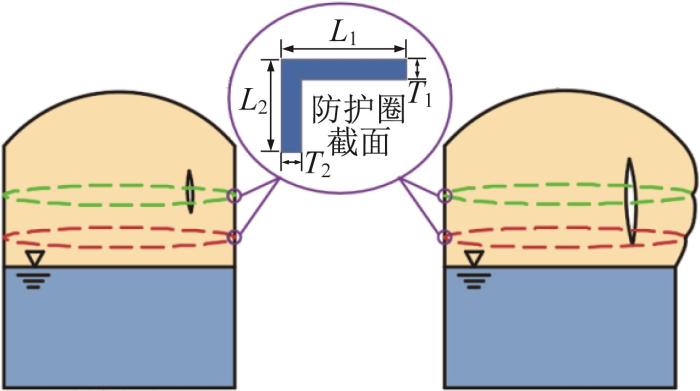
结合上文分析发现，当储罐产生裂纹时，裂纹初始出现在液位以上并靠近起爆位置。随着爆炸载荷的传播，裂纹向下扩展，最终穿过液位，致使罐内储液流出。为了避免裂纹在储罐爆炸过程中扩展到液位以下，采用设置防护圈的方法对储罐进行弱顶优化。在储罐的实际应用中，半罐以上液位是最常见且最经济的运行状态。因此，以半罐状态下1 000，3 000，5 000 m3的储罐为例，在液位以上设置除标准要求外的2个防护圈，保证最终裂纹下端点在液位以上，达到非弱顶储罐优化设计的目的。非弱顶储罐的优化过程如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   非弱顶储罐优化过程示意

Fig.8   Schematic diagram of optimization process of non-weak roof storage tank


在优化过程中，结合GB 50341—2014对防护圈尺寸的规定，不同容积储罐优化过程中使用的防护圈尺寸以及安装位置如表5所示。

表5   不同容积储罐的防护圈尺寸

Table 5  Dimensions of protective rings for storage tanks with different volumes

容积/m3L1/mT1/mL2/mT2/m液位高度/m防护圈1安装高度/m防护圈2安装高度/m
1 0000.0750.0080.0750.0085.759.1257.250
3 0000.1050.0080.0630.0088.4013.10010.400
5 0000.1300.0080.0800.0088.4013.10010.400

新窗口打开| 下载CSV


4.2　优化后的储罐弱顶性能分析

由于本文的优化设计方案对储罐内压力和应力的影响较小，假设优化后储罐基于压力和应力的弱顶性能评价结果与优化前相同。优化前后储罐弱顶性能评价结果对比如表6所示。

表6   优化前后储罐的弱顶性能评价结果对比

Table 6  Comparison of weak roof performance evaluation results of storage tank before and after optimization

新窗口打开| 下载CSV


结合表5和表6可知，1 000，3 000，5 000 m3储罐分别在距离罐底7.25 m和10.40 m的罐壁处设置防护圈后，有效阻止了裂纹向液位以下扩展。优化后，1 000 m3和3 000 m3储罐最危险的裂纹向下延伸到第2个防护圈附近，5 000 m3储罐最危险的裂纹延伸到第2个防护圈以下、液位以上。根据基于多判别条件的储罐内爆弱顶性能评价方法，半罐状态下3种容积的储罐在优化前均不具备弱顶性能，但在优化后均具备。结果表明，在液位以上设置防护圈可以有效阻止储罐裂纹向下扩展，使得非弱顶储罐满足弱顶结构设计要求。因此，即使储罐液位超过了防护圈的安装高度，防护圈的作用仍然能够达到。

5 结 论

1）以立式拱顶储罐为研究对象，考虑罐内流体、储罐、罐外气体之间的多相耦合，采用CEL流固耦合算法建立储罐内爆三维有限元模型；综合考虑储罐破坏过程中内部的压力、应力以及裂纹扩展等因素，建立弱顶性能多判别方法，为储罐弱顶性能的评价提供了依据。

2）通过对内爆载荷作用下储罐的弱顶性能进行分析，以压力和应力为判别条件的评价结果表明：若各观测点处的峰值压力比大于1，且峰值压力出现时间比小于1，则储罐具备弱顶性能；若观测点处的峰值压力比及峰值压力出现时间比均大于1，但只要应力没有超过材料内聚力强度，则储罐仍具备弱顶性能。以结构破坏为判别条件的评价结果表明：若储罐在内爆载荷作用下发生结构破坏，只要产生的裂纹没有延伸到液位以下，则具备弱顶性能。

3）当储罐液位高度不变时，容积越大，储罐的弱顶性能越好；当容积不变时，液位高度越高，储罐的弱顶性能越好。针对1 000，3 000，5000 m3储罐，采用在液位以上设置防护圈的方法进行优化设计。结果表明，防护圈有效提升了储罐的弱顶性能，说明所采取的优化方法可以满足提升储罐弱顶性能的结构设计要求。

参考文献

刘巨保，门建斌，丁宇奇，等.

2万m3立式网壳顶储罐破坏分析及弱顶性能评价

［J］.石油化工设备，2013，42（3）：48-53.

[本文引用: 1]

LIU J B， MENG J B， DING Y Q， et al.

Failure analysis and evaluation for weak roof performance of 2×104 m3 vertical latticed shell roof storage tank

［J］. Petro-chemical Equipment， 2013， 42（3）： 48-53.

[本文引用: 1]

丁宇奇.

立式拱顶储罐超压破坏机理与弱顶结构研究

［D］.大庆：东北石油大学，2014：111-115.

DING Y Q.

Research on broken mechanism of vertical dome roof tank overpressure and weak roof structure

［D］. Daqing： Northeast Petroleum University， 2014： 111-115.

DING Y， DAI Z， LU Y， et al.

The influence of tank roof form on weak roof performance based on preventing environmental pollution

［J］. Ekoloji， 2019， 28（107）： 3773-3781.

[本文引用: 1]

李成兵，雷鹏.

5000 m3立式拱顶储罐应力分析与弱顶性能评价

［J］.工程设计学报，2020，27（2）：182-190.

[本文引用: 1]

LI C B， LEI P.

Stress analysis and weak roof performance evaluation for 5000 m3 vertical dome storage tank

［J］. Chinese Journal of Engineering Design， 2020， 27（2）： 182-190.

[本文引用: 1]

万昊天.

固定顶储罐弱壁防护结构设计及优化研究

［D］.大连：大连理工大学，2015：4-13.

[本文引用: 1]

WAN H T.

Design and optimization of weak wall protective structure of fixed roof storage tank

［D］. Dalian： Dalian University of Technology， 2015： 4-13.

[本文引用: 1]

刘博，唐辉永，张学恭.

微内压大型立式圆筒储罐设计原理及应用分析

［J］.化工设备与管道，2014，51（5）：1-4. doi：10.3969/j.issn.1009-3281.2014.05.001

[本文引用: 1]

LIU B， TANG H Y， ZHANG X G.

Design principle and application analysis of large vertical cylindrical tank subjected to minor internal pressure

［J］. Process Equipment & Piping， 2014， 51（5）： 1-4.

DOI:10.3969/j.issn.1009-3281.2014.05.001      [本文引用: 1]

丁旭明，李明波.

设计压力对储罐结构设计的影响

［J］.油气储运，2018，37（5）：563-567.

[本文引用: 1]

DING X M， LI M B.

The effect of design pressure on tank structure design

［J］. Oil & Gas Storage and Transportation， 2018， 37（5）： 563-567.

[本文引用: 1]

万昊天，喻健良，焦国栋.

静压下固定顶储罐弱壁结构保护性能研究

［J］.河南科技，2017（9）：71-74. doi：10.3969/j.issn.1003-5168.2017.09.036

[本文引用: 1]

WAN H T， YU J L， JIAO G D.

Study of weak wall structure of fixed roof storage tank under static pressure

［J］. Henan Science and Technology， 2017（9）： 71-74.

DOI:10.3969/j.issn.1003-5168.2017.09.036      [本文引用: 1]

刘巨保，许蕴博.

基于GB 50341标准设计的立式拱顶储罐弱顶结构分析与评价

［J］.化工机械，2011，38（4）：423-427.

[本文引用: 1]

LIU J B， XU Y B.

Weak-roof structure analysis and evaluation of vertical dome tank based on GB 50341

［J］. Chemical Engineering & Machinery， 2011， 38（4）： 423-427.

[本文引用: 1]

丁宇奇，刘巨保，武铜柱，等.

基于三维模型的立式拱顶储罐应力分析与弱顶影响因素分析

［J］.压力容器，2011，28（12）：11-17. doi：10.3969/j.issn.1001-4837.2011.12.003

[本文引用: 1]

DING Y Q， LIU J B， WU T Z， et al.

Stress analysis of vertical dome tank and influencing factors analysis of weak roof based on three-dimensional model

［J］. Pressure Vessel Technology， 2011， 28（12）： 11-17.

DOI:10.3969/j.issn.1001-4837.2011.12.003      [本文引用: 1]

张宇.

池火灾场景下拱顶油罐失效过程的数值模拟与实验研究

［D］.鞍山：辽宁科技大学，2021：17-18.

[本文引用: 1]

ZHANG Y.

Numerical simulation and experimental study on failure process of dome roof oil tank under pool fire scenario

［D］. Anshan： University of Science and Technology Liaoning， 2021： 17-18.

[本文引用: 1]

李永华.

事故多米诺效应与罐区安全设计探讨

［J］. 安全、健康和环境，2018，18（11）：17-20.

[本文引用: 1]

LI Y H.

Domino effect of accidents and safety design of tank farms

［J］. Safety Health & Environment， 2018， 18（11）： 17-20.

[本文引用: 1]

戴希明.

储罐内爆破坏形式预测与弱顶优化方法研究

［D］.大庆：东北石油大学，2019：66-73.

[本文引用: 1]

DAI X M.

Study on prediction of damage form of blasting in storage tank and optimization method of weak roof

［D］. Daqing： Northeast Petroleum University， 2019： 66-73.

[本文引用: 1]

DING Y， LU Y， CHEN Z.

Study on the influence of frangible roof performance of tank explosion under multi-field coupling

［J］. Journal of Failure Analysis and Prevention， 2019， 19（5）： 1455-1463.

DING Y， ZHOU H， LU Y， et al.

Design of foot bolts for weak roof storage tanks to avoid environmental pollution

［J］. Ekoloji， 2019， 28（107）： 3643-3651.

[本文引用: 1]

孙延廷.

3000 m3立式固定顶储罐设计方法与罐顶失效分析

［D］.大庆：东北石油大学，2014：10-23.

[本文引用: 1]

SUN Y T.

The analysis and design methods of 3000 m3 vertical dome tanks and analysis of roof failure

［D］. Daqing： Northeast Petroleum University， 2014： 10-23.

[本文引用: 1]

侯海量，朱锡，李伟，等.

舱内爆炸冲击载荷特性实验研究

［J］.船舶力学，2010，14（8）：901-907. doi：10.3969/j.issn.1007-7294.2010.08.011

[本文引用: 1]

HOU H L， ZHU X， LI W， et al.

Experimental studies on characteristics of blast loading when exploded inside ship cabin

［J］. Journal of Ship Mechanics， 2010， 14（8）： 901-907.

DOI:10.3969/j.issn.1007-7294.2010.08.011      [本文引用: 1]

LU Y， XU K.

Prediction of debris launch velocity of vented concrete structures under internal blast

［J］. International Journal of Impact Engineering， 2007， 34（11）： 1753-1767.

CHAN P C， KLEIN H H.

A study of blast effects inside an enclosure

［J］. Journal of Fluids Engineering， 1994， 116（3）： 450-455.

[本文引用: 1]

芦烨，丁宇奇，王学勇，等.

考虑温压载荷耦合作用的储罐内爆破坏与辐射区域

［J］.化工机械，2021，48（6）：839-846. doi：10.3969/j.issn.0254-6094.2021.06.010

[本文引用: 1]

LU Y， DING Y Q， WANG X Y， et al.

Internal explosion damage and radiation area of storage tank considering coupling effect of temperature and pressure

［J］. Chemical Engineering & Machinery， 2021， 48（6）： 839-846.

DOI:10.3969/j.issn.0254-6094.2021.06.010      [本文引用: 1]

苗婷，苗张木，冷晓畅.

基于内聚力模型的X65管线钢稳定裂纹扩展研究

［J］.船舶力学，2017，21（2）：192-200. doi：10.3969/j.issn.1007-7294.2017.02.009

[本文引用: 2]

MIAO T， MIAO Z M， LENG X C.

Study of stable crack growth through X65QO pipeline steel using cohesive zone modeling

［J］. Journal of Ship Mechanics， 2017， 21（2）： 192-200.

DOI:10.3969/j.issn.1007-7294.2017.02.009      [本文引用: 2]

傅伟庆，张文伟，孙正国，等. 立式圆筒形钢制焊接油罐设计规范： ［S］.北京：中国计划出版社，2014：17-145.

[本文引用: 1]

FU W Q， ZHANG W W， SUN Z G， et al. Code for design of vertical cylindrical welded steel oil tanks： ［S］. Beijing： China Planning Press， 2014： 17-145.

[本文引用: 1]

ZHANG R， JIA J， WANG H， et al.

Shock response analysis of a large LNG storage tank under blast loads

［J］. KSCE Journal of Civil Engineering， 2018， 22（9）： 3419-3429.

[本文引用: 1]

王晓辉，褚学森，冯光.

基于ABAQUS显式CEL方法的球体入水数值研究

［J］.船舶力学，2018，22（7）：838-844. doi：10.3969/j.issn.1007-7294.2018.07.007

[本文引用: 1]

WANG X H， CHU X S， FENG G.

Numerical simulation of sphere’s water-entry based on coupled Eulerian-Lagrangian method

［J］. Journal of Ship Mechanics， 2018， 22（7）： 838-844.

DOI:10.3969/j.issn.1007-7294.2018.07.007      [本文引用: 1]

RASAEE S， MIRZAEI A H.

Constitutive modeling of 2024 aluminum alloy based on the Johnson-Cook model

［J］. Transactions of the Indian Institute of Metals， 2019， 72（4）： 1023-1030.

[本文引用: 1]

XU H， ZHAO B， LU X， et al.

A modified Johnson-Cook constitutive model for the compressive flow behaviors of the SnSbCu alloy at high strain rates

［J］. Journal of Materials Engineering and Performance， 2019， 28（11）： 6958-6968.

[本文引用: 1]

王博，刘雄飞，胡佳，等.

缝内暂堵转向压裂数值模拟方法

［J］.石油科学通报，2021，6（2）：262-271. doi：10.3969/j.issn.2096-1693.2021.02.020

[本文引用: 1]

WANG B， LIU X F， HU J， et al.

Numerical simulation of in-fracture temporary plugging and diverting fracturing （ITPDF）

［J］. Petroleum Science Bulletin， 2021， 6（2）： 262-271.

DOI:10.3969/j.issn.2096-1693.2021.02.020      [本文引用: 1]

/

〈 〉