对转圆柱滚子轴承动态特性分析

doi:10.3785/j.issn.1006-754X.2023.00.014

对转圆柱滚子轴承动态特性分析

张龙隆^,^,¹, 肖正明^,¹, 刘江¹, 刘卫标²

1.昆明理工大学机电工程学院，云南昆明 650500

2.云南昆钢重型装备制造集团有限公司，云南昆明 650501

Dynamic characteristics analysis of counter-rotating cylindrical roller bearing

ZHANG Long-long^,^,¹, XIAO Zheng-ming^,¹, LIU Jiang¹, LIU Wei-biao²

1.Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China

2.Yunnan Kunming Iron & Steel Heavy Equipment Manufacturing Group Co. , Ltd. , Kunming 650501, China

通讯作者: 肖正明（1982—），男，江西吉安人，教授，博士生导师，博士，从事机械动力学分析与控制、机器人机构学研究，E-mail: suzem@sina.com

收稿日期: 2022-06-23 修回日期: 2022-09-05

基金资助:

国家自然科学基金资助项目.  51965025
云南省重点研发计划国际科技合作专项.  202003AF140007
云南省基础研究计划面上项目.  202201AT070103

Received: 2022-06-23 Revised: 2022-09-05

作者简介 About authors

张龙隆（1996—），男，贵州兴义人，硕士生，从事机械动力学研究，E-mail:1476146576@qq.com，https://orcid.org/0000-0001-5608-3552 , E-mail：1476146576@qq.com

摘要

针对内外圈对转圆柱滚子轴承内部复杂的运动特性及相互作用力，通过分析轴承径向游隙的影响因素以及考虑滚子与滚道的接触变形和热效应对油膜厚度的影响，利用拟静力学法建立了轴承的分析模型，并采用Newton-Raphson法进行求解；同时，利用该模型对滚子打滑率进行计算，以验证所采用分析方法的正确性和可靠性。然后，进一步探讨了不同工况下对转圆柱滚子轴承内部组件的转速变化规律与接触特性。结果表明：滚子的自转转速、滚子与滚道的接触载荷均随径向载荷的增大而增大；内、外圈转速变化会使受载区滚子与滚道的接触载荷以一定的规律重新分配，且转速对最小油膜厚度的影响较径向载荷更为明显。研究结果可为对转圆柱滚子轴承的结构优化和生热机理分析提供理论依据。

关键词： 对转圆柱滚子轴承 ; 动态特性 ; 拟静力学法 ; 接触载荷 ; 最小油膜厚度

Abstract

Aiming at the complex internal motion characteristics and interaction forces of cylindrical roller bearings with counter-rotating inner and outer rings, through analyzing the factors affecting the radial clearance of bearing and considering the contact deformation between rollers and raceway and the influence of thermal effect on oil film thickness, the analytical model of bearing was established by the quasi-static method and solved by the Newton-Raphson method; at the same time, the model was used to calculate the roller slip rate to verify the correctness and reliability of the analysis method. Then, the rotation speed variation and contact characteristics of internal components of counter-rotating cylindrical roller bearing under different working conditions were further discussed. The results showed that the rotation speed of roller and the contact load between rollers and raceway increased with the increase of radial load; the rotation speed change of inner and outer rings could make the contact load between rollers and raceway in the loaded area redistributed regularly, and the influence of rotation speed on the minimum oil film thickness was more obvious than that of radial load. The research results can provide a theoretical basis for structure design and heat generation mechanism analysis of counter-rotating cylindrical roller bearings.

Keywords： counter-rotating cylindrical roller bearing ; dynamic characteristics ; quasi-static method ; contact load ; minimum oil film thickness

PDF (3162KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张龙隆, 肖正明, 刘江, 刘卫标. 对转圆柱滚子轴承动态特性分析. 工程设计学报[J], 2023, 30(1): 93-101 doi:10.3785/j.issn.1006-754X.2023.00.014

ZHANG Long-long, XIAO Zheng-ming, LIU Jiang, LIU Wei-biao. Dynamic characteristics analysis of counter-rotating cylindrical roller bearing. Chinese Journal of Engineering Design[J], 2023, 30(1): 93-101 doi:10.3785/j.issn.1006-754X.2023.00.014

对转主轴系统可减小内、外转子陀螺力矩的影响，扭矩均匀且机械效率高，在机械传动中得到了广泛应用。对转轴承是对转主轴系统中的重要支撑元件，具有复杂的运动特性及相互作用力，准确预测其内部的接触载荷和转速等特性具有重要意义。Gamble等^[1]通过搭建对转轴承实验装置，对转子转速、轴承的载荷和温度等特征进行了测试。Bill^[2]对比分析了不同支撑方式下对转轴承的温度变化，并对代表性轴承保持架的转速和温度场进行了进一步分析。Cavallaro等^[3]基于Roark公式，在轴承动力学平衡方程中考虑轴承滚道的变形，建立了更加复杂的拟动力学模型。林国昌等^[4]开展了对转圆柱滚子轴承打滑率的实验研究。杨喜关^[5]采用拟动力学法分析了保持架引导方式对轴承动态特性的影响规律，并进行了实验验证。符毅强^[6]建立了对转轴承内外滚道表面的波纹度模型，探索了波纹度对双转子系统振动特性的影响规律。侯磊等^[7]建立了考虑波纹度的轴承动力学模型，并运用龙格-库塔法分析了对转轴承的波数、初始波纹度等因素影响下双转子系统的动态特性。胡绚等^[8-9]采用拟静力学法研究了对转圆柱滚子轴承的保持架转速、滚子自转转速及内部接触载荷，并对比分析了同向转动与反向转动圆柱滚子轴承的动态特性。任国哲等^[10]运用拟动力学法对比分析了正装与倒装工况下对转圆柱滚子轴承的接触载荷、内部转速等动态特性。李静等^[11]通过建立双转子系统的动力学模型，分析了对转轴承波纹度对双转子系统动力学特性的影响。高朋等^[12-13]结合双转子系统在临界转速下产生的不平衡响应，分析了同向转动轴承的动态载荷，并通过整体生热法计算得到轴承的生热情况。晏资文^[14]利用有限元分析软件分析了对转轴承刚度对双转子系统的影响，并搭建实验台进行了动力学特性验证。曹宏瑞等^[15]建立了对转轴承的动力学模型，并通过实验完成了轴承保持架转速的测量，验证了动力学模型的正确性，同时在此基础上，进一步分析了轴承出现故障后的振动响应。蒋云帆等^[16]分析了不同因素对同转/对转轴承径向刚度的影响程度，其中内、外圈转动方向对轴承径向刚度的影响较大。

综上所述，在对转轴承的相关分析中，学者们分别对轴承保持架、滚道波纹及轴承内部相互作用力进行了研究，部分学者还通过搭建实验台分析了对转轴承的相关特性，并讨论了轴承的刚度、游隙等对双转子系统响应特性的影响。但是，目前关于对转轴承自身动态特性分析的研究较少，且存在以下不足：一是对轴承进行建模时忽略了轴承径向游隙受实际工况的影响，虽减小了计算难度，但所得结果并不能精确反映轴承的运动状态；二是滚子与滚道的接触载荷采用的是静态工况下的，忽略了滚子的变形与离心力对接触载荷的影响。

为此，笔者以对转圆柱滚子轴承为研究对象，综合分析内、外圈过盈配合与转速对轴承径向游隙的影响，并考虑径向游隙、油膜厚度及接触载荷对滚子与滚道之间接触变形的影响以及热效应对油膜厚度的影响，基于弹性流体动力润滑与流体动压润滑理论，采用拟静力学法建立对转圆柱滚子轴承的分析模型，以研究其在不同工况下的动态特性。

1 对转圆柱滚子轴承径向游隙的影响因素分析

轴承的径向游隙是轴承应用时的一个重要参考指标，其不仅对轴承的磨损、振动和噪声等特性均有不可忽视的影响，还会改变轴承内部载荷的分布情况。因此，在分析轴承的动态特性时，必须考虑径向游隙的影响因素^[17]。

在安装对转圆柱滚子轴承时，轴承内圈与实心内轴过盈配合，内圈与内轴共同转动，故内圈受撑向外膨大；轴承外圈与空心外轴同样过盈配合，外圈受压向内收缩。根据弹性力学理论，内圈过盈配合造成的轴承径向游隙减少量u_i为^[18]：

$u i = 2 I 1 - I i d i / d d i / d 2 - 1 d i / d 2 + 1 d i / d 2 - 1 + v 1 + E 1 E 2 1 - v 2$ (1)

式中：I₁为考虑表面粗糙度的轴承内圈与内轴的过盈量；d、d_i分别为轴承内径和内圈滚道直径；E₁、v₁，E₂、v₂分别为轴承内圈与内轴材料的弹性模量和泊松比；I_i为轴承内圈因高速转动而产生的过盈变化量，忽略内轴因高速转动而产生的过盈量变化。

外圈过盈配合造成的轴承径向游隙减少量u_o为：

$u o = 2 I 2 + I o - I w / d n 2 - d o 2 d n / d o 2 + 1 d n / d o 2 - 1 + v 3 + E 3 E 4 d w / d n 2 + 1 d w / d n 2 - 1 - v 4$ (2)

式中：I₂为考虑表面粗糙度的轴承外圈与外轴的过盈量；d_o为外圈滚道直径；d_n、d_w为外轴内、外径；E₃、v₃，E₄、v₄分别为轴承外圈与外轴材料的弹性模量和泊松比；I_o、I_w分别为轴承外圈与外轴因高速转动而产生的过盈变化量。

将轴承内、外圈看作高速旋转的空心轴，通过几何方程与弹性本构方程，可求得内、外圈因转动而产生的离心力所引发的轴承径向游隙变化量u_n与u_w，为：

$u n w = r i o E 1 (3) σ c - v 1 (3) σ r + σ z$ (3)

式中：r_i(o)为轴承内、外圈滚道的半径；σ_c、σ_r、σ_z分别为半径r处的周向应力、径向应力和轴向应力。

综合分析可知，轴承径向游隙受过盈配合和高速转动时离心效应的影响。由此可得，轴承的径向游隙u为：

$u = u r - u i - u o - u n + u w$ (4)

式中：u_r为初始径向游隙。

2 对转圆柱滚子轴承拟静力学模型建立

2.1　轴承运动分析

通过分析对转圆柱滚子轴承的运动可得，内、外圈滚道与滚子接触处的相对滑动速度V_i_j 与V_o_j 分别为：

V_{i j} = \frac{D_{m}}{2} [(1 - γ) (ω_{i} - ω_{m}) - γ ω_{b j}]

(5)

V_{o j} = \frac{D_{m}}{2} [(1 + γ) (ω_{o} + ω_{m}) - γ ω_{b j}]

(6)

其中：

γ = \frac{D_{m}}{D_{b}}

式中：D_m为节圆直径；D_b为滚子直径；ω_i、ω_m、ω_o和ω_b_j 分别为内圈、保持架和外圈的角速度以及受载区滚子的自转角速度。

则受载区滚子与内、外圈滚道接触处的平均线速度U_i_j 与U_o_j 分别为：

U_{i j} = \frac{D_{m}}{4} [(1 - γ) (ω_{i} - ω_{m}) + γ ω_{b j}]

(7)

U_{o j} = \frac{D_{m}}{4} [(1 + γ) (ω_{o} + ω_{m}) + γ ω_{b j}]

(8)

非受载区滚子与外圈滚道接触处的平均线速度U_ou为：

U_{o u} = \frac{D_{m}}{4} [(1 + γ) (ω_{o} + ω_{m}) + γ ω_{b u}]

(9)

其中：

ω_{b u} = \frac{(1 + γ) (ω_{o} + ω_{m})}{γ}

(10)

式中：ω_bu为非受载区滚子的自转角速度。

2.2　轴承内部载荷分析

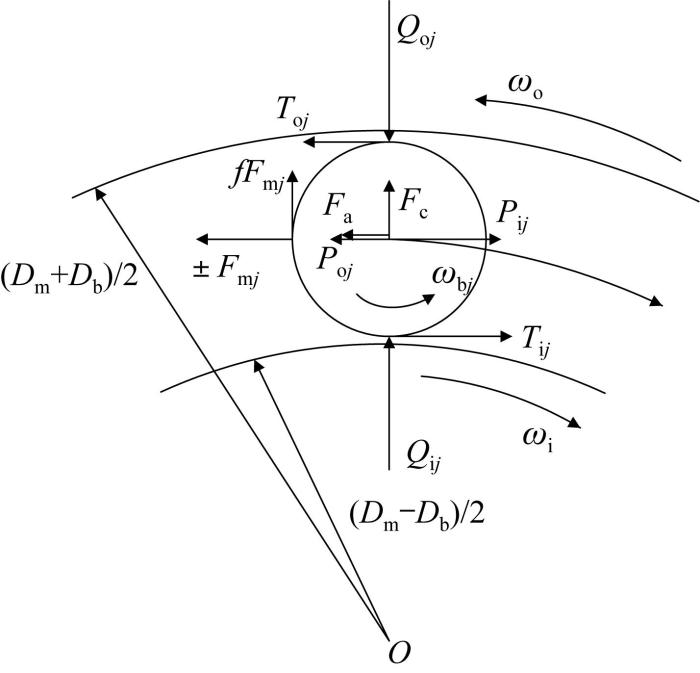
忽略滚子的歪斜，分析受载区滚子的受力情况，如图1所示。定义图示转动方向与力方向为正方向。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 受载区滚子受力分析

Fig.1 Force analysis of roller in loading region

2.2.1　流体动压力

根据图1，当滚子在油气混合的空间内转动时，滚子在与内、外圈滚道接触时受到的流体动压力P_i_j 、P_o_j 的无量纲形式为^[19]：

{\bar{P}}_{i j} = \frac{P_{i j}}{l_{e} E R_{i}} = 18.4 (1 - γ) G^{- 0.3} {(\frac{η_{0} U_{i j}}{E R_{i}})}_{}^{0.7}

(11)

{\bar{P}}_{o j} = \frac{P_{o j}}{l_{e} E R_{o}} = 18.4 (1 + γ) G^{- 0.3} {(\frac{η_{0} U_{o j}}{E R_{o}})}_{}^{0.7}

(12)

式中：G为材料参数；E为当量弹性模量；l_e为滚子有效长度；R_i、R_o分别为轴承内、外圈的当量曲率半径；η₀为润滑油动力黏度。

非受载区滚子所受的流体动压力P_ou的无量纲形式为：

{\bar{P}}_{o u} = \frac{P_{o u}}{l_{e} E R_{o}} = 18.4 (1 + γ) G^{- 0.3} {(\frac{η_{0} U_{o u}}{E R_{o}})}_{}^{0.7}

(13)

2.2.2　切向摩擦力

根据图1，轴承内、外圈滚道分别作用在滚子上的切向摩擦力T_i_j、T_o_j 的无量纲形式为：

{\bar{T}}_{i j} = \frac{T_{i j}}{l_{e} E R_{i}} = - 9.2 G^{- 0.3} {(\frac{η_{0} U_{i j}}{E R_{i}})}^{0.7} + \frac{η_{0} V_{i j} I_{i j}}{E R_{i} {\bar{H}}_{i j}}

(14)

{\bar{T}}_{o j} = \frac{T_{o j}}{l_{e} E R_{o}} = - 9.2 G^{- 0.3} {(\frac{η_{0} U_{o j}}{E R_{o}})}^{0.7} + \frac{η_{0} V_{o j} I_{o j}}{E R_{o} {\bar{H}}_{o j}}

(15)

其中：

{I_{i (o)}}_{j} = 2 \int_{0}^{4 {\bar{q}}_{i (o) j}} e x p [G {\bar{q}}_{i (o) j} \sqrt[]{1 - {(\frac{\bar{x}}{4 {\bar{q}}_{i (o) j}})}^{2}}] d \bar{x}

{\bar{q}}_{i (o) j} = \sqrt[]{Q_{i (o) j} / (l_{e} E R_{i (o)} 2 π)}

式中： $\bar{H}$ _i_j 、 $\bar{H}$ _o_j 分别为第j个滚子与内、外圈滚道之间的无量纲油膜厚度^[20]；Q_i_j 、Q_o_j 分别为滚子与内、外圈滚道的接触载荷。

非受载区滚子所受的切向摩擦力T_ou的无量纲形式为：

{\bar{T}}_{o u} = \frac{T_{o u}}{l_{e} E R_{o}} = - 9.2 G^{- 0.3} {(\frac{η_{0} U_{o u}}{E R_{o}})}^{0.7}

(16)

2.2.3　滚子与滚道的接触载荷

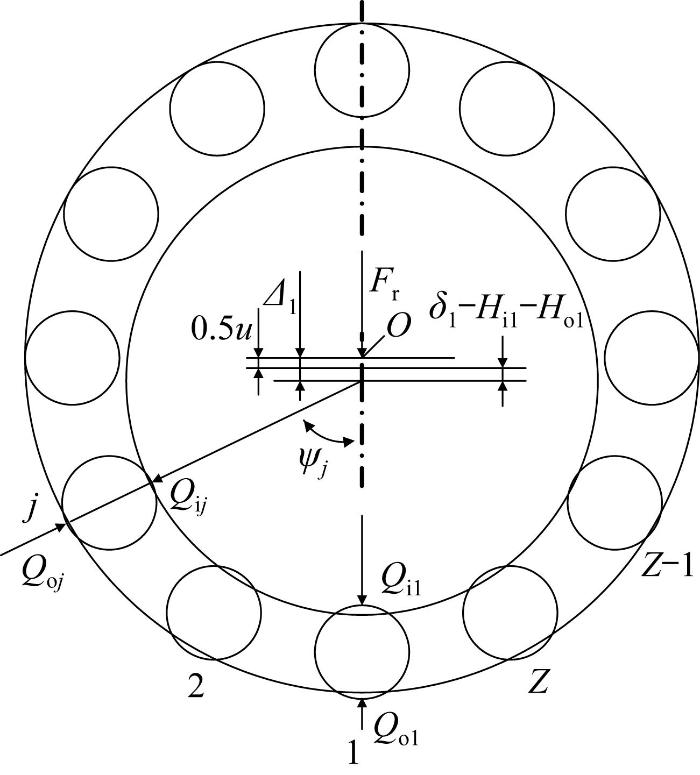
对转圆柱滚子轴承的内、外圈分别与实心内轴和空心外轴联结安装，且外轴上还装有固定轴承，以保证轴承内圈外加径向载荷F_r时，外圈不发生偏移。轴承内圈在向下径向载荷的作用下产生了一定的位移，其内部接触载荷的分布如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 对转圆柱滚子轴承载荷分布

Fig.2 Load distribution of counter-rotating cylindrical roller bearing

根据图2，轴承的静力平衡方程可表示为：

F_{r} = Q_{i 1} + 2 \sum_{j = 2}^{(N + 1) / 2} Q_{i j} c o s ψ_{j}

(17)

式中：N为受载区滚子的个数；Ψ_j 为第j个滚子的角度，ψ_j=2π $(j - 1) / Z$ ，其中Z为滚子总数；Q_i1为第1个滚子与内圈滚道的接触载荷。

在向下径向载荷F_r的作用下，内圈相对于外圈的径向位移Δ_j 可表示为：

Δ_{j} = Δ_{1} c o s ψ_{j} = δ_{j} + 0.5 u - H_{i j} - H_{o j}

(18)

其中：

H_{i (o) j} = 2.65 \frac{C_{i (o) j} α^{0.54} {(η_{0} U_{i (o) j})}^{0.7} R_{i (o)}^{0.43} l_{e}^{0.13}}{E^{0.03} {Q_{i (o) j}}^{0.13}}

C_{i (o) j} = \frac{1 - 13.2 (p_{0} / E) L_{T}^{0.42}}{1 + 0.213 (1 + 2.23 S^{0.83}) L_{T}^{0.64}}

式中：Δ₁为第1个滚子处内圈相对于外圈的径向位移；δ_j 为第j个滚子与内、外圈滚道的接触变形量；C_i(o)_j 为润滑油膜的热修正系数^[21]；L_T为热负荷参数，L_T=ßη₀U_i(o)_j /k_d，其中ß、k_d分别为润滑油的黏‒温系数和导热系数；p₀为接触面之间的接触应力；S为接触面运动滑滚比，S=V_i(o)_j /U_i(o)_j。

由图2可知，滚子与内、外圈滚道的接触变形受轴承径向游隙和最小油膜厚度的共同影响，可得不同角位置处滚子的接触变形量为：

\begin{array}{l} δ_{j} = [δ_{1} + 0.5 u - (H_{i 1} + H_{o 1})] c o s ψ_{j} - \\ 0.5 u + (H_{i j} + H_{o j}) \end{array}

(19)

其中：

δ1=δ_i1+δ_o1

式中：δ1为第1个滚子与内、外圈滚道的接触变形量。

由文献[20]可知，滚子与内、外圈滚道的接触变形量分别为：

\{\begin{array}{l} δ_{i j} = {(\frac{Q_{i j}}{K_{}})}_{}^{0.9} - 0.13 H_{i j} \\ δ_{o j} = {(\frac{Q_{o j}}{K_{}})}^{0.9} - 0.13 H_{o j} \end{array}

(20)

式中：δ_i_j 、δ_o_j 分别为滚子与内、外圈滚道的接触变形量，δ_j =δ_i_j +δ_o_j；K为变形协调系数。

联立式(19)和式(20)可得，受载区滚子的变形协调方程为：

\begin{array}{l} [{(\frac{Q_{i 1}}{K_{}})}^{0.9} + {(\frac{Q_{o 1}}{K_{}})}^{0.9} + 0.5 u - 1.13 (H_{i 1} + H_{o 1})] c o s ψ_{j} - \\ [{(\frac{Q_{i j}}{K_{}})}^{0.9} + {(\frac{Q_{o j}}{K_{}})}^{0.9} + 0.5 u - 1.13 (H_{i j} + H_{o j})] = 0 \end{array}

(21)

2.2.4　滚子离心力

由于滚子绕内圈滚道高速公转，单个滚子的离心力F_c为^[22]：

F_{c} = \frac{1}{2} m_{b} D_{m} ω_{m}^{2}

(22)

式中：m_b为滚子质量。

2.2.5　油气混合物对滚子的绕流阻力

当轴承转动时，滚子通过油气混合环境，此时作用在滚子上的绕流阻力F_a可近似表示为^[23]：

F_{a} = \frac{1}{8} P_{d} ρ D_{m} l_{e} D_{m}^{2} ω_{m}^{2}

(23)

式中：P_d为绕流阻力系数；ρ为油气混合物的密度^[24]。

2.3　轴承受力平衡方程组建立

为便于计算，特作以下假设：

1）忽略非受载区滚子与内圈滚道的切向摩擦力；

2）非受载区滚子的受力情况相同，且滚子沿外圈滚道作纯滚动。

根据滚子与内、外圈滚道和保持架的受力关系，可得受载区滚子的受力平衡方程：

\{\begin{array}{l} P_{i j} + T_{i j} - P_{o j} - T_{o j} \pm F_{m j} \pm F_{a} = 0 \\ Q_{i j} + F_{c} - Q_{o j} \pm f F_{m j} = 0 \\ 0.5 D_{b} (T_{i j} + T_{o j} \pm f F_{m j}) = 0 \end{array}

(24)

式中：F_m_j 为保持架与滚子的接触力；f为摩擦因数。

保持架的受力平衡方程为：

\frac{D_{m}}{2} (F_{m 1} + 2 \sum_{j = 2}^{(N - 1) / 2} F_{m j} - (Z - N) F_{m u}) - M_{C L} = 0

(25)

式中：F_mu为非受载区滚子与保持架的接触力；M_CL为保持架与轴承外圈挡边引导面产生的摩擦力矩^[18]。

根据式(17)和式(21)，可求得N个受载滚子与内圈滚道的接触载荷Q_i1，Q_i2，…，Q_i_N，方程数为N个；根据式(24)和式(25)，可求得N个受载滚子的自转角速度与保持架角速度，方程数为N+1个。考虑到轴承受力的对称性，为简化计算，将滚子与内圈滚道的接触载荷的方程数减少至 $(N + 1) / 2$ ，滚子自转角速度的方程数减少至 $(N + 3) / 2$ ，并采用Newton-Raphson法对上述方程组进行联合求解。

3 对转圆柱滚子轴承滚子打滑率计算验证

为验证上文所构建的对转圆柱滚子轴承拟静力学模型的正确性，以型号为D1002928NQ1K的轴承为分析对象，对其滚子打滑率与径向载荷的关系进行计算（转速、载荷等工况与文献[4]一致），并与文献[4]中的实验结果进行对比。该轴承的节圆直径为165 mm，滚子的直径与有效长度均为12 mm，滚子个数为32；内圈转速为13 280 r/min，外圈转速为7 220 r/min。基于对转轴承特殊的运动关系，定义滚子的打滑率s_r为：

s_{r} = |\frac{ω_{m t} - ω_{m}}{ω_{m t} + 0.5 ω_{o} D / D_{m}}| \times 100 %

式中：ω_mt为保持架的理想角速度；D为轴承外径。

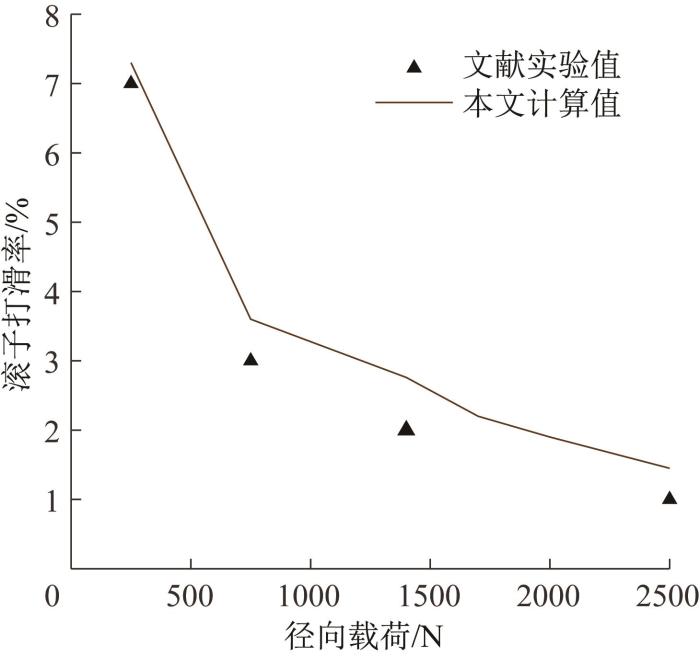
运用本文构建的拟静力学模型计算得到的轴承滚子打滑率与文献[4]实验值的比较如图3所示。由图可知，当径向载荷由250 N增大至2 500 N时，滚子打滑率的计算值由7.30%减小至1.45%，实验值由7%减小至1%，计算值与实验值的吻合程度较高，说明本文所采用的分析方法正确、可靠，即所建立的拟静力学模型正确。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 滚子打滑率与径向载荷的关系

Fig.3 Relation between roller slip rate and radial load

4 对转圆柱滚子轴承动态特性计算与分析

使用所构建的拟静力学模型分析对转圆柱滚子轴承的动态特性。如图4所示，对转圆柱滚子轴承在由对转主轴和双转子电机联结而成的双转子系统实验台上工作，双转子电机通过实心内轴和空心外轴输出到轴承内、外圈的转速大小相同、方向相反，且最大转速为5 000 r/min。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 对转圆柱滚子轴承安装示意

Fig.4 Installation diagram of counter-rotating cylindrical roller bearing

以NU1014圆柱滚子轴承（采用MIL-L-7808润滑油，油气比5%）为例，进行动态特性计算与分析，其主要参数如表1所示。

表1 NU1014圆柱滚子轴承主要参数

Table 1 Main parameters of NU1014 cylindrical roller bearing

参数	数值
轴承外径/mm	110
轴承内径/mm	70
节圆直径/mm	90
初始径向游隙/mm	0.04
滚子数	26
滚子直径/mm	10
泊松比	0.3
弹性模量/Pa	2.07×10¹¹

新窗口打开| 下载CSV

4.1　转速分析

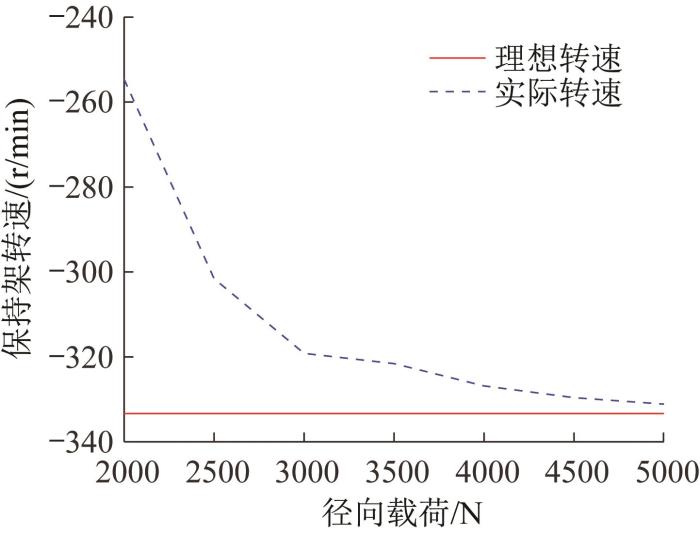
图5所示为对转圆柱滚子轴承保持架转速随径向载荷的变化曲线。由图5可知，不同径向载荷下保持架转速均小于0 r/min，说明此时保持架的转动方向因受外圈高转速影响而与外圈转动方向一致。当径向载荷由2 000 N增大至5 000 N时，保持架转速由254.6 r/min增大至331.1 r/min。这是因为随着径向载荷的增大，滚子与内、外圈滚道的切向摩擦力增大，使得滚子的打滑率减小，故保持架的转速提高。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 保持架转速与径向载荷的关系

Fig.5 Relationship between cage rotation speed and radial load

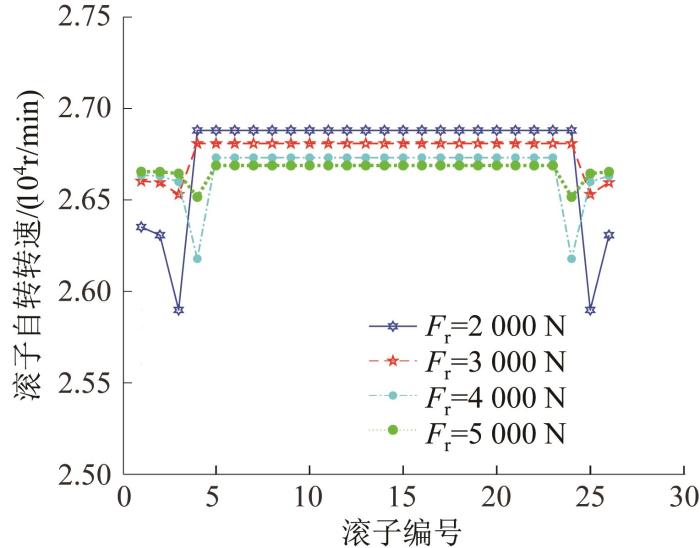
图6所示为相同转速、不同径向载荷下对转圆柱滚子轴承的滚子在不同角位置处的自转转速。设定径向载荷作用线下的滚子编号为1，其余滚子按顺时针方向依次编号。由图6可知，曲线部分为受载区，受载区滚子的自转转速随径向载荷的增大而增大，这是因为滚子与内、外圈滚道的接触载荷增大，使得滚子受到的切向摩擦力增大，而切向摩擦力产生的力矩方向与滚子自转方向相同，故滚子自转转速提高。在相同径向载荷下，1号滚子的自转转速最高，并向两侧逐渐减小；在非受载区，同一径向载荷下滚子的自转转速相等。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同径向载荷下滚子的自转转速

Fig.6 Rotation speed of roller under different radial loads

4.2　接触特性分析

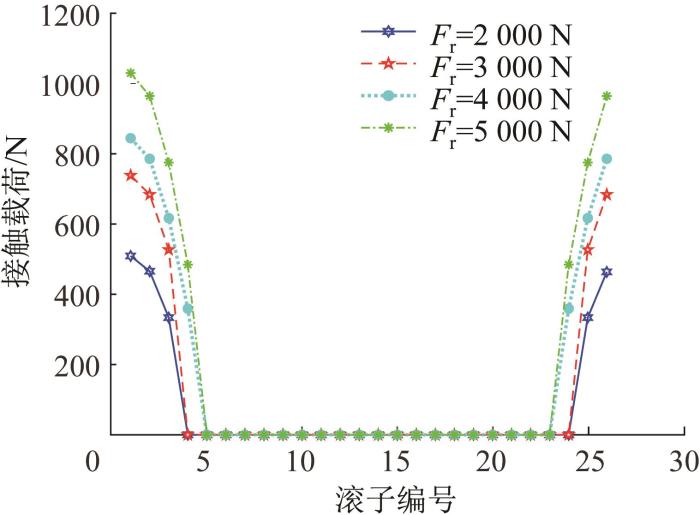
图7所示为内、外圈转速均为3 000 r/min，不同径向载荷下对转圆柱滚子轴承的滚子与内圈滚道的接触载荷变化曲线。由图7可知，当径向载荷由2 000 N逐渐增大到5 000 N时，轴承的受载区变大，受载区滚子数从5个增加到7个。在受载区，当径向载荷相同时，1号滚子所受的接触载荷最大，其余滚子所受的接触载荷随着角位置的增大而减小；在非受载区，内圈滚道因受向下径向载荷的作用而产生相应的位移，同时滚子因受离心力作用而挤压外圈滚道，导致滚子与内圈滚道失去接触，与外圈滚道的接触载荷等于滚子所受的离心力。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同径向载荷下滚子与内圈滚道的接触载荷

Fig.7 Contact load between roller and inner ring raceway under different radial loads

表2所示为径向载荷为2 000 N时，静态工况和不同转速（内、外圈转速同）工况下滚子与内圈滚道的接触载荷。其中，静态工况下的接触载荷由文献[23]的方法计算得到。为方便表述，表2中将静态工况表示为内、外圈转速为0 r/min工况。由上文分析可知，轴承在径向载荷为2 000 N时的受载滚子为5个，鉴于轴承的结构对称，仅列举一半数据。

表2 不同转速下滚子与内圈滚道的接触载荷 (N)

Table 2 Contact load between roller and inner ring raceway under different rotation speeds

转速/(r/min)	1号滚子	2号滚子	3号滚子
0	603.31	506.02	231.92
2 000	511.49	464.77	330.88
3 000	508.95	463.59	333.62
4 000	507.49	462. 91	335.19
5 000	506.51	462.46	336.23

新窗口打开| 下载CSV

由表2结果可知，当内、外圈转速提高时，3号滚子所受的接触载荷增大，而1号和2号滚子所受的接触载荷减小。这是因为在径向载荷不变的情况下，滚子的公转转速增大，滚子因离心力增大而与内圈呈分离趋势，从而导致接触载荷减小；同时，为保证滚子受载区静力平衡，边缘滚子所受载荷增大。由于轴承的对称性，另一半受载区内滚子所受的载荷亦是如此。相比于静态工况，内、外圈转动工况下滚子与内圈滚道的接触载荷的分布较为分散，避免了因滚子与滚道的接触载荷过大而产生接触变形。

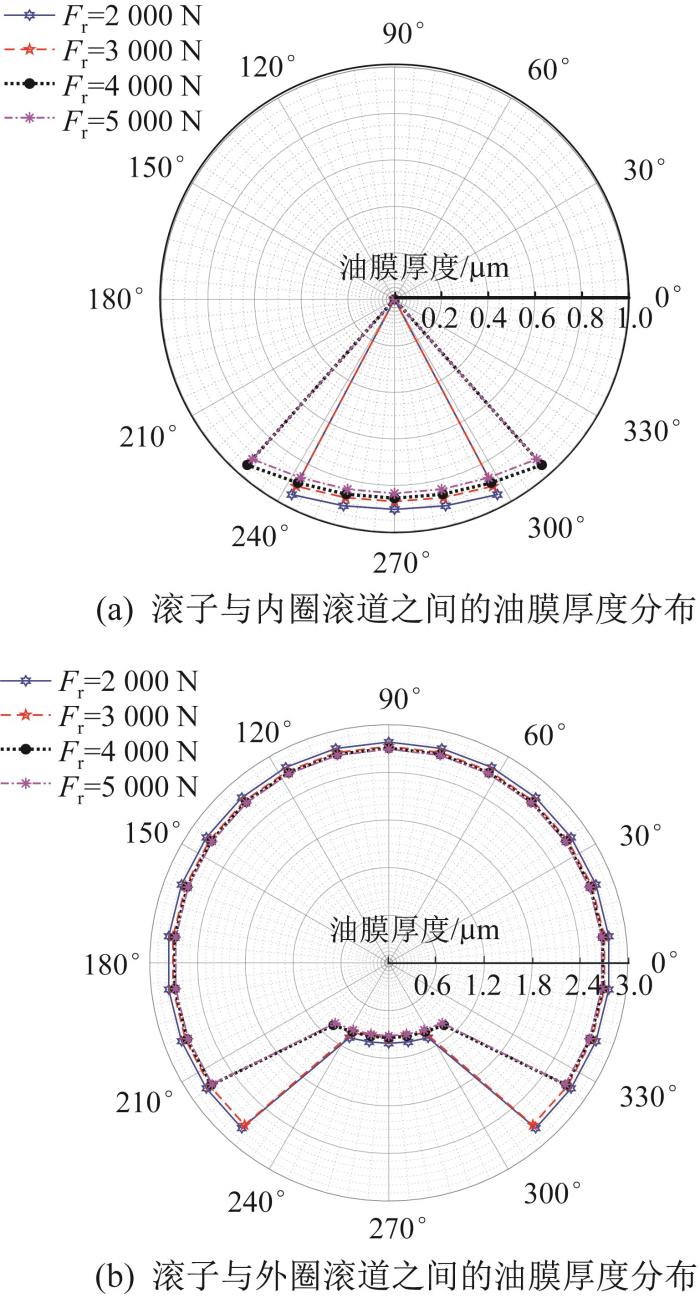
图8所示为相同转速、不同径向载荷下对转圆柱滚子轴承不同角位置处滚子与内、外圈滚道之间的最小油膜厚度，假设在270°角位置处的为1号滚子。由图8可知，随着径向载荷的增大，滚子与内、外圈滚道之间的油膜厚度均减小；当径向载荷相同时，1号滚子与内、外圈滚道之间的油膜厚度最小，越偏离径向载荷作用线，油膜厚度越大。这是因为越偏离1号滚子，滚子与内、外圈滚道的接触载荷越小。从图8(a)可以看出，当径向载荷由2 000 N逐渐增大到5 000 N时，1号滚子与内圈滚道之间的油膜厚度由0.903 4 μm减小到0.834 1 μm；在非受载区，由于滚子与内圈滚道分离，故不形成油膜。从图8(b)可以看出，1号滚子与外圈滚道之间的油膜厚度由1.013 1 μm减小到0.918 6 μm；在非受载区，各滚子与外圈滚道接触而形成油膜，油膜厚度约为2.726 6 μm，这是因为离心力较小，油膜厚度偏大。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同径向载荷下滚子与滚道之间的油膜厚度分布

Fig.8 Oil film thickness distribution of roller and raceway under different radial loads

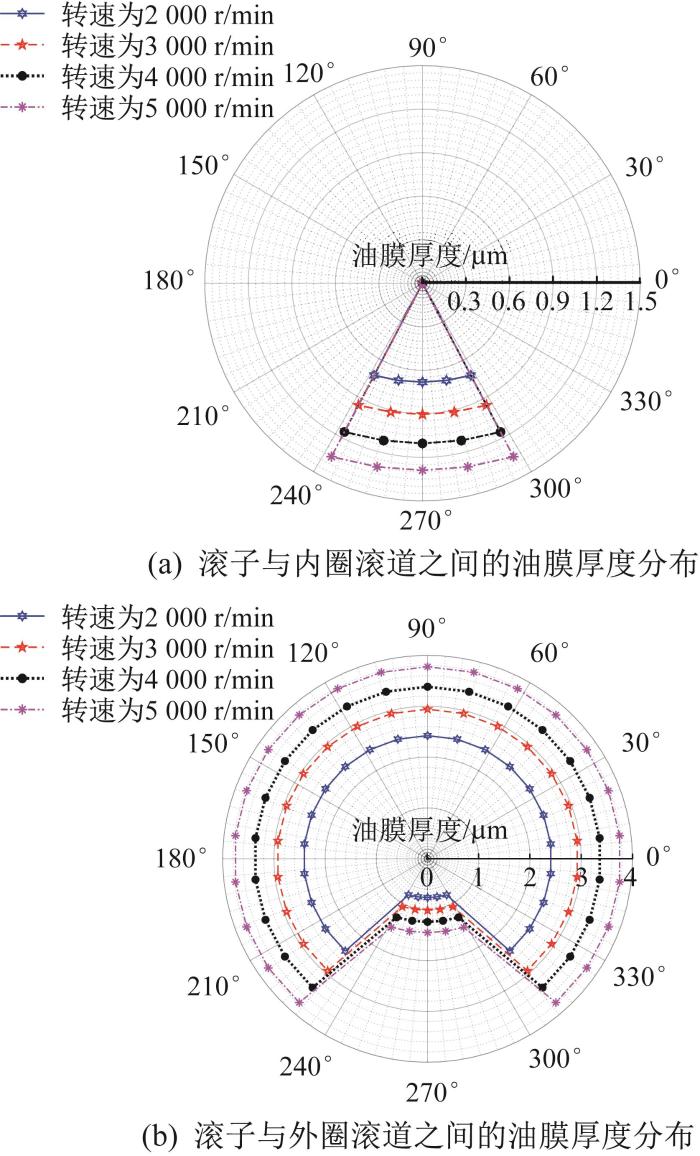
图9所示为相同径向载荷、不同转速下对转圆柱滚子轴承不同角位置处滚子与内、外圈滚道之间最小油膜厚度的分布规律。由图9可知，随着内、外圈转速的增大，滚子与滚道接触处的平均线速度增大，故滚子与内、外圈滚道之间的油膜厚度增大。从图9(a)可以看出，当内、外圈转速同时由2 000 r/min逐渐增大到5 000 r/min时，1号滚子与内圈滚道之间的油膜厚度由0.681 0 μm增大到1.288 4 μm；从图9(b)可以看出，1号滚子与外圈滚道之间的油膜厚度由0.761 6 μm增加到1.451 4 μm；在非受载区，外圈滚道仅受到滚子的离心力，油膜厚度相对较大，不同转速下油膜厚度最大相差1.354 3 μm。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同转速下滚子与滚道之间的油膜厚度分布

Fig.9 Oil film thickness distribution of roller and raceway under different rotation speeds

5 结论

本文综合分析了对转圆柱滚子轴承径向游隙的影响因素，同时考虑滚子的变形和热效应对油膜厚度的影响，采用拟静力学法建立了更加符合实际工况的轴承分析模型，并研究了轴承在不同工况下的动态特性，主要结论如下。

1）对滚子打滑率和径向载荷之间的关系进行了解析，完成了打滑率计算值与文献实验值的对比验证，结果表明计算结果与实验结果的吻合性较好，验证了所构建拟静力学模型的正确性。

2）随着径向载荷的增大，轴承保持架和滚子的转速均增大；在非受载区，同一径向载荷下滚子的自转转速相等。

3）轴承内部的接触载荷和受载区与径向载荷呈正相关。当径向载荷不变时，提高内、外圈转速，受载区边缘的2个滚子所受的接触载荷增大，其他滚子所受的接触载荷减小。相较于静态工况，不同转动工况下滚子所受的接触载荷分布较均匀。

4）滚子与滚道之间的最小油膜厚度随径向载荷的增大而逐渐减小，随内、外圈转速的增大而增大，且转速对油膜厚度的影响较为明显。因此，合理降低径向载荷和提高运行转速，有助于润滑油膜的形成，从而保证润滑效果，避免因干摩擦而导致轴承快速升温。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

GAMBLE

， VALORI

Development of counter-rotating intershaft support bearing technology

［J］. Journal of Aircraft， 1983， 20（6）： 557-563.