陶瓷浆料3D打印机料筒的结构与注射器类似。在微流挤出成形的作业过程中,采用柱塞式或螺杆式推杆将浆料从料筒挤出。本文采用由300 nm粒径的ZrO2陶瓷粉末制备的陶瓷浆料。由于浆料的化学特性,螺杆式机构易被腐蚀,因此选用柱塞式推杆[4]。
陶瓷浆料在制备及装填过程中会不可避免地出现气泡、板结颗粒等缺陷,在挤出过程中也会受到外部随机影响,导致挤压力不稳定即挤出速度不稳定。陶瓷部件的打印成形要求陶瓷浆料挤出时具有相对稳定的挤出速度,以保证打印进程的连续性、稳定性,因此提出了挤压力稳定控制策略,使在打印时实际压力值快速逼近参考压力值,这对保证打印精度是至关重要的。浆料挤出时挤压力的稳定控制并不能直接实现,通常通过调节推杆的进给速度或进给距离来间接控制[5]。许多学者对挤压力稳定控制策略进行了研究。如:刘志鹏[5]提出了一种浆料挤压力预测方法,设计了适用于微流挤出工艺的基于传统PID(proportion-integral-derivative,比例‒积分‒微分)控制的压力稳定控制器,但该控制器的参数设置后无法实现在线整定,会影响控制效果;Mason等[6]采用Bang-bang压力控制器对浆料在低温成形过程中的挤压力进行反馈控制;焦盼德等[7]采用基于最小方差的控制策略,在一定程度上解决了由水基膏体中气泡和结块导致的系统不稳定问题,但该控制策略有一定的局限性,难以实现精准控制;李聪[8]提出了压力系统的模糊自适应控制策略,采用模糊PID方法有效解决了在高固相陶瓷浆料挤出过程中压力无法快速稳定的问题,但该模糊控制策略在环境变化时缺乏自我调节和自学习能力,因此须进一步优化。
神经网络具有传播速度快、可实现自我权值更新等优点,可以弥补模糊控制缺乏自学习能力的缺陷。因此,本文以模糊PID控制为基础,结合神经网络,提出了模糊神经网络PID控制策略,并进行仿真及实验验证。
1 挤压力稳定控制原理
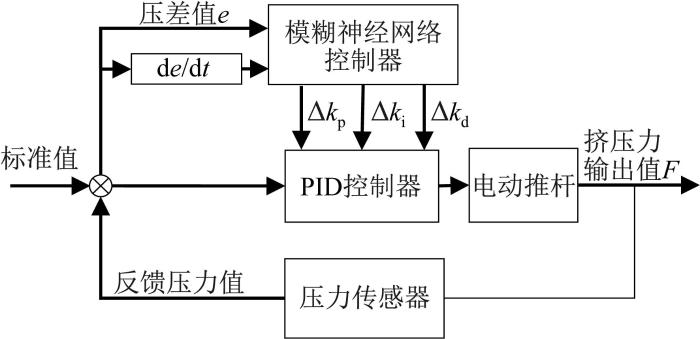
图1
PID控制参数的计算公式为:
传统PID控制器表示为:
式中:
式中:
2 模糊神经网络设计
2.1 模糊控制设计
结合陶瓷浆料3D打印经验及控制需求,定义模糊控制器输入变量
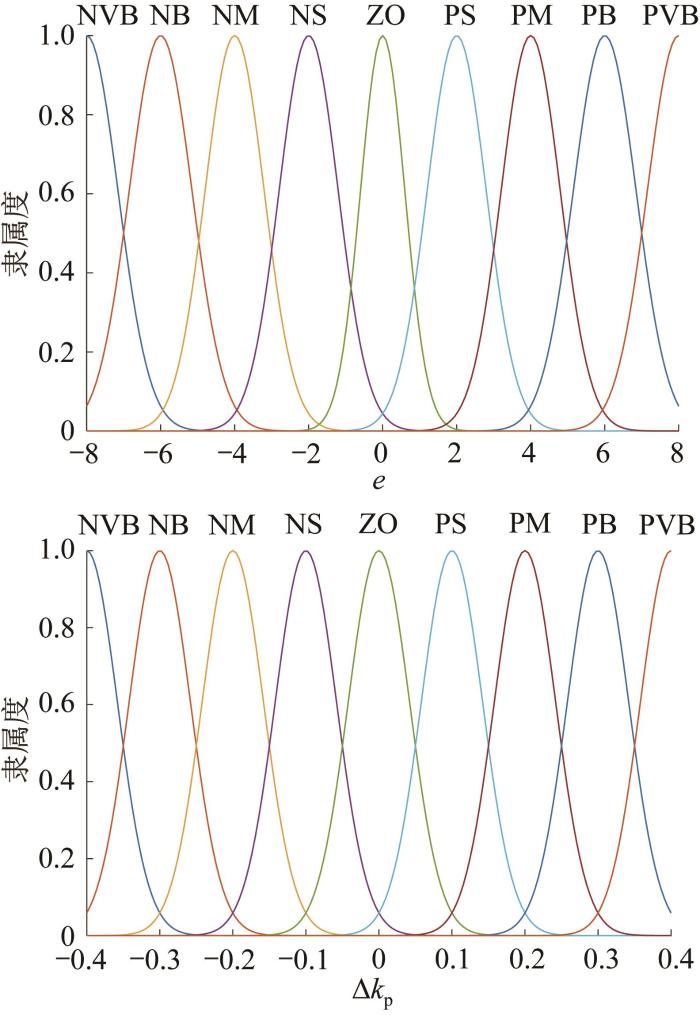
图2
根据陶瓷浆料3D打印经验建立模糊控制规则,采用形如“If
表1 模糊控制规则表
Table 1
| Δkp | Δki | Δkd | ||
|---|---|---|---|---|
| NVB | NB | PVB | NVB | NVB |
| NB | NM | PB | NB | NS |
| NM | NVB | PVB | NVB | PS |
| NS | NM | PM | NM | NS |
| ZO | PS | NS | PS | NS |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| PB | NB | ZO | ZO | PB |
| PS | PB | NM | PB | ZO |
| PM | NS | NS | PS | PS |
| NS | PS | ZO | ZO | NS |
| NM | PVB | NM | PS | PS |
利用上述规则完成推理过程,得到输出变量的模糊子集,再采用重心法等解模糊化方法处理所需控制量。
2.2 模糊神经网络推理结构
模糊神经网络是利用神经网络每一层中的神经元功能实现模糊推理的,同时,在推理过程中可以实现快速收敛和使控制精度逼近理想状态[15]。
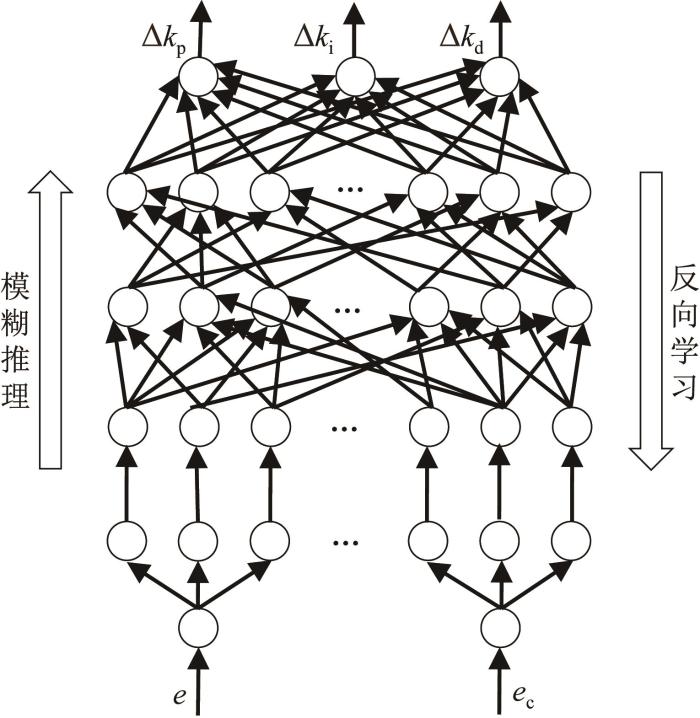
将模糊控制输入、输出变量及控制规则嵌入神经网络。网络结构如图3所示。
图3
第1层:输入层。
在输入层将模糊控制的2个输入变量
式中:
第2层:隶属度函数模拟层。
神经网络中单个神经元可模拟隶属度函数,此处神经元激励函数取S函数。将第1层的各输出值与权值相乘再相加后形成的和函数输入S函数,再形成第2层输出函数,即:
式中:
第3层:隶属度函数实现层。
根据模糊控制设计,隶属度函数选择为高斯函数。利用2个S函数的差,模拟高斯型隶属度函数。
式中:
第2、3层可看作模糊化层,其作用是模糊化处理输入变量,并确定隶属度函数。
第4层:模糊推理层。
在第4层确立模糊规则,进行模糊运算。共确立81条模糊规则,每一个神经元节点代表一条规则,利用玛达尼(Mamdani)推理法完成模糊“与”运算即取小运算,节点的输出即为运算结果。
式中:
第5层:隶属度函数模拟层。
第5层的神经元用以模拟输出变量的隶属度函数,对结果进行模糊化处理。其中,每一个神经元的激励函数均选择S函数。
式中:
第6层:清晰化输出层。
在第6层采用重心法对输出结果进行解模糊化处理,即精确计算出PID控制器的3个参数:Δkp、Δki、Δkd。
式中:
2.3 模糊神经网络反向学习算法
根据自学习算法,取评价函数为:
式中:
权值更新:
式中:
隶属度函数中心值
式中:
隶属度函数宽度
3 挤压力稳定控制仿真
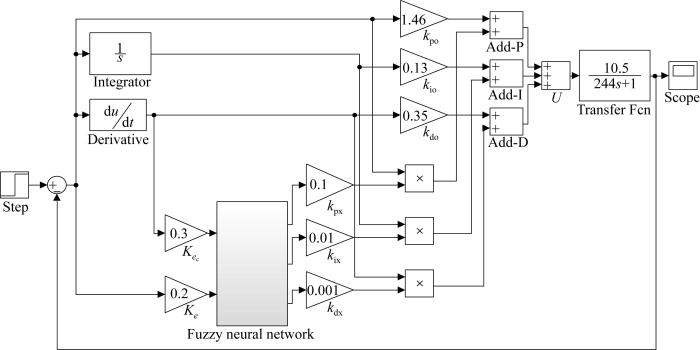
3.1 仿真系统搭建
图4
3.2 仿真结果分析
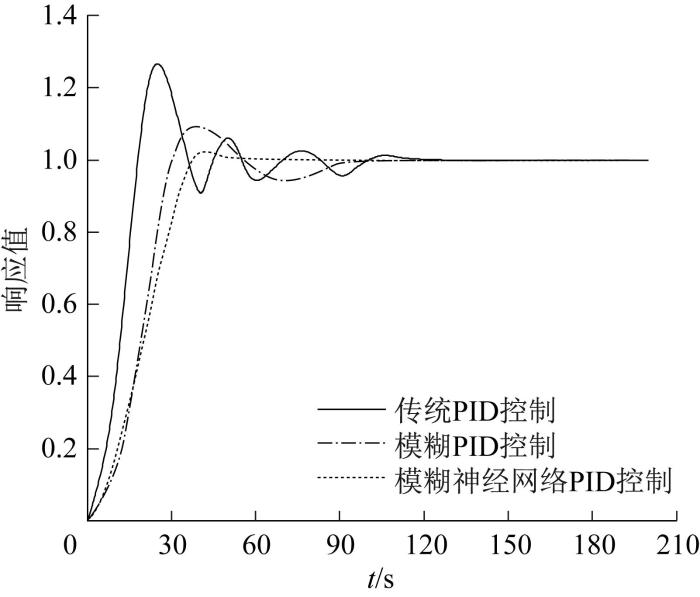
在3种控制策略下挤压力稳定控制仿真结果如图5所示。由图可知:
图5
图5
3种控制策略下挤压力稳定控制仿真结果
Fig.5
Simulation results of extrusion force stability control under three control strategies
1)在传统PID控制下,系统经过25 s后达到最大偏差值,超调量为22.5%;经过125 s后达到稳定状态。可见该控制器调节时间较长,波动较大。
2)在模糊PID控制下,系统经过40 s后达到最大偏差值,超调量为3.33%;经过94 s后达到稳定状态。可见该控制器波动较小,但调节时间也较长。
3)在模糊神经网络PID控制下,系统经过42 s后达到最大偏差值,超调量为1.6%;经过50 s后达到稳定状态。可见该控制器波动较小,调节时间较短。
通过对比可知,相较于传统PID控制策略和模糊PID控制策略,采用模糊神经网络PID控制策略可使超调量分别减小20.9%和1.73%,达到稳定状态的时间分别缩短75 s和44 s。综上,模糊神经网络PID控制策略具有波动小、调节速度快的优点。
4 挤压力稳定控制实验
4.1 控制流程
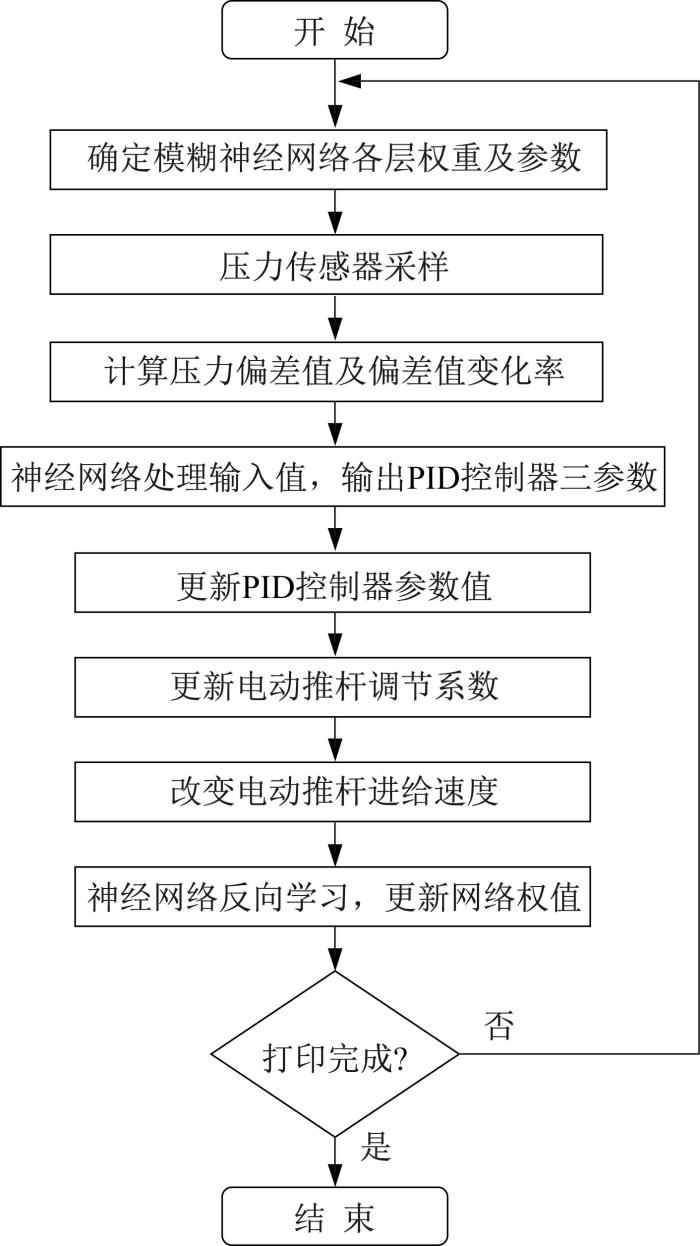
挤压力稳定控制流程如图6所示。控制流程为:开机,输入打印参数,初始化控制模块参数(参考压力读取),开始打印;压力传感器采集数据并处理(数模转换),挤压力稳定控制器处理输入数据并输出控制信号;电动推杆动作,其间压力传感器采集数据并反馈至控制器,进行控制器参数优化,直至打印完成。
图6
4.2 实验方案
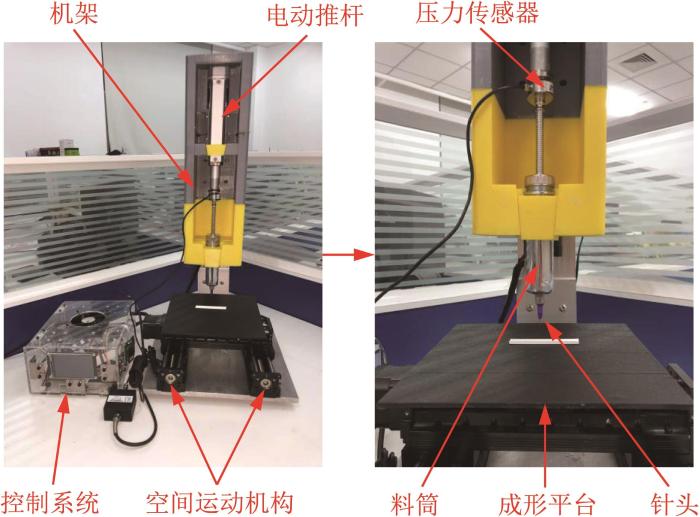
分别采用传统PID、模糊PID和模糊神经网络PID三种控制策略进行挤压力稳定控制实验。作者研制的陶瓷浆料3D打印机如图7所示。
图7
实验1:挤压力控制实验。由粒径为300 nm的ZrO2陶瓷粉末制备而成的浆料作为挤出浆料,料筒针头直径选择为0.5 mm,挤出速度设为0.03 mm/s,3D成形平台不移动,由压力传感器记录不同控制策略下挤压力数据,分析其波动情况。
实验2:陶瓷坯体打印实验。浆料和料筒针头直径与实验1一致,3D成形平台移动,打印速度为10 mm/s,打印尺寸为65 mm
4.3 实验结果及分析
4.3.1 挤压力控制结果及分析
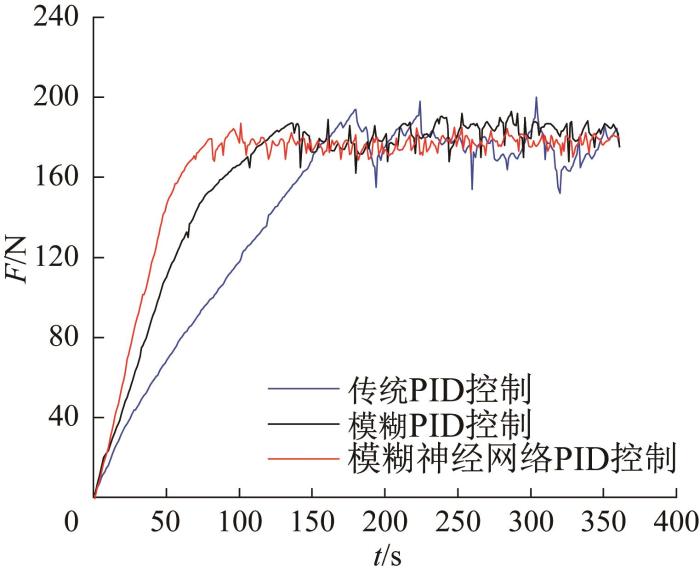
在不同控制策略下挤压力控制结果如图8所示。由图可知:
图8
1)在传统PID控制下,经过170 s左右挤压力达到稳定状态,压力最大值为200 N,最小值为152 N。
2)在模糊PID控制下,经过136 s左右挤压力达到稳定状态,压力最大值为192 N,最小值为162 N。
3)在模糊神经网络PID控制下,经过80 s左右挤压力达到稳定状态,压力最大值为188 N,最小值为170 N。
通过对比可知:相较于传统PID控制,采用模糊神经网络PID控制可使挤压力提前90 s达到稳定状态,压力峰值减小12 N,压力谷值增大18 N;相较于模糊PID控制,采用模糊神经网络PID控制可使挤压力提前56 s达到稳定状态,压力峰值减小4 N,压力谷值增大8 N。综上,采用模糊神经网络PID控制策略可以最快达到稳定打印状态,并在稳定打印后挤压力波动范围最小,总体压力最稳定,超调量最小。
4.3.2 陶瓷坯体形貌及分析
陶瓷坯体表面和侧面的形貌特征如图9所示。由图可知:
图9
1)在传统PID控制下,图中箭头1、6、7所示打印缺陷是电动推杆速度过快、挤压力过大、浆料挤出速度快于3D成形平台移动速度而导致的明显的浆料过堆积现象;方框1所示缺陷则是推杆速度过慢、挤压力过小、浆料挤出速度慢于3D成形平台移动速度而导致的浆料欠堆积现象;方框4所示出现了打印丝不连续现象,即过堆积、欠堆积现象交替出现。可见,传统PID控制策略对挤压力稳定具有一定的调节作用,但是响应速度较慢,调节时间较长,易超调,易出现浆料过堆积、欠堆积交替的现象,坯体打印缺陷较多。
2)在模糊PID控制下,方框2所示浆料堆积不匀,造成打印丝弯曲的缺陷;方框3所示则是由于浆料欠堆积,出现了一长段打印丝缺失;箭头8所示出现了塌陷现象,是由于下一层的一段打印丝缺失致使上一层打印丝失去支撑。可见,模糊PID控制策略对挤压力稳定的调节作用较明显,坯体表面和侧面的形貌较好,但响应仍不够及时,超调量仍较大,坯体存在一长段打印缺陷。
3)在模糊神经网络PID控制下,箭头3、4、5所示打印丝有细小的凹坑,方框6所示打印丝形貌有波动,出现轻微的浆料堆积不均匀现象。
可见,模糊神经网络PID控制策略对挤压力稳定调节的作用最为显著,调节速度最快,调节最为平稳,所以打印的坯体表面和侧面的形貌平整,没有大的打印缺陷。
从2个实验结果来看,采用模糊神经网络PID控制策略相较于传统PID控制、模糊PID控制策略对挤压力的调节更为迅速和平稳,超调量更小,调节效果更优,能够更好地适配微流挤出陶瓷浆料3D打印机。
5 结 论
根据陶瓷浆料3D打印过程中挤压力快速稳定、高效调节的控制要求,鉴于传统PID无法实现理想控制及模糊PID控制缺乏自学习能力,提出了一种模糊神经网络PID控制策略,并设计了模糊神经网络控制器。该控制器通过六层神经网络实现了整个模糊控制过程,即实时输出PID控制器的控制参数Δkp、Δki、Δkd并将其输入传统PID控制器,计算后输出电动推杆的速度变化信号,进而调节挤压力,实现挤压力的快速稳定控制。模糊神经网络PID控制策略基于神经网络的自学习能力,采用负梯度方法,实时更新模糊神经网络参数值,增强了控制器的自适应性和鲁棒性,使挤压力稳定控制更为精准。搭建了3种控制器的仿真模型,并进行阶跃信号响应测试,验证了模糊神经网络PID控制策略的优越性。同时,设计了挤压力控制实验和陶瓷坯体打印实验,分别采用3种控制策略打印陶瓷样件并进行坯体形貌对比。仿真及实验结果表明:模糊神经网络PID控制策略相较于其他两种控制策略具有自适应能力更强、控制精度更高、响应速度更快和鲁棒性更强等优点,能够满足微流挤出陶瓷浆料3D打印机挤压力稳定控制的要求。
参考文献
基于浆料形态的陶瓷3D打印技术的浆料体系研究进展
[J].
Research progress on slurry system of ceramic 3D printing technology based on slurry morphology
[J].
Indirect 3D printed ceramic: A literature review
[J].
陶瓷浆料微流挤压成形关键问题研究
[J].
Research on several key problems of microflow extrusion forming of ceramic slurry
[J].DOI:10.3969/j.issn.1004-132X.2015.22.018 [本文引用: 1]
Optimization of 3D printing parameters of screw type extrusion (STE) for ceramics using the Taguchi method
[J].
基于微流挤出工艺的3D打印机控制系统研究
[D].
Research on 3D printer control system based on microfluidic extrusion process
[D].DOI:10.13433/j.cnki.1003-8728.20190249 [本文引用: 3]
Freeform extrusion of high solids loading ceramic slurries, part I: extrusion process modeling
[C]//
功能梯度材料快速成形过程建模与控制
[J].
Modeling and control of rapid deposition for functionally gradient material components
[J].DOI:10.3969/j.issn.1004-132X.2017.06.016 [本文引用: 1]
基于STM32的陶瓷浆料3D打印机控制系统研究
[D].
Research on the control system of ceramic slurry 3D printer based on STM32
[D].
Bookshelf: analytical design of PID controllers
[J].
Grey wolf optimizer based PID controller for speed control of BLDC motor
[J].
Fuzzy fractional-order PID controller for fractional model of pneumatic pressure system
[J].
PID参数先进整定方法综述
[J].
A survey of advanced PID parameters turning methods
[J].
基于BP-PID的选择性激光烧结温度控制系统设计
[J].
Design of temperature control system based on BP-PID for selective laser sintering
[J].DOI:10.3969/j.issn.1001-3881.2021.24.019
基于STM32小型四轴飞行器PID参数整定
[J].
PID parameter tuning based on STM32 small quadcopter
[J].
基于模糊神经网络PID控制的花茶烘焙温控系统设计
[J].
Design of tea baking temperature control system based on fuzzy neural network PID control
[J].
基于自适应神经网络模糊PID的磨煤机控制研究
[J].
Research on coal mill control based on adaptive neural network fuzzy PID
[J].
Chaotic self-tuning PID controller based on fuzzy wavelet neural network model
[J].
Online tuning of PID controller using a multilayer fuzzy neural network design for quadcopter attitude tracking control
[J].
基于S函数的BP神经网络PID控制器及Simulink仿真
[J].
Simulink simulation of BP neural network PID controller based on S-function
[J].DOI:10.3969/j.issn.1674-6236.2014.04.009 [本文引用: 1]
基于S函数的RBF神经网络PID控制器Simulink仿真
[J].
Simulink simulation of RBF network PID controlle based on S-function
[J].DOI:10.3969/j.issn.1672-9994.2008.01.007
Design of conventional and neural network based controllers for a single-shaft gas turbine
[J].