机床热误差占机床误差的70%以上,而电主轴是热误差的主要误差源之一。由于自身结构特点,电主轴内部温度场分布复杂,且结构的热不对称比较剧烈,会对转轴的形变产生较大影响,从而严重影响机床的加工精度。
为了有效降低电主轴发热对数控机床的影响,各国科研人员开展了大量研究。Grama等[1]提出了一种冷却器触发模型,该模型在稳定电机和轴承温度方面具有一定的优势。Xiang等[2]、Yan等[3]和Zhang等[4]通过分析电主轴的热特性,分别提出了不同的电主轴热误差预测模型,有效提高了热误差计算精度。Zhang等[5]、He等[6]和Lei等[7]对电主轴水冷系统的冷却效果和温度分布进行了仿真分析,为冷却水流量的计算提供了理论依据。Tang等[8]和Xia等[9]为改善电主轴水冷通道的冷却效果,设计了不同的冷却结构,并通过有限元仿真验证了冷却效果。Li等[10]采用实验设计法对电主轴冷却流道的尺寸进行了优化。Ma等[11]和Meng等[12]建立了电主轴有限元分析模型,通过仿真模拟了其温度场和形变场。Brecher等[13]针对电主轴设计了一个在线热模拟模型,并对其进行了参数化和验证。Li等[14]设计了一种基于环形热虹吸管的磨削电主轴冷却结构,使得电主轴的最高温度约降低了28%。Shi等[15]采用流体体积法结合Lee相变模型的方法,研究了转速、加热功率对电主轴热变形的影响。Liu等[16]、Zhang等[17]和Liu等[18]分别对电主轴热行为与热误差之间的关系进行了定性分析,并提出了一些热误差补偿方法。Li等[19]建立了冷却剂泵驱动频率与电主轴转速和冷却剂温差的回归模型,并利用实验对回归模型进行了验证。Chien等[20]利用数值和实验相结合的方法,分析了内置高速电主轴螺旋水冷流道内的三维流体运动和温度分布情况。
综上所述,对于电主轴的发热问题,仍有2个技术难点未得到妥善解决:第一,冷却效果差,即未根据电主轴内部温度场的分布差异进行差异化冷却;第二,缺乏主动热误差控制平台,即未搭建相关热控制平台来对电主轴温度进行主动控制。为了实现对电主轴热源的主动控制与精确冷却,笔者设计了一种用于电主轴冷却的水冷机系统,并提出了水冷机冷却方案,同时通过温度‒流速控制模型来实现电主轴温度的主动控制。最后通过流体冷却有限元仿真和冷却实验来验证水冷机系统的有效性。
1 电主轴水冷机系统设计
1.1 电主轴热特性分析
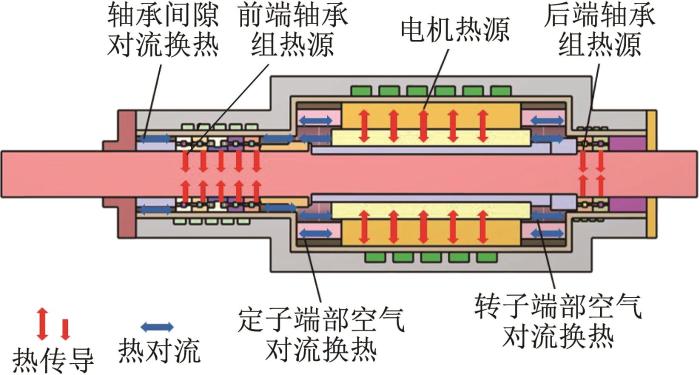
电主轴的主要结构如图1所示。在电主轴运行过程中,各零部件的运动状态不同,其发热情况也不同。其中,电主轴电机和前后端轴承组的发热损耗较大。电机发热损耗主要包含3个部分,分别为机械损耗、电损耗和磁损耗。轴承摩擦发热过程比较复杂,在一般工况条件下,主要考虑轴承内部滚动体、保持架与内外圈之间的摩擦发热。
图1
图2所示为电主轴的热量分布和传递情况。通过分析可知,电主轴温度场分布不均匀及热应力分布不对称的原因主要有以下3点:第一,不同零部件的结构形状和材料性能不同,造成电主轴内部不同热源的产热机理不同,从而导致产热量存在差异;第二,内部热源位置不同造成不同热源的热传递过程不同;第三,结构和材料的差异造成不同零部件受热不均匀。
图2
图2
电主轴热量分布与传递示意
Fig.2
Schematic diagram of heat distribution and transfer of motorized spindle
1.2 电主轴冷却方案设计
图3
图4
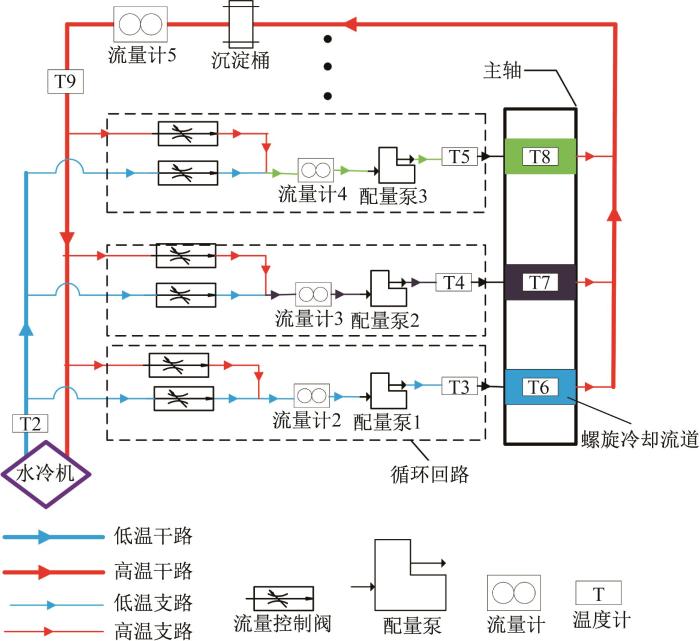
综上,水冷机系统的主要技术特点如下:1)设计多回路供液装置,布置水冷机供水管路,在较短时间内实现冷却水的变温变速,缩短热反应时间;2)建立温度‒流速控制模型,实现不同冷却流道制冷参数的优化。
1.3 电主轴冷却流道设计
图5
表1 电主轴冷却流道的几何尺寸 (mm)
Table 1
| 几何尺寸 | 前端流道 | 中部流道 | 后端流道 |
|---|---|---|---|
| 截面尺寸(L×H) | 12×6 | 20×10 | 6×3 |
| 长度S | 1 522 | 3 129 | 1 124 |
2 电主轴温度‒控制模型
2.1 电主轴发热量与载荷计算
本文以数格AMS-120型高速电主轴为研究对象,其主要技术参数如表2所示。
表2 AMS-120型高速电主轴主要技术参数
Table 2
| 技术参数 | 数值 |
|---|---|
| 额定功率/kW | 7.5 |
| 额定电压/V | 380 |
| 额定电流/A | 17 |
| 额定频率/Hz | 545 |
| 最高扭矩/Nm | 4.4 |
| 最高转速/(r/min) | 16 000 |
1)电机发热量。电机理论发热量包括机械损耗、电损耗和磁损耗,根据公式计算电机实际发热量
2)轴承组发热量。轴承发热是由动摩擦引起的,根据公式计算轴承实际发热量
2.2 电主轴传热计算
有学者研究了电主轴电机温度与冷却水流速之间的关系,并提出了温度‒流速数学模型[24]。但根据对电主轴温升实验结果的分析,该模型存在2个不足:第一,分析对象少,只考虑了电主轴电机部分的热量,未考虑前后端轴承组的热量;第二,计算误差大,未考虑转子端面和轴承间隙处对流换热所造成的热量损失。
为了降低计算误差,应考虑主要热源对流换热所造成的热量损失。故本文在计算电主轴的发热量时,在上述温度‒流速数学模型中引入对流热量损失项。则电主轴的实际发热量为:
式中:
电主轴电机的热量损失主要来自转子对流换热。将转子等效为均匀圆柱体,则电机的实际发热量
其中:
式中:Pz为电机的理论发热量,W;Piz为转子的对流热量损失,W;
基于上述电主轴的技术参数,可得电机转子端部的对流换热系数hz:
其中:
式中:
电机转子端部的对流换热面积Azx为:
式中:
将轴承的内、外圈和滚动体视为均匀发热体,其实际发热量Qa为:
其中:
式中:Pa为轴承的理论发热量,W;Pia为轴承的对流热量损失,W;
前、后端轴承组的对流换热系数
其中:
式中:u为轴承内部空气的平均流速,m/s;
轴承的对流换热面积
式中:
2.3 电主轴温度‒流速控制模型建立
根据上述分析结果,可以推导出电主轴电机和轴承的温度‒流速控制方程,表示为:
式中:
3 电主轴流‒热耦合仿真
3.1 有限元仿真模型构建
利用ANSYS SpaceClaim软件构建电主轴三维模型,并按仿真要求对模型进行简化,主要包括电主轴的各类孔结构、内部拉刀机构和各类圆弧角的简化。
将电主轴三维模型导入ANSYS Fluent软件,使用Fluent Mesh对模型进行网格划分,并对划分的网格进行节点控制和质量控制。
表3 电主轴仿真模型材料参数
Table 3
| 零件与冷却介质 | 材料 | 密度/ (kg/m3) | 导热率/ [W/(m·K)] | 比热容/ [J/(kg·K)] |
|---|---|---|---|---|
| 转轴 | 45号钢 | 7.85 | 60.5 | 434 |
| 轴承 | GCr15 | 7.83 | 30 | 670 |
| 定子 | 铜 | 8.93 | 401 | 390 |
| 转子 | 铜 | 8.93 | 401 | 390 |
| 冷却介质 | 水 | 1 | 0.599 | 4 184 |
表4 电主轴内部换热系数
Table 4
| 位置 | 对流换热系数/[W/(m2·K)] |
|---|---|
| 前端流道 | 1 463.65~1 765.87 |
| 中部流道 | 2 257.39~2 628.49 |
| 后端流道 | 1 067.35~1 325.41 |
| 转轴端部 | 8 |
3.2 仿真监测对象确定
对电主轴进行仿真分析时,主要监测3个参数的变化:热源温度、转轴形变量和关键部位温度。监测电主轴关键部位温度主要是为了避免因温度过低而出现冷凝现象。
在仿真过程中,在电主轴内部设置多个温度监测点,如图6所示。
图6
图6
电主轴温度监测点分布
Fig.6
Distribution of temperature monitoring points of motorized spindle
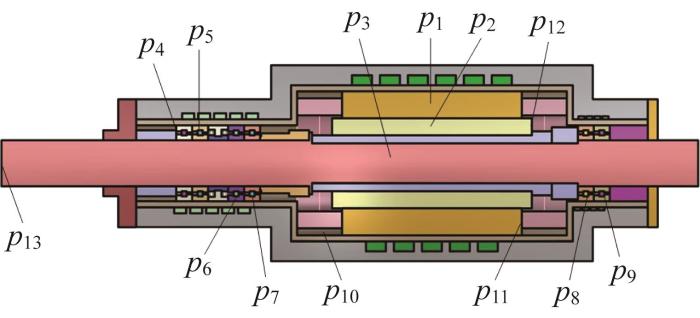
图6中的温度监测点主要分为以下2类:
1)关键结构监测点:p1为定子中心温度监测点;p2为转子中心温度监测点;p3为转轴中心温度监测点;p4、p5、p6、p7为前端轴承组滚动体边缘温度监测点;p8、p9为后端轴承组滚动体边缘温度监测点。
2)关键部位监测点:p10为机壳内腔表面温度监测点;p11为定子端部温度监测点;p12为转子端部温度监测点;p13为转轴端部温度监测点。
3.3 仿真结果分析
利用Steady-State Thermal模块和Fluent模块对电主轴开展稳态热仿真和流固耦合仿真分析,共开展3组仿真实验(转轴转速均为8 000 r/min)。其中,第1组不通冷却水;第2组通入冷却水,前端流道冷却水温度为17 ℃,流速为2.6 m/s,中部流道冷却水温度为18 ℃,流速为2.4 m/s,后端流道冷却水温度为16 ℃,流速为3.4 m/s;第3组通入冷却水并优化制冷参数,前端流道冷却水温度为15 ℃,流速为2.6 m/s,中部流道冷却水温度为16 ℃,流速为2.4 m/s,后端流道冷却水温度为14 ℃,流速为3.4 m/s。对比冷却前后电主轴温度场和形变场的变化以及冷却后电主轴主要结构的温度场变化。
3.3.1 电主轴整体温度与形变分析
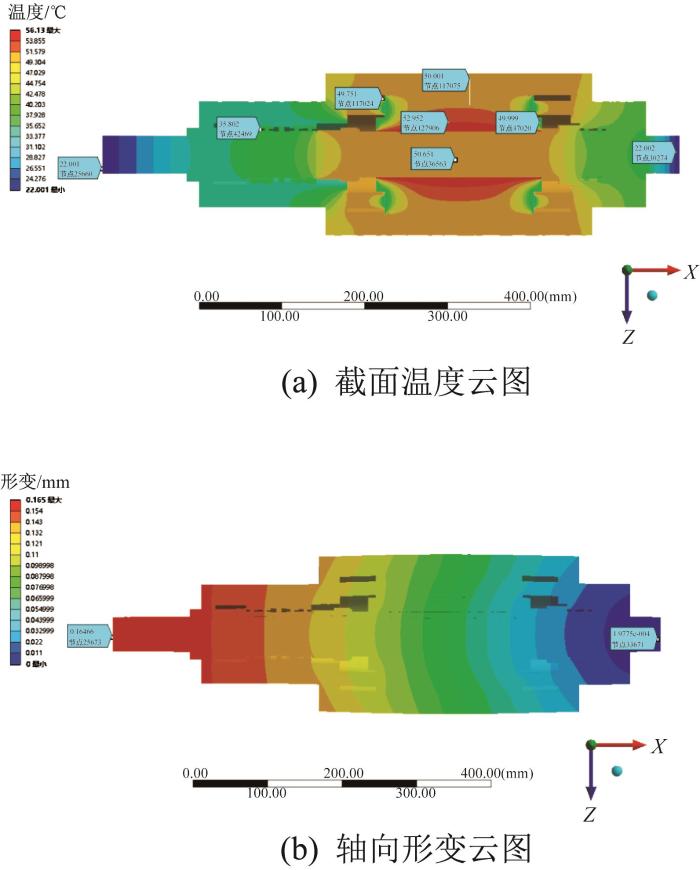
开展第1组仿真分析,得到冷却前电主轴的温度云图和形变云图,如图7所示。由图可知,冷却前电主轴定子的最高温度为56.00 ℃,前端轴承组的最高温度为38.95 ℃,后端轴承组的最高温度为38.50 ℃;最大形变量为0.165 mm,最小轴向形变发生在电主轴后端。
图7
图7
冷却前电主轴的温度云图和形变云图
Fig.7
Temperature and deformation nephogram of motorized spindle before cooling
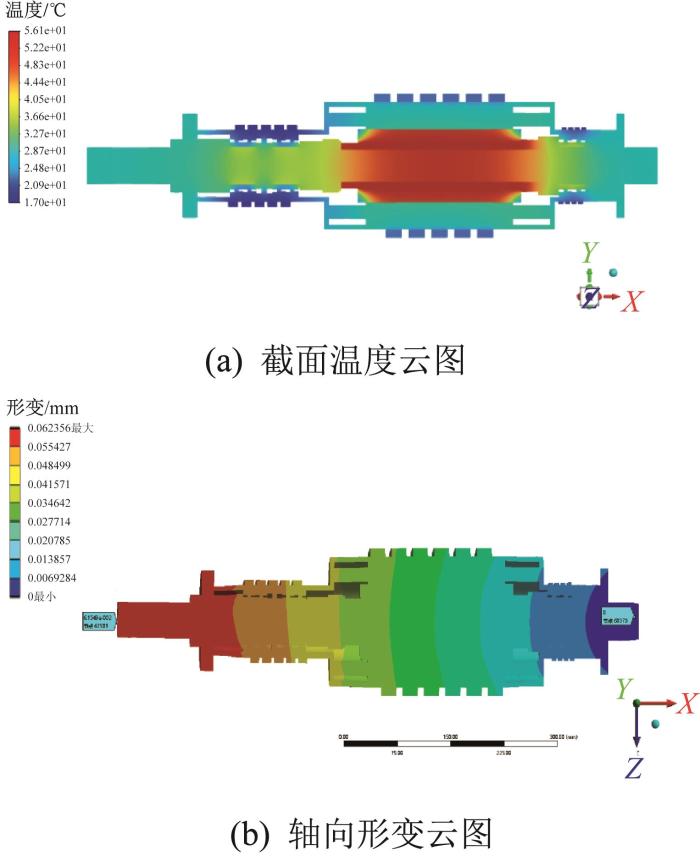
开展第2组仿真分析,得到冷却后电主轴的温度云图和形变云图,如图8所示。由图可知,冷却后电主轴定子的最高温度为28.34 ℃,前端轴承组的最高温度为24.90 ℃,后端轴承组的最高温度为24.23 ℃;最大形变量为0.062 mm,最小轴向形变发生在电主轴后端。
图8
图8
冷却后电主轴的温度云图和形变云图(制冷参数优化前)
Fig.8
Temperature and deformation nephogram of motorized spindle after cooling (before optimization of refrigeration parameters)
图9
图9
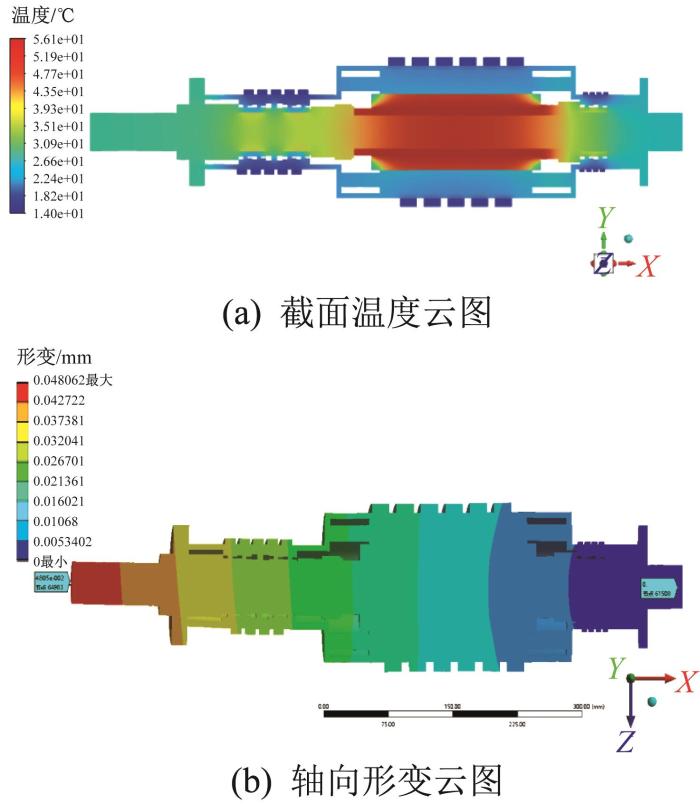
冷却后电主轴的温度云图和形变云图(制冷参数优化后)
Fig. 9
Temperature and deformation nephogram of motorized spindle after cooling (after optimization of refrigeration parameters)
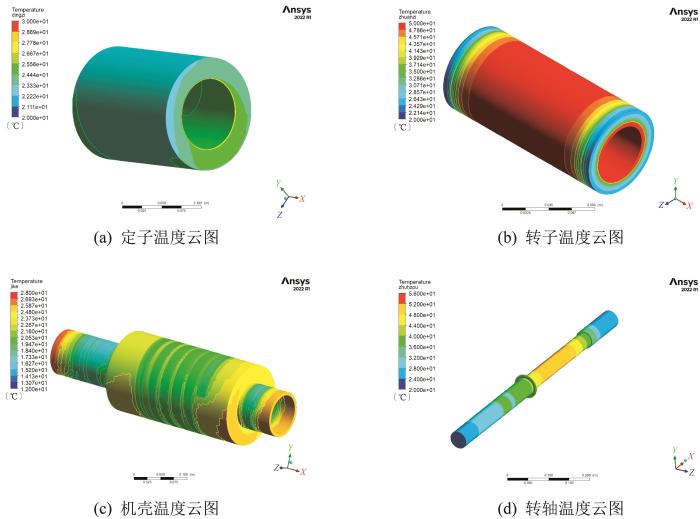
提取第3组仿真实验中电主轴主要结构的温度进行分析,结果如图10所示。由图可知,冷却后电主轴定子外表面的温度为22.00 ℃,内表面温度为45.00 ℃;转子外表面温度为45.00 ℃,内表面温度为50.00 ℃,端面温度为28.00 ℃;机壳的最高温度为28.00 ℃,最低温度为14.00 ℃;转轴最高温度为50.00 ℃,最低温度为26.00 ℃,最高温度出现在转轴前端。
图10
图10
冷却后电主轴主要结构的温度云图
Fig.10
Temperature nephogram of main structure of motorized spindle after cooling
3.3.2 电主轴监测点温度分析
1)关键结构监测点。
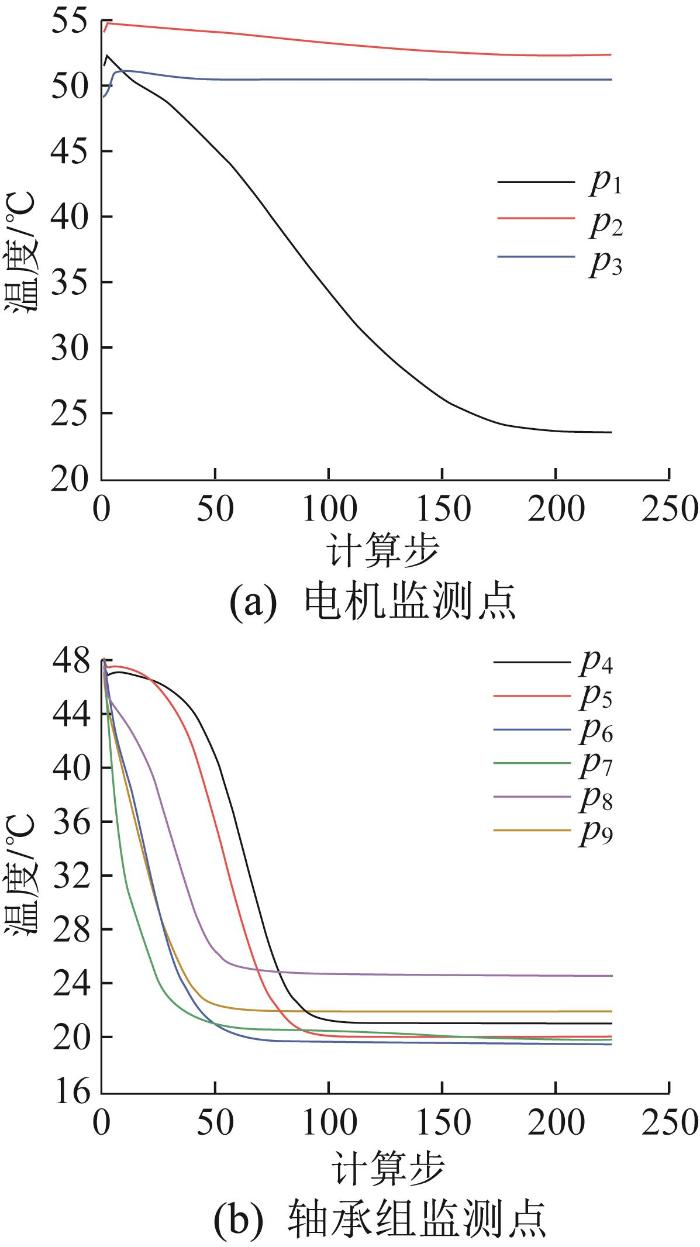
通过仿真可得,电主轴各关键结构监测点的温度变化如图11所示。由监测点p1至p3处的温度变化数据可知,冷却后电机温度变化如下:定子温度由51.56 ℃降低至23.52 ℃,降温幅度为54.83%;转子温度由56.00 ℃降低至52.43 ℃;转轴的稳定温度为50.48 ℃。根据监测点p4至p9处的温度变化数据,冷却后前后轴承组各测点的温度为20~25 ℃。
图11
图11
电主轴关键结构监测点温度变化
Fig.11
Temperature change of key structure monitoring points of motorized spindle
2)关键部位监测点。
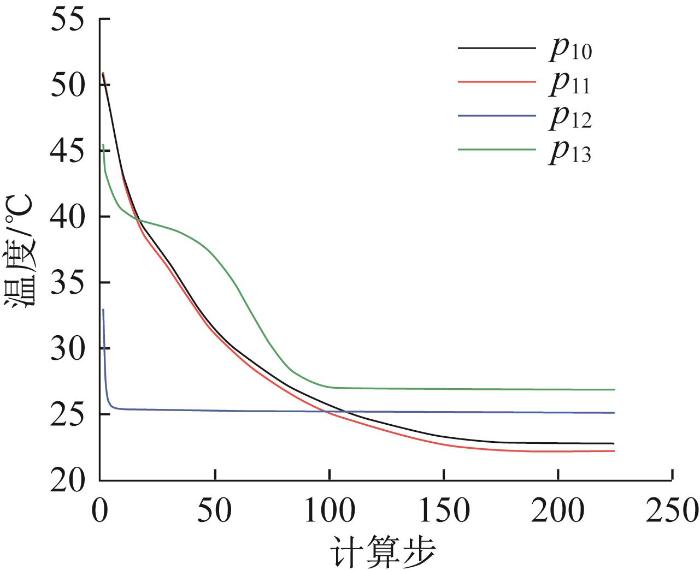
通过仿真可得,电主轴各关键部位监测点的温度变化如图12所示。由监测点p10至p13处的温度变化数据可知,电主轴最高温度出现在转轴端部处,为26.80 ℃;最低温度出现在定子端部处,为22.10 ℃。电主轴的温度均大于20 ℃的环境温度,可有效避免冷凝现象。
图12
图12
电主轴关键部位监测点温度变化
Fig.12
Temperature change of key part monitoring points motorized spindle
4 实验验证
为进一步验证所设计水冷机系统的冷却效果,开展了3组电主轴冷却实验,各组参数设置与仿真实验一致。对比冷却前后电主轴进入热平衡状态的时间和转轴伸长量的变化情况。
实验设备为XHK-715数控加工中心、温度传感器和主轴分析仪等。实验步骤与仿真分析时保持一致,并对比仿真结果和实验结果。
电主轴冷却实验现场如图12所示,采集上述3组实验中电主轴的温度变化数据以及转轴形变数据。
图13
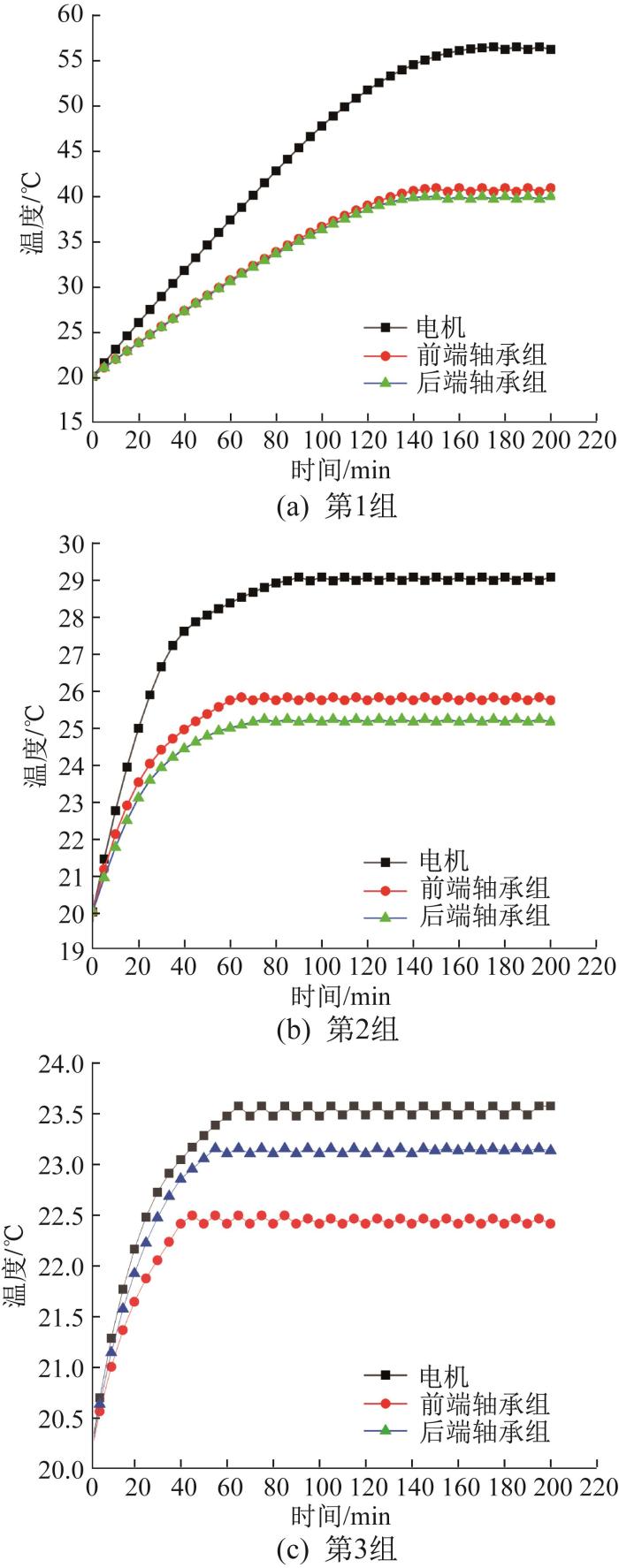
3组冷却实验中电主轴的温度变化如图14所示。通过分析可知,在不通冷却水的情况下,电主轴电机的热平衡温度为56.60 ℃,热平衡时间为160 min;前端轴承组的热平衡温度为40.80 ℃,热平衡时间为143 min;后端轴承组的热平衡温度为39.90 ℃,热平衡时间为140 min。通入冷却水后,电主轴电机的热平衡温度为29.05 ℃,热平衡时间为90 min,前端轴承组的热平衡温度为25.73 ℃,热平衡时间为60 min,后端轴承组的热平衡温度为24.98 ℃,热平衡时间为70 min。通入冷却水并优化制冷参数后,电主轴电机的热平衡温度为23.50 ℃,热平衡时间为75 min,前端轴承组的热平衡温度为22.40 ℃,热平衡时间为45 min,后端轴承组的热平衡温度为23.10 ℃,热平衡时间为60 min。
图14
图14
电主轴温度变化实验结果
Fig.14
Experimental results of temperature change of motorized spindle
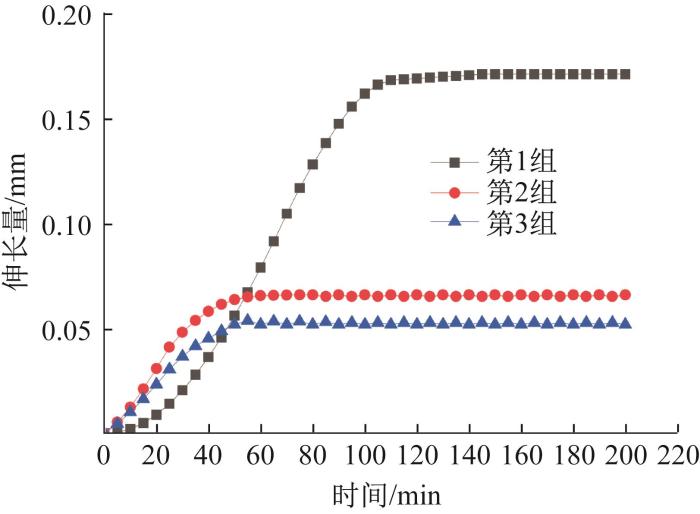
3组冷却实验中电主轴转轴的伸长量如图15所示。通过分析可知,在不通冷却水的情况下,转轴达到热平衡状态时的伸长量为0.165 mm,热平衡时间为160 min。通入冷却水后,转轴达到热平衡状态时的伸长量为0.065 mm,热平衡时间为80 min。通入冷却水并优化制冷参数后,转轴达到热平衡状态时的伸长量为0.051 mm,热平衡时间为60 min。
图15
图15
电主轴转轴伸长量实验结果
Fig.15
Experimental results of rotating shaft elongation of motorized spindle
表5 电主轴温度仿真结果与实验结果对比 (℃)
Table 5
| 组别 | 对比项 | 前端轴承组 | 电机 | 后端轴承组 |
|---|---|---|---|---|
| 第1组 | 仿真值 | 38.95 | 56.00 | 38.50 |
| 实验值 | 40.80 | 56.60 | 39.90 | |
| 相对误差/% | 4.75 | 1.07 | 3.64 | |
| 第2组 | 仿真值 | 24.90 | 28.34 | 24.23 |
| 实验值 | 25.73 | 29.05 | 24.98 | |
| 相对误差/% | 3.33 | 2.50 | 3.09 | |
| 第3组 | 仿真值 | 21.10 | 22.00 | 21.90 |
| 实验值 | 22.40 | 23.50 | 23.10 | |
| 相对误差/% | 6.16 | 6.82 | 5.48 |
表6 电主轴转轴伸长量仿真结果与实验结果对比 (mm)
Table 6
| 对比项 | 第1组 | 第2组 | 第3组 |
|---|---|---|---|
| 相对误差/% | 3.64 | 4.83 | 6.25 |
| 仿真值 | 0.165 | 0.062 | 0.048 |
| 实验值 | 0.171 | 0.065 | 0.051 |
5 结 论
1)电主轴温度场分布仿真结果表明,采用多流道异温差速的冷却方法对电主轴进行冷却,具有良好的冷却效果。
2)通过仿真得到的电主轴各监测点的温度变化情况表明,利用水冷机系统对电主轴进行冷却,很好地避免了其内部的冷凝问题。
3)利用仿真和实验得到的电主轴热平衡温度和热平衡时间表明,通过温度‒流速控制模型计算制冷参数可达到优化冷却效果的目的。
参考文献
A model-based cooling strategy for motorized spindle to reduce thermal errors
[J].
Dynamic linearization modeling approach for spindle thermal errors of machine tools
[J].
A new modeling method for thermal errors of motorized spindle based on the variation characteristics of spindle temperature field
[J].
Thermal deformation prediction of high-speed motorized spindle based on biogeography optimization algorithm
[J].
Design and thermal characteristic analysis of motorized spindle cooling system
[J].
Thermal characteristics of high speed motorized spindle with helical water cooling channel
[J].
Simulation and analysis for cooling system of high-speed motorized spindle
[J].
Analysis of influence of different convex structures on cooling effect of rectangular water channel of motorized spindle
[J].
Conjugate heat transfer in fractal tree-like channels network heat sink for high-speed motorized spindle cooling
[J].
Machining accuracy enhancement of a machine tool by a cooling channel design for a built-in spindle
[J].
Simulation and experimental study on the thermally induced deformations of high-speed spindle system
[J].
Simulation and analysis on temperature field of bearingless high speed motorized spindle
[J].
Thermal condition monitoring of a motorized milling spindle
[J].
Experimental investigation of single loop thermosyphons utilized in motorized spindle shaft cooling
[J].
Numerical study on two-phase flow and heat transfer characteristics of loop rotating heat pipe for cooling motorized spindle
[J].
Thermo-mechanical behavior analysis of motorized spindle based on a coupled model
[J].
Active and intelligent control onto thermal behaviors of a motorized spindle unit
[J].
Temperature detection based transient load/boundary condition calculations for spindle thermal simulation
[J].
Increase in accuracy of a built-in spindle by adaptive cooling control with varied coolant volume and temperature
[J].
3-D numerical and experimental analysis of a built-in motorized high-speed spindle with helical water cooling channel
[J].
基于热载荷优化修正的电主轴热特性分析方法
[J].
Thermal characteristic analysis method of motorized spindle based on thermal load optimization correction
[J].
基于CFX的高速电主轴水冷系统的仿真分析
[J].
Simulation analysis for water cooling system of high-speed motorized spindle based on CFX
[J].DOI:10.3969/j.issn.1001-3881.2014.07.007
高速电主轴新型层板冷却水套的热特性研究
[D].
Study on thermal characteristics of new laminated cooling water jacket for high-speed motorized spindle
[D].
Analysis on the effects of cooling water velocity on temperature rise of motorized spindle
[J].
A thermal model for high speed motorized spindles
[J].