陶瓷、硬质合金和光学玻璃等硬脆材料具有优异的机械、物理和化学性能，是特殊环境下内圆柱表面零部件的理想材料^[1]。近年来，具有内圆柱表面的机械精密部件，例如陶瓷轴承的内圈、汽车发动机的喷油嘴和小型玻璃透镜的套筒模具等，在航空航天、生物制造、医疗器械和微电子制造等诸多领域中得到了广泛应用^[2-4]。目前，内圆磨削是机械零部件内表面精密加工的主要方法。但在硬脆材料加工过程中，存在刀具磨损严重、切削力大、加工效率低及高精度内表面获取难等问题，不利于硬脆材料的推广使用^[5-7]。因此，硬脆材料内表面的高效加工方法成为研究热点。

旋转超声内圆磨削是一种具有高精度、高表面质量、高效率和低成本等优点的特种加工方法，能够有效地加工硬脆材料^[8-9]。相比于传统磨削，旋转超声内圆磨削在加工过程中施加了超声振动，主要有将超声振动作用于工件或砂轮两种方式^[10]。超声振动加工装备不仅对零部件的几何尺寸精度和形位精度有要求，还对系统的谐振特性提出了较高的要求。为此，面向新复合工艺的应用，正确建立超声谐振系统的理论分析模型，对提高超声谐振系统的工作性能和推广旋转超声内圆磨削工艺具有重要意义。

在旋转超声内圆磨削加工系统的制备过程中，设计纵向谐振系统的关键环节是正确设计磨削主轴中的砂轮变幅器。付俊帆等^[11]、周瑞峰等^[12]将多种材料的阶梯环盘负载（平行砂轮）与变幅杆组合成纵弯谐振变幅器，并提出了一种基于Mindlin中厚板理论的变幅器设计方法，为纵弯谐振砂轮变幅器的研制提供了一种有效的设计方法。牛金荣等^[13]基于Mindlin理论建立了杯形砂轮变幅器的理论模型,研制了以杯形砂轮为加工工具的超声辅助磨削主轴附件式工具系统，为主轴附件式超声磨削装置的设计提供了理论参考。赵波等^[14]采用分段近似趋近法建立了砂轮变幅器的动力学模型，得到了各段直径、长度对整个砂轮变幅器放大系数的影响，并进行了ANSYS有限元优化和动力学特性测试，实现了对非谐振大工具头变幅杆的设计。

当砂轮的厚径比大于0.3时，其适用于加工纵向谐振砂轮变幅器。吕明等^[15]将齿轮简化为短粗圆柱体，利用非谐振设计方法建立了齿轮纵向谐振系统，另外还推导了圆锥形、悬链线形和指数形复合纵向谐振变幅器的频率方程，为超声珩齿变幅器的设计提供了理论基础。顾荣华等^[16]基于变幅杆设计理论设计了一种圆锥过渡型阶梯变幅杆，并分析了变幅杆的面积比、端口直径和圆锥过渡长度对其共振频率、放大系数及最大响应应力的影响，为纵向振动变幅器尺寸的优化设计提供了技术参考。

然而，上述文献所研究的砂轮变幅器的理论分析模型仅针对某一种特定形状的砂轮变幅器。为提高砂轮变幅器理论分析模型的通用性，笔者拟针对旋转超声内圆磨削工艺，以非谐振设计方法为基础，建立圆锥过渡阶梯形、圆锥圆柱形和阶梯形砂轮变幅器的统一理论分析模型并推导频率方程，并设计了3种纵向谐振砂轮变幅器。经有限元仿真分析后，对变幅杆进行连接法兰设计，并加工圆锥过渡阶梯形变幅杆。最后，加工制作纵向谐振砂轮变幅器，并通过阻抗特性分析试验、超声谐振试验和振动位移测量试验来验证理论分析模型的正确性，旨在为旋转超声内圆磨削砂轮变幅器的设计提供一种方法。

旋转超声内圆磨削加工是一种将普通内圆磨削与超声加工技术相结合的特种加工方法，可使内圆磨削砂轮在以大于20 kHz频率纵向谐振的同时进行旋转运动，利用超声振动和砂轮磨削的复合作用形成加工表面，实现工件表面材料的去除，从而获得优异的加工表面质量^[17-18]。

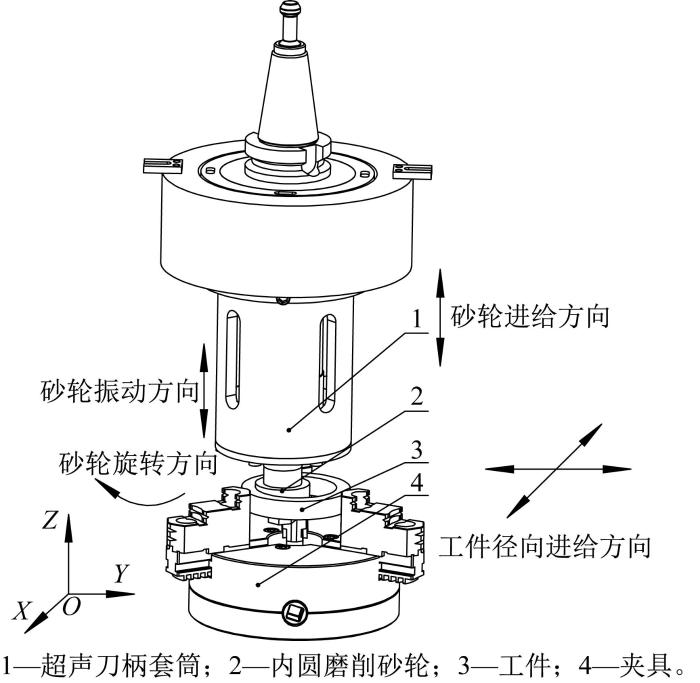
图1所示为旋转超声内圆磨削加工的示意图。超声刀柄套筒连接在机床主轴上，机床主轴工作时带动超声刀柄套筒旋转，超声刀柄套筒通过变幅杆上的法兰将扭矩传递给变幅杆，进而带动内圆磨削砂轮作回转运动，以完成工件内表面的磨削加工。同时，换能器将电信号转化为高频振动并传递至变幅杆，使得砂轮在作回转运动的同时产生沿纵向的超声振动，从而实现对工件的超声精密磨削加工^[19]。

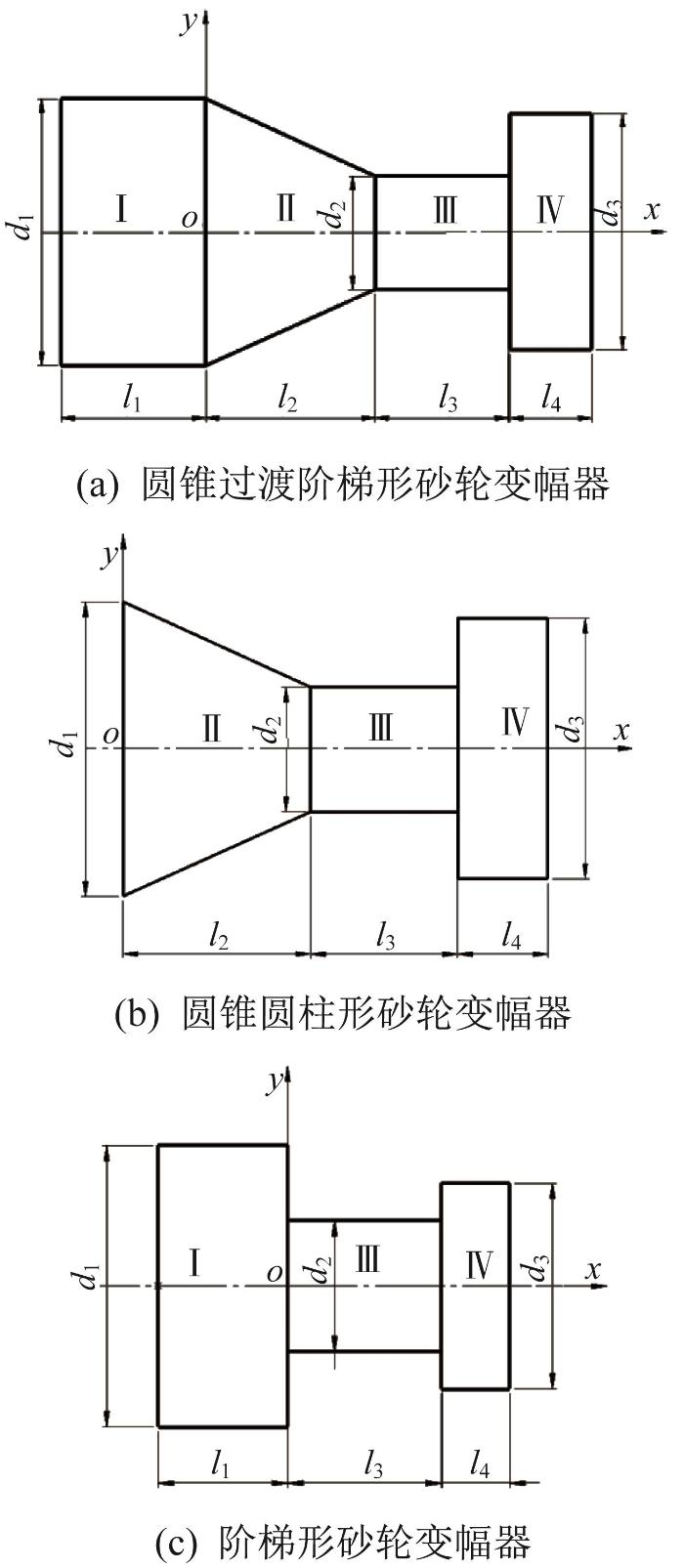
纵向谐振砂轮变幅器由变幅杆和内圆磨削砂轮组成，砂轮通过螺母与变幅杆小端刚性连接。为了满足工程应用需求，变幅杆有圆锥过渡阶梯形变幅杆、圆锥圆柱形变幅杆和阶梯形变幅杆。分别建立由3种变幅杆与砂轮组成的纵向谐振砂轮变幅器的理论分析模型，如图2所示，并以图2(a)所示模型作为该类砂轮变幅器统一的理论分析模型。其中，砂轮采用电镀金刚石砂轮。由于电镀磨料层厚度远小于砂轮径向尺寸，理论分析建模时将电镀金刚石砂轮等效为单一材料均质圆柱，并忽略圆角、倒角等工艺结构，以及螺母对纵向谐振砂轮变幅器的影响。

图2(a)所示的圆锥过渡阶梯形砂轮变幅器理论分析模型可简化为圆柱杆Ⅰ、圆锥杆Ⅱ、圆柱杆Ⅲ和圆柱砂轮Ⅳ四部分的组合体。其中：圆柱杆Ⅰ、圆锥杆Ⅱ和圆柱杆Ⅲ共同组成变幅杆。在圆柱杆Ⅰ和圆锥杆Ⅱ的连接面中心处建立坐标系o-xy，d₁、d₂和d₃分别为圆柱杆Ⅰ、圆柱杆Ⅲ和圆柱砂轮Ⅳ的直径，l₁、l₂、l₃和l₄分别为圆柱杆Ⅰ、圆锥杆Ⅱ、圆柱杆Ⅲ的长度和圆柱砂轮Ⅳ的厚度。

当圆锥过渡阶梯形砂轮变幅器理论分析模型中圆柱杆Ⅰ长度l₁趋于0或无限小时，可简化为圆锥圆柱形砂轮变幅器；当理论分析模型中圆锥杆Ⅱ长度l₂趋于0或无限小时，可简化为阶梯形砂轮变幅器。

基于图2(a)所示的圆锥过渡阶梯形砂轮变幅器理论分析模型，对纵向谐振砂轮变幅器进行理论分析并求解。纵向谐振砂轮变幅器左端的变幅杆大端通过螺纹与换能器紧密连接，在接通电源工作时，变幅杆与砂轮在换能器的激励作用下纵向振动，则圆柱杆Ⅰ的纵向振动位移ξ₁和应变ε₁的解析表达式分别为：

式中：C₁₁、C₁₂为由边界条件和力、位移连续条件确定的待定常数，下文的C_ij （i=1, 2, 3, 4; j=1, 2）同；k₁为变幅杆的波数。

圆锥杆Ⅱ的纵向振动位移ξ₂和应变ε₂的解析表达式分别为：

其中：

式中：α、N分别为圆锥杆的锥度系数和面积系数。

圆柱杆Ⅲ的纵向振动位移ξ₃和应变ε₃的解析表达式分别为：

圆柱砂轮Ⅳ的纵向振动位移ξ₄和应变ε₄的解析表达式分别为：

式中：k₂为砂轮的波数。

变幅杆和砂轮的波数k₁、k₂的计算式为：

其中：

式中：ω为砂轮变幅器的圆频率；c₁、c₂分别为变幅杆和砂轮的纵波波速；E₁、ρ₁，E₂、ρ₂分别为变幅杆和砂轮的弹性模量、密度。

鉴于变幅杆在换能器的激励作用下纵向振动，其圆柱杆Ⅰ左侧端面满足受力为0，即：

式中：S₁为变幅杆大端圆柱的横截面积。

变幅杆圆柱杆Ⅰ右侧端面与圆锥杆Ⅱ左侧端面的连接区域满足力相等与纵向振动位移相等的连续条件，即：

变幅杆圆锥杆Ⅱ右侧端面与圆柱杆Ⅲ左侧端面连接区域满足力相等与纵向振动位移相等的连续条件，即：

式中：S₂为变幅杆小端圆柱的横截面积。

变幅杆圆柱杆Ⅲ右侧端面与圆柱砂轮Ⅳ左侧端面连接区域满足力相等与纵向振动位移相等的连续条件，即：

式中：S₃为砂轮的横截面积。

忽略砂轮变幅器最右端砂轮所受的磨削力，即砂轮处于自由振动状态，则圆柱砂轮Ⅳ右侧端面为自由振动端面，满足受力为0，即：

将式(1)至式(4)代入式(5)至式(9)，联立并整理可得以下八阶齐次方程组：

即：

式中：D_mn （m、n=1, 2, …, 8）为待定常数C_ij （i=1, 2, 3, 4; j=1, 2）前的系数，其值可由式(5)至式(9)解得。

当待定常数C_ij （i=1, 2, 3, 4; j=1, 2）不全为0时，八阶齐次方程组有解的充要条件为由D_mn 组成的行列式的值为0，即：

式(11)即为纵向谐振砂轮变幅器的频率方程。当纵向谐振砂轮变幅器的材料性能参数和结构尺寸参数已知时，由频率方程可求得其纵向谐振频率；当纵向谐振理论设计频率已知且只有一个未知尺寸参数时，由频率方程可求得该未知尺寸参数。

已知换能器纵向振动输出的最大振动位移为6 μm，假设纵向谐振砂轮变幅器左端的位移为ξ₀，则有边界条件ξ1=ξ0x=-l1，即：

联立式(11)与式(12)可求得待定常数C_ij （i=1, 2, 3, 4; j=1, 2）的一组特解。将这组特解分别代入纵向谐振砂轮变幅器不同区域的振动位移解析表达式，即可得到其沿x方向的振动位移曲线。

所设计的3种纵向谐振砂轮变幅器的尺寸参数如表1所示，其中l₃为待求值。

将表1中各纵向谐振砂轮变幅器的尺寸参数代入所编写的程序，并利用MATLAB软件进行求解，得到圆锥过渡阶梯形、圆锥圆柱形和阶梯形砂轮变幅器的未知尺寸l₃=19，34，39 mm。在确定了上述3种纵向谐振砂轮变幅器的基本尺寸参数后，利用SolidWorks软件分别建立其三维实体模型。

将纵向谐振砂轮变幅器的三维实体模型导入有限元分析软件ANSYS，并设置其材料性能参数，如表2所示。其中，变幅杆的材料选用45钢，砂轮的基体材料选用40Cr。通过模态分析得到3种砂轮变幅器纵向谐振的理论设计频率和有限元仿真频率以及两者的相对误差，结果如表3所示。

如表3所示，3种砂轮变幅器纵向谐振的理论设计频率与有限元仿真频率存在误差，主要原因包括以下2点。

1）在建立理论分析模型时，忽略了变幅杆两端芯轴以及螺母尺寸对砂轮变幅器整体纵向谐振频率的影响；

2）在求解理论分析模型时，根据声波在砂轮变幅器各区域之间的传递建立了力与位移的连续条件，但变幅杆最右端与砂轮左端接触区域存在截面变化，忽略了声波在截面变化处传播的影响。阶梯形砂轮变幅器存在2处截面变化，因此相较于其他2种砂轮变幅器的误差更大。

在设计纵向谐振砂轮变幅器的尺寸参数时，根据理论分析模型求解结果，在不改变其他尺寸的情况下，适当调整尺寸l₃的大小，以满足其谐振频率的要求。考虑到工艺与加工效果，为降低阶梯形砂轮变幅器在2个圆柱截面突变处的应力集中现象，在该砂轮变幅器截面突变处添加一段半径为15 mm的过渡圆弧。利用ANSYS软件对3种纵向谐振砂轮变幅器进行模态分析，其尺寸l₃的调整值以及仿真求解得到的谐振频率如表4所示。

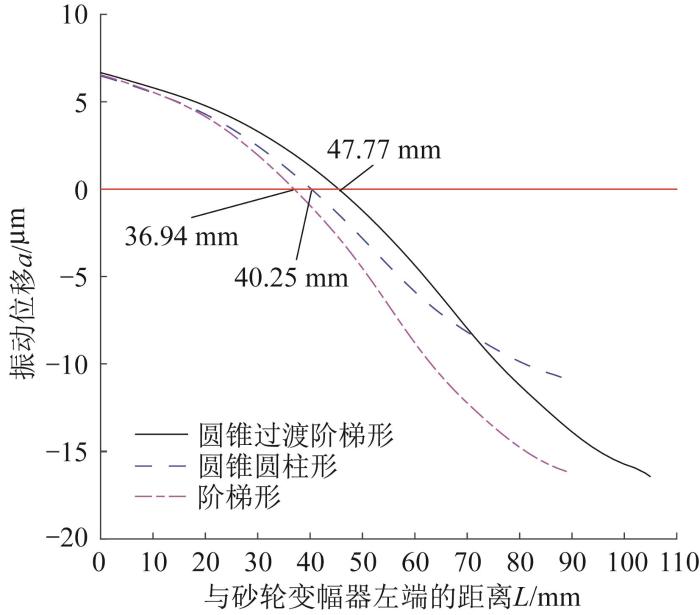
在调整并确定3种纵向谐振砂轮变幅器的尺寸参数后，利用ANSYS软件对其进行谐响应分析，设置其左端端面的最大输入位移为6 μm，求解得到3种砂轮变幅器的振动位移曲线，如图3所示。位移曲线与横坐标轴的交点为振动位移等于0 μm处，即变幅杆的节面位置。由图3可知，这3种砂轮变幅器的节面位置分别在距其左端端面的47.77，40.25，36.94 mm处；3种砂轮变幅器输出端的振动位移分别为17.38，10.77，16.16 μm，可满足旋转超声内圆磨削的要求。

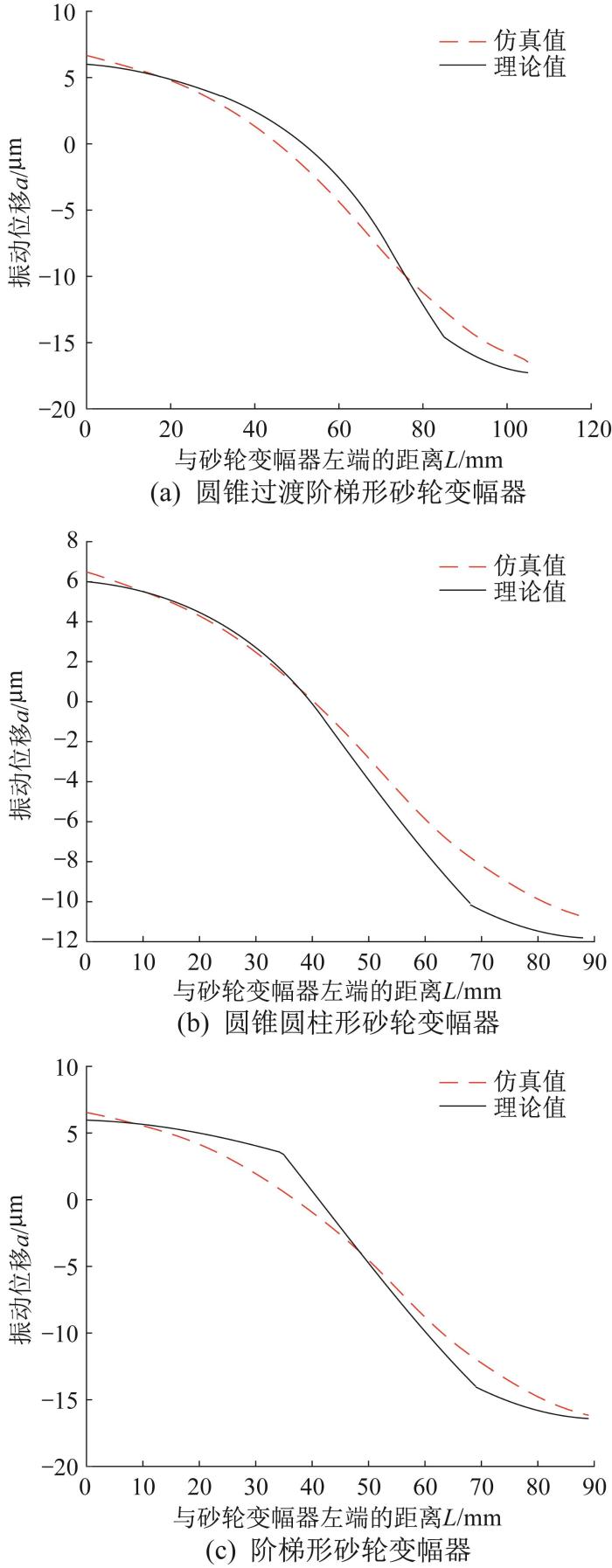
将上述3种纵向谐振砂轮变幅器的材料性能参数和尺寸参数代入式(11)和式(12)，通过MATLAB软件编写对应的求解程序，分别求解3种砂轮变幅器的理论振动位移曲线，并与有限元仿真分析曲线进行对比，结果如图4所示。

通过对比图4所示的振动位移曲线可知，3种砂轮变幅器振动位移的仿真分析曲线与理论求解曲线基本吻合。3种砂轮变幅器最右端振动位移的仿真值与理论值相对误差最大的为圆锥圆柱形砂轮变幅器，为1.03 μm。在阶梯形砂轮变幅器的振动位移曲线中，距其左端约35 mm处，仿真分析与理论求解的振动位移误差较大，可能是此处（截面突变）为避免应力集中现象而添加过渡圆弧所导致的。

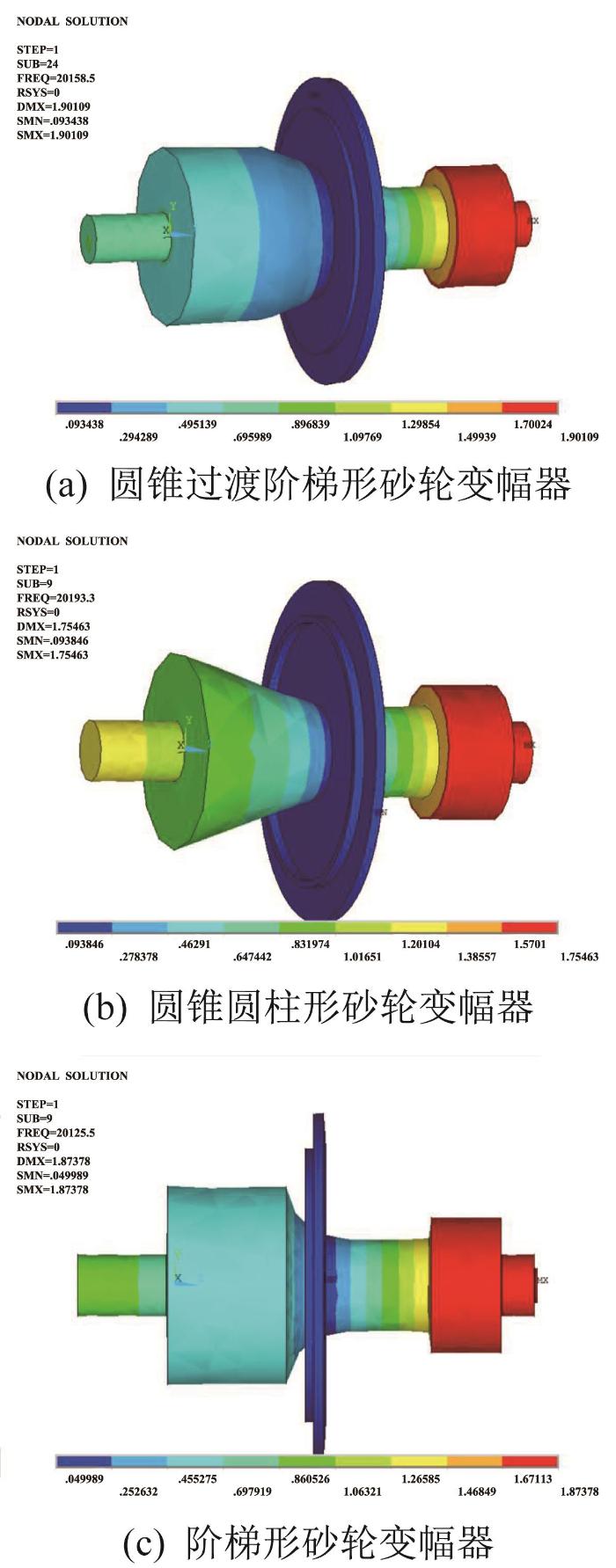
为实现纵向谐振砂轮变幅器与超声刀柄套筒的连接，分别在3种砂轮变幅器的节面位置处安装厚度为5 mm的法兰盘，因砂轮变幅器节面位置处的振动位移为0 μm，在此处安装法兰盘可最大限度地降低对系统振动效果的影响。安装法兰盘后，利用ANSYS软件对3种砂轮变幅器进行模态分析，其纵向谐振模态振型如图5所示，由此得到其谐振频率分别为20 158.3，20 193.3，20 125.5 Hz，满足设计要求。

为验证所设计的纵向谐振砂轮变幅器理论分析模型的正确性，依据表1和表4的尺寸参数加工圆锥过渡阶梯形变幅杆，如图6所示。购置基体材料为40Cr的电镀金刚石砂轮，与圆锥过渡阶梯形变幅杆组成纵向谐振砂轮变幅器，并加工超声刀柄套筒。所设计的纵向谐振砂轮变幅器的工作频率为20 000 Hz，选用由森瑞普电子有限公司生产的H100-185导电滑环，杭州成功超声设备有限公司生产的ZJS-2000超声波发生器和YP-5520-4BZ柱形换能器。将上述设备按要求装配，得到如图7所示的纵向谐振砂轮变幅器工具系统。

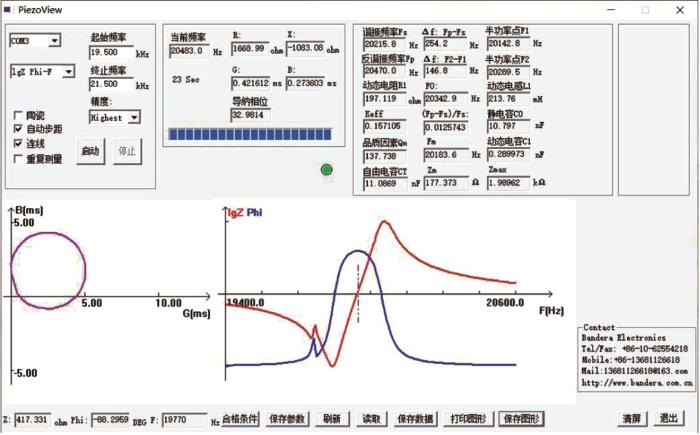
为分析纵向谐振砂轮变幅器的阻抗特性，使用 PV70A型阻抗分析仪对其进行阻抗特性分析试验，试验装置如图8所示，分析结果如图9所示。

阻抗特性分析测试结果表明，纵向谐振砂轮变幅器的导纳曲线呈较为完整的单圆，说明换能器与变幅杆的连接阻抗匹配较好；在幅相特性曲线中，阻抗特性曲线只有一对极小值和极大值，相位角曲线呈较为明显的“几”字形，说明该砂轮变幅器的内部结构合理，但谐振频率带宽稍窄，可能是因装配质量不佳而导致砂轮变幅器存在机械损耗。参数栏中显示所测砂轮变幅器的谐振频率f₁=20 215 Hz，与理论设计频率f_D=20 000 Hz相差215 Hz，试验相对误差δ₁=f_D-f₁/f_D=1.08%，误差较小，满足设计要求，说明砂轮变幅器处于一个较为理想的工作状态。

为得到上述砂轮变幅器的实际谐振频率，连接图7所示纵向谐振砂轮变幅器工具系统与超声波发生器的电源线，组成超声谐振试验装置，如图10所示。

启动超声波发生器的电源后观察到，整个纵向谐振砂轮变幅器工具系统的振动声音较小且无异响，并能持续振动较长时间，表明整个工具系统可稳定工作。记录超声波发生器显示屏上的谐振频率f₂=19 735 Hz，与理论设计频率f_D=20 000 Hz的相对误差δ₂=1.3%。

砂轮变幅器输出端的振动位移在旋转超声内圆磨削工具系统中是一个重要的性能指标，符合工艺要求的输出端振动位移对工件的加工具有至关重要的作用。为此，对图7所示纵向谐振砂轮变幅器工具系统的谐振频率和输出端的振动位移进行测量。采用挚感（苏州）光子科技有限公司生产的MV-H200的激光振动传感器，搭建如图11所示的振动位移测量试验装置，对上述砂轮变幅器砂轮末端的谐振频率和振动位移进行测量。

在砂轮末端端面上选取一条半径为18 mm的圆弧，该圆弧位于砂轮的电镀磨料层上，可最大程度地反映砂轮工作时端面的振动状态。在该圆弧上依次选取10个采样点进行振动位移测量。打开超声波发生器电源，当砂轮变幅器工具系统稳定振动时，在样点处利用激光振动传感器测量系统的谐振频率f₃和砂轮末端的振动位移a，具体结果如表5所示。

表5所示的振动位移测量结果表明：采样点处测得的谐振频率f₃=19 500~19 650 Hz，平均值为19 592 Hz；振动位移a=14.50~17.00 μm，平均值为16.02 μm。理论求解和仿真分析所得到的砂轮变幅器输出端各采样点的振动位移是相同的。但从振动位移测量结果可以看出，砂轮变幅器输出端各采样点处的振动位移并不完全一致，不过各采样点处振动位移的绝对值最大相差1.84 μm。砂轮变幅器输出端振动位移的变化可能受到以下因素的影响：1）变幅杆选用的45钢与砂轮基体选用的40Cr并非均质材料；2）砂轮的制造精度导致砂轮电镀磨料层端面并非绝对的平面。

本文基于非谐振设计理论提出了一种纵向谐振砂轮变幅器的设计方法。通过分析各振动单元之间的力、位移连续条件和边界条件建立了3种纵向谐振砂轮变幅器统一的理论分析模型并推导了频率方程，同时利用ANSYS软件进行了模态分析与谐响应分析，实现了对3种纵向谐振砂轮变幅器的设计。最后，加工制作了纵向谐振砂轮变幅器并进行了阻抗特性分析试验、超声谐振试验与振动位移测量试验，具体结论如下。

1）基于非谐振设计理论建立了3种纵向谐振砂轮变幅器的统一理论分析模型，提高了理论分析模型的通用性，减少了工程设计人员的理论计算量，可为旋转超声内圆磨削砂轮变幅器的设计提供理论技术参考。

2）对于所设计的3种纵向谐振砂轮变幅器，其纵向谐振的理论设计频率与仿真分析频率的相对误差最小为6.81%，最大为10.81%，满足工程应用的要求。圆锥过渡阶梯形砂轮变幅器输出端的振动位移最大，为17.38 μm，圆锥圆柱形砂轮变幅器输出端的振动位移最小，为10.77 μm，但均满足旋转超声内圆磨削的要求。对于阶梯形砂轮变幅器，其添加法兰后虽可满足谐振频率与振动位移放大的要求，但考虑到工艺加工效果，法兰处不宜加工。综合考虑，圆锥过渡阶梯形砂轮变幅器的整体效果最优。

3）加工制作了纵向谐振砂轮变幅器工具系统，通过阻抗特性分析试验、超声谐振试验与振动位移测量试验测得，其谐振频率分别为20 215，19 735，19 592 Hz，与理论设计频率f_D的相对误差分别为1.08%，1.33%和2.04%。砂轮变幅器输出端的实际测量振动位移与仿真分析振动位移的相对误差为7.83%。

4）阻抗特性分析试验、超声谐振试验与振动位移测量试验初步验证了所建立的统一理论分析模型的正确性以及所设计纵向谐振砂轮变幅器的可行性，为旋转超声内圆磨削砂轮变幅器的设计提供了理论技术参考。

下一步将进行陶瓷材料轴承内圈零件的旋转超声磨削加工实验，研究所设计砂轮变幅器的应用性能。