Al/CFRP混合薄壁结构耐撞性能可靠性优化设计

doi:10.3785/j.issn.1006-754X.2022.00.090

Al/CFRP混合薄壁结构耐撞性能可靠性优化设计

张正峰^,^,¹^,², 宋小雨³, 袁晓磊^,^,¹, 陈文娟², 张伟东⁴

1.长安大学汽车学院，陕西西安 710064

2.陕西汽车控股集团有限公司，陕西西安 710042

3.中铝材料应用研究院有限公司，北京 102209

4.上海捷能汽车技术有限公司，上海 201804

Reliability optimization design for crashworthiness of Al/CFRP hybrid thin-walled structure

ZHANG Zheng-feng^,^,¹^,², SONG Xiao-yu³, YUAN Xiao-lei^,^,¹, CHEN Wen-juan², ZHANG Wei-dong⁴

1.School of Automobile, Chang’an University, Xi’an 710064, China

2.Shaanxi Automobile Holding Group Co. , Ltd. , Xi’an 710042, China

3.Chinalco Material Application Research Institute Co. , Ltd. , Beijing 102209, China

4.Shanghai Jieneng Automobile Technology Co. , Ltd. , Shanghai 201804, China

通讯作者: 袁晓磊（1988—），男，陕西西安人，工程师，硕士，从事分布式驱动电动汽车控制系统开发研究，E-mail: yuanxiaolei@chd.edu.cn，https://orcid.org/0000-0002-7189-0245

收稿日期: 2022-05-17 修回日期: 2022-07-13

基金资助:

陕西省科技重大专项.  2020zdzx06-01-01
陕西省自然科学基金资助项目.  2020JQ-368
长安大学中央高校基础研究基金资助项目.  300102221201

Received: 2022-05-17 Revised: 2022-07-13

作者简介 About authors

张正峰（1979—），男，甘肃兰州人，高级工程师，硕士，从事汽车制造工艺设计与材料应用研究，E-mail:zhangzf1979@yeah.net，https://orcid.org/0000-0002-0991-4453 , E-mail：zhangzf1979@yeah.net

摘要

轻量化是实现汽车产业向安全、节能、环保发展的一个重要途径。Al/CFRP（carbon fiber reinforced plastic，碳纤维增强复合材料）混合材料能够在提升轻量化效果的同时兼顾材料成本和结构耐撞性能。为探索方形截面Al/CFRP混合薄壁结构的最佳组合方式，首先，制备了Al方管、CFRP方管和Al/CFRP混合方管，并开展准静态压溃实验。然后，建立能够精确模拟Al/CFRP混合方管压溃响应的有限元模型。最后，将试验设计方法、代理模型技术、多目标优化算法和蒙特卡罗模拟技术相结合，对Al/CFRP混合方管分别进行多目标确定性与可靠性优化设计，并对效果较好的可靠性优化解进行仿真验证。准静态压溃实验结果表明，Al/CFRP混合方管具有优异的耐撞性能；优化结果表明，可靠性优化解的约束可靠度相比于确定性优化解提高了10.96%，大大降低了失效概率，具有更强的实用性。研究结果有望对Al/CFRP混合薄壁吸能构件的优化设计提供参考。

关键词： Al/CFRP（碳纤维增强复合材料）混合材料 ; 有限元分析 ; 可靠性 ; 优化设计

Abstract

Lightweight is an important way to make automobile industry develop towards safety, energy conservation and environmental protection. The Al/CFRP (carbon fiber reinforced plastic) hybrid material can improve the lightweight effect while taking into account the material cost and structural crashworthiness. In order to explore the best combination mode of Al/CFRP hybrid thin-walled structure with square cross section, firstly, Al square tubes, CFRP square tubes and Al/CFRP hybrid square tubes were prepared, and quasi-static crushing experiments were carried out. Then, the finite element model that could accurately simulate the crushing response of Al/CFRP hybrid square tube was established. Finally, the multi-objective certainty and reliability optimization design for the Al/CFRP hybrid square tube was carried out by combining experimental design method, agent model technique, multi-objective optimization algorithm and Monte Carlo simulation technology, and the reliability optimization solution with good effect was verified by simulation. The quasi-static crushing experiment results showed that the Al/CFRP hybrid square tube had excellent crashworthiness; the optimization results showed that the constraint reliability of the reliability optimization solution was 10.96% higher than that of the certainty optimization solution, which greatly reduced the failure probability and had stronger practicability. The research results are expected to provide a reference for the optimal design of Al/CFRP hybrid thin-walled energy-absorbing components.

Keywords： Al/CFRP (carbon fiber reinforced plastic) hybrid material ; finite element analysis ; reliability ; optimization design

PDF (3798KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张正峰, 宋小雨, 袁晓磊, 陈文娟, 张伟东. Al/CFRP混合薄壁结构耐撞性能可靠性优化设计. 工程设计学报[J], 2022, 29(6): 720-730 doi:10.3785/j.issn.1006-754X.2022.00.090

ZHANG Zheng-feng, SONG Xiao-yu, YUAN Xiao-lei, CHEN Wen-juan, ZHANG Wei-dong. Reliability optimization design for crashworthiness of Al/CFRP hybrid thin-walled structure. Chinese Journal of Engineering Design[J], 2022, 29(6): 720-730 doi:10.3785/j.issn.1006-754X.2022.00.090

随着汽车保有量逐年增多，交通安全问题频发，能源短缺与环境污染问题也日益严峻。提高汽车安全性能、节约资源和减少污染已成为汽车行业的当务之急。为了实现上述目标，学者们致力于开发轻质高效的车身吸能构件来代替传统钢制构件，以提升汽车轻量化水平。CFRP（carbon fiber reinforced plastic，碳纤维增强复合材料）因具有优异的力学性能和显著的轻量化效果，被广泛应用于汽车薄壁结构的轻量化设计。尽管CFRP展现了优异的能量吸收效果，但高昂的材料成本制约了其在汽车行业中的大规模应用。因此，有学者提出可将CFRP与金属材料混合，制成金属/CFRP混合材料，替代传统钢材，以实现汽车轻量化^[1]。

为了实现CFRP在汽车车身上的合理应用，学者们针对金属/CFRP混合薄壁结构进行了大量研究。例如：Sun等^[2]采用试验方法对比了Al管、CFRP管和Al/CFRP混合管的变形失效形式和吸能效果，并采用数值研究方法进行了耐撞性能参数化分析和优化设计。Zhu等^[3]采用试验方法研究了具有2种不同Al、CFRP相对位置的Al/CFRP混合圆管在准静态轴向载荷作用下的耐撞性能，结果表明，通过将CFRP粘贴在Al管内部制成的混合圆管具有优异的能量吸收能力。Shi等^[4]采用试验与仿真相结合的方法，从耐撞性能与材料成本两个方面验证了Al/CFRP混合圆管具有优异的能量吸收能力。上述研究表明，Al/CFRP混合薄壁结构能够成为优异的汽车吸能构件。

鉴于金属部分尺寸、CFRP的铺层数和铺层角度等因素会对Al/CFRP混合薄壁结构的能量吸收能力有较大影响，一些学者采用有限元分析与优化设计相结合的方法对其进行耐撞性能优化设计。例如：孙光永等^[5]采用结合试验设计、响应面法和蒙特卡罗模拟技术的6σ优化方法对汽车薄壁构件进行了优化设计；Wang等^[6]采用多目标优化算法对Al/CFRP混合薄壁结构进行了优化设计，优化后薄壁结构的耐撞性能相较于初始方案有了很大程度的提升。上述研究表明，优化设计方法的应用能够提升薄壁结构的能量吸收能力；此外，与传统试验设计相比，优化设计方法也实现了薄壁结构设计效率的提升。

综上所述，Al/CFRP混合薄壁结构在汽车轻量化设计和耐撞性能的提升上有很大优势。因此，笔者制备了方形截面的Al管、CFRP管和Al/CFRP混合管，研究其在准静态轴向载荷下的承载能力。同时，采用多目标优化设计方法对Al/CFRP混合方管进行优化设计，旨在对汽车薄壁吸能构件的设计提供指导。

1 Al/CFRP混合方管耐撞性能实验研究

1.1　试样制备

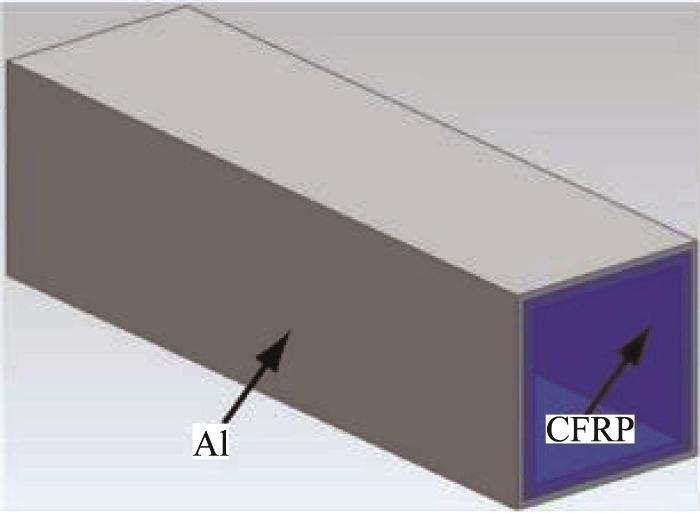
由文献[1]可知，CFRP粘接在Al管内部时，Al/CFRP混合管各部分的吸能效果较好。为了进一步研究Al/CFRP混合方管（CFRP粘接在方形截面Al管内部）的吸能特性，采用AA6061-O铝合金和T300机织平纹CFRP预浸料制备了Al/CFRP混合方管和相应尺寸的Al方管、CFRP方管，并开展准静态压溃实验。Al/CFRP混合方管和CFRP方管中CFRP部分的铺层角度均为0°。Al/CFRP混合方管的几何构型如图1所示。Al方管、CFRP方管和Al/CFRP混合方管试样的制备方案如表1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Al/CFRP混合方管几何构型示意

Fig.1 Schematic diagram of geometric configuration of Al/CFRP hybird square tube

表1 各试样制备方案

Table 1 Preparation scheme of each sample

试样	Al管厚度/mm	CFRP铺层数/层
Al方管	1	—
CFRP方管	—	8
Al/CFRP混合方管	1	8

新窗口打开| 下载CSV

采用吹气模压法制备Al/CFRP混合方管和CFRP方管。Al/CFRP混合方管的制备流程（见图2）如下：首先，将Al管内表面打磨粗糙，利于粘接；然后，将8层CFRP预浸料依次缠绕在芯棒上；接着，将已取出芯棒的CFRP预浸料层置入Al管内部，并在预浸料层内部置入气囊；最后，将带有气囊的Al/CFRP混合方管放入模具，在热压机中将模具加热至150 ℃，并将气囊压力调节至1.5 MPa，保温保压1.5 h，即可制成Al/CFRP混合方管试样。最终制成的Al方管、CFRP方管和Al/CFRP混合方管试样的几何尺寸如表2所示。此外，在各试样上端打磨出45°的倒角，以降低初始峰值载荷。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Al/CFRP混合方管制备流程

Fig.2 Preparation process of Al/CFRP hybird square tube

表2 各试样最终的几何尺寸参数

Table 2 Final geometric dimension parameters of each sample

试样

CFRP铺层数/层

外径

D/mm

长度

L/mm

厚度

T/mm

质量

m/g

Al方管

—

40.0

120.2

1.00

46.396

CFRP方管

40.5

120.9

2.03

50.601

Al/CFRP混合方管

40.0

120.1

3.07

94.762

新窗口打开| 下载CSV

1.2　轴向准静态压溃实验

采用万能试验机对Al方管、CFRP方管和Al/CFRP混合方管试样施加准静态轴向载荷，压缩位移为80 mm，上压盘压缩速度为4 mm/min。实验过程中试样的载荷—位移数据由万能试验机记录，试样变形模式由相机记录。轴向准静态压溃实验装置如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 轴向准静态压溃实验装置

Fig.3 Axial quasi-static crushing experimental device

1.3　耐撞性能指标

基于载荷—位移曲线计算得到总能量吸收值（energy absorption, EA）、比吸能（specific energy absorption, SEA）和压溃力效率（crush force efficiency, CFE）等指标，用于评价Al方管、CFRP方管和Al/CFRP混合方管试样的耐撞性能^[6]。

1）总能量吸收值为压溃过程中薄壁结构吸收的总能量，表示为：

W_{e} = \int_{0}^{s} F (x) d x

(1)

式中：W_e为总能量吸收值； $F (x)$ 为压溃过程中某一时刻的压溃载荷；s为压溃位移。

薄壁结构的总能量吸收值越大，其吸收能量的能力越强。

2）比吸能为薄壁结构的总能量吸收值与质量的比值，表示为：

W_{s} = \frac{W_{e}}{m}

(2)

式中：W_s为比吸能；m为薄壁结构的质量。

薄壁结构的比吸能越大，其能量吸收效率越高。

3）压溃力效率为薄壁结构平均压溃力与峰值压溃力的比值，表示为：

λ_{c} = \frac{F_{a v e}}{F_{m a x}}

(3)

式中：λ_c为压溃力效率；F_max为峰值压溃力；F_ave为平均压溃力。

薄壁结构的压溃力效率越接近于1，其吸能过程越平稳。

1.4　实验结果

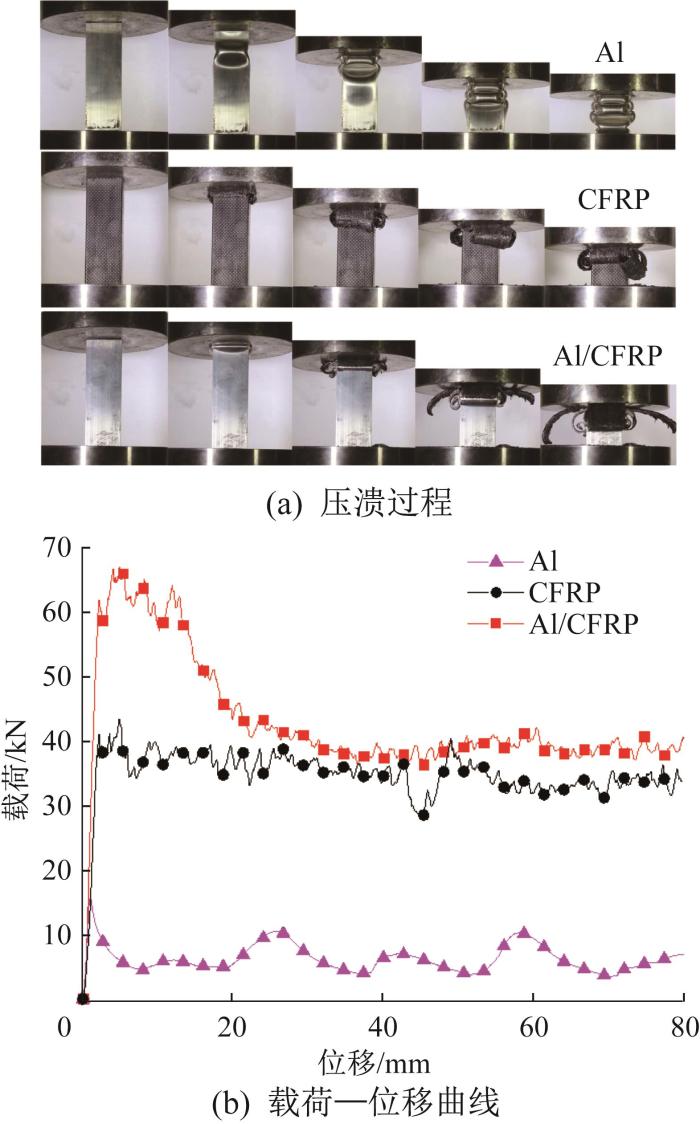
Al方管、CFRP方管和Al/CFRP混合方管试样的压溃过程及载荷—位移曲线如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 各试样的压溃过程及载荷—位移曲线

Fig.4 Crushing process and load‒displacement curve of each sample

由图4可知：

Al方管的变形模式为自上而下折叠变形；随着压缩过程的推进，Al方管逐渐从顶端形成塑性铰；Al方管的压溃力在短时间内达到峰值，随后下降，最后在某一值附近上下波动。

CFRP方管自上而下逐渐被破坏，呈渐进破坏变形模式；随着压缩过程的推进，CFRP方管逐渐产生向内和向外卷曲的叶片；CFRP方管的压溃力并未直接达到峰值，这可能是因为倒角的作用。CFRP方管压溃力的波动程度远小于Al方管，展现出平稳的承载能力。

Al/CFRP混合方管在压缩初期先形成了一个并未完全折叠的塑性铰；随着压缩过程的推进，其内部的CFRP阻止了外部Al管继续向内塑性折叠，导致Al管在边角处产生了不断延伸的4条裂缝；随着压缩位移的增大，内部的CFRP表现出与纯CFRP方管相似的卷曲分层变形模式；Al/CFRP混合方管的压溃力在外部Al管产生裂缝后迅速降低，但略高于纯CFRP方管，不过两者的变化趋势较为相似。值得注意的是，Al/CFRP混合方管的承载能力在外部Al管产生裂缝后逐渐平稳。

2 Al/CFRP混合方管有限元模型

2.1　CFRP损伤本构模型

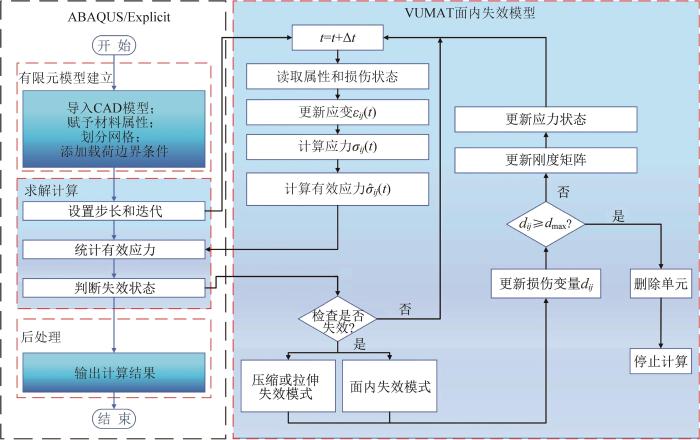
分别采用层内损伤模型、层间损伤模型来模拟CFRP在轴向压溃时的层内和层间失效。其中，CFRP层内失效采用有限元软件ABAQUS/Explicit中的用户子程序（VUMAT）实现，其流程如图5所示。CFRP层间损伤模型参考文献[3]建立，模型参数如表3所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于ABAQUS/Explicit用户子程序（VUMAT）的CFRP层内失效实现流程

Fig.5 Implementation flow of CFRP layer failure based on user subroutine (VUMAT) in ABAQUS/Explicit

表3 CFRP层间失效模型参数

Table 3 Parameters of CFRP interlaminar failure model

参数	数值
$t_{n}^{0}$ /MPa	54
$t_{s}^{0}$ /MPa	70
$t_{t}^{0}$ /MPa	70
$G_{n}^{c}$ /MPa	504
$G_{s}^{c}$ /MPa	1 556
$G_{t}^{c}$ /MPa	1 556
$η$	2.284

注：n和s、t分别表示法向与切向； $t 0$ 、 $G c$ 分别表示强度与断裂能；η表示粘接属性参数。

新窗口打开| 下载CSV

实验中采用的机织CFRP在弹性阶段的应力—应变关系如下：

[\begin{matrix} ε_{11} \\ ε_{22} \\ ε_{12} \end{matrix}] = [\begin{matrix} \frac{1}{(1 - d_{11}) E_{11}} & \frac{- ν_{12}}{E_{11}} & 0 \\ \frac{- ν_{21}}{E_{22}} & \frac{1}{(1 - d_{22}) E_{22}} & 0 \\ 0 & 0 & \frac{1}{2 (1 - d_{12}) G_{12}} \end{matrix}] [\begin{matrix} σ_{11} \\ σ_{22} \\ σ_{12} \end{matrix}]

(4)

式中： $σ$ =[σ₁₁σ₂₂σ₁₂]^T，为应力矢量； $ε$ =[ $ε$ ₁₁ $ε$ ₂₂ $ε$ ₁₂]^T，为弹性应变矢量；下标1，2分别为2个纤维方向；E₁₁、E₂₂分别为2个纤维方向的弹性模量；G₁₂为面内剪切模量；v₁₂、v₂₁为泊松比，v₂₁=(E₂₂/E₁₁)v₁₂；d₁₁、d₂₂分别为2个纤维方向的损伤变量，用于判断纤维的损伤状态；d₁₂为面内剪切损伤变量。

机织CFRP在面内剪切工况下会产生纤维的塑性变形和树脂的开裂，其应力—应变关系呈非线性^[1,7-8]。因此，采用塑性准则与硬化准则来描述CFRP的面内应力—应变关系，具体公式如下：

H = |{\hat{σ}}_{12}| - {\hat{σ}}_{0} ({\bar{ε}}^{p l}) \leq 0

(5)

其中：

{\hat{σ}}_{0} ({\bar{ε}}^{p l}) = {\hat{σ}}_{y 0} + C {({\bar{ε}}^{p l})}^{a}

(6)

式中：H为屈服函数； ${\hat{σ}}_{12}$ 为对应σ₁₂的有效应力； ${\hat{σ}}_{y 0}$ 为机织CFRP受到面内剪切载荷时的剪切屈服应力初始值； ${\bar{ε}}^{p l}$ 为等效塑性应变；C与a为剪切屈服应力的拟合参数，由实验推算得出^[9]。

采用失效方程(7)和(8)来推断机织CFRP是否发生损伤（ $i$ =11, 22）：

\{\begin{matrix} B_{i +} = \frac{{\hat{σ}}_{i +}}{X_{i +}} \\ B_{i -} = \frac{{\hat{σ}}_{i -}}{X_{i -}} \\ B_{12} = \frac{{\hat{σ}}_{12}}{S_{12}} \end{matrix}

(7)

\{\begin{matrix} {\hat{σ}}_{i +} = \frac{< σ_{i} >}{1 - d_{i +}} \\ {\hat{σ}}_{i -} = \frac{< - σ_{i} >}{1 - d_{i -}} \\ {\hat{σ}}_{12} = \frac{σ_{12}}{1 - d_{12}} \end{matrix}

(8)

式中：B_i 为不同方向上的损伤因子，下标中的+、-分别表示拉伸与压缩工况； ${\hat{σ}}_{i}$ 为有效应力； $X_{i +}$ 、 $X_{i -}$ 分别为机织CFRP沿 $i$ 方向的拉伸和压缩强度； $S_{12}$ 为机织CFRP的面内剪切强度。

当CFRP发生失效时，采用损伤演化法则对其进行损伤演化，以判断残余应力状态。损伤演化法则中的损伤变量演化关系定义如下（ $i$ =11, 22）：

\{\begin{matrix} r_{i +} (t) = m a x (\frac{{\hat{σ}}_{i +}}{X_{i +}}) \\ r_{i -} (t) = m a x (\frac{{\hat{σ}}_{i -}}{X_{i -}}) \\ r_{12} (t) = m a x (\frac{{\hat{σ}}_{12}}{S_{0}}) \end{matrix}

(9)

d_{α} = 1 - \frac{1}{r_{α}} e x p [- \frac{2 g_{0}^{α} L_{c}}{G_{f}^{α} g_{0}^{α} L_{c}} (r_{α} - 1)]

(10)

式中： $r_{α}$ 为损伤阈值， $α = 1 \pm, 2 \pm, 12$ ； $L_{c}$ 为单一有限元网格特征长度； $g_{0}^{α}$ 为单轴拉伸或压缩载荷下损伤起始点处单位体积的弹性能； $G_{f}^{α}$ 为纤维方向单位面积的拉伸或压缩破坏断裂能；S₀为基体的初始损伤剪切应力。

CFRP的面内剪切损伤演化规律定义为：

d_{12} = m i n (β_{12} l n r_{12}, d_{12 m a x}^{})

(11)

式中： $β_{12}$ 为拟合参数； $d_{12 m a x}^{}$ 为最大的面内剪切损伤变量。

2.2　有限元建模

Al/CFRP混合方管中Al管部分采用单层壳单元建模，网格的轴向与横向尺寸分别为1 mm和1.5 mm。AA6061-O铝合金材料的弹塑性行为由ABAQUS软件内置弹塑性模型表征，其材料参数参考文献［1］，如表4所示。

表4 AA6061-O铝合金材料参数

Table 4 AA6061-O aluminum alloy material parameters

参数	数值
密度/(g/cm³)	2.7
弹性模量/MPa	69.87
泊松比	0.37
屈服应力/MPa	143.1

新窗口打开| 下载CSV

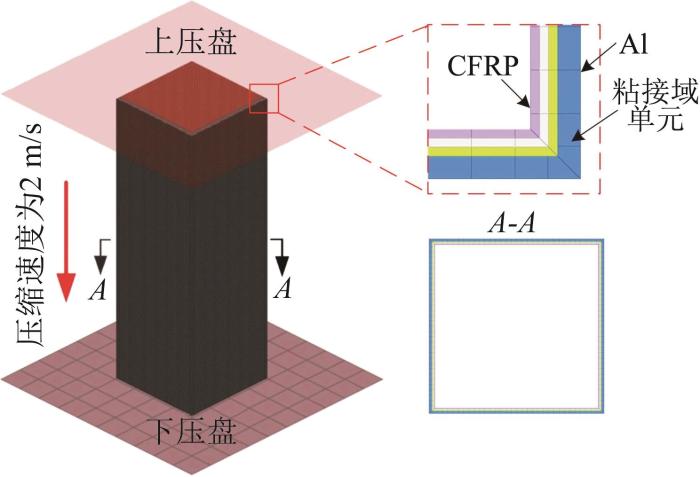
Al/CFRP混合方管中CFRP部分采用多层壳单元建模，每层壳单元代表一层机织CFRP，每层CFRP的铺层角度均为0°，网格尺寸与外部Al管保持一致。机织CFRP的层内、层间损伤模型按2.1节构建，材料参数取值参考文献[1]，其弹性参数、强度参数、面内剪切参数和损伤断裂参数分别如表5至表7所示。Al/CFRP混合方管轴向压溃有限元模型如图6所示。

表5 CFRP的弹性参数和强度参数

Table 5 Elastic parameters and strength parameters of CFRP

参数	数值
E₁₁/GPa	57
E₂₂/GPa	57
v₁₂，v₂₁	0.067
X₁₁₊/MPa	679
X₂₂₊/MPa	679
X_11-/MPa	512
X_22-/MPa	512

新窗口打开| 下载CSV

表6 CFRP的面内剪切参数

Table 6 In-plane shear parameters of CFRP

参数	数值
G₁₂/MPa	8 400
S₀/MPa	71
${\hat{σ}}_{y 0}$ /MPa	115
$r_{12}$	0.154
C	3 080
a	0.810 6

新窗口打开| 下载CSV

表7 CFRP的面内损伤断裂参数 (kJ/m²)

Table 7 In-plane damage fracture parameters of CFRP

参数	数值
$G_{f}^{1 +}$	155
$G_{f}^{1 -}$	255
$G_{f}^{2 +}$	155
$G_{f}^{2 -}$	255

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Al/CFRP混合方管轴向压溃有限元模型

Fig.6 Finite element model for axial crushing of Al/CFRP hybird square tube

由于Al/CFRP混合方管的Al管部分与CFRP部分之间采用树脂粘接，有限元模型中Al管部分与CFRP部分之间的粘接关系与机织CFRP的层间损伤模型保持一致。

为了提高计算效率，对CFRP与层间单元进行质量缩放^[10-11]，且采用2 m/s（12 000 mm/min）的压缩速度（高于实验压缩速度）对Al/CFRP混合方管有限元模型进行压缩^[12]，但要保证仿真动能低于总内能的5%~10%^[13-14]。在仿真过程中，Al/CFRP混合方管有限元模型放置在固定的刚性下压盘上，刚性上压盘匀速下压80 mm，刚性盘为壳单元。使用通用接触来模拟加载过程中Al/CFRP混合方管与上、下压盘的接触行为，摩擦系数为0.3^[15]。

2.3　有限元模型准确性验证

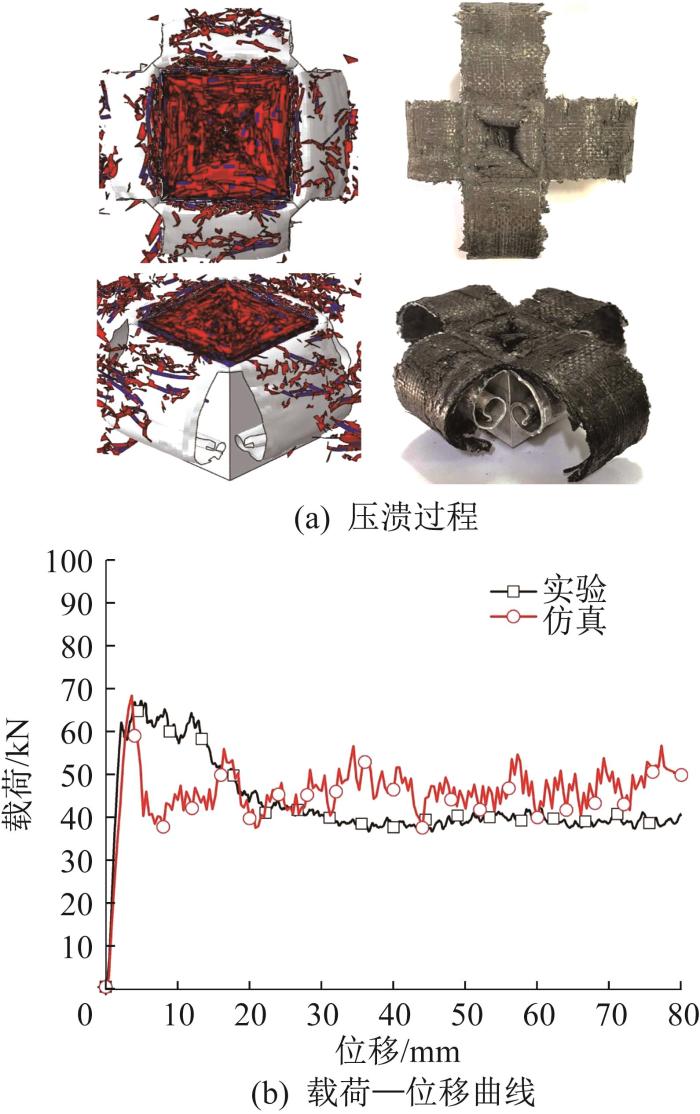
为了验证Al/CFRP混合方管轴向压溃有限元模型的准确性，基于图6模型开展Al/CFRP混合方管轴向准静态压溃仿真分析，其压溃过程及载荷—位移曲线的仿真与实验结果对比如图7所示。由图可知，基于仿真与实验所得的Al/CFRP混合方管的变形模式极为相似：外部Al管在边角处产生了不断延伸的4条裂缝，内部CFRP随着压缩位移的增大呈卷曲分层。Al/CFRP混合方管载荷—位移曲线的仿真与实验结果的差异表现在仿真分析并没有很好地复现实验初期载荷—位移曲线的波动阶段，这可能是实验中试样倒角不均匀所导致的。综合表8所示的Al/CFRP混合方管的耐撞性能指标，仿真结果与实验结果的差异在可接受范围内，由此说明所构建的有限元模型是准确的。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Al/CFRP混合方管轴向压溃的仿真与实验结果对比

Fig.7 Comparison between simulation and experimental results of axial crushing of Al/CFRP hybrid square tube

表8 Al/CFRP混合方管耐撞性能指标的仿真与实验结果对比

Table 8 Comparison between simulation and experimental results of crashworthiness index of Al/CFRP hybrid square tube

对比项	W_e/J	W_s/(J/g)	F_max/kN	F_ave/kN	λ_c
相对误差/%	6.17	6.13	1.85	5.89	4.68
实验值	3 444.74	36.35	66.87	43.07	0.64
仿真值	3 657.47	38.58	68.11	45.61	0.67

新窗口打开| 下载CSV

3 Al/CFRP混合方管多目标优化设计

3.1　优化问题定义

为了获取耐撞性能最优的Al/CFRP混合方管设计方案，选取Al管厚度、CFRP铺层角度为设计变量，基于代理模型开展多目标优化设计。将Al管厚度记作T_Al，其取值范围为0.5~2 mm；CFRP铺层数设为8，内、外4层CFRP的铺层角度对称，故整个Al/CFRP混合方管的铺层角度有4个，自外而内记作θ₁、θ₂、θ₃、θ₄，其取值范围为0°~45°。在优化设计中，以压溃力效率λ_c $\geq$ 0.65为约束条件，以达到Al/CFRP混合方管比吸能最大及峰值压溃力最小的优化目标。

3.2　试验设计

采用代理模型能够有效减少有限元计算次数，进而实现优化设计效率的大幅提升。建立准确的代理模型的关键是样本点的选取，本文采用优化拉丁超立方采样技术选取样本点：在各设计变量的取值范围内选取60个样本点。利用所构建的Al/CFRP混合方管轴向压溃有限元模型对60个样本点的设计目标响应进行计算，结果如表9所示。

表9 Al/CFRP混合方管的试验设计样本点及响应

Table 9 Experimental design sample points and responses of Al/CFRP hybrid square tube

样本点	设计变量					响应
样本点	T_Al/mm	θ₁/(°)	θ₂/(°)	θ₃/(°)	θ₄/(°)	F_max/kN	W_s/(J/g)	λ_c
1	1.4	7	1	8	35	71.39	28.79	0.58
2	1.3	17	33	1	3	70.56	31.74	0.63
3	0.6	39	0	7	4	51.64	38.95	0.75
︙	︙	︙	︙	︙	︙	︙	︙	︙
58	0.7	25	0	23	3	55.33	38.89	0.74
59	1.1	12	22	22	10	60.59	38.18	0.81
60	1.5	1	12	40	43	80.09	31.74	0.59

新窗口打开| 下载CSV

3.3　代理模型构建及其精度评估

根据选取的样本点及对应响应，利用插值等方法建立代理模型，将设计变量与优化目标之间的关系以函数形式近似表达，可大大降低优化过程中有限元仿真的时间成本^[16]。代理模型的精度对于优化设计结果的准确性至关重要，本文采用交叉验证方法来评价代理模型的准确性^[17]。交叉验证方法通常利用确定性系数R²、均方根误差R_MSE进行验证，其具体公式如下：

R^{2} = 1 - \sum_{u = 1}^{n} \frac{{(y_{u} - {\hat{y}}_{u})}^{2}}{\sum_{u = 1}^{n} {(y_{u} - \bar{y})}^{2}}

(12)

R_{M S E} = \frac{1}{n} \sqrt[]{{\sum_{u = 1}^{n} (y_{u} - {\hat{y}}_{u})}^{2}}

(13)

式中： $y_{u}$ 为真实响应； ${\hat{y}}_{u}$ 为近似响应； $\bar{y}$ 为真实响应的平均值。

精度越高的代理模型的 $R^{2}$ 越接近于1，R_MSE越小。当 $R^{2} \geq 0.9$ 时，认为代理模型的精度达到要求^[16]。

响应面法（response surface methodology, RSM）、克里金（Kriging）法及径向基函数（radial basis function, RBF）是常见的3种代理模型构建方法，但针对同一优化目标，基于这3种方法得到的代理模型的精度也有所差异。为此，分别采用上述3种方法对Al/CFRP混合方管的耐撞性能指标W_s、F_max与λ_c搭建代理模型，并选取精度最高的代理模型。基于不同方法的Al/CFRP混合方管耐撞性能指标代理模型的精度对比如表10所示。根据对比结果，F_max、W_s与λ_c分别采用RSM和Kriging来构建相应的代理模型。

表10 基于不同方法的Al/CFRP混合方管耐撞性能指标代理模型的精度对比

Table 10 Accuracy comparison of agent models for crashworthiness indexes of Al/CFRP hybrid square tube based on different methods

耐撞性能指标	代理模型构建方法	精度评价指标
耐撞性能指标	代理模型构建方法	$R^{2}$	R_MSE
F_max	RSM	0.911 8	0.105 6
	Kriging	0.831 4	0.116 7
	RBF	0.753 2	0.249 6
W_s	RSM	0.689 3	0.345 6
	Kriging	0.904 7	0.100 2
	RBF	0.758 3	0.255 2
λ_c	RSM	0.806 5	0.185 6
	Kriging	0.926 3	0.099 8
	RBF	0.796 5	0.213 5

新窗口打开| 下载CSV

3.4　多目标确定性优化设计

Al/CFRP混合方管的多目标确定性优化设计数学模型如下：

\{\begin{array}{l} m i n F_{m a x} \\ m a x W_{s} \\ s . t . λ_{c} \geq 0.65 \\ 0.5 \leq T_{A l} \leq 2 m m \\ 0 ° \leq θ_{1} \leq 45 ° \\ 0 ° \leq θ_{2} \leq 45 ° \\ 0 ° \leq θ_{3} \leq 45 ° \\ 0 ° \leq θ_{4} \leq 45 ° \end{array}

(14)

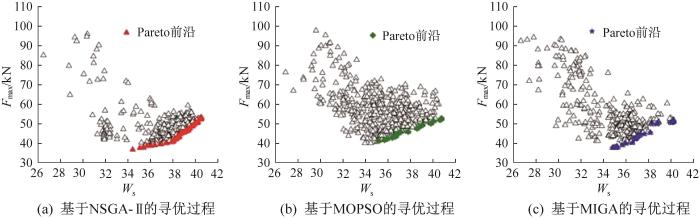
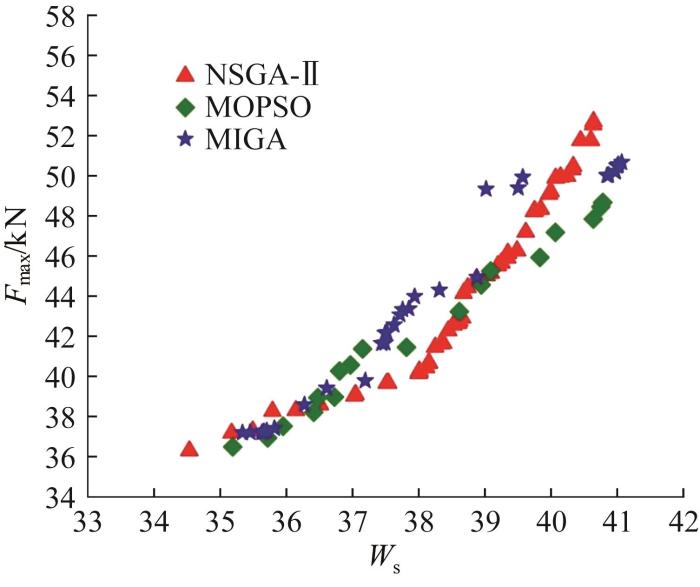
基于上文所构建的各耐撞性能指标的代理模型，选用3种常用启发式优化算法——NSGA-II（elitist non-dominated sorting genetic algorithm，精英非支配排序遗传算法）、MOPSO（multi-objective particle swarm optimization，多目标粒子群算法）和MIGA（multi-island genetic algorithm，多岛遗传算法），分别对各耐撞性能指标进行寻优，结果如图8所示。基于不同优化算法得到的Pareto前沿最优解集如图9所示。由图可知，采用不同优化算法得到的Pareto前沿最优解集具有较高的一致性。本文采用最小距离法从Pareto前沿最优解集中选择最优解^[18]，最优解及其响应如表11所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Al/CFRP混合方管多目标确定性优化寻优过程

Fig.8 Multi-objective certainty optimization process of Al/CFRP hybrid square tube

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 基于不同优化算法的Al/CFRP混合方管多目标确定性优化的Pareto前沿最优解集对比

Fig.9 Comparison of Pareto frontier optimal solution sets of multi-objective certainty optimization for Al/CFRP hybrid square tube based on different optimization algorithms

表11 Al/CFRP混合方管多目标确定性优化的最优解

Table 11 Optimal solution of multi-objective certainty optimization for Al/CFRP hybrid square tube

设计变量与耐撞性能指标	数值
T_Al/mm	0.59
θ₁/(°)	5.37
θ₂/(°)	43.92
θ₃/(°)	22.46
θ₄/(°)	44.79
F_max/kN	38.24
W_s/(J/g)	36.56
λ_c	0.71

新窗口打开| 下载CSV

3.5　多目标可靠性优化设计

复合材料的力学性能受制造精度的影响较大，设计参数在实际生产过程中的微小误差可能会对Al/CFRP混合方管的耐撞性能造成很大程度的削弱^[19]。因此，在实际生产过程中，应在设计阶段考虑设计参数的不确定性。此外，为了降低实际生产过程中的失效概率，要求优化结果远离设计边界，故在每个样本点处均要进行可靠性评估。本文采用蒙特卡洛法来计算失效概率，即采用描述性抽样方法在样本点正态分布范围内选取模拟点，每个样本点处抽样模拟500次后，计算该样本点处的可靠度，可靠度不达标的样本点为失效点。基于多目标确定性优化，考虑Al管厚度及4个CFRP铺层角度的不确定性，并使约束条件满足给定的可靠度要求，由此建立Al/CFRP混合方管的多目标可靠性优化数学模型，表示为：

\{\begin{array}{l} m i n F_{m a x} (μ_{T_{A l}}, μ_{θ_{1}}, μ_{θ_{2}}, μ_{θ_{3}}, μ_{θ_{4}}) \\ m a x W_{s} (μ_{T_{A l}}, μ_{θ_{1}}, μ_{θ_{2}}, μ_{θ_{3}}, μ_{θ_{4}}) \\ s . t . P (λ_{c} (μ_{T_{A l}}, μ_{θ_{1}}, μ_{θ_{2}}, μ_{θ_{3}}, μ_{θ_{4}}) \geq 0.65) \geq 0.98 \\ 0.5 m m + Δ T_{A l} \leq μ_{T_{A l}} \leq 2 m m - Δ T_{A l} \\ 0 ° + Δ θ_{1} \leq μ_{θ_{1}} \leq 45 ° - Δ θ_{1} \\ 0 ° + Δ θ_{2} \leq μ_{θ_{2}} \leq 45 ° - Δ θ_{2} \\ 0 ° + Δ θ_{3} \leq μ_{θ_{3}} \leq 45 ° - Δ θ_{3} \\ 0 ° + Δ θ_{4} \leq μ_{θ_{4}} \leq 45 ° - Δ θ_{4} \end{array}

(15)

假定设计变量服从正态分布，并根据典型的加工精度和装配误差，设计变量的变异系数一般设置为5%^[20]。根据5%变异系数确定的Al/CFRP混合方管多目标可靠性优化设计变量的初始值及不确定性概率分布，如表12所示。

表12 Al/CFRP混合方管多目标可靠性优化设计变量的初始值及其概率分布

Table 12 Initial value and probability distribution of design variables of multi-objective reliability optimization for Al/CFRP hybrid square tube

设计变量	概率分布	相关系数	初始值	取值范围
设计变量	概率分布	相关系数	初始值	上限	下限
T_Al/mm	正态分布	0.05	0.59	0.5	2
θ₁/(°)	正态分布	0.05	5.37	0	45
θ₂/(°)	正态分布	0.05	43.92	0	45
θ₃/(°)	正态分布	0.05	22.46	0	45
θ₄/(°)	正态分布	0.05	44.79	0	45

新窗口打开| 下载CSV

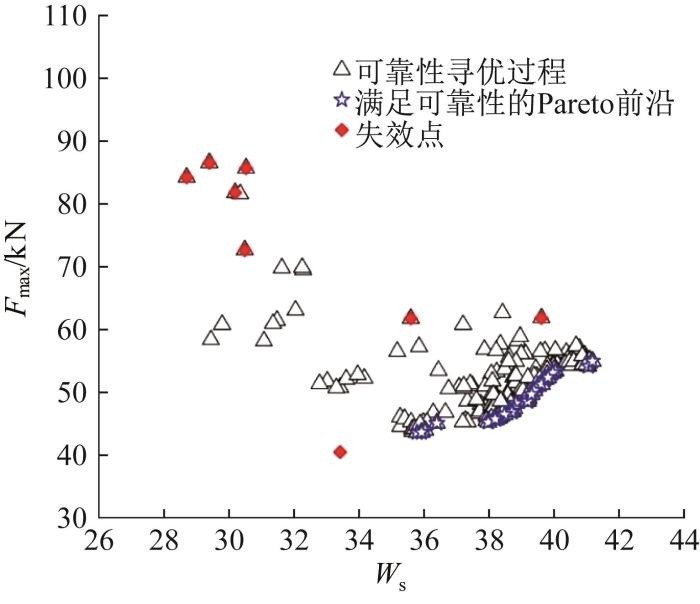
基于NSGA-Ⅱ的Al/CFRP混合方管多目标可靠性优化过程如图10所示，采用确定性优化及可靠性优化得到的Pareto前沿最优解集如图11所示。由图11可知，利用可靠性优化得到的Pareto前沿最优解集与采用确定性优化得到的有一定差别。可靠性最优解同样由最小距离法确定，基于2种优化方法的最优解及其响应如表13所示。从耐撞性能指标来看，采用确定性优化得到的F_max、W_s分别小于和高于采用可靠性优化得到的，但可靠度却远低于可靠性优化。因此，针对Al/CFRP混合方管耐撞性能的优化设计，可靠性优化具有更高的可靠度与更好的实用性。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 基于NSGA-Ⅱ的Al/CFRP混合方管多目标可靠性寻优过程

Fig.10 Multi-objective reliability optimization process of Al/CFRP hybrid square tube based on NSGA-Ⅱ

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 Al/CFRP混合方管确定性与可靠性优化的Pareto前沿最优解集对比

Fig.11 Comparison of Pareto frontier optimal solution sets of certainty and reliability optimization for Al/CFRP hybrid square tube

表13 Al/CFRP混合方管的确定性与可靠性优化最优解对比

Table 13 Comparison of certainty and reliability optimal solutions of Al/CFRP hybrid square tube

设计变量、优化目标及约束	确定性优化解	可靠性优化解
T_Al/mm	0.59	0.79
θ₁/(°)	5.37	16.62
θ₂/(°)	43.92	25.70
θ₃/(°)	22.46	20.99
θ₄/(°)	44.79	37.97
F_max/kN	38.24	42.11
W_s/(J/g)	36.56	35.75
λ_c	0.71	0.76
可靠度/%	87.36	98.32

新窗口打开| 下载CSV

将可靠性优化结果进行圆整处理，得到Al/CFRP混合方管的最优设计参数组合：T_Al=0.8 mm，θ₁=17°，θ₂=26°，θ₃=21°，θ₄=38°。基于最优设计参数组合，构建Al/CFRP混合方管轴向压溃有限元模型并进行仿真分析，以判断所构建代理模型的准确性。基于可靠性最优解的Al/CFRP混合方管压溃过程仿真结果如图12所示，其最终的变形模式和载荷—位移曲线如图13所示。基于代理模型和有限元仿真的Al/CFRP混合方管耐撞性能指标对比如表14所示。由表可知，基于代理模型和有限元仿真得到的W_s与λ_c具有很高的一致性，而F_max的误差较大，达到了-13.47%，但在可接受的误差范围之内。因此，所构建的代理模型准确，且可靠性优化结果可靠。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 基于可靠性最优解的Al/CFRP混合方管压溃过程仿真结果

Fig.12 Simulation results of Al/CFRP hybrid square tube crushing process based on reliability optimal solution

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 基于可靠性最优解的Al/CFRP混合方管的变形模式和载荷—位移曲线仿真结果

Fig.13 Simulation results of deformation mode and load‒displacement curve of Al/CFRP hybrid square tube based on reliability optimal solution

表14 基于代理模型和有限元仿真的Al/CFRP混合方管耐撞性能指标对比

Table 14 Comparison of crashworthiness indexes of Al/CFRP hybrid square tube based on agent model and finite element simulation

对比项	F_max/kN	W_s/(J/g)	λ_c
相对误差/%	-13.47	2.52	3.79
代理模型预测结果	42.11	35.75	0.76
有限元仿真结果	48.67	34.87	0.79

新窗口打开| 下载CSV

4 结论

为实现Al/CFRP混合方管的优化设计，采用实验方法对比了3种由不同材料制成的方管的耐撞性能，并基于实验验证的有限元模型，使用确定性优化及可靠性优化方法对Al/CFRP混合方管的耐撞性能进行优化，得到以下结论：

1）CFRP方管的比吸能及压溃力效率远高于相同尺寸的Al方管；Al/CFRP混合方管的变形模式为渐进失效，其承载能力稳定，具有较好的耐撞性能，达到了预期的效果。

2）基于有限元软件ABAQUS/Explicit建立的Al/CFRP混合方管轴向压溃有限元模型可用于其准静态轴向压溃模拟与优化设计。

3）确定性优化及可靠性优化结果显示，采用可靠性优化得到的压溃力效率的可靠度为98.32%，远大于采用确定性优化得到的87.36%，大幅降低了失效概率，即可靠性优化具有更高的可靠度与更好的实用性。

上述结果表明，Al/CFRP混合方管可为汽车车身薄壁吸能构件的轻量化设计提供参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

朱国华

金属/碳纤维混合材料薄壁结构耐撞性研究

［D］.长沙：湖南大学，2018：14-32. doi：10.1016/j.tws.2018.02.029

[本文引用: 5]

ZHU

Guo-hua

On crashworthiness of metal/CFRP hybrid thin-walled structures

［D］. Changsha： Hunan University， 2018： 14-32.

DOI:10.1016/j.tws.2018.02.029 [本文引用: 5]

[2]

SUN

， YU

， WANG

， et al.

Energy absorption mechanics and design optimization of CFRP/alumimun hybrid structures for tra+nsverse loading

［J］. International Journal of Mechanical Sciences， 2019， 150： 767-783.