<img src="https://www.zjujournals.com/gcsjxb/images/1006-754X/images/logo.png" class="img-responsive">

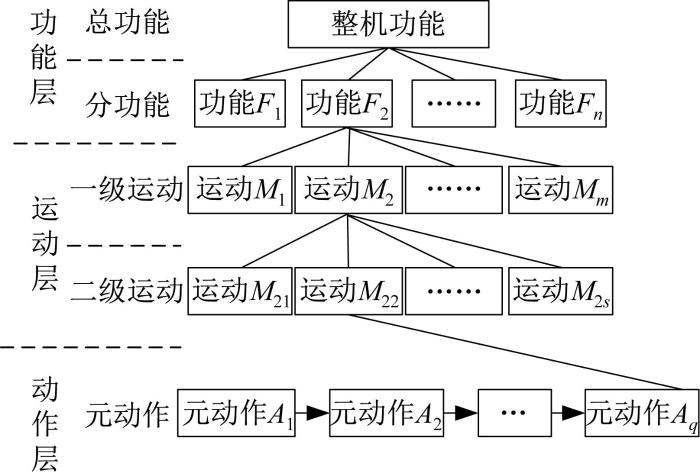
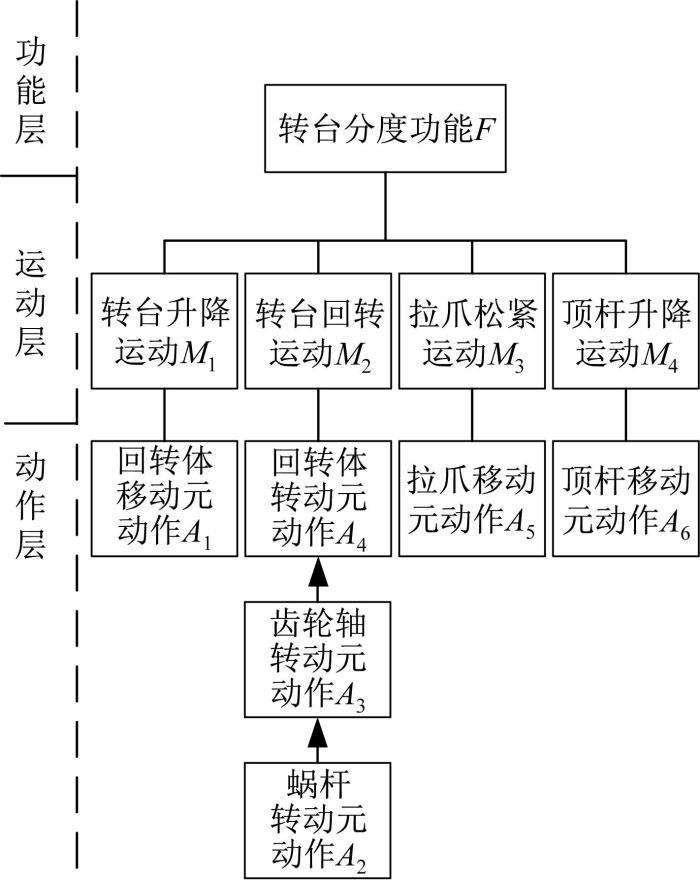
图1 FMA结构层次分解过程

Fig.1 FMA structure hierarchical decomposition process

1.2　元动作单元

在机械产品中，单个零件无法完成规定的运动。因此，为了保证元动作能够正常传递动力和运动，将零件按照装配关系组成的能够实现元动作正常运行且在结构上不可再分的统一整体确定为元动作单元。根据各装配零件在元动作运动过程中的不同作用，将组成元动作单元的不同零件分为输入件、中间件、输出件、支撑件和紧固件^［14］。其具体的定义如表1所示。

表1 元动作单元组成零件的分类及定义

Table 1 Classification and definition of components of meta-action unit

零件分类	定义
输入件	接收邻接上游元动作或提供动力和运动的零件
中间件	连接输入件和输出件并传递动力和运动的零件
输出件	输出动力和运动到邻接下游元动作的零件或该元动作的运动执行件
支撑件	提供装配基准，保证各零件相互位置精度的零件
紧固件	连接2个或多个零件为一体，且使被连接件间无相对运动的零件

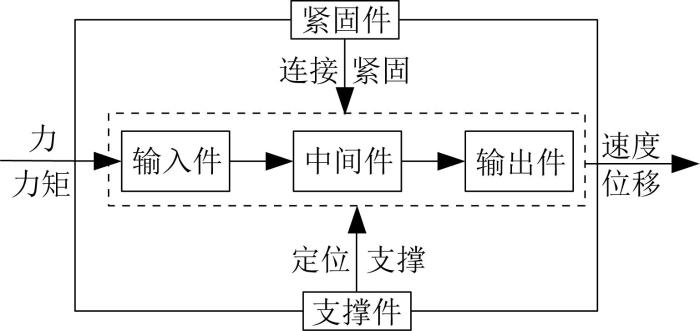
力和力矩是元动作运动状态改变的原因。因此，任意元动作实现运动都须依靠输入件接收外部的动力和运动，并通过中间件传递给输出件，从而改变元动作运动参数。同时，为了保障元动作的运动性能满足要求，支撑件和紧固件也起着至关重要的作用。故将上述五类零件按照一定的装配关系构成完整的元动作单元，如图2所示。

图2

图2 元动作单元结构示意

Fig.2 Schematic of meta-action unit structure

2 多准则模糊关联的关键元动作识别建模

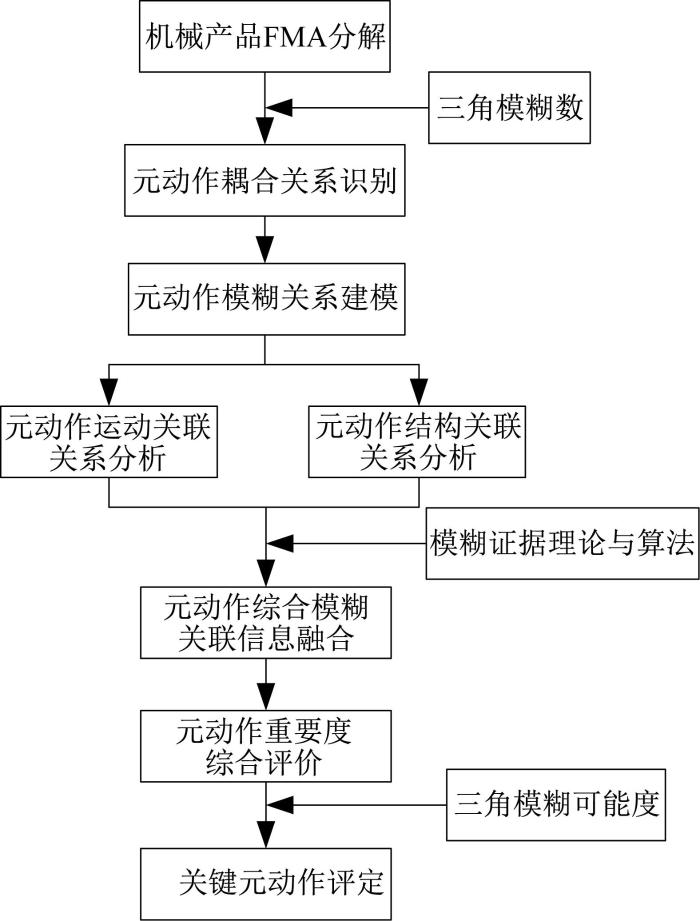
针对传统识别关键单元的不足，本文提出一种基于元动作的关键运动单元识别方法。首先，根据FMA结构化分解方法对机械产品进行分解，得到元动作集合，并将其作为研究对象；其次，从运动关系和结构关系两个角度结合专家评价讨论元动作之间的关联关系，并建立模糊关系矩阵；然后，基于模糊证据理论对元动作之间的模糊关系进行定量分析，并融合不同准则下的元动作之间的关联信息；最后，基于获得的元动作之间的综合模糊关系结果计算元动作所占权重，并对其重要度进行排序，识别考虑综合关联关系的关键元动作。其具体流程如图3所示。

图3

图3 关键元动作识别流程

Fig.3 Key meta-action identification process

与传统的关键单元识别不同，传统的关键单元识别只从零件与结构关系进行，本文从运动角度对机械产品进行分解——FMA结构化分解。同时，针对领域内多专家评价时出现的信息不完整或信息缺失等问题，提出了用模糊证据理论推算来融合元动作之间的多准则关联关系，为后续对关键元动作的可靠性分析奠定基础。

2.1　元动作模糊关联分析

机械产品元动作之间的关联关系与零件之间的关联关系不同，其除了考虑结构间的相互影响，还要考虑运动关系的影响。一般来说，主要通过调研和专家经验来评估机械产品关键单元^［15］。然而，当信息模糊或不完整时，专家无法用准确的数值表示他们的观点。本文利用三角模糊数与模糊语义之间的关系，将模糊数值转化为评价元动作之间模糊关联关系的输入。其中，任一三角模糊数可以表示为 $A = (A_{l}, A_{m}, A_{u})$ ， $A_{l}, A_{m}, A_{u}$ 分别表示三角模糊元素中的最小值、最可能值和最大值。任意两个三角模糊数的加法运算公式为：

\begin{array}{l} A_{1} + A_{2} = (A_{l 1}^{}, A_{m 1}^{}, A_{u 1}^{}) + (A_{l 2}^{}, A_{m 2}^{}, A_{u 2}^{}) = \\ (A_{l 1}^{} + A_{l 2}^{}, A_{m 1}^{} + A_{m 2}^{}, A_{u 1}^{} + A_{u 2}^{}) \end{array}

(1)

对于任意三角模糊数，其隶属度函数可以表示为：

μ_{A} (x) = \{\begin{matrix} \frac{x - A_{l}}{A_{m} - A_{l}}, A_{l} < x < A_{m} \\ 0, 其 他 \\ \frac{A_{u} - x}{A_{u} - A_{m}}, A_{m} < x < A_{u} \end{matrix}

(2)

建立不同三角模糊数与模糊语义的对应关系，并对其进行等级划分，如表2所示。

表2 三角模糊数与模糊语义的对应关系

Table 2 Corresponding between triangular fuzzy numbers and fuzzy semantics

三角模糊数	模糊语义	等级
（0，1，2）	无关紧要的	1
（2，3，4）	不重要的	2
（4，5，6）	一般重要的	3
（6，7，8）	重要的	4
（8，9，10）	非常重要的	5

本文结合FMA结构化分解的特点，基于不同元动作之间的运动关联关系和结构关联关系，分析元动作之间的相关性，求解元动作之间的综合关联关系。

其中，元动作之间的运动关联性主要表示为元动作与运动层中同一运动的相关性，可以通过元动作之间的协同必要性或程度衡量。比如，为实现数控转台回转运动，蜗杆转动元动作和转台转动元动作缺一不可，可以认为它们之间具有很强的运动关联关系。元动作运动关联性的语义描述与三角模糊数的对应关系如表3所示。

表3 元动作运动关联性的语义描述与三角模糊数的对应关系

Table 3 Corresponding relation between semantic description of meta-action motion relevance and triangular fuzzy number

运动关联关系	三角模糊数
两元动作对某一运动的实现不存在关联性	（0，1，2）
一元动作对另一元动作完成同一运动的协同作用较弱	（2，3，4）
一元动作对另一元动作完成同一运动的协同作用一般	（4，5，6）
一元动作对另一元动作完成同一运动的协同作用较强	（6，7，8）
两元动作对完成同一运动缺一不可	（8，9，10）

元动作之间的结构关联关系主要表示为两元动作之间是否存在共用件，若存在共用件，共用件是否传递信息。比如，拉爪移动元动作和顶杆移动元动作共用拉钉和公锥活塞中间件，用于传递动力和运动，可以认为它们之间具有很强的结构关联关系。元动作结构关联性的语义描述与三角模糊数的对应关系如表4所示。

表4 元动作结构关联性的语义描述与三角模糊数的对应关系

Table 4 Corresponding relationship between semantic description of meta-action structure relevance and triangular fuzzy number

结构关联关系	三角模糊数
两元动作不存在联系	（0，1，2）
两元动作无共用件，但传递某介质	（2，3，4）
两元动作有共用件，但不传递介质	（4，5，6）
两元动作无共用件，但传递能量	（6，7，8）
两元动作的共用件传递扭矩等能量	（8，9，10）

2.2　元动作之间综合关联关系分析

分析元动作运动关联关系和结构关联关系之后，根据模糊证据理论对关联关系进行进一步融合。具体方法和步骤如下。

1）建立专家评价矩阵。根据运动关联关系和结构关联关系成立一个不少于5人的评估小组来评估不同关联准则下的元动作关联关系。专家的评估结果 $R_{i j}^{P s}$ 用三角模糊矩阵表示：

R_{i j}^{P s} = \begin{matrix} A_{1} \\ ⋮ \\ A_{n} \end{matrix} (\begin{matrix} γ_{11}^{P s} & \dots & γ_{1 n}^{P s} \\ ⋮ & ⋮ & ⋮ \\ γ_{n 1}^{P s} & \dots & γ_{n n}^{P s} \end{matrix})

(3)

式中： $γ_{i j}^{P s}$ 表示在元动作关联关系s下专家P对元动作 $A_{i}$ 和 $A_{j}$ 的关联性评价。

2）融合专家评价信息。采用模糊证据理论，将三角模糊数与证据理论相结合进行专家评价信息融合。模糊识别框由N个评价等级组成。其中， $G_{k}^{s} (k = 1,2, \dots, N)$ 表示在元动作关联关系 $s$ 下的k个评价等级。p位专家在关联关系 $s$ 下给出的元动作 $A_{i}$ 与元动作 $A_{j}$ 的相关度置信水平 $β_{k}^{s} (i, j)$ 为：

β_{k}^{s} (i, j) = \frac{Z (G_{k}^{s})}{p}, β_{k}^{s} (i, j) \in [0, 1]

(4)

式中： $Z (G_{k}^{s})$ 表示在元动作关联关系s下评价元动作 $A_{i}$ 与元动作 $A_{j}$ 之间的关系为 $G_{k}^{s}$ 的专家数量。

根据式（3）和式（4），可以将p位专家在关联关系s下给出的元动作 $A_{i}$ 与元动作 $A_{j}$ 的相关性评价值相结合，得到模糊矩阵：

γ_{i j}^{s} = \{\begin{matrix} (G_{k}^{s}, β_{k}^{s} (i, j)), i \neq j \\ 1, i = j \end{matrix}

(5)

假设元动作 $A_{i}$ 与元动作 $A_{j}$ 之间的基本质量概率为 $m_{k}^{s} (i, j)$ ，即元动作 $A_{i}$ 和元动作 $A_{j}$ 在关联关系s下评价等级为k的概率，则其残差质量概率为 $m_{G}^{s} (i, j)$ ，即在评价过程中没有任何评价等级的概率。残差质量概率可以划分为由相对重要度引起的残差质量概率 ${\bar{m}}_{G}^{s} (i, j)$ 和由信息不完整引起的残差质量概率 ${\tilde{m}}_{G}^{s} (i, j)$ ，具体表达式分别为：

m_{k}^{s} (i, j) = ω_{s} \cdot β_{k}^{s} (i, j)

(6)

\begin{array}{l} m_{G}^{s} (i, j) = 1 - \sum_{k = 1}^{N} m_{k}^{s} (i, j) = 1 - ω_{s} \cdot \sum_{k = 1}^{N} β_{k}^{s} (i, j) = \\ {\bar{m}}_{G}^{s} (i, j) + {\tilde{m}}_{G}^{s} (i, j) \end{array}

(7)

{\bar{m}}_{G}^{s} (i, j) = 1 - ω_{s}

(8)

{\tilde{m}}_{G}^{s} (i, j) = ω_{s} \cdot (1 - \sum_{k = 1}^{N} β_{k}^{s} (i, j))

(9)

式中： $ω_{s}$ 表示元动作之间关联关系s的权重， $\sum ω_{s \in \{m, l\}} = 1$ ， $m$ 表示运动关联关系， $l$ 表示结构关联关系。

每种关联关系的权重可以通过层次分析法获得^［16］。

3）多关联关系评价信息融合。基于模糊分析证据推理算法融合多关联关系下的专家评价信息，具体表达如下：

\begin{array}{l} K = \sum_{k = 1}^{N} \prod_{s \in \{m, l\}} (m_{k}^{s} (i, j) + {\bar{m}}_{G}^{s} (i, j) + {\tilde{m}}_{G}^{s} (i, j)) - \\ (N - 1) \prod_{s \in \{m, l\}} ({\bar{m}}_{G}^{s} (i, j) + {\tilde{m}}_{G}^{s} (i, j)) \end{array}

(10)

\begin{array}{l} m_{k} (i, j) = K^{- 1} \prod_{s \in \{m, l\}} (m_{k}^{s} (i, j) + m_{G}^{s} (i, j)) - \\ K^{- 1} \prod_{s \in \{m, l\}} m_{G}^{s} (i, j) (11) \end{array}

{\bar{m}}_{G} = K^{- 1} \prod_{s \in \{m, l\}} {\bar{m}}_{G}^{s} (i, j) (12)

{\tilde{m}}_{G} (i, j) = \prod_{s \in \{m, l\}} m_{G}^{s} (i, j) - \frac{\prod_{s \in \{m, l\}} {\bar{m}}_{G}^{s} (i, j)}{K} (13)

β_{k} (i, j) = \frac{m_{k} (i, j)}{1 - {\bar{m}}_{G} (i, j)}

(14)

式中： $K$ 表示规模化比例因子； $m_{k} (i, j)$ 表示元动作 $A_{i}$ 与元动作 $A_{j}$ 在综合关联关系下评价等级为k的基本质量概率； $β_{k} (i, j)$ 表示元动作 $A_{i}$ 和元动作 $A_{j}$ 在综合关联关系下的相关度置信水平。

通过融合不同关联关系下专家评价信息后可以得到元动作 $A_{i}$ 与元动作 $A_{j}$ 的综合模糊关联关系 $γ_{i j}$ ：

γ_{i j} = \{\begin{matrix} \sum_{k = 1}^{N} β_{k} (i, j) \cdot G_{k}, i \neq j \\ 1, i = j \end{matrix}

(15)

2.3　关键元动作识别

对元动作的模糊关联关系进行分析得到所需的评价结果后，还须进一步计算各元动作在该机械产品中的权重，并对其重要度进行排序，最终得到关键元动作。采用三角模糊数可能度关系的指标权重确定方法，实现对关键元动作的识别。该方法的具体步骤如下^［17］：

1）计算元动作 $A_{i}$ 与所有元动作之间的综合模糊值 $γ_{i j}$ 的初始权重 $D_{i}$ ：

D_{i} = \frac{\sum_{j = 1}^{n} γ_{i j}}{\sum_{i = 1}^{n} \sum_{j = 1}^{n} γ_{i j}}

(16)

2）去模糊化。将三角模糊值转化为定值，定义 $A_{i} > A_{j}$ 的可能度，其中 $A_{i} = (A_{l i}^{}, A_{m i}^{}, A_{u i}^{})$ ， $A_{j} = (A_{l j}^{}, A_{m j}^{}, A_{u j}^{})$ ，则可得三角模糊数为：

P (A_{i} > A_{j}) = \{\begin{array}{l} 1, A_{m i}^{} > A_{m j}^{} \\ \frac{A_{l j}^{} - A_{u i}^{}}{(A_{m i}^{} - A_{u i}^{}) - (A_{m j}^{} - A_{l j}^{})}, A_{m i}^{} < A_{m j}^{}, A_{u i}^{} > A_{l j}^{} \\ 0, 其 他 \end{array}

(17)

定义一个元动作模糊数大于其他k个元动作模糊数的可能度为：

\begin{array}{l} P (A_{i} > A_{1}, A_{2}, \dots, A_{k}) = m i n P (A_{i} > A_{m}) \\ m = 1, 2, \dots, k \end{array}

(18)

3）将求得的各元动作权重标准化，得到所有元动作的最终权重为：

\{\begin{array}{l} W = (d (A_{1}), d (A_{2}), \dots, d (A_{n})) \\ d (A_{1}) = m i n P (A_{i} > A_{m}) \end{array}

(19)

3 实例分析

以国内某型号数控加工中心转台（以下简称数控转台）为例，进行其FMA结构化分解，并在此基础上完成对该转台关键元动作的识别。

3.1　转台FMA结构化分解

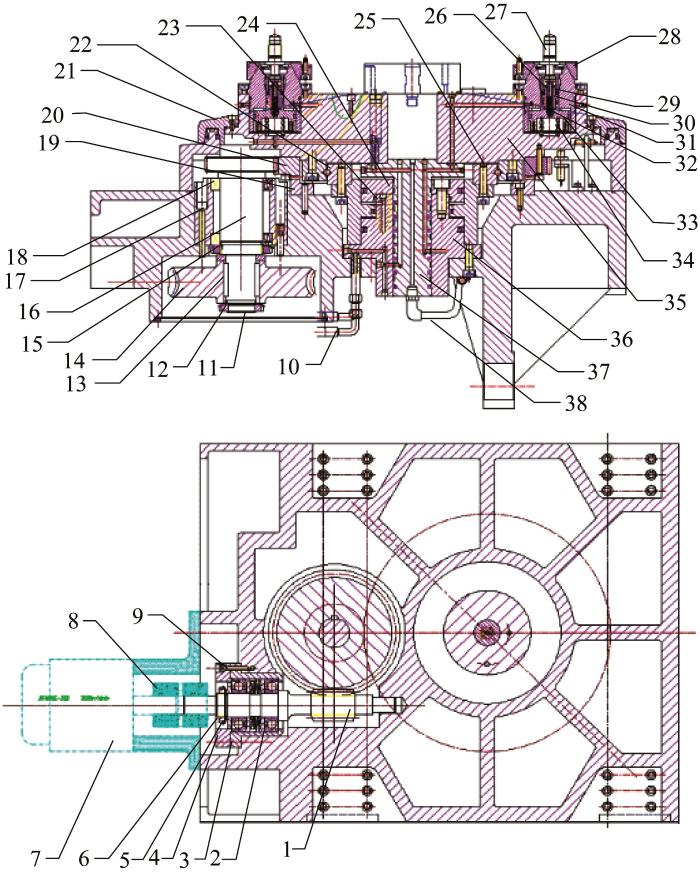
数控转台的结构如图4所示。

图4

图4 数控转台结构

1—蜗杆；2—轴承；3—隔套；4—端盖；5—止动垫圈；6—螺母；7—电机；8—联轴器；9—螺钉；10—锁紧油路；11—密封盖；

12—止动垫圈；13—平键；14—蜗轮；15—螺母；16—齿轮轴；17—螺钉；18—齿轮轴轴承；19—下齿盘； 20—上齿盘；

21—密封罩壳；22—轴承；23—升降油缸；24—活塞；25—螺钉；26—顶杆；27—顶杆螺钉；28—母锥；29—拉爪；30—拉钉；

31—公锥；32—小弹簧；33—活塞；34—大弹簧； 35—回转体；36—托架；37—活塞；38—心轴； 39—升降油路。

Fig.4 NC turntable structure

据数控转台“功能—运动—动作”的运动特性，利用FMA结构化分解得到6个元动作，如图5所示。每个元动作都是确保数控转台正常运行的最基本运动单元。

图5

图5 数控转台FMA结构化分解

Fig.5 FMA structural decomposition of NC turntable

3.2　数控转台元动作模糊关联分析

5位该领域内的专家分别从元动作之间的运动关联关系和结构关联关系进行评价，并构建各关联关系下的矩阵。不同关联关系所占权重通过层次分析法进行计算，得到元动作之间运动关联关系和结构关联关系的权重分别为： $ω_{m} = 0.593$ ， $ω_{l} = 0.407$ ，因此，得到元动作之间不同关联关系下5位专家的评价结果，如表5和表6所示。

表5 数控转台元动作之间运动关联关系评价结果

Table 5 Evaluation results of motion association between NC turntable meta-actions

A₁

A₂

A₃

A₄

A₅

A₆

A₁

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0.6

(8,9,10),0.4

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

A₂

(0,1,2),0.2

(2,3,4),0.6

(4,5,6),0.2

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

A₃

(0,1,2),0.2

(2,3,4),0.6

(4,5,6),0.2

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

A₄

(0,1,2),0

(2,3,4),0

(4,5,6),0.4

(6,7,8),0.4

(8,9,10),0.2

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),0.2

(2,3,4),0.8

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0.4

(2,3,4),0.6

(4,5,6),0

(6,7,8),0

(8,9,10),0

A₅

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.8

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0.2

(8,9,10),0.8

A₆

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.8

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0.2

(8,9,10),0.8

表6 数控转台元动作之间结构关联关系评价结果

Table 6 Evaluation results of structural association between NC turntable meta-actions

A₁

A₂

A₃

A₄

A₅

A₆

A₁

(0,1,2),0.6

(2,3,4),0.4

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2)0.2

(2,3,4)0.4

(4,5,6),0.4

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

A₂

(0,1,2),0.6

(2,3,4),0.4

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),1

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),1

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

A₃

(0,1,2),0.2

(2,3,4),0.4

(4,5,6),0.4

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),1

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),1

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

A₄

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),1

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),1

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),1

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

A₅

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0.2

(8,9,10),0.8

A₆

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),1

(2,3,4),0

(4,5,6),0

(6,7,8),0

(8,9,10),0

(0,1,2),0.2

(2,3,4),0.2

(4,5,6),0.6

(6,7,8),0

(8,9,10),0

(0,1,2),0

(2,3,4),0

(4,5,6),0

(6,7,8),0.2

(8,9,10),0.8

根据式（10）至式（14）将元动作运动关联关系和结构关联关系下的评价结果进行融合，得到数控转台所有元动作之间的模糊关联关系，如表7所示。

表7 数控转台元动作之间综合关联关系评价结果

Table 7 Evaluation results of comprehensive association between NC turntable meta-actions

	A₁	A₂	A₃	A₄	A₅	A₆
A₁	1	(0.20,1.20,2.20)	(0.70,1.70,2.70)	(7.31,8.31,9.31)	(0.82,1.82,2.82)	(0.82,1.82,2.82)
A₂	(1.58,2.58,3.58)	1	(7.36,8.36,9.36)	(7.36,8.36,9.36)	(0,1,2)	(0,1,2)
A₃	(2.14,3.14,4.14)	(7.36,8.36,9.36)	1	(7.36,8.36,9.36)	(0,1,2)	(0,1,2)
A₄	(6.51,7.51,8.51)	(7.36,8.36,9.36)	(7.36,8.36,9.36)	1	(1.95,2.95,3.95)	(1.67,2.67,3.67)
A₅	(0.82,1.82,2.82)	(0,1,2)	(0,1,2)	(1.95,2.95,3.95)	1	(7.67,8.67,9.67)
A₆	(0.82,1.82,2.82)	(0,1,2)	(0,1,2)	(1.95,2.95,3.95)	(7.67,8.67,9.67)	1

3.3　数控转台关键元动作识别

根据表7对数控转台各元动作之间的综合关联关系进行去模糊化处理，并根据式（16）至式（18）可以得到数控转台各元动作所占权重结果：

W = (0.094, 0.194, 0.202, 0.304, 0.103, 0.103)

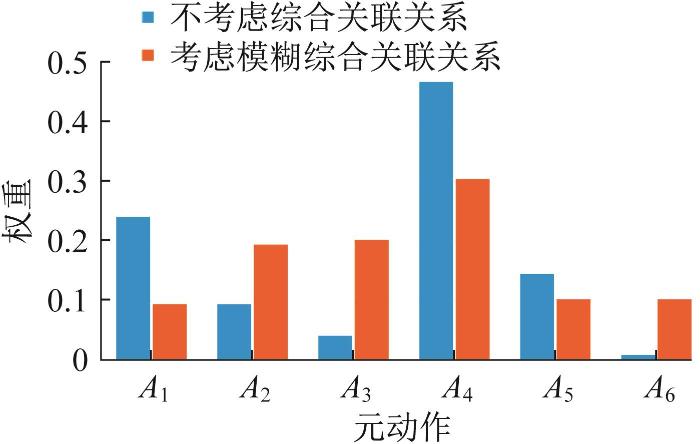
在考虑运动和结构的综合关联关系下，数控转台元动作的重要度排序为： $w_{A_{4}} > w_{A_{3}} > w_{A_{2}} > w_{A_{5}} = w_{A_{6}} > w_{A_{1}}$ 。其中 $A_{4}$ 在数控转台所有元动作中所占权重最高，可以解释为： $A_{4}$ 既与 $A_{1}$ 存在共用件，又与 $A_{2}$ 和 $A_{3}$ 对数控转台回转运动起着不可或缺的协同作用，还与 $A_{5}$ 和 $A_{6}$ 共用支撑件，因此， $A_{4}$ 分配更高的权重是合理的。

此外，以本文提出的考虑模糊综合关联关系的元动作重要度排序结果与不考虑综合关联关系的重要度排序结果进行对比^［18］，结果如图6所示。

图6

图6 数控转台元动作重要度对比

Fig.6 Comparison of importance of NC turntable meta-actions

由图6可知，考虑模糊综合关联关系的元动作重要度与不考虑综合关联关系的元动作重要度差异较大，不考虑关联关系的元动作重要度排序为： $w_{A_{4}} > w_{A_{1}} > w_{A_{5}} > w_{A_{2}} > w_{A_{3}} > w_{A_{6}}$ 。比如，在不考虑关联关系时 $A_{1}$ 排序第2，而在考虑关联关系时排序第6。可以解释为：在运动层，转台升降运动和转台的转动存在先后关系，这2条传动链的任一环节出问题，整机的功能将无法实现。不仅如此， $A_{1}$ 和 $A_{4}$ 元动作共用上端齿盘，其分别作为中间件和输入件，均用于传递动力，且 $A_{1}$ 中的输出件（回转体）是 $A_{5}$ 和 $A_{6}$ 的支撑件，该作用也不可忽视。综上，元动作之间的综合关联关系对该元动作的重要度影响较大。因此，在识别机械产品关键元动作的过程中，为保证最终识别的关键元动作的完备性，应该将元动作之间的综合关联关系予以考虑。

4 结论

1）针对机械产品元动作之间关联关系的确定问题，基于三角模糊数和模糊证据理论从元动作运动关系和结构关系的角度构建了具有不确定信息的多准则综合关联关系的模糊度量，有效解决了领域内多专家评价时出现的信息不完整或信息缺失等问题。下一步将在此基础上优化方法，分析不同元动作之间的关联性，并进行方法对比验证。

2）利用FMA分解得到最小运动单元——元动作，将其作为研究对象，有利于减轻研究工作量，并且将元动作运动关系作为影响重要度的因素，能够有效解决关联准则分析不完整的问题，也为下一步关键零件的分析奠定了基础。

3）以数控转台为例，对比验证了所提出方法的可行性。基于模糊关联分析实现了元动作关联关系作用下的关键元动作识别，有效解决了产品模糊信息转化和传递的问题，改善了由经验不足或精确知识缺乏带来的不确定。该方法还可以用于不同质量特性耦合关系的识别，以确定机械产品的关键质量特性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周宏根，景旭文，高安丽.

柴油机关键零件工艺规划支持系统研究

［J］.组合机床与自动化加工技术，2009（6）：84-87. doi：10.3969/j.issn.1001-2265.2009.06.024

DOI:10.3969/j.issn.1001-2265.2009.06.024 [本文引用: 1]

ZHOU

Hong-gen

， JING

Xu-wen

， GAO

An-li

The research on process planning and supporting system of the diesel engine critical parts

［J］. Modular Machine Tool & Automatic Manufacturing Technique， 2009（6）： 84-87.

[2]

宫中伟，莫蓉，杨海成，等.

基于产品开发网络Hub节点的工程变更

［J］.计算机集成制造系统，2012， 18（1）：40-46. doi：10.4028/www.scientific.net/amr.314-316.1607

DOI:10.4028/www.scientific.net/amr.314-316.1607 [本文引用: 1]

GONG

Zhong-wei

， MO

Rong

， YANG

Hai-cheng

， et al.

Engineering change based on Hub nodes of product development network

［J］. Computer Integrated Manufacturing Systems， 2012， 18（1）： 40-46.

[3]

郏维强，刘振宇，刘达新，等.

基于模糊关联的复杂产品模块化设计方法及其应用

［J］.机械工程学报， 2015，51（5）：130-142. doi：10.3901/jme.2015.05.130

JIA

Wei-qiang

， LIU

Zhen-yu

， LIU

Da-xin

， et al.

Modular design method and application for complex product based on fuzzy correlation analysis

［J］. Journal of Mechanical Engineering， 2015， 51（5）： 130-142.

DOI:10.3901/jme.2015.05.130 [本文引用: 1]

[4]

郝丽，莫蓉，魏斌斌，等.

粗糙集理论在关键功能零件识别中的应用

［J］.哈尔滨工业大学学报，2021，53（2）：61-70. doi：10.11918/202001068

HAO

， MO

Rong

， WEI

Bin-bin

， et al.

Application of rough set theory in identification of key functional parts

［J］. Journal of Harbin Institute of Technology， 2021， 53（2）： 61-70.

DOI:10.11918/202001068 [本文引用: 1]

[5]

BELHADJ

， TRIGUI

， BENAMARA

Sub-assembly generation algorithm from a CAD model

［J］. The International Journal of Advanced Manufacturing Technology， 2016， 87： 2829-2840. doi：10.1007/s00170-016-8637-x

[6]

HAN

Zhou-pei

， MO

Rong

， CHANG

Zhi-yong

， et al.

Key assembly structure identification in complex mechanical assembly based on multi-source information

［J］. Assembly Automation， 2017， 37（2）： 208-218. doi：10.1108/aa-09-2016-121

[7]

袁博

基于复杂网络的装配过程关键零件识别和故障传播评价

［D］.武汉：武汉理工大学，2020：42-50. doi：10.29252/jafm.13.03.30747

YUAN

Identification of key parts and evaluation of fault propagation

［D］. Wuhan： Wuhan University， 2020： 42-50.

DOI:10.29252/jafm.13.03.30747 [本文引用: 1]

[8]

李冬英，李梦奇，张根保，等.

元动作装配单元误差源及误差传递模型研究

［J］.机械工程学报，2015， 51（17）：146-155. doi：10.3901/jme.2015.17.146

Dong-ying

， LI

Meng-qi

， ZHANG

Gen-bao

， et al.

Mechanism analysis of deviation sourcing and propagation for meta-action assembly unit

［J］. Journal of Mechanical Engineering， 2015， 51（17）： 146-155.

DOI:10.3901/jme.2015.17.146 [本文引用: 1]

[9]

Hui

， ZHANG

Gen-bao

， RAN

Yan

， et al.

A reliability allocation method for mechanical product based on meta-action

［J］. IEEE Transactions on Reliability， 2020， 69（1）： 373-381. doi：10.1109/tr.2019.2907517

[10]

柯磊

数控机床基于元动作的故障溯源与分析技术研究

［D］.重庆：重庆大学，2019：19-27.

Lei

Research on fault trace and analysis technology of NC machine tool based on meta action

［D］. Chong-qing： Chongqing University， 2019： 19-27.

[11]

CHEN

Yi-fan

， ZHANG

Gen-bao

， RAN

Yan

Risk analysis of coupling fault propagation based on meta-action for computerized numerical control （CNC） machine tool

［J］. Complexity， 2019（8）： 1-11. doi：10.1155/2019/3237254

[12]

RAN

Yan

， ZHANG

Gen-bao

， ZHANG

Lian

Quality characteristic association analysis of computer numerical control machine tool based on meta-action assembly uni

［J］ Advances in Mechanical Engineering， 2016， 8（1）： 1-10. doi：10.1177/1687814016629344

[13]

Dong-ying

， ZHANG

Gen-bao

， LI

Meng-qi

， et al.

Assembly reliability modeling technology based on meta-action

［J］. Procedia CIRP， 2015， 27： 207-215. doi：10.1016/j.procir.2015.04.068

[14]

李宇龙，张根保，王勇勤，等.

数控机床基于元动作的FMEA分析技术研究

［J］.湖南大学学报（自然科学版），2019，46（10）：64-75.

Yu-long

， ZHANG

Gen-bao

， WANG

Yong-qin

， et al.

Research on FMEA analysis technology based on meta-action for numerical control machine tool

［J］. Journal of Hunan University （Natural Sciences）， 2019， 46（10）： 64-75.

[15]

WANG

Xin

， LUO

， SERGIO

Application of service modular design based on a fuzzy design structure matrix： A case study from the mining industry

［J］. Mathematical Problems in Engineering， 2021： 1-19. doi：10.1155/2021/5067092

[16]

FANG

Ming

， LIU

Hong-wei

A Research on the Reliability allocation of complex equipment based on improved fuzzy analytic hierarchy process

［C］//2013 International Conference on Industrial Engineering and Management Science （ICIEMS 2013）， Shanghai， China， 2013-09-28.

[17]

黄智力，罗键.

三角模糊数型不确定多指标决策的可能度关系法

［J］.控制与决策，2015，30（8）： 1365-1371.

HUANG

Zhi-li

， LUO

Jian

Possibility degree relation method for triangular fuzzy number-based uncertain multi-attribute decision making

［J］. Control and Decision， 2015， 30（8）： 1365-1371.

[18]

陈一凡，张根保，冉琰，等.

面向元动作的机械传动系统可靠性分配方法

［J］.中国机械工程，2021，32（17）：2032-2039. doi：10.3969/j.issn.1004-132X.2021.17.003