半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] 。但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] 。性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] 。
在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] 。因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] 。目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究。邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估。Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证。李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法。徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测。然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差。Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型。该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量。但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度。
针对上述问题,笔者拟建立一种基于双方差随机过程的半导体激光器性能退化评估方法,以评估其寿命。首先,同时考虑半导体激光器性能退化数据中的固有随机误差和测量随机误差,并采用自相关时间序列过程来表征测量随机误差项,建立其性能退化模型以及模型未知参数的极大似然估计方法;然后,基于首达时的概念推导失效时间分布函数和概率密度函数的解析表达式,以对半导体激光器进行可靠性评估与寿命预测。最后,通过半导体激光器的寿命评估工程实例来验证所提出方法的适用性和有效性。
1 半导体激光器性能退化模型构建
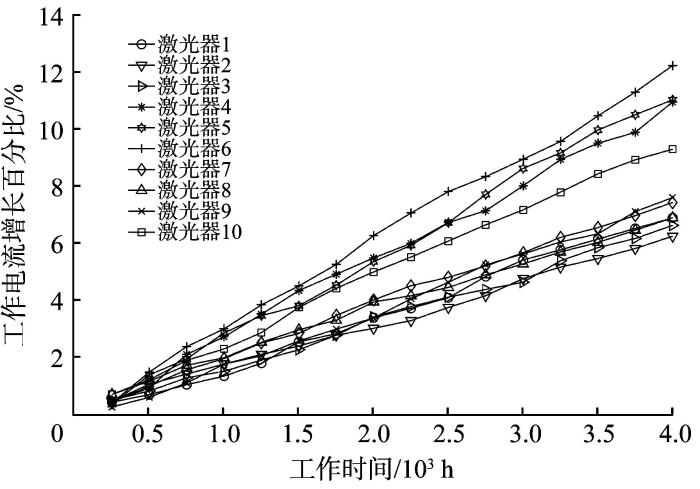
图1 所示为测量得到的恒定输出功率下10个GaAs激光器的工作电流增长百分比,测量间隔时间为250 h,共试验4 000 h[8 ] 。由图1 可知,GaAs激光器的工作电流增长百分比随时间递增,当其达到失效阈值时,该激光器即被认定为失效。
图1
图1
恒定输出功率下不同GaAs激光器的工作电流增长百分比
Fig.1
Percentage increase of working current of different GaAs lasers at constant output power
将工作电流增长百分比看作半导体激光器的性能参数,令Y t t Y t , t ≥ 0 图1 中可以看出,半导体激光器的性能退化量Y t t
Y t = a + b t + ε t + e t
式中:a 为初始性能退化量,由图1 可知初始性能退化量一般为0,则可假设a = 0 b b μ b σ b 2 σb 为与性能退化率相关的扩散系数)的正态分布的随机变量,即b ~ N μ b , σ b 2 ε t e t
对于固有随机误差项ε t [15 ] :
1)对于任意n 0 < t 1 < t 2 < … < t n t 1 ε t 1 ~ N 0 , σ 2 t 1 σ
2)对于任意测量时刻t i > t j ε t i - ε t j σ 2 t i - t j ε t i - ε t j ~ N 0 , σ 2 t i - t j i , j = 1 , 2 , … , n
3)初始固有随机误差ε t 1 ε t 2 - ε t 1 ε t 3 - ε t 2 ε t n - ε t n - 1
对于测量随机误差项e t [16 ] :
1)对于任意n 个测量时刻0<t 1 <t 2 <…<tn ,测量误差时间序列e t i i = 1,2 , ⋯ , n
e t i = ξ i , i = 1 ρ e t i - 1 + ξ i , i ≥ 2
式中:ρ ρ < 1 ζ i ζ i ~ i i d N 0 , σ e 2 σe 为与测量误差相关的扩散系数。
2)根据定义推导得到随机测量误差项e t
E e t = 0 E e 2 t = σ e 2 ∑ i = 0 n ρ 2 i
为便于分析,令γ 0 = σ e 2 ∑ i = 0 n ρ 2 i ρ < 1 γ 0 = σ e 2 / 1 - ρ 2 [16 ] 。
3)对于任意测量时刻t i > t j i , j = 1 , 2 , … , n C o v e t i , e t j = ρ i - j γ 0 e t i i = 1,2 , … , n Q
γ 0 1 ρ ρ 2 ⋯ ρ n - 1 ρ 1 ρ ⋯ ρ n - 2 ρ 2 ρ 1 ⋯ ρ n - 3 ⋮ ⋮ ⋮ ⋮ ρ n - 1 ρ n - 2 ρ n - 3 ⋯ 1
另外,假设性能退化率b ε t e t
2 半导体激光器性能退化模型未知参数估计
令Θ = μ b σ b 2 σ 2 σ e 2 ρ
假设有m 个半导体激光器参与寿命试验,第k 个激光器在预定的nk 个测量时刻t k 1 < t k 2 < … < t k n k y k 1 < y k 2 < … < y k n k y k j = Y t k j k 个激光器在第j t k j k = 1,2 , … , m j = 1,2 , … , n k
令y k = y k 1 y k 2 … y k n k T t k = t k 1 t k 2 … t k n k T y k n k y k ~ N μ b t k , Σ k Σ k = σ b 2 t k t k T + σ 2 Ω k + γ 0 Q k
Ω k = t 1 t 1 ⋯ t 1 t 1 t 2 ⋯ t 2 ⋮ ⋮ ⋮ t 1 t 2 ⋯ t n k
Q k = 1 ρ ρ 2 ⋯ ρ n k - 1 ρ 1 ρ ⋯ ρ n k - 2 ρ 2 ρ 1 ⋯ ρ n k - 3 ⋮ ⋮ ⋮ ⋮ ρ n k - 1 ρ n k - 2 ρ n k - 3 ⋯ 1
为简化估计过程,重新定义参数,令σ ˜ = σ / σ b γ ˜ 0 = γ 0 / σ b Ψ k = t k t k T + σ ˜ 2 Ω k + γ ˜ 0 Q k Σ k = σ b 2 Ψ k Θ = μ b σ b 2 σ ˜ 2 γ ˜ 0 ρ y = y 1 y 2 … y m
𝓁 Θ y = - N 2 l n 2 π - N 2 l n σ b 2 - 1 2 ∑ k = 1 m l n Ψ k -
1 2 σ b 2 ∑ k = 1 m y k - μ b t k T Ψ k - 1 y k - μ b t k
N = ∑ k = 1 m n k
分别求式(5)关于参数μ b σ b 2
∂ 𝓁 Θ y ∂ μ b = ∑ k = 1 m t k T Ψ k - 1 y k - μ b t k
∂ 𝓁 Θ y ∂ σ b 2 = - N 2 σ b 2 + 1 2 σ b 4 ∑ k = 1 m y k - μ b t k T Ψ k - 1 y k - μ b t k
分别令式(6)和式(7)等于0,联立两式可得参数μ b σ b 2
μ ̂ b = ∑ k = 1 m t k T Ψ k - 1 t k - 1 ∑ k = 1 m t k T Ψ k - 1 y k
σ ̂ b 2 = 1 N ∑ k = 1 m y k - μ ̂ b t k T Ψ k - 1 y k - μ ̂ b t k
将式(8)和式(9)代入式(5),可得关于未知参数矩阵Θ ˜ = σ ˜ 2 γ ˜ 0 ρ
𝓁 Θ ˜ y = - N 2 l n 2 π + 1 - N 2 l n σ ̂ b 2 - 1 2 ∑ k = 1 m l n Ψ k
首先,通过多维搜索算法对式(10)进行最大化处理,可得未知参数矩阵Θ ˜ Θ ˜ ̂ = σ ˜ ̂ 2 γ ˜ ̂ 0 ρ ̂ 式(8)和式(9)可得参数μ b σ b 2 μ ̂ b σ ̂ b 2 σ 2 γ 0 σ ̂ 2 = σ ̂ b 2 σ ˜ ̂ 2 γ ̂ 0 = σ ̂ b 2 γ ˜ ̂ 0 σ e 2 σ ̂ e 2 = γ ̂ 0 1 - ρ ̂ 2
在进行多维优化之前,需给定参数的取值区间。本文通过对半导体激光器性能退化数据进行预处理,得到各参数的初始估计值,并将其作为对应参数取值区间选取的依据,从而提高参数估计的效率。获取参数初始估计值的具体步骤如下。
1)结合半导体激光器的性能退化数据y = y 1 y 2 … y m J MSE :
J M S E = ∑ k = 1 m y k - b k t k T y k - b k t k
2)根据最小二乘法,通过最小化均方误差来获取m b ̂ 1 , b ̂ 2 , … , b ̂ m μ b σ b
μ ̂ b = 1 m ∑ k = 1 m b ̂ k σ ̂ b = ∑ k = 1 m b ̂ k - μ ̂ b 2 m - 1
3)将b ̂ 1 , b ̂ 2 , … , b ̂ m 式(13),并通过最大化处理来获取参数σ 2 、 σ e 2 和 ρ
𝓁 σ 2 , σ e 2 , ρ = - N 2 l n 2 π - 1 2 ∑ k = 1 m l n Σ k -
1 2 ∑ k = 1 m y k - b k t k T Σ k - 1 y k - b k t k
通过上述3个步骤得到未知参数矩阵Θ = μ b σ b 2 σ 2 σ e 2 ρ σ ˜ γ ˜ 0 式(10)进行最大化处理,并依次代入式(8)和式(9),便可得到半导体激光器性能退化模型参数的极大似然估计结果。
3 半导体激光器寿命评估
为了对半导体激光器的寿命进行评估,需确定其可靠度分布函数。令T T X (t )首次达到失效阈值D f [15 ,17 ] ,即有:
T = i n f t : X t ≥ D f X 0 < D f
X t = a + b t + ε t
由文献[14 ]可知,当b N μ b , σ b 2 T F T t f T t
F T t = Φ μ b t - D f σ b 2 t 2 + σ 2 t + e x p 2 μ b D f σ 2 + 2 σ b 2 D f 2 σ 4 × Φ - σ 2 μ b t + 2 σ b 2 t + σ 2 D f σ 2 σ b 2 t 2 + σ 2 t
f T t = D f 2 2 π t 3 σ b 2 t + σ 2 e x p - D f - μ b t 2 2 t σ b 2 t + σ 2
由此可得,半导体激光器的可靠度分布函数RT (t )可表示为:
R T t = 1 - F T t = Φ D f - μ b t σ b 2 t 2 + σ 2 t - e x p 2 μ b D f σ 2 + 2 σ b 2 D f 2 σ 4 ×
Φ - σ 2 μ b t + 2 σ b 2 t + σ 2 D f σ 2 σ b 2 t 2 + σ 2 t
t M T T F = E T = ∫ 0 + ∞ t f T t d t = D f σ b 2 e x p - μ b 2 2 σ b 2 ∫ 0 μ b e x p u 2 2 σ b 2 d u =
2 D f σ b D μ b 2 σ b
D z = e x p - z 2 ∫ 0 z e x p x 2 d x
式中:E T T D z
根据道森积分的性质可知,当z D z ≈ 1 2 z μ b ≫ σ b
t M T T F = E T ≈ D f μ b
在实际工程应用中,人们常常比较关心产品失效时间的百分位值,即可靠寿命或安全寿命。给定失效阈值D f t R R
R T t R = R
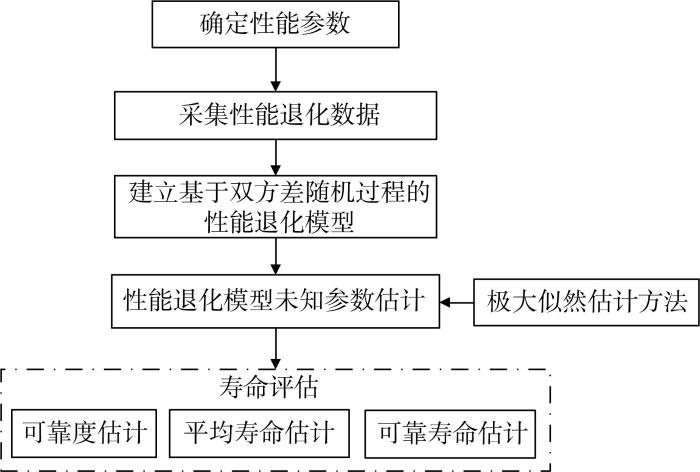
通过求解式(20)可以得到半导体激光器可靠寿命的估计值t ̂ R = R T - 1 R R T t t R 图2 所示。
图2
图2
半导体激光器寿命评估流程
Fig.2
Lifetime evaluation process of semiconductor laser
4 工程实例验证
为了验证本文所提出方法的适用性和有效性,结合图1 所示的GaAs激光器性能退化数据,进行工程实例分析。为了验证考虑测量误差间自相关性和同时考虑固有随机误差和测量随机误差的必要性,用M0表示本文构建的GaAs激光器性能退化模型,并将文献[14 ]中的模型和文献[11 ,13 ]中的模型看作对比模型,分别为M1和M2。
分别利用模型M0、M1和M2对上述GaAs激光器性能退化数据进行统计分析,得到各模型未知参数的极大似然估计值。为了评价各性能退化模型的拟合效果,选用对数似然函数(Log-likelihood function,Log-LF)值和赤池信息量准则(Akaike information criterion, AIC)值这2个指标来进行评价。由极大似然估计方法的定义可知,极大似然估计值越大,则性能退化模型的拟合效果越好。本文模型M0的未知参数比模型M1和M2多,其求解复杂度较大。为了验证该模型提出的必要性及其性能,进一步采用AIC值来进行对比。AIC值A 定义为[18 ] :
A = - 2 L m a x + 2 q
式中:L m a x q 为性能退化模型未知参数的个数。
AIC值不仅考虑了模型拟合的极大似然估计值,而且能够同时考虑模型未知参数的个数q
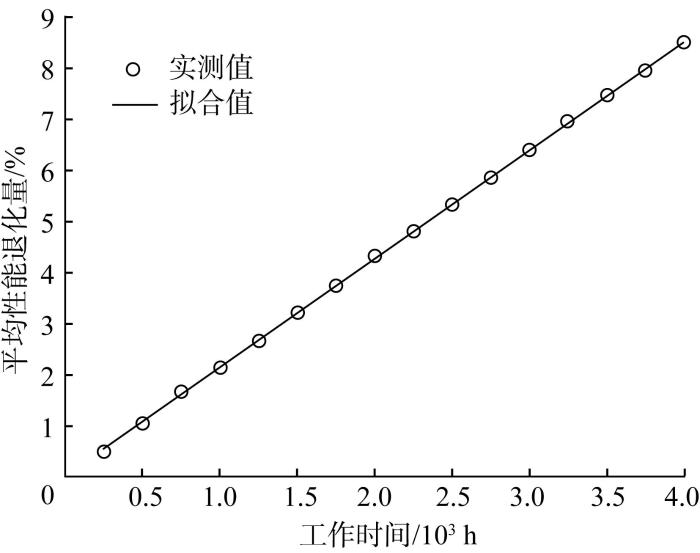
性能退化模型M0、M1和M2的未知参数估计值及其对应的Log-LF值和AIC值如表1 所示。从表1 中可以看出,无论是从Log-LF值还是从AIC值看,本文模型M0的拟合效果都要优于模型M1和M2。此外,从表1 中还可以看出,一旦忽略测量误差间的自相关性,本文模型M0将变为模型M2,从而导致寿命评估结果不准确,最终造成错误的维修决策,增大了事故率。图3 所示为基于本文模型M0拟合得到的GaAs激光器平均性能退化曲线。从图中可以很明显地看出,拟合得到的平均性能退化量与实际测得的平均性能退化量符合较好,进一步证明了本文方法的有效性。
图3
图3
基于模型M0拟合得到的GaAs激光器平均性能退化曲线
Fig.3
Average performance degradation curve of GaAs laser fitted by the model M0
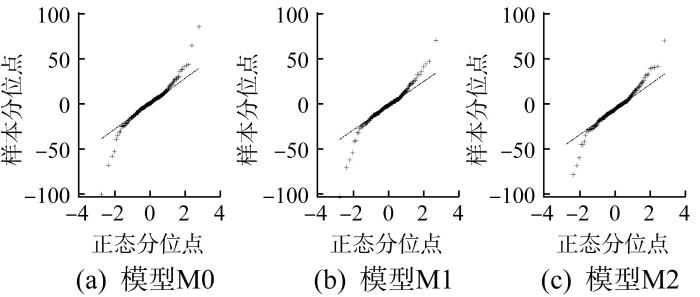
为了更进一步验证本文模型的拟合效果,结合GaAs激光器的性能退化数据和表1 所示的参数估计结果,得到3个性能退化模型的分位数-分位数图(简称为Q-Q图),如图4 所示。由定义可知,Q-Q图的线性关系越强表明模型的拟合效果越好。由图4 可以看出,与模型M1和M2相比,本文模型M0的拟合效果更好。
图4
图4
不同GaAs激光器性能退化模型的Q-Q图对比
Fig.4
Comparison of Q-Q plot of different GaAs laser performance degradation models
假设GaAs激光器的性能退化失效阈值D f = 30 % 表1 中各模型未知参数的估计结果,计算得到激光器在可靠度R = 0.99 t 0.99 表2 所示。由表2 可以看出,基于模型M1和M2得到的GaAs激光器可靠寿命估计结果偏大,可能导致事后维修或更换,增大了事故率。
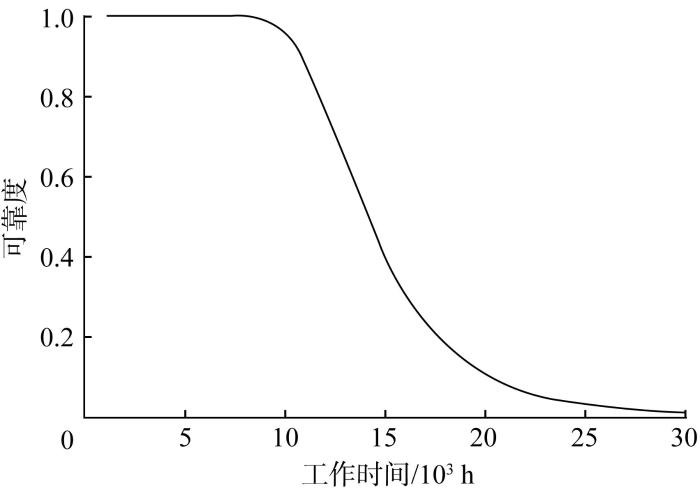
根据GaAs激光器的可靠寿命,利用式(17)计算其可靠度,得到可靠度估计曲线,用于评价其可靠性。基于本文模型M0计算得到GaAs激光器的可靠度估计曲线,结果如图5 所示。
图5
图5
基于模型M0的GaAs激光器可靠度估计曲线
Fig.5
Reliability estimation curve of GaAs laser based on model M0
5 结 论
1) 建立了基于双方差随机过程的半导体激光器性能退化评估方法,用于评估其寿命。该方法同时考虑了半导体激光器性能退化数据中的固有随机误差和测量随机误差。
2) 半导体激光器的连续测量数据的误差为时间序列数据,其存在的自相关性不容忽视,有必要在构建性能退化模型时考虑。
3) 所提出的评估方法能够更加准确地描述半导体激光器的性能退化过程,其拟合效果较好,寿命评估精度较高且适用性较强。
参考文献
View Option
[2]
[本文引用: 1]
WANG Wen-zhi JING Hong-qi QI Qiong et al Reliability test and failure analysis of high power semicounductor laser
[J]. Chinese Journal of Luminescence , 2017 , 38 (2 ): 165 -169 .
DOI:10.3788/fgxb20173802.0165
[本文引用: 1]
[3]
[本文引用: 1]
ZHANG Jian-ping ZHANG Bei Rapid life assessment model of optoelectronic devices based on three-parameter Weibull function method and its applications
[J]. Electronic Components and Materials , 2021 , 40 (2 ): 137 -143 .
DOI:10.14106/j.cnki.1001-2028.2021.1106
[本文引用: 1]
[4]
LEI Y LI N GUO L et al Machinery health prognostics: a systematic review from data acquisition to RUL prediction
[J]. Mechanical Systems and Signal Processing , 2018 , 104 : 799 -834 . doi:10.1016/j.ymssp.2017. 11.016
[本文引用: 1]
[5]
GAO H CUI L DONG Q Reliability modeling for a two-phase degradation system with a change point based on a Wiener process
[J]. Reliability Engineering & System Safety , 2020 , 193 : 106601 . doi:10.1016/j.ress.2019.106601
[本文引用: 1]
[6]
[本文引用: 1]
NIE Zhi-qiang WANG Ming-pei SUN Yu-bo et al Thermally accelerated aging test of conduction-cooled-packaged high power diode laser bar in CW mode
[J]. Chinese Journal of Luminescence , 2019 , 40 (9 ): 1136 -1145 .
DOI:10.3788/fgxb20194009.1136
[本文引用: 1]
[7]
[本文引用: 1]
YUAN Qing-he JING Hong-qi ZHANG Qiu-yue et al Development and applications of GaAs-based near-infrared high power semiconductor lasers
[J]. Laser & Optoelectronics Progress , 2019 , 56 (4 ): 040003 .
DOI:10.3788/lop56.040003
[本文引用: 1]
[8]
MEEKER W Q ESCOBAR L A Statistical methods for reliability data [M]. 2nd ed . New York : John Wiley & Sons , 2021 : 254 -256 .
[本文引用: 2]
[9]
MEEKER W HONG Y ESCOBAR L Encyclopedia of statistical sciences [M]. New York : John Wiley & Sons , 2011 : 1 -27 .
[本文引用: 1]
[11]
SU C ZHANG Y System reliability assessment based on Wiener process and competing failure analysis
[J]. Journal of Southeast University (English Edition) , 2010 , 26 (4 ): 554 -557 . doi:10.3321/j.issn:1000-1328. 2006.03.044
[本文引用: 2]
[13]
[本文引用: 2]
XU Ting-xue WANG Hao-wei ZHANG Xin Application of EM algorithm to estimate hyper parameters of the random parameters of Wiener process
[J]. Systems Engineering and Electronics , 2015 , 37 (3 ): 707 -712 .
DOI:10.3969/j.issn.1001-506X.2015.03.36
[本文引用: 2]
[14]
PENG C Y TSENG S T Mis-specification analysis of linear degradation models
[J]. IEEE Transactions on Reliability , 2009 , 58 (3 ): 444 -455 . doi:10.1109/tr.2009. 2026784
[本文引用: 3]
[15]
COX D R MILLER H D WEISS G et al The theory of stochastic processes [M]. New York : Routledge , 1965 : 81 -83 . doi:10.1063/1.3047872
[本文引用: 2]
[16]
MADSEN H Time series analyses [M]. Boca Raton : Chapman and Hall/CRC , 2007 : 103 -121 .
[本文引用: 2]
[17]
TANG S YU C WANG X et al Remaining useful life prediction of lithium-ion batteries based on the Wiener process with measurement error
[J]. Energies , 2014 , 7 (2 ): 520 -547 . doi:10.3390/en7020520
[本文引用: 1]
[18]
AKAIKE H A new look at the statistical model identification
[J]. IEEE Transactions on Automatic Control , 1974 , 19 (6 ): 716 -723 . doi:10.1109/tac.1974.1100705
[本文引用: 1]
大功率半导体激光器研究进展
1
2015
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
大功率半导体激光器研究进展
1
2015
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
大功率半导体激光器可靠性研究和失效分析
1
2017
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
大功率半导体激光器可靠性研究和失效分析
1
2017
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
基于三参数威布尔函数法的光电器件寿命快速评估模型及其应用
1
2021
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
基于三参数威布尔函数法的光电器件寿命快速评估模型及其应用
1
2021
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
Machinery health prognostics: a systematic review from data acquisition to RUL prediction
1
2018
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
Reliability modeling for a two-phase degradation system with a change point based on a Wiener process
1
2020
... 半导体激光器已被广泛应用于工业、通信、医疗和国防等领域,在实际应用中,可靠性和寿命是评估其性能的重要技术指标[1 -2 ] .但是,半导体激光器具有可靠性高、寿命长的特点,这给以失效时间为基础的传统可靠性分析方法带来了巨大的挑战[3 ] .性能退化建模与分析是解决该类产品可靠性和寿命评估难题的有效途径之一,也是目前可靠性工程研究的热点和难点[4 -5 ] . ...
传导冷却高功率半导体激光器单巴器件CW工作模式下的热加速寿命试验
1
2019
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
传导冷却高功率半导体激光器单巴器件CW工作模式下的热加速寿命试验
1
2019
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
砷化镓基近红外大功率半导体激光器的发展及应用
1
2019
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
砷化镓基近红外大功率半导体激光器的发展及应用
1
2019
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
2
2021
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
... 图1 所示为测量得到的恒定输出功率下10个GaAs激光器的工作电流增长百分比,测量间隔时间为250 h,共试验4 000 h[8 ] .由图1 可知,GaAs激光器的工作电流增长百分比随时间递增,当其达到失效阈值时,该激光器即被认定为失效. ...
1
2011
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
基于性能退化数据的可靠性评估
1
2006
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
基于性能退化数据的可靠性评估
1
2006
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
System reliability assessment based on Wiener process and competing failure analysis
2
2010
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
... 为了验证本文所提出方法的适用性和有效性,结合图1 所示的GaAs激光器性能退化数据,进行工程实例分析.为了验证考虑测量误差间自相关性和同时考虑固有随机误差和测量随机误差的必要性,用M0表示本文构建的GaAs激光器性能退化模型,并将文献[14 ]中的模型和文献[11 ,13 ]中的模型看作对比模型,分别为M1和M2. ...
基于GaAs激光器性能退化的可靠性度量方法
1
2012
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
基于GaAs激光器性能退化的可靠性度量方法
1
2012
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
EM算法在Wiener过程随机参数的超参数值估计中的应用
2
2015
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
... 为了验证本文所提出方法的适用性和有效性,结合图1 所示的GaAs激光器性能退化数据,进行工程实例分析.为了验证考虑测量误差间自相关性和同时考虑固有随机误差和测量随机误差的必要性,用M0表示本文构建的GaAs激光器性能退化模型,并将文献[14 ]中的模型和文献[11 ,13 ]中的模型看作对比模型,分别为M1和M2. ...
EM算法在Wiener过程随机参数的超参数值估计中的应用
2
2015
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
... 为了验证本文所提出方法的适用性和有效性,结合图1 所示的GaAs激光器性能退化数据,进行工程实例分析.为了验证考虑测量误差间自相关性和同时考虑固有随机误差和测量随机误差的必要性,用M0表示本文构建的GaAs激光器性能退化模型,并将文献[14 ]中的模型和文献[11 ,13 ]中的模型看作对比模型,分别为M1和M2. ...
Mis-specification analysis of linear degradation models
3
2009
... 在恒定输出功率下,半导体激光器的工作电流会随时间增大,当达到失效阈值时其将丧失预期功能,即被认定为失效[6 -7 ] .因此,半导体激光器的失效过程可看作性能退化过程[8 -9 ] .目前,已有很多学者针对基于性能退化的半导体激光器可靠性评估进行了研究.邓爱民等[10 ] 提出了基于退化轨迹与基于性能退化量分布的可靠性评估方法,并对半导体激光器进行了可靠性评估.Su等[11 ] 考虑到产品突发失效和退化失效并存的情况,提出了基于Wiener过程的性能退化模型,并以GaAs(砷化镓)激光器为例进行了可靠性评估验证.李玲玲等[12 ] 针对利用传统的基于失效时间的可靠性分析方法评估GaAs激光器可靠性精度不高的问题,提出了基于性能退化的可靠性度量方法.徐廷学等[13 ] 建立了基于Wiener过程的激光器性能退化模型,并对GaAs激光器的剩余寿命进行了预测.然而,上述方法在对半导体激光器进行性能退化建模时,均只考虑了其性能退化数据中的固有随机误差或测量随机误差.Peng等[14 ] 在分析半导体激光器性能退化数据时发现,其性能退化过程不仅受内部失效机理固有随机性的影响,还受由人为因素、测量仪器等引起的测量随机误差的影响,为此建立了一种同时考虑固有随机误差和测量随机误差的性能退化模型.该方法在考虑测量随机误差时,假设其为独立同分布的正态随机变量.但是,由于半导体激光器性能退化数据为时间序列数据,连续测量数据的误差之间不可避免地会存在自相关性且不容忽视,否则会严重影响可靠性评估的精度. ...
... 由文献[14 ]可知,当b N μ b , σ b 2 T F T t f T t
... 为了验证本文所提出方法的适用性和有效性,结合图1 所示的GaAs激光器性能退化数据,进行工程实例分析.为了验证考虑测量误差间自相关性和同时考虑固有随机误差和测量随机误差的必要性,用M0表示本文构建的GaAs激光器性能退化模型,并将文献[14 ]中的模型和文献[11 ,13 ]中的模型看作对比模型,分别为M1和M2. ...
2
1965
... 对于固有随机误差项ε t [15 ] : ...
... 为了对半导体激光器的寿命进行评估,需确定其可靠度分布函数.令T T X (t )首次达到失效阈值D f [15 ,17 ] ,即有: ...
2
2007
... 对于测量随机误差项e t [16 ] : ...
... 为便于分析,令γ 0 = σ e 2 ∑ i = 0 n ρ 2 i ρ < 1 γ 0 = σ e 2 / 1 - ρ 2 [16 ] . ...
Remaining useful life prediction of lithium-ion batteries based on the Wiener process with measurement error
1
2014
... 为了对半导体激光器的寿命进行评估,需确定其可靠度分布函数.令T T X (t )首次达到失效阈值D f [15 ,17 ] ,即有: ...
A new look at the statistical model identification
1
1974
... 分别利用模型M0、M1和M2对上述GaAs激光器性能退化数据进行统计分析,得到各模型未知参数的极大似然估计值.为了评价各性能退化模型的拟合效果,选用对数似然函数(Log-likelihood function,Log-LF)值和赤池信息量准则(Akaike information criterion, AIC)值这2个指标来进行评价.由极大似然估计方法的定义可知,极大似然估计值越大,则性能退化模型的拟合效果越好.本文模型M0的未知参数比模型M1和M2多,其求解复杂度较大.为了验证该模型提出的必要性及其性能,进一步采用AIC值来进行对比.AIC值A 定义为[18 ] : ...