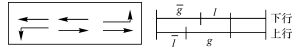干线协调控制的基本方法是通过对主路沿线多个交叉口协调控制, 使行驶车辆尽可能不停车通过.大量研究表明, 与单点控制相比, 干线协调控制可以得到较好的控制效果, 同时可以有效减少车辆延误、停车次数和尾气排放, 提高路网的通行效率, 对于交通状况的整体改善具有重要意义[1].
目前, 干线协调控制方法主要有最小延误法和最大绿波带法.与最小延误法相比, 最大绿波带法所需的条件较少, 可以更加直观地反映出协调控制效果, 应用较广泛, 国内外进行了大量研究.基于半整数算法, Messer等[2]提出多相位相序绿波带协调控制优化方法.基于混合整数线性规划, Little[3]建立经典MAXBAND模型, 可以同时优化周期时长、相序、相位差和绿波速度, 使带宽达到最大.基于路网层面, Chang等[4]对MAXBAND进行扩展, 提出协调控制模型MAXBAND-86.考虑路段交通的需求, Gartner等[5]建立多带宽协调模型MULTIBAND, 允许不同路段不同带宽, 以满足信号控制实时性的要求.随后, Stamatiadis等[6]进行完善, 提出MULTIBAND-96模型, 设计优化算法[7], 大大缩减了模型运算时间.针对交通流的离散特性, Lu等[8]将Robertson模型引入MAXBAND, 得到新的协调控制模型.陈宁宁等[9]分析下游交叉口排队消散时间与相位差的函数关系, 建立红灯排队消散时间模型, 结合MAXBAND模型, 降低了绿波带受排队消散过程的影响.通过分析相邻交叉口车流驶离与相位差的关系, Wang等[10]结合车辆动态排队消散时间与MAXBAND模型, 提出改进的绿波带模型, 增加了有效带宽比例, 降低了干线车辆延误.面向双向不同带宽的需求, 卢凯等[11]引入带宽分配影响因子与带宽需求比例系数, 分别对MAXBAND和MULTIBAND模型进行优化, 得到绿波协调控制优化模型.刘小明等[12]考虑路口协调相位不同方向放行重要程度, 以绿波带宽内连续通过车辆数最多为控制目标, 提出考虑红灯排队消散的绿波带搜索算法, 实用性更强.针对MULTIBAND模型存在绿波带求解范围小和位置不合理问题, 唐克双等[13]进行改进, 取消绿波带中心对称, 增加绿波带位置约束, 取得了较好的效果.Zhang等[14]提出改进的非对称多带宽绿波带模型AM-BAND, 有效利用绿灯时间, 得到了更大的绿波带宽.Ye等[15]考虑排队清空时间和非协调相位相序优化, 提出双向绿波协调控制模型.
虽然现有研究对MAXBAND和MULTIBAND模型进行了改进, 但仍然存在不足.现有的绿波干线协调控制模型所求得的绿波带大多沿着中心线对称, 容易造成绿灯时间利用不充分;此外大多忽略车辆排队过程, 排队消散时间大多根据人为经验指定, 主观性较强.针对上述问题, 基于现有的研究成果, 结合混合整数线性规划, 本文提出基于MULTIBAND模型改进的干线协调控制方法.首先优化绿波带形式;其次, 分析上下游交叉口车辆排队, 建立红灯排队消散时间模型;最后, 对模型进行验证.结果表明, 与MULTIBAND模型相比, 本文算法能够得到更大的绿波带宽, 且车辆延误和停车次数更小, 证明了本文算法的有效性.
1 MULTIBAND模型
通常, 双向绿波控制适用于交叉口间距适中的未饱和干线系统, 以保证干线行驶车辆具有相对稳定的速度, 避免因流量过大或离散导致行驶速度降低.研究表明, 当交通流处于饱和状态时, 双向绿波协调难以发挥效用[3].本文针对非饱和干线系统进行研究.
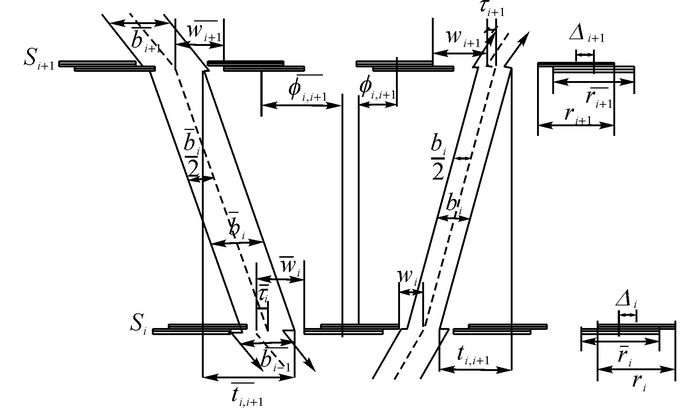
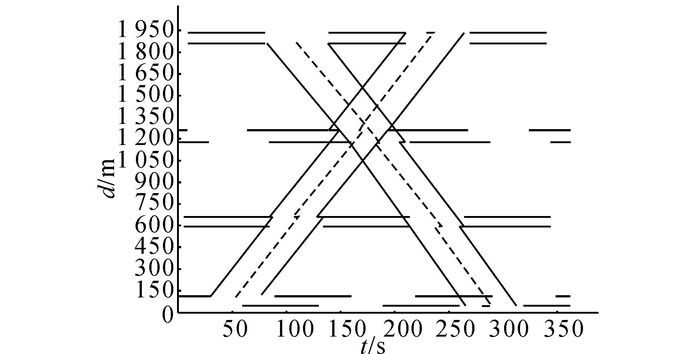
假设一干线协调控制系统包含n个交叉口, 控制方式为定时控制.干线方向车流分为上行和下行两股, 定义从交叉口i至i+1方向为上行方向, 反之为下行方向;干线方向直行车流所在相位为协调相位.经典的MULTIBAND模型时距图[6]如图 1所示.
图 1中, bi( $\overline {{b_i}} $ )为交叉口i(1, 2, …, n)与i+1之间上行(下行)方向绿波带宽度;ri( $\overline {{r_i}} $ )为交叉口i上行(下行)红灯时长;wi( $\overline {{w_i}} $ )为干扰变量, 表示上行(下行)交叉口i处红灯结束(开始)时刻到绿波带中心线的时间;τi( $\overline {{\tau _i}} $ )为交叉口i上行(下行)排队清空时间, 用来清空红灯期间主路上的排队车辆; ${\phi _{i,i + 1}}\left( {\overline {{\phi _{i,i + 1}}} } \right)$ 为上行(下行)交叉口i与i+1之间的相对相位差, 指交叉口i上行(下行)方向红灯中点到最近的交叉口i+1上行(下行)红灯中点的时间, 若交叉口i+1红灯时间在交叉口i红灯时间的右侧(左侧), 则值为正, 否则为负;Δi为红灯时长ri中心到最近的 $\overline {{r_i}} $ 中心的距离, 当ri中心在 $\overline {{r_i}} $ 右侧时, 取值为正;ti( $\overline {{t_i}} $ )为交叉口i到i+1(i+1到i)的行程时间;mi为整数变量.
MULTIBAND模型可以通过二进制变量δi和 $\overline {{\delta _i}} $ 实现对干线左转相位相序的优化, 共存在4种相位组合方式, 如表 1所示.其中, li( $\overline {{l_i}} $ )为交叉口i处上行(下行)左转相位的绿灯时长.
MULTIBAND模型允许不同交叉口之间的绿波带宽度不同, 决策变量为:bi、 $\overline {{b_i}} $ 、z、wi、 $\overline {{w_i}} $ 、ti、 $\overline {{t_i}} $ 、δi、 $\overline {{\delta _i}} $ 和mi, 目标函数如下:
|
$
\max B = \frac{1}{{n - 1}}\sum\limits_{i = 1}^{n - 1} {\left( {{a_i}{b_i} + {{\bar a}_i}{{\bar b}_i}} \right)} .
$
|
(1) |
|
$
{a_i} = {\left( {\frac{{{V_i}}}{{{S_i}}}} \right)^p},\overline {{a_i}} = {\left( {\frac{{\overline {{V_i}} }}{{{{\bar S}_i}}}} \right)^p}.
$
|
(2) |
式中:ai(ai)为交叉口i处上行(下行)绿波带宽比例系数;Vi( $\overline {{V_i}} $ )为交叉口i处上行(下行)流量;Si( $\overline {{S_i}} $ )为交叉口i处上行(下行)饱和流量;p为指数, 通常取值为0, 1, 2, 4, 可以根据实际情况进行确定.
模型的约束条件如下.
|
$
\left( {1 - {k_i}} \right){{\bar b}_i} \ge \left( {1 - {k_i}} \right){k_i}{b_i};i = 1,2, \cdots ,n - 1.
$
|
(3) |
|
$
1/{C_{\max }} \le z \le 1/{C_{\min }}.
$
|
(4) |
|
$
\left. \begin{array}{l}
{b_i}/2 \le {w_i} \le \left( {1 - {r_i}} \right) - {b_i}/2,\\
{b_i}/2 \le {w_{i + 1}} + {\tau _{i + 1}} \le \left( {1 - {r_{i + 1}}} \right) - {b_i}/2,\\
{{\bar b}_i}/2 \le {{\bar w}_i} - {{\bar \tau }_i} \le \left( {1 - {{\bar r}_i}} \right) - {{\bar b}_i}/2,\\
{{\bar b}_i}/2 \le \overline {{w_{i + 1}}} \le \left( {1 - \overline {{r_{i + 1}}} } \right) - {{\bar b}_i}/2;i = 1,2, \cdots ,n - 1.
\end{array} \right\}
$
|
(5) |
|
$
\begin{array}{l}
\left( {{w_i} + \overline {{w_i}} } \right) - \left( {{w_{i + 1}} + \overline {{w_{i + 1}}} } \right) + \left( {{t_i} + \overline {{t_i}} } \right) + {\delta _i}{l_i} + \overline {{\delta _{i + 1}}{l_{i + 1}}} = \\
\left( {{r_{i + 1}} - {r_i}} \right) + \left( {\overline {{\tau _i}} + {\tau _{i + 1}}} \right) + \overline {{\delta _i}} \overline {{l_i}} + {\delta _{i + 1}}{l_{i + 1}} + {m_i};i = 1,\\
2, \cdots ,n - 1.
\end{array}
$
|
(6) |
|
$
\left. \begin{array}{l}
\left( {{d_i}/{f_i}} \right)z \le {t_i} \le \left( {{d_i}/{e_i}} \right)z,\\
\left( {\overline {{d_i}} /\overline {{f_i}} } \right)z \le \overline {{t_i}} \le \left( {\overline {{d_i}} /\overline {{e_i}} } \right)z;i = 1,2, \cdots ,n - 1.
\end{array} \right\}
$
|
(7) |
|
$
\left. \begin{array}{l}
\left( {{d_i}/{h_i}} \right)z \le \left( {{d_i}/{d_{i + 1}}} \right){t_{i + 1}} - {t_i} \le \left( {{d_i}/{g_i}} \right)z,\\
\left( {\overline {{d_i}} /\overline {{h_i}} } \right)z \le \left( {\overline {{d_i}} /\overline {{d_{i + 1}}} } \right)\overline {{t_{i + 1}}} - \overline {{t_i}} \le \left( {\overline {{d_i}} /\overline {{g_i}} } \right)z;\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,n - 2.
\end{array} \right\}
$
|
(8) |
|
$
\left. \begin{array}{l}
{b_i}、\overline {{b_i}} 、z、{w_i}、\overline {{w_i}} 、{t_i}、\overline {{t_i}} \ge 0;\\
{m_i}\;为整数;{\delta _i},\overline {{\delta _i}} \;为\;0/1\;变量.
\end{array} \right\}
$
|
(9) |
式中:ki为上、下行的带宽需求比例, 通常等于上、下行总流量之比;z=1/C为信号频率, 等于周期时长的倒数;Cmin和Cmax分别为信号周期时长的最小值和最大值;di( $\overline {{d_i}} $ )为交叉口i与i+1上行(下行)之间的距离;ei、fi( $\overline {{e_i}} $ 、 $\overline {{f_i}} $ )分别为上行(下行)方向速度的下/上限值;gi、hi( $\overline {{g_i}} $ 、 $\overline {{h_i}} $ )分别为上行(下行)方向速度变化量的下/上限值.
2 MULTIBAND模型改进
经典MULTIBAND模型要求绿波带左、右等距对称, 若一侧带宽受到约束, 则另一侧将受到影响, 甚至出现零带宽, 造成绿灯时间利用不充分;其次, 对于红灯排队消散时间考虑不足, 没有考虑与相位差的关系, 大多根据经验进行取值, 容易造成误差.针对上述问题, 从绿波带形式和排队消散时间两个方面对MULTIBAND模型进行改进, 以得到更加优化的信号配时方案.
2.1 绿波带形式优化
首先, 通过取消绿波带对称约束和增加左、右带宽比例约束实现对绿波带形式优化[14].
在MULTIBAND模型中, 绿波带沿带宽进程线严格对称, 进程线是绿波带中心线, 容易限制绿波带宽, 造成一侧绿灯时间浪费.本文的改进模型运用进程线来保证干线绿波带的连续性, 但不等同于绿波带中心线, 进程线位置取决于决策变量取值.通过将上行绿波带宽bi分解为bi′和bi″, 下行绿波带宽 $\overline {{b_i}} $ 分解为 $\overline {{{b'}_i}} $ 和 $\overline {{{b''}_i}} $ , 降低绿波带两侧带宽的相互影响, 左、右带宽取值可以不相等, 即绿波带无须对称于进程线;额外的带宽可以用来释放绿灯初期的排队车辆.综上所述, 存在关系如下:
|
$
{b_i} = {{b'}_i} + {{b''}_i},{{\bar b}_i} = \overline {{{b'}_i}} + \overline {{{b''}_i}} .
$
|
(10) |
改进模型的目标函数与传统MULTIBAND模型类似, 区别在于带宽形式的变化.将式(10) 代入式(1), 可得新的目标函数:
|
$
\max B' = \frac{1}{{n - 1}}\sum\limits_{i = 1}^{n - 1} {\left[ {{a_i}\left( {{{b'}_i} + {{b''}_i}} \right) + {{\bar a}_i}\left( {{{\bar b'}_i} + {{\bar b''}_i}} \right)} \right]} .
$
|
(11) |
相应地, 冲突限制条件发生改变, 经过整理, 可以得到绿波带宽约束条件.原模型约束条件(6) 转变为
|
$
\left. \begin{array}{l}
{{b'}_i} \le {w_i} \le \left( {1 - {r_i}} \right) - {{b''}_i},\\
{{b'}_i} \le {w_{i + 1}} + {\tau _{i + 1}} \le \left( {1 - {r_{i + 1}}} \right) - {{b''}_i},\\
{{\bar b''}_i} \le \overline {{w_i}} - \overline {{\tau _i}} \le \left( {1 - {{\bar r}_i}} \right) - {{\bar b'}_i},\\
{{\bar b''}_i} \le \overline {{w_{i + 1}}} \le \left( {1 - \overline {{r_{i + 1}}} } \right) - \overline {{{b'}_i}} .
\end{array} \right\}
$
|
(12) |
为了充分利用绿灯时长, 保证干线绿波带的连续性, 同时使得带宽不为零, 增加左、右带宽比例约束, 如下所示:
|
$
\left. \begin{array}{l}
\left( {1/q} \right){{b''}_i} \le {{b'}_i} \le q{{b''}_i},\\
\left( {1/q} \right)\overline {{{b''}_i}} \le {{b'}_i} \le q\overline {{{b''}_i}} .
\end{array} \right\}
$
|
(13) |
式中:q可以为任意的正实数.基于经验分析可知, 本文取q=2.综上所述, 改进的MULTIBAND模型对绿波带形式进行了优化.
2.2 排队消散时间建模
在信号控制过程中, 当相邻的交叉口之间的相位差发生变化时, 下游交叉口的红灯排队车辆会变化[15].在流量和信号配时确定的情况下, 排队消散时间对绿波带的影响将随之改变.在干线绿波协调控制中, 需要考虑车辆排队消散时间.本文建立车辆排队消散时间与相位差的关系模型, 对经典的MULTIBAND模型进行改进.
由于在绿灯初期, 车辆以饱和流率进行消散, 可以得到红灯排队消散时间计算模型:
|
$
{\tau _{i + 1}} = \frac{{q_{i + 1}^{\rm{r}}}}{{{S_{i + 1}}{n_{i + 1}}}} + {t_1},
$
|
(14) |
|
$
\overline {{\tau _i}} = \frac{{\overline {q_i^{\rm{r}}} }}{{\overline {{S_i}} \overline {{n_i}} }} + \overline {{t_1}} .
$
|
(15) |
式中:τi+1( $\overline {{\tau _i}} $ )为交叉口i+1上行(i下行)方向协调相位进口道车辆排队消散时间;qi+1r( $\overline {q_i^{\rm{r}}} $ )为交叉口i+1上行(i下行)协调相位排队车辆数;ni+1( $\overline {{n_i}} $ )为交叉口i+1上行(i下行)协调相位进口道车道数;Si+1( $\overline {{S_i}} $ )为交叉口i+1上行(i下行)协调相位单车道饱和流率;tl( $\overline {{t_1}} $ )为车辆启动损失时间, 本文取3 s.
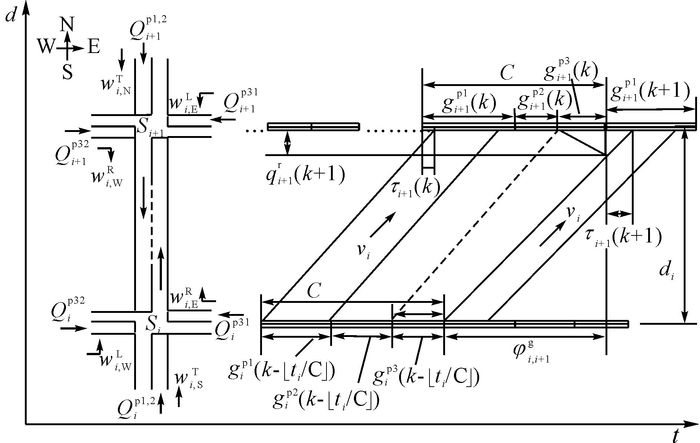
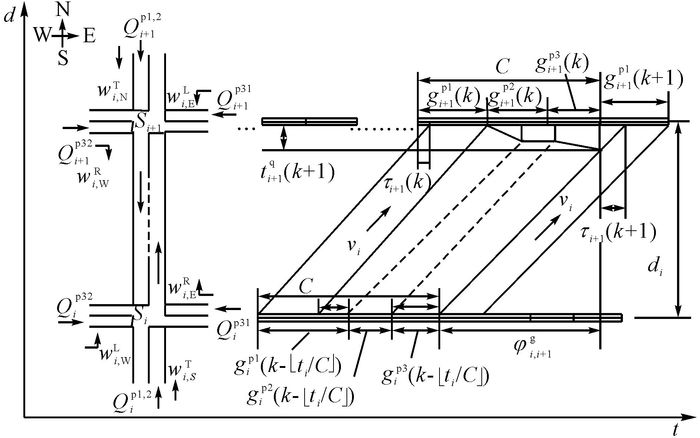
与文献[15]的分析方法类似, 以双向混合放行三相位干线系统的上行车流为例, 分析相邻交叉口车辆排队;其他的相序配置情况可以类似分析.为了清晰描述相邻交叉口之间的车辆排队长度, 对变量进行周期循环标注.定义干线直行相位为相位1, 干线左转相位为相位2, 支路相位为相位3.
如图 2、3所示, 交叉口i第 $\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ 个周期与交叉口i+1的第k个周期协调相位形成了一个绿波带.通过流量分析可知, 在第k+1个周期, 协调相位的排队长度qi+1r(k+1) 由两部分组成:交叉口i处 $\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ 周期驶来未能在交叉口i+1第k周期绿灯结束前驶离的直行车辆qT, i;在干线红灯期间, 由交叉口i支路方向驶出的左转车流qL, i和右转车流qR, i.qi+1r(k+1) 可由下式计算得到:
|
$
q_{i + 1}^{\rm{r}}\left( {k + 1} \right) = {q_{{\rm{T}},i}} + {q_{{\rm{L}},i}} + {q_{{\rm{R}},i}}.
$
|
(16) |
依据图 2、3, 对红灯期间车辆排队进行具体分析, 分为以下2种情况.
1) 当上游交叉口i绿灯末期最后一辆驶出车辆到达下游交叉口i+1时, 交叉口i+1绿灯未结束, 如下:
|
$
g_i^{{\rm{pl}}} + {t_i} - \left( {\varphi _{i,i + 1}^{\rm{g}} + g_{i + 1}^{{\rm{pl}}}} \right) \le 0.
$
|
(17) |
式中:φi, i+1g为交叉口i与i+1之间干线协调相位的绿时差, gip1为交叉口i协调相位绿灯时长.此时不存在直行滞留车辆qT, i, 排队车辆仅为上游非协调相位驶出车辆数qL, i和qR, i, 如图 2所示.由于各交叉口采取定时控制, 各周期配时参数相等, 即存在关系gip1(k)=gip1.由图 1可知, 有以下关系成立:
|
$
\varphi _{i,i + 1}^{\rm{g}} = {w_i} + {t_i} - {w_{i + 1}} + {\tau _{i + 1}}.
$
|
(18) |
此时, 排队长度qi+1r(k+1) 可由下式计算得到:
|
$
\begin{array}{*{20}{c}}
{q_{i + 1}^{\rm{r}}\left( {k + 1} \right) = \left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + } \right.}\\
{\left. {Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}}.}
\end{array}
$
|
(19) |
式中:Qip31 $\left[ {\left. {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)} \right.$ 和Qip32 $\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ 为交叉口i第 $\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ 个信号周期支路两个方向进口道的输出车辆数, wi+1, dx为由交叉口i的d(N, S, E, W)进口道x(L, T, R)转向交叉口i+1的车流比例, wi+1T为由交叉口i驶入i+1直行车流的比例.
2) 当上游交叉口i绿灯末期最后一辆驶出车辆到达下游交叉口i+1时, 交叉口i+1绿灯已结束, 如图 3所示, 有
|
$
g_i^{{\rm{pl}}} + {t_i} - \left( {\varphi _{i,i + 1}^{\rm{g}} + g_{i + 1}^{{\rm{pl}}}} \right) \ge 0.
$
|
(20) |
此时存在直行滞留车辆qT, i.排队长度可由下式计算得到:
|
$
\begin{array}{l}
q_{i + 1}^{\rm{r}}\left( {k + 1} \right) = \left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + } \right.\\
\;\;\;\;\;\;\left. {Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}} + \\
\;\;\;\;\;\;{\mu _i}Q_i^{{\rm{p1,2}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{s}}}^{\rm{T}}w_{i + 1}^{\rm{T}}/g_i^{{\rm{pl}}}.
\end{array}
$
|
(21) |
式中:Qip1, 2 $\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ 为第 ${k - \left\lfloor {{t_i}/C} \right\rfloor }$ 个信号周期交叉口i干线上行方向进口道输出车辆数.
在定时控制中信号配时方案固定, 因此假设车辆排队消散时间不随周期变化, 进口道流量和排队长度在短期内不发生变化, 即Qip1, 2 $\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ =Qip1, 2(k).
令μi=gip1-gi+1p1+τi+1-wi+wi+1, 经过整理, 可以得到交叉口i+1处上行协调相位排队长度:
|
$
q_{i + 1}^{\rm{r}} = \left\{ \begin{array}{l}
\left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right]w_{i + 1,{\rm{E}}}^{\rm{R}} + Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}},{\mu _i} \le 0;\\
\left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}} + {\mu _i}Q_i^{{\rm{pl}},2}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{s}}}^{\rm{T}}w_{i + 1}^{\rm{T}}/g_i^{{\rm{pl}}},{\mu _i} > 0.
\end{array} \right.
$
|
(22) |
将式(22) 代入式(14), 可得上行方向车辆消散时间:
|
$
{\tau _{i + 1}} = \left\{ \begin{array}{l}
\frac{{\left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}}}}{{{S_{i + 1}}{n_{i + 1}}}} + {t_1},{\mu _i} \le 0;\\
\frac{{\left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}} + {\mu _i}Q_i^{{\rm{pl}},2}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{s}}}^{\rm{T}}w_{i + 1}^{\rm{T}}/g_i^{{\rm{pl}}}}}{{{S_{i + 1}}{n_{i + 1}}}} + {t_1},{\mu _i} > 0.
\end{array} \right.
$
|
(23) |
同理, 令 $\overline {{\mu _i} + 1} = \overline {{\tau _i}} - \overline {{\omega _i}} + \overline {{\omega _{i + 1}}} $ , 可以得到交叉口i下行协调相位红灯排队车辆数:
|
$
\overline {{\tau _i}} = \left\{ \begin{array}{l}
\frac{{\left[ {Q_{i + 1}^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{E}}}^{\rm{L}}} + Q_{i + 1}^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{W}}}^{\rm{R}}} } \right]\overline {w_i^{\rm{T}}} }}{{\overline {{S_i}} \overline {{n_i}} }} + {t_1},\overline {{\mu _{i + 1}}} \le 0;\\
\frac{{\left[ {Q_{i + 1}^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{E}}}^{\rm{L}}} + Q_{i + 1}^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{W}}}^{\rm{R}}} } \right]\overline {w_i^{\rm{T}}} + \overline {{\mu _{i + 1}}} \overline {Q_{i + 1}^{{\rm{pl}},2}} \left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{N}}}^{\rm{T}}} \overline {w_i^{\rm{T}}} /\overline {g_{i + 1}^{{\rm{pl}}}} }}{{\overline {{S_i}} \overline {{n_i}} }} + {t_1},\overline {{\mu _{i + 1}}} > 0.
\end{array} \right.
$
|
(24) |
式中: $\overline {Q_{i + 1}^{{\rm{p}}1,2}} \left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)$ 为交叉口i干线下行方向 ${k - \left\lfloor {{t_i}/C} \right\rfloor }$ 周期进口道输出车辆数, $\overline {\omega _{i,d}^x} $ 为由交叉口i+1的d(N, S, E, W)进口道x(L, T, R)转向交叉口i的车流比例, $\overline {\omega _i^{\rm{T}}} $ 为由交叉口i+1驶入i的直行车流比例.
2.3 改进的MULTIBAND模型
基于传统MULTIBAND模型, 优化绿波带形式, 同时考虑红灯排队消散时间, 得到改进的MULTIBAND模型如下.
|
$
\max B' = \frac{1}{{n - 1}}\sum\limits_{i = 1}^{n - 1} {\left[ {{a_i}\left( {{{b'}_i} + {{b''}_i}} \right) + {{\bar a}_i}\left( {{{\bar b'}_i} + {{\bar b''}_i}} \right)} \right]} .
$
|
(25) |
|
$
\begin{array}{l}
{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\\
\left( {1 - {k_i}} \right)\left( {{{\bar b'}_i} + {{\bar b''}_i}} \right) \ge \left( {1 - {k_i}} \right){k_i}\left( {{{b'}_i} + {{b''}_i}} \right);i = 1,2, \cdots ,n - 1.
\end{array}
$
|
(26) |
|
$
1/{C_{\max }} \le z \le 1/{C_{\min }}.
$
|
(27) |
|
$
\left. \begin{array}{l}
{{b'}_i} \le {w_i} \le \left( {1 - {r_i}} \right) - {{b''}_i},\\
{{b'}_i} \le {w_{i + 1}} + {\tau _{i + 1}} \le \left( {1 - {r_{i + 1}}} \right) - {{b''}_i},\\
{{\bar b''}_i} \le \overline {{w_i}} - \overline {{\tau _i}} \le \left( {1 - {{\bar r}_i}} \right) - {{\bar b'}_i},\\
{{\bar b''}_i} \le \overline {{w_{i + 1}}} \le \left( {1 - \overline {{r_{i + 1}}} } \right) - \overline {{{b'}_i}} ;i = 1,2, \cdots ,n - 1.
\end{array} \right\}
$
|
(28) |
|
$
\left. \begin{array}{l}
\left( {1/q} \right){{b''}_i} \le {{b'}_i} \le q{{b''}_i},\\
\left( {1/q} \right)\overline {{{b''}_i}} \le \overline {{{b'}_i}} \le q\overline {{{b''}_i}} ;i = 1,2, \cdots ,n - 1.
\end{array} \right\}
$
|
(29) |
|
$
\begin{array}{l}
\left[ {{w_i} + \overline {{w_i}} } \right) - \left( {{w_{i + 1}} + \overline {{w_{i + 1}}} } \right) + \left( {{t_i} + \overline {{t_i}} } \right) + \\
\;\;{\delta _i}{l_i} + \overline {{\delta _{i + 1}}{l_{i + 1}}} = \left( {{r_{i + 1}} - {r_i}} \right) + \left( {\overline {{\tau _i}} + {\tau _{i + 1}}} \right) + \overline {{\delta _i}{l_i}} + \\
\;\;{\delta _{i + 1}}{l_{i + 1}} + {m_i};i = 1,2, \cdots ,n - 1.
\end{array}
$
|
(30) |
|
$
\left. \begin{array}{l}
{\mu _i} = g_i^{{\rm{pl}}} - g_{i + 1}^{{\rm{pl}}} + {\tau _{i + 1}} - {w_i} + {w_{i + 1}},\\
\overline {{\mu _{i + 1}}} = \overline {{\tau _i}} - \overline {{w_i}} + \overline {{w_{i + 1}}} .
\end{array} \right\}
$
|
(31) |
|
$
{\tau _{i + 1}} = \left\{ \begin{array}{l}
\frac{{\left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}}}}{{{S_{i + 1}}{n_{i + 1}}}} + {t_1},{\mu _i} \le 0;\\
\frac{{\left[ {Q_i^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{E}}}^{\rm{R}} + Q_i^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{W}}}^{\rm{L}}} \right]w_{i + 1}^{\rm{T}} + {\mu _i}Q_i^{{\rm{pl}},2}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)w_{i + 1,{\rm{s}}}^{\rm{T}}w_{i + 1}^{\rm{T}}/g_i^{{\rm{pl}}}}}{{{S_{i + 1}}{n_{i + 1}}}} + {t_1},{\mu _i} > 0.
\end{array} \right.
$
|
(32) |
|
$
\overline {{\tau _i}} = \left\{ \begin{array}{l}
\frac{{\left[ {Q_{i + 1}^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{E}}}^{\rm{L}}} + Q_{i + 1}^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{W}}}^{\rm{R}}} } \right]\overline {w_i^{\rm{T}}} }}{{\overline {{S_i}} \overline {{n_i}} }} + {t_1},\overline {{\mu _{i + 1}}} \le 0;\\
\frac{{\left[ {Q_{i + 1}^{{\rm{p31}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{E}}}^{\rm{L}}} + Q_{i + 1}^{{\rm{p32}}}\left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{W}}}^{\rm{R}}} } \right]\overline {w_i^{\rm{T}}} + \overline {{\mu _{i + 1}}} \overline {Q_{i + 1}^{{\rm{pl}},2}} \left( {k - \left\lfloor {{t_i}/C} \right\rfloor } \right)\overline {w_{i,{\rm{N}}}^{\rm{T}}} \overline {w_i^{\rm{T}}} /\overline {g_{i + 1}^{{\rm{pl}}}} }}{{\overline {{S_i}} \overline {{n_i}} }} + {t_1},\overline {{\mu _{i + 1}}} > 0.
\end{array} \right.
$
|
(33) |
|
$
\left. \begin{array}{l}
\left( {{d_i}/{f_i}} \right)z \le {t_i} \le \left( {{d_i}/{e_i}} \right)z,\\
\left( {\overline {{d_i}} /\overline {{f_i}} } \right)z \le \overline {{t_i}} \le \left( {\overline {{d_i}} /\overline {{e_i}} } \right)z;i = 1,2, \cdots ,n - 1.
\end{array} \right\}
$
|
(34) |
|
$
\left. \begin{array}{l}
\left( {{d_i}/{h_i}} \right)z \le \left( {{d_i}/{d_{i + 1}}} \right){t_{i + 1}} - {t_i} \le \left( {{d_i}/{g_i}} \right)z,\\
\left( {\overline {{d_i}} /\overline {{h_i}} } \right)z \le \left( {\overline {{d_i}} /\overline {{d_{i + 1}}} } \right)\overline {{t_{i + 1}}} - \overline {{t_i}} \le \left( {\overline {{d_i}} /\overline {{g_i}} } \right)z;\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,n - 2.
\end{array} \right\}
$
|
(35) |
|
$
{{b'}_i}、{{b''}_i}、\overline {{{b'}_i}} 、\overline {{{b''}_i}} 、z、{w_i}、\overline {{w_i}} 、{t_i}、\overline {{t_i}} \ge 0.
$
|
(36) |
|
$
{m_i}\;为整数;{\delta _i},\overline {{\delta _i}} \;为\;0/1\;变量.
$
|
(37) |
其中, 决策变量为b′i、b″i、 $\overline {{{b'}_i}} $ 、 $\overline {{{b''}_i}} $ 、z、wi、 $\overline {{\omega _i}} $ 、ti、 $\overline {{t_i}} $ 、δi、 $\overline {{\delta _i}} $ 、mi.
3 模型验证
3.1 路网选取
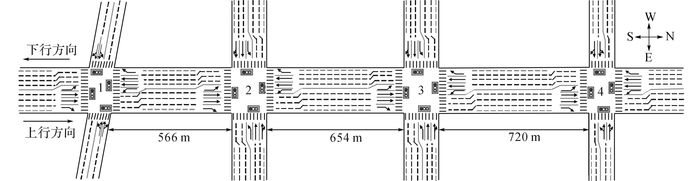
选取1个典型干线系统, 对改进MULTIBAND模型进行验证.该干线共含有4个交叉口, 间距分别为566、654和720 m, 适合干线协调控制.交叉口渠化情况如图 4所示.选取平峰时段(9:00-10:00), 对交叉口的流量情况进行调查, 结果如表 2所示.表中, E为东进口, W为西进口, S为南进口, N为北进口, L为左转车流, T为直行车流, R为右转车流.
表 2
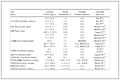
表 2 交叉口流量调查结果
Table 2 Traffic volume of different intersections along arterial
| 辆/h |
| 交叉口 | E | | W | | S | | N |
| L | T | R | | L | T | R | | L | T | R | | L | T | R |
| 1 | 176 | 328 | 115 | | 143 | 286 | 106 | | 256 | 1 285 | 182 | | 192 | 1 043 | 146 |
| 2 | 166 | 402 | 112 | 178 | 316 | 142 | 201 | 1 136 | 206 | 196 | 1 073 | 178 |
| 3 | 118 | 299 | 108 | 162 | 388 | 98 | 132 | 1 152 | 142 | 154 | 1 231 | 124 |
| 4 | 107 | 360 | 96 | 132 | 426 | 142 | 156 | 1 168 | 98 | 205 | 1 260 | 102 |
|
表 2 交叉口流量调查结果
Table 2 Traffic volume of different intersections along arterial
|
依据流量调查结果和渠化情况, 利用Webster模型求解各交叉口的最佳信号周期, 得到交叉口2为关键交叉口, 周期时长为140 s;将其他交叉口的周期时长调整为公共周期140 s, 进而得到交叉口各相位的车流方向及绿信比, 如表 3所示.车辆启动损失时间为3 s, 黄灯时间为3 s, 全红时间为2 s;直行车道的饱和流率为1 650辆/h, 其他车道饱和流率为1 550辆/h.其中, 交叉口1和4为3相位信号配时;交叉口2和3为4相位信号配时.
3.2 模型求解
通过前文计算, 得到公共周期时长为140 s, 因此在求解绿波带模型时, 将周期确定为130~150 s, 即满足约束1/150≤z≤1/130[13].通过调查分析和城市交通流特性, 确定路段限速为50 km/h, 速度为36~54 km/h, 即ei=10 m/s, fi=15 m/s.为了保证干线车流的平稳性, 相邻路段间的速度波动范围不应超过一定的阈值, 因此, 将相邻路段间的速度变化范围设为6 km/h[13], 则-1/hi=1/gi=0.008 9 s/m.代入交叉口调查数据, 分别建立MULTIBAND模型、AM-BAND模型[14]和改进的MULTIBAND模型, 利用Lingo软件进行求解.在干线协调优化时, 主路方向允许相位搭接, 基本结构如表 1所示.由于研究路网的上、下行流量相差不大, 模型中的p取为1, 3种模型的求解结果如表 4~6所示.
表 4

表 4 MULTIBAND模型求解结果
Table 4 Solving results of MULTIBAND model
|
i | bi | bi | z | wi | wi | ti | $\overline {{t_i}} $ | δi | δi | mi | φi, i+1g
|
| 1 | 0.37 | 0.36 | 1/130 | 0.18 | 0.27 | 0.44 | 0.44 | 1 | 0 | 1 | 0 |
| 2 | 0.34 | 0.36 | 1/130 | 0.17 | 0.22 | 0.50 | 0.50 | 1 | 1 | 1 | 0.41 |
| 3 | 0.43 | 0.43 | 1/130 | 0.22 | 0.25 | 0.55 | 0.55 | 0 | 1 | 1 | 0.41 |
| 4 | - | - | 1/130 | 0.18 | 0.22 | - | - | 1 | 1 | - | 0.55 |
|
表 4 MULTIBAND模型求解结果
Table 4 Solving results of MULTIBAND model
|
表 5

表 5 AM-BAND模型求解结果
Table 5 Solving results of AM-BAND model
|
i | b′i | b″i | b′i | b″i | z | wi | wi | ti | $\overline {{t_i}} $ | i | δi | mi | φi, i+1g
|
| 1 | 0.21 | 0.18 | 0.17 | 0.22 | 1/130 | 0.21 | 0.31 | 0.42 | 0.44 | 1 | 1 | 1 | 0 |
| 2 | 0.17 | 0.22 | 0.21 | 0.18 | 1/130 | 0.17 | 0.22 | 0.50 | 0.50 | 0 | 1 | 1 | 0.42 |
| 3 | 0.14 | 0.29 | 0.29 | 0.14 | 1/130 | 0.14 | 0.18 | 0.55 | 0.55 | 0 | 1 | 1 | 0.50 |
| 4 | - | - | - | - | 1/130 | 0.11 | 0.14 | - | - | 1 | 1 | - | 0.55 |
|
表 5 AM-BAND模型求解结果
Table 5 Solving results of AM-BAND model
|
表 6

表 6 改进的MULTIBAND模型求解结果
Table 6 Solving results of improved MULTIBAND model
|
i | b′i | b″i | b′i | b″i | z | wi | wi | ti | $\overline {{t_i}} $ | δi | δi | mi | φi, i+1g |
| 1 | 0.26 | 0.14 | 0.13 | 0.26 | 1/130 | 0.31 | 0.35 | 0.40 | 0.36 | 1 | 0 | 1 | 0 |
| 2 | 0.22 | 0.17 | 0.16 | 0.23 | 1/130 | 0.22 | 0.26 | 0.50 | 0.46 | 1 | 1 | 1 | 0.45 |
| 3 | 0.19 | 0.24 | 0.24 | 0.19 | 1/130 | 0.19 | 0.23 | 0.50 | 0.50 | 1 | 1 | 1 | 0.50 |
| 4 | - | - | - | - | 1/130 | 0.17 | 0.19 | - | - | 1 | 1 | - | 0.49 |
|
表 6 改进的MULTIBAND模型求解结果
Table 6 Solving results of improved MULTIBAND model
|
如表 4~6所示, 采用3种模型求得的公众周期时长均为130 s.为了在方案仿真评价时快速输入配时参数, 选取交叉口之间的干线上行相对绿灯相位差φi, i+1g, 可由式(19) 求得.经计算可知, 利用MULTIBAND模型求得的交叉口之间的上行相对绿时差为0、54、54、72 s;AM-BAND模型中上行方向绿时差为0、55、64、71 s;利用本文模型求得的结果为0、59、64、63 s.对比表 1可知, 利用3种模型得到的相位结构分别为2, 4, 1, 4;4, 1, 1, 4和2, 4, 4, 4;交叉口信号配时方案如表 7所示.
表 7

表 7 3种模型交叉口信号配时方案
Table 7 Signal timing schemes of three models
| 交叉口 | MULTIBAND模型 | AM-BAND模型 | 本文模型 |
| 1 | 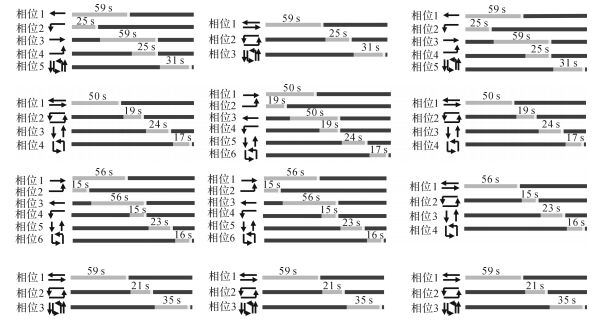
|
| 2 |
| 3 |
| 4 |
|
表 7 3种模型交叉口信号配时方案
Table 7 Signal timing schemes of three models
|
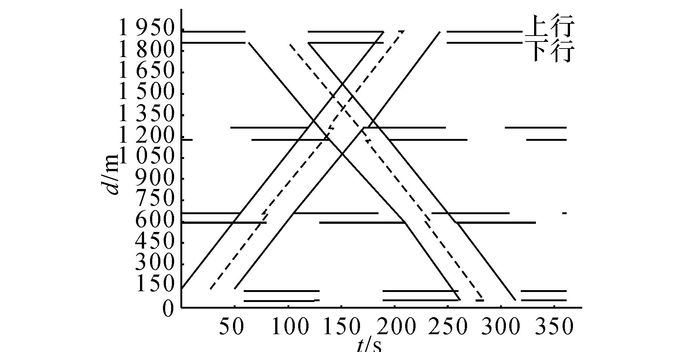
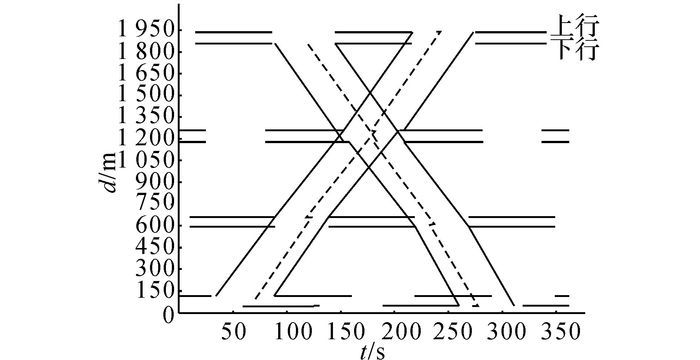
根据Lingo软件的求解结果, 可以得到3种模型的绿波时间-距离图, 如图 5~7所示.如图 5所示为由MULTIBAND模型得到的绿波时距图, 如图 6所示为由AM-BAND模型得到的绿波时距图;如图 7所示为利用本文改进模型得到的绿波时距图.由图 5可知, MULTIBAND模型可以实现干线相位相序的优化, 依据实际流量得到带宽可变的绿波带, 且绿波带沿着中心线对称.由图 6、7可知, AM-BAND模型与本文改进模型在优化相位相序的同时优化绿波带形式, 允许绿波带不完全对称, 得到较宽的带宽, 有效利用绿灯时间.与AM-BAND模型相比, 本文模型能够根据实际流量计算车辆排队消散时间, 更加符合实际的交通流特性.
3.3 仿真验证分析
为了验证本文方法的有效性, 将3种模型得到的信号配时方案分别输入到VISSIM仿真软件中, 进行效果评价.考虑到干线协调的控制目标, 选取干线方向车辆平均总延误和平均停车次数作为评价指标, 取5 min为评价参数输出时间间隔, 仿真时长设为2 h.
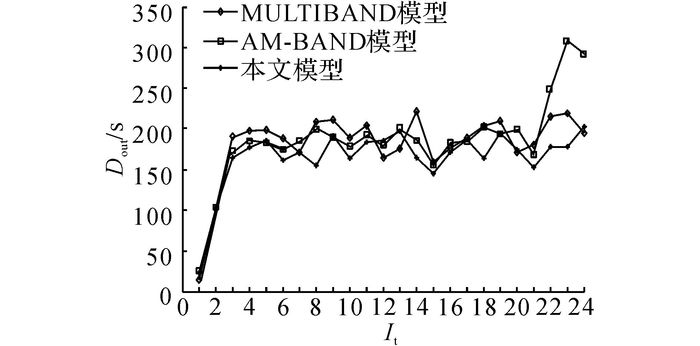
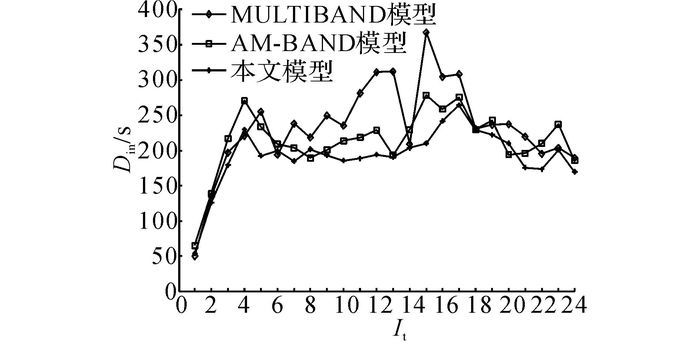
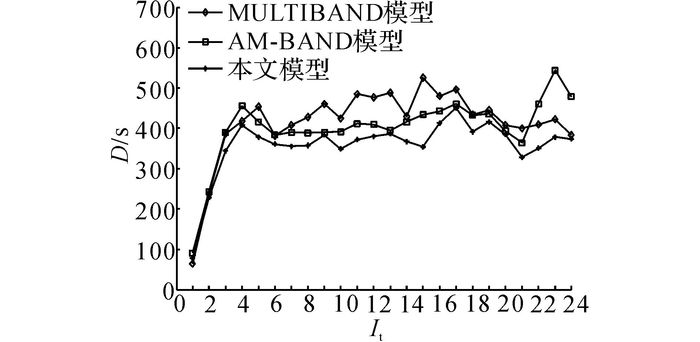
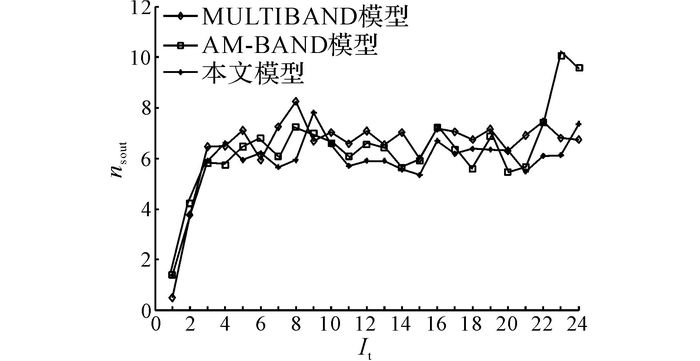
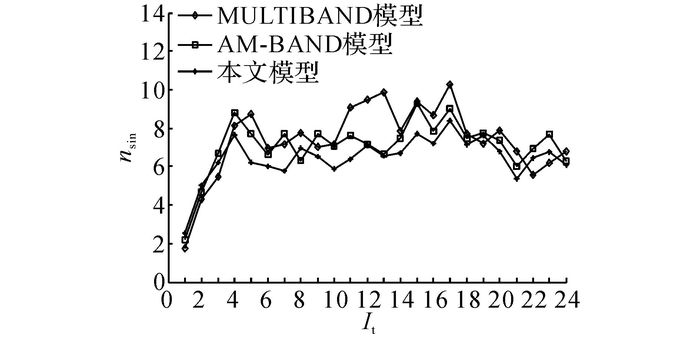
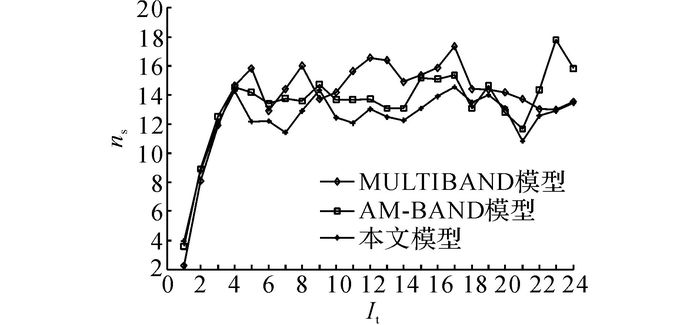
如图 8、9所示分别为输出时间间隔It内3种方案的干线上行方向平均总延误Dout和下行方向平均总延误Din对比图;如图 10所示为干线双向总体时间间隔内的平均总延误D.如图 11、12所示分别为干线上行平均停车次数nsout和下行平均停车次数nsin对比图, 如图 13所示为干线双向总体平均停车次数ns.3种方案的平均效益对比情况如表 8所示.
表 8

表 8 间隔时间内3种方案的平均效益对比
Table 8 Average performance at time interval comparison of three schemes
| 方向 | 平均延误 | | 平均停车次数 |
| MULTIBAND | AM-BAND | 本文模型 | | MULTIBAND | AM-BAND | 本文模型 |
| 干线上行 | 181.58 | 187.55 | 165.67 | | 6.46 | 6.59 | 5.88 |
| 干线下行 | 232.84 | 213.04 | 192.26 | 7.38 | 7.3 | 6.46 |
| 干线总体 | 414.41 | 400.60 | 357.93 | 13.84 | 13.89 | 12.34 |
| 支路 | 48.23 | 47.35 | 41.14 | 0.85 | 0.84 | 0.78 |
|
表 8 间隔时间内3种方案的平均效益对比
Table 8 Average performance at time interval comparison of three schemes
|
由图 8、9可知, 与传统MULTIBAND模型相比, AM-BAND模型和本文模型都能降低干线车辆延误, 且下行方向的延误改善效果优于上行方向.与MULTIBAND相比, AM-BAND模型对于上行方向延误的最大改善率为15.95%;对于下行延误, 最大改善率为38.15%;对于干线双向, 总体延误的最大改善率为19.04%.与MULTIBAND模型相比, 本文模型对于干线上行方向5 min平均总延误的最大改善率为25.71%;对于下行方向, 延误改善效果明显, 最大改善率为42.82%;对于干线双向, 总体延误的最大改善率为32.55%.与其他两个模型相比, 本文模型在降低车辆平均延误方面的效果最好.
由图 11、12可知, AM-BAND模型和本文模型均可以降低干线上行和下行方向车辆平均停车次数, 且下行方向的改善效果优于上行方向.与MULTIBAND模型相比, AM-BAND模型对于上行和下行方向停车次数的最大改善率分别为20.20%和32.45%;本文模型对于上行和下行停车次数的最大改善率分别为28.21%和33.37%.由图 13可知, AM-BAND模型和本文模型对于干线双向总体停车次数的改善率分别为20.12%和23.34%.
由表 8可知, 就方案平均效益而言, 本文模型的数值最小.与MULTIBAND模型相比, 干线总体平均延误和平均停车次数均有较大改善.AM-BAND模型虽然有改善, 但总体指标情况不如本文模型.此外, 仿真结果显示, 3种方案的支路评价指标值虽然相差不大, 但本文模型的数值最小.综上所述, 与MULTIBAND模型相比, AM-BAND模型和本文模型均能够降低干线车辆延误和停车次数, 提高路网的整体运行效率, 且本文模型的信号配时方案优于AM-BAND模型, 从而证明了本文方法的有效性.
4 结语
基于传统MULTIBAND模型, 本文提出新的干线协调控制优化方法.对绿波带形式进行优化, 取消了绿波带对称约束, 增加了左、右带宽比例约束;在绿波带形式优化的基础上, 分析下游交叉口红灯排队情况, 建立排队消散时间模型, 进而得到改进的MULTIBAND模型.选取1个典型路网, 将Lingo软件求解结果输入到VISSIM仿真软件中进行验证.结果表明, 与MULTIBAND模型相比, 采用本文方法能够有效地降低干线总延误和停车次数, 提高干线整体通行效益, 证明了该方法的有效性.本文研究存在一定的局限性.本文研究的交通特性单一, 未考虑混合交通流和饱和交通状态;对于支路的相位相序考虑不足, 在后续的研究中将进行完善.